Summary
The virologically confirmed cases of a new coronavirus disease (COVID‐19) in the world are rapidly increasing, leading epidemiologists and mathematicians to construct transmission models that aim to predict the future course of the current pandemic. The transmissibility of a virus is measured by the basic reproduction number ( R 0 ), which measures the average number of new cases generated per typical infectious case. This review highlights the articles reporting rigorous estimates and determinants of COVID‐19 R 0 for the most affected areas. Moreover, the mean of all estimated R 0 with median and interquartile range is calculated. According to these articles, the basic reproduction number of the virus epicentre Wuhan has now declined below the important threshold value of 1.0 since the disease emerged. Ongoing modelling will inform the transmission rates seen in the new epicentres outside of China, including Italy, Iran and South Korea.
Keywords: the basic reproduction number ( R 0 ), COVID‐19, pandemic, SARA‐CoV‐2
1. INTRODUCTION
The appearance of a new infectious disease is always a complex phenomenon, especially if it becomes pandemic. Globally, infections by SARS‐CoV‐2 that causes COVID‐19 are rapidly growing, and they extended very fast with transmission chains throughout the world since the first case was detected in the Chinese city of Wuhan in December 2019. Imported cases and secondary cases have been reported in more than 1 436 198 confirmed cases globally. 1 On 11 March 2020, the World Health Organization (WHO) declared COVID‐19 a pandemic and called for governments to take urgent actions to change the course of the outbreak. 2
An infectious disease outbreak can be characterised by its basic reproductive number, known as R 0 , which represents the average number of secondary infections generated by each infected person. If R 0 is equal to 1 or less, this indicates that the number of secondary cases will decrease over time and, eventually, the outbreak will peter out. If it is higher than one, the outbreak is expected to increasingly transmit infection to secondary cases, indicating the need to use control measures to limit its extension.
As governments and WHO work together to treat infected people and control the spread of the hitherto unknown SARS‐CoV‐2, several mathematical modelling groups in the China, United Kingdom, Europe and United States have rushed to estimate the basic reproduction number and predict the spread of SARS‐CoV‐2 infections and cases of COVID‐19 disease. These groups used different approaches as illustrated in Table 1 with estimates hovering between 0.32 and 6.47 in Tables 2 and 3. These differences are not surprising, as there is uncertainty about many of the factors go into estimating R 0 , such as different methods for modelling, different variables considered, and various estimation procedures.
TABLE 1.
Description of R 0 estimation methods with list of used abbreviations
| ID | Methods | Method description with its abbreviation |
|---|---|---|
| 1 | SIR model3, 4, 5, 6, 7, 8, 9 | It is a compartmental model in epidemiology that divides an infectious disease into three parts: Susceptible‐Infectious‐Removed (SIR), which is represented as a dynamical system in mathematics. |
| 2 | SEIR model10, 11, 12, 13, 14, 15 | Susceptible‐Exposed‐Infectious‐Removed (SEIR) model which is another type of compartmental model which differs from SIR model by adding exposed part that represents the delay time of infected by virus and apparing symptoms (latency period). |
| 3 | MSIR model 16 | Maternally derived immunity‐Susceptible‐Infectious‐Removed (MSIR) compartmental model that babies got protection from maternal antibodies. |
| 4 | MSEIR model 16 | It is the same as the model MSIR by joining Exposed component and becoming Maternally derived immunity‐Susceptible‐Exposed‐Infectious‐Removed (MSEIR). |
| 5 | SEIHR model17, 18 | Entering the Hospitalized class to SEIR model to obtain: Susceptible‐Exposed‐Infectious‐Hospitalized‐Removed (SEIHR). |
| 6 | SEIAR model 19 | A modified SEIR model with another movement class of compartmental model known as Asymptomatic, to get: Susceptible‐Exposed‐Infectious‐Asymptomatic‐Removed (SEIAR). |
| 7 | SEQR model 20 | Incorporating the quarantine policy to a mathematical model and obtaining Susceptible‐Exposed‐Quarantined‐Removed (SEQR) model. |
| 8 | SIRD model 21 | It is the SIR model that addresses the removed class with recovered and dead class to be Susceptible‐Infectious‐Recovered‐Dead (SIRD) model. |
| 9 | SUQC model 22 | In this model, the infectious class of transmission model is separeted as un‐quanrantined, quarantined and confirmed infected. The model is named Susceptible‐Unquanrantined‐Quarantined‐Confirmed (SUQC) model. |
| 10 | SIQR model 23 | Its modified SIR model with considering quarantine, Susceptible‐Infectious‐Quarantined‐Recovered (SIQR). |
| 11 | S E1E2I1I2HR time‐dependent model 24 | It is a mathematical model focusing on the effects of medical resourceson transmission of COVID‐19, stands for susceptible S (t), pre‐stage exposed E1(t), post‐stage exposed E2(t), infected with mild symptoms I1(t), infected with serious symptoms I2(t), hospitalized H(t) and recovered R(t) individuals. |
| 12 | SIDARTHE model 25 | It is a mathematical model that designed to show transsimssion between different stages in infectious disease. The abbrevation refers to: Susceptible‐Infected ‐Diagnosed‐Ailing‐Recognised‐Threatened‐Healed‐Extinct (SIDARTHE) model. In this model, being infected is dividing into 5 types as: undetected asymptomatic infected, detected asymptomatic infected, undetected symptomatic infected, detected symptomatic infected, and infected with detected life‐threatening symptoms; whereas the removed class in compartmental model is classfied into recovered and dead. |
| 13 | Exponential growth9, 26, 27, 28, 29, 30, 31 | It is a model that varies exponentially with the time by a specific rate. |
| 14 | Generalized growth model 32 | It is the growth model with two parameters: (r) represents the growth rate parameter with (p) that is the scaling growth rate parameter. Whenever P = 1, the generalized growth model returns to exponential growth and if 0 < P < 1, then it is sub‐exponential (polynomial) growth. |
| 15 | Logistic growth model 33 | It is a mathematical model that starts exponentially but it gets stabilized due to the capacity of population. |
| 16 | Bayesian estimation method 34 | It is a paramter estimation method that deals with paramters as random variables in a statistical model. |
| 17 | Fudan‐CCDC model 12 | Developed model for the growth rate and CCDC stands for Chinese Center for Disease Control. |
| 18 | Least square based method 35 | It is a procedure to best fit data in statistics. |
| 19 | MCMC method 36 | Markov Chain Monte Carlo (MCMC) method. In this technique, the posterior distribution of a desired parameter can be found. |
| 20 | Maximum Likelihood Estimation30, 37 | It is a method used to estimate parameters with knowing their distributions. |
| 21 | Phenomenological modelling 33 | Statistical method for modelling. |
TABLE 2.
The basic reproduction number ( R 0 ) from the published articles in Wuhan
| ID | Researcher | Date | Location | Methods | Ro Est. | Ro (%95 CI) |
|---|---|---|---|---|---|---|
| 1 | Imai 38 | 18 January 2020 | Wuhan | Epidemic trajectories | 2.60 | (1.50‐3.50) |
| 2 | Li et al 39 | 22 January 2020 | Wuhan | Exponential growth | 2.20 | (1.40‐3.90) |
| 3 | Majumder et al 33 | 26 January 2020 | Wuhan | Phenomenological modelling | 2.55 | (2.00‐3.10) |
| 4 | Park et al 40 | 24 February 2020 | Wuhan | 2.20 | ||
| 5 | Read et al 11 | 1‐22 January 2020 | Wuhan | SEIR | 3.11 | (2.39‐4.13) |
| 6 | Shao et al 12 | 16‐February‐20 | Wuhan | SEIR model and Gamma distribution | 3.12 | |
| 7 | Shao et al 12 | 16 February 20 | Wuhan | Fudan‐CCDC model | 3.32 | |
| 8 | Tuite et al 29 | 24 January 20 | Wuhan | Disease transmission model | 2.30 | |
| 9 | WHO 2 | 22 January 20 | Wuhan | 1.95 | (1.40‐2.50) | |
| 10 | Wu et al 41 | 25 January 20 | Wuhan | Markov Chain Monte Carlo methods | 2.68 | (2.47‐2.86) |
| 11 | Zhang et al 19 | 27 January 2020‐10 February 2020 | Wuhan | SEIAR model | 2.88 | |
| 12 | Zhao & Chen 22 | Before 30 January 2020 | Wuhan | SUQC Model (Stage I) | 4.70 | |
| 13 | Zhao & Chen 22 | After 30 January 2020 | Wuhan | SUQC Model (Stage II) | 0.75 | |
| 14 | Zhao & Chen 22 | After 13 Feb 2020 | Wuhan | SUQC Model (Stage III) | 0.47 | |
| 15 | Wang et al 24 | 23 January 2020 | Wuhan | SE1E2I1I2HR time‐dependent model | 2.71 |
TABLE 3.
The basic reproduction number ( R 0 ) from the published articles
| ID | Researcher | Date | Location | Methods | Ro Est. | Ro (%95 CI) |
|---|---|---|---|---|---|---|
| 1 | Anastassopoulou et al 21 | 11‐17 January 2020 | Hubei, China | SIRD model | 4.60 | %90 CI (3.56‐5.65) |
| 2 | Choi et al 17 | 17 February 2020 | Hubei, China | Deterministic mathematical model (SEIHR) | 4.26 | (4.24‐4.29) |
| 3 | Choi et al 17 | 17 February 2020 | South Korea | Deterministic mathematical model (SEIHR) | 0.55 | (0.51‐0.60) |
| 4 | Choi et al 17 | 05 March 2020 | NGP‐South Korea | Deterministic mathematical model(SEIHR) | 3.50 | (3.47‐3.54) |
| 5 | Di Lauro et al 42 | 02 March 2020 | World | Metapopulation model | 2.50 | |
| 6 | Hao 16 | 17 February 2020 | World | MSIR | 1.50 | |
| 7 | Hao 16 | 17 February 2020 | World | MSEIR | 3.50 | |
| 8 | Hellewell et al 43 | 05 February 2020 | World | Branching process model | 2.50 | (1.50–3.50) |
| 9 | Hossain et al 4 | 13 March 2020 | China | SIR (44 days quarantined) | 1.40 | |
| 10 | Hossain et al 4 | 13 March 2020 | China | SIR (24 days quarantine) | 1.68 | |
| 11 | Hossain et al 4 | 13 March 2020 | China | SIR (10 days quarantined) | 2.92 | |
| 12 | Imai et al 38 | 18 January 2020 | Wuhan | Computational modelling of potential epidemic trajectories | 2.60 | (1.50–3.50) |
| 13 | Jung et al 36 | 08 December 2020 | China | Developed exponential growth model and using MCMC techinqe. | 2.10 | (2.00‐2.20) |
| 14 | Jung et al 36 | 24 January 2020 | China with exported cases | Developed exponential growth model and using MCMC techinqe. | 3.20 | (2.70‐3.70) |
| 15 | Ku et al 7 | 12 February 2020 | Anhui, China | SIR after lockdown of Wuhan | 3.89 | (3.27‐4.50) |
| 16 | Ku et al 7 | 12 February 2020 | Beijing, China | SIR after lockdown of Wuhan | 3.30 | (1.89‐4.32) |
| 17 | Ku et al 7 | 12 February 2020 | Chongqing, China | SIR after lockdown of Wuhan | 2.22 | (1.26‐3.14) |
| 18 | Ku et al 7 | 12 February 2020 | Fujian, China | SIR after lockdown of Wuhan | 1.66 | (0.72‐2.87) |
| 19 | Ku et al 7 | 12 February 2020 | Gansu, China | SIR after lockdown of Wuhan | 2.30 | (1.02‐3.96) |
| 20 | Ku et al 7 | 12 February 2020 | Henan, China | SIR after lockdown of Wuhan | 3.70 | (3.16‐4.25) |
| 21 | Ku et al 7 | 12 February 2020 | Hubei, China | SIR after lockdown of Wuhan | 4.65 | (4.10‐5.15) |
| 22 | Ku et al 7 | 12 February 2020 | Tianjin, China | SIR after lockdown of Wuhan | 2.17 | (1.23‐3.54) |
| 23 | Ahmadi et al 44 | 19 March 2020 | Iran | Logistic growth model | 4.70 | |
| 24 | Kuniya 35 | 15 January 2020‐29 February 2020 | Japan | Least‐square‐based method with Poisson noise | 2.60 | (2.40‐2.80) |
| 25 | Lai et al 45 | 11 February 2020 | World | 2.91 | (2.24‐3.58) | |
| 26 | Li et al 39 | 22 January 2020 | Wuhan | Exponential growth | 2.20 | (1.40–3.90) |
| 27 | Lui et al 30 | 22 January 2020 | World | Exponential growth | 2.90 | (2.32‐3.63) |
| 28 | Lui et al 30 | 22 January 2020 | World | Maximum Likelihood Estimation | 2.92 | (2.28‐3.67) |
| 29 | Luo et al 13 | 13 February 2020 | China (except Hubei) | Develped SEIR model. | 1.17 | (1.15‐1.16) |
| 30 | Luo et al 13 | 13 February 2020 | Hubei Province, China | Develped SEIR model. | 1.49 | (1.48‐1.51) |
| 31 | Majumder et al 33 | 26 January 2020 | Wuhan | Phenomenological modeling | 2.55 | (2.00–3.10) |
| 32 | Meng et al 8 | 12 February 2020 | China (except Hubei) | Devloped SIR Model | 2.81 | (2.72‐2.93) |
| 33 | Muniz‐Rodriguez et al 32 | 19‐29 February 2020 | Iran | Generalized growth model | 3.60 | (3.20‐4.20) |
| 34 | Muniz‐Rodriguez et al 32 | 19‐29 February 2020 | Iran | Growth model with doubling times which is equal ln (2)/r where r is grwoth rate. | 3.58 | (1.29‐8.46) |
| 35 | Park et al 40 | 24 February 2020 | Wuhan | 2.20 | ||
| 36 | Read et al 11 | 1‐22 January 2020 | Wuhan | SEIR | 3.11 | (2.39–4.13) |
| 37 | Remuzzi et al 27 | 08 March 2020 | Italy | Exponential growth | 3.00 | (2.76‐3.25) |
| 38 | Riou et al 31 | 18 January 2020 | China | Computational modelling of potential epidemic trajectories | 2.20 | %90 CI (1.40‐3.80) |
| 39 | Rocklöv et al 14 | 21 January 2020‐19 February 2020 | Diamond Princess Cruise Ship | SEIR Model | 3.70 | |
| 40 | Shao et al 12 | 16 February 2020 | Wuhan | SEIR model and Gamma distribution | 3.12 | |
| 41 | Shao et al 12 | 16 February 2020 | Hubei (without Wuhan) | SEIR model and Gamma distribution | 3.01 | |
| 42 | Shao et al 12 | 16 February 2020 | China (except Hubei) | SEIR model and Gamma distribution | 3.04 | |
| 43 | Shao et al 12 | 16 February 2020 | Beijing | SEIR model and Gamma distribution | 3.25 | |
| 44 | Shao et al 12 | 16 February 2020 | Shanghai | SEIR model and Gamma distribution | 3.24 | |
| 45 | Shao et al 12 | 16 February 2020 | Wuhan | Fudan‐CCDC model | 3.32 | |
| 46 | Shao et al 12 | 16 February 2020 | Hubei (without Wuhan) | Fudan‐CCDC model | 3.37 | |
| 47 | Shao et al 12 | 16 February 2020 | China (except Hubei) | Fudan‐CCDC model | 3.34 | |
| 48 | Shao et al 12 | 16 February 2020 | Beijing | Fudan‐CCDC model | 3.27 | |
| 49 | Shao et al 12 | 16 February 2020 | Shanghai | Fudan‐CCDC model | 3.31 | |
| 50 | Shen et al 15 | 12 December 2019 | Hubei Province, China | By SEIR simulation | 4.71 | (4.50‐4.92) |
| 51 | Shim et al 46 | 26 February 2020 | South Korea | Exponential growth | 1.50 | (1.40‐1.60) |
| 52 | Sugishita et al 5 | 14 January 2020‐28 February 2020 | Japan | SIR Model | 2.50 | (2.43‐2.55) |
| 53 | Sugishita et al 5 | 11 March 2020 | Japan | %35 reduction of basic reproduction number (2.5), 0.65*2.5 = 1.625, by voluntary event cancellation | 1.62 | |
| 54 | Tang et al 10 | 23 January 2020 | China | SEIR Model | 6.47 | (5.71‐7.23) |
| 55 | Tang et al 18 | 03 February 2020 | Shaanxi Province, China | Developed SEIHR Model | 1.69 | |
| 56 | Tapiwa et al 34 | 14 January 2020‐27 February 2020 | Tianjin, China | Bayesian estimation method | 1.59 | (1.42‐1.78) |
| 57 | Tapiwa et al 34 | 21 January 2020‐26 February 2020 | Singapore | Bayesian estimation method | 1.27 | (1.19‐1.36) |
| 58 | Traini et al 3 | 20 February 2020‐11 March 2020 | Italy | SIR Model | 3.40 | |
| 59 | Tuite et al 29 | 24 January 2020 | Wuhan | Disease transmission model | 2.30 | |
| 60 | Wang & You et al 47 | 17 January 2020‐8 February 2020 | Hubei, China | Exponential growth | 3.49 | (3.42‐3.58) |
| 61 | Wang & You et al 47 | 17 January 2020‐8 February 2020 | Hubei, China | Exponential growth (After including control measure) | 2.95 | (2.86‐3.03) |
| 62 | Wang et al 48 | 27 February 2020 | China | 2.75 | (2.00‐3.50) | |
| 63 | WHO 2 | 22 January 2020 | Wuhan | 1.95 | (1.40–2.50) | |
| 64 | Wu et al 41 | 25 January 2020 | Wuhan | Markov Chain Monte Carlo methods | 2.68 | (2.47–2.86) |
| 65 | Wu et al 9 | 10 February 2020 | Henan, China &China(without Hubei) | SIR Model | 2.44 | |
| 66 | Wu et al 9 | 16 February 2020 | Hubei, China | SIR Model | 6.27 | |
| 67 | Yang et al 49 | 26 January 2020 | China | Transmission model | 3.77 | (3.51‐4.05) |
| 68 | Zhang et al 19 | 27 January 2020‐10 February 2020 | Wuhan | SEIAR model | 2.88 | |
| 69 | Zhang et al 37 | 16 February 2020 | Diamond Princess cruise ship | Maximum Likelihood Estimation | 2.28 | (2.06‐2.52) |
| 70 | Zhao & Chen 22 | Before 30 January 2020 | Wuhan | SUQC Model (Stage I) | 4.71 | |
| 71 | Zhao & Chen 22 | After 30 January 2020 | Wuhan | SUQC Model (Stage II) | 0.75 | |
| 72 | Zhao & Chen 22 | After 13 February 2020 | Wuhan | SUQC Model (Stage II) | 0.48 | |
| 73 | Zhao & Chen 22 | Before 30 January 2020 | Hubei (without Wuhan) | SUQC Model (Stage I) | 5.93 | |
| 74 | Zhao & Chen 22 | After 30 January 2020 | Hubei (without Wuhan) | SUQC Model (Stage II) | 0.60 | |
| 75 | Zhao & Chen 22 | Before 30 Jan 2020 | China (excluding Hubei) | SUQC Model (Stage I) | 1.52 | |
| 76 | Zhao & Chen 22 | After 30 January 2020 | China (excluding Hubei) | SUQC Model (Stage II) | 0.57 | |
| 77 | Zhao & Chen 22 | Before 30 January 2020 | Beijing | SUQC Model (Stage I) | 0.88 | |
| 78 | Zhao & Chen 22 | After 30 January 2020 | Beijing | SUQC Model (Stage II) | 0.52 | |
| 79 | Zhao & Chen 22 | Before 30 January 2020 | Shanghai | SUQC Model (Stage I) | 3.62 | |
| 80 | Zhao & Chen 22 | After 30 Jan 2020 | Shanghai | SUQC Model (Stage II) | 0.51 | |
| 81 | Zhao & Chen 22 | Before 30 January 2020 | Guangzhou | SUQC Model (Stage I) | 1.20 | |
| 82 | Zhao & Chen 22 | After 30 Jan 2020 | Guangzhou | SUQC Model (Stage II) | 0.50 | |
| 83 | Zhao & Chen 22 | Before 30 January 2020 | Shenzhen | SUQC Model (Stage I) | 5.93 | |
| 84 | Zhao & Chen 22 | After 30 January 2020 | Shenzhen | SUQC Model (Stage II) | 0.53 | |
| 85 | Zhao et al 50 | 10‐24 January 2020 | China | Exponential growth | 2.24 | (1.96‐2.55) |
| 86 | Zhao et al 50 | 10–24 January 2020 | China | Exponential growth | 3.58 | (2.89‐4.39) |
| 87 | Zhuang et al 26 | 31 January 20 | Republic of Korea | Exponential growth | 2.60 | (2.30‐2.90) |
| 88 | Zhuang et al 26 | 05 February 2020 | Republic of Korea | Exponential growth | 3.20 | (2.90‐3.50) |
| 89 | Zhuang et al 26 | 05 February 2020 | Italy | Exponential growth | 2.60 | (2.30–2.90) |
| 90 | Zhuang et al 26 | 10 February 2020 | Italy | Exponential growth | 3.30 | (3.00‐3.60) |
| 91 | Giordano et al 25 | 20 February 2020‐12 March 2020 | Italy | SIDARTHE model | 2.38 | |
| 92 | Giordano et al 25 | 16 March 2020 | Italy | SIDARTHE model (Public health care) | 1.66 | |
| 93 | Hamidouche et al 51 | 21 March 2020 | Algeria | Mathematical model (Alg‐COVID‐19) | 2.55 | |
| 94 | Klausner et al 28 | 21 February 2020‐20 March 2020 | Israel | Exponential Growth | 2.19 | |
| 95 | Sahafizadeh et al 6 | 28 February 2020 | Iran | SIR Model | 4.86 | |
| 96 | Sahafizadeh et al 6 | 7 March 2020 | Iran | SIR Model | 4.5 | |
| 97 | Sahafizadeh et al 6 | 14 March 2020 | Iran | SIR Model | 4.29 | |
| 98 | Sahafizadeh et al 6 | 18 March 2020 | Iran | SIR Model | 2.10 | |
| 99 | Tian et al 20 | prior to 23 January 2020 | Anhui, China | SEQR model (Phase I) | 2.97 | |
| 100 | Tian et al 20 | 23 January 2020‐6 February 2020 | Anhui, China | SEQR model (Phase II) | 0.86 | |
| 101 | Tian et al 20 | after 6 February 2020 | Anhui, China | SEQR model (Phase III) | 0.57 | |
| 102 | Wang et al 24 | 23 January 2020‐6 March 2020 | Wuhan | S E1E2I1I2HR time‐dependent model | 2.71 | |
| 103 | Crokidakis, N 23 | 26 February 2020 | Brazil | SIQR model | 5.25 |
In this review, we summarise the basic reproduction number R 0 of multiple published articles for pandemic COVID‐19. Screening from 1 January 2020 to 6 April 2020, yielded 50 articles which estimated the basic reproduction number for COVID‐19. Most of these studies concern China, some of them are from Italy, Iran, South Korea, Singapore, Japan, Israel and Brazil.
Initially, the WHO estimated the basic reproduction number for COVID‐19 between 1.4 and 2.5, as declared in the statement regarding the outbreak of SARS‐CoV‐2, dated 23 January 2020. 52 Additionally, several articles aimed to more precisely estimate the COVID‐19 R 0 . A review written by Liu et al 53 compared 12 published articles from the first January to the seventh of February 2020 which estimated for the R 0 for COVID‐19 a range of values between 1.5 and 6.68.The authors of the review evaluated the mean and median of R 0 estimated by the 12 articles and they calculated a final mean and median value of R 0 for COVID‐19 of 3.28 and 2.79, respectively, with an interquartile range (IQR) of 1.16. Zhao and Chen 22 developed a Susceptible, Un‐quanrantined infected, quarantined infected, confirmed infected (SUQC) model to characterise the dynamics of COVID‐19; suggesting that this model was more suitable for analysis and prediction than adopting existing epidemic models. Using daily confirmed cases, they applied the SUQC model to analyse the outbreak of COVID‐19 in Wuhan, Hubei (excluding Wuhan), China (excluding Hubei) and four first‐tier cities of China (only Wuhan considered in Table 1). They found that the reproduction number R 0 > 1 for all mentioned regions except Beijing, before 30 January 2020, was defined as stage I, R 0 < 1 for all regions after 30 January known as stage II, R 0 even smaller after 13th February called stage III. The article by Kucharski and colleagues 54 combined mathematical modelling with multiple datasets to calculate the median daily reproduction number in Wuhan, within 2 weeks of introducing travel restrictions; this crucial number began at 2.35 and declined to 1.05 throughout December 2019 and January 2020.
In order to understand a measure of transmissibility of the new disease, a lot of preprints and papers were published in the last months (Table 3), modelling various mathematical and statistical techniques, considering different compartment models in epidemiology and analysing its evolution in some countries. In this paper, we highlight the articles' estimates of COVID‐19 R 0 , explore the assumptions of the preditive methods of R 0 and illustare values of R 0 in differing geographic regions.
2. METHODS
Along with reviewing articles and presenting their computing basic reproduction numbers, the mean; dividing the total of values by their number, of all R 0 that calculated by participating finding of it in each. The median, anothor measure of central is found for ungrouped ordering data which returns to the middle number among the whole values by Microsoft Excel 2010. A measure of variability, finally, named the interquartile range (IQR); is computed by dividing rank‐ordered data into 4 parts and finding quarties as follows: Q 1 is the middle of first two parts and Q 3 is the middle of last two parts, while Q 2 is the median and it is the middle of all values as it is mentioned before. IQR, thus, is the difference between Q 3 and Q 1 also it found via Excel 2010.
LOESS method is utilised to sketch the curve of R 0 values in Wuhan with their range. LOESS stands for local regression; it is a non‐parametric approach that fits multiple regressions in the local neighbourhood. LOESS can be particularly useful when the x‐axis variables are bound within a range. It allows greater flexibility than traditional modelling tools because it can be used for situations in which we do not know which the parametric form of the regression surface is. A regression line (or curve) is fitted to the observations that fall within the window, the points closest to the centre of the window being weighted to have the most significant effect on the calculation of the regression line. It uses nearest neighbour algorithm. However, the predictor variable can just be indices from 1 to the number of observations in the absence of explanatory variables (as in Figure 1). A window of a specified width is placed over the data. The wider the window, the smoother the resulting loess curve. In other words, the size of the neighbourhood controls the degree of smoothing. 55
FIGURE 1.
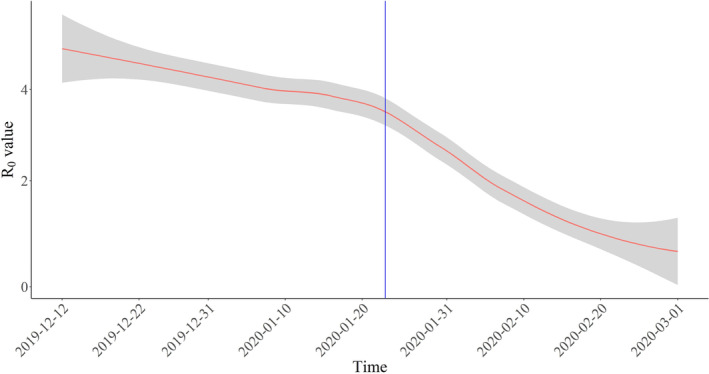
Smoothed curve showing the R 0 value in Wuhan city in the period from the 12th of December to the 1st of March 2020. The blue line marks travel restrictions starting on 23 January 2020, red line represents R 0, and grey shading represents 95% confidence intervals of the models estimate
The articles are estimated COVID‐19 R 0 that were published from 1 January 2020 to 6 April 2020, searched in Science Direct, Google Scholar, PubMed, Scopus and MedRxiv, using the keywords “basic reprodation number,” “ R 0 ,” “SARS‐CoV‐2,” and “COVID‐19,” and yielded more than 60 articles. After screening relevancy, 50 studied met inclsion criteria, providing 103 R 0 estimaties. The reason for exclusion the rest of them due to have R t , R c and R e instead of R 0 with couple of papers written in different languages. However, no research were excluded because of poor quality.
3. RESULTS
As recently announced by WHO, the virus epicentre Wuhan and its surrounding Hubei province have not recorded new cases of COVID‐19, 56 which shows the researchers' prediction on R 0 are on track (Figure 1 and Table 1). Figure 1 presents different estimated values of the R 0 in Wuhan city, Hubei province in China in the period between 12 December and 1 March 2020. It shows different estimated values R 0 in Wuhan city through the papers reviewed sorted by chronological order; we can see how the reproduction rate smoothed with LOESS regression method shows a decreasing trend over time. It is worth noting that after the control measures were introduced in Wuhan on 23 January 2020, 52 shown by a vertical blue line in Figure 1, the R 0 started dropping down, based on the data in Table 1.
The dot chart in Figures 2 and 3 stratifies COVID‐19 R 0 estimates in the period between the first of January to the 18th of March 2020 by authors in the analysed papers in Table 2. Figure 2 illustrates 68 R 0 values over 17 different regions in China. Tang et al 10 show the highest R 0 = 6.47 in China based on early outbreak data following the SEIR model, while Zhao and Chen 22 estimated the number to be 0.47, which is the lowest R 0 in the entire China through SUQC model, after 13 February 2020.
FIGURE 2.
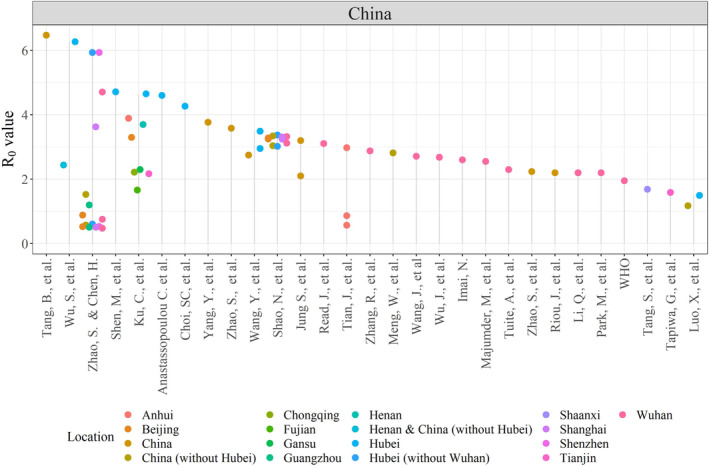
Dot chart showing the R 0 value estimated in the analysing papers coloured by location of interest in China
Figure 3 illustrates 35 R 0 values over 10 different countries. Brazil has the highest R 0 outside China, estimated more than 5. 23 In Iran, Muniz‐Rodriguez et al 32 estimated a value of about 3.5. Zhuang et al, 26 Traini et al 3 and Remuzzi et al 27 estimated range of basic reproduction number from 2.6 to 3.4 in Italy. Kuniya 35 estimated R 0 to be 2.60 in Japan, Hamidouche et al 51 estimated R 0 to be 2.55 in Algeria, Klausner et al 28 estimatied R 0 to be 2.19 in Israel and Tapiwa et al, 34 estimated R 0 to be 1.27 in Singapore. Regarding the Republic of Korea, Choi et al 17 reported a value below 1 on 17 February 2020.
FIGURE 3.
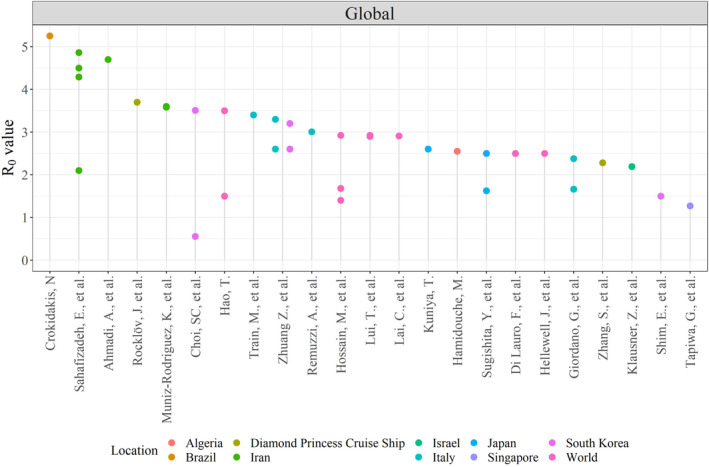
Dot chart showing the R 0 value estimated in the analysing papers coloured by location of interest in the global
With available articles regarding R 0 in Italy, Iran, South Korea, Singapore, Japan, Israel, Algeria, Brazil and China, we calculated the estimated mean R 0 = 2.71 for COVID‐19, with median = 2.73 and interquartile range (IQR) = 1.73. This mean R 0 is very close to the upper boundary estimated by WHO but lower than the previous review by Liu et al. 53 However, the average R 0 between 2 and 3 seems to have stabilised in recent articles shown in Table 2.
As more results to mention, there are various methods utilised in estimating R 0 as listed in Table 1, some of them being special compartmental models which are mathematical models in epidemlogy, while others are statistical models and techniques; whereas some others are mix of mathematical and statistical approaches. More accurately, from 103 findings of R 0 , 28 of them estimated it using statistical approaches, reported a range of 1.27 to 4.70 with an average 2.71, and 6 obtained of R 0 were found by mathematical models with statistics techniques estimated R 0 ranging from 3.01 to 4.71, with an average 3.39, the remaining 66 used mathematical models to estimate R 0 calculated a range from 0.47 to 6.47, with an average of 2.69.
4. CONCLUSION
In the globalised world of today, the evolution of the outbreak and information on COVID‐19 have become available at an unprecedented pace. Still, R 0 is not easy to calculate, especially there is much more to know about this new infection. The articles in Table 3, estimated different values of R 0 , using results obtained from their respective models. The discrepancies observed among the studies of R 0 COVID‐19 depend on a variety of assumptions in mathematical and statistical techniques, namely, the duration of contagiousness, the likelihood of infection per contact and the contact rate. 57 Due to variation in the assumptions and control strategies with time, the intervention measures, such as border control and quarantine in China, reduces R 0 from 2.92 to 1.40, 4 voluntary event cancellation in Japan reduced COVID‐19 infectiousness by 35%, 5 social distancing and strict restriction on travelling in Iran during 4 weeks reduced from 4.86 to 2.1 6 and closing schools and remote working with some basic recommendations in Italy reduced R 0 from 2.38 to 1.66. 25 Moreover, the basic reproduction number is continuously modified during a pandemic by accurate assumptions introduced and becomes more reliable R 0 as more data and information come to light.
In this article, the potential transmission of the SARS‐COV‐2 virus results in COVID‐19 that is expressible in basic reproduction number R 0 is summarised from 50 publishes with identifying their used approaches in finding it across the world. This review found that the estimated R 0 for COVID‐19 in the case of Wuhan has decreased below the threshold of 1, and the estimated mean of R 0 is around 2.71 for COVID‐19, with a median of 2.73 and IQR of 1.73. Our review coincides with a recent published article by Wang et al, 24 they estimated COVID‐19 R 0 to be 2.71 in Wuhan. More reasonable match in their article showed that the epidemic gradually died out from calculating effective reproduction ratio, which is used to measure the daily reproduction number, started from 2.71 as of 23 January, has declined rapidly to below 1 since eighth February 2020 and dropped to 0.06 at 6 March 2020.
Along with new pandemic control measures introducing and treating procedures more mathematically desiged models are required to take account of all factors, in this point of view, the mathematical models are more recommended to be used. All in all, still R 0 is not easy to calculate especially there is much more to know about this novel virus.
Rahman B, Sadraddin E, Porreca A. The basic reproduction number of SARS‐CoV‐2 in Wuhan is about to die out, how about the rest of the World? Rev Med Virol. 2020;30:e2111. 10.1002/rmv.2111
REFERENCE
- 1.WHO. Coronavirus disease 2019 (COVID‐19), situation report‐80, Accessed 9th April 2020. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200319-sitrep-59-covid-19.pdf?sfvrsn=c3dcdef9_2
- 2. WHO . Emergency Committee regarding theoutbreak of Coronavirus disease 2019. (COVID‐19), Retrieved on 11 March 2020 from https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19-11-march-2020
- 3. Traini MC, Caponi C, De Socio GV Fisica D. Modelling the Epidemic 2019‐nCoV Event in Italy: a preliminary note. 2020;0: 1–5.
- 4. Hossain MP, Junus A, Zhu X, Jia P, Wen T, Pfeiffer D. The effects of border control and quarantine measures on global spread of COVID‐19. 2020: 1–24. [DOI] [PMC free article] [PubMed]
- 5. Sugishita Y, Kurita J, Sugawara T, Ohkusa Y. Preliminary evaluation of voluntary event cancellation as a countermeasure against the COVID‐19 outbreak in Japan as of 11 March 2020. 2020; 21(1): 1–9.
- 6. Sahafizadeh E, Sartoli S. Estimating the reproduction number of COVID‐19 in Iran using epidemic modeling. medRxiv. January 2020: 2020.03. 20.20038422. 10.1101/2020.03.20.20038422 [DOI]
- 7. Ku C‐C, Ng T‐C, Lin H‐H. Epidemiological benchmarks of the COVID‐19 outbreak control in China after Wuhan's lockdown: a modelling study with an empirical approach. 2020. 10.2139/ssrn.3544127 [DOI] [Google Scholar]
- 8. Meng W, Jingtao QI. The Emergence of COVID‐19 in China. 2020: 1–11.
- 9. Shan WS, Pan SP, Ling LR, et al. Epidemiological development of novel coronavirus pneumonia in China and its forecast. medRxiv. 2020: 21 February 2020. 20026229. doi: 10.1101/2020.02.21.20026229 [DOI]
- 10. Tang B, Wang X, Li Q, et al. Estimation of the transmission risk of the 2019‐nCoV and its implication for public health interventions. J Clin Med. 2020;9(2):462. 10.3390/jcm9020462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Read JM, Bridgen JRRE, Cummings DATA, Ho A, Jewell CP. Novel coronavirus 2019‐nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv. 2020; 53(9):11. 10.1017/CBO9781107415324.004 [DOI] [PMC free article] [PubMed]
- 12. Shao N, Cheng J, Chen W. The reproductive number R0 of COVID‐19 based on estimate of a statistical time delay dynamical system. medRxiv. 2020: 17 February 2020. 20023747. 10.1101/2020.02.17.20023747 [DOI]
- 13. Luo X, Feng S, Yang J, et al. Analysis of potential risk of COVID‐19 infections in China based on a pairwise epidemic model. Preprints. 2020; February: 1–18. 10.20944/preprints202002.0398.v1 [DOI]
- 14. Rocklöv J, Sjödin H, Wilder‐Smith A. COVID‐19 outbreak on the Diamond princess cruise ship: estimating the epidemic potential and effectiveness of public health countermeasures. 2020; 3700. [DOI] [PMC free article] [PubMed]
- 15. Shen M, Peng Z, Xiao Y, Zhang L. Modelling the epidemic trend of the 2019‐nCOV outbreak in Hubei Province, China. medRxiv. 2020: 30 January 2020. 20019828. 10.1101/2020.01.30.20019828 [DOI]
- 16. Hao T. Infection dynamics of coronavirus disease 2019 (Covid‐19) modeled with the integration of the Eyring rate process theory and free volume concept. medRxiv. 2020; 26 February 2020. 20028571. 10.1101/2020.02.26.20028571 [DOI]
- 17. Choi S, Ki M. Estimating the Reproductive Number and the Outbreak Size of Novel Coronavirus Disease (COVID‐19) in South Korea. Epidemiol Health. 2020;12:e2020011. 10.4178/epih.e2020011 [DOI] [PMC free article] [PubMed]
- 18. Tang S, Tang B, Bragazzi NL, et al. Stochastic discrete epidemic modeling of COVID‐19 transmission in the province of Shaanxi incorporating public health intervention and case importation. medRxiv. 2020: 25 February 2020. 20027615. 10.1101/2020.02.25.20027615 [DOI]
- 19. Zhang R, Zhang R. Impact of Wuhan's Epidemic Prevention Policy on the Outbreak of COVID‐19 in Wuhan, China. 2020.
- 20. Tian J, Wu J, Bao Y, et al. Modeling analysis of COVID‐19 based on morbidity data in Anhui, China. Math Biosci Eng. 2020;17(4):2842‐2852. 10.3934/mbe.2020158 [DOI] [PubMed] [Google Scholar]
- 21. Anastassopoulou C, Russo L, Tsakris A, Siettos C. Data‐based analysis, modelling and forecasting of the COVID‐19 outbreak. 2020: 1–28. [DOI] [PMC free article] [PubMed]
- 22. Zhao S, Chen H. Modeling the epidemic dynamics and control of COVID‐19 outbreak in China. Quant Biol. 2020;8(1):11‐19. 10.1007/s40484-020-0199-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Crokidakis N. Data analysis and modeling of the evolution of COVID‐19 in Brazil. 2020. http://arxiv.org/abs/2003.12150
- 24. Wang L, Wang J, Zhao H, et al. Modelling and assessing the effects of medical resources on transmission of novel coronavirus (COVID‐19) in Wuhan, China. Math Biosci Eng. 2020;17(4):2936‐2949. 10.3934/mbe.2020165 [DOI] [PubMed] [Google Scholar]
- 25. Giordano G, Blanchini F, Bruno R, et al. A SIDARTHE Model of COVID‐19 Epidemic in Italy. 2020. Retrieved from http://arxiv.org/abs/2003.09861
- 26. Zhuang Z, Zhao S, Lin Q, et al. Preliminary estimating the reproduction number of the coronavirus disease (COVID‐19) outbreak in Republic of Korea and Italy by 5 March 2020. medRxiv. 2020: March 2, 2020. 20030312. 10.1101/2020.03.02.20030312 [DOI] [PMC free article] [PubMed]
- 27. Remuzzi A, Remuzzi G. Health policy COVID‐19 and Italy: what next? The Lancet. 2020;2:10‐13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Klausner Z, Fattal E, Hirsch E, Shapira SC. A single holiday was the turning point of the COVID‐19 policy of Israel. medRxiv. January 2020: March 26, 2020. 20044412. 10.1101/2020.03.26.20044412 [DOI] [PMC free article] [PubMed]
- 29. Tuite AR, Fisman DN. Reporting, epidemic growth, and reproduction numbers for the 2019 novel coronavirus (2019‐nCoV) epidemic. Ann Intern Med. 2020;172:567. 10.7326/m20-0358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Liu T, Hu J, Kang M. Transmission dynamics of 2019 novel coronavirus (2019‐nCoV). 2020; 61: 122–128.
- 31. Riou J, Althaus CL. Pattern of early human‐to‐human transmission of Wuhan 2019 novel coronavirus (2019‐nCoV), December 2019 to January 2020. Euro Surveill. 2020;25(4):1‐5. 10.2807/1560-7917.ES.2020.25.4.2000058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Muniz‐Rodriguez K, Fung IC‐H, Ferdosi SR, et al. Transmission potential of COVID‐19 in Iran. medRxiv. January 2020: 8 March 2020. 20030643. 10.1101/2020.03.08.20030643 [DOI]
- 33. Majumder M, Mandl KD. Early transmissibility assessment of a novel coronavirus in Wuhan, China. 2020. 10.2139/ssrn.3524675 [DOI]
- 34. Ganyani T, Kremer C, Chen D, et al. Estimating the generation interval for COVID‐19 based on symptom onset data. medRxiv. 2020: March 5, 2020. 20031815. 10.1101/2020.03.05.20031815 [DOI] [PMC free article] [PubMed]
- 35. Kuniya T. Prediction of the epidemic peak of coronavirus disease in Japan, 2020. J Clin Med. 2020;9:1‐7. 10.3390/jcm9030789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Jung S‐M, Akhmetzhanov AR, Hayashi K, et al. Real‐time estimation of the risk of death from novel coronavirus (COVID‐19) infection: inference using exported cases. J Clin Med. 2020;9(2):523. 10.3390/jcm9020523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Zhang S, Diao MY, Yu W, Pei L, Lin Z, Chen D. Estimation of the reproductive number of novel coronavirus (COVID‐19) and the probable outbreak size on the Diamond princess cruise ship: a data‐driven analysis. Int J Infect Dis. 2020;93:201‐204. 10.1016/j.ijid.2020.02.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Imai N, Cori A, Dorigatti I, et al. Report 3: transmissibility of 2019‐nCoV. Imp Coll London 2020: 2–6. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-2019-nCoV-transmissibility.pdf
- 39. Li Q, Guan X, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N Engl J Med. 2020;382:1‐9. 10.1056/nejmoa2001316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Park M, Thwaites RS, Openshaw PJM. COVID‐19: lessons from SARS and MERS. Eur J Immunol. 2020;50:308‐311. 10.1002/eji.202070035 [DOI] [Google Scholar]
- 41. Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019‐nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689‐697. 10.1016/S0140-6736(20)30260-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Lauro F Di, Kiss IZ , Miller J. The timing of one‐shot interventions for epidemic control. medRxiv. 2020: 2 March 2020. 20030007. 10.1101/2020.03.02.20030007 [DOI]
- 43. Hellewell J, Abbott S, Gimma A, et al. Feasibility of controlling COVID‐19 outbreaks by isolation of cases and contacts. Lancet Global Health. 2020;20:1‐9. 10.1016/s2214-109x(20)30074-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Ahmadi A, Shirani M, Rahmani F. Modeling and forecasting trend of COVID‐19 epidemic in Iran. medRxiv. January 2020: 17 March 2020. 20037671. 10.1101/2020.03.17.20037671 [DOI] [PMC free article] [PubMed]
- 45. Lai CC, Shih TP, Ko WC, Tang HJ, Hsueh PR. Severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2) and coronavirus disease‐2019 (COVID‐19): the epidemic and the challenges. Int J Antimicrob Agents. 2020;2:105924. 10.1016/j.ijantimicag.2020.105924 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Shim E, Tariq A, Choi W, Lee Y, Chowell G. Transmission potential of COVID‐19 in South Korea. medRxiv. January 2020: 27 February 2020. 20028829. 10.1101/2020.02.27.20028829 [DOI] [PMC free article] [PubMed]
- 47. Wang Y, You XY, Wang YJ, Peng LP, Du ZC, Gilmour S, Yoneoka D, Gu J, Hao C, Hao YT et al. Estimating the basic reproduction number of COVID‐19 in Wuhan, China 2020: 1–11. [DOI] [PubMed]
- 48. Wang Y, Wang Y, Chen Y, Qin Q. Unique epidemiological and clinical features of the emerging 2019 novel coronavirus pneumonia (COVID‐19) implicate special control measures. J Med Virol. 2020;92:568‐576. 10.1002/jmv.25748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Yang Y, Lu Q, Liu M, et al. Epidemiological and clinical features of the 2019 novel coronavirus outbreak in China. medRxiv. January 2020: 10 February 2020. 20021675. 10.1101/2020.02.10.20021675 [DOI]
- 50. Zhao S, Lin Q, Ran J, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019‐nCoV) in China, from 2019 to 2020: a data‐driven analysis in the early phase of the outbreak. Int J Infect Dis. 2020;92:214‐217. 10.1016/j.ijid.2020.01.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Hamidouche M. COVID‐19 outbreak in Algeria: a mathematical model to predict cumulative cases. medRxiv. January 2020:March 20, 2020. 20039891. 10.1101/2020.03.20.20039891 [DOI]
- 52. WHO . Emergency Committee regarding theoutbreak of novel coronavirus 2019. (n‐CoV), Retrieved on 23 January 2020 from https://www.who.int/news-room/detail/23-01-2020-statement-on-the-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov)
- 53. Liu Y, Gayle AA, Wilder‐Smith A, Rocklöv J. The reproductive number of COVID‐19 is higher compared to SARS coronavirus. J Travel Med. 2020;27(2):1–4. 10.1093/jtm/taaa021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Kucharski AJ, Russell TW, Diamond C, et al. Early dynamics of transmission and control of COVID‐19: a mathematical modelling study. medRxiv. 2020; 3099(20): January 31, 2020. 20019901. 10.1101/2020.01.31.20019901 [DOI] [PMC free article] [PubMed]
- 55. Cleveland WS, Grosse E, Shyu WM. Local regression models. In: Chambers JM, Hastie TJ, eds. Chapter 8 in Statistical Models. Pacific Grove, CA: Wadsworth Brooks/Cole ; 1992:608. [Google Scholar]
- 56. Nature . Coronavirus latest: Italy death toll overtakes China's, Retrieved on 18 March 2020 from https://www.nature.com/articles/d41586-020-00154-w
- 57. Viceconte G, Petrosillo N. COVID‐19 R0: magic number vidual affected by a transmittable disease is or conundrum? Infect Dis Rep. 2020;12:12‐13. 10.4081/idr.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]


