Abstract
We have applied mathematical modeling to investigate the infections of the ongoing coronavirus disease‐2019 (COVID‐19) pandemic caused by SARS‐CoV‐2 virus. We first validated our model using the well‐studied influenza viruses and then compared the pathogenesis processes between the two viruses. The interaction between host innate and adaptive immune responses was found to be a potential cause for the higher severity and mortality in COVID‐19 patients. Specifically, the timing mismatch between the two immune responses has a major impact on disease progression. The adaptive immune response of the COVID‐19 patients is more likely to come before the peak of viral load, while the opposite is true for influenza patients. This difference in timing causes delayed depletion of vulnerable epithelial cells in the lungs in COVID‐19 patients while enhancing viral clearance in influenza patients. Stronger adaptive immunity in COVID‐19 patients can potentially lead to longer recovery time and more severe secondary complications. Based on our analysis, delaying the onset of adaptive immune responses during the early phase of infections may be a potential treatment option for high‐risk COVID‐19 patients. Suppressing the adaptive immune response temporarily and avoiding its interference with the innate immune response may allow the innate immunity to more efficiently clear the virus.
Keywords: adaptive immunity, antiviral drugs, COVID‐19, innate immunity, SARS‐CoV‐2, target cell‐limited model
1. INTRODUCTION
Since December 2019, coronavirus severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2) has rapidly spread across the globe and become the top issue affecting millions of people around the world. Although most of the patients of coronavirus disease‐2019 (COVID‐19) show mild symptoms and can recover on their own, about 20% of the patients develop severe symptoms. Common symptoms include fever, cough, shortness of breath, as well as other flu‐like symptoms (sore throat, chills, fatigue, etc.). Patients with severe illness tend to have severe pneumonia, sometimes acute respiratory distress, which could lead to multiple organ failures and death. The hospital stay can be weeks for such patients. 1 , 2 , 3 , 4 There is no proven cure or antiviral drugs available yet.
The influenza virus typically binds to the sialic acid receptors on the surface of epithelial cells in the upper respiratory tracks and the upper divisions of bronchi. 5 In very severe, and often fatal cases of influenza, the infection will spread to the lower lungs. 6 , 7 Similarly, the SARS‐CoV‐2 virus binds to the angiotensin‐converting enzyme 2 (ACE2) receptors on the surface epithelial cells. 8 These cells with ACE2 expression are hence vulnerable to virus attack and are called target cells in mathematical models. The density of the target cells has been found to vary significantly in different regions of the respiratory tracks, with the highest in the lungs, followed by the nose, and lastly, the trachea/bronchi tissues. 9 , 10 , 11 As such pneumonia is relatively common among COVID‐19 patients.
The incubation time for influenza is typically 48 hours or less. 12 The eclipse phase is reported to be around 6 hours, with viral load peaks around 2 to 3 days postinfection (dpi). 5 The infection typically resolves in 3 to 5 days. In typical influenza patients, the adaptive immune responses (AIRs) including pathogen‐specific antibodies (Abs) and CD8+ cytotoxic T lymphocytes (CTL) are first observed around 5 dpi, peaking around 7 dpi. 13 The mean incubation period for COVID‐19 patients is estimated to be 6 days, with a range distribution of 13 days. 14 , 15 The median time from symptoms to discharge from the hospital was about 22 days, whereas the median time to death was 18 days. 4 Among this study of 191 patients, the shortest observed duration of viral shedding among survivors was 8 days, whereas the longest was 37 days. Among 29 patients who received the antiviral drug lopinavir/ritonavir and were discharged, the median time from illness onset to initiation of antiviral treatment was 14 days and the median duration of viral shedding was 22 days. The median duration of viral shedding was 19 days in patients with severe disease status and 24 days in patients with critical disease status. The median time from illness onset to dyspnea was similar in survivors and non‐survivors, with a median duration of dyspnea of 13 days for survivors. The much longer incubation time, duration of viral shedding, and time it takes from disease onset to discharge in COVID‐19 patients are critical in our modeling study, which puts a strong constraint on what the model outputs should look like.
In this paper, we used mathematical modeling to investigate the dynamics of the viral infection/replication inside a human host, in particular, the influenza and the SARS‐CoV‐2 virus, as well as the interactions of target cells with the innate and AIRs. Our model suggests that most of the differences between the two types of infections can potentially be attributed to the timing mismatch between the two immune responses. More specifically, influenza is a very acute infection; all vulnerable cells are completely depleted and viruses are more or less cleared by the innate immune response, before the adaptive immune response (AIR), which has a transient nature, reaches a significant level. The arrival of AIR may seem futile but it helps to completely clear the remaining viruses. On the other hand, the peak level of the AIR of the COVID‐19 patients is more likely to come before the number of infected cells reaches its peak, due to the slower disease progression outlined above. As such the AIR helps to eliminate more viruses in the rapid growth phase and slow down the infection and depletion of vulnerable epithelial cells in the lungs of COVID‐19 patients. A strong AIR, in this case, may be bad for the patients, as the disease progression is extended longer while a weaker AIR can be beneficial for the patients due to the rapid depletion of the target cells. One recent observation puzzling for many is the apparent resurgence of the disease for some “cured” patients. Based on our theory and modeling, this phenomenon can be explained by that of a strong interaction of innate and AIRs in a host, which can sometimes create double peaks in viral load, separated by weeks. In the second part of our study, we applied our modeling to the current bedside treatment regimen. Antiviral drugs and immunosuppressive drugs have been evaluated as potential treatments for high‐risk patients. We proposed an immune‐suppressing treatment based on the leanings of our modeling study, which is to apply immunosuppressive drugs during the early phase of infection to reduce the AIRs to a level low enough not to interfere with the innate immune response. Once the vulnerable cells are depleted, the drug should be removed to let the AIR run its course to clear the remaining virus. This new approach can potentially lead to fast and complete recovery. This counter‐intuitive approach aims to mimic the excellent job human immune systems have done with the influenza infection. Further studies on immune responses of COVID‐19 patients and validation of our core assumptions and theory are needed before this can be applied in real patients' situations.
2. MATHEMATICAL MODELS
Mathematical models have been developed to understand the dynamics of viral infections. 16 , 17 , 18 , 19 , 20 Most of them fall into the category of the target cell‐limited model with some variations. The simplest version includes three species: uninfected susceptible target cells (T), which in our case is the surface epithelial cells with ACE2 receptors, located at the respiratory tracks including lungs, nasal and trachea/bronchial tissues, infected virus‐producing cells (I), and the virus particles (V). They can be described by the following set of differential equations:
| (1) |
Detailed descriptions and definitions of the parameters are shown in Table 1. Notice that uninfected target cells (T) are produced and die at the same rate d. This ensures that without infection, the number of target cells remains the same. The density of target cells is different for different tissues, and we specifically included the effective surface area here so that the constants (except and A) remain the same for different parts of the respiratory tracks of the same patient. These constants can be different for different patients. By the interaction of virus (V) with uninfected target cells (T) at a constant infectivity rate k, the target cells become infected cells (I), which in turn produce virus (V) with production rate p. Due to viral cytopathicity, immune elimination and/or apoptosis, infected cells (I) die at a rate . The virus is cleared at rate c from the cells by mechanisms such as immune elimination. This set of equations essentially describes the innate immune response of the host. is a dimensionless variable describing the time t in units of , tracking how many cycles of replications the virus has gone through since the inoculation, while is the average cycle time for virus reproduction including the eclipse and burst phase. The reason for us to use instead of the familiar time variable t is to simplify numerical simulation, as well as making the constants more intuitively understandable.
Table 1.
Parameters in Equations (1)
| Parameters | Definition | |
|---|---|---|
|
|
Average cycle time for virus replication | |
|
|
, the number of cycles of virus replication | |
| T | Target cells at | |
| I | Infected cells at | |
| V | Total virus particles at | |
| A | Effective surface area of the tissue | |
| d | % of normal target cells died during each cycle | |
|
|
% of infected cells died during each cycle | |
| c | % of virus particle cleared during each cycle | |
|
|
Ratio of the number of virus particles and the number of virions | |
| k | % target cells infected during each cycle by unit density of virions | |
| p | Number of virus particles each infected cell produces during each cycle | |
|
|
Target cells at = 0 | |
|
|
Virus count at = 0 | |
|
|
Infected cell count at |
The ability of a virus to grow the infection or to be cleared is determined by the basic reproductive ratio R:
where R represents the number of infected cells newly generated by one infected cell. With R 1 the infection grows, while with R 1 infected cells decrease and the virus is cleared out. 21
Here it is important to note that T is a variable. When the target cells are depleted, T goes down, and so does R. This is a very simple yet critically important concept for understanding the virus clearance. Complete depletion of the target cells, namely , leads to , hence achieving the best virus clearing ability. is the native R at , when the target cells are not depleted at all. It should be pointed out that with the innate immunity alone, the Equations (1) always lead to a stable equilibrium, which is achieved when the elimination of infected cells is equal to the regeneration of the target cells at any given time. This is why the AIR is so important, without which the host may not be able to completely clear all virus particles.
Multiple studies have suggested that both the innate and AIRs are important in modeling virus infections. 22 , 23 , 24 To account for the AIR and the dynamic interactions among multiple players (target epithelial cells, virus, CTLs, and antibodies), we used the equations employed by Miao et al 25 with minor modifications, shown as Equations (2). Table 2 described the new parameters introduced in Equations (2).
| (2) |
Table 2.
Definition of adaptive immune responses in Equations (2)
|
|
Activity level for cells | |
|
|
Normalized profile for T cells killing activity at | |
|
|
Activity level for IgG antibody | |
|
|
Normalized profile for serum IgG antibody activity at | |
|
|
Activity level for IgM antibody | |
|
|
Normalized profile for serum IgM antibody activity at |
In their experiment, the authors found that the viral load peaked at 2 to 3 dpi. The level of cells and IgM data shows a very narrow peak at about 8 days dpi, while the level of IgG antibody shows a relatively broad peak lasting well over 50 days. We seek to mimic these temporal profiles, using as an example:
With such a profile, we can choose the peak position , and the rising and falling width and in our simulation to see the effects of these parameters on the viral infection dynamics. Our main assumption is that the AIR is a short term effect, which assumes that the virus is successfully cleared timely and the patient survived. As such, it is not our goal to develop a detailed model for AIRs, but rather to understand the necessary conditions that are needed for a successful outcome for the patients. Other components like IgA, CD4+ T cells, and a number of other components of the AIR could also play important roles here. 13 Although we have used the three components of CD8+ and antibodies of IgM and IgG as a representation of the AIR, our conclusions are more general. This is because the conclusions are based on the overall effect of the AIR, rather than the details of how each component of AIR works. If we change the number of AIR components to 2 or 4, as long as they have a similar transient profile, the conclusions should remain the same.
To analyze the effect of antiviral drugs that either block infection and/or production of viral particles , the target cell‐limited model is modified as follows:
| (3) |
with . 26 Here, describes no antiviral drug effect while refers to a drug that is 100% effective. With the action of the drug, the reproduction number R is revised as follows:
Finally, we want to add another component to describe the effect of a drug that suppresses the innate immune response, for reasons that will be discussed in the section of treatments by immunosuppressive drugs. Equations (1), (2), and (3) are changed to the following:
| (4) |
with . Here, describes no effect of immune‐suppressing drugs while refers to complete suppression.
3. RESULTS
3.1. Modeling influenza infections
Mathematical models of influenza infections have been studied extensively, 5 , 22 , 23 , 24 , 25 our interest is to use it as a starting point before we embark on more challenging work on SARS‐CoV‐2 infections. We have carefully evaluated the parameter values tabulated by Beauchemin et al 5 and decided to use the values shown in Table 3.
Table 3.
Parameters used for Influenza simulation
| Parameters | Values | ||
|---|---|---|---|
|
|
7 h | ||
| d | 2.9x | ||
|
|
0.4 | ||
| c | 0.4 | ||
|
|
0.075 | ||
| p | 100 | ||
|
|
|
||
|
|
100 | ||
|
|
10 |
The choice of the parameters is based on cross‐checking multiple sources, and testing many simulation runs with variations of parameters to ensure that the output agrees with what is known about influenza infections. It is not our intent to fit the model to any specific set of data, but rather to be able to reproduce the general features of the influenza infections. The result is shown at Figure 1. With these parameters, the infected cell count peaks at 2.45 dpi; viral load peaks at 2.98 dpi, and and the is about 47. , which describes an exponential growth rate (shown in Appendix) is 2.34. As we should expect, the target cells are depleted shortly following the peak of the infected cells, after which the virus count decays exponentially.
Figure 1.
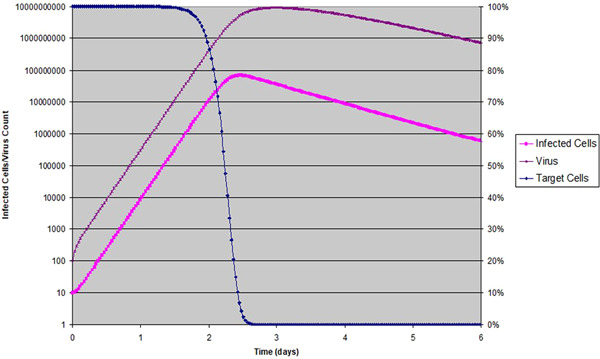
Target cell‐limited model of Influenza virus infection in human host: Target cells as a ratio is shown in percentage with linear scale to the right; infected cells and virus counts are shown in log scale to the left
The situation with regard to the decay portion is more complicated, and the consideration of the AIR is warranted if one is to understand it beyond 6 dpi. Table 4 shows the parameters for the three components we considered in Equations (2).
Table 4.
Parameters used for adaptive immune response (AIR), modeling
| Parameters | Values |
|---|---|
| Component | kτ, peak time (dpi), rising width (d), falling width (d) |
| CD8 + | 0.3, 9, 2, 10 |
| IgM | 0.3, 8, 2, 10 |
| IgG | 0.3, 10, 10, 40 |
These values are chosen so that the temporal profiles resemble what was presented by Miao et al 25 The choice of the peak time is based on Beauchemin et al 5 We should clarify that the temporal profiles are not completely the same as in reference, 25 as some other literature has shown broader profiles. 5 We have done sensitivity analysis by doing multiple simulations, and find that as long as the width is not too narrow, the results are not sensitive to the width or shape of the peak. On the other hand, the location of the peak time is very important for the complete clearing of the virus. The result is shown in Figure 2.
Figure 2.
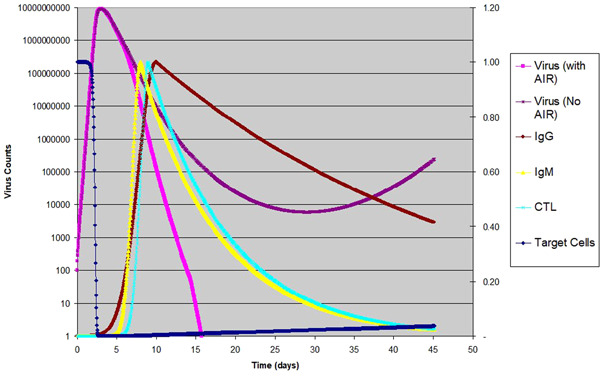
Influenza virus infection in human host: Virus counts of the same infection with and without AIR are shown in log scale to the left; target cells is shown with linear scale to the right; normalized temporal profile for are shown in linear scale to the right
In Figure 2, we included the same graph for virus count without the AIR, as shown in Figure 1, except with a longer time scale. From this point on, in all of the figures, we show the virus counts only, as the infected cells counts always follow the same pattern as the virus counts, except with a small time shift. At about 30 dpi, the virus count goes to a small number and then gradually climbs up. This tail is caused by the cell regeneration, as the newly generated epithelial cells provide the target cells for the viral infection to stay on at a relatively low level, eventually reaching equilibrium at a later time. As long as the native is greater than 1, this pattern is the universal behavior of the Equations (1), namely, a rapid exponential rise followed by an exponential decay, then eventually reaching an equilibrium at a low level of infection. Changing parameters in Table 3 will change the time scale, the peak/trough levels and locations of virus count etc., but the general pattern is the same. When the AIR is included, the virus clears out much faster. By day 15, the virus is completely gone. Mathematically virus and infected cells count never actually go to zero. However, we know that the infected cell count has to be an integer. Therefore when this number is below 1, one can safely consider it game‐over for the virus. In our modeling, we set this cutoff to be 0.2 infected cell to be conservative.
The temporal profile of the three components of the AIR are also shown in Figure 2 so that the readers can see their peak positions as compared to the actual virus counts over time. After the AIR becomes active, the decay of virus count becomes much faster. We also tried to vary the parameters around what is listed in Table 3. In the case of the influenza virus, if the peak time of the AIR is adjusted, only under some extreme conditions (e.g., reducing the AIR activity level to below 0.08, or raising the to above 90 and keeping the AIR activity to 0.2 or lower), one can make the tail end of the viral load survive and potentially thrive. In other words, this ability to completely and swiftly clear the influenza virus is common across a broad spectrum of parameters, which means that most people can successfully clear influenza infections quickly and completely. This has a lot to do with the acute nature of the influenza infection, namely, the peak viral load is at 2 to 3 dpi and the target cells are completely depleted before 3 dpi, much before the AIR reaches its peak level, which is at around 8 dpi. With few new cells generated, it takes only a very low level of AIR to completely clear the remaining virus. We reason that the acute nature and an appropriately timed adaptive immunity is key to completely eradicate all influenza virus. The fact that the adaptive immunity works so well with the innate immunity can probably be traced back to the long history of human evolution and its constant battles with acute virus infections. As our immune system against viral infection is so optimized against acute viral infections such as influenza, it may have some limitations against other infections by slow‐progressing viruses, such as the coronavirus SARS‐CoV‐2.
3.2. The role of innate and AIRs on SARS‐CoV‐2 virus infection
Due to the lack of experimental data, the discussions below are based on our best assumptions and observations. When shifting gears from the influenza virus to the novel corona virus, the most important difference we noticed is the difference in the pace of infection progression. Multiple reports suggested that the viral counts of SARS‐CoV‐2 do not reach a peak until 2 to 3 weeks postinoculation. 2 , 3 , 4 Here we will make a bold assumption that, if without the AIR, the peak time is around 8 to 14 days, if not more. As most of the severe cases result in pneumonia and the lungs are significantly larger than the nose, is estimated to be higher by a factor of . Table 5 lists the only two parameters that are changed from Tables 3 and 4, together with the three dependent variables as outputs from the model. Here we aimed to have a peak time for infected cells at around 12 dpi if considering the effect of innate immune response only. Together with a times increase of , these constraints essentially limited our choice for the only other variable to a very narrow range. The result is shown in Figure 3.
Table 5.
Parameters used for corona virus modeling
| Parameters | Values | ||
|---|---|---|---|
|
|
0.01125 | ||
|
|
|
||
|
|
7.03 | ||
|
|
0.66 | ||
| Peak time for infected cells | 12.02 dpi |
Figure 3.
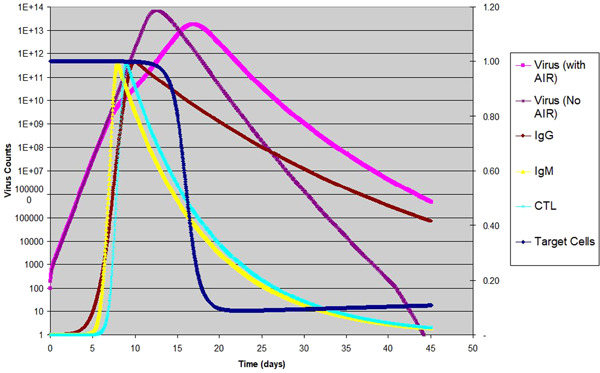
Corona virus infection in human host: Virus counts of the same infection with and without AIR are shown in log scale to the left; target cells is shown with linear scale to the right; normalized temporal profile for are shown in linear scale to the right
As we can see in Figure 3, the curve of virus count for an innate immune response only (no AIR) is similar to that of influenza infections, except with a longer time scale. With AIR the peak of the viral count is shifted from 12.02 to 16.33 dpi, and the decay becomes much slower, indicating much slower recovery. We have also shown the three components of the AIR on the same graph, which peak at 8 to 10 dpi. Once the AIR is activated, the steep rise of virus count is slowed, and the maximum viral load is reduced by a factor of 3.3. Another point we noticed is that the target cells are not depleted completely, with about 6.5% being the lowest; this explains why the decay is slower when compared to the innate‐only scenario, which has complete depletion of target cells (not shown in the graph). What does this mean for the severity of the disease? We hypothesize that the AIR is not helping in the case of COVID‐19 due to a longer duration of virus activity.
From a mathematical standpoint, there is a huge advantage to quickly deplete all target cells, namely, fast and complete elimination of the virus. In reality, one critical question that remains is what are the target cells and whether elimination of all target cells poses a critical risk for patients. We hereby make the assumption that the target cells are mainly epithelial cells with ACE2 expression, and the complete elimination of these cells is not in itself causing failure of lung function in patients. Rather, the extended duration of viral activity may have led to hyperactive immune responses at a later stage, which eventually leads to tissue damage and potentially ARDS. Our assumption is based on the observation that only about 2% to 4% of the epithelial cells have ACE2 receptors, 4 giving us hope that the loss of these cells is not going to cause a major loss of air exchange capability. Another indication is that a large number of patients with CT scans showing ground‐glass opacity do not necessarily have severe COVID‐19 symptoms. 2 In influenza infections, most of the patients experience total depletion of target cells and recover without any consequences.
Our initial choice of AIR activity of 0.3 is purely artificial at this point, so we want to explore the effect of different levels of AIR activity. The result is shown in Figure 4.
Figure 4.
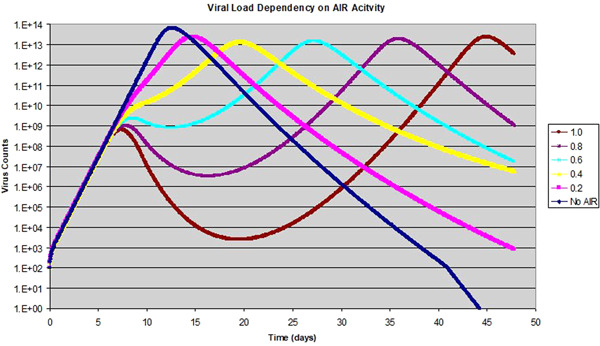
Effect of adaptive immuneresponse (AIR) activity on the viral infection: The AIR activity level varies from 0 to 1.0, while the peak of the AIR is fixed at 8 dpi
As we can see, with the AIR activity level of 0.2–0.4, the virus count reaches a high level, and then the growth is slowed with the activation of the AIR at around 8 dpi. After the effect of the AIR wanes, the virus count continues its ascent, reaching its peak at a later date. At a higher AIR activity level, we start to see an apparent drop in virus count after the onset of AIR, reaching a trough then rising to its peak at a much later day. Overall, an increase in the AIR activity tends to increase the duration of viral activity extensively in this case. This is because early activation of the AIR helps to reduce infection and depletion of target cells before it reaches a peak level, which saves a large number of uninfected target cells for later infection. When the effect of the AIR wanes, the virus takes control again when the effective R rises above 1. Whether the virus count grows or drops during the peak AIR activity is dependent on how strong the AIR effect is, and whether the effective reproductive ratio R at the time is greater or less than 1. This situation resembles a rampant forest fire. If the fire is left alone, when all the trees are burnt out, the fire loses its fuel and dies out quickly. Trying to fight the fire halfheartedly before that can only result in partial control of the fire. Once the fire fighting stops, the fire resumes in vengeance until all trees are burnt out. We believe that this is the reason why a lot of severe patients cannot leave hospital beds, and eventually develop ARDS and multiple organ failure. The examples in Figure 4 with the AIR activity level greater or equal to 0.8 offers a ready explanation for some perplexing clinical observations that some patients can appear to be recovered, but have the virus level resurges at a later time.
What's even more interesting is when we shift the day that the AIR activity peaks, as shown in Figure 5.
Figure 5.
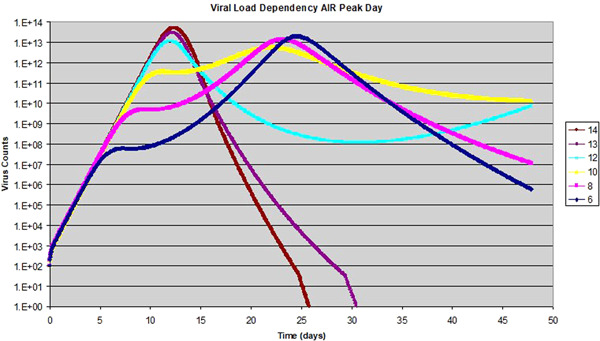
Effect of adaptive immuneresponse (AIR) peak day on viral dynamics: data shows the viral load over time when the day of AIR peak is changed from 6 to 14 days
To show the AIR effect on viral replication in a more pronounced fashion, we fix the AIR activity level at 0.5, and vary the day of its peak time from 6 to 14 dpi. The virus peak time without the AIR is at 12 dpi. As we can see, if the AIR peaks before 12 dpi, its effect is to lower the maximum viral load somewhat, but extend the duration of viral activity quite substantially. On the other hand, if the AIR peaks after 12 dpi, it helps to clear out the remainder of the viral load more efficiently, as shown by a sharper decay of virus. This ensures a quick and complete clearance of the virus, resembling the scenario of influenza infections. With additional simulations, we have found that if the AIR peak is after the viral peak, a higher level of AIR activity always helps to clear the virus faster. Contrarily, if the AIR peaks before the viral peak, higher AIR activity can increase the duration of viral activity. We also found that if the AIR level is low enough, for example below 0.1, its effect becomes negligible and the virus replication and clearing process is dictated by the innate immune response alone. As discussed earlier, the consequences of extended duration of viral activity may be detrimental to the patients, which include a prolonged disease process, increase of the patient's risk in secondary infections, tissue/organ damage caused by an over‐active immune system and potential virus spreading to other parts of the body.
These dramatic effects due to the AIR timing is mainly caused by two factors: the presence of a large number of uninfected target cells, and the AIR as a transient effect. A short‐term antiviral activity during the exponential growth of the virus will always slow down the growth of the virus and infection, leaving more target cells as a source for continued infections later. This result is very general and does not depend on the source of antiviral activity, as we can see later with the analysis of antiviral drugs.
In essence, our modeling aims to explore potential means to manage the COVID‐19 infections so that it can be similar to influenza infections. When the virus can be quickly and completely cleared, the AIR should be transient, similar to the influenza infections. Our modeling then establishes that one of the requirements is that the peak of AIR needs to come after the peak of infected cells, or equivalently, the peak of viral load. This can be viewed as a necessary condition for fast and complete clearing of virus. To achieve rapid clearing of the virus, it is also desirable to have the target cells more or less completely depleted. In reality, when the virus cannot be cleared timely, it is likely that the AIR will also be extended longer, so the conclusions from our modeling related to the later stage development may need to be modified.
3.3. Antiviral drugs on SARS‐CoV‐2 virus infection
When searching for a cure for COVID‐19 patients, an effective antiviral drug is highly anticipated, so we decided to model the effect of the antiviral drug on the corona virus infection. We started our base case with a peak of the AIR at 8 dpi, and AIR activity level of 0.3, as shown before. From Equations (3), the expression for is revised as follows:
| (5) |
Here is the native reproductive ratio; is the percentage of the target cells that are not depleted. The first two brackets show the effect of the antiviral drugs on the reproductive ratio R, which shows that the drug has an equivalent effect regardless of whether it is acting on k or p. Next, we tried to simulate the effect of an antiviral drug with 50% efficacy on k, namely, , taken for 15 days consecutively. Taking this drug for a longer time does not necessarily make it more beneficial in this particular scenario. As a comparison, the base scenario is also included with a native of 7.03, and AIR activity of 0.3 peaking at 8 dpi. The base scenario is shown as a blue line in Figure 6. When the drug is applied, the effective R is reduced to 3.52, according to the formula above, not considering the effect of target cell depletion.
Figure 6.
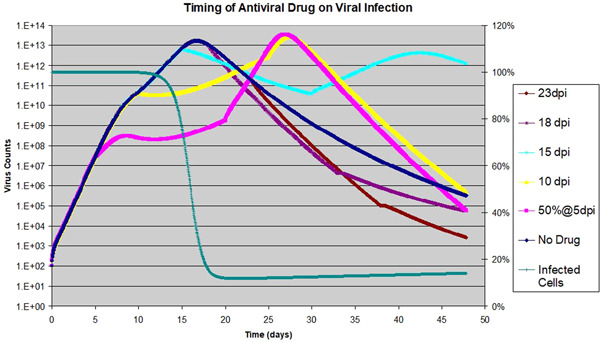
Effect of Antiviral drug on viral dynamics: The drug is assumed to be 50% effective on k, and applied to a host with of 7.03 for 15 days consecutively with various starting dates; viral counts to the left with exponential scale; target cell is shown for the scenario of the drug applied at 18 dpi, to the right with linear scale
Similar to the AIR effects shown in Figure 5, Figure 6 shows that additional drug‐induced antiviral activity has a pronounced effect on the duration of viral activity within the host for the three scenarios when the antiviral drug is started on 5 dpi, 10 dpi, or 15 dpi. During the 15 days when the antiviral drug is effective, the virus growth rate is reduced. After the drug is removed, the virus either resumes its growth or remains at a plateau. In all three scenarios, the duration of virus activity is extended substantially, which can lead to detrimental consequences for the patients. On the other hand, if the drug is started 18 or 23 dpi, after the peak of infected cells, the effect of the antiviral drug is to speed up the virus clearing, which is beneficial for the patient. In Figure 6, the depletion of target cells is also shown for the scenario of the drug started at 18 dpi. As we can see, the depletion is not complete (12% target cells remain), which explains why the decay is slow even with the additional drug activity.
The situation is very different if the antiviral drug efficacy is raised to 90%, namely, . When the drug is applied, the effective R becomes 0.7, which leads to virus clearance. We ran the same set of scenarios as above and the results are shown in Figure 7. The blue line again shows the base scenario with no drug applied. If the drug is applied early, as shown for the scenario with a start date of 5 dpi, the infection can be stopped completely before it makes any real progress. When the drug is started at 10 or 15 dpi, double peaks of viral count are observed. The reason is that when the drug is stopped, R jumps back to 7, so that virus resumes its rapid growth until the target cells are depleted, causing a second peak in virus count. Therefore if the drug is stopped before the virus is cleared out completely, the infection will resurge. This is similar to what we have seen in Figure 4 with the transient antiviral activity of strong AIR, except the peak‐trough‐peak curve is smoother there. When the drug is applied after the viral peak is reached, it has a small but positive effect of faster recovery, similar to the scenario shown in Figure 6. The level of target cell depletion is also shown for the scenario of the drug started at 15 dpi. At the first peak of viral load, less than 30% of the target cells are depleted by the infection. This is why a second exponential growth starts after the drug is removed. To avoid this kind of unwanted effect, the antiviral drug needs to be maintained until the virus is completely cleared. In the Appendix, we showed the relationship between the duration the drug needs to be administered, and the time the drug is started. The simple rule of thumb is that the later the drug is started, the longer it is required to be applied to ensure complete clearing of the virus.
Figure 7.
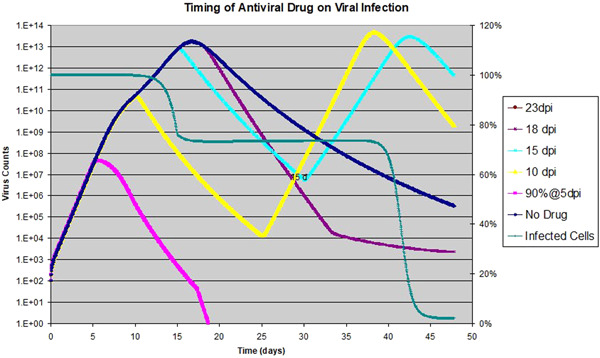
Effect of antiviral drug on viral dynamics: the drug is assumed to be 90% effective on k, and is applied for 15 days consecutively with various starting dates; viral counts to the left with exponential scale; target cell is for drug started on 15 dpi only, shown with linear scale to the right
It is interesting to note that ‐immunoglobulin has been widely used to treat COVID‐19 patients in China. In a way, injection of ‐immunoglobulin can be modeled similarly as antiviral drugs (assuming that it is able to deliver some antiviral function). It will be interesting to know if some researchers have compiled data to correlate the efficacy of this treatment with the timing of the injections. Our theory predicts that if the ‐immunoglobulin is used early on, it will most likely delay the depletion of target cells so the duration of the disease will be extended for the patients, hence with poor prognosis. On the other hand, if it is applied after the peak of infected cells, it should be helpful to some extent.
In summary, for an antiviral drug to be useful, the drug needs to be effective enough so that the effective reproductive ratio R falls below 1 (see Equation (5) for the factors affecting R). Under such a condition, it is desirable to apply it early on and must be maintained until the viral load is completely cleared (in the Appendix we provide an estimate for the duration of the regimen). When a drug cannot meet this criterion, applying it before the target cells are fully depleted is typically not beneficial to the patient, and likely will make things worse for the patients. This should have some significant implications for drug companies when they design the clinical trials. At this point, as we do not know much about the potential level of the AIR, , and the efficacy of the antiviral drug, it is difficult to identify a risk‐free way of applying the antiviral drug. A prudent approach is to measure the viral loads frequently post‐drug administration. If the viral load does not drop rapidly shortly after, it may indicate that the effective R is not below 1, and the drug should be stopped. If the drug is known to be effective but not effective enough to cause R to go below 1, it might still be useful to apply it after a large percentage of the target cells have been depleted. As a safety measure, it may be desirable to continue the regimen for a few more days after the viral load drops below the detection limit to ensure complete clearance.
3.4. Effect of drugs to suppress AIR temporarily
Currently, there is already a class of drugs called immunosuppressive drugs (drugs to suppress AIRs). A large body of research has been done on the effects of the drugs on different parts of immune response. 27 , 28 The goal of investigating immunosuppressive drugs is to explore their possible applications in COVID‐19 disease management.
Immunosuppressants such as corticosteroids have been applied to SARS and COVID‐19 patients, with positive results. 29 , 30 From the previous discussions, we propose a potential treatment plan by applying immunosuppressive drugs as soon as an infection is detected in the lungs, and remove the drug as soon as the target cells are fully depleted. This approach is simple and only requires the immunosuppressive drugs to be able to reduce the AIR activity to a level low enough not to interfere with the innate immunity. From the discussions around Figure 4, this approach should clear out the virus quickly if the AIR activity level is below 0.1. If the drug effect is not removed quickly, and the AIR does not rise after the drug is removed, the patients may not be able to completely clear the residue level of the virus. We projected that a short regimen of antiviral drugs 3 to 5 days after the peak of virus counts may help to completely clear the remaining low level of virus load. The purpose of the antiviral drug regimen is to mimic the effect of the AIR in patients with influenza infections.
If the drug effect can be removed immediately after the peak infection, so that the AIR level increases after the drug is removed, we then have a situation that the AIR peaks after the target cells are depleted. The discussions around Figure 5 established that with this scenario, the virus can always be cleared completely, regardless of the level of the AIR. With this approach, the novel coronavirus infections are essentially reduced to influenza‐like infections in adults, except with slower disease progression.
One possible concern with our proposed approach is that the immunosuppressive drugs may inevitably have some limited side effects on the innate immune response, in addition to the intended effect on the AIR. This is considered by Equations (4), which gives us the following (see Appendix):
| (6) |
From the above, it is clear that the effect on is to raise R and reduce . On the other hand, if the drug also has some effect on the infection of target cells and the production of virus particles by infected cells, due to its immune‐suppressing nature, the effect should be negative , which also raises R, and reduces . The effect of reducing is beneficial for the patients, as it reduces the duration of viral activity in the host. On the other hand, an increasing R tends to increase the maximum virus count at the peak, which may or may not have a significant effect on the patients, as the virus are quickly cleared out.
To address this possible concern, we did some simulations with the following: the immunosuppressive drug is assumed to have either a 50% or 90% effect on , the drug with 50% effect on is applied from 1 dpi up to 12 dpi, while the second drug is applied from 1 dpi up to 10 dpi. The choice to apply the drug from 1 dpi is merely to simplify our simulation, and may not be necessary, as our main goal is to suppress the AIR. The AIR peak day is assumed to be the same as the base scenario at 8 dpi, and the AIR activity level is reduced to 0.1. The same base scenario without drug is also shown as the blue line in Figure 8. With both scenarios, we observed a big reduction of the duration of viral activity. Not only the date of viral peak is moved from 16 to 11 dpi, but the decay from the peak is also much faster. This rapid decay is beneficial for the patients as well, and it's due to the complete depletion of the target cells. The overall virus replication curve with the immunosuppressive drug resembles closely the curve for adult influenza infections (shown in Figure 2) except with a longer time scale. When compared to the base scenario with AIR (the blue line in Figure 8), we find that the maximum viral load is increased by a factor of 3.6–4.7. However, if we compare it to the base scenario of innate response alone without AIR, the maximum viral load varies by less than 15%. In summary, we think that the benefit of shortening the disease duration outweighs the cost of increased viral load for a short period.
Figure 8.
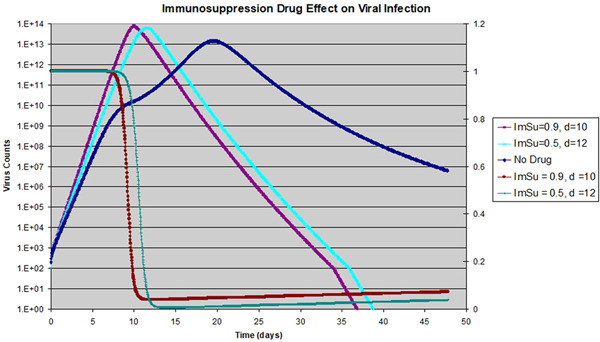
Effect of immunosuppressive drug on viral dynamics: The drug is assumed to be 50 or 90% effective so or 0.9; drug is applied from 1 dpi until 10 or 12 dpi (with the end day shown on legend); viral counts shown to the left with exponential scale; target cell is shown for 10 dpi for both 50% and 90% drugs, with linear scale to the right
We see multiple potential advantages of this novel approach. There are a number of well‐studied, FDA‐approved drug candidates to choose from. Animal models can help to define the range for the main parameters quickly. Finally, as long as the drug is applied for enough days so that the suppression of the AIR is beyond the peak of virus load, this approach always resulted in a quick clearance of the virus. Removing the drug in time should enable the AIR to be fully stimulated, so the patient most likely can have antibody‐based immunity for the virus in the near future, as in the case of patients recovered from influenza infections. In our discussion so far, we have assumed that the drug effect is immediate, namely, the drug effect shows up immediately after its application and the effect goes away immediately after the drug is removed. This is clearly not realistic, so one of the key considerations when selecting the right immunosuppressive drugs is its pharmacokinetics; a drug with short elimination and absorption half time is more desirable, considering the time‐sensitive nature of the effect. In a recent study by Wang et al, 29 the authors reviewed the effect of a low‐dose and short‐term application of corticosteroid to COVID‐19 patients at an early stage, and found some clear benefits of for the patients as compared to the patients without the treatment, including the shortening the disease course. This is consistent with our findings. In their study, the drug corticosteroid was applied for 11 days or more, which according to our theory, might be a little too long for optimal results, considering its half time of 12 to 36 days.
4. DISCUSSIONS AND CONCLUSIONS
Previous studies have investigated the RNA expression of ACE2 in 72 human tissues. 9 Two more recent studies have shown that the percentage of epithelial cells with ACE2 receptors in bronchial is much lower than in turbinate and lung tissues (0.2% vs 2–3%). 10 , 11 Considering the difference in surface area between the lungs and the nasal cavity, 31 , 32 , 33 we arrived at a rough estimate of as the ratio of target cells in these two organs. A quick simulation using the much lower suggests that the peak of infected cells is changed from 12 to 8 dpi in the nose with the innate immune response alone. If infection is localized at the nasal cavity only, it is then much more likely for the peak of the AIR to come after the peak of infected cells. In this case, most likely the infection will resolve itself just like influenza infections, except the disease may take a few more days. This may explain why a lot of people do not develop severe symptoms or remain asymptomatic if the infection is localized in the nasal area without reaching and propagating in the lungs. If our analysis can be verified clinically, methods and techniques (for example antiviral nasal sprays) to enhance trachea/bronchial tubes as a barrier to stop the spread of the virus from upper respiratory tracks to the lungs can be effective in reducing the percentage of patients with pneumonia.
Another important parameter we have not discussed is the cell regeneration rate, , of the epithelial cells. In Table 3, we have listed it as 2.9 × 10−4, which corresponds to 10−3 day−1 for d. This is based on a study by Rawlins and Hogan 34 on the half‐life of epithelial cells in the mouse lung. This parameter, if it is higher, will make the depletion of the target cells more difficult. This is because as the target cells are depleted, new target cells are generated. The higher the regeneration rate, the more new target cells are available for viruses to infect and stay alive. Our simulation results remain essentially the same if this parameter is lower or increased by no more than a factor of 20. Beyond that, depletion of the target cells becomes substantially more difficult to achieve. Thereby, clearing the virus also becomes harder to accomplish. Could this be the reason for the observed higher severity rate among older patients? We reason that this is not likely, as the cell regeneration rate should be higher for younger patients, while older people are known to have more difficulty repairing lung damage. 35
In this article, we have applied the target cell‐limited model to study the novel corona virus infections mostly in human lungs. Through comparison between SARS‐CoV‐2 and influenza viruses, and by analyzing the interactions among various players (target cells, innate and AIRs, and different types of drugs), we propose that the main reason for the higher probability of severe symptoms, prolonged hospital stays, and even fatal outcomes for COVID‐19 patients 2 , 3 may be that the peak of infected cells and virus counts often comes after the peak of the AIR in these patients. This mismatch of timing and the resulted interference with innate immunity by adaptive immunity, leads to incomplete depletion of the target cells, thus providing uninfected target cells for continued infection. Prolonged infection can induce overactive immune responses, secondary complications, and sometimes fatal outcomes.
We also discussed the prospects of antiviral drugs and immunosuppressive drugs in combating COVID‐19 infections. Our proposal to apply immunosuppressive drugs at an early stage to reduce the interference from adaptive immunity so that the innate immunity and the depletion of target cells can together achieve fast elimination of the virus seems to be unconventional. However, it is particularly interesting to note that, as we were working on our mathematical modeling, the recent study by Wang et al 29 demonstrated that an early stage low‐dose and short‐term application of corticosteroid treatment in patients with severe COVID‐19 pneumonia was beneficial and essentially validated our findings. We envision that new insights from our analysis and modeling will encourage more work in this direction.
CONFLICT OF INTERESTS
The authors declare that there are no conflict of interests.
ACKNOWLEDGMENTS
The authors would like to express their appreciation for Professor Yong‐Zhong Qian for some productive discussions. Weiming Yuan is supported by the NIH grant (R21 AI 149365) and partially supported by NIH grant P30CA014089 to the University of Southern California Norris Comprehensive Cancer Center from the National Cancer Center.
From Figure 1, two distinctive regions are easily identifiable: an exponential growth for viral load/infected cells, followed by an exponential decay after reaching the peak. To figure out what determines the time it takes for infected cells to reach the peak, we make an approximation of (for most part of the exponential growth, the target cells depletion is minimal) in Equations (1) and get the following:
| (A1) |
Let and , we get the following:
| (A2) |
Solving the above equation, we find the following:
When , we have
The time it takes for the infected cells to reach the peak, , is as follows, assuming complete depletion of the target cells:
| (A3) |
If the exponential growth is interrupted by an antiviral drug, the should be replaced with . Similar to the result (A3), we can derive the following for clearing/decay time:
| (A4) |
Notice that here we used I max and I min, because to clear virus completely we need to get to a level lower than the initial level of infected cells. Immediately we can see that when , we have the lowest , which means the fastest clearing of virus. If we assume that I min = 1, and , the above result can be further simplified:
Combining with (A3) we can calculate the ratio of decay time vs rise time:
If we assume that the infection is inoculated with 1 infected cell, then the above can be further simplified as
| (A5) |
This above ratio is important for estimating how long the antiviral drug needs to be taken to clear out the virus in the host. Notice that we made the assumption of ; if the opposite is true, then in formula (A5) we simply need to exchange the positions of c with .
Du SQ, Yuan W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID‐19 and implications for viral pathogenesis. J Med Virol. 2020;92:1615–1628. 10.1002/jmv.25866
Contributor Information
Sean Quan Du, Email: seand168@gmail.com.
Weiming Yuan, Email: weiming.yuan@usc.edu.
REFERENCES
- 1. Huang C, Zhang L, Fan G, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan. China Lancet. 2020;395(10223):497‐506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Wang D, Hu B, Hu C, et al. Clinical Characteristics of 138 Hospitalized Patients With 2019 Novel Coronavirus‐Infected Pneumonia in Wuhan, China. JAMA. 2020;323(11):1061‐1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Chen N, Zhou M, Dong X, et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: a descriptive study. Lancet. 2020;395(10223):507‐513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Zhou F, Yu T, Du R, et al. Clinical course and risk factors for mortality of adult inpatients with COVID‐19 in Wuhan, China: a retrospective cohort study. Lancet. 2020;395(10229):1054‐1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Beauchemin CA, Handel A. A review of mathematical models of influenza A infections within a host or cell culture: lessons learned and challenges ahead. BMC Public Health. 2011;1(11 Suppl):S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. van Riel D, Munster VJ, de Wit E, et al. H5N1 virus attachment to lower respiratory tract. Science. 2006;312(5772):399. [DOI] [PubMed] [Google Scholar]
- 7. Nicholls JM, Chan MC, Chan WY, et al. Tropism of avian influenza A (H5N1) in the upper and lower respiratory tract. Nat Med. 2007;13(2):147‐149. [DOI] [PubMed] [Google Scholar]
- 8. Xu X, Chen P, Wang J, et al. Evolution of the novel coronavirus from the ongoing Wuhan outbreak and modeling of its spike protein for risk of human transmission. Sci China Life Sci. 2020;63(3):457‐460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Hamming I, Timens W, Bulthuis ML, et al. Tissue distribution of ACE2 protein, the functional receptor for SARS coronavirus. A first step in understanding SARS pathogenesis. J Pathol. 2004;203(2):631‐637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Zhao YZZ, Wang Y, Zhou Y, Ma Y, Zuo W. Single‐cell RNA expression profiling of ACE2, the putative receptor of Wuhan 2019‐nCov. BioRxiv. 2020.
- 11. Wu CZ, Chen S, Zheng Y. Single‐cell RNA expression profiling of ACE2, the putative receptor of Wuhan 2019‐nCoV, in the nasal tissue. medRxiv. 2020.
- 12. Potter CW. Influenza. In: Zuckerman AJB, Pattison JE, Griffiths JR, Schoub PDBD, eds. Principles and Practice of Clinical Virology. 5th ed. John Wiley & Sons, Ltd; 2004:271‐297. [Google Scholar]
- 13. Tamura S, Kurata T. Defense mechanisms against influenza virus infection in the respiratory tract mucosa. Jpn J Infect Dis. 2004;57(6):236‐247. [PubMed] [Google Scholar]
- 14. Backer JA, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019‐nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Euro Surveill. 2020;25(5). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Li Q, Guan X, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus‐infected pneumonia. N Engl J Med. 2020;382(13):1199‐1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Zitzmann C, Kaderali L. Mathematical analysis of viral replication dynamics and antiviral treatment strategies: from basic models to age‐based multi‐scale modeling. Front Microbiol. 2018;9:1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Nowak MA, Bangham CR. Population dynamics of immune responses to persistent viruses. Science. 1996;272(5258):74‐79. [DOI] [PubMed] [Google Scholar]
- 18. Nowak MA, Bonhoeffer S, Hill AM, Boehme R, Thomas HC, McDade H. Viral dynamics in hepatitis B virus infection. Proc Natl Acad Sci USA. 1996;93(9):4398‐4402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bonhoeffer S, May RM, Shaw GM, Nowak MA. Virus dynamics and drug therapy. Proc Natl Acad Sci USA. 1997;94(13):6971‐6976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Wodarz D, Nowak MA. Mathematical models of HIV pathogenesis and treatment. Bioessays. 2002;24(12):1178‐1187. [DOI] [PubMed] [Google Scholar]
- 21. Nowak MAMR. Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford University Press; 2001. [Google Scholar]
- 22. Doherty PC, Turner SJ, Webby RG, Thomas PG. Influenza and the challenge for immunology. Nat Immunol. 2006;7(5):449‐455. [DOI] [PubMed] [Google Scholar]
- 23. Thomas PG, Keating R, Hulse‐Post DJ, Doherty PC. Cell‐mediated protection in influenza infection. Emerg. Infect. Dis. 2006;12(1):48‐54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Maines TR, Szretter KJ, Perrone L, et al. Pathogenesis of emerging Avian influenza viruses in mammals and the host innate immune response. Immunol Rev. 2008;225:68‐84. [DOI] [PubMed] [Google Scholar]
- 25. Miao H, Hollenbaugh JA, Zand MS, et al. Quantifying the early immune response and adaptive immune response kinetics in mice infected with influenza a virus. J Virol. 2010;84(13):6687‐6698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Neumann AU, Lam NP, Dahari H, et al. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon‐alpha therapy. Science. 1998;282(5386):103‐107. [DOI] [PubMed] [Google Scholar]
- 27. Zaza G, Leventhal J, Signorini L, Gambaro G, Cravedi P. Effects of antirejection drugs on innate immune cells after Kidney transplantation. Front Immunol. 2019;10:2978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Janeway CAJTP, Walport M, et al. Immunobiology: The Immune System in Health and Disease. 5th ed. New York: Garland Science; 2001. [Google Scholar]
- 29. Wang YJW, He Q, Wang C, et al. Early, low‐dose and short‐term application of corticosteroid treatment in patients with severe COVID‐10 pneumonia: single‐center experience from Wuhan, China. medRxiv. 2020.
- 30. Zhao Z, Zhang F, Xu M, et al. Description and clinical treatment of an early outbreak of severe acute respiratory syndrome (SARS) in Guangzhou, PR China. J Med Microbiol. 2003;52(Pt 8):715‐720. [DOI] [PubMed] [Google Scholar]
- 31. Levy M, Koeppen B, Stanton B. Berne & Levy Physiology. Philadelphia: Mosby/Elsevier; 2008. [Google Scholar]
- 32. Pawlina W. Histology a Text & Atlas. 7th ed. Philadelphia: Mosby/Elsevier; 2015. [Google Scholar]
- 33. Gizurarson S. Anatomical and histological factors affecting intranasal drug and vaccine delivery. Curr Drug Deliv. 2012;9(6):566‐582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Rawlins EL, Hogan BL. Ciliated epithelial cell lifespan in the mouse trachea and lung. Am J Physiol Lung Cell Mol Physiol. 2008;295(1):L231‐234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Navarro S, Driscoll B. Regeneration of the aging lung: a mini‐review. Gerontology. 2017;63(3):270‐280. [DOI] [PubMed] [Google Scholar]


