Fast and robust ancestry prediction using principal component analysis

Abstract

Motivation

Population stratification (PS) is a major confounder in genome-wide association studies (GWAS) and can lead to false-positive associations. To adjust for PS, principal component analysis (PCA)-based ancestry prediction has been widely used. Simple projection (SP) based on principal component loadings and the recently developed data augmentation, decomposition and Procrustes (ADP) transformation, such as LASER and TRACE, are popular methods for predicting PC scores. However, the predicted PC scores from SP can be biased toward NULL. On the other hand, ADP has a high computation cost because it requires running PCA separately for each study sample on the augmented dataset.

Results

We develop and propose two alternative approaches: bias-adjusted projection (AP) and online ADP (OADP). Using random matrix theory, AP asymptotically estimates and adjusts for the bias of SP. OADP uses a computationally efficient online singular value decomposition algorithm, which can greatly reduce the computation cost of ADP. We carried out extensive simulation studies to show that these alternative approaches are unbiased and the computation speed can be 16–16 000 times faster than ADP. We applied our approaches to the UK Biobank data of 488 366 study samples with 2492 samples from the 1000 Genomes data as the reference. AP and OADP required 0.82 and 21 CPU hours, respectively, while the projected computation time of ADP was 1628 CPU hours. Furthermore, when inferring sub-European ancestry, SP clearly showed bias, unlike the proposed approaches.

Availability and implementation

The OADP and AP methods, as well as SP and ADP, have been implemented in the open-source Python software FRAPOSA, available at github.com/daviddaiweizhang/fraposa.

Contact

leeshawn@umich.edu

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Population stratification (PS) is a major confounder for genetic association analysis (Price et al., 2006), and the adjustment of PS requires the estimation of the ancestry structure among the study samples. Principal component analysis (PCA) is a multivariate statistical method which finds the direction of the maximal variability (Jolliffe, 2002). By aggregating information across all the genetic markers, PCA has been effective for PS adjustment (Reich et al., 2008). To adjust for PS, PCA can be applied to study data to calculate the principal component (PC) scores, which are regarded as variables of ancestry and can be used as covariates to adjust for. An alternative approach is predicting the PC scores of the study samples by using reference genotyped samples with detailed ancestry information. This prediction-based approach allows not only adjustment for PS but also inference of the ancestry memberships of the study samples. In addition, by using a common reference panel, predicted PC scores across different studies can be directly comparable, allowing to integrate and match the different study samples (Wang et al., 2015). For example, using the predicted PC scores, Zhan et al. (2013) identified the ancestry-matched control samples from the publicly available NHLBI ESP sequencing data, which helped to identify rare variant associations.

The standard approach of predicting PC scores is to project the study samples onto the maximal variability directions, called PC loadings. In this article, we call this approach simple projection (SP). However, when the number of features greatly exceeds the size of the reference samples, which is common for data in genome-wide association studies (GWAS), the PC scores predicted by SP are known to be systematically biased toward NULL (Dey and Lee, 2019). This shrinkage bias can cause inaccurate prediction of the ancestry of each study sample and inappropriate adjustment of PS.

One way of addressing this shrinkage bias is presented by Wang et al. (2014, 2015). Their solution is to combine one study sample with all the reference samples and find the PC scores of this augmented dataset. The PC scores of the study individuals are then mapped to the reference sample PC space by a Procrustes transformation. We call this method ‘augmentation, decomposition and Procrustes transformation’ (ADP). This method has been shown to be effective in eliminating the shrinkage bias of study PC scores. However, since ADP needs to run PCA separately for each of the augmented datasets, it is computationally expensive, especially with large reference samples. For example, the estimated computation time for predicting the ancestry of the UK Biobank data of 488 366 samples with 2492 reference samples is 1628 CPU hours. Since the computation time is cubic to the reference sample size, the computation time will rapidly increase for larger reference samples.

To address the limitations of SP and ADP, we develop and propose two alternative methods for ancestry prediction and apply them to the UK Biobank data. The first approach removes the bias in SP by estimating the asymptotic bias factor, which is calculated based on random matrix theory (Dey and Lee, 2019). The second approach improves the computational efficiency of ADP by using an online singular value decomposition (SVD) algorithm (Halko et al., 2011), which obtains the SVD results of the augmented matrix by updating the SVD results of the reference matrix, since the latter only differs slightly from the former and many of the overlapping calculations can be avoided. We call the first approach ‘bias-adjusted projection’ (AP) and the second approach ‘online augmentation, decomposition and Procrustes transformation’ (OADP).

In this article, we evaluate the accuracy and computational efficiency of AP and OADP as compared to SP and ADP through extensive simulation studies and the analysis of the UK Biobank data. In the simulation studies, we show that AP and OADP have both achieved accuracy similar to or higher than that of ADP and computational efficiency close to that of SP. The UK Biobank data analysis shows that the proposed approaches are 80–2000 times faster than ADP. In addition, we have developed the open-source software FRAPOSA in Python that implements AP, OADP, SP and ADP.

2 Materials and methods

2.1 Model and PCA on the reference data

For PC score prediction, we have the reference samples and the study samples, which can be represented by two matrices. Let $\underset{¯}{\mathbf{X}}$ be a p × n matrix of reference genotypes and $\underset{¯}{\mathbf{Y}}$ be a p × m matrix of study genotypes, where p is the number of genetic markers, n is the number of reference samples and m is the number of study samples. In our study, we only consider genotypes composed of biallelic single-nucleotide polymorphisms (SNPs), so each entry of $\underset{¯}{\mathbf{X}}$ and $\underset{¯}{\mathbf{Y}}$ is a minor allele count of 0, 1 or 2. For PCA, the reference data matrix is commonly standardized by subtracting the marker mean from each marker genotype and then dividing it by the marker standard deviation. The sample matrix $\underset{¯}{\mathbf{Y}}$ also can be standardized using marker means and standard deviations calculated from the reference samples. Suppose $\mathbf{X}$ and $\mathbf{Y}$ are the standardized reference and study data matrices, respectively. The sample covariance matrix is $\mathbf{S}=\mathbf{X}{\mathbf{X}}^{\mathrm{\top }}/n$, and then by eigen decomposition,

$$n\mathbf{S}=\mathbf{X}{\mathbf{X}}^{\mathrm{\top }}=\mathbf{U}{\mathbf{D}}^2{\mathbf{U}}^{\mathrm{\top }}$$

where ${\mathbf{D}}^2=\text{diag}(d_1^2,\dots ,d_n^2)$ is an n × n diagonal matrix of ordered sample eigenvalues and $\mathbf{U}=({\mathbf{u}}_1,\dots ,{\mathbf{u}}_n)$ is a p × n corresponding eigenvector matrix. The $j\text{th}$ PC score vector is ${\mathbf{v}}_j={\mathbf{X}}^{\mathrm{\top }}{\mathbf{u}}_j/d_j$, where ${\mathbf{u}}_j$ is the $j\text{th}$ sample eigenvector, which is also called the $j\text{th}$ PC loading. Alternatively, PC loadings and scores can be calculated using SVD, which is computationally more efficient when p is larger than n. By SVD

$$\mathbf{X}=\mathbf{U}\mathbf{D}{\mathbf{V}}^{\mathrm{\top }},$$ (1)

where $\mathbf{V}=({\mathbf{v}}_1,\dots ,{\mathbf{v}}_n)$ is the right singular-vector matrix and ${\mathbf{v}}_j$ is the $j\text{th}$ PC scores. From (1),

$${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}=\mathbf{V}{\mathbf{D}}^2{\mathbf{V}}^{\mathrm{\top }}.$$

After calculating ${\mathbf{v}}_j$ and d_j from the eigen decomposition of ${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}$, the $j\text{th}$ loading, ${\mathbf{u}}_j$, can be calculated as ${\mathbf{u}}_j=\mathbf{X}{\mathbf{v}}_j/d_j$.

2.2 Predicting the PC scores of the study samples

Here, we describe the existing approaches, SP and ADP, and the proposed approaches, AP and OADP, and their computation complexity (CC) to predict the top K PC scores. For practical purposes, we assume that $K\ll n\ll p$. Table 1 summarizes the CC of the four methods.

Table 1.

CC of SP, AP, ADP and OADP

Method	Reference complexity	Study complexity
SP	$\mathcal{O}[n^{2}p]$	$\mathcal{O}[\mathit{mKp}]$
AP	$\mathcal{O}[n^{2}p]$	$\mathcal{O}[\mathit{mKp}]$
ADP	$\mathcal{O}[n^{2}p]$	$\mathcal{O}[m(np+n^3)]$
OADP	$\mathcal{O}[n^{2}p]$	$\mathcal{O}[m(K″p+K{\prime }^{2}n)]$

Simple projection (SP) SP directly uses the PC loadings of the reference sample PCA to predict the PC scores of the study samples. The SP algorithm of predicting the top K PC scores and the CC of each step is as follows:

1. Perform the reference sample PCA: ${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}=\mathbf{V}{\mathbf{D}}^2{\mathbf{V}}^{\mathrm{\top }}$. (CC: $\mathcal{O}[p{n}^2]$.)

2. Compute the PC loading matrix for the top K PCs: ${\mathbf{U}}_K=\mathbf{X}{\mathbf{V}}_K{\mathbf{D}}_K^{-1}$. Here, ${\mathbf{V}}_K$ and ${\mathbf{D}}_K$ are the first K columns of $\mathbf{V}$ and the upper-left K × K sub-matrix of $\mathbf{D}$, respectively. (CC: $\mathcal{O}[\mathit{npK}]$.)

3. Compute the predicted study PC scores for the top K PCs: ${\mathbf{W}}_K={\mathbf{Y}}^{\mathrm{\top }}{\mathbf{U}}_K$. (CC: $\mathcal{O}[\mathit{mpK}]$.)

The total CC is $\mathcal{O}[p{n}^2+\mathit{mpK}]$ (assuming $K\ll n\ll p$), which is the lowest among all the methods discussed in this article. However, a major weakness of SP is the loss of accuracy when the number of makers, p, greatly exceeds the reference sample size, n, a situation that is common in GWAS. Lee et al. (2010) have shown that when n < p, the predicted PC scores can be shrunken toward NULL. This shrinkage bias limits the accuracy of SP for high-dimensional data.

Bias-adjusted projection (AP) AP calculates the asymptotic shrinkage bias of SP and adjusts the predicted PC scores using the estimated bias. The estimation of the bias requires all the eigenvalues of the reference data matrix. The details for estimating the shrinkage factor are described in Dey and Lee (2019). Suppose the population covariance matrix $\mathbf{\Sigma }=\mathrm{E}(\mathbf{X}{\mathbf{X}}^{\mathrm{\top }}/n)$ has (population) eigenvalues ${\lambda }_1^2,\dots ,{\lambda }_{\mathrm{p}}^2$, and the sample covariance matrix $\mathbf{S}=\mathbf{X}{\mathbf{X}}^{\mathrm{\top }}/n$ has nonzero (sample) eigenvalues $d_1^2,\dots ,d_n^2$. First, the population eigenvalues are assumed to follow a generalized spiked population (GSP) model, where only a few eigenvalues are large (which are called distant spikes) compared to the rest of them. The rest of the eigenvalues are relatively small but not necessarily all equal to each other. Then for the top few PCs that correspond to the distant spikes, the ratio of the variance of the reference PC scores and that of the study PC scores predicted by SP converges in probability to the ratio of the corresponding population eigenvalues (distant spikes) and the sample eigenvalues as $p\to \infty ,\hspace{0.17em}n\to \infty ,\hspace{0.17em}p/n\to \gamma <\infty$. Formally, suppose $v_{kj}={\mathbf{x}}_j^{\mathrm{\top }}{\mathbf{u}}_k$ is the kth PC score of the jth subject in the standardized reference data $\mathbf{X}$, and $w_{kl}={\mathbf{y}}_l^{\mathrm{\top }}{\mathbf{u}}_k$ is the kth PC score of the lth subject in the standardized study data $\mathbf{Y}$. Then the shrinkage factor along the kth PC score is defined as ${\tau }_k=\sqrt{\text{Var}(w_{kl})/\text{Var}(v_{kj})}$, and when λ_k is a distant spike with multiplicity one, $|{\tau }_k-d_k/{\lambda }_k|\stackrel{p}{\to }0$. Dey and Lee (2019) provides two consistent estimators of λ_k for the distant spikes (i.e. ${\hat{\lambda }}_k$). The consistent estimator of τ_k can be obtained as ${\hat{\tau }}_k=d_k/{\hat{\lambda }}_k$. Among the two estimators of λ_k, we used the method called d-estimation, which is faster (CC: $\mathcal{O}[Kn]$) than the other l-estimation approach (CC: $\mathcal{O}[Kp]$).

The method for approximating the shrinkage factors has been implemented in the hdpca package in the R language (Dey and Lee, 2016). The algorithm of AP is summarized below.

1. Perform the reference sample PCA: ${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}=\mathbf{V}{\mathbf{D}}^2{\mathbf{V}}^{\mathrm{\top }}$. (CC: $\mathcal{O}[p{n}^2]$.)

2. Estimate the shrinkage factors ${\hat{\tau }}_1,\dots ,{\hat{\tau }}_K$ for the top K PCs, where ${\hat{\tau }}_k=d_k/{\hat{\lambda }}_k$ as defined above. (CC: $\mathcal{O}[Kn]$.)

3. Compute the PC loading matrix for the top K PCs with the adjustment for the shrinkage bias: ${\mathbf{U}}_K=\mathbf{X}{\mathbf{V}}_K{\mathbf{D}}_K^{-1}{\mathbf{F}}_K^{-1}$, where ${\mathbf{F}}_K=\text{diag}(f_1,\dots ,f_K)$. (CC: $\mathcal{O}[\mathit{pnK}]$.)

4. Compute the predicted study PC scores for the top K PCs: ${\mathbf{W}}_K={\mathbf{Y}}^{\mathrm{\top }}{\mathbf{U}}_K$. (CC: $\mathcal{O}[\mathit{mpK}]$.)

The total CC is $\mathcal{O}[p{n}^2+\mathit{mpK}]$ (assuming $K\ll n\ll p$), which is the same as that of SP. This is because shrinkage factor estimation is asymptotic based and can be computed rapidly with the sample eigenvalues. In addition, the shrinkage factor only needs to be calculated once for all the study samples.

Augmentation, decomposition, and Procrustes transformation (ADP) ADP, such as LASER and TRACE (Wang et al., 2014, 2015), predicts the study PC scores by using a different approach compared to SP and AP. ADP first augments the (standardized) reference matrix by appending a column vector of a (standardized) study sample. Then SVD is applied to the $p\times (n+1)$ augmented matrix $\tilde{\mathbf{X}}$. The resulted $(n+1)\times (n+1)$ right singular-vector matrix $\tilde{\mathbf{V}}$ can be divided into two parts: the first n rows ${\tilde{\mathbf{V}}}_{\text{ref}}={({\tilde{\mathbf{v}}}_{\text{ref},1}^{\mathrm{\top }},\dots ,{\tilde{\mathbf{v}}}_{\text{ref},n}^{\mathrm{\top }})}^{\mathrm{\top }}$, which correspond to the reference samples, and the last row ${\tilde{\mathbf{v}}}_{\text{stu}}$, which corresponds to the one study sample. Since ${\tilde{\mathbf{V}}}_{\text{ref}}$ is different (though only slightly when n is large) from $\mathbf{V}$, the n × n right singular-vector matrix of the reference data, ADP uses the Procrustes transformation to map ${\tilde{\mathbf{V}}}_{\text{ref}}$ to $\mathbf{V}$ in the original reference PC space. That is, it finds a linear transformation of the form

$$f({\tilde{\mathbf{v}}}_{\text{ref},i,K\prime })=\rho {\tilde{\mathbf{v}}}_{\text{ref},i,K\prime }\mathbf{A}+\mathbf{c}$$

that minimizes the mean-squared difference between ${\mathbf{V}}_K$ and the transformed ${(f{({\tilde{\mathbf{v}}}_{\text{ref},1,K\prime })}^{\mathrm{\top }},\dots ,f{({\tilde{\mathbf{v}}}_{\text{ref},n,K\prime })}^{\mathrm{\top }})}^{\mathrm{\top }}$, where ${\mathbf{V}}_K$ is the first K columns of $\mathbf{V}$, ${\tilde{\mathbf{v}}}_{\text{ref},i,K\prime }$ is the first $K\prime$ columns of ${\tilde{\mathbf{v}}}_{\text{ref},i}$, and $K\le K\prime$. Here, ρ is a non-negative scaler, $\mathbf{A}$ is an $K\prime \times K$ orthogonal matrix, and $\mathbf{c}$ is an $1\times K$ row vector. We then apply this transformation to ${\tilde{\mathbf{v}}}_{\text{stu},K\prime }$, the first $K\prime$ columns of ${\tilde{\mathbf{v}}}_{\text{stu}}$, to obtain the predicted PC score, $f({\tilde{\mathbf{v}}}_{\text{stu},K\prime })$. The algorithm is summarized as follows.

1. Perform the reference sample PCA. ${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}$ is obtained in this process. (CC: $\mathcal{O}[p{n}^2]$.)

2. For a study sample $\mathbf{y}$, obtain ${\tilde{\mathbf{X}}}^{\mathrm{\top }}\tilde{\mathbf{X}}$ by computing ${\mathbf{X}}^{\mathrm{\top }}\mathbf{y},\hspace{0.17em}{({\mathbf{X}}^{\mathrm{\top }}\mathbf{y})}^{\mathrm{\top }}$, and ${\mathbf{y}}^{\mathrm{\top }}\mathbf{y}$ appending them to the right edge, bottom edge and bottom-right corner of ${\mathbf{X}}^{\mathrm{\top }}\mathbf{X}$, respectively. (CC: $\mathcal{O}[pn]$.)

3. Apply eigen decomposition on ${\tilde{\mathbf{X}}}^{\mathrm{\top }}\tilde{\mathbf{X}}$ to get ${\tilde{\mathbf{X}}}^{\mathrm{\top }}\tilde{\mathbf{X}}=\tilde{\mathbf{V}}{\tilde{\mathbf{D}}}^2{\tilde{\mathbf{V}}}^{\mathrm{\top }}$. (CC: $\mathcal{O}[n^3]$.)

4. Find the Procrustes transformation f from ${\tilde{\mathbf{V}}}_{\text{ref},K\prime }$, the first n rows and first $K\prime$ columns of $\tilde{\mathbf{V}}$, to ${\mathbf{V}}_K$, the first K columns of $\mathbf{V}$. Note that $K\prime \ge K$. (CC: $\mathcal{O}[nK{\prime }^2]$)

5. Apply f to ${\tilde{\mathbf{v}}}_{\text{stu},K\prime }$, the last row and first $K\prime$ columns of $\tilde{\mathbf{V}}$, to obtain the top K PC scores of the current study sample. (CC: $\mathcal{O}[KK\prime ]$)

6. Go to Step 2 for the next study sample unless all the study samples have been analyzed.

The total CC is $\mathcal{O}[p{n}^2+m(np+n^3)]$ given that $K\prime \ll n\ll p$. In our simulation studies and UK Biobank data analysis, setting K = 4 and $K\prime =8$ was sufficient for separating the ancestry groups.

ADP is a non-parametric approach that does not require any assumption on the distribution of the eigenvalues and therefore can be more robust than AP. It does not suffer the shrinkage bias. A major disadvantage of ADP, however, is its high computation cost. In particular, as the reference size increases, the computation cost for a study sample increases cubicly.

Online augmentation, decomposition, and Procrustes transformation (OADP) Since the augmented data matrix $\tilde{\mathbf{X}}$ differs in only one column from the reference matrix $\mathbf{X}$, the computational process for the SVD of $\tilde{\mathbf{X}}$ is numerically close to that for the SVD of $\mathbf{X}$. If we avoid the repeated computation and obtain the SVD of $\tilde{\mathbf{X}}$ by updating the SVD of $\mathbf{X}$, the computation cost can be greatly reduced. One of such ‘online’ algorithms for SVD has been proposed for imaging processing (Brand, 2002). This algorithm calculates SVD in an incremental manner and has the ability to rapidly update the top few singular values and vectors. Here, we propose to use this online SVD algorithm to replace the standard SVD algorithm for ADP and call it OADP. The algorithm for this method is as follows:

1. Perform the reference sample PCA. (CC: $\mathcal{O}[p{n}^2]$.)

2. Calculate the top $K″$ PC loadings: ${\mathbf{U}}_{K″}=\mathbf{X}{\mathbf{V}}_{K″}{\mathbf{D}}_{K″}^{-1}$. (CC: $\mathcal{O}[K″np]$.)

3. Calculate

   $$b=U_{K″}^{\mathrm{\top }}y\hspace{1em}\text{and}\hspace{1em}g=y^{\mathrm{\top }}h,$$

   where $\mathbf{h}$ is the normalized $\mathbf{y}-{\mathbf{U}}_{K″}\mathbf{b}$. (CC: $\mathcal{O}[K″p]$.)
4. Calculate ${\mathbf{Q}}^{\mathrm{\top }}\mathbf{Q}$, where

   $$\begin{array}{l}Q=\left[\begin{array}{cc}{D}_{K″}& b\\ 0& g\end{array}\right].\end{array}$$

   $(\text{CC}:\mathcal{O}[K″{ }^3].)$

5. Apply eigen decomposition to ${\mathbf{Q}}^{\mathrm{\top }}\mathbf{Q}$ get ${\mathbf{Q}}^{\mathrm{\top }}\mathbf{Q}=\ddot{V}{\ddot{D}}^2{\ddot{V}}^{\mathrm{\top }}$. (CC: $\mathcal{O}[K″3]$.)

6. Calculate

   $$\begin{array}{l}\tilde{V}=\left[\begin{array}{cc}{V}_{K″}& 0\\ 0& 1\end{array}\right]\ddot{V}.\end{array}$$

   $(\text{CC}:\hspace{0.17em}\mathcal{O}[nK″{ }^2].)$

7. Find the Procrustes transformation f from ${\tilde{\mathbf{V}}}_{\text{ref},K\prime }$, the first n rows and first $K\prime$ columns of $\tilde{\mathbf{V}}$, to ${\mathbf{V}}_K$, the first K columns of $\mathbf{V}$. Note that $K″\ge K\prime \ge K$. (CC: $\mathcal{O}[nK{\prime }^2]$)

8. Apply f to ${\tilde{\mathbf{v}}}_{\text{stu},K\prime }$, the last row and first $K\prime$ columns of $\tilde{\mathbf{V}}$, to obtain the top K PC scores of the current study sample. (CC: $\mathcal{O}[KK\prime ]$)

9. Go to step 3 for the next study sample unless all the study samples have been analyzed.

The total CC is $\mathcal{O}[n^{2}p+m(K″p+K{\prime }^{2}n)]$ provided $K″\ll n\ll p$. In our simulation studies and UK Biobank data analysis, setting K = 4, $K\prime =8$, and $K″=16$ was sufficient for the online SVD algorithm to approximate regular SVD well and separating the ancestry groups. The CC of OADP for analyzing the study individuals increases linearly with respect to the reference sample size, which is much more efficient than ADP’s cubicly increasing rate. The closeness between the results given by OADP and ADP is empirically shown in Section 3.

2.3 Simulation studies

We simulated the genotype data using a coalescence-based grid simulation approach with population migration by Mathieson and McVean (2012). In this approach, we simulated four different population groups in a 2 × 2 grid. In each population, we generated $(n+m)/2$ haploid genotypes with 100 000 biallelic genetic markers. Then we combined every two of the haploid genotypes to form $(n+m)/4$ diploid genotypes in each population. A large migration rate (M = 100) was used to evaluate the performance of the proposed and existing methods in fine-scale population differentiation. Among the $(n+m)$ generated samples, we randomly selected reference and study samples. The reference sample size n ranged from 1000 to 3000, and the study sample size m was fixed to 200. The proportion of variants with minor allele frequency <0.05, 0.005 and 0.0005 was 0.66, 0.37 and 0.12, respectively.

After the individual genotypes were simulated, we applied SP, ADP, AP and OADP to the data to predict the PC scores for the study samples. We only calculated the Top 2 PCs, and for OADP and ADP, we calculated the Top 8 PC scores (i.e. $K\prime =8$) for the study samples and project them to the 2D reference PC score space through the Procrustes transformation. For OADP, we calculated the Top 16 PC scores in the online SVD algorithm (i.e. $K″=16$) but used only the Top 8 PCs for the Procrustes transformation (i.e. $K\prime =8$). Finally, we used the 20-nearest-neighbor method to predict each study sample’s population membership. It classified a study sample by the votes of the 20 nearest neighboring reference samples, where the weight of each neighbor was inversely proportional to the distance in between.

To evaluate the accuracy of each method, we obtained the population means of the reference PC scores and calculated the scaled mean-squared difference (MSD) between the reference population means and the corresponding study population means, that is,

$$\text{MSD}=\frac{{\sum }_{q=1}^Q{\sum }_{k=1}^K{(D_{q,k}-C_{q,k})}^2}{{\sum }_{q=1}^Q{\sum }_{k=1}^K{C}_{q,k}^2},$$

where $C_{q,k}$ and $D_{q,k}$ are population q’s reference and study sample means, respectively, for the $k\text{th}$ PC.

To determine the proportion of the MSD that is caused by the prediction of the study samples rather than random variations, in each population we randomly selected some reference samples whose number is the same as that of the study samples. Then we calculated the MSD of these selected reference samples as if they are study samples. We repeated this procedure for 100 times to obtain an empirical null distribution of the MSD.

In addition, to directly compare different methods’ predicted PC scores, we calculated their pairwise mean-squared difference across all the samples and PCs.

For the comparison of computation cost, we applied each method 10 times for each experimental setting and obtained the mean of the study runtimes. Note that the study runtime did not include the time for running the reference sample PCA, reading and writing files, or predicting the population membership of the study samples from their predicted PC scores. For SP, AP and OADP, we used our FRAPOSA software, which implements the methods using Python. For ADP, we used the TRACE software by Wang et al. (2015). All the programs were run on a single-core CPU.

2.4 UK Biobank data analysis

We applied the proposed and existing methods to the UK Biobank data (Bycroft et al., 2018; Sudlow et al., 2015), which contained the genotypes of 488 366 individuals in the UK. The 1000 Genomes Project data served as our reference panel (1000 Genomes Protection Consortium et al., 2015). We used the Phase 3 release of the 1000 Genomes data, which contained 84.4 million variants and 2504 individuals from five super-populations: Africans, admixed Americans, East Asians, Europeans and South Asians (Table 2). These populations were further divided into 26 sub-populations. By using the family structure information provided by the 1000 Genomes Project, we excluded all the individuals with at least one parent that was included in the dataset, which resulted in 2492 individuals for the reference panel. Furthermore, we intersected the 147 604 high-quality genotyped SNPs in the UK Biobank data with the 1000 Genomes SNPs, which gave us 145 282 SNPs in common.

Table 2.

Super-population and sub-population sizes in the 1000 Genomes used for references in UK Biobank data analysis

Super-population	Size	Sub-population	Size
Africans	657	ACB (African Caribbeans in Barbados)	96
		ASW (Americans of Afr. Ancestry in SW. USA)	61
		ESN (Esan in Nigeria)	99
		GWD (Gambian in W. Divisions in the Gambia)	113
		LWK (Luhya in Webuye, Kenya)	97
		MSL (Mende in Sierra Leone)	84
		YRI (Yoruba in Ibadan, Nigeria)	107
Americans	347	CLM (Colombians from Medellin, Colombia)	94
		MXL (Mexican Ancestry from Los Angeles, USA)	64
		PEL (Peruvians from Lima, Peru)	85
		PUR (Puerto Ricans from Puerto Rico)	104
East Asians	503	CDX (Chinese Dai in Xishuangbanna, China)	92
		CHB (Han Chinese in Beijing, China)	103
		CHS (Southern Han Chinese)	105
		JPT (Japanese in Tokyo, Japan)	104
		KHV (Kinh in Ho Chi Minh City, Vietnam)	99
Europeans	498	CEU (Utah Residents with N. and W. Eur. Ancestry)	95
		FIN (Finnish in Finland)	99
		GBR (British in England and Scotland)	90
		IBS (Iberian Population in Spain)	107
		TSI (Toscani in Italia)	107
South Asians	487	BEB (Bengali from Bangladesh)	86
		GIH (Gujarati Indian from Houston, Texas)	102
		ITU (Indian Telugu from the UK)	102
		PJL (Punjabi from Lahore, Pakistan)	96
		STU (Sri Lankan Tamil from the UK)	101
Total	2492		2492

Note: Americans are described as admixed Americans by the 1000 Genomes Project.

After predicting PC scores, we further predicted the ancestry membership by using the 20-nearest-neighbor method, as in the simulation studies (Section 2.3). If a study sample’s highest voted population had received ≤0.875 of the total weighted votes, we classified it as an admixed individual. Then, we investigated the finer-scale ancestry structures using the population-specific reference samples. For example, we used the 498 European 1000 Genomes samples, which consisted of Iberians, Britons, Finns, Toscani and Utah resident with Northern and Western European ancestry, as the reference panel to predict the sub-population membership of the UK Biobank samples that had been predicted to be Europeans.

Since ADP was very slow for such large reference and study sample sizes, we did not apply ADP to all the study samples. Instead, we randomly selected 5000 study samples and used them to compare the performance of ADP against the other methods. The other three methods, SP, AP and OADP, were applied to all the study samples. As in the simulation studies, accuracy was measured by MSD, and runtime excluded the time for PCA on the reference samples.

3 Results

3.1 Simulation studies

We applied the proposed (AP and OADP) and the existing methods (SP and ADP) to the grid-simulated genotypes with the reference sample sizes ranged from 1000 to 3000. Figure 1 shows the PC scores calculated by using 1000 reference samples. It shows that PCA has successfully clustered four different groups. As expected, SP showed systematic shrinkage, but AP, OADP and ADP did not show the bias and had very similar predicted PC scores (Fig. 2). As the reference sample size increased, the bias in SP was reduced, but it was still visible even when the reference sample size was 3000 (Supplementary Figs S1 and S2).

Fig. 1.

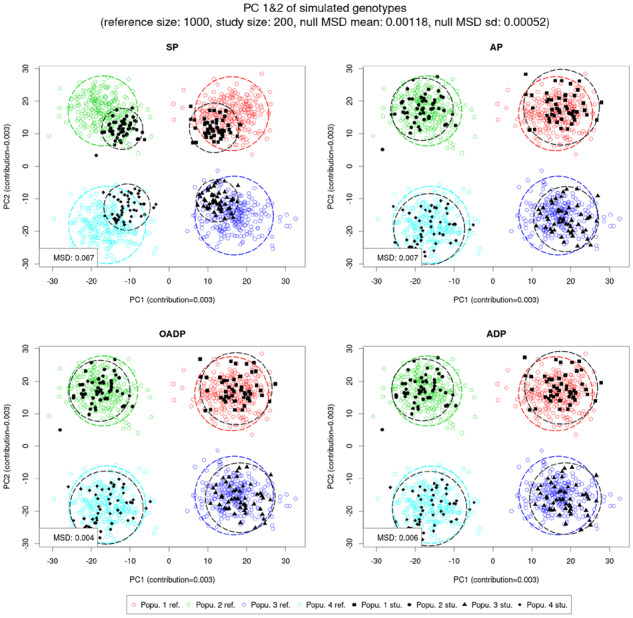
The Top 2 PC scores of the simulated genotypes as predicted by SP, AP, OADP and ADP when the reference size was 1000. In each of the four populations, there were 250 reference samples and 50 study samples, where each sample contained 100 000 variants. The colored/black circle is centered at the reference/study sample mean and encloses 90% of the reference/study samples. The MSD has been scaled with the average distance between the reference population means and the reference global mean. (Color version of this figure is available at Bioinformatics online.)

Fig. 2.

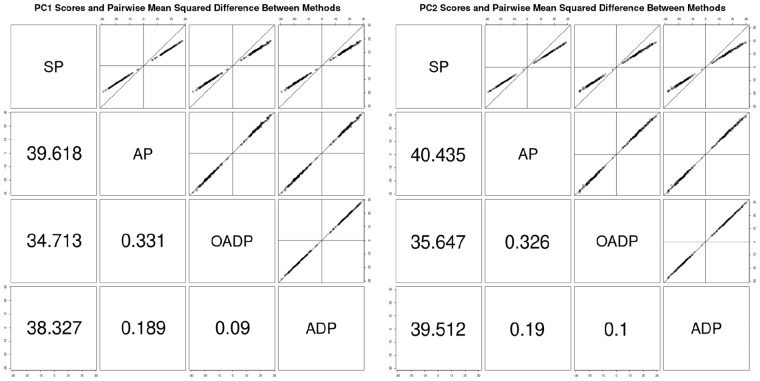
Pairwise comparison of the simulated genotype data’s PC1 and PC2 scores as predicted by SP, AP, OADP and ADP. The reference and study sizes were 1000 and 200, respectively. Each sample contained 100 000 variants. The upper panels show the PC scores, while the lower panels show the pairwise mean-squared difference between the methods

Moreover, SP’s MSD was more than 10 times higher than those of AP, OADP and ADP when the reference sample size was 1000. SP’s MSD was reduced as the number of reference samples increased, but even when the reference sample size was 3000, the MSD of SP was still at least four times higher than that of the other methods, which indicated a higher magnitude of shrinkage for SP. See Figure 3 and Supplementary Table S1. Among the proposed approaches, OADP generally had the smallest MSD.

Fig. 3.

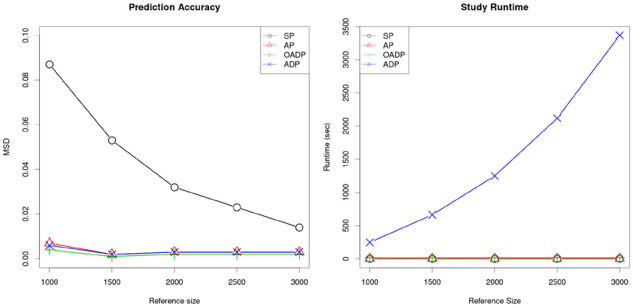
Comparison of the accuracy and runtimes of SP, AP, OADP and ADP in the simulated datasets. Accuracy was measured by the MSD between the population means of the reference samples and the corresponding population means of the study samples, scaled by the average distance between the reference population means and the reference global mean. The runtimes only included the time for analyzing the study samples, and the computation cost for analyzing the reference samples was ignored. Each experimental setting’s runtime was the average of 10 replications. A single-core CPU was used for all the cases. The study sample size was 200, and there were 100 000 variants. Only the Top 2 PCs were calculated

When compared to the empirical null distribution, SP’s MSD exceeded the mean of the empirical null distribution by 33–172 SDs. In comparison, the MSDs of AP, OADP and ADP were only 6–12 SDs away from the mean of the empirical null distribution when the reference size was 1000, and 0.2–5 SDs away when the reference size was 1500 or greater. These observations indicated that the differences in MSD across different methods were mostly due to prediction error.

Figure 3 and Supplementary Table S1 report the computation time. For all the simulation settings, the runtime of ADP greatly exceeded those of the other methods and increased faster than linearly with the number of reference samples. In comparison, the runtime of OADP only grew slightly, and the runtimes of AP and SP remained almost unchanged, as the reference size increased. These observations were consistent with the $\mathcal{O}[n^3],\hspace{0.17em}\mathcal{O}[n],\hspace{0.17em}\mathcal{O}[1]$ and $\mathcal{O}[1]$ CC of ADP, OADP, AP and SP, respectively, with respect to reference size (for fixed data dimension and study size, see Table 1). When the reference size reached 3000, ADP’s runtime for predicting 200 study samples was 3369 s, which was more than 200 times of OADP’s (16 s) and more than 16 000 times of AP’s (0.20 s). In a study of 500 000 samples with a reference size of 3000, the projected computation time of ADP would be 2340 CPU hours (97 CPU days), while OADP and AP would only require 11 and 0.14 CPU h, respectively.

3.2 UK Biobank data analysis

To identify the ancestry structure of the UK Biobank data, we applied the proposed and existing approaches by using the 1000 Genomes data as references. The UK Biobank data contained 488 366 samples collected over multiple centers in the UK. The 2492 independent samples from the 1000 Genomes data were used as the reference set. Sample sizes of the super-populations and sub-populations are given in Table 2. The predicted super-populations (by OADP) of the UK Biobank samples are shown in Table 3. Since ADP was computationally too expensive, we only applied ADP to 5000 randomly selected samples for method comparison. All the other methods were applied to all the 488 366 samples.

Table 3.

Population memberships of the UK Biobank samples as predicted by OADP

Predicted population	Size
Africans	8169
Admixed Americans	2149
East Asians	2569
Europeans	461 807
South Asians	10 250
Admixed	3422
Total	488 366

Note: Admixed samples are defined to be those whose highest vote is 0.875 or less of the total weighted votes, as determined by the 20-nearest-neighbor method.

Figure 4 shows the Top 4 PC scores of all the UK Biobank samples as predicted by SP, AP and OADP. The super-populations (Africans, admixed Americans, East Asians, Europeans and South Asians) were distinguishable by all these three methods. Even SP did not show strong shrinkage. The shrinkage factors for the Top 4 PCs predicted by AP were 0.99, 0.99, 0.96 and 0.94.

Fig. 4.

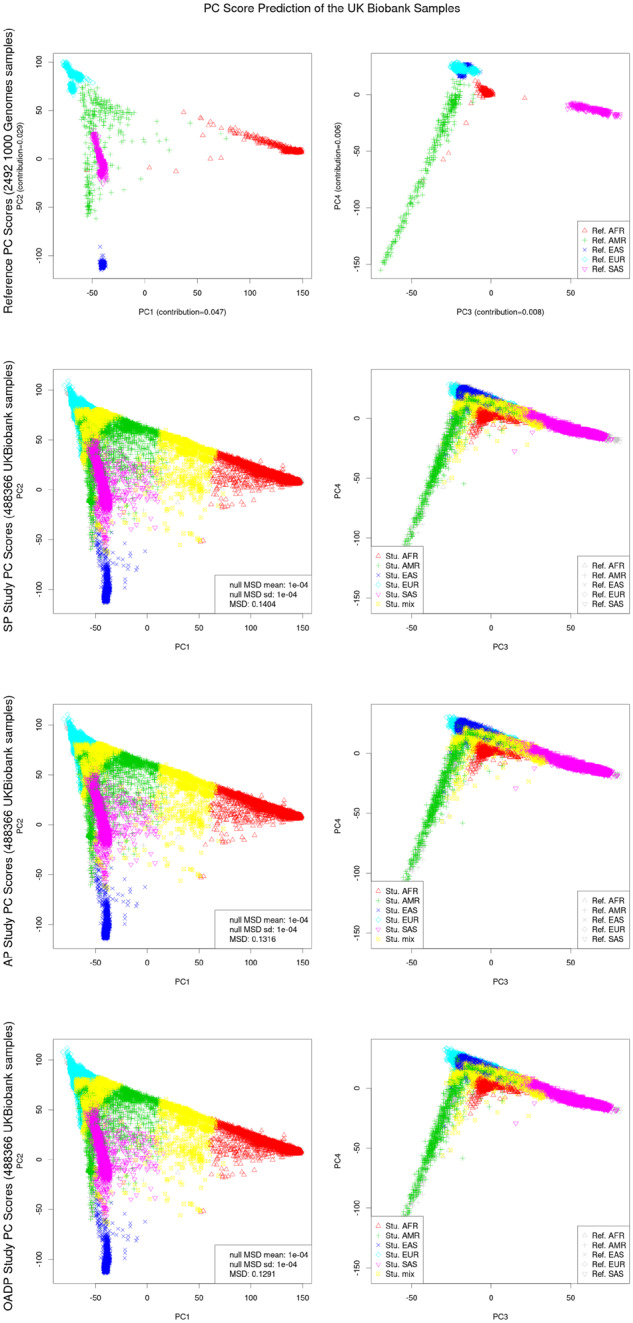
PC scores of all the UK Biobank samples, as predicted by SP, AP and OADP. The reference panel consisted of all the 2492 samples in the 1000 Genomes data. The population membership of each study sample was predicted by the votes of the 20 nearest reference samples with weights inversely proportional to the distance in between. The MSD was scaled with the average distance between the reference population means and the reference global mean. The shrinkage factors for the Top 4 PCs predicted by AP were 0.99, 0.99, 0.96 and 0.94. The F_st statistic was 0.10, and the total variation contributed from the Top 4 PCs was 0.09

To compare the PC score prediction of SP, AP and OADP against ADP’s, we applied each method to the 5000 randomly selected UK Biobank samples. The PC scores are plotted in Supplementary Figure S4. All the methods gave similar predicted PC scores (Supplementary Fig. S4), and the MSDs were also very close (Table 4).

Table 4.

Estimated runtimes and MSDs of SP, AP, OADP and ADP for the UK Biobank data analysis

	Runtime (h)		MSD
Population	Global	European	Global	European
Ref. size	2492	498	2492	498
Study size	488 366	461 807	5000	5000
SP	0.82	0.69	0.156	0.360
AP	0.82	0.69	0.156	0.107
OADP	20.71	17.75	0.156	0.100
ADP	1628.22a	58.93a	0.153	0.102

^aRuntime was estimated from the 5000 randomly selected study samples.

Next, among the 461 807 UK Biobank samples that had been predicted to be Europeans by OADP, we further estimated their sub-population memberships. For the reference panel, we used the 498 European samples in the 1000 Genomes data, where each of them was Iberian, British, Finnish, Toscani or a Utah resident with Northern and Western European ancestry. Each European UK Biobank study sample was predicted to be one of these sub-populations by using the 20-nearest-neighbor method on the PC scores in the same way as in the analysis of the global samples, except that the possibility of being identified as an admixed sample was not included. The Top 4 reference and study PC scores of the European samples are shown in Figure 5. Compared to AP and OADP, SP clearly showed shrinkage in PC1–PC4. The shrinkage factors for the Top 4 PCs predicted by AP were 0.70, 0.40, 0.21 and 0.14.

Fig. 5.

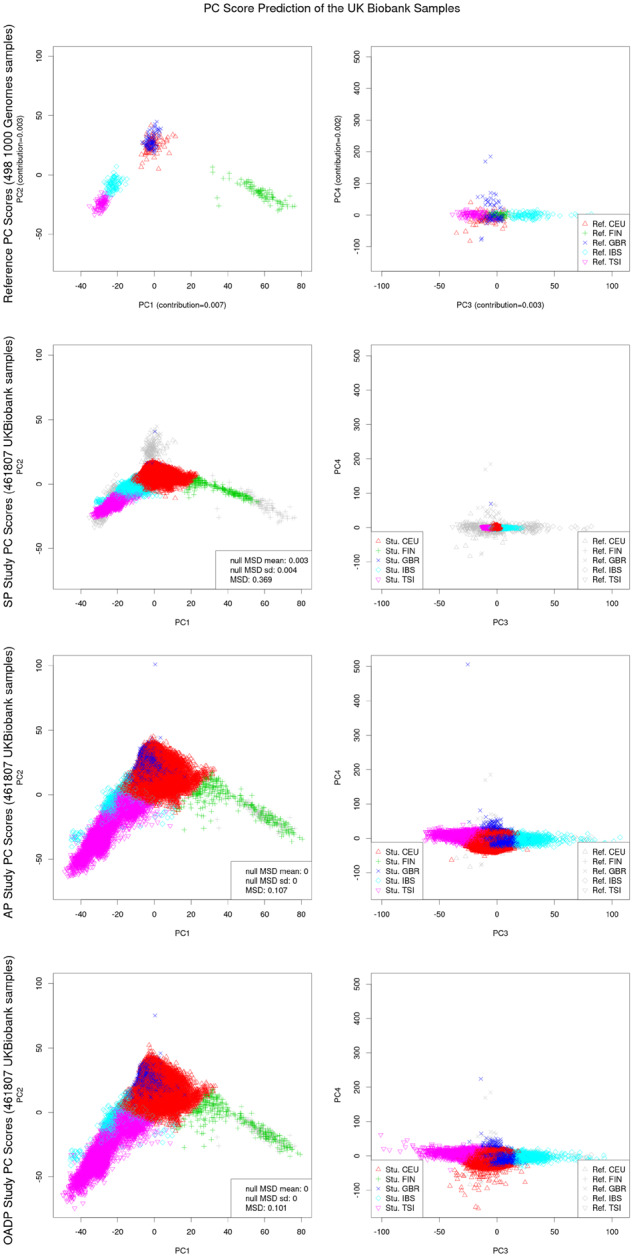
PC scores of the European UK Biobank samples, as predicted by SP, AP and OADP. European samples were identified by OADP using global 1000 Genome reference samples. The reference panel consisted of all the 498 European 1000 Genomes samples. The population membership of each study sample was predicted by the votes of the 20 nearest reference samples with weights inversely proportional to the distance in between. The MSD was scaled with the average distance between the reference population means and the reference global mean. The shrinkage factors for the Top 4 PCs predicted by AP were 0.70, 0.40, 0.21 and 0.14. The F_st statistic was 0.01, and the total variation contributed from the Top 4 PCs was 0.02

Supplementary Figure S5 shows the PC scores predicted by SP, AP, OADP and ADP of the 5000 randomly selected European UK Biobank study samples. The comparison of the PC scores is illustrated in Supplementary Figure S6. Compared to the other methods, PC scores predicted by SP were much closer to NULL. Unlike in the analysis of the global samples, SP had a much higher MSD between the population means for the European samples (Table 4).

In addition, we identified the African, East Asian, admixed American, South Asian and admixed samples by using the OADP-predicted PC scores based on the global 1000 Genomes reference samples. Then SP, AP and OADP were used to predict their finer-scale PC scores and ancestry memberships. The results are shown in Supplementary Figures S7–S11.

The computation cost is shown in Table 4. For the analysis of all the 488 366 UK Biobank samples, SP and AP both took 0.82 CPU hour, while OADP took 21 CPU hour. For ADP, because of its high computation cost, we only ran it on 500 study samples and then scaled its runtime to all the 488 366 samples. The projected runtime for ADP was 1682 h, which was almost 80 times higher than OADP and 2000 times higher than SP and AP. For the computation cost of the analysis of the European samples, SP and AP both took 0.69 h, and OADP took 17.75 h. Because there were only 498 European reference samples, ADP was estimated to cost only 58.93 CPU hours when applied to the European samples.

4 Discussion

In this article, we have compared two existing (SP and ADP) and two novel methods (AP and OADP) of predicting PC scores for the purpose of predicting population structure. The CC calculation shows that our methods greatly exceed the speed of the existing ADP method when the reference sample size is large. Moreover, AP improves the accuracy of SP by adjusting for the shrinkage bias, which is asymptotically estimated from random matrix theory. Our simulation study and the analysis of the UK Biobank data have empirically demonstrate the efficiency and unbiasedness of our methods. AP and OADP have been shown to be 16–16 000 times faster than ADP. They have also successfully separated the sub-populations in the UK Biobank data when SP shrinks most of the study samples toward NULL and is unable to cluster them.

In our simulation studies, we set the number of markers to 100 000. In studies focusing on specific regions in the genome, such as exome-chip or exome-sequencing studies, the number of variants available for ancestry prediction can be substantially smaller. To investigate the performance of the methods in such situations, we reduced the number of variants from 100 000 to 50 000 and 10 000. Supplementary Figures S12 and S13 show that when the reference size was 1000, reducing the number of variants caused all the samples, reference and study, to be close to NULL. This would cause difficulties for predicting the population membership of the study samples, as there were more study samples on the boundaries of the reference populations. ADP, OADP and AP could still separate most of the samples from different populations. In comparison, SP’s study PC scores clustered much more closely around NULL, although their population memberships were mostly distinguishable. On the other hand, Supplementary Figure S14 shows that the MSD remained almost unchanged as the number of variants was reduced. This was due to the fact that MSD was scaled with the scale of the reference PC scores and therefore would change little when the reference and study PC scores shrank by approximately the same magnitude.

In the UK Biobank data analysis, we observed that the PC scores predicted by SP had shrunken much more in the analysis of the European samples than in the analysis of the global samples. This difference could be caused by the sample size difference and the population diversity difference. To further investigate this issue, we randomly selected 498 global 1000 Genomes reference samples to analyze the 5000 randomly selected global UK Biobank samples. With the reference size, the same as the European samples, the 5000 global samples’ PC scores shrank more than when using all the 2492 global reference samples, as shown in Supplementary Figures S15 and S16. The shrinkage factors for the Top 4 PCs predicted by AP were 0.96, 0.93, 0.80 and 0.70, which indicated stronger shrinkage effect compared to the analysis using all the 2492 reference samples, especially in PC3 and PC4, though the shrinkage was not as strong as the shrinkage in the analysis of the European samples. For differences in population diversity, the global samples in the 1000 Genomes data had a fixation statistic F_st (Weir and Cockerham, 1984) of 0.087, while that of the Europeans samples was 0.005. Similarly, the proportion of the total variation explained by Top 4 PCs was 0.090 for the global samples and 0.015 for the European UK Biobank samples. Both population diversity statistics show that the European populations did not differ as much as the global populations. We conclude that both the reference size difference and the population diversity difference contributed to SP’s large shrinkage in the European sample analysis as compared to the global sample analysis.

Throughout the article, we estimate the ancestry membership of the study samples by predicting their PC scores with a reference panel. An alternative method would be combining the reference samples with the study samples and applying PCA to the combined data. However, a major drawback of this alternative is that when most of the study samples belong to one population, this population would dominate the analysis and cause inaccurate PC score prediction for samples in other populations. To illustrate this, we combined the European 1000 Genomes samples with the European UK Biobank samples and applied the FastPCA algorithm (Galinsky et al., 2016) to the combined data. The PC scores were then used to estimate the ancestry membership through the 20-nearest-neighbor method, as described in Section 2.3. Supplementary Figure S17 shows the PC scores estimated by FastPCA, and Supplementary Table S2 compares the ancestry membership estimated by FastPCA and OADP. The two methods estimated very similar numbers of samples to be British or Utah residents of Northern and Western European ancestry, which is what we would expect since the study data were dominated by these two populations. However, the two methods gave very different results for the other three European populations. In the most extreme case, the difference in the number of Finnish samples was more than 10-fold between the two methods’ predictions. We note that, due to the lack of the fine-scale ancestry information, we cannot confirm that our method has provided more accurate results. However, considering the unsupervised nature of the alternative approach, it is reasonable to assume that the alternative approach would be less accurate. In addition, the alternative approach does not allow to compare samples in different studies, so it cannot be used for the sample matching in integrative analysis (Zhan et al., 2013).

An interesting phenomenon we have observed is that in most cases of the simulation studies and the UK Biobank analysis, OADP outperformed ADP in terms of prediction accuracy as measured by MSD, even though OADP is an approximation method of ADP. One possible explanation for this phenomenon is that OADP only uses the first 16 PCs to update the Top 8 PCs. OADP sacrifices the information of the lower-rank PCs in order to gain computation speed, but this might turn out to be an advantage for OADP’s prediction accuracy, since it makes this method less vulnerable to outliers in the lower-rank PCs.

We have also noticed a limitation of AP. While the CC and memory usage of SP can be further reduced by using some truncated SVD algorithm [such as the randomized SVD algorithm by Halko et al. (2011)] to compute the SVD for only the top K PCs of the reference matrix, AP requires all the eigenvalues and thus a full SVD or eigen decomposition of the reference matrix. This becomes especially important when the reference set is extremely large. In contrast, OADP needs only the top few singular values and vectors, which can be computed by randomized approaches even for large reference sets.

In addition, for concerns about relatedness in the samples, the proposed methods AP and OADP can in general be applied to high-dimensional genotype data as long as the reference samples are all unrelated. Relatedness among study samples would not affect PC score prediction accuracy.

As the cost of genotyping continues to decrease, larger genotype datasets will become available. High-dimensional large-sized data will be essential for identifying and adjusting for fine-scale population structure in GWAS but they also create a demand for computationally efficient algorithms. When the size of the reference samples increases, existing methods such as ADP would become impractical to use. But our methods will continue to operate within a reasonable computation time frame without losing accuracy and serve as useful tools for genetic studies. The SP, AP, OADP and ADP methods have been implemented in the open-source software FRAPOSA (github.com/daviddaiweizhang/fraposa).

Funding

This work was supported by the National Institutes of Health [R01 HG008773 to D.Z. and S.L.]. It was conducted using the UK Biobank Resource under application number 45227.

Conflict of Interest: none declared.