forgeNet: a graph deep neural network model using tree-based ensemble classifiers for feature graph construction

Abstract

Motivation

A unique challenge in predictive model building for omics data has been the small number of samples (n) versus the large amount of features (p). This ‘$n\ll p$’ property brings difficulties for disease outcome classification using deep learning techniques. Sparse learning by incorporating known functional relationships between the biological units, such as the graph-embedded deep feedforward network (GEDFN) model, has been a solution to this issue. However, such methods require an existing feature graph, and potential mis-specification of the feature graph can be harmful on classification and feature selection.

Results

To address this limitation and develop a robust classification model without relying on external knowledge, we propose a forest graph-embedded deep feedforward network (forgeNet) model, to integrate the GEDFN architecture with a forest feature graph extractor, so that the feature graph can be learned in a supervised manner and specifically constructed for a given prediction task. To validate the method’s capability, we experimented the forgeNet model with both synthetic and real datasets. The resulting high classification accuracy suggests that the method is a valuable addition to sparse deep learning models for omics data.

Availability and implementation

The method is available at https://github.com/yunchuankong/forgeNet.

Contact

tianwei.yu@emory.edu

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

In the study of bioinformatics, one important problem is the prediction of clinical outcomes using profiling datasets with a large amount of variables such as gene expression data, proteomics data and metabolomics data. In such datasets, major challenges lie in the relatively small number of samples compared to the large number of predictors (genes/proteins/metabolites), namely the ‘$n\ll p$’ issue. In addition, the complex unknown correlation structure among predictors results in more difficulty in prediction and feature selection. To tackle this challenging situation, machine learning approaches have been introduced for the prediction task (Cai et al., 2015; Chen et al., 2014; Kursa, 2014; Liang et al., 2013; Vanitha et al., 2015). While the primary interest of these studies is to achieve high prediction accuracy, contributions have also been made for feature selection or learning effective feature representations (Cai et al., 2015; Kursa, 2014). Based on the biological property of profiling data, i.e. functionally associated biological units tend to be statistically dependent and contribute to a biological outcome in a synergistic manner, a branch of classification research has been focused on integrating prior knowledge on the relationships between features into predictive models, to improve both classification performance and learning the structure of feature space. A critical data source to achieve this goal is the biological networks constructed from existing biological knowledge, such as signal transduction network or protein–protein interaction network (Chowdhury and Sarkar, 2015; Szklarczyk and Jensen, 2015). A biological network is a graph-structured dataset with biological units as the graph vertices and their functional relations as graph edges. In terms of classification tasks, each vertex in the biological network corresponds to a predictor, and it is expected that the biological network can provide useful information for a learning process. Motivated by this idea, certain classification methods have been developed where biological networks are integrated as additional information for the prediction and feature selection procedure. For example, support vector machines and traditional linear models such as logistic regression classifier can be modified by adding penalty terms to the objective function, where the penalty is defined according to pairwise distances between biological units in a network (Kim et al., 2013; Lavi et al., 2012; Zhao et al., 2014; Zhu et al., 2009). Dutkowski and Ideker (2011) develop a random forest (RF)-based method, called Network-Guide Forest, where the feature subsampling in building decision trees is guided by graph search on the given biological network. Also, a recent study (Kong and Yu, 2018) brings biological networks to deep learning, where applications on profiling data were restricted primarily due to the $n\ll p$ issue (Min et al., 2016). In Kong and Yu (2018), a deep learning model graph-embedded deep feedforward network (GEDFN) is proposed with the biological network embedded as a hidden layer in deep neural networks to achieve an informative sparse structure. In GEDFN, the graph-embedded layer helps achieve two effects. One is model sparsity, and the other is the informative flow of information for prediction and feature evaluation. These two effects allow GEDFN to outperform other methods in profiling data classification given an appropriately specified feature graph.

Authors of these methods have demonstrated that combining biological networks with profiling data results in better classification performance and more interpretable feature selection. However, these methods bear a common limitation, which is the potential mis-specification of the required biological network. In practice, profiling data are used for various clinical outcomes, and the mechanistic relationships between biological units and different clinical outcomes can be quite different. Hence, there does not exist a single known network that uniformly fits all classification problems. Thus, biological networks used in graph-embedded methods can only be ‘useful’ but not ‘true’. Consequently, how to decide if a known biological network is useful in predicting a certain clinical outcome with a certain gene expression dataset remains an unsolved problem, causing difficulties in applying graph-embedded methods in practice. Kong and Yu (2018) discuss the feature graph mis-specification issue of the GEDFN model and shows that the method is robust with mis-specified biological networks. Nevertheless, it is unrealistic to guarantee that the robustness applies in a broad sense, as feature graph structures can be extremely diverse such that simulation would not be able to cover all scenarios.

To address these issues, in this paper, we aim at developing a method that does not rely on a given feature network, yet can still benefit from the idea of building a model with sparse and informative flow of information. Instead of using known feature graphs, we try to construct a feature graph within the feature space. We propose a supervised feature graph construction framework using tree-based ensemble models, as literature shows that tree-based ensemble methods such as the RF (Breiman, 2001) and the Gradient Boosting Machine (GBM) (Friedman, 2002) are excellent tools for feature selection (Tang and Foong, 2014; Vens and Costa, 2011). These tree-based methods also provide relational information between features in terms compensating each other in the classification task. We develop the forest graph-embedded deep feedforward network (forgeNet) model, with a built-in tree-based ensemble classifier as a feature graph extractor on top of a modified GEDFN model. The feature extractor selects features that span a reduced feature space, and constructs a graph between the selected features based on their directional relations in the decision tree ensemble.

The application of tree-based ensemble methods as feature graph extractor is mainly based on two considerations: (i) the extractor selects effective features in a supervised manner. Thus, the target outcome directly participates the feature graph construction. Compared to unsupervised feature construction such as using marginal or conditional correlation graphs, the resulting graph from trees is more informative and relevant to the specific classification task; (ii) the feature extraction procedure helps reduce the dimension of the original feature space, alleviating the $n\ll p$ problem for the downstream neural network model.

2 Materials and methods

2.1 Review of GEDFNs

We first briefly review the GEDFN model as our new method utilizes a similar neural network architecture. Recall a deep feedforward network with l hidden layers:

$$\text{Pr}(\mathbf{y}|\mathbf{X},\mathbf{\Psi })=\text{softmax}({\mathbf{Z}}_{\text{out}}{\mathbf{W}}_{\text{out}}+{\mathbf{b}}_{\text{out}}){\mathbf{Z}}_{\text{out}}=\sigma ({\mathbf{Z}}_l{\mathbf{W}}_l+{\mathbf{b}}_l)\dots {\mathbf{Z}}_{k+1}=\sigma ({\mathbf{Z}}_k{\mathbf{W}}_k+{\mathbf{b}}_k)\dots {\mathbf{Z}}_1=\sigma (\mathbf{X}{\mathbf{W}}_{\text{in}}+{\mathbf{b}}_{\text{in}}),$$

where $\mathbf{X}\in {\mathcal{R}}^{n\times p}$ is the feature matrix with n samples and p features, $\mathbf{y}\in {\mathcal{R}}^n$ is the outcome containing classification labels, $\mathbf{\Psi }$ denotes all parameters, ${\mathbf{Z}}_k$ ($k=1,\dots ,l-1,\text{out}$) are hidden layers with corresponding weights ${\mathbf{W}}_k$ and bias ${\mathbf{b}}_k$. The dimensions of Z and W depend on the number of hidden neurons h_k ($k=1,\dots ,l,\text{in}$) of each hidden layer, as well as the input dimension p and the number of classes h_out. We mainly focus on binary classification problems hence the elements of y simply take binary values and $h_{\text{out}}\equiv 2$. The function $\sigma (·)$ is the nonlinear activation such as sigmoid, hyperbolic tangent or rectifiers. The $\text{softmax}(·)$ function converts values of the output layer into probability prediction.

The graph-embedded feedforward net is a variant of the regular feedforward net with modified first hidden layer:

$${\mathbf{Z}}_1=\sigma (\mathbf{X}({\mathbf{W}}_{\text{in}}\odot A)+{\mathbf{b}}_{\text{in}}),$$ (1)

where A is the adjacency matrix of a feature graph and $\odot$ is the Hadamard (element-wise) product. As in regular deep neural networks, the parameters to be estimated are all the weights and biases. The model is trained using a stochastic gradient decent-based algorithm by minimizing the cross-entropy loss function (Goodfellow et al., 2016).

2.2 The forgeNet model

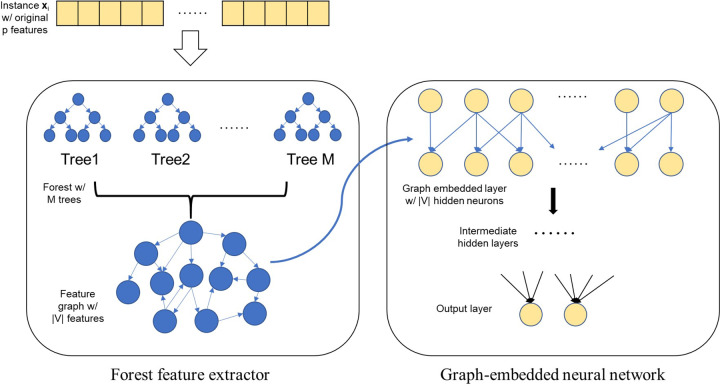
Our newly proposed forgeNet model consists of two components—the extractor component and the neural network component. The extractor component uses a forest model to select useful features from raw inputs with the supervision of training labels, as well as constructs a directed feature graph according to the splitting order in the individual decision trees. The neural network component feeds the generated feature graph and the raw inputs to GEDFN, and serves as the learner to predict outcomes. In forgeNet, a forest is defined as any ensemble of decision trees but not limited to RFs. In fact, any tree-based ensemble approach is applicable within the forgeNet framework. Besides RF and GBM mentioned in Section 1, their variants with similar outputs are also possible options, or the forest can be simply built through bagging trees (Breiman, 1996). However, since RF and GBM models are the most commonly used tree ensembles, in this paper, we only employ these two methods for a proof-of-concept purpose.

In forgeNet, a forest $\mathcal{F}$ is denoted as a collection of decision trees:

$$\mathcal{F}(\Theta )=\{{\mathcal{T}}_m({\Theta }_m)\},\hspace{0.17em}m=1,\dots ,M,$$

where M is the total number of trees in the forest, $\Theta =\{{\Theta }_1,\dots ,{\Theta }_M\}$ represents the parameters, which include splitting variables and splitting values. In the feature graph extraction stage, $\mathcal{F}$ is fitted by training data ${\mathbf{X}}_{\text{train}}$ and training label ${\mathbf{y}}_{\text{train}}$, where ${\mathbf{X}}_{\text{train}}\in {\mathcal{R}}^{n_{\text{train}}\times p}$ and ${\mathbf{y}}_{\text{train}}\in {\mathcal{R}}^{n_{\text{train}}}$. After fitting the forest, we obtain M decision trees, each of which contains a subset of features and their directed connections according to the tree splitting. At the same time, a binary tree can be viewed as a special case of a graph with directed edges. Hence, we can construct a set of graphs:

$$\mathcal{G}=\{G_m(V_m,E_m)\},\hspace{0.17em}m=1,\dots ,M,$$

where V_m and E_m are collections of vertices and edges in G_m, respectively. Next, by merging all graphs in $\mathcal{G}$, the aggregated feature graph

$$\mathbf{G}(V,E)=\underset{m=1}{\overset{M}{\cup }}{G}_m(V_m,E_m)$$

is obtained, where $V=\underset{m=1}{\overset{M}{\cup }}{V}_m$ and $E=\underset{m=1}{\overset{M}{\cup }}{E}_m$.

In the form of its adjacency matrix, G is the feature graph to be embedded into the second stage of the forgeNet. Note that regardless which tree-based ensemble methods we use, it is likely that not all predictors in the original feature space can enter the forest model. A feature is included in G if and only if it is used at least once by the forest to split samples. As a result, the original feature space is reduced after the feature extraction. Denoting the number of vertices of G as $\left|V\right|$, we have $\left|V\right|<p$, and the input data matrix for the second stage is thus ${\tilde{\mathbf{X}}}_{\text{train}}\in {\mathcal{R}}^{n\times \left|V\right|}$. The columns in ${\tilde{\mathbf{X}}}_{\text{train}}$ corresponds to selected features in the original data ${\mathbf{X}}_{\text{train}}\in {\mathcal{R}}^{n\times p}$, and the order of columns does not matter.

The resulting feature graph G of feature extraction is a directed network, which differs from the one used in the original GEDFN. In Kong and Yu (2018), the adjacency matrix A in Equation (1) represents an undirected feature graph. In the case of forgeNet, the adjacency matrix is naturally generalized to the directed version, and replacing A in Equation (1) with an asymmetric adjacency does not affect the model construction and training. A visualization of the entire forgeNet architecture is seen in Figure 1.

Fig. 1.

Illustration of the forgeNet model. Notations are consistent with those in the text

After fitting forgeNet with the training data, only the reduced input ${\tilde{\mathbf{X}}}_{\text{test}}$ and the testing label ${\mathbf{y}}_{\text{test}}$ are required for testing the prediction results, as ${\tilde{\mathbf{X}}}_{\text{test}}$ can be directly fed into the downstream neural nets together with the feature graph constructed from the forest.

2.3 Evaluation of feature importance

The selection of predictors that significantly contribute to the prediction is another major aspect of the analysis of profiling data, as they can reveal underlying biological mechanisms. Thus in forgeNet, we introduce a feature importance evaluation mechanism, which is closely related to the Graph Connection Weights (GCW) method proposed in Kong and Yu (2018) for the original GEDFN model. However, since the feature graph used in forgeNet has a different property from that in GEDFN where the feature graph is given, certain modifications of GCW are needed.

The main idea of GCW is that, the contribution of a specific predictor is directly reflected by the magnitude of all the weights that are directly associated with the corresponding hidden neuron in the graph-embedded layer (the first hidden layer). In forgeNet, since the connection between the input layer and the first hidden layer is no longer symmetric due to the directed feature graph structure, to evaluate the importance of a given feature, we examine both hidden neurons in the first hidden layer and the nodes in the input layer. The importance score is thereby calculated as the summation of absolute values of the weights that are directly associated with the feature node itself and its corresponding hidden neuron in the graph-embedded layer:

$$\begin{array}{c}{s}_j=\sum _{u=1}^p|w_{ju}^{\left(\text{in}\right)}\mathcal{I}(A_{ju}=1)|+\sum _{v=1}^p|w_{vj}^{\left(\text{in}\right)}\mathcal{I}(A_{vj}=1)|\\ +\sum _{m=1}^{h_1}\left|w_{jm}^{(1)}\right|,\hspace{1em}j=1,\dots ,p,\end{array}$$

where s_j is the importance score for feature j, $w^{\left(\text{in}\right)}$ denotes weights between the input and first hidden layers and $w^{(1)}$ denotes weights between the first hidden layer and the second hidden layer. The score consists of three parts: the first two terms summarize the importance of a feature according to the directed edge connection in the feature graph G; the third term summarizes the contribution of the feature according to the connection with the second hidden layer ${\mathbf{Z}}_2$. Note that the input data X are required to be Z-score transformed (the original value minus the mean across all samples and then divided by the SD), ensuring all variables are of the same scale so that the magnitude of weights is comparable. Once the forgeNet is trained, the importance scores for all the variables can be calculated using trained weights.

2.4 Implementation

We employ the Scikit-learn (Pedregosa et al., 2011) package for the implementation of RF, the Xgboost package (Chen and Guestrin, 2016) for GBM, and the Tensorflow library (Abadi et al., 2016) for deep neural networks. For the choice of activation functions of neural nets, the rectified linear unit (ReLU) (Nair and Hinton, 2010) is employed. This nonlinear activation has an advantage over the sigmoid function and the hyperbolic tangent function as it avoids the vanishing gradient problem (Hochreiter et al., 2001) during model training. The entire neural net part of forgeNets is trained using the Adam optimizer (Kingma and Ba, 2014), which is the state-of-the-art version of the popular stochastic gradient descent algorithm. Also, we use the mini-batch training strategy by which the optimizer loops over randomly divided small proportions of the training samples in each iteration. Details about the Adam optimizer and the mini-batch strategy applications in deep learning can be found in Goodfellow et al. (2016) and Kingma and Ba (2014).

The performance of a deep neural network model is associated with many hyper-parameters, including the number of hidden layers, the number of hidden neurons in each layer, the dropout proportion of training, the learning rate and the batch size. As the hyper-parameters are not of primary interest in our research, in the simulation and real data experiments, we simply tune hyper-parameters using grid search in a feasible parameter space. An example of hyper-parameter tuning can be found in Supplementary File S1. Also, since our experiments contain a number of datasets, it is not plausible to fine tune models for each dataset. Instead, we tune hyper-parameters using some preliminary synthetic datasets, and apply the set of parameters to all experimental data. For simulation experiments, the number of trees of our forgeNets is 1000 and the number of hidden layers of the neural net is three with p (graph-embedded layer), 64 and 16 hidden neurons, respectively. For real data analyses, the number of trees in the forest part is adjusted according to the size of the corresponding feature space, and the neural net structure is the same as it is in simulation.

3 Simulation experiments

The goal of the simulation experiments is to mimic disease outcome classification using profiling data with $n\ll p$. Effective features are sparse and potentially correlated through an underlying unknown structure. Several benchmark methods are experimented in addition to the new forgeNet model for comparison purpose. Through simulation, we intend to investigate whether the forgeNet model is able to outperform other classifiers without knowing the underlying structure of features.

3.1 Synthetic data generation

We follow a similar procedure described in Kong and Yu (2018). For a given number of features p, the preferential attachment algorithm (BA model) (Barabási and Albert, 1999) is employed to generate a scale-free network as the underlying true feature graph. Defining the distance between two features in the network as the shortest path between them, we calculate the p × p matrix D recording pairwise distances among features. Next, the distance matrix is transformed into a covariance matrix Σ by letting

$${\Sigma }_{ij}={0.6}^{D_{ij}},i,j=1,\dots ,p.$$

After obtaining the covariance matrix between features, we generate n multivariate Normal samples as the data matrix $\mathbf{X}={({\mathbf{x}}_1,\dots ,{\mathbf{x}}_n)}^T$ i.e.

$${\mathbf{x}}_i\sim \mathcal{N}(0,\Sigma ),i=1,\dots n,$$

where $n\ll p$ for imitating gene expression data. To add negative correlations as well, we randomly flipped the signs of 1% of the X columns (genes). Supplementary Figure S1 shows empirical pairwise feature correlation distributions for the simulated data. The plots confirm that there are significant proportions of negative correlations. To generate outcome variables, we first select a subset of features to be ‘true’ predictors. Among vertices with relatively high degrees (‘hub nodes’) in the feature graph, part of them are randomly selected as ‘cores’, and a proportion of the neighboring vertices of cores are also selected. Denoting the number of true predictors as p₀, we uniformly sample a set of parameters $\beta ={({\beta }_1,\dots ,{\beta }_{p_0})}^T$ and an intercept β₀ from a small range, say $(-0.15,0.15)$. Finally, the outcome variable y is generated through a procedure similar to the generalized linear model framework

$$y_i=\mathcal{I}\{g({\beta }_0+{(x_i{}^{(\text{true})})}^T\beta )>t\},i=1,\dots n,$$

where ${\mathbf{x}}_{\mathbf{i}}^{(\text{true})}\in {\mathcal{R}}^{p_0}$ is the subvector of ${\mathbf{x}}_{\mathbf{i}}$ and t is a threshold. For the transformation function $g(·)$, we consider a weighted sum of hyperbolic tangent and quadratic function

$$g(x)=0.7\varphi (\text{tan}\hspace{0.17em}h(x))+0.3\varphi (x^2).$$

The reason of using this $g(·)$ function is that the transformation is nonmonotone, which brings in more challenges for classification. The function $\varphi (·)$ is the min–max transformation scaling the input to $[0,1]$, i.e. the original value minus the sample minimum and then divided by the difference between the sample maximum and the sample minimum.

Following the above data generation scheme, we simulate a set of synthetic datasets with P = 5000 features and n = 400 samples. Since in profiling data, the true signals for a certain prediction task are sparse ($p_0\ll p$), We choose $p_0=15,30,45,60$ and 75 as the numbers of true predictors, corresponding to 1–5 cores selected among all hub nodes in the feature graph.

3.2 Evaluation of simulation experiments

We compare our method with several benchmark models. First, since the true feature graphs are known for simulation data, we are able to test the original GEDFN model with correctly specified feature graphs. At the same time, we also experiment GEDFN with mis-specified feature graphs by randomly generating Erdös–Rényi random graphs (Erdös and Rényi, 1959), which have a different graph topology structure from the true scale-free networks. Also, since forgeNet inherently fits a tree-based ensemble classifier, it is natural to compare the performance of a forgeNet with its forest part alone. We choose two representative tree methods RF and GBM for the experiments, and correspondingly test two versions of forgeNets—forgeNet-RF and forgeNet-GBM. Finally, the logistic regression classifier with lasso (LRL) (Tibshirani, 1996) is also added as a representative of linear machines.

For each of the data generation settings, 50 independent datasets are generated. For each dataset, we randomly split samples into training and testing sets at a ratio of 4:1. All models are fitted using the training dataset and then used to predict the testing dataset. To evaluate classification results, areas under receiver operating characteristic curves (ROC-AUCs) are calculated using the predicted class probabilities and the labels of the testing set. The final testing result for a simulation case is then given by the average testing ROC-AUC across the 50 datasets.

As for feature selection, all the methods except LRL provide relative feature importance scores; LRL does not rank features but directly gave the selected feature subset. Knowing the true predictors for simulated data, we could use the binary true predictor labels to evaluate the accuracy of feature selection. However, in preliminary numerical experiments, it is observed that though we fix the number of true features in each case, neighboring features of true predictors in the feature graph are also informative for classification even if they are not in the true feature set. This is because these neighboring features have a relatively high correlation with selected true predictors (0.6 according to Section 3.1). Therefore, when evaluating the results of feature selection, it is more appropriate to investigate a set of ‘relevant’ features including those neighboring features, rather than the ‘true’ feature set only. The average numbers of relevant features are 208.8, 460.4, 615.4, 717.8 and 864.7, respectively, corresponding to the five cases of true features $p_0=15,30,45,60$ and 75.

Since the relevant feature sets are still small compared to the entire feature space (P = 5000), the AUC of the precision–recall curve is a more appropriate metric here. We thus compare feature selection results using binary labels of relevant features for all methods providing feature scores. As for LRL, for each dataset, we compare recall values of our methods and LRL given the precision value of LRL. That is, the precision of LRL helps locate points on the precision–recall curves of forgeNets, and corresponding recall values are used for comparison.

3.3 Simulation results

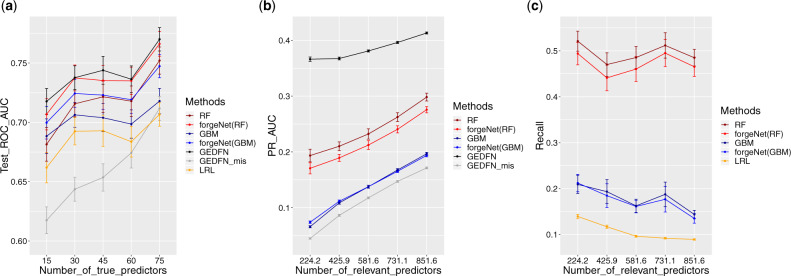
Figure 2a shows the results of classification accuracy comparison. With the increasing number of true predictors, all of the methods performed better as there were more signals in the entire feature space. From the figure, the two versions of forgeNets, forgeNet-RF and forgeNet-GBM, significantly improved the classification performance of their forest counterparts, i.e. RF and GBM. Also, the forgeNet-RF was the only method that achieved similar classification accuracy as GEDFN which benefited from the use of true feature graphs. When GEDFN was given mis-specified feature graphs (GEDFN_mis), its classification ability was weakened with AUC values even worse than LRL. In summary, in terms of prediction, forgeNets beat all classic machine learning methods compared here (RF, GBM, LRL), achieved very similar accuracy compared to GEDFN using true feature graphs, and significantly outperformed GEDFN once its feature graphs were mis-specified.

Fig. 2.

Comparison of classification and feature selection for the simulation study. (a) AUC of ROC for classification; (b) AUC of precision–recall for feature selection; and (c) recall plots given fixed precision from LRL. Error bars represent the estimated mean quantities plus/minus the estimated standard errors

Feature selection results can be seen in Figure 2b and c. Comparing the precision–recall AUCs from Figure 2b, it can be observed that GEDFN using true feature graph was the best method for feature importance ranking, yet again the outstanding performance was ruined by mis-specified feature graphs. The results of forgeNets were significantly better than GEDFN_mis, and were consistent with their forest counterparts. As the training of neural networks in forgeNets largely relied on feature graphs given by forests, it is not surprising to see that forgeNets could achieve similar feature selection results as their forest counterparts. In Figure 2c, both forgeNet-RF and forgeNet-GBM were able to achieve higher recall values than LRL. In summary, in terms of feature selection, forgeNets outperformed the traditional lasso method and had consistent performance with their forest counterparts. Although not as good as GEDFN with true feature graphs, forgeNets produced significantly better feature selection than GEDFN using mis-specified feature graphs. Finally, we observe that the choice of the forest in forgeNets mattered, and among the two versions in our experiments, forgeNet-RF was a more powerful model.

The simulation study proved the forgeNet a powerful classifier, with reasonably good feature selection ability. Through the experiment results, one can easily conclude the novelty of forgeNets is that, by borrowing the neural net architecture of the original GEDFN, forgeNets utilize feature information more effectively in classification tasks compared to regular tree-based ensemble methods.

ForgeNets involve stochastic model fitting. There can be concerns about forgeNet’s stability and scalability. The former refers to the sensitivity regarding different initial values in training the deep neural network. To test the reproducibility of the forgeNet model, we examined the classification accuracy of 10 repeated forgeNet runs for fixed synthetic datasets. The results for both forgeNet-RF and forgeNet-GBM are shown in Supplementary Table S1. Despite a little variability in cases where the numbers of true features are small, forgeNets exhibited robustness with respect to initial values in general. The second aspect is forgeNet’s capability of tackling large-scale datasets (i.e. larger samples and/or extremely large feature spaces) without inducing impractical cost in time and memory, compared to traditional classification methods. To answer this question, we designed additional experiments for forgeNet-RF and forgeNet-GBM to analyze their computational cost and compared the cost with their tree-ensemble counterparts, respectively. The analysis is reported in Supplementary Tables S3–S6, where we concluded that the extra computation time and memory usage induced by forgeNets stayed in a limited scale, indicating the usability of the method for large-scale data.

3.4 Analysis of estimated feature graphs

ForgeNets use feature graphs constructed by tree-ensemble methods. It is of interest to investigate the feature graphs constructed by the tree-based feature extractors. The comparison between the estimated feature graphs and the true simulated feature graphs were based on two aspects, vertices and edges. For each synthetic dataset, we selected the subnetwork, denoted as H, containing all relevant features defined in Section 3.2 and their neighbors (i.e. second neighbors of true features) in the true feature graph. To compare vertices, we calculated the proportion of features in the estimated feature graph that fell in H. Table 1 [row ‘RF (vertex)’ and row ‘GBM (vertex)’] shows the averaged vertex proportions for different simulation cases. As for edges, it is noted that the feature graph construction by tree-based methods is not for recovering the original correlation feature graph. Instead, two adjacent features in a tree are more likely to be complementary to each other regarding a given classification task. Consequently, the estimated feature graphs were expected to be more similar to the complement graph of H, denoted as ${\mathbf{H}}^c$, rather than H itself. In graph theory, the complement graph ${\mathbf{H}}^c$ of H is a graph with the same vertices such that two vertices of ${\mathbf{H}}^c$ are connected if and only if they are not connected in H (Bondy et al., 1976). The averaged proportions of the estimated feature graph edges that fell in the edge set of ${\mathbf{H}}^c$ can be also found in Table 1 [row ‘RF (edge)’ and row ‘GBM (edge)’].

Table 1.

Analysis of feature graphs constructed by RF and GBM

No. of true features	15	30	45	60	75
RF (vertex)	0.429	0.585	0.663	0.723	0.768
RF (edge)	0.284	0.447	0.546	0.625	0.692
GBM (vertex)	0.437	0.582	0.660	0.718	0.764
GBM (edge)	0.226	0.376	0.467	0.548	0.609

Note: Proportions are averaged across the 50 datasets in each simulation case.

The analysis of estimated feature graphs indicates that forgeNet selects relevant features but views the feature interactions from a different perspective. On the one hand, forgeNet’s tree-based feature extractor identifies relevant features for classification that are consistent with those in the original correlation feature graph. On the other hand, the feature extractor constructs feature graphs based on a complementary relationship among features instead of direct correlation. This again aligns with the concept of the supervised feature extractor, as the estimated feature graph is not necessarily recovering the correlation graph, as long as it contains useful information of feature interactions in predicting a certain classification outcome.

4 Real data applications

4.1 Breast invasive carcinoma RNAseq data

We applied forgeNets to the Cancer Genome Atlas (TCGA) breast cancer (BRCA) RNA-seq dataset (Koboldt et al., 2012). The dataset consists of a gene expression matrix with 20 155 genes and 1097 cancer patients, as well as the clinical data including survival information. The classification task is to predict the 3-year survival outcome. We excluded patients with missing or censored survival time for which the 3-year survival outcome could not be decided. Also, genes with more than 10% of zero values were screened out. As a result, the final dataset contains a total of P = 16 027 genes and n = 506 patients, with 86% positive cases. For each gene, its expression value was Z-score transformed.

Using the BRCA data, we again tested two versions of forgeNets together with RF, GBM and LRL. The classification was conducted using a 5-fold stratified cross-validation process, and the final prediction AUC for each method is computed by averaging the five validation results.

Table 2 summarizes the classification results. From the table, forgeNets again outperformed their forest counterpart models and LRL. Therefore, this real data application also led to a similar conclusion as in Section 3 that forgeNets brought in significant improvement for classification.

Table 2.

Classification results for BRCA data

Methods	forgeNet-RF	RF	forgeNet-GBM	GBM	LRL
Average ROC-AUC	0.742	0.672	0.716	0.691	0.689
SD	0.066	0.048	0.100	0.022	0.084

Feature selection was also conducted for BRCA data. We obtained ranked gene importance lists by averaging importance scores across the five cross-validation results from all methods except LRL. For LRL, the intersection (456 genes) of the five selected feature sets is used as the final selected features. We chose top 500 ranked genes for each ranked list so that the numbers are of a similar magnitude as the genes selected by LRL. Functional analysis of all final gene lists was conducted by the Gene Ontology (GO) enrichment test using GOstats package (Falcon and Gentleman, 2007). We limited the analysis to GO biological processes containing 10–500 genes, and a P-value cutoff of 0.005. After manual removal of highly overlapping GO terms, the top 3 GO terms that contained the most number of selected genes are found in Table 3.

Table 3.

Top 3 GO biological processes for each method, after manual removal of redundant GO terms

ID	Term	P-value	Count	Size
forgeNet-RF
GO:0031647	Regulation of protein stability	0.00123	17	229
GO:0090502	RNA phosphodiester bond hydrolysis, endonucleolytic	0.00369	7	62
GO:1901998	Toxin transport	0.00499	5	35
RF
GO:2000679	Positive regulation of transcription regulatory region DNA binding	0.00255	4	19
GO:0010172	Embryonic body morphogenesis	0.00313	3	10
GO:0090042	Tubulin deacetylation	0.0042	3	11
forgeNet-GBM
GO:0001676	Long-chain fatty acid metabolic process	0.00138	9	84
GO:0032890	Regulation of organic acid transport	0.00155	6	40
GO:0046470	Phosphatidylcholine metabolic process	0.00449	7	65
GBM
GO:0006633	Fatty acid biosynthetic process	0.000454	12	121
GO:0030520	Intracellular ER signaling pathway	0.000643	7	47
GO:0010763	Positive regulation of fibroblast migration	0.00322	3	10
LRL
GO:0051047	Positive regulation of secretion	0.000609	20	317
GO:0006090	Pyruvate metabolic process	0.000911	9	90
GO:0019359	Nicotinamide nucleotide biosynthetic process	0.00204	8	82

The top GO term selected by forgeNet-RF was regulation of protein stability. It has been found that estrogen receptor (ER) alpha has increased abundance and activity in breast cancer. One of the mechanisms facilitating this change is the protection of ER from degradation by the ubiquitin–proteasome system (Tecalco-Cruz and Ramírez-Jarquín, 2017). Another critical protein, HER2 (human epidermal growth factor receptor 2), has also been found to have increased stability and activity in some breast cancer tissues through the formation of Her2-Heat-shock protein 27 (HSP27) complex (Kang et al., 2008). The protein stability mechanism has not been previously linked to the survival outcome of breast cancer. The second GO term found by forgeNet-RF, RNA phosphodiester bond hydrolysis, endonucleolytic, is part of rNRA and tRNA processing. It plays a critical role in the protein synthesis of the cancer cells. The third term, toxin transport, is specific to breast cancer. It is suggested that increased toxin presence in the mammary tissue is a predisposing factor to breast cancer (McManaman and Neville, 2003; Quezada and Vafai, 2014).

The forgeNet-GBM and GBM results both point to fatty acid metabolism, which is known to be dysregulated in breast cancer (Monaco, 2017). The GBM selected the ER signaling pathway, which is critically important in breast cancer development. The LRL selected GO terms include positive regulation of secretion, which includes lactation, in addition to a number of metabolic processes.

In this real data analysis, we were also interested in examining the feature graphs constructed by the two tree-based ensemble methods. We compared the estimated feature graphs with the real gene network employed in the original GEDFN paper (Kong and Yu, 2018) from the HINT database (Das and Yu, 2012). Among the 16 027 genes, 7816 of them were involved in the HINT network, and there was no connectivity (edge) information for the remaining 8211 genes. The estimated feature graphs by forgeNet-RF had an average (The average was taken over the graphs constructed from different folds of samples.)¹ of 8997.8 vertices, and 44.2% of them overlapped with the HINT gene network. The estimated feature graphs by forgeNet-GBM had an average of 428 vertices, and 52.6% of them fell in the HINT network. The difference of vertex numbers of the two tree-based methods was caused by their own tree construction mechanisms, and the percentages were roughly proportional to the genes covered by the HINT network.

Unlike the analysis in Section 3.4, comparison between the estimated feature graphs and the HINT network regarding edges was not feasible, as the underlying true predictive feature subgraph structure was unknown. We observed few overlapping edges between the estimated feature graphs and the HINT network, for both forgeNet-RF and forgeNet-GBM. This is expected. As seen in the simulation study, the estimated edges by RF and GBM tend to be the complimentary edges in the subnetwork involving true predictors. In addition, the true biological network is much more complex than a simple correlation network.

It can be noted that, in the case of real data applications, both GEDFN and forgeNet can be regarded as a way of feature prescreening. GEDFN utilizes external knowledge (e.g. the HINT network data), which cannot utilize features not presenting in the known feature graph. In contrast, forgeNet examines initial input with a larger feature space and screens features in a supervised manner, following the philosophy that the forest feature extractor should be able to decide the usefulness of a feature. Depending on the real dataset and the classification outcome of interest, the two ways of prescreening can agree or differ with each other, and there is no way to guarantee which mechanism dominates the other.

4.2 Breast invasive carcinoma microRNA data

We further applied forgeNets to the BRCA microRNA dataset (Koboldt et al., 2012). There was no readily available feature graph for the microRNA data. The dataset consists of 2588 microRNAs and 848 BRCA patients. Again, we examined the classification task for predicting the 3-year survival outcome. Similar to Section 4.1, we excluded patients with missing or censored survival time for which the 3-year survival outcome could not be determined. MicroRNAs with more than 50% of missing values were also screened out. As a result, the final dataset contained a total of P = 310 microRNAs and n = 424 patients, with 85% positive cases. Although this was not strictly an ‘$n\ll p$’ dataset, the number of features was on the same scale as the sample size. Therefore, it was still a problem that challenges traditional classification methods. We applied the K-Nearest Neighbor imputation (Troyanskaya et al., 2001) for the remaining missing values, and each microRNA was Z-score transformed.

Following the same 5-fold stratified cross-validation procedure as in Section 4.1, we obtained the classification results of the microRNA data, shown in Table 4. The microRNA data were more challenging than the gene expression data, as the ROC-AUCs for all methods were lower. Nevertheless, the forgeNets were again able to outperform their tree-based counterparts, as well as the LRL.

Table 4.

Classification results for BRCA microRNA data

Methods	forgeNet-RF	RF	forgeNet-GBM	GBM	LRL
Average ROC-AUC	0.637	0.528	0.617	0.560	0.571
SD	0.066	0.123	0.052	0.042	0.061

We analyzed the functions of the selected microRNAs using DIANA mirPath V.3 using a microT score threshold of 0.95 (Vlachos et al., 2012). The top 5 KEGG pathways for each method are shown in Table 5. As the LRL selected 29 microRNAs, we used the top 30 microRNAs for each of the other methods. All five methods selected ‘Hippo signaling pathway’ among the top pathways. The dysregulation of the pathway is associated with the metastasis and resistance to chemotherapy in breast cancer (Wei et al., 2018; Wu et al., 2020).

Table 5.

Top 5 pathways selected by each method using mirPath V.3

Methods	No. of significant pathways (P< 0.01)	Top 5 pathways	P-value
forgeNet-RF	12	Hippo signaling pathway	6.63E−06
		Glycosaminoglycan biosynthesis—KS	0.000752
		Rap1 signaling pathway	0.000882
		AMPK signaling pathway	0.000928
		Glycosphingolipid biosynthesis—lacto and neolacto series	0.00119
RF	3	Prion diseases	2.67E−20
		Hippo signaling pathway	4.69E−10
		Thyroid hormone synthesis	0.00651
		Adrenergic signaling in cardiomyocytes	0.0165
		Long-term potentiation	0.0165
forgeNet-GBM	6	Pathways in cancer	0.000248
		Transcriptional misregulation in cancer	0.000248
		Hippo signaling pathway	0.000417
		AMPK signaling pathway	0.000950
		Maturity onset diabetes of the young	0.00127
GBM	15	Prion diseases	3.75E−20
		Hippo signaling pathway	3.87E−16
		Signaling pathways regulating	5.31E−06
		pluripotency of stem cells
		Proteoglycans in cancer	0.000532
		Colorectal cancer	0.000794
LRL	8	GABAergic synapse	2.19E−05
		ECM–receptor interaction	2.19E−05
		Hippo signaling pathway	2.19E−05
		Morphine addiction	8.90E−05
		Proteoglycans in cancer	0.000251

Among the top 5 pathways selected by forgeNet-RF, three were signaling pathways, which was the most among all methods. The Rap1 signaling pathway is well -known for regulating breast cancer cell migration through modulating matrix metalloproteinases (McSherry et al., 2011). AMP-activated protein kinase (AMPK) signaling responds to a number of endocrine signals, and regulates energy, growth and motility of cells (Zhao et al., 2017). Its role in breast cancer progression and therapy has been well documented (Cao et al., 2019; Zou et al., 2017). The AMPK pathway was selected by both forgeNet-RF and forgeNet-GBM as the top 5.

Besides signaling pathways, forgeNet-RF also selected the glycosaminoglycan–keratan sulfate (KS) pathway and the glycosphingolipid pathway. KS is the newest glycosaminoglycan, and its roles in cancer have not been clearly elucidated (Caterson and Melrose, 2018). Recently it’s been found that increased KS epitope is associated with worse survival in pancreatic cancer (Leiphrakpam et al., 2019). Glycolipids are essential in maintaining plasma membrane stability. Aberrant glycosphingolipid metabolism plays critical roles in cancer progression and metastasis (Zhuo et al., 2018).

Comparatively, among the top five pathways selected by LRL, two were neurological pathways that bear no clear relation to breast cancer—GABAergic synapse, and morphine addiction. The extracellular matrix (ECM)–receptor interaction pathway is important in cancer progression (Walker et al., 2018), and proteoglycans are important for cell surface adhesion and cancer invasion (Nikitovic et al., 2018). Overall, forgeNet-RF achieved better performance in classification, as well as selected more interpretable features.

4.3 Healthy human metabolomics dataset

Another real dataset, we experimented, was the untargeted metabolomics dataset measured by high-resolution liquid chromatography–mass spectrometry from the Emory/Georgia Tech Center for Health Discovery and Well Being. The cohort was made up of healthy adults. The data were processed using apLCMS with hybrid mode (Yu et al., 2009, 2013). We limited the analysis to the baseline measurements of the subjects with available clinical data. The metabolic feature matrix contained 8807 features and 382 subjects, as well as clinical and demographic information. The classification task was to predict obesity as indicated by the body mass index (BMI). Metabolites with more than 10% of zero values were screened out. Other general confounders, including age, gender (male/female) and ethnicity (three races), were included as predictors. As a result, the final dataset contained a total of P = 4997 predictors, including 4993 metabolic features and 4 confounding variables. The obesity outcome was defined as BMI >30, and 25.6% of the subjects were positive cases. For each continuous predictor, its value was Z-score transformed.

The 5-fold stratified cross-validation classification results of the metabolomics data are shown in Table 6. Although the data were again challenging and no method performed very well, the forgeNets were better classifiers compared to other benchmarks. Using the top 10% of the metabolic features selected by each method, we conducted pathway analysis using Mummichog (Li et al., 2013). As shown in Table 7, RF selected the largest number of significant metabolic pathways, followed by forgeNet-RF. This is consistent with the simulation results. The top pathways selected by RF were all focused on amino acids metabolism. The top pathways selected by forgeNet-RF included amino acids metabolism, membrane lipid metabolism and reduction–oxidation pathways, most of which were also in the list of the RF results. LRL selected a slightly smaller number of pathways than forgeNet-RF. Its top pathways were diverse with some pathways with no apparent relation to BMI, such as the prostaglandin and arachidonic metabolism pathways. The pathways selected by GBM were more focused on glycolipid metabolism, and those selected by forgeNet-GBM were diverse, some of which do not have a clear link to BMI. Overall, RF and forgeNet-RF showed the most interpretable pathway analysis results. Combined with its better predictive power, forgeNet-RF was again the preferred method among all those being compared.

Table 6.

Classification results for healthy human metabolomics data

Methods	forgeNet-RF	RF	forgeNet-GBM	GBM	LRL
Average ROC-AUC	0.686	0.649	0.682	0.666	0.649
SD	0.066	0.042	0.044	0.039	0.077

Table 7.

Top 5 pathways selected by each method using Mummichog

Methods	No. of significant pathways (P < 0.05)	Top 5 pathways	P-value
forgeNet-RF	17	Tryptophan metabolism	0.00126
		Histidine metabolism	0.00681
		Lipoate metabolism	0.00832
		Glycosphingolipid metabolism	0.00865
		Glutathione metabolism	0.00924
RF	26	Alanine and aspartate metabolism	0.00008
		Urea cycle/amino group metabolism	0.00134
		Nitrogen metabolism	0.00185
		Aspartate and asparagine metabolism	0.00294
		Tryptophan metabolism	0.00378
forgeNet-GBM	5	Histidine metabolism	0.00059
		Vitamin B12 (cyanocobalamin) metabolism	0.00681
		Squalene and cholesterol biosynthesis	0.01949
		Androgen and estrogen biosynthesis and metabolism	0.0268
		Ubiquinone biosynthesis	0.03655
GBM	14	Glycosphingolipid metabolism	0.00823
		Blood group biosynthesis	0.01361
		Glycosylphosphatidylinositol-anchor biosynthesis	0.01361
		Glycosphingolipid biosynthesis—lactoseries	0.01361
		Glycosphingolipid biosynthesis—neolactoseries	0.01361
LRL	14	Glycerophospholipid metabolism	0.00151
		Lysine metabolism	0.00176
		Prostaglandin formation from dihomo gama-linoleic acid	0.00193
		Arachidonic acid metabolism	0.00378
		Saturated fatty acids beta-oxidation	0.01294

5 Conclusion

We presented forgeNet that uses tree-based ensemble methods to extract feature connectivity information, and uses GEDFN for graph-based predictive model building. The new method was able to achieve sparse connection for neural nets without seeking external information, i.e. known feature graphs. It works well in the ‘$n\ll p$’ situation. Simulation experiments showed forgeNets’ relatively higher classification accuracy compared to existing methods; the TCGA BRCA RNA-seq dataset, the TCGA BRCA microRNA dataset and a metabolomics dataset demonstrated the utility of forgeNets in both classification and the selection of biologically interpretable predictors.

Funding

This study was supported by National Institutes of Health [R01GM124061].

Conflict of Interest: none declared.