Abstract
Motivation
In the analysis of high-throughput omics data from tissue samples, estimating and accounting for cell composition have been recognized as important steps. High cost, intensive labor requirements and technical limitations hinder the cell composition quantification using cell-sorting or single-cell technologies. Computational methods for cell composition estimation are available, but they are either limited by the availability of a reference panel or suffer from low accuracy.
Results
We introduce TOols for the Analysis of heterogeneouS Tissues TOAST/-P and TOAST/+P, two partial reference-free algorithms for estimating cell composition of heterogeneous tissues based on their gene expression profiles. TOAST/-P and TOAST/+P incorporate additional biological information, including cell-type-specific markers and prior knowledge of compositions, in the estimation procedure. Extensive simulation studies and real data analyses demonstrate that the proposed methods provide more accurate and robust cell composition estimation than existing methods.
Availability and implementation
The proposed methods TOAST/-P and TOAST/+P are implemented as part of the R/Bioconductor package TOAST at https://bioconductor.org/packages/TOAST.
Contact
ziyi.li@emory.edu or hao.wu@emory.edu
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Complex samples are mixtures of different cell types, where alterations in cell compositions have been reported to associate with etiology and progression of many diseases. For example, neuronal cell death is a prominent pathological feature of Alzheimer’s disease (AD) (Yang et al., 2001), and immune infiltration is significantly correlated with tumor progression in various cancer types (Li et al., 2016). In addition to its direct link with diseases, cell composition is also an important covariate to estimate and account for in analyzing high-throughput data from complex tissues. Studies have found that ignoring the composition may produce biased results in high-throughput data analysis (Jaffe and Irizarry, 2014; Zheng et al., 2017) and mask critical disease-related changes in distinct cell types (Guintivano et al., 2013).
Cell compositions can be experimentally obtained through technologies, such as immunohistochemistry, flow cytometry and single-cell sequencing. However, all of these approaches are costly and labor intensive, and thus, cannot be applied widely to large-scale studies. As alternatives, efficient in silico computational methods for estimating cell compositions (referred to as the ‘deconvolution’ methods) have been developed. These methods can be roughly categorized into three groups: reference-based (RB) (Clarke et al., 2010; Gong et al., 2011; Newman et al., 2015), reference-free (RF) (Houseman et al., 2014; Repsilber et al., 2010) and partial reference-free (PRF) methods (Brunet et al., 2004; Lee and Seung, 2001; Rahmani et al., 2018; Zhong et al., 2013).
The RB methods require reference panel data obtained from purified tissues. The deconvolution is based on some type of regression, where the reference data are used as predictors and the regression coefficients are estimated compositions (Abbas et al., 2009; Newman et al., 2015; Zheng et al., 2018). They are in general believed to be the most accurate approach among the three groups (Li et al., 2019; Newman et al., 2015; Teschendorff et al., 2017). The reference panels required in the RB methods, however, are expensive to obtain and only available for a limited number of tissue types. In addition, the reference panels are platform-dependent. For example, reference from microarray data cannot be used in the deconvolution of RNA-seq data. Moreover, variations between the reference and samples to be deconvolved, which could be caused by different biological and clinical conditions, have been found to lead to inaccurate proportion estimation from RB (Li and Wu, 2019; Yousefi et al., 2015). For tissues without proper references, RF methods provide a feasible solution (Johnson et al., 2016, 2017). They are based on some type of factor analysis, such as non-negative matrix factorization (NMF) (Houseman et al., 2014; Repsilber et al., 2010), where the pure cell-type profiles and cell compositions are jointly estimated. However, the RF applications can suffer from low accuracy and difficulty in assignment of cell-type labels. More importantly, the RF method usually requires a large sample size because there are many parameters that need to be estimated. This greatly limits its application in small-scale studies.
The PRF methods are similar to RF in that they do not require a reference panel. However, they incorporate additional biological information in the model to improve estimation results. Because they do not rely on the reference panel, they have wider applications than RB methods and reduce the biases caused by inaccurate reference panels. They incorporate biological information, such as cell-type-specific markers, which helps to improve the estimation and avoid the difficulty in cell-type labeling. The additional biological information required for the PRF methods are typically easy and cheap to obtain from either existing data or light experiments.
PRF is a promising deconvolution approach that provides a feasible solution for scenarios where RF and RB methods do not work well, in particular for small-sized experiments without a reference panel. Currently there are a few PRF methods available. Digital sorting algorithm (DSA) uses known cell-type-specific marker genes to reduce the number of model parameters (Zhong et al., 2013). It averages the expression of marker genes for each cell type as a surrogate for reference panels, and deconvolves mixed expression data. The simple averaging step does not handle noise in the marker gene expression well, often resulting in biased estimates. The semi-supervised NMF algorithm for KL divergence (ssKL) (Brunet et al., 2004) and for Euclidean distance (ssFrobenius) (Lee and Seung, 2001) are similar PRF methods but use different converging criteria. Bayesian Cell Count Estimation (BayesCCE) improves the RF model through a Bayesian framework by imposing a prior on cell composition estimators. However, BayesCCE has a heavy computation burden because of the usage of Dirichlet prior and is only designed for DNA methylation data (Rahmani et al., 2018).
Here, we present two novel partial RF algorithms for estimating cell compositions from gene expression profiles of complex tissues. The essence of our method is to run RF deconvolution on pre-specified cell-type-specific markers. In addition, the prior knowledge of cell compositions can be incorporated, which further improves the accuracy and robustness of the method. Through extensive simulation studies and real data analyses, we demonstrate that the proposed method has more robust and accurate proportion estimations than existing RF, PRF and even RB methods. We also show that the prior knowledge (for cell-type-specific markers and prior cell compositions) can be obtained from various sources, and we evaluate the performance of the methods when the priors are from different platforms, including microarray, RNA-seq, single-cell RNA-seq (scRNA-seq) and existing marker repositories. The proposed method is implemented as part of the Bioconductor package TOols for the Analysis of heterogeneouS Tissues (TOAST) (https://bioconductor.org/packages/TOAST).
Previously, we developed a feature selection method to improve RF deconvolution (Li and Wu, 2019). Although the same name ‘TOAST’ is used, the proposed methods in this work differ in motivation, method design and application. Li and Wu (2019) focus on data with large sample size (N>50), and it is a feature selection tool compatible with most existing RF deconvolution algorithms. This work focuses on small sample application and is a partial RF method with requirements for cell-type-specific marker information and optionally prior knowledge of proportions. Both are named TOAST, because both methods are developed for the same general purpose of cell composition estimation and are implemented in our Bioconductor package TOAST.
2 Materials and methods
2.1 Overview of TOAST/-P and TOAST/+P
The required input for the proposed method includes a data matrix of expression profiles (Y) and a list of cell-type-specific marker genes. Here, the cell-type-specific markers are defined as genes that are only expressed in one cell type and have zero or low expressions in other cell types. An additional option is that users can provide prior knowledge of cell compositions for calibrating estimation scales. The procedures without and with the prior cell compositions are referred to as TOAST/-P and TOAST/+P, respectively.
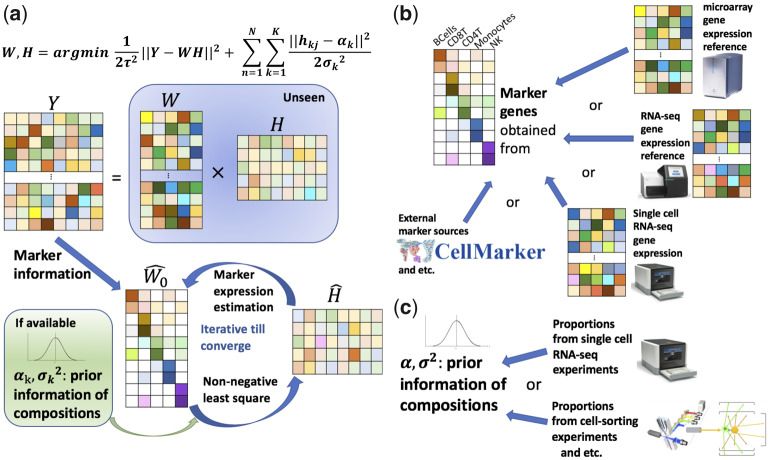
Figure 1a illustrates the general workflow of the proposed method. TOAST(/-P or/+P) is an iterative algorithm consisting of two steps: estimating marker expressions in a reference panel (), and solving for cell compositions (). As shown in Figure 1b and c, the biological information can be acquired from existing data without additional experiments. The cell-type-specific markers can be obtained by analyzing gene expression profiles in reference panels from different platforms, e.g. microarray, RNA-seq, or scRNA-seq. Vast amounts of existing public data make it possible to identify these markers for many cell types. In addition, existing marker repositories [e.g. CellMarker by Zhang et al. (2019)] provide information on many cell-type-specific genes, which can be used. The prior knowledge of cell compositions can be obtained from cell-sorting or single-cell experiments. The wide application of scRNA-seq experiments on many tissues, e.g. by the Human Cell Atlas (Rozenblatt-Rosen et al., 2017), will eventually provide reference expressions and prior cell compositions for virtually a majority of cell types in most tissues. These resources will greatly benefit our proposed method.
Fig. 1.
A schematic workflow of TOAST. We assume five cell types and eight subjects. (a) TOAST requires a data matrix of tissue expression profiles (Y) and cell-type-specific marker informtion as inputs. Prior information of cell compositions is optional but highly recommended. TOAST adopts an iterative algorithm to solve for pure cell-type profile () and cell compositions (). (b) Cell-type-specific markers can be selected from gene expression reference by microarray or RNA-seq or scRNA-seq, or from existing marker repository, etc. (c) Prior information of cell compositions can be obtained from scRNA-seq or cell-sorting experiments, etc
2.2 Model formulation
The gene expression matrix is denoted by Y, a P × N matrix representing the expression from P genes and N samples. All the deconvolution methods, whether RB or RF, try to decompose Y into the multiplicity of two matrices, . Here, W is a P × K matrix representing the pure cell-type profiles for K cell types and H is a K × N matrix representing the cell compositions of K cell types in N samples. Additional constraints are usually imposed on the model, which require that all elements in W and H are non-negative and each column of H sums up to one.
The list of cell-type-specific marker genes is denoted by , where represents a vector of cell-type-specific genes for cell type k. We assume the length of is lk, thus, the total length of M is . Optionally, the prior knowledge of cell compositions can be provided. We denote the prior means and variances for the proportions for all K cell types as and , respectively.
Given Y and M, TOAST first subsets the observations corresponding to the genes in the marker list and obtains an L × N expression matrix . Assume
| (1) |
where and H are unseen parameters for pure cell-type profiles of marker genes and mixing proportions that we aim to estimate. Since contains expressions for marker genes, which are assumed to be expressed in only one cell type, each row of should only have one non-zero entry. This greatly reduces the number of parameters to be estimated in an RF deconvolution, and is the foundation of the proposed method. We initialize by if , and otherwise for
Our algorithm iterates between two steps. Without and , the first step is to estimate H with and using non-negative least square (Chen and Plemmons, 2010) subject to hkj>0, . The second step is to estimate marker-specific expression values by if , and otherwise for
When cell compositions of the same tissue types from previous studies are known, we denote the composition matrix by . Rows of represent samples and columns for cell types. We can easily calculate the mean and SD priors through and , where and are the operations to compute the column-wise mean and column-wise SD of a matrix. Thus, and are two vectors of length K representing the prior knowledge of mean and SD for each cell type. With and , the second step is unchanged while the first step becomes solving for H by incorporating prior knowledge in a Bayesian framework. Specifically, we write Equation (1) into a probabilistic model as
where yij is the (i, j)-th element in matrix is the i-th row in matrix and is the j-th column in matrix H. We further assume that each element of H follows a prior distribution
We adopt a Normal prior here instead of Dirichlet prior for computation convenience and efficiency. Deriving a maximum likelihood-based solution for this model and including the previously mentioned constraints lead to the following optimization problem:
| (2) |
where . Solving (2) immediately results in an explicit solution for :
| (3) |
where and are estimates for and H from previous iteration. We then impose post hoc constraints and on . Detailed derivations for Equations (2) and (3) are presented in Supplementary Section S5.
We summarize the procedure in Supplementary Algorithm S1. The algorithm without prior (empty α), i.e. switching to step 5(a), is TOAST/-P; otherwise, with step 5(b), it is TOAST/+P. The stopping criterion, absolute maximum difference between from two consecutive iterations being smaller than , is applied for all our simulation studies and real data analyses. Due to the adoption of a linear model and a Normal prior, the proposed algorithm has superior computational speed and efficiency. We benchmark the proposed methods on a laptop computer with 4 GB RAM and Intel Core i5 CPU. For a dataset with 100 samples and 4 cell types with 20 marker genes per cell type (i.e. contains 100 columns and 80 rows), it takes less than a second for both TOAST/-P and TOAST/+P to estimate cell compositions.
TOAST/-P and TOAST/+P have been implemented as parts of R/Bioconductor package TOAST. In addition to estimating cell compositions, we also provide functions to select cell-type-specific markers from bulk pure cell-type profiles or scRNA-seq data. The tissues that have prior knowledge of compositions provided in the current package include human PBMC, brain, pancreas, liver and skin. We provide detailed descriptions about our simulation study design (Supplementary Section S1), real datasets and pre-processing (Supplementary Section S2), implementation of existing methods (Supplementary Section S3) and prior knowledge of cell compositions (Supplementary Section S4) in Supplementary Material.
2.3 Design of simulation studies
The simulations are based on a real gene expression dataset obtained from Gene Expression Omnibus with accession number GSE11058 (Abbas et al., 2009). This dataset contains microarray gene expression of four immune cell lines, thus, we assume there are four cell types in the mixture. For all simulations, we generate the expressions for pre-specified (also randomly selected) marker genes () instead of all genes (Y). The first step is to simulate subject-specific pure cell-type profiles. For a subject, we randomly generate pure cell-type expressions from the Normal distribution for marker genes. The cell-type-specific mean and variance of each gene, denoted by μik and , are estimated from the expressions of randomly selected genes in the immune dataset. For markers of cell type k, their corresponding gene expressions in cell type k are drawn from . The expressions in cell type j () are drawn from , where ϕ is the parameter controlling magnitude of non-specific expressions ranging from 0 to 1. When the number of incorrectly selected markers r is specified as non-zero, we let for r randomly selected markers per cell type.
The above procedure allows cross-subject heterogeneity in pure profiles, which more accurately mimics the real scenarios where each sample has its own distinct cell-type expression. After pure cell-type profiles are generated, we simulate cell compositions from Dirichlet distribution with parameters , and mix the pure cell-type profiles with corresponding cell compositions. Random measurement errors are added to the mixed signals with similar procedures as Li et al. (2019). For all simulation settings, results from 100 Monte Carlo experiments are summarized and presented.
3 Results
3.1 Simulation studies
We compared TOAST/-P and TOAST/+P against two state-of-the-art RF/PRF methods for microarray gene expression data: NMF (Repsilber et al., 2010) and DSA (Zhong et al., 2013). We considered various experimental designs, including different sample sizes, number of markers per cell type, magnitude of noises and number of wrong markers.
3.1.1 Benchmark for sample sizes and numbers of marker genes
We first evaluated the impact of sample size and number of markers. To fairly assess all methods, we adopt two evaluation metrics, absolute mean bias (Abs Mean Bias) and averaged Pearson correlation of estimated versus true proportions over all cell types. Abs Mean Bias reflects the accuracy of estimated proportions, while correlation with true proportions shows whether the general trend of estimated proportions is aligned with true proportions in every cell type.
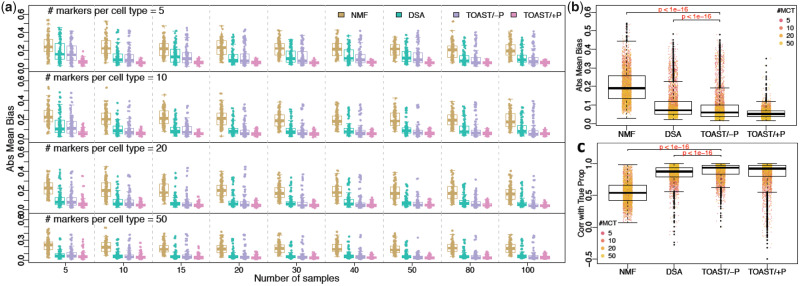
As shown in Figure 2a and Supplementary Figure S1, TOAST/-P consistently achieves lower Abs Mean Biases and higher correlations with true proportions (Corr with True Prop) than NMF and DSA averaged over 100 Monte Carlo datasets, while TOAST/+P further outperforms TOAST/-P in reducing Abs Mean Bias. The advantages of TOAST/-P over NMF and DSA are statistically significant (Fig. 2b and c). It is also important to note that DSA and the proposed methods all have better performance than NMF, demonstrating the benefits of utilizing marker information in the algorithm. From left to right columns of Figure 2a, with sample sizes increasing from 5 to 100 and all methods have decreased biases, indicating that greater sample sizes lead to better proportion estimation. For top to bottom rows, the number of markers per cell type increases from 5 to 50, and the accuracy from all PRF methods TOAST/-P, TOAST/+P and DSA further increases, suggesting more markers also help improve the PRF performance.
Fig. 2.
Results of simulation studies to evaluate the performance of TOAST/-P, TOAST/+P and existing methods. (a) Boxplots of Abs Mean Bias of estimated versus true proportions, by NMF, DSA, TOAST without prior (TOAST/-P) and TOAST with prior (TOAST/+P). Four rows from top to bottom are results with 5, 10, 20 and 50 markers per cell type. Nine columns from left to right are results with 5, 10, 15, 20, 30, 40, 50, 80 and 100 samples in total. (b and c) Abs Mean Biases and Corr with True Prop of four methods across different sample sizes and marker numbers. The P-values are obtained using paired t-test. The presented results are summarized over 100 Monte Carlo simulation experiments
We further investigate the impact of number of markers on deconvolution performance by extending the range of marker numbers (from 2 to 100). The detailed simulation setting and results are described in Supplementary Section S1. Supplementary Figure S7 demonstrates that, a large number of markers (e.g. 100) do not necessarily lead to better results. Instead, a moderate number of markers, 10–60, provide the most ideal results.
In addition, we compare TOAST/-P and TOAST/+P with two other PRF methods: ssKL (Brunet et al., 2004) and ssFrobenius (Lee and Seung, 2001). Supplementary Figure S8 shows that ssKL and ssFrobenius have comparable correlation with true proportions and Abs Mean Bias with DSA, and are worse than the proposed methods. Based on these results and the finding from a previous study that DSA has superior deconvolution performance over ssKL and ssFrobenius (Hunt et al., 2019), we use DSA as the comparison PRF method for the rest of our evaluation.
3.1.2 Robustness to non-specific expressions
We next evaluated the robustness of all methods against non-specific expressions. An ideal cell-type-specific marker should have high expression in one cell type (specific), but zero expression in all other cell types (non-specific). The existence of non-specific expressions is a violation of model assumptions, but commonly occurs in real data settings. Supplementary Figures S2a and S3 summarize the Abs Mean Biases and Corr with True Prop of all methods with the increase of non-specific expression from 1% to 50% of specific expression (x-axis) in different sample sizes (top to bottom panels).
Supplementary Figure S2a shows that the increase of non-specific expressions has no impacts on the RF method (NMF), which is as expected since the RF method does not consider cell-type specificity. The PRF methods (DSA, TOAST/-P and TOAST/+P) are much better than the RF method under all scenarios because these models use additional information. Furthermore, the PRF methods are mostly robust against the increase of non-specific expressions, especially for Corr with True Prop (Supplementary Fig. S3). This confirms the robustness and validity of the PRF method in real applications, since the cell-type specificity assumption could be moderately violated. Compared with correlations, Abs Mean Bias is more affected by the increase of non-specific expression (Supplementary Fig. S2a). From left to right in each panel of Supplementary Figure S2a, DSA and TOAST/-P have larger biases, while the biases for TOAST/+P are almost constant. The bias increase is more substantial when sample size is small (upper rows) than large (bottom rows), suggesting the benefits of increasing sample size when selected markers are of low quality. Among all PRF methods, TOAST/-P maintains the highest correlation with the increase of non-specific expression (Supplementary Fig. S3), with small advantages over TOAST/+P and DSA. TOAST/+P has the lowest Abs Mean Bias against non-specific expression, with only minimum biases increase for larger non-specific expression. This demonstrates that the incorporation of prior composition knowledge can improve estimation even when the model assumption does not entirely hold.
Supplementary Figure S2b and c summarizes the results of all scenarios presented in Supplementary Figures S2a and S3. They confirm the above observations from separate scenarios, including the highest correlation using TOAST/-P and lowest bias using TOAST/+P. TOAST/-P significantly outperforms DSA and NMF in both metrics. TOAST/+P sometimes has slightly lower correlation than TOAST/-P when the ranks of prior means are different from the true value, especially for cell types with similar proportions. However, as long as the scale of the prior means is close to the true value, it is more likely to lead to lower biases.
3.1.3 Robustness to the inclusion of wrong markers
We next evaluated the impact of another commonly present scenario: the inclusion of wrong markers. Here, the wrong markers are selected as genes with similar expression levels in all cell types, which violate the assumption that one cell type has much higher expression than others. We allow up to 40% wrong markers in the simulations.
Although all methods perform worse with more wrong markers, Supplementary Figures S2d, S4 and S5 demonstrate that both TOAST/-P and TOAST/+P have comparable correlations and much lower biases than existing methods, suggesting their outstanding robustness against the inclusion of wrong markers. DSA shows comparable and sometimes slightly higher correlations than the proposed methods (Supplementary Fig. S4). We suspect that by averaging all markers for each cell type, DSA alleviates the impact of wrong markers on correlation more than our proposed methods. However, the proposed methods have much lower Abs Mean Bias (Supplementary Fig. S2d), indicating that overall they have more accurate estimations than DSA with the inclusion of wrong markers. From the upper to lower panel in Supplementary Figures S2d and S4, the number of markers per cell type increases from 5 to 30. We find that increasing the number of markers helps reduce bias for all PRF methods, and helps even more in improving correlations. When number of markers per cell type increases from 5 to 30, the mean correlations of all PRF methods almost doubled. However, when the number of wrong markers selected increase from 1 to 6 out of 30 markers per cell type, the mean correlations of all PRF methods decreased by almost one-third. These observations hold when sample size is relatively large (50 for Supplementary Figs S2d and S4) and small (10 for Supplementary Fig. S5). Our findings emphasize the importance of choosing high-quality markers.
3.1.4 Impacts of cell-type composition variations
Lastly, we designed a simulation setting to evaluate the magnitude of cell-type composition variations on the accuracy of cell composition estimations. Intuitively, there should be a reasonably large variation in cell-type composition among samples so that RF/PRF algorithm can effectively solve for such compositions. Our simulation setting (details presented in Supplementary Section S1) evaluates the variations of cell-type compositions ranging from large () to small (). The correlation of estimated proportions versus true proportions and Abs Mean Bias from the existing method DSA and our proposed method TOAST/-P and TOAST/+P are presented in Supplementary Figure S6. We observe that larger variation in cell-type compositions is associated with better cell composition estimations. All our previous simulation results are based on mean cell-type composition SD being around 0.11, which is close to the level we observed from the Cibersort blood data (introduced later). We believe that our simulation settings more accurately mimic real data and should in general perform well in real data, but we acknowledge that the accuracy could be lower when the variation of proportions is very small.
3.2 Real data analyses
We next benchmarked the proposed methods on in vitro and in vivo mixtures of distinct cell types, including both solid tissues and blood. For the first part of the evaluation, we obtained three microarray gene expression datasets: the Mouse-Mix data (Shen-Orr et al., 2010), the CiBerSort Peripheral Blood Mononuclear Cell (CBS PBMC) data (Newman et al., 2015) and the Diabetes PBMC data (Kaizer et al., 2007). For the second part of the evaluation, we obtained gene expression data from two AD studies, which will described in detail later. The Mouse-Mix data contains 33 manually mixed tissues of rat brain, liver and lung with known-mixing proportions. The CBS PBMC data contain 20 human PBMC samples, with cell compositions previously quantified by flow cytometry. The Diabetes PBMC data contain 117 children PBMC samples, including 24 samples from healthy subjects, 81 from Type I and 12 from Type II Diabetes patients. Details about reference panels and prior parameters are presented in the Supplementary Sections S2 and S4.
3.2.1 Cell composition estimation using markers from microarray gene expression reference
When an accurate reference panel is available, RB methods are often used to estimate cell compositions, as they have been shown to be more accurate than RF/PRF methods (Li et al., 2019; Newman et al., 2015). Here, our focus is not to compare with RB methods, but to benchmark the proposed methods under different scenarios.
For each dataset, we evaluated DSA, TOAST/-P and TOAST/+P with varying numbers of selected markers, sample sizes and number of wrong markers. In all the real data analyses, we select the markers using limma (Ritchie et al., 2015) with FDR<0.05 as the significance criteria. Similar to our simulation studies, we evaluate the Abs Mean Bias and correlations of estimated versus true proportions. Because we only obtain one bias and correlation evaluation for each scenario, we summarize the results from all scenarios by method and dataset in boxplots, i.e. Supplementary Figure S9a, c and e for MouseMix, CBS PBMC and Diabetes PBMC datasets. TOAST/-P shows significantly lower biases and higher correlations than DSA across the three datasets and different settings. TOAST/+P has similar correlations as TOAST/-P, but much lower estimation biases, which is consistent with what we observe in our simulation studies.
Supplementary Figure S9b, d and f shows the estimated versus true (or RB) proportions and confirm the proposed methods have more accurate estimations than DSA. Moreover, the performance improvement of TOAST over DSA is higher in the CBS PBMC and Diabetes PBMC data than in the MouseMix data. As described above, the MouseMix data were generated by manually mixing tissues while the CBS PBMC and Diabetes PBMC are measured from real human PBMC. Thus, the latter two datasets are more noisy than the MouseMix data, due to cross-subject heterogeneity and the existence of unmeasured cell types. This indicates that the benefits of TOAST become more obvious when noise levels are higher.
TOAST also provides advantages over DSA when sample size is smaller, e.g. in CBS PBMC (N=20, Supplementary Fig. S9c and d) compared to Diabetes PBMC data analysis (N=117, Supplementary Fig. S9e and f). To further demonstrate this point, we perform deconvolution on the healthy subjects of the Diabetes study (N=24). Results from this analysis (Supplementary Fig. S10) show that both TOAST/+P and TOAST/-P have better Corr with True Prop (0.82 for TOAST/+P and TOAST/-P, 0.78 for DSA), and reduce Abs Mean Bias by more than a third in comparison with DSA. The advantages of TOAST over DSA are greater for the healthy subjects only study (Supplementary Fig. S10) compared to using all samples (Supplementary Fig. S9f), confirming the benefits of TOAST in deconvolution with smaller sample sizes.
3.2.2 Cell composition estimation using markers from different sources
An important advantage of PRF methods is the possibility to borrow information across platforms. Consider the situation where one wants to deconvolve microarray data, but there is only a reference panel available from RNA-seq data. The quantitative values of the reference panel cannot be used in an RB deconvolution, but the expression status of the genes is very likely to be consistent from both platforms. Thus, the information of cell-type specificity can be transferred from RNA-seq to microarray. That is, one can identify markers from RNA-seq and then use them in microarray deconvolution through PRF methods.
We compared the performance of PRF methods (DSA, TOAST/-P and TOAST/+P) in deconvolving CBS and Diabetes PBMC data, with markers obtained from different platforms including RNA-seq, scRNA-seq, or from existing knowledge database CellMarker (Zhang et al., 2019), which provides a catalog of marker genes for many cell types in human and mouse. We also tried to use mouse marker genes to test the possibility of borrowing marker information across species (the CBS and Diabetes data are from human). Independent prior knowledge of PBMC cell types is used in TOAST/+P for both CBS and Diabetes datasets. When reference panels from other platforms are available, we also compare the performance of PRF versus RB methods (Cibersort). For the RB method, the references from RNA-seq and scRNA-seq (averaged profiles), i.e. cross-platform references, are used. It would be useful to understand how RB with cross-platform reference actually performs in reality.
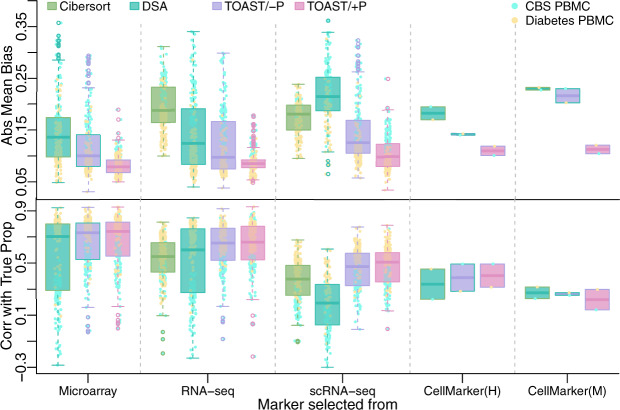
To obtain a fair evaluation and reduce randomness in the results, we again considered different selections of marker numbers, sample sizes and number of wrong markers as described in the previous section. Figure 3 summarizes the absolute biases and Corr with True Prop for all methods across different information sources. First, the proportion estimations from the proposed methods achieve lower biases and higher correlations than existing methods, including Cibersort with cross-platform references. Notably, TOAST/+P can greatly reduce estimation bias compared to existing methods regardless of where the markers are selected. Second, it is interesting that using bulk samples as references to select markers (Fig. 3, Microarray and RNA-seq columns) leads to similar deconvolution accuracy, and is better than using markers and references from scRNA-seq (scRNA-seq column). Moreover, having a reference panel, regardless of the platform, is better than using markers from CellMarker, i.e. CellMarker(H) column in Figure 3 (H is for human), and much better than human-symbol-mapped mouse markers, i.e. CellMarker(M) column in Figure 3 (M is for mouse). In addition, the results show that when the reference profiles are from the wrong platform (e.g. using RNA-seq or scRNA-seq reference to deconvolve microarray), the RB method is worse than TOAST (Fig. 3, RNA-seq and scRNA-seq columns). Overall, these results demonstrate that the proposed method is the most accurate and robust, especially when prior knowledge of composition is used in TOAST/+P.
Fig. 3.
Deconvolution performance in two real datasets with markers selected from different sources. From left to right, cell-type-specific markers are selected from microarray, RNA-seq, scRNA-seq immune references, CellMarker (http://biocc.hrbmu.edu.cn/CellMarker/) human immune cell-type markers and mouse immune cell-type markers (mapped to human symbols). Four methods under evaluations are Cibersort, DSA, TOAST/- and TOAST/+P. For the left three columns, Abs Mean Bias and correlation with true proportions are obtained from different combinations of marker number selections (5, 10, 15, 20, 30 and 50), sample size selections (5, 10, 15 and 20 for CBS PBMC data and 5, 10, 20, 30, 50 and 100 for Diabetes PBMC data) and number of wrong markers (0, 1, 2 and 3)
We visualize the proportions estimated from different methods versus true proportions using markers obtained from RNA-seq and scRNA-seq in Supplementary Figures S11 (CBS PBMC data) and S12 (Diabetes PBMC data). For scenarios of using scRNA-seq data as reference, we also evaluated the performance of a recently developed method MuSiC (Wang et al., 2019), which is designed to deconvolve bulk RNA-seq gene expression data with scRNA-seq profiles. It is not an entirely fair evaluation for MuSiC since the bulk data used here are from microarray instead of RNA-seq. However, it provides useful information to benchmark the methods. Again, the proposed methods outperform MuSiC in both correlation and bias (Supplementary Figs S11b and S12b). The proportions estimated using CellMarker information are shown in Supplementary Figures S13 and S14. They confirm our observations from Figure 3 that TOAST has a more accurate proportion estimation than DSA using markers from CellMarker. They also show using same-species markers are better than using cross-species markers (in this case, using mouse markers to deconvolve human data).
3.2.3 Brain cell composition estimation in AD
AD is an irreversible, progressive and detrimental brain disorder that causes degeneration in brain cells. Existing study of inferring cell compositions from bulk gene expression data usually considers two or three cell types (Gasparoni et al., 2018; Hagenauer et al., 2018). Here, we apply RB and PRF deconvolution methods on bulk microarray gene expression data using scRNA-seq data as reference, in order to understand the cell compositions of more cell types.
We first obtained the microarray gene expression data from the Religious Orders Study and Memory and Aging Project (ROS/MAP) (Bennett et al., 2018). Among all samples, 25 of them have also been sequenced by scRNA-seq (Mathys et al., 2019). We perform deconvolution on these 25 bulk microarray samples, and compare the estimated proportions against the cell compositions summarized from scRNA-seq study (SC proportions). As the scRNA-seq study profiles, 48 subjects in total, we use cell compositions from the other 23 samples to calculate prior parameters for TOAST/+P. Supplementary Figure S15a presents the estimated proportions from all methods against SC proportions. All methods perform worse compared to previous studies, which we suspect is for several reasons: small sample size (25), large number of cell types (8) and the discrepancy between bulk and single-cell experiments. Nevertheless, we still find TOAST/+P has the highest correlations and lowest Abs Mean Bias with SC proportions among all methods.
We further evaluated the performance of the proposed method from another microarray gene expression dataset (Patel et al., 2019) (GSE118553), which includes 27 controls (CTRL), 33 asymptomatic AD (AsympAD) and 52 AD subjects. There are expression profiles for three brain regions that are known to be affected by AD neuropathology (entorhinal cortex, temporal cortex and frontal cortex), and one region that is partially spared by the disease (cerebellum). Supplementary Figure S15b shows the estimated proportions for frontal cortex (top four panels), and the proportions from 48 prefrontal cortex samples of ROS/MAP study by scRNA-seq (bottom panel). Although the samples from the two datasets are different, the comparisons between the proportions could provide hints about the method performance, e.g. by comparing the scale of the same cell types or trends across the cell types between ROS/MAP and AD/AsympAD studies. As expected, after incorporating the prior knowledge of compositions, the scale of results by TOAST/+P is the closest to the single-cell results. Among all existing methods, Cibersort appears to provide results the most similar to that from scRNA-seq. However, it greatly overestimates compositions for oligodendrocytes and astrocytes, and its proportions are zero for inhibitory neurons and oligodendrocytes progenitor cells. In comparison, the proportions estimated by DSA and MuSiC are completely different in scale from single-cell proportions.
In addition to the comparisons with single-cell proportions, we also compared the estimated proportions across different brain regions. One prominent pathology feature of AD is the loss of neuronal cells (Yang et al., 2001, 2003). Interestingly, we observe a decrease of neuronal cell proportions in AD compared to CTRL and AsympAD samples by all methods in the three regions that are affected by the disease (Supplementary Figs S16–S19). In contrast, the neuronal cells remain stable or even increase using all four methods in the cerebellum. In this analysis, we do not have a gold standard to benchmark the performance. But the interesting results observed in estimated proportions suggest that the in silico deconvolution methods included in the proposed algorithm can provide insights about cell compositions of complex tissues.
4 Discussion
In summary, we present a partial RF deconvolution method that utilizes cell-type-specific markers and prior composition knowledge to guide cell composition estimation. The proposed method provides a satisfactory solution for the deconvolution of microarray gene expression data. It will be particularly useful when an appropriate reference panel is unavailable (i.e. when the RB method cannot be applied) and the sample size is small (i.e. when the RF method will be unstable).
TOAST/+P is recommended when prior knowledge on cell compositions is available, since the incorporation of such information can stabilize the scales of estimation. Systematic estimation bias is often observed in RF deconvolution due to the existence of unseen cell types, measurement noises and non-identifiability issue (Rahmani et al., 2018). Our comprehensive evaluations demonstrate the desirable performance of TOAST/+P in various datasets under different settings.
As we previously discussed in Li and Wu (2019), RF methods usually require a large sample size in order to obtain accurate cell composition estimations. This hinders the application of RF deconvolution in small-scale studies where the reference panel that is needed in RB deconvolution is lacking. Our proposed methods, however, can accurately estimate cell compositions with sample sizes ranging from very small (e.g. 5) to relatively large (e.g. a few hundreds). As shown in our simulation studies (Fig. 2 and Supplementary Figs S1–S3 and S20), increasing sample size from 5 to 100 provides some accuracy improvement, but not a dramatic change. Using only five samples gives reasonable performance from the proposed method.
In the analyses of the two PBMC datasets, we evaluate cell-type-specific markers selected from microarray, RNA-seq references and scRNA-seq profiles using data-driven methods. We also consider the human markers and human-symbol-mapped mouse markers from existing repository CellMarker. We find that markers from bulk reference (by microarray or RNA-seq) are better than those from scRNA-seq or CellMarker. We acknowledge this is not an exhaustive assessment of markers from various sources. For example, we use domain knowledge to help further filter the marker list. In reality, it is possible that the markers confirmed by biological experiments or identified by domain experts are more trustworthy than those obtained using data-driven methods.
The proposed method is primarily focused on microarray gene expression data. However, the same principal is applicable to other data types, such as RNA-seq data. As mentioned above, a number of methods have been proposed to deconvolve bulk RNA-seq with scRNA-seq data (Frishberg et al., 2019; Wang et al., 2019). Thus, it is important to fully compare the performance of the proposed method against existing methods designed for RNA-seq. A comprehensive assessment of the proposed method on RNA-seq is beyond the scope of this article, but we plan to provide such comparisons in our future work.
Funding
This project was partially supported by the National Institutes of Health [R01GM122083 to H.W. and Z.L., P01NS097206, U01MH116441 to H.W. and P.J. and NS111602 to P.J.); and the Emory University WHSC 2018 Synergy Award (to H.W. and P.J.). The study was supported by the National Institutes of Health [P30AG10161, R01AG17917 and U01AG61356].
Conflict of Interest: none declared.
Supplementary Material
References
- Abbas A.R. et al. (2009) Deconvolution of blood microarray data identifies cellular activation patterns in systemic lupus erythematosus. PLoS One, 4, e6098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett D.A. et al. (2018) Religious orders study and rush memory and aging project. J. Alzheimers Dis., 64, S161–S189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunet J.-P. et al. (2004) Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl. Acad. Sci. USA, 101, 4164–4169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D., Plemmons R.J. (2010) Nonnegativity constraints in numerical analysis In: The Birth of Numerical Analysis. World Scientific, Singapore, pp. 109–139. [Google Scholar]
- Clarke J. et al. (2010) Statistical expression deconvolution from mixed tissue samples. Bioinformatics, 26, 1043–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frishberg A. et al. (2019) Cell composition analysis of bulk genomics using single-cell data. Nat. Methods, 16, 327–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasparoni G. et al. (2018) DNA methylation analysis on purified neurons and glia dissects age and Alzheimer’s disease-specific changes in the human cortex. Epigenetics Chromatin, 11, 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong T. et al. (2011) Optimal deconvolution of transcriptional profiling data using quadratic programming with application to complex clinical blood samples. PLoS One, 6, e27156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guintivano J. et al. (2013) A cell epigenotype specific model for the correction of brain cellular heterogeneity bias and its application to age, brain region and major depression. Epigenetics, 8, 290–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagenauer M.H. et al. (2018) Inference of cell type content from human brain transcriptomic datasets illuminates the effects of age, manner of death, dissection, and psychiatric diagnosis. PLoS One, 13, e0200003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houseman E.A. et al. (2014) Reference-free cell mixture adjustments in analysis of DNA methylation data. Bioinformatics, 30, 1431–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunt G.J. et al. (2019) dtangle: accurate and robust cell type deconvolution. Bioinformatics, 35, 2093–2099. [DOI] [PubMed] [Google Scholar]
- Jaffe A.E., Irizarry R.A. (2014) Accounting for cellular heterogeneity is critical in epigenome-wide association studies. Genome Biol., 15, R31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson K.C. et al. (2016) 5-Hydroxymethylcytosine localizes to enhancer elements and is associated with survival in glioblastoma patients. Nat. Commun., 7, 13177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson K.C. et al. (2017) Normal breast tissue DNA methylation differences at regulatory elements are associated with the cancer risk factor age. Breast Cancer Res., 19, 81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaizer E.C. et al. (2007) Gene expression in peripheral blood mononuclear cells from children with diabetes. J. Clin. Endocrinol. Metab., 92, 3705–3711. [DOI] [PubMed] [Google Scholar]
- Lee D.D., Seung H.S. (2001) Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst., 556–562. [Google Scholar]
- Li B. et al. (2016) Comprehensive analyses of tumor immunity: implications for cancer immunotherapy. Genome Biol., 17, 174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z., Wu H. (2019) TOAST: improving reference-free cell composotion estimation by cross-cell type differential analysis. Genome Biol., 1, 190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z. et al. (2019) Dissecting differential signals in high-throughput data from complex tissues. Bioinformatics, 35, 3898–3905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathys H. et al. (2019) Single-cell transcriptomic analysis of Alzheimer’s disease. Nature, 571, 332–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman A.M. et al. (2015) Robust enumeration of cell subsets from tissue expression profiles. Nat. Methods, 12, 453–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel H. et al. (2019) Transcriptomic analysis of probable asymptomatic and symptomatic Alzheimer brains. Brain Behav. Immun., 80, 644–656. [DOI] [PubMed] [Google Scholar]
- Rahmani E. et al. (2018) BayesCCE: a Bayesian framework for estimating cell-type composition from DNA methylation without the need for methylation reference. Genome Biol., 19, 141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Repsilber D. et al. (2010) Biomarker discovery in heterogeneous tissue samples-taking the in-silico deconfounding approach. BMC Bioinformatics, 11, 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie M.E. et al. (2015) limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res., 43, e47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rozenblatt-Rosen O. et al. (2017) The Human Cell Atlas: from vision to reality. Nature, 550, 451–453. [DOI] [PubMed] [Google Scholar]
- Shen-Orr S.S. et al. (2010) Cell type–specific gene expression differences in complex tissues. Nat. Methods, 7, 287–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teschendorff A.E. et al. (2017) A comparison of reference-based algorithms for correcting cell-type heterogeneity in epigenome-wide association studies. BMC Bioinformatics, 18, 105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X. et al. (2019) Bulk tissue cell type deconvolution with multi-subject single-cell expression reference. Nat. Commun., 10, 380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y. et al. (2001) DNA replication precedes neuronal cell death in Alzheimer’s disease. J. Neurosci., 21, 2661–2668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y. et al. (2003) Neuronal cell death is preceded by cell cycle events at all stages of Alzheimer’s disease. J. Neurosci., 23, 2557–2563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yousefi P. et al. (2015) Estimation of blood cellular heterogeneity in newborns and children for epigenome-wide association studies. Environ. Mol. Mutagen., 56, 751–758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X. et al. (2019) CellMarker: a manually curated resource of cell markers in human and mouse. Nucleic Acids Res., 47, D721–D728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng S.C. et al. (2018) A novel cell-type deconvolution algorithm reveals substantial contamination by immune cells in saliva, buccal and cervix. Epigenomics, 10, 925–940. [DOI] [PubMed] [Google Scholar]
- Zheng X. et al. (2017) Estimating and accounting for tumor purity in the analysis of DNA methylation data from cancer studies. Genome Biol., 18, 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong Y. et al. (2013) Digital sorting of complex tissues for cell type-specific gene expression profiles. BMC Bioinformatics, 14, 89. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.