DeCoDe: degenerate codon design for complete protein-coding DNA libraries

Abstract

Motivation

High-throughput protein screening is a critical technique for dissecting and designing protein function. Libraries for these assays can be created through a number of means, including targeted or random mutagenesis of a template protein sequence or direct DNA synthesis. However, mutagenic library construction methods often yield vastly more nonfunctional than functional variants and, despite advances in large-scale DNA synthesis, individual synthesis of each desired DNA template is often prohibitively expensive. Consequently, many protein-screening libraries rely on the use of degenerate codons (DCs), mixtures of DNA bases incorporated at specific positions during DNA synthesis, to generate highly diverse protein-variant pools from only a few low-cost synthesis reactions. However, selecting DCs for sets of sequences that covary at multiple positions dramatically increases the difficulty of designing a DC library and leads to the creation of many undesired variants that can quickly outstrip screening capacity.

Results

We introduce a novel algorithm for total DC library optimization, degenerate codon design (DeCoDe), based on integer linear programming. DeCoDe significantly outperforms state-of-the-art DC optimization algorithms and scales well to more than a hundred proteins sharing complex patterns of covariation (e.g. the lab-derived avGFP lineage). Moreover, DeCoDe is, to our knowledge, the first DC design algorithm with the capability to encode mixed-length protein libraries. We anticipate DeCoDe to be broadly useful for a variety of library generation problems, ranging from protein engineering attempts that leverage mutual information to the reconstruction of ancestral protein states.

Availability and implementation

github.com/OrensteinLab/DeCoDe.

Contact

yaronore@bgu.ac.il

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

A protein’s function is inextricably linked to its amino acid sequence. Stability, flexibility, enzymatic turnover and binding affinity all depend directly on the specific structures available to the sequence of a given protein (Eisenmesser et al., 2005; Motlagh et al., 2014). Due to the critical importance of protein products in medicine and industry, a number of high-throughput screening techniques, including cell-surface display (Barbas et al., 1991; Boder and Wittrup, 1997; Freudl et al., 1986; Rockberg et al., 2008), phage display (Smith, 1985), mRNA display (Roberts and Szostak, 1997; Tabuchi et al., 2001) and droplet-based enzyme screens (Agresti et al., 2010; Romero et al., 2015) have been developed to link protein sequence to function. These techniques all require starting libraries of DNA encoding a vast number of protein variants, generally $>{10}^6$. Consequently, a number of strategies have been developed to quickly and cheaply generate pools of synthetic DNA templates to express the desired protein libraries.

The gold standard for DNA library construction is direct synthesis of each individual library member followed by pooling (Beaucage and Caruthers, 1981). This strategy guarantees the inclusion of each desired DNA sequence without introducing any undesired constructs. However, direct synthesis is often prohibitively expensive for large libraries and has limitations on both the length of each synthesized construct and the total number of constructs that can be synthesized in parallel. While recent advances in DNA synthesis technology are enabling direct and specific synthesis for longer and larger libraries (LeProust et al., 2010; Oling et al., 2018; Plesa et al., 2018), the number of possible full-length protein-coding constructs (10³–10⁶) remains several orders of magnitude below the desired library sizes for most protein-screening methods (10⁶–10¹³).

Methods that exploit the redundancy of the genetic code to generate large, semi-targeted libraries balance low cost, simple production with library output sizes suitable for protein screening. A degenerate codon (DC) is a mixture of nucleotide triplets capable of collectively encoding more than one amino acid (Arkin and Youvan, 1992; LaBean and Kauffman, 1993; Schultz and Richards, 1986; Wolf and Kim, 1999). DC libraries combine mixtures of nucleotides at specific positions during DNA synthesis to include only specific subsets of the codon table and ultimately allow expression of protein mixtures from a single pooled DNA synthesis reaction. However, as each DC is independent of each other DC in the construct, including a large number of DCs can quickly generate a library of possible DNA and protein sequences too large to be screened.

A number of groups have developed computational methods to maximize the number of desired target sequences created using DCs under a user-specified library size limit. Unfortunately, this problem is NP-hard (Parker et al., 2011; Pierce and Winfree, 2002), meaning that a fast (polynomial time) algorithmic solution is extremely unlikely to exist. Instead, researchers have had to rely on a variety of heuristics or relaxations of the problem to algorithmically design DC libraries. One of the first methods to allow simultaneous optimization of all covarying sites was LibDesign (Mena and Daugherty, 2005). LibDesign optimizes DC usage to include as many complete targeted protein sequences as possible in the final library under a limit on the total number of sequences produced. As a result, LibDesign libraries directly account for the three main structures of protein covariation as shown in Figure 1(A–C). However, because this algorithm relies on brute-force search, it is computationally inefficient and intractable for modern protein library designs that may vary at dozens or more positions. Moreover, LibDesign is incapable of accounting for length variation within the target library or using multiple synthesis reactions (i.e. a DNA library comprised of multiple sublibraries with each sublibrary produced according to a separate DNA template) to cover more targets without incurring large library size penalties.

Fig. 1.

Examples of covariation structures within protein target sets (top row). For each covariation pattern, an optimal library was generated with a total size limit of six DNA sequences. The amino acid sequences encoded by this optimized library are shown (bottom row) and the corresponding library quality, as measured by the number of target sequences covered, is shown below each optimized library. (A) A set with two independently varying positions. The DC library generated for this set of sequences codes all six targets. (B) A set with two covarying positions. The DC library generated for this set of sequences codes only four of the six targets. The third variable position is not degenerate in the optimal library. (C) A set with multiple covarying positions and an indel mutation. The DC library generated for this set of sequences codes only three of the six targets. By adding a second sublibrary, the indel mutation is handled by templates with different lengths and the total coverage is five targets

As an alternative to total-library optimization, optimization of combinatorial mutagenesis (OCoM) measures library quality by the maintenance of single and pairwise mutational frequencies (Fig. 1A and B) and optimizes libraries using integer linear programming (ILP) (Parker et al., 2011). However, the pairwise sequence potential employed by OCoM fails to capture higher-order covariation patterns (Fig. 1C) that would be explicitly considered under LibDesign’s objective. Such patterns are particularly important for functional networks within proteins (Halabi et al., 2009; Lockless and Ranganathan, 1999; Socolich et al., 2005) and could prove critical for the generation of libraries optimized for inclusion of functional variants. Furthermore, OCoM cannot design libraries of multiple lengths.

Due to the problem’s hardness, some groups have introduced relaxations to solve it in polynomial time with respect to the input size. SwiftLib is a DC optimization algorithm based on dynamic programming (Jacobs et al., 2015). To reduce computational complexity, SwiftLib considers each position of the protein library independently. Critically, SwiftLib can include multiple DCs at a given position to better cover the target library while staying under the same diversity limit. This strategy dramatically reduces the total size of the final library by minimizing or eliminating undesired amino acid inclusion at a given position. Despite these advantages, the simplification of the DC design problem used by SwiftLib eliminates its ability to account for covariation. Moreover, while SwiftLib allows for the use of multiple degenerate DNA templates, it does not account for a gap and, therefore, lacks the ability to encode mixed-length libraries.

Here, we present degenerate codon design (DeCoDe), an algorithm for total-library DC optimization based on ILP that simultaneously addresses three critical gaps in current algorithmic solutions to DC library design: (i) direct accounting for high-order covariation, (ii) optimization over mixed-length libraries and (iii) inclusion of multiple degenerate DNA templates to cover more proteins of the input library under experimental constraints. For small libraries (up to a hundred proteins with a dozen of variable positions), DeCoDe often achieves optimal library designs in a reasonable amount of time (hours to days). For larger libraries, DeCoDe will output a feasible solution after a given time limit, and will report the gap between the current best number of targets covered and an upper bound on the optimal design. Because of its distinct advantages, we expect DeCoDe to be applicable to numerous protein engineering challenges including library design for directed evolution, reconstruction of ancestral protein states and high-throughput biochemical analysis.

2 Materials and methods

2.1 Preliminaries

We start with a few formal definitions that will aid in the problem definition and ILP formulation. A list of notations, proofs supporting all ILP constraints, and the complete ILP formulations can be found in the Supplementary Material.

Definition 1. An amino acid sequence is a string over the amino acid alphabet ${\Sigma }_{\text{AA}}$ plus a gap character indicating the absence of an amino acid at a given position.

Definition 2. A codon is a DNA triplet coding a single amino acid or stop or a gap character indicating the absence of a DNA triplet at a given position.

Definition 3. A degenerate nucleotide represents a subset of $\{\mathrm{A},\mathrm{C},\mathrm{G},\mathrm{T}\}$.

In general, a symbol in an alphabet is said to be degenerate if it represents a set of symbols within the same alphabet and that set has a cardinality >1. Nucleotide degeneracy allows DNA molecules to be synthesized with a mixture of nucleotides at one or more specified positions, giving direct rise to DCs.

Definition 4. A degenerate codon is a triple of degenerate nucleotides and, thus, codes a subset of ${\Sigma }_{\text{AA}}$.

Whereas a non-DC codes one and only one amino acid residue or stop, a DC can code multiple amino acids or stops by representing a mixture of non-DCs. If we denote the DNA triplets represented by DC x as ${\text{span}}_{\text{DNA}}(x)$, then, x covers non-DC c if and only if $c\in {\text{span}}_{\text{DNA}}(x)$.

Definition 5. A DC covers the DNA triplets represented by it and codes the amino acids they code.

If we denote the amino acids encoded by DC x by ${\text{span}}_{\text{AA}}(x)$, then, x codes a if and only if $a\in {\text{span}}_{\text{AA}}(x)$.

Definition 6. A sequence of DCs, a degenerate template $T=\{t_1,\dots ,t_P\}$, codes a sequence of amino acids $A=\{a_1,\dots ,a_P\}$ if and only if $a_p\in {\text{span}}_{\text{AA}}(t_p)\forall 1\le p\le P$.

A sequence of DCs can be assembled to cover a DNA library coding a large number of protein sequences. We denote by ${\text{span}}_{\text{AA}}(T)$ the set of amino acid sequences coded by degenerate template T.

Definition 7. ${\text{span}}_{\text{DNA}}(T)$ of degenerate template T is called a sublibrary.

We note that the cardinality of ${\text{span}}_{\text{DNA}}(T)$ will grow exponentially with the number of DCs included in T, quickly outstripping the capacity of all available experimental screening methods. Therefore, it is necessary to constrain the maximum number of non-degenerate DNA sequences produced, i.e. limit the cardinality of ${\text{span}}_{\text{DNA}}(T)$.

Definition 8. A library is made up of one or more sublibraries, each covered by a single degenerate template T_j. Formally, a library is denoted by $\underset{j}{\cup }{\text{span}}_{\text{DNA}}(T_j)$.

By grouping similar sequences together in a sublibrary, each covered by a single degenerate template, then combining the sublibraries to generate the final library, more protein sequences can be encoded under the same DNA diversity limit.

2.2 Problem definition

We define our problem as that of taking a set of desired protein sequences and producing a degenerate template coding as many of those sequences as possible while limiting the total number of DNA sequences covered as shown in Figure 1A and B. We explicitly consider only the variable positions in an alignment of protein sequences. Fixed positions are removed as the optimal solution to cover them is any of the non-DCs covering that amino acid. These positions do not grow the size of the output library.

2.2.1. Max-coverage degenerate single-template design

• INSTANCE:

• Set S of aligned amino acid sequences $\left\{S_i\right\}$ varying at P positions and DNA library size limit M.

• VALID SOLUTION:

• Template T with at most P degenerate positions s.t. $|{\text{span}}_{\text{DNA}}(T)|\le M$.

• GOAL:

• Maximize $|{\text{span}}_{\text{AA}}(T)\cap S|$.

Optionally, we allow the library to be constructed as a combination of smaller sublibraries (Fig. 1C), each covered by a single degenerate template, and coding a fraction of the total number of targeted proteins. By using multiple sublibraries, the overall quality of the optimized library, measured as the total number of target sequences covered, can be increased while the total number sequences generated remains under the same limit.

2.2.2. Max-coverage degenerate multi-template design

• INSTANCE:

• Set S of aligned amino acid sequences $\left\{S_i\right\}$ varying at P positions, DNA library size limit M and number of degenerate templates J.

• VALID SOLUTION:

• A set of degenerate templates $\{T_1,\dots ,T_J\}$, each with at most P degenerate positions, such that ${\sum }_{j=1}^J|{\text{span}}_{\text{DNA}}(T_j)|\le M$.

• GOAL:

• Maximize $|{{\cup }_{j=1}^J\text{span}}_{\text{AA}}(T_j)\cap S|$.

Proteins of multiple lengths are allowed only in the multiple template design, as a single degenerate template codes for proteins of only one specific length. By using x gap codons in a template with at most P degenerate positions, the template will have at most P – x degenerate positions and the length of the produced proteins will be reduced by x.

As noted by Parker et al. (2011), it follows from the NP-hardness of the protein design problem (Pierce and Winfree, 2002) that the design of degenerate templates to cover aligned sequences varying non-independently at multiple positions is NP-hard (for reader convenience, we provide a proof in the Supplementary Material). This finding holds whether designing a single template or multiple degenerate templates. Consequently, we devise a solution to this problem using ILP. ILP is a method with efficient solvers that has previously been applied to solve various NP-hard problems in numerous domains, including computational biology. Examples include the gene duplication problem (Chang et al., 2011) and instances of the DC design problem considering pairwise sequence propensities (Parker et al., 2011).

2.3 MC-DSTD: single library formulation

We first present a solution to the problem in which we cover the input set using only a single sublibrary (one degenerate template). This restriction simplifies the calculation of the total produced library size $|{\text{span}}_{\text{DNA}}(T)|$, which ordinarily requires multiplication of independent variables, an operation that is disallowed in linear programs.

2.3.1. Objective

To address this problem, we introduce the objective function:

$$\text{max}\sum _i{s}_i,$$

where i indexes an indicator variable such that s_i denotes whether target protein sequence S_i in target set S can be translated from the set of DNA sequences covered by T. Formally, $s_i=1\iff S_i\in {\text{span}}_{\text{AA}}(T)$. By optimizing for inclusion of full-length sequences, DeCoDe implicitly captures covariation structures within the library (Fig. 1B and C).

2.3.2. Single DC per position constraint

We introduce the variable Y_jpd where j denotes the index of the degenerate template, p denotes the position of the DC in the degenerate template and d denotes the use of the dth DC at that specified position. In the max-coverage degenerate single-template design (MC-DSTD) case, j = 1 as we are only considering the special case of having a single degenerate template cover the entire library. Upon the variable Y_jpd, we introduce the following constraint:

$$\sum _d{Y}_{\mathit{jpd}}=1\hspace{1em}\hspace{1em}1\le j\le J,\hspace{0.17em}1\le p\le P,$$

so that only a single DC can be employed at each position of each degenerate template.

2.3.3. Coverage constraints

We introduce integer matrix D and binary matrix $\widehat{D}$. In matrix D, D_da corresponds to the number of non-DCs covered by DC d that code the ath amino acid, gap, or stop. Matrix ${\widehat{D}}_{da}$ is a binary copy of matrix D where each value ${\widehat{D}}_{da}$ is the evaluated truth of D_da > 0. Variable C_jpa is an indicator variable for coding the ath amino acid at position p by degenerate template T_j. Therefore, the following relationship exists between Y and C variables:

$$\begin{array}{c}{C}_{\mathit{jpa}}=\sum _d{Y}_{\mathit{jpd}}{\widehat{D}}_{da}\\ 1\le j\le J,\hspace{0.17em}1\le p\le P,\hspace{0.17em}1\le a\le \left|{\Sigma }_{\text{AA}}\right|.\end{array}$$

To indicate whether target sequence S_i can be encoded by the sublibrary set, we introduce variable X_ij. X_ij indicates whether degenerate template T_j can code the target protein sequence S_i. These variables are shared between the MC-DSTD and max-coverage degenerate multi-template design (MC-DMTD) instances and are introduced here for completeness. In the MC-DSTD instance j = 1 while in the MC-DMTD instance $1\le j\le J$. We introduce the following constraints upon this variable, where O is defined such that O_ipa is a one-hot encoded representation of target sequence S_i:

$$\begin{array}{c}\sum _p\sum _a{O}_{\mathit{ipa}}{C}_{\mathit{jpa}}-P+(P+1)(1-X_{ij})\le P\\ 1\le i\le \left|S\right|,\hspace{0.17em}1\le j\le J\\ \sum _p\sum _a{O}_{\mathit{ipa}}{C}_{\mathit{jpa}}-P+(P+1)(1-X_{ij})\ge 0\\ 1\le i\le \left|S\right|,\hspace{0.17em}1\le j\le J.\end{array}$$

Finally, we can impose the following constraints to solve s_i for all values of i to ensure that it is covered by at least one degenerate template in T:

$$\begin{array}{ccc}-\sum _j{X}_{ij}+(J+1)s_i\hfill & \le J\hfill & 1\le i\le \left|S\right|\hfill \\ -\sum _j{X}_{ij}+(J+1)s_i\hfill & \ge 0\hfill & 1\le i\le \left|S\right|\hfill \end{array}.$$

2.3.4. Total-library size constraint

We note that the calculation of total produced library size, $|{\text{span}}_{\text{DNA}}(T)|$, requires multiplication of the total possible number of incorporated codons at each position. Because multiplication of variables is a non-linear operation, we instead calculate the log of the span of T and introduce the following constraint against the technology-imposed diversity limit M to ensure that $\text{log}(|{\text{span}}_{\text{DNA}}(T)|)\le \text{log}(M)$ and, therefore $|{\text{span}}_{\text{DNA}}(T)|\le M$ in the case of a single sublibrary, j = 1:

$$\begin{array}{ccc}\sum _p\sum _d{Y}_{\mathit{jpd}}\hspace{0.17em}\text{log}\hspace{0.17em}\left(\sum _a{D}_{da}\right)\hfill & \le \text{log}\hspace{0.17em}\left(M\right)\hfill & j=1\hfill \end{array}.$$

2.4 MC-DMTD: multiple degenerate templates extension

To extend the ILP for use with multiple degenerate templates, we must adjust the calculation of the constraint on the size of the total produced library. Because this calculation requires a sum of products, it is not trivial to devise a linear solution. Instead, we approximate the solution by binning the log of the sublibrary size produced by each degenerate template into discrete bins ranging from size 1 to size $\text{log}(M)$. We then approximate the size of each sublibrary as the exponentiated value of the upper bound of the bin, thus ensuring that the calculated approximate sublibrary size is always greater than or equal to the true sublibrary size across all sublibraries. Therefore, the constraint that the total-library size must be less than or equal to the user-defined limit will always hold for a valid solution of the ILP.

To calculate the appropriate bin for the size of the sublibrary produced by each degenerate template, we define two constant vectors U and L such that U_n and L_n define the upper and lower bound of bin n, respectively. We then let variable Q_j denote the log size of the sublibrary ${\text{span}}_{\text{DNA}}(T_j)$ calculated as $Q_j=\sum _p\sum _d{Y}_{\mathit{jpd}}\hspace{0.17em}\text{log}\hspace{0.17em}\left(\sum _a{D}_{da}\right)$. We then introduce a binary-valued variable B_jn to indicate whether the size of sublibrary j falls into the range of bin n such that $L_n\le \text{log}(|{\text{span}}_{\text{DNA}}(T_j)|)\le U_n$. Upon B_jn, we place the following constraints:

$$\begin{array}{ccc}\sum _n{B}_{jn}\hfill & =1\hfill & 1\le j\le J\hfill \\ \sum _n{B}_{jn}{L}_n\hfill & \le Q_j\hfill & 1\le j\le J\hfill \\ \sum _n{B}_{jn}{U}_n\hfill & \ge Q_j\hfill & 1\le j\le J\hfill \end{array}.$$

Our upper bound on total-library size when combining multiple sublibraries is therefore calculated as:

$$\sum _j\sum _n{B}_{jn}{e}^{U_n}.$$

The following constraint can be introduced to ensure that the maximum possible library size when combining multiple sublibraries does not exceed the user-defined limit:

$$\sum _j\sum _n{B}_{jn}{e}^{U_n}\le M.$$

2.5 DC table

To reduce unnecessary search over equivalent solutions, we formulate the DC table D to minimize the degeneracy of the constructed DNA library while maintaining access to all subsets of 20 amino acid residues, stop codons and gaps. Though 3376 possible DCs exist (15³ plus the empty set to account for a gap), many of these codons are redundant in the amino acids they encode. We therefore employ and load a pre-generated, non-redundant codon table that groups all codons covering the same set of amino acids. We select and return from this set the subset of codons that display the least degeneracy in nucleic acid space. By removing redundant codons from the codon table, we reduce the number of possible codon selections from 3376 to 841. Upon parsing the optimized library, DeCoDe returns the set of all equivalent DCs, allowing the user to select the codon best suited to their expression system (e.g. selecting the DC that encodes the fewest rare Escherichia coli codons).

2.6 Implementation

DeCoDe was implemented in Python using the CVXPY package (Diamond and Boyd, 2016). All results presented here employed the Gurobi solver (Gurobi Optimization, 2018), which provides a free licence to academic users. CVXPY also provides interfaces to most common alternative ILP solvers including free and open-source options. All results presented here were run on a server with two Intel Xeon CPU E5-2630 v4 @ 2.20 GHz CPUs and 256 GB of memory. Each run of DeCoDe was allocated 12 hyper-threads for the Gurobi solver and multiple runs were conducted in parallel using GNU Parallel (Tange, 2018). We provide a command-line interface to DeCoDe at github.com/OrensteinLab/DeCoDe.

3 Results

We sought to apply DeCoDe to a set of library optimization problems closely mimicking those required for a standard protein engineering project. Specifically, we elected to first benchmark DeCoDe’s performance against a dataset employed in the initial demonstration of SwiftLib (Jacobs et al., 2015): covering a set of 200 Rosetta-designed sequences altering nine surface residues at the interacting interface of crystal structure 1XBI from the Protein Data Bank (Suryadi et al., 2005). We then extend our analysis of DeCoDe’s performance by targeting the documented lineage of the Aequorea victoria green fluorescent protein (avGFP) (Prasher et al., 1992). We refer to these to tasks as ‘1XBI’ and ‘GFP’, respectively. All of the template sequences and resulting output files presented in the results below are available in the DeCoDe GitHub repository.

We selected the GFP task as a new benchmark for several reasons. First, avGFP and its laboratory-derived descendants have provided a critical suite of research tools and, consequently, are the subject of ongoing research to map the protein’s sequence onto its functional characteristics (Sarkisyan et al., 2016). Second, the exact lineage of the entire family of laboratory-derived avGFP variants is known, making the tasks of sequence alignment and variant identification trivial (Lambert, 2019). Third, the high total number of variable sites and the length variation within the protein family causes this design problem to be particularly challenging or impossible for existing DC library design algorithms.

For each of these tasks, we measure the quality of the optimized library by three metrics. The first is the total coverage count of the input target sequences. The second is the fraction of total target k-mers covered. The third is the fraction of unique target k-mers covered. For the last two metrics, we extract all amino acid k-mers, both contiguous and discontiguous for k = 2, 3, 4, present in the target sequence set. We then calculate the fraction of the total and unique k-mers present in each of the optimized libraries, respectively. These secondary metrics better measure the extent to which lower-order covariation is maintained by each of the optimized libraries. By measuring total k-mer coverage, we assess the extent to which each library is able to capture high-abundance, and therefore theoretically important, covariation structures. In the case of unique k-mer coverage, we assess the generated library’s ability to explore the breadth of sequence space, as each unique k-mer represents a potentially novel functional property of the protein. The relative value of each of these metrics to the user will be a function of the desired balance between exploiting the known, frequently-occurring k-mer patterns present in the target library and exploring a larger area of sequence space through the inclusion of a large number of unique k-mer patterns.

We compared DeCoDe to an existing DC library design algorithm. As the most recently published method and the only open-source algorithm allowing multiple DC usage per position, SwiftLib (Jacobs et al., 2015) represents a natural point of comparison.

3.1 Performance on the 1XBI benchmark

We compared the performance of DeCoDe to that of SwiftLib on the 1XBI task using both a single sublibrary and four sublibraries under a library size limit of 3.2 × 10⁸, corresponding to the analogous libraries listed as ‘Problem 1, DP Solution 1’ and ‘Problem 1, DP Solution 2’, respectively, in the SwiftLib text. When employing only a single sublibrary, DeCoDe produced an optimized library identical to the SwiftLib solution. This result is not unexpected as, for target sequence sets with relatively few variable positions, the optimal library by SwiftLib’s objective may also be optimal by DeCoDe’s objective.

However, when the number of sublibraries was increased to 4, as in SwiftLib’s ‘DP Solution 2’, DeCoDe outperformed SwiftLib based on both the target coverage and the k-mer coverage criteria. The DeCoDe library covers 191 of the target input sequences while the SwiftLib library covers only 173 (Fig. 2A). Beyond the full-length sequences, DeCoDe was also able to cover a larger fraction of the total covariation present in the set of target sequences. For all analyzed values of k, the DeCoDe library covered a greater proportion of the total and unique target library k-mers, indicating that covariation is maintained at a higher rate not only in the extreme of full-length target coverage, but also in lower-order cases (Fig. 2B and C, respectively).

Fig. 2.

DeCoDe and SwiftLib performance on the 1XBI benchmark using four sublibraries. (A) The total number of full-length target sequences covered by each optimized library. (B, C) Comparison of total higher-order covariation. Each point represents the fraction of total (B) or unique (C) target k-mers covered by the optimized libraries generated by each method. Values of k are indicated by the color of each point

3.2 Performance on the limited GFP benchmark

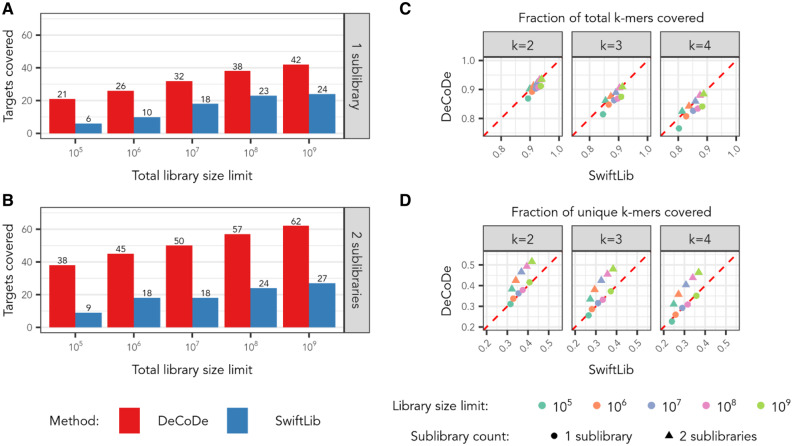
We next sought to test the performance of DeCoDe on a more challenging set of target proteins: the lab-derived lineage of avGFP. The total set of these avGFP-derived proteins spans several different lengths, the most common being 238 or 239 amino acids. The two exceptions include large, unique insertions and were excluded from our benchmarks since each would need to be ordered as individual, non-degenerate constructs in any DC library. While DeCoDe permits libraries of varying length, SwiftLib requires all target proteins to be the same length. To allow for a direct comparison between the two methods on the GFP benchmark, we therefore subset the GFP lineage to include only proteins of length 239 amino acids (the most common length).

We performed library optimization for this reduced target protein set with both DeCoDe and SwiftLib. As both algorithms are capable of increasing performance by employing multiple degenerate DNA templates, we optimized for a range of library size limits using either 1 or 2 sublibraries, where each sublibrary represents an independently synthesized DNA construct. We then measured the quality of each algorithm’s generated library by the number of full-length sequences out of the target set of 94 proteins covered by that DC library and their k-mer coverage.

For library designs comprised of only a single sublibrary, we find that DeCoDe consistently outperforms SwiftLib in the total number of target sequences covered for a given library size limit (Fig. 3A). Across all limits for a single sublibrary, DeCoDe offers an improvement of between 58% and 250%. DeCoDe’s improvement over SwiftLib is even more apparent when comparing libraries comprised of two sublibraries (Fig. 3B). For all diversity limits, DeCoDe outputs a library that covers more than twice the number of proteins covered by SwiftLib’s library.

Fig. 3.

Comparison of full-length target and k-mer coverage by DeCoDe and SwiftLib on the target sequence set of 94 avGFP-descended target proteins of length 239 amino acids, where 73 positions are variable between proteins. (A, B) Total targets covered for libraries comprised of one sublibrary and two sublibraries, respectively. (C, D) Fraction of total and unique target k-mers covered. Various library sizes are denoted by color and the use of one or two sublibraries is denoted by shape

For the k-mer coverage analysis, we find a strong dependence of DeCoDe’s performance on the number of sublibraries it is allowed to use. For instance, SwiftLib outperforms DeCoDe in all cases by the measure of covering the total target k-mers when using only a single sublibrary (Fig. 3C, circles). However, the performance of the two techniques is roughly equivalent across diversity limits when both methods employ a second sublibrary (Fig. 3C, triangles).

When comparing unique k-mer coverage, we find that DeCoDe and SwiftLib cover a nearly identical fraction of the target k-mers when using only a single sublibrary (Fig. 3D, circles). The addition of a second sublibrary dramatically improves the proportion of unique target k-mers covered by DeCoDe while offering only a marginal improvement for SwiftLib (Fig. 3D, triangles). This pattern holds for the instances of both total and unique k-mer coverage. Taken together with the full-length target coverage results, these findings indicate that DeCoDe can better utilize additional sublibraries to cover both high- and low-order covariation and support the importance of multiple DNA constructs to the performance of DeCoDe.

The returned total-library sizes for both DeCoDe and SwiftLib approach, but do not exceed, the user-specified limit (Supplementary Fig. S1). However, because the problem of linked variation addressed by DeCoDe is NP-hard, both the runtime (Supplementary Fig. S2) and memory requirements (Supplementary Fig. S3) of DeCoDe tend to be much higher than those of SwiftLib. Since SwiftLib does not attempt to optimize over the problem of covariation between multiple sites, the algorithm can find an optimal solution for its library quality metric in polynomial time.

3.3 Performance on the complete GFP benchmark

In addition to the 94 proteins of length 239 amino acids explored in the above optimization task, the avGFP family includes 37 additional proteins of length 238 amino acids. Because DeCoDe can employ multiple sublibraries and the gap codon, it is, to our knowledge, the first algorithm able to perform total-library optimization for libraries composed of mixed-length protein targets. Here, we use DeCoDe to optimize a library targeting the set of 131 avGFP-derived proteins of both 238 and 239 amino acid lengths (Supplementary Fig. S4).

For this task, we selected a total-library size limit of 10⁷ unique DNA species. This limit is consistent with yeast-based assays (e.g. yeast display) frequently used in conjunction with fluorescence-activated cell sorting to enrich for fluorescent proteins with desirable properties (Swers et al., 2004). Because the avGFP family is relatively diverse, we explored different sublibrary counts to maximize coverage under the 10⁷ diversity limit. Specifically, we optimized libraries comprising 1, 2, 3, 4, 8 and 12 sublibraries. Each sublibrary represents an additional monetary and labor cost that is, in most instances, offset by the improved coverage that the sublibraries achieve under the total diversity limit.

On the computational side, libraries comprised of a high number of sublibraries will likely require a prohibitively long runtime to reach a guaranteed optimal solution as each additional sublibrary further complicates the optimization procedure. Because the problem of DC design with explicit consideration of full coverage is NP-hard, no solution, including one based on ILP solvers, can guarantee a feasible runtime, i.e. terminating in days. To address this issue, we limited the total runtime to a maximum of 48 h and selected the solution reached by the ILP solver under that time limit. We expect this time limit to be within reason for researchers since, when added to the synthesis and delivery time, it represents a total turnaround time from design to delivery of roughly 1 week through existing commercial sources. In practice, the user is free to set any time limit they deem appropriate.

The inclusion of additional sublibraries dramatically improved overall coverage of the lineage tree (Supplementary Fig. S5) while keeping the total-library diversity under the 10⁷ limit (Supplementary Fig. S6). When only a single sublibrary is used, DeCoDe outputs an optimal library. However, this library only covers 32 of the 131 target sequences and all of the covered sequences are of length 239. When 2 additional sublibraries are added (for a total of 3), the library produced by DeCoDe covers 66 proteins, or just over half of all sequences in the lineage. This 3-member library begins to cover sequences of length 238 with diverse functions, including CFP and BFP. With 12 sublibraries, DeCoDe covers 121 of the 131 total target sequences while generating only 7 640 832 total DNA sequences, which is well within the range of modern DNA synthesis techniques. With this library, nearly all of the significant functional variants are covered. As expected, there is a positive correlation between the number of sublibraries included and the runtime (Supplementary Fig. S7) and maximum memory usage (Supplementary Fig. S8) for each optimization problem.

While we were able to obtain guaranteed optimal solutions for the case of 1 and 2 sublibraries, we were unable to obtain optimality guarantees for the libraries comprising 3, 4, 8 and 12 sublibraries under the 48-h time limit. However, solutions tend to rapidly improve on the objective function and yield diminishing returns with increased runtimes (Supplementary Fig. S9). The ILP solver computes an upper bound for the value of the optimal solution for each point during the run, which can inform the user how far the current library is from a theoretical optimum. Given these findings, we suggest that DeCoDe is unlikely to significantly improve on the presented results with increased time and that reaching a guaranteed optimal solution may require a dramatic increase in runtime, perhaps weeks, months, or even longer for the more challenging library designs.

4 Discussion

The synthesis of large, protein-coding DNA libraries is a necessary step for high-throughput protein-screening assays. This synthesis step often incurs a high cost, even for libraries of closely related genes. Many research groups have focused significant efforts on reducing this prohibitive cost through innovations in software (Jacobs et al., 2015; Mena and Daugherty, 2005; Parker et al., 2011), hardware (LeProust et al., 2010; Oling et al., 2018), or chemistry (Plesa et al., 2018). Among these techniques, DC libraries stand out as a particularly attractive method, as they can cover large swaths of sequence space without a proportional rise in synthesis cost. However, existing DC library design solutions lack the ability to account for linked variation, multiple protein lengths or both. DeCoDe was written with careful consideration of both linked and length variation, making it a particularly useful solution for a variety of DC library design tasks.

Covariation between amino acid positions underlies the evolutionary structure of protein families. Naturally evolved proteins rely on evolutionarily conserved, interconnected networks of residue interactions to carry out their functions (Halabi et al., 2009; Lockless and Ranganathan, 1999; Socolich et al., 2005). These networks can often be disrupted by even a single amino acid change if that change is non-conservative in a necessary physical property (Goldberg and Wittes, 1966). Several research groups have exploited the preservation of these networks over time to reconstruct ancestral protein lineages and better understand the link between protein sequence, structure and function (Lim et al., 2016; Shi and Yokoyama, 2003; Thornton et al., 2003). Due to the highly correlated, chemically conserved sequence patterns present in these reconstructed lineages, DeCoDe offers an attractive solution to the problem of synthesizing the complete protein family for functional testing simultaneously.

Expansions or reductions in protein domain lengths represent another type of variation with significant implications for protein function (Brocchieri and Karlin, 2005). As an example, size differences in the complementarity-determining regions of immunoglobulin proteins can differentiate success and failure of antigen binding (Teplyakov and Gilliland, 2014). Because DeCoDe can simultaneously optimize constructs of various lengths under a single library size constraint, it is ideal for generating DC libraries to screen immunoglobulin proteins for specific, desired binding properties.

While DeCoDe can tackle these previously untenable challenges, DeCoDe’s direct solution for the linked variation problem can require significant computational resources. We implemented two features to overcome this limit. The first is the use of a non-redundant codon table in the ILP formulation, which reduces the number of constraints and variables to consider. The second is a user-defined limit on the runtime of the ILP solver. While the ILP may not find an optimal solution with limited runtime, it will output a feasible solution that may be very close to the optimum.

The utility of DeCoDe optimized libraries depends heavily on the method used to define the target sequences in the input set. Historically, targeted protein library design has relied on the expertise of trained biochemists. However, beginning in the early 2000s, computational methods for linking protein sequence to function started to emerge. Initial methods, such as those underpinning the software suite Rosetta, employed biophysical models of protein structure and enabled computational design of hundreds to thousands of protein variants prior to experimental screening (Kuhlman et al., 2003; Leaver-Fay et al., 2011). More recent developments employ machine learning to rapidly predict the function of a novel protein sequence without the computational expense of simulating protein dynamics (Cadet et al., 2018; Saito et al., 2018; Wu et al., 2019). All of these methods have shown promise for the task of protein design when used appropriately. Here, we explored two sets of input sequences with a high likelihood of containing functional variants: one designed by the industry standard protein modeling tool Rosetta (1XBI) and one based on an existing protein family with experimentally verified functional properties (GFP). Ultimately, it is up to the user to ensure that the method being used to generate targets can effectively predict and return functional protein sequences to include in the target set.

DeCoDe-generated libraries will be most useful when coupled with high-throughput screening methods, as many functional variants may reside in the sequence space covered by the optimized library but not specifically present in the target set. When used in this manner, DeCoDe-generated libraries stand to make a significant impact in the field of protein engineering, as they have the capacity to more efficiently screen sequence space for functional variants. Future extensions of DeCoDe could include optimization of the PCR assembly process necessary to generate long protein-coding constructs. Such an implementation could potentially allow even better capture of local covariation structures within the sequence library and generate combinatorially-assembled libraries that have been proven useful in directed evolution experiments.