Computer animation body surface analysis of total skin electron radiation therapy dose homogeneity via Cherenkov imaging

Abstract.

Purpose: Quality assurance (QA) of dose homogeneity in total skin electron therapy (TSET) is challenging since each patient is positioned in six standing poses with two beam angles. Our study tested the feasibility of a unique approach for TSET QA through computational display of the cumulative dose, constructed and synthesized by computer animation methods.

Approach: Dose distributions from Cherenkov emission images were projected onto a scanned 3D body model. Topographically mapped surfaces of the patient were recorded in each of six different delivery positions, while a Cherenkov camera acquired images. Computer animation methods allowed a fitted 3D human body model of the patient to be created with deformation of the limbs and torso to each position. A two-dimensional skin map was extracted from the 3D model of the full surface of the patient. This allowed the dose mapping to be additively accumulated independent of body position, with the total dose summed in a 2D map and reinterpreted on the 3D body display.

Results: For the body model, the mean Hausdorff error distance was below 2 cm, setting the spatial accuracy limit. The dose distribution over the patient’s 3D model generally matched the Cherenkov/dose images. The dose distribution mapping was estimated to be near 1.5 cm accuracy based upon a phantom study. The body model must most closely match at the edges of the mesh to ensure that high dose gradients are not projected onto the wrong location. Otherwise 2 to 3 cm level errors in positioning in the mesh do not appear to cause larger than 5% dose errors. The cumulative dose images showed regions of overlap laterally and regions of low intensity in the posterior arms.

Conclusions: The proposed modeling and animation can be used to visualize and analyze the accumulated dose in TSET via display of the summed dose/Cherenkov images on a single body surface.

1. Introduction

Mycosis fungoides is the most common form of cutaneous T-cell lymphoma,¹ and some patients have superficial lesions throughout the skin of the body, which can require radiation over large areas or even the whole skin surface.² Therefore, total body dose uniformity can be the goal for radiation therapy of this disease to achieve partial remission and low toxicity.^3–5 In most TSET setups, the Linac gantry points toward the standing patient, and a broad electron beam treatment is delivered to cover the patient’s entire skin area.^6,7 There are largely three techniques to achieve total skin coverage, with one having the patient rotate slowly on a stand while standing with arms and legs spread,⁸ another having the beam scan across the patient in prone and supine positions near the floor, and the third being the Stanford technique in which the patient stands in six different limb and body positions that are designed to expose many body surfaces to the beam sequentially.⁴ The vast majority of centers appear to use the latter Stanford technique for historical reasons, although little published data exist documenting this method. Validation of the coverage homogeneity is challenging, and while phantom tests can be done,⁹ this is labor intensive, and more commonly, dosimeters, such as TLDs, OSLDs, and diodes, are attached at multiple positions on the patient, to directly monitor the dose delivered to specified verification points.¹⁰

In particular, the curvature of the body and the complexity of trying to get a relatively homogeneous dose over the entire skin surface are extremely challenging. There is a goal of ±10% agreement in dose over all of the skin relative to the dose at the midline,^11,12 but this is rarely checked with dose measurement over the large area of the patient’s body surface because of the logistics and the length of time required for the setup. As such, there is relatively little published or expected in any individual TSET treatment about confirmation of dose homogeneity. Yet, imaging tools and surface capture tools are actually inexpensive and readily available and could be used to test the homogeneity of coverage with the use of animation tools to map the dose onto the anatomic locations. The goal of this study was to test the ability to visualize noncontact Cherenkov imaging on an anatomic surface map of the 3D patient skin as a surrogate of dose delivery to determine if computer animation methods could be better utilized to map out the homogeneity of the coverage to the skin.

Cherenkov photons are generated from relativistic electrons traveling through dielectric materials, such as water and human tissue.^13,14 This Cherenkov emission can be imaged from the surface of tissue,^15,16 during x ray or electron beam in radiotherapy, with the intensified time-gated camera.¹⁷ Experiments and theory have shown that the intensity generated in tissue is generally linear with the dose deposited on the corresponding surfaces, but that there are variations in intensity, largely due to blood vessels, capillary blood volume, and surface reflectivity that can be corrected for by either reflectance or CT number.⁹ The Cherenkov imaging was used to derive the 2D dose distribution in TSET treatment.¹¹ Thus, to a first approximation, the superficial Cherenkov emission distribution is generally representative of the relative dose distribution. Surface images of Cherenkov emission present a view of dose delivery that provides an intuitive understanding of the beam–tissue interactions. This approach to imaging dose delivery has a major potential advantage for large area irradiation such as TSET where total skin coverage needs to be verified to check the anomalous regions, such as overlaps or gaps in field uniformity.

The Stanford technique is one of the three main treatment techniques used in TSET and is the only approved TSET technique in the study sites of Dartmouth Hitchcock Medical Center and the Hospital of the University of Pennsylvania. In the Stanford technique for TSET, the patient is placed in six distinct anatomic positions throughout treatment. There is no anatomical imaging technique that can capture all six limbs and body positions for planning in a single or fused 3D image set; therefore, classical 3D CT information is unavailable. It is, however, relatively easy to create 3D optical surface scans of the body since these scanners are now commonly used for daily position verification during radiation treatment.¹⁸ In this study, 2D Cherenkov image data were projected onto the 3D optical scan surfaces through texture mapping, which is widely used in computer graphics and photogrammetry research. Medical use of these animation methods has occurred in endoscopic imaging, where optical images are textured onto the 3D meshes of the CT images to visualize the internal structures and locate fiducial markers as a surgical aid.¹⁹ In our study, texture mapping of radiation dose as estimated from Cherenkov emission imaging was mapped onto a single 3D body mesh. The study presents the first use of a 3D animated model of the patient during the TSET treatment, which is digitally altered to match the six positions of the Stanford technique, such that a cumulative dose image can be mapped onto the surface.

2. Material and Method

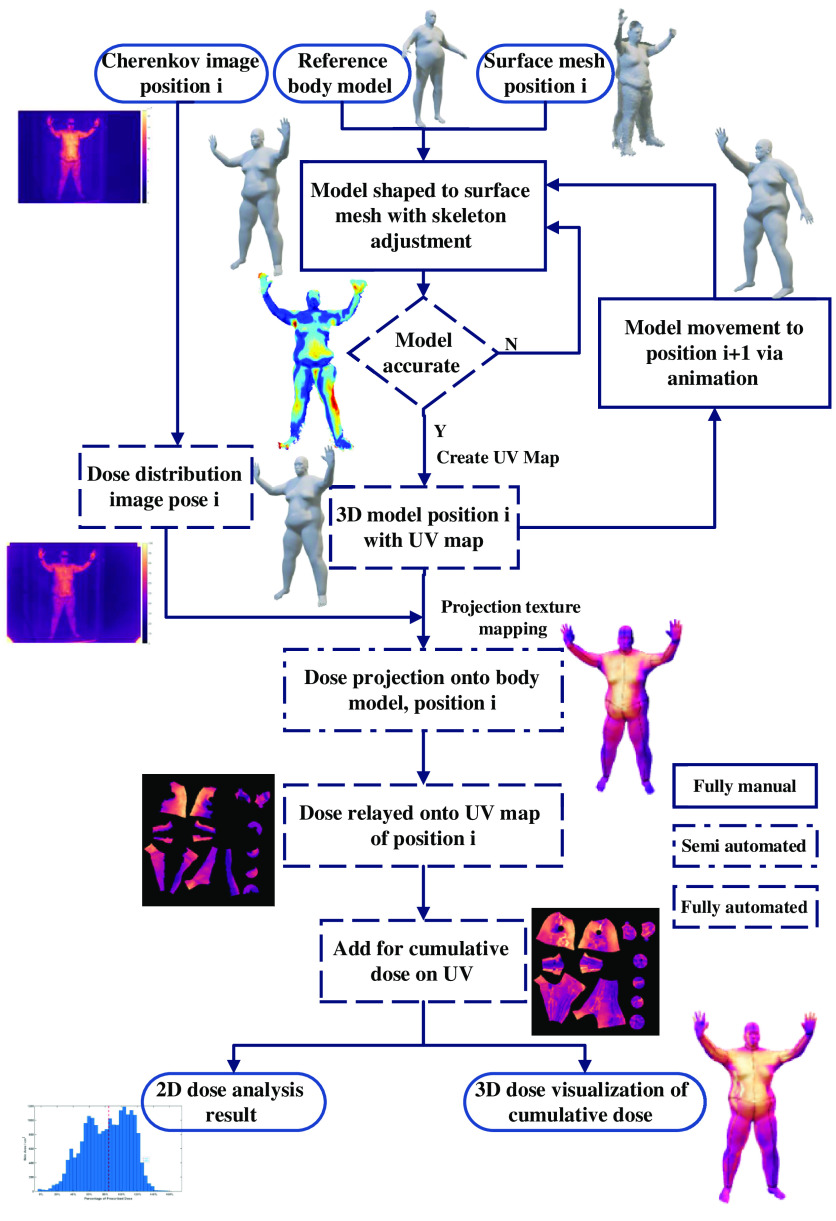
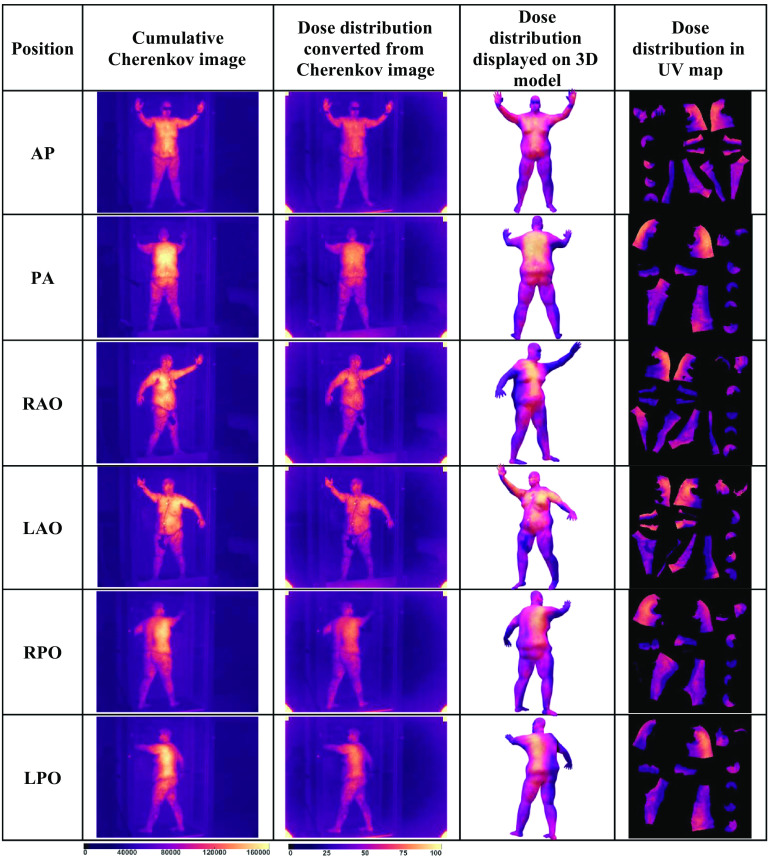
The overall concept of the study is illustrated graphically in the flow chart of Fig. 1. The 2D Cherenkov images and partial 3D body contour meshes of the patient were acquired during a clinical TSET treatment using the Stanford technique.¹¹ The Cherenkov images were converted into the 2D dose distribution images, with the point dose measurement in the patient body and flat field correction.¹¹ The partial 3D body contour meshes for the anterior–posterior (AP) and posterior–anterior (PA) positions were used to build a 3D model of the complete patient body contour, based on warping a reference human body model to match the measured partial 3D meshes. The patient-specific 3D model was evaluated and refined through iterative comparisons with the measured partial 3D body meshes, and manual editing of the 3D model was done to minimize discrepancies. After the 3D body model matched the measured data, a mapping was defined between the 3D surface and a fixed 2D representation of the whole-body surface, called a UV map, where U and V refer to the axis of this 2D texture space. The use of a UV map enables the summation of the 3D Cherenkov data across different patient positions, independent of patient rotation or alternations of limb and body positions. Variants of the 3D body model were then created with adjustments to match each of the remaining positions, such as right anterior oblique (RAO) and left posterior oblique (LPO). With 3D models now available for each patient position, the 2D dose distribution image data for each position were projected onto the 3D models and then cast onto UV maps. The UV maps for each position were then summed up to generate a cumulative dose distribution for the entire body for the complete TSET treatment. This cumulative dose distribution could then be visualized on the 3D body model of the patient as a delivery verification tool and used for 3D Cherenkov emission distribution analysis.

Fig. 1.

The analysis workflow of mesh creation and Cherenkov mapping onto the different distributions, from TSET images, using computer animation techniques.

2.1. Human Imaging and Treatments

The total skin electron therapy treatments (TSET) were conducted in the linear accelerator (Linac) room of Perelman Center of Advanced Medicine of the University of Pennsylvania. All imaging was approved by the Institutional Review Board (IRB), and all procedures followed this approved protocol. The experimental setup included the patient in a wooden stand with handles for patient position support. A clear plastic spoiler was positioned in front of the patient to provide electron scattering and beam energy degradation of the electron beam from the Linac (Varian Truebeam, Palo Alto, California). The patient was 5 m away from the Linac nominal electron source, which pointed toward the patient with two specific angles. Laser line positioning was used on the stand to make sure it was in the same position for different patients and each daily treatment fraction. Before TSET, certain parts of patient’s skin, such as the nails or eyes, were shielded with lead, to reduce the radiation dose in these regions where prescribed by the physician.

The Stanford technique was used for treatment. The whole TSET treatment was divided into two cycles, with three of the six patient positions treated each cycle. Each patient position was irradiated using an upper field and lower field, in which the gantry angles were set at 106 deg and 74 deg. On cycle A, the patient stood in the AP, LPO, and RPO positions, while on cycle B, the patient stood in the PA, LAO, and RAO positions. Before the treatment, multiple OSLDs or diodes were attached to the patient to monitor the dose delivery at specific point locations across the patient’s skin. Dose measurements were acquired for the first fraction of cycles A and B. The laser alignment is turned off during treatment, and the room light was dimmed above the patient to minimize background light reflected from the front of the spoiler during Cherenkov imaging.

2.2. Camera Systems

There were two camera system setups in the Linac, one to acquire the 2D Cherenkov frames during the TSET and the second to acquire the 3D skin surface contour of the patient before TSET. The Cherenkov camera (CDose, DoseOptics, Lebanon, New Hampshire) was located beside the couch, which served as the reference location to make sure the Cherenkov camera was in the same position for different TSET treatment days, and used a 28-mm lens (Sigma, Ronkonkoma, New York) for similar field of view as the Linac beam coverage. The 3D structured light surface camera (generation 1, Occipital, San Francisco, California) was positioned in front of the patient, and the distance between the patient and the 3D camera was $\sim 2\mathrm{m}$, the optimum distance for a useful 3D scan. Before and in between the irradiation, the therapists helped the patient stand in each of the different positions, and the patient held these positions with the support of handles during the treatment. Immediately after each position was set, the 3D camera recorded the skin surface contours. Through classical 2D camera calibration methods, the position of the Cherenkov camera was derived relative to the TSET isocenter, which is located at the patient’s standing position and at the same height of the Linac isocenter. The position information of the Cherenkov camera was used in the projection texture mapping stage of 3D image processing. The 3D contour mesh of the patient includes partial contouring of the wooden stand, which served as the position reference for the patient’s skin surface contour.

2.3. Three-Dimensional Human Model Construction

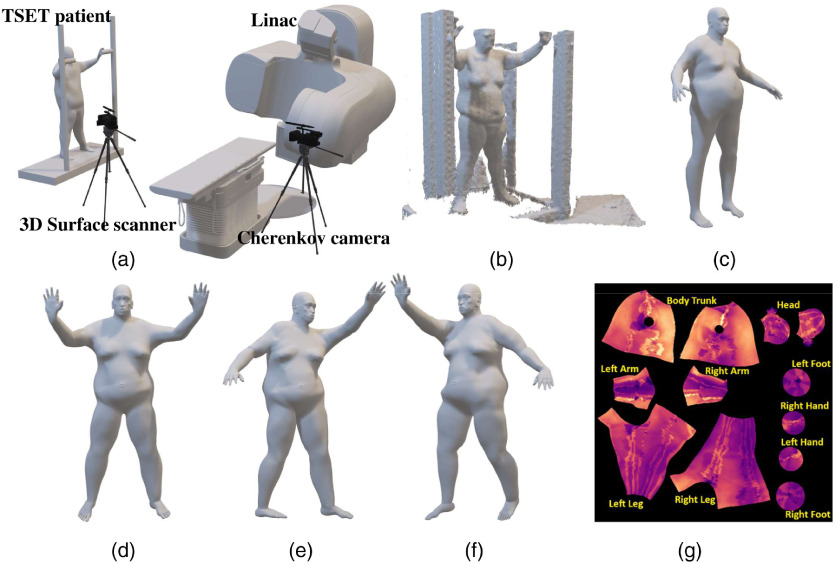
Due to its limited perspective view, a single 3D structured light sensor only extracts partial meshes of the patient’s position. While this limitation can be mitigated in future studies through the installation of multiple 3D sensors, definitions of the unmeasured regions were resolved using a full body reference mesh purchased for this purpose (Turbosquid, New Orleans, Louisiana). The reference contour mesh of the human body was manually edited using the sculpture tools in 3D animation software (Maya, Autodesk, Mill Valley, California) to fit the partial meshes of the patient’s AP and PA positions by expansion. The body regions needing the most additional reference mesh information were the feet and hand areas.

The manually edited mesh accuracy was evaluated by iterative calculation of the Hausdorff distance,²⁰ which estimates a metric of distance from vertices of the edited patient body mesh to the nearest point on the contour surface mesh extracted from the 3D sensor. This Hausdorff distance evaluation was used to provide feedback for editing of the patient’s 3D model. Many reference body model shapes are available for use, such that a reference model that closely matches the body mass and relative shape of each patient can be chosen. The reference body models include animation skeletons used for altering the body model into different limb and body positions. During the editing process, the skeleton of the body model was also adjusted to fit the body shape and size, providing the ability to move the arms and legs to match the six positions as well as possible, as illustrated in Fig. 2.

Fig. 2.

(a) The TSET clinical setup with Cherenkov camera behind the treatment table and 3D sensor beside the TSET stand. (b) The 3D raw mesh of the patient in AP position with TSET stand, extracted from 3D sensor. (c) The 3D human body model used as reference to make the patient’s 3D model. (d) The 3D body model of the patient in AP position manually created based on the reference body mesh to match the raw mesh, with the 3D model in (e) RAO and (f) LAO positions altered from the AP position through animation. (g) All of the 3D body models share the same UV map layout.

Computer animation software uses a surface space mapping plane called the UV map, which is a 2D layout presented or displayed on a square, to record the surface texture of the animated 3D mesh,²¹ as shown in Fig. 2(c). The UV map is usually represented by a 2D square image and is invariant in animiation.²¹ In Stanford technique, the patient deformed to different positions during the treatment, which made it hard to sum up dose values directly in the patient’s 3D model. However, the UV map is invariant in the deformation process of moving the limbs or posture, which makes it the ideal tool to examine total Cherenkov/dose summed from all fractions. The UV map is created in Maya by manually defining the cutting seams, which are the boundaries of textured region in the UV map. Most vertices in the 3D body model map to a single point in the UV map. In some regions, such as the edges and corners of the cutting seams, a single vertex corresponded to multiple points in the 2D UV map. The correspondence relationship between the UV map and 3D model was recorded with the 3D body model and used for texture mapping and texture recording in later steps.

The reference body model has a built-in animation skeleton. Through the animation skeleton, the 3D body model based on the AP and PA positions was altered to those of other positions, such as the LPO and RAO positions. The animation process was manually done by rotating the joint of the animation skeleton to simulate the patient’s movement and to change their position. After altering the animation skeleton, there were some mismatched regions between the body model and the body contour mesh. Additional detailing steps using the 3D editing tools are needed to make the body models fit the contour meshes that are extracted from the 3D body scanner.

2.4. Three-Dimensional Dose Distribution Analysis

After flat field correction, the cumulative Cherenkov image of each position was converted to dose distribution with the Cherenkov-to-dose conversion ratio.¹¹ The conversion ratio was derived by the ratio of the diode measurement in the chest region to the mean Cherenkov intensity in the corresponding region. Projective texture mapping²² used a ray-tracing algorithm, which is one of the classical rendering algorithms in computer graphics. As shown in Algorithm 1, the method tracked the light rays from each pixel of the Cherenkov camera sensor back to the 3D body model of the patient. The ray-tracing algorithm located the vertex corresponding to the image pixel through the first intersection of the light ray and the 3D model. If there were no light rays intersecting with one vertex on the 3D body surface, the texture value of that vertex was assigned zero. The texture values of the vertices in the 3D model were mapped onto the points in the UV map, and the 2D texture distribution was interpolated from the texture values of the individual points in the UV map.

Algorithm 1.

Projection texture mapping.

Input: Cherenkov/dose image $I_{\mathrm{ch}}$, 3D body model $G$, UV map correspondence $\mathbf{F}$

Loop: Pixel $(m,n)$ in $I_{\mathrm{ch}}$

Generate camera ray $\mathbf{R}(x,y)$

If$\mathbf{R}(m,n)$ intersect with $G$ at location $(x,y,z)$

Search the UV location $(i,j)$ of $(x,y,z)$ through $(i,j)=\mathbf{F}(m,n)$

$UV(i,j)=I_{\mathrm{ch}}(x,y)$

end if

end Loop

Output: UV as the Cherenkov/dose UV map of the 3D body model

The projective texture mapping method included the modules of ray tracing and the interpolation of the texture values. The ray-tracing module was an interactive graphical user interface implemented in VTK toolkit (Kitware, Clinton Park, New York) with support from DoseOptics, LLC. It reads the dose distribution images and the patient’s 3D body model to create the textures on the 3D body model. The projection approach used the Cherenkov camera information from the positional calibration file, such as its location and orientation relative to the patient, to simulate the Cherenkov camera view of the patient. However, the camera calibration was not done at the same time as the patient’s Cherenkov imaging, and the camera position was not fixed between different fractions. Thus, some manual adjustment, which was included in the module, was needed to tune the Cherenkov camera parameters for accurate texture mapping. The interpolation module was implemented with the scatter points interpolated in MATLAB (Mathwork, Natick, Massachusetts), converting the dose distribution from the 3D body contour to the UV map that represented the body skin in 2D.

With the dose distribution recorded over the 3D body model and the 2D UV map, it is then possible to complete further analysis. For example, in this study, the mean and the standard deviation could be extracted from the area dose distribution, and body components that had significantly higher or lower overall dose could be identified from the cumulative dose values of the whole treatment (Algorithm 2).

Algorithm 2.

Statistical analysis of dose distribution on body area.

Input: Dose distribution UV, triangulated 3D body model $G$

Loop: Face $f_i$ in $G$

$A(i)=\text{area}[f_i(1),f_i(2),f_i(3)]$

$D(i)=\text{mean}\{UV[f_i(1)],UV[f_i(2)],UV[f_i(3)]\}$

end Loop

Output:$\mathbf{A}$ as the arrays of area for all faces, $\mathbf{D}$ as the dose value for all faces.

Even though the UV map is a 2D array representing the dose distribution over the patient’s surface, it cannot be used directly to analyze the area dose distribution due to the area distortion of converting a 3D model to a 2D area. To analyze the area dose distribution, we assumed that the planner geometry with a small area had uniform dose distribution. The 3D model of the patient’s body consists of multiple polygonal faces with small areas. The body model was first triangulated to make sure all faces on the surface of the body model were triangles. The area of each triangle was calculated from the locations of its vertices. The dose values in the vertices were extracted from their UV locations, and the dose value of the triangle was derived as the mean of the dose values of its three vertices. Finally, the area distributions of the dose value were derived by calculating the areas and dose values of all triangular faces in the 3D body model.

2.5. Verification Analysis on a Cylindrical Phantom

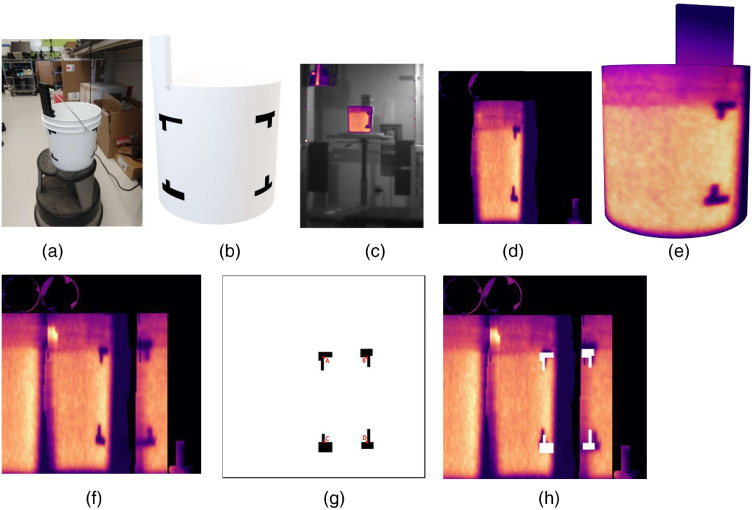
A basic phantom experiment to validate the positional accuracy involved imaging a cylindrical water bucket as a tissue phantom; it was placed on a rotary table on the TSET stand with its center aligned with the height of the Linac isocenter. The Cherenkov and 3D scanning cameras were placed similarly to the human TSET setup to extract the 3D contour of the bucket and image Cherenkov emissions. A turntable was used to rotate the water bucket, emulating variations in the rotational position of a TSET patient. Pieces of black marker tape were affixed to the outer wall as marker fiducials that could be viewed by both cameras.

The cylinder was irradiated by a 6-MeV electron beam to capture Cherenkov imaging. The gantry angle was set at 270 deg so that the gantry head faced the water bucket along the isocenter line. In the experiment, the bucket was irradiated twice with turntable rotations. For each rotation angle, 200 MU of electron beam was delivered to the bucket.

Before this experiment, the locations of the tape markers in the film edge were recorded as texture in the 3D bucket model, using a marker plate on the top. The black tape markers were visible in the Cherenkov intensity, such that these locations could be compared with prerecorded texture in the 3D bucket model to measure the accuracy of the projective texture mapping.

3. Results

3.1. Cylindrical Phantom Study

The experiment using the cylindrical phantom was to test the accuracy of the texture projection. During the process of projection texture mapping, a square plate on the top of the cylinder was used as a fiducial marker to provide a reference for the camera location. The black marker-taped corners were used to test the spatial accuracy of texture mapping, as shown in Fig. 3(h), for Cherenkov distribution in the UV map, to match with their real locations on the UV map. Four corner locations, marked by the red dots, were used to evaluate the spatial accuracy of the projection algorithm. The deviations of these four locations are (A) 10.1 mm, (B) 8.7 mm, (C) 7.5 mm, and (D) 12.8 mm, with a mean value of 9.8 mm. These distance errors would result in a minimal lateral dose error for regions within the bucket, likely $<1\%$ because the dose intensity map varies slowly with lateral position. However, if these distance errors were near the edge of a sharp falloff in dose, then there could be considerable dose mapping error.

Fig. 3.

Phantom study using a water-filled bucket. (a) Photograph of the bucket with black fiducial corner markers and reference positioning plate above. (b) A simplified 3D model of the water bucket from the surface scan. (c) The cumulative Cherenkov image of the water bucket in one rotational position, with corresponding (d) Cherenkov UV map layout and (e) Cherenkov texture on the 3D model. (f) The cumulative Cherenkov distribution from the water bucket in rotations 1 and 2 projected onto a UV map for the bucket. (g) The locations of the black fiducial marker corners in the UV map with a red dot marking the corners used to evaluate spatial accuracy, and (h) compared with the cumulative Cherenkov distribution.

3.2. Human Study

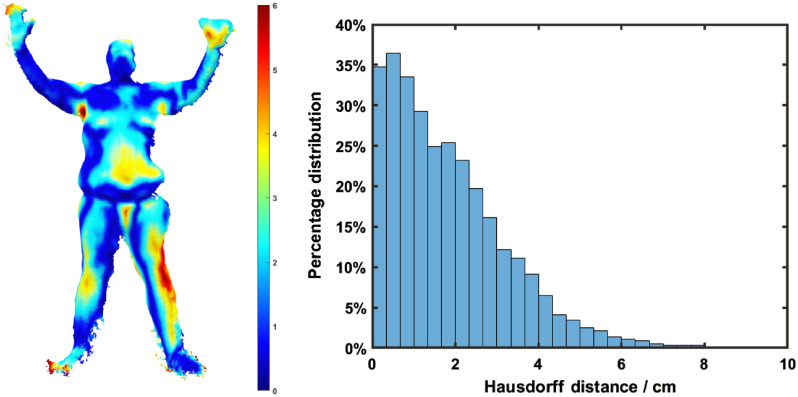
The mean Hausdorff distances representing the difference between the raw meshes extracted from the 3D sensor and the model mesh created manually are listed below. The mean distance, which is the average distance from the vertices in the raw mesh to the model mesh, was between 1.84 and 3.23 cm with a mean of 2.54 cm (as listed in Table 1). The 3D sensor extracted high-resolution raw meshes of human body, with many noisy regions, especially on the boundaries. The mesh resolution of the reference model is much lower, which provides a lower number of control vertices for manual mesh editing. The lower resolution of the reference human model can be regarded as the 3D fit of the raw mesh, resulting in the deviations of the reference model from the raw mesh, represented by the Hausdorff distance metrics.

Table 1.

The mean Hausdorff distance from the extracted raw mesh to the body model for the six positions in TSET treatment.

Positions	AP	PA	LAO	RAO	LPO	RPO
Mean distance (cm)	1.84	3.23	2.81	2.18	2.23	2.95

These distance errors would translate into Cherenkov intensity projection errors in estimating the dose on the skin surface at these positions. There is no exact translation in how a distance translates into dose because the dose values vary across the body, as some distance errors would provide very little dose error, but some distance errors such as those near the edge of the patient could produce 100% dose error (Fig. 4).

Fig. 4.

(a) Hausdorff distance distribution from the raw mesh to the model mesh in AP position. (b) Histogram of the Hausdorff distance distribution in AP position, with the mean value of 2.54 cm for all positions.

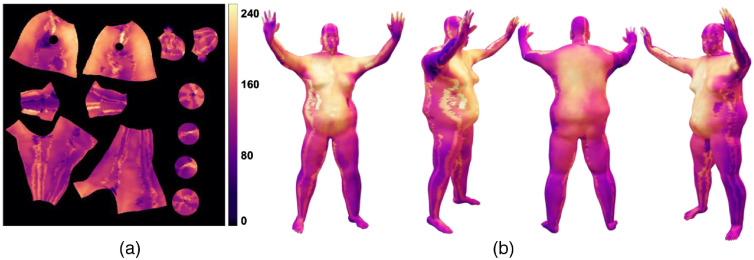
The body surface analysis workflow using computer animation techniques was verified on two patients. Patient 1 had a more obese body shape, while patient 2 was thinner. For each patient, the dose distributions were derived from the cumulative Cherenkov images in all six positions. The dose distributions were then projected onto the patient’s 3D models and recorded on the single UV map. The final cumulative dose distribution was derived by summing up the dose distributions of all positions on the UV map (Fig. 5).

Fig. 5.

The summary of the results of 3D dose (cGy)/Cherenkov (intensity count) study in TSET patient 1.

This 3D dose visualization can be used to find regions of low or high exposure from the electron beam treatments. Cumulative dose summaries across all positions can be created by summing across the sets of 2D UV data and reprojecting onto the 3D model, as shown in Fig. 6. The locations of the fiducial feature points in the texture, such as the scintillators in AP, RAO, and LAO, match the physical attachment locations, which are near the region of the chest and umbilicus.

Fig. 6.

The cumulative dose distribution of patient 1 by adding up dose distributions (cGy) in UV map for six positions, (a) visualized in UV map, and (b) the patient’s 3D model in AP position with different perspective views.

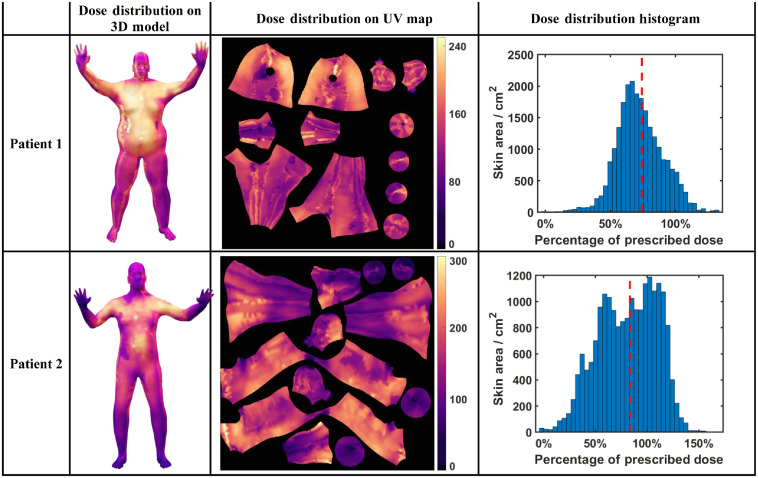
A similar workflow was applied to patient 2 to study the dose distribution over the body. The area dose distributions were derived for both patients from their dose distributions on the 3D models and UV maps. The histograms of their dose distributions in reference to the dose value measured on the umbilicus are plotted in Fig. (7), with the dashed red line representing the mean values of the dose distributions. The reference dose of patient 1 measured at the umbilicus by OSLD is 198.4 cGy, compared with the mean dose derived from Cherenkov of 147.0 cGy and standard deviation of 35.3 cGy. The reference dose of patient 2 is 186.9 cGy, with the mean dose derived from Cherenkov of 155.8 cGy and standard deviation of 52.7 cGy.

Fig. 7.

The comparison between the dose distribution of patients 1 and 2 throughout the TSET, represented in the 3D model, UV map, and dose distribution histogram.

The statistical analysis generally matches the in vivo diode measurement in different locations of the patient during the TSET, as the chest and the umbilicus regions had higher doses while the regions of legs, feet, and hands had lower doses. The scintillator also affected the dose reading from Cherenkov imaging as the scintillation signal was much higher than the Cherenkov signal.

4. Discussion

The cumulative 3D dose distribution provides a possible comprehensive surface view to display the total dose distribution from different body positions. Visualization of this total dose distribution shows that the body trunk coverage was relatively uniform. However, there are clearly regions of overlap between the fields that lead to the bright lines present in the lateral areas of the legs and body. Simulation studies indicate that the vertical lines represent true overlap regions between the different fields, which makes these regions over- or underexposed as compared to the midline. Perhaps the most interesting observation are the areas of very low Cherenkov intensity that were not expected, such as the underside and back of the arms, the head, and the lateral aspect of the legs. It is worth reiterating that Cherenkov intensity is known to be slightly different from dose, due to attenuation by blood, body hair, etc. So, the lower intensity at the legs is not entirely indicative of lower dose at the legs; however, lateral or rotational variations in the dose distribution are likely indicative of dose heterogeneity. In addition, features such as the back versus the front of the arms are likely indicative of lower dose levels.

The error of the final cumulative dose distribution could be attributed to two steps in the workflow. The first type of error is derived from the interpretation of the dose value in the 3D Cherenkov imaging. After camera and dose calibration, the dose interpretation could achieve good agreement with OSLD measurement (within 6.1% error) and diode measurement (within 10.9% error).¹⁵ The second type of error is derived from the geometries of the cameras and projection texture mapping. The projection error was between 2 and 3 cm in phantom measurement, and this was the focus in this study. The 3D dose/Cherenkov analysis on both a patient and the bucket phantom tested the limits of spatial accuracy in this setup, for the current geometry of a single Cherenkov camera and a single 3D body sensor camera. The slight differences in positioning between the two cameras provide some nonoverlapping spaces from the differences in perspective view, although this was largely solved using a common reference mesh that was warped to fit the body surfaces. In addition to testing the positioning accuracy, the projection of Cherenkov light onto the human animation mesh can be ensured for accuracy by testing for coverage to match at geometrical features on the patient body, such as the joints and the edges of the body in view. These implicit fiducials, together with other fiducial markers, such as the scintillation dots at the chest and umbilicus regions, serve to ensure that Cherenkov mapping can fit the body mesh within the accuracy specified by the bucket testing. There are peripheral limits on the perspective view of the Cherenkov camera and 3D sensor, as well as choices in lenses and positioning used on the cameras. In the positions, such as PA, RPO, and LPO, the TSET stand occludes the image view of the left hand and arm, which make the corresponding 3D body model miss texture regions on the left hand and arm. The 3D sensor did not have high enough spatial resolution to extract the shape of hands or feet, which makes the 3D textures in these regions different from the Cherenkov images. The handles blocked the line of sight for the 3D sensor in the hand regions. The shielding regions in the patient’s lower body limited the perspective views of the Cherenkov camera, as shown in the RAO and LAO positions. Each of these limitations can be overcome by a stand that incorporates multiple 3D scanning cameras within the stand itself, and this design is in progress.

Many modules in the workflow of projecting dose/Cherenkov images onto the patient’s 3D body model can be automated, even though some manual labor is needed for some modules. The workload of editing the patient’s 3D model is similar to contouring work in treatment planning systems. But the procedures of editing the body model are clear and the number of editing tools is limited. The health care practitioner can be familiar with the editing tool after training similar to CT contouring in treatment planning systems. The premade 3D human body models with animation skeletons save significant work in editing and animating the body models. With the premade 3D model, users only need to detail the body surface with common sculpture tools to match the patient’s raw mesh scanned from the 3D sensor. The 3D software with the calculation module of Hausdorff distance can automatically create the Hausdorff distances between the body model and raw meshes, which provides quick feedback of the performance of mesh editing and animation. After the body model is created for one position, the UV map can be constructed automatically from the 3D software. In the projective texture mapping module, manual input is needed to tune the camera view angle and position. The rest of the texture mapping can be done automatically by software, with the dose/Cherenkov distribution in the UV map as the output of this module. The dose/Cherenkov UV map is finally used to texture the 3D body model by the 3D software. Therefore, in the whole workflow, manual inputs are only needed to create human body models for the six positions and adjust the camera parameters in the texture mapping process. In future improvements, the camera alignment can be done once, with the fixed installation of the Cherenkov camera in the room. The workload of editing and animating the body mesh can be further reduced with more types of reference body models, allowing the user to choose the reference body model that is closest to the new TSET patient.

Minimizing the distance errors from mesh creation is critical because they can directly influence dose mapping errors, which would be largest near the periphery of the body. The key factor in this process is to keep the lateral errors as small as possible so that the projection of dose onto the 3D mesh does not have large error because a distance that moves the body out of the project would have a 100% dose error, for example. Otherwise, lateral shifts in the center of the body would not be that large, likely being just a few percent dose error. In the shifts reported here, the alignment of the fingers and toes was not highly accurate due to limited resolution of the mesh, so the dose values at these locations would be unreliable. However, the mesh accuracy throughout most of the body had a median Hausdorff distance of 2 to 3 cm error, which would translation to a mean dose mapping error of 3% to 5%, but the range could be anywhere from 0% up to about 20%. While the mean dose error is reasonable, the absolute error range would be unacceptably high, so the key factor in this type of display is to place accuracy error bounds on the resultant dose map, with calculated confidence intervals estimated based upon the known Hausdorff distances.

Even though the Stanford technique is the only approved technique in our sites, the workflow introduced in this study can be easily applied to other main TSET techniques. The other TSET techniques do not require the patient’s anatomical movement during the treatment. Thus, the animation procedures in the workflow can be skipped. In the technique using a rotary table, the researcher extracts the 3D body model of the patient’s initial position. During the treatment, the researcher can take the Cherenkov images and record the rotation angles without the 3D scanners. The Cherenkov/dose images are projected to the body model from the corresponding rotation angles using the projection texture mapping methods, and the cumulative Cherenkov/dose distribution is derived through summing up the distribution on the UV map.

5. Conclusion

Three-dimensional modeling and animation methods can be used to visualize and analyze the accumulated dose in TSET via display of the summed dose/Cherenkov images on a single body surface. With the help of 2D UV surface mapping between 3D surface maps in different body positions, the total dose/Cherenkov distribution can be summed to allow for inspection of the regions of field overlap and possible lack of field coverage. The fiducial markers used to test human body TSET and cylinder phantom experiments indicate that spatial accuracy in the range of 2 cm is currently feasible and is most critical near the edges of the body mesh to ensure that projection of high dose gradients are not misprojected. Areas of poor spatial agreement were largely due to limitations of the body surface camera used, which is readily solved with a more complete camera system for surface scanning. In this preliminary study, the areas of least coverage appeared to be the back of the arms and legs, while lateral areas on the torso and legs appeared to have overlap regions of higher coverage. Further quantitative investigation with full body scanning and calibrated Cherenkov to dose conversion are likely possible in future systems.

Biographies

Tianshun Miao is a graduate research assistant at Thayer School of Engineering in Dartmouth College. He received his MSc degree from Dartmouth College and is working toward completion of his PhD.

Heather Petroccia is a medical physicist at the University of Colorado Heath in Fort Collins, Colorado, USA. She was the chief medical physics resident at the Perelman School of Medicine in the University of Pennsylvania. She received her PhD from the University of Florida in medical physics.

Yunhe Xie is a medical physicist at Massachusetts General Hospital in Boston, Massachusetts, USA. She was the chief medical physics resident at the Perelman School of Medicine in the University of Pennsylvania. She received her PhD from Brown University in high energy physics.

Michael Jermyn is an assistant professor at Thayer School of Engineering in Dartmouth College and lead software developer at DoseOptics LLC. He received his PhD from Dartmouth College.

Maxine Perroni-Scharf is an undergraduate student in the Department of Computer Science at Dartmouth College.

Namit Kapoor is an undergraduate student in the Department of Computer Science at Dartmouth College.

James M. Mahoney is a lecturer of computer animation in the Department of Computer Science at Dartmouth College. He received his MSc degree from Cornell University.

Timothy C. Zhu is a professor of radiation oncology at the Perelman School of Medicine in the University of Pennsylvania. He received his PhD in physics from Brown University.

Petr Bruza is an assistant professor at the Thayer School of Engineering at Dartmouth College. He received his PhD in biomedical physics from Czech Technical University.

Benjamin B. Williams is the medical physicist at the Geisel School of Medicine at Dartmouth College and Dartmouth-Hitchcock Health. He received his PhD in physics from the University of Chicago.

David J. Gladstone is the chief medical physicist in radiation oncology at the Geisel School of Medicine and Dartmouth Hitchcock Health. He received his ScD degree from Massachusetts Institute of Technology.

Brian W. Pogue is the MacLean professor of engineering at the Thayer School of Engineering at Dartmouth College. He received his PhD in medical physics from McMaster University in Canada.

Disclosures

Authors Brian Pogue and Michael Jermyn both disclose that they are employed by the company DoseOptics LLC, whose camera and software were used in the acquisition of data in this manuscript. Author Petr Bruza has sponsored research financially supported by DoseOptics LLC, through his employment at Dartmouth College. Authors Tianshun Miao, Heather Petroccia, Yunhe Xie, Maxine Perroni-Scharf, Namit Kapoor, James Mahoney, Timothy Zhu, Benjamin Williams, and David Gladstone have no financial interests to disclose related to this work.