CONTROLLING PHYSICAL INTERACTIONS: HUMANS DO NOT MINIMIZE MUSCLE EFFORT

Abstract

Physical interaction with tools is ubiquitous in functional activities of daily living. While tool use is considered a hallmark of human behavior, how humans control such physical interactions is still poorly understood. When humans perform a motor task, it is commonly suggested that the central nervous system coordinates the musculo-skeletal system to minimize muscle effort. In this paper, we tested if this notion holds true for motor tasks that involve physical interaction. Specifically, we investigated whether humans minimize muscle forces to control physical interaction with a circular kinematic constraint.

Using a simplified arm model, we derived three predictions for how humans should behave if they were minimizing muscular effort to perform the task. First, we predicted that subjects would exert workless, radial forces on the constraint. Second, we predicted that the muscles would be deactivated when they could not contribute to work. Third, we predicted that when moving very slowly along the constraint, the pattern of muscle activity would not differ between clockwise (CW) and counterclockwise (CCW) motions.

To test these predictions, we instructed human subjects to move a robot handle around a virtual, circular constraint at a constant tangential velocity. To reduce the effect of forces that might arise from incomplete compensation of neuro-musculoskeletal dynamics, the target tangential speed was set to an extremely slow pace (~1 revolution every 13.3 seconds). Ultimately, the results of human experiment did not support the predictions derived from our model of minimizing muscular effort. While subjects did exert workless forces, they did not deactivate muscles as predicted. Furthermore, muscle activation patterns differed between CW and CCW motions about the constraint. These findings demonstrate that minimizing muscle effort is not a significant factor in human performance of this constrained-motion task. Instead, the central nervous system likely prioritizes reducing other costs, such as computational effort, over muscle effort to control physical interactions.

1. INTRODUCTION

Many of the motor actions performed in our daily lives involve physical interaction. And yet, our knowledge of human motor control results largely from studies focused solely on free motion. Neural control of physical interaction is under-studied largely due to the fact that physical interaction is vastly more complex than free motion. Object interaction introduces bidirectional forces that pose a new challenge, absent in free movements [1–3]. Furthermore, a tool may have complex internal dynamics (e.g., a circular power saw) which may change in response to forces from the human (friction increases with applied normal force). Intermittent contact also introduces switching between discrete regimes of continuous dynamics [4,5].

Even though teasing out the control strategies humans use for physical interaction can be challenging, the need is significant and widespread. For instance, the ultimate goal of rehabilitation and assistive technology is to increase the number of activities of daily living that an individual can perform independently. A vast majority of these tasks require physical interaction with a tool or object, such as brushing teeth, buttoning a shirt, opening a door, walking etc. To repair or replace such control in impaired humans, a basic understanding of how unimpaired humans control such interactions is first needed.

Knowledge of how humans control physical interactions is similarly important for robotic systems where a human is in the loop. Such insight would aid the design of teleoperation systems where humans must interact with an unknown physical environment through a robotic device for applications in space and disaster relief. Additionally, understanding human control of interaction is necessary in cases where the human must physically interact either directly with a robot or indirectly through a shared object (e.g., each holding the end of a table). Especially when performing cooperative tasks, it would be ideal for the robot to interact with objects as humans do, such that the behavior is more legible and predictable to humans [6]. At the very least, this requires a competent model of how humans control physical interactions.

To render the study of tool use manageable, a task of intermediate complexity is needed. Physical interaction with a kinematic constraint is a key intermediate point between simple reaching and complex tool use. Kinematic constraints introduce many challenges of complex tool use. For instance, they may evoke instabilities not present in free movements [7]. They also profoundly change the multi-joint interaction torques that confront the neural controller. Moreover, many tools introduce kinematic constraints. For example, a simple lever imposes a circular constraint on hand motion but assists the motion by enhancing applied force. Continuous circularly-constrained rotation is required by tools such as a traditional coffee-mill and a yarn winder. Thus experimental and theoretical studies of how humans manually interact with a circular kinematic constraint provide a first step towards understanding complex tool use and the human control of physical interactions.

In previous work, Russell and Hogan showed that when humans operate a frictionally loaded crank in a vertical plane, they exert forces normal to the crank [8]. Such forces are considered workless as they do not contribute to motion or mechanical work. This finding suggests that humans use a control strategy that takes advantage of motion constraints to reduce required effort. The question is, what form of effort or cost do humans reduce when controlling physical interactions?

Ohta and colleagues similarly found that when rotating a crank in a horizontal plane, humans exert workless forces [9]. To determine what criterion humans might optimize to control interaction, they compared human experimental data with data simulated with a variety of optimality criteria. Their results suggest that subjects minimized a combined criterion of the change in hand contact force and the change in muscle force. However, it is also possible that while subjects attempted to reduce muscle force, non-minimal muscle forces resulted from imperfect compensation for neuro-musculo-skeletal dynamics.

In this paper, we further investigated if humans minimize muscle forces to control physical interaction with a circular kinematic constraint. First, we used a simplified arm model to derive predictions for the existence of workless forces and specific characteristics of muscle activity consistent with the hypothesis that humans reduce muscle effort. Next, we conducted an experiment to test whether human subjects exhibited the same behavior as predicted by our model with minimized muscle effort. In the human experiment, we instructed subjects to move a robot handle around a virtual, circular constraint at a constant tangential velocity in both clockwise (CW) and counter-clockwise (CCW) directions. To reduce the effect of forces that might arise from incomplete compensation of neuro-musculo-skeletal dynamics, the target tangential speed was set to an extremely slow pace (~1 revolution every 13.3 seconds). This allowed us to assume that subjects moved around the constraint under quasi-static conditions.

2. MODEL-BASED PREDICTIONS OF MINIMIZING MUSCULAR EFFORT

Exerting muscular force without doing work consumes metabolic energy, so we might expect workless forces to be minimized. However, exerting such seemingly unnecessary forces on a kinematic constraint can actually reduce muscular effort while still achieving the task goal [10]. To demonstrate this point, we refer to a simplified model of a human ann with 3 major muscle types: one-joint elbow muscles, one-joint shoulder muscles, and two-joint elbow and shoulder muscles (Figure 1). For any given posture of the upper limb, each muscle exerts hand force in a particular direction. Activating one-joint elbow muscles exerts a force vector directed from the hand to the shoulder joint. Activating a one-joint shoulder muscle exerts a hand force vector oriented along a line joining the elbow axis with the point of contact. The activation of two-joint muscles exerts a force vector oriented parallel to the upper arm link, assuming that their moment anns about shoulder and elbow joints are all equal.

Figure 1.

In this simplified two-link arm model, the moment arms of all muscles are assumed to be constant. The links of the arm are of equal length (30cm each). The center of the circular constraint (radius = 10cm) is aligned with the shoulder joint and 45cm in front of the shoulder joint. Colored radial lines depict reversal positions for the 3 muscle types. Dark and light shading denotes two distinct reversals for each muscle group. At these positions along the circular constraint, the respective muscle cannot generate tangential force. If subjects are minimizing muscle effort to perform this task, we predict that the respective muscles will be deactivated at these positions along the constraint.

In the position shown in Figure 1, the one-joint shoulder muscles project a force component along the tangent, as well as a substantial component along the radius. To strictly exert tangential hand force and avoid workless forces, the one-joint elbow flexors must be activated to offset or cancel radial hand force due to shoulder muscles. However, if workless forces are permitted, the same tangential hand force may be generated by one-joint shoulder muscles activated at the same level with no exertion of one-joint elbow muscles. This latter scenario requires less total muscular effort, regardless of whether such effort is measured by metabolic energy consumption, sum of squares of muscle stresses, muscle forces or joint torques, or any other reasonable measure.

Thus, minimizing muscle effort requires the exertion of workless radial forces against the circular constraint. Accordingly, when muscles can only generate radial forces (i.e. they cannot generate tangential force needed to contribute to the task), they should be deactivated. Figure 1 shows the distinct hand positions around the constraint where the different muscle types cannot generate tangential force. These positions correspond to where the muscles reverse from shortening to lengthening and vice versa. In addition, activity of the corresponding muscle type should be minimized, regardless of the direction of motion around the constraint. In fact, the pattern of muscle activity should be identical, assuming static or quasi-static conditions.

To summarize, if humans minimize muscular effort as they interact with the circular constraint, we would expect subjects to exhibit the following behaviors as derived from the model. First, we predicted that subjects would exert workless, radial forces along the constraint as previously reported [8,9]. Second, we predicted that the muscle activation would be minimal at the respective muscle reversal positions. Third, the pattern of muscle activity would not differ between CW and CCW motion around the constraint.

3. METHODS

3.1. Participants

Three right-handed subjects (2 males and 1 female, mean age 26 ± 9.6 years) with no history of neurological or biomechanical disorders took part in the experiment. Subjects participated voluntarily and provided written informed consent according to procedures approved by the Institutional Review Board of the Massachusetts Institute of Technology.

3.2. Experimental Setup

Seated subjects held the handle of a planar horizontal robot, the InMotion 2 (Interactive Motion Technologies, Watertown, MA), with their right, dominant hand (Figure 2). To restrain shoulder and torso movements, subjects were strapped to the seat with a shoulder harness. A wrist brace discouraged wrist rotation, and a hanging sling supported the elbow against gravity.

Figure 2.

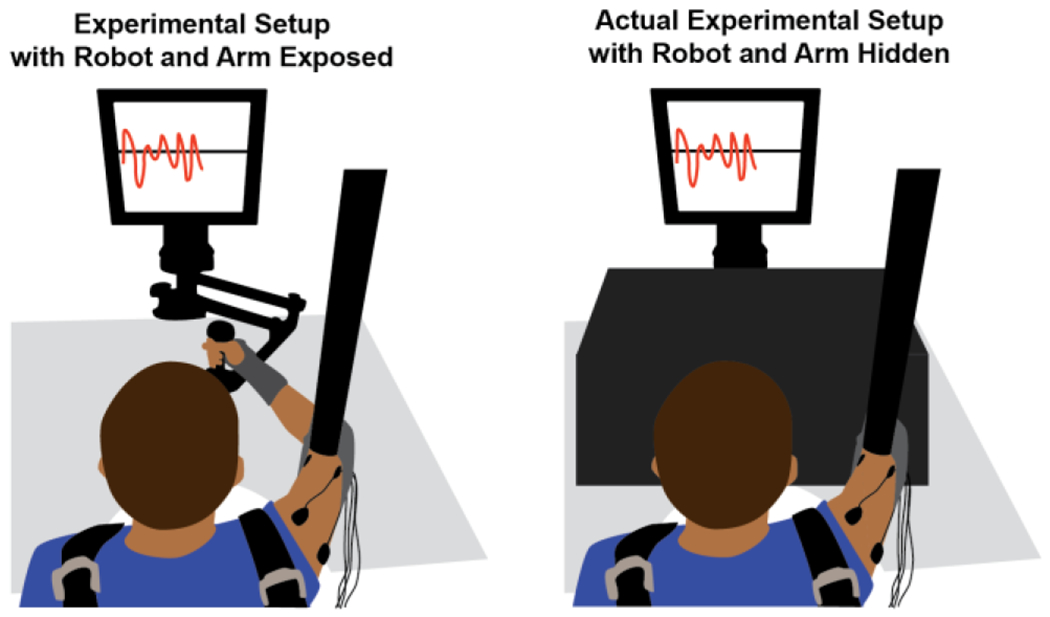
Experimental Setup. The panel on the left shows how subjects held onto the planar InMotion 2 robot to perform the task. During the actual experiment, however, the view of the robot and subject’s arm was occluded by a wooden box draped with black cloth as shown in the right panel. Subjects were instructed to match their current tangential speed with a target value, both of which were displayed to the subject on a computer monitor.

Subjects were instructed to move the robot handle around a virtual, circular constraint at a constant velocity. To simulate the constraint haptically, the robot controller implemented zero impedance along the tangent to a circle of radius of 10cm and an effective mechanical impedance of 3000N/m stiffness and 100N-s/m damping in the radial direction normal to that circle.

The endpoint position of the robot was recorded at 200Hz. The endpoint velocity was approximated by computing the backward difference of the position values. From the endpoint velocity, the tangential speed of the endpoint along the circular constraint was calculated. The subject’s current and target tangential speed were displayed on a computer monitor directly in front of the subject. The target tangential velocity was 0.047m/s. As the radius of the constraint was 10cm, the target angular speed was 0.075 revolutions per second (i.e., 1 revolution per 13.3 seconds). Force applied to the robot handle was measured at 200Hz with a 6-axis force transducer mounted on the robot handle (ATI Industrial Automation, Inc., Apex, NC).

3.3. Experimental Design

At the start of the experiment, subjects performed a familiarization trial with the virtual constraint to become acquainted with the robotic system. This trial lasted for approximately 1 minute. Subjects then performed 4 experimental trials. Each trial was 2 minutes long and consisted of approximately 9 revolutions. For 2 trials, subjects moved around the constraint in the clockwise (CW) direction and in the counterclockwise (CCW) direction for the other 2 trials. The order of these trials was randomized for each subject.

3.4. Electromyographic (EMG) Measurements and Onset/Offset Detection

To measure muscle activation levels, EMG signals were recorded from surface electrodes (Delsys, Inc., Natick, MA) placed on 6 muscles of the subject’s right upper extremity. Table 1 describes each muscle recorded. Placement location and orientation of surface electrodes were determined using guidelines from SENIAM, and standard clinical tests were used to confirm correct detection of each muscle [11]. EMG signals were collected at 1 kHz through an NI-USB-6343 data acquisition board (National Instruments, Austin, TX) with custom software developed in MATLAB (The Mathworks, Natick, MA).

Table 1.

Muscles recorded with EMG and the corresponding positions along the circular constraint where they should be deactivated to minimize muscle effort.

Muscle Name	Type	Reversal Positions
Brachioradialis	One joint – elbow	90°, 270°
Biceps Brachii	Two-joint	57.9°, 229.2°
Triceps Brachii (Lateral Head)	Two-joint
Anterior Deltoid	One joint – shoulder	122.1°, 310.8°
Pectoralis Major	One joint – shoulder
Posterior Deltoid	One joint – shoulder

At the end of the experiment, subjects were instructed to lie on a padded surface and remain as relaxed as possible while EMG signals were sampled for approximately 30 seconds. From this sample, baseline resting activity in each channel of the EMG system was estimated. These measures served to evaluate the appropriateness of signal levels of the data after collection. The EMG signals during the familiarization trial were visually inspected to verily that the signals were not contaminated with excessive noise or movement artifact. Electrodes were adjusted as necessary based on EMG signals from this familiarization trial but were not adjusted after collection of experimental data began.

We predicted that muscle activity would be minimal at the corresponding muscle reversal positions along the circular constraint. To accurately test this prediction, it was important to correctly detect when each muscle was on and off from the EMG signals. One popular method for determining muscle onset involves detecting when the amplitude of a rectified and low-pass filtered EMG signal exceeds a threshold value set above baseline activity [12]. However, the low-pass filter smooths the EMG signal, such that the exact onset of muscle activity becomes difficult to detect. In fact, onset detection is sensitive to the parameters used for the low-pass filtering. Additionally, examination of the low-pass filtered signals to determine muscle onsets can be susceptible to bias from the individual inspecting the data. Thus, we used a statistics-based, double-threshold detection algorithm [13]. Compared to using a single threshold, this method has been shown to have less error in detecting the onset of muscle activity [14]. In addition, the performance of the double-threshold method degrades at a slower rate as signal-to-noise ratio of the EMG signal decreases [14]. With the double-threshold method, the EMG signals were transformed into binary signals. In these signals, a value of 0 indicated that the muscle was not active, and a value of 1 indicated that the muscle was active.

3.5. Data Processing and Dependent Measures

While data from the robot and EMG were collected through different systems, a trigger signal sent from the robot to the EMG data acquisition system was used to synchronize the two sets of acquired data. Radial forces and the binary muscle activation signals were parsed into revolutions based on the angular position of the robot handle around the circular constraint. Only full revolutions were included in the analysis in order to exclude transient effects at the beginning and end of each trial. For each subject, approximately 16 revolutions were analyzed for each direction.

To test our predictions, we performed the following analysis across all subjects in each of the two conditions (CW and CCW rotation). To assess if subjects exerted workless forces as predicted, the average radial force for each position on the constraint (between 0° and 360°) was calculated. For each binary muscle activation signal, the percentage of revolutions where each muscle was activated was calculated for each position on the constraint. We predicted that the percentage of revolutions where the muscle was active would be low at the respective muscle reversal positions, regardless of movement direction. Given the slow speed, we also expected this distribution of the percentage of muscle-active revolutions to be the same in each direction of movement around the constraint.

4. RESULTS

If humans minimize muscular effort as they interact with the circular constraint, we expected them to exert workless forces. Figure 3 shows that subjects did exert such radial forces as predicted.

Figure 3.

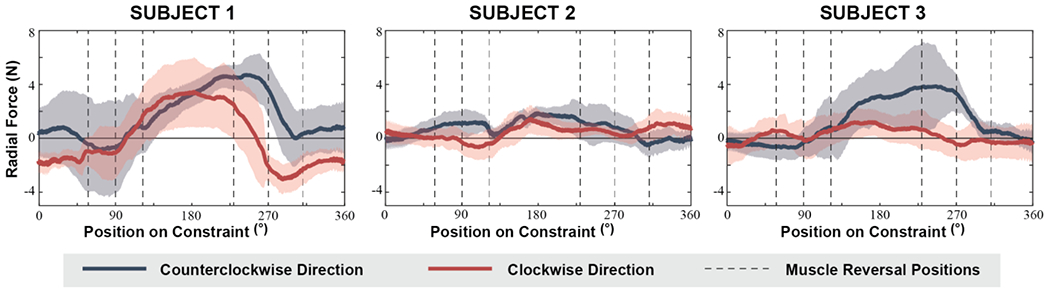
Average radial forces over angular position on the constraint for individual subjects. The thick lines show the average radial force at each position, and the shaded regions represent ± 1 standard deviation. The vertical lines indicate the muscle reversal positions as detailed in Table 1. The 0° position corresponds to 3 o’clock as shown in Figure 1. Positive radial forces are tensile, away from the center of constraint and vice versa. Consistent with the hypothesis that subjects minimize muscles effort, subjects exerted radial forces, even though they do not contribute to work in this task.

We posited that the exertion of workless forces is due to the deactivation of muscles when they cannot contribute work (i.e. they cannot generate hand force tangential to the constraint). Thus, muscle activation at the corresponding reversal positions was expected to be zero. However, Figure 4 shows that subjects consistently did not deactivate muscles at the predicted positions. Moreover, the muscle activity at these positions was not even consistently at a minimum value (Figure 5).

Figure 4.

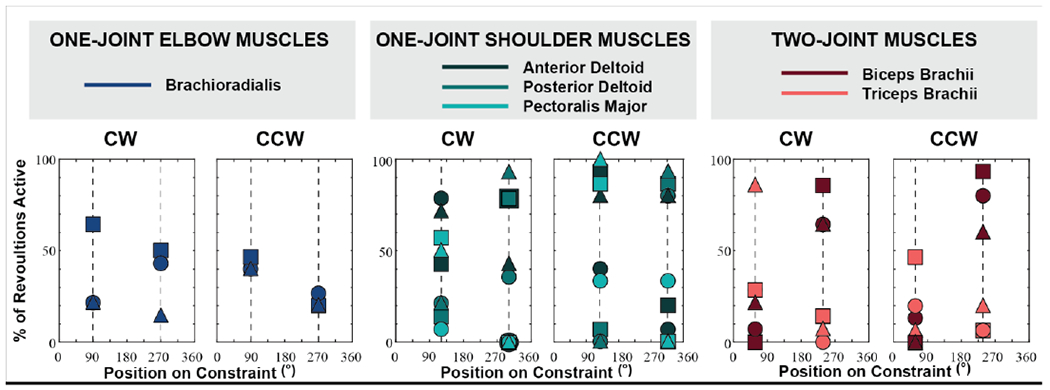
Percentage of the revolutions where the muscle was activated at respective reversal positions. Data from each subject is represented by a different shape (circle for Subject 1, triangle for Subject 2, and square for Subject 3). The dotted lines indicate the muscle reversal positions specific to each muscle type. We predicted that muscle activity should be minimal at these reversal positions where they cannot contribute work. Contrary to this prediction, subjects consistently did not minimize muscle activation at these points.

Figure 5.

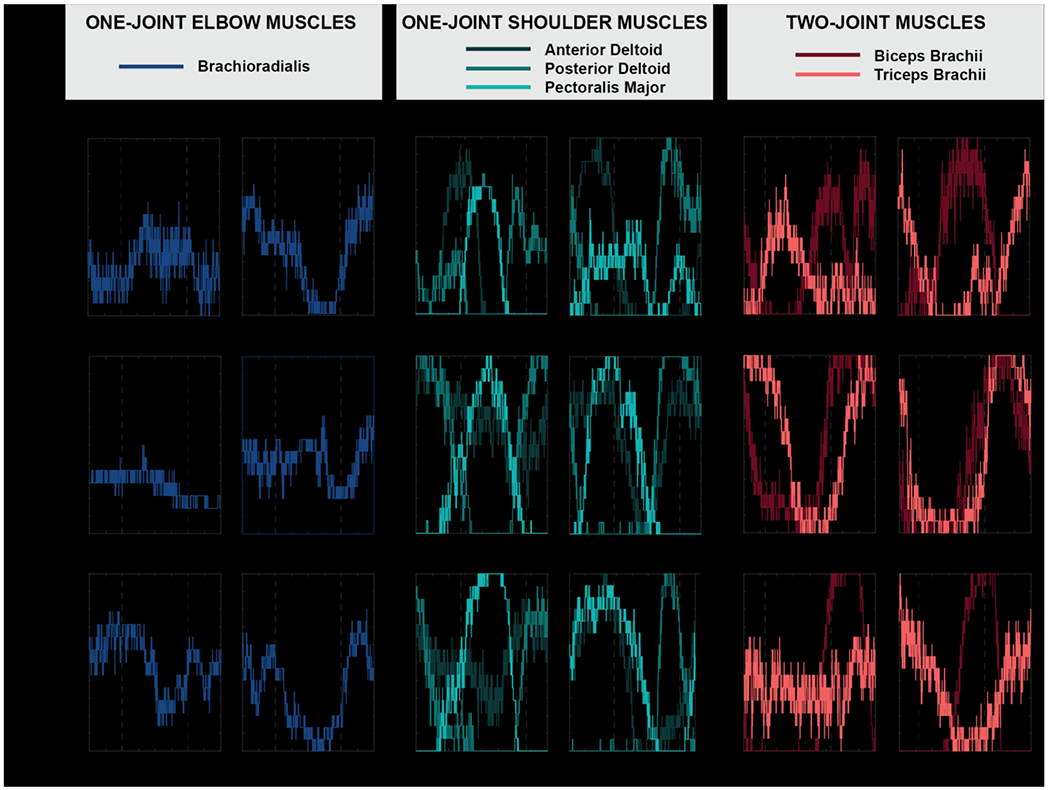
Individual plots of the percentage of the revolutions where the muscle was activated for each angular position. The dotted lines indicate the muscle reversal positions specific to each muscle type. Subjects consistently did not minimize muscle activation at these points. They also exhibited different patterns of EMG activity in each movement direction.

It is also important to remember that the speed at which subjects moved along the constraint was extremely slow. Subjects were instructed to move with a tangential speed of 0.047m/s. Overall, subjects were able to maintain a tangential speed close to the target value. The average tangential speed across subjects was 0.043m/s in the CW direction and 0.041m/s in the CCW direction. There were, however, significant fluctuations in their tangential speed within each trial. The average coefficient of variation of tangential speed across subjects was 35.49% in the CW direction and 39.83% in the CCW direction. While subjects had difficulty moving with a constant tangential speed as instructed, they still moved about the constraint at a very slow rate. Because of this slow speed, it was assumed that subjects moved under quasi-static conditions. Hence, we expected that subjects would exhibit the same muscle activation patterns in both CW and CCW directions. Figure 5 shows that counter to this prediction, muscle activation was different in each movement direction. This was especially evident from the activity at the muscle reversal positions. At these positions, the percentage of revolutions where the muscle was active was expected to be equal, but this was not the case. The most prominent example was the difference between motion directions in the activation of the triceps brachii at its reversal position of Subject 2.

5. DISCUSSION

If humans minimize muscular effort as they interact with a circular constraint, we predicted that subjects would deactivate muscles when they could not contribute to the task (i.e. generate force tangent to the constraint). Consequently, subjects would exert workless, radial forces. Consistent with prior research, subjects exerted workless radial forces on the constraint. They did not, however, deactivate muscles when they could not contribute to the task.

It is possible that failure to inactivate muscles at these positions might result from addressing other aspects of performance, such as a perceived need to stabilize limb posture by antagonist muscle co-activation. If this were the case, we would expect muscle activations to at least reach a local minimum at the expected positions. However, they did not. Regardless of how muscular effort is quantified, be it metabolic energy consumption, sum of squares of muscle stresses, muscle forces or joint torques, our results showed that humans did not minimize muscular effort to control physical interaction in this task. Furthermore, subjects did not produce the same pattern of muscle activity in the CW direction as in the CCW direction as predicted. Together, these results demonstrate that minimizing muscle effort is not a significant factor in human performance of this constrained-motion task.

It is possible that the simplifying assumptions in the model influenced the estimation of the muscle reversal positions. First, we assumed that all muscles had constant moment arms. In reality, these moment arms change with joint configuration. Second, we assumed that the length of each arm link was 30cm. However, it is important to note that the muscle reversal positions for the one-joint elbow muscles do not depend on muscle moments arms or link lengths (the latter due to how subjects were positioned relative to the constraint). The muscle reversal positions for one-joint shoulder and two-joint muscles depend on link length. However, the link lengths measured from the 3 subjects changed the reversal positions by an average of only 1.7°. Thus, we submit that these modeling assumptions did not materially affect our predictions. Finally, it should be noted that the existence of muscle reversal positions is not limited to the two-link planar arm model we used. This analysis can readily be extended to kinematic chains with more degrees of freedom (as in the human arm).

To determine whether muscles were on or off at these reversal points, we elected to use a double-threshold detection method on the raw EMG signals. This method has several advantages over the more common approach of rectifying and filtering the signals. First, our hypotheses were only concerned with whether a muscle was active or not, rather than the signals’ relative amplitudes. When the raw EMG signals were converted into a binary signal, activation could be measured as a simple proportion without the need to interpret arbitrary EMG signal amplitudes. That proportion provides an unbiased estimate of the probability that a muscle is active. Second, the double-threshold method is an unbiased, probability-based approach to detecting the onset of muscle activation. Thresholds for the detection process were calculated based on signal strength and an underlying statistical model of the EMG signal rather than selected at the discretion of the researcher. If the signals were filtered and/or a single-threshold detection were employed, sections of filtered data where the activation level was ambiguous might be vulnerable to potential bias from the researcher. Finally, a double-threshold method is more sensitive to the onset and offset of muscle activations compared to single threshold methods.

While optimization is an appealing way to describe the basis of human coordination, identifying the objective function is challenging. To minimize muscular effort, humans must have knowledge of the tangential and radial directions of the constraint. The combined optimization criterion of the change in hand contact force and the change in muscle force proposed by [9] similarly requires this knowledge. Hence, it is possible that our ability to minimize muscle effort is limited by our inability to construct such a detailed internal model of the task.

This study focused on the strategies humans might extemporaneously use to control physical interaction. Thus, we did not rule out the possibility that subjects could develop a control strategy that minimizes muscle effort if given enough practice or explicitly trained to do so. Still, motions subject to a circular constraint are commonplace in daily life and should not require a lot of practice. It is therefore significant that the “off the cuff’ approach that subjects used to control physical interaction in this task did not result in minimal muscular effort.

Prior work of Kistemaker et al. has similarly shown that subjects do not prioritize the minimization of muscular energy in a force-field reaching task [15]. While subjects did not minimize muscular effort in our task, it is important to note that they still exerted workless forces. This observation offers insight as to what criterion humans may be optimizing to perform this task. One possible explanation is that subjects exerted workless forces as a consequence of optimizing “computational effort”.

It is possible that reducing “computational effort” over “muscle effort” is a strategy that the central nervous system could use in order to minimize overall “effort”. Huang et al. showed that during force-field reaching adaptation, net metabolic power continues to decrease, even after muscle activity and antagonist coactivation reached an asymptote [16]. Nasseroleslami et al. also found that when interacting continuously with a complex dynamic object, humans learned a strategy that rendered the object’s behavior more predictable [17]. It was proposed that humans adopted this strategy to avoid excessive sensorimotor processing [18]. They did not minimize exerted forces or maximize smoothness of the object’s motion.

To move around the circular constraint, subjects may have adopted a similar strategy of minimizing computational effort. To reduce the knowledge and information processing required to perform the task, the central nervous system may have used a combination of dynamic primitives (e.g., submovements and mechanical impedances) to control physical interactions [19,20]. This possible explanation for the exertion of workless forces remains to be investigated in future work.

6. CONCLUSION

We investigated whether humans minimize muscular effort to control physical interaction with a circular kinematic constraint. Consistent with this hypothesis, we predicted that subjects would exert workless forces. We further predicted that these workless forces would result from the deactivation of muscles when they could not contribute to work done in this task (i.e., at muscle reversal positions). Additionally, we predicted that muscle activity would be the same in each direction of motion. Ultimately, the results of our experiment did not support these predictions derived from our model with minimized muscular effort. While subjects exerted workless forces, they did not minimize muscle activation at the muscle reversal positions. Moreover, muscle activation patterns differed between CW and CCW motions about constraint. This finding suggests that the central nervous system prioritizes reducing other costs, such as “computational effort”, over “muscle effort” to minimize overall “effort”.