The Efficacy of Lockdown Against COVID-19: A Cross-Country Panel Analysis

Abstract

Background

There has been much debate about the effectiveness of lockdown measures in containing COVID-19, and their appropriateness given the economic and social cost they entail. To the best of our knowledge, no existing contribution to the literature has attempted to gauge the effectiveness of lockdown measures over time in a longitudinal cross-country perspective.

Objectives

This paper aims to fill the gap in the literature by assessing, at an international level, the effect of lockdown measures (or the lack of such measures) on the numbers of new infections. Given this policy’s expected change in effectiveness over time, we also measure the effect of having a lockdown implemented over a given number of days (from 7 to 20 days).

Methods

We pursue our objectives by means of a quantitative panel analysis, building a longitudinal dataset with observations from countries all over the world, and estimating the impact of lockdown via feasible generalized least squares fixed effect, random effects, generalized estimating equation, and hierarchical linear models.

Results

Our results show that lockdown is effective in reducing the number of new cases in the countries that implement it, compared with those countries that do not. This is especially true around 10 days after the implementation of the policy. Its efficacy continues to grow up to 20 days after implementation.

Conclusion

Results suggest that lockdown is effective in reducing the R0, i.e. the number of people infected by each infected person, and that, unlike what has been suggested in previous analyses, its efficacy continues to hold 20 days after the introduction of the policy.

Electronic supplementary material

The online version of this article (10.1007/s40258-020-00596-3) contains supplementary material, which is available to authorized users.

Key Points for Decision Makers

Lockdown is effective in reducing the number of new COVID-19 infections.

Lockdown starts to reduce the number of COVID-19 infections around 10 days after implementation.

Lockdown continues to reduce the number of new cases as much as 20 days after the initiation of the policy.

Introduction and Research Question

Diffusion of a novel coronavirus infectious disease (COVID-19) began in China in December 2019, when the first cases were identified in the province of Wuhan. Since then, COVID-19 has spread quickly all over the world [1]. For this reason, on 11 March 2020, the World Health Organization (WHO) declared COVID-19 a pandemic. According to WHO data, on 12 May 2020 there were more than 4 million confirmed cases, approximately 280,000 confirmed deaths, and at least 215 countries, areas or territories that had reported confirmed cases of infection. Starting in April, the US observed swift growth of COVID-19, and by 12 May 2020 was the country with the highest number of confirmed cases (approximately 1,300,000). In May, Europe and North America were the most severely affected continents, with 1,755,790 and 1,743,717 cases, respectively (as of 12 May 2020). By 12 May 2020, Spain was the most badly affected European country, with over 224,000 confirmed cases, followed by Russia (221,334), the UK (219,187), Italy (219,070) and Germany (169,575). It should be noted that the situation is rapidly evolving and continuously changing.

Although the approaches taken by national governments to deal with the emergency have varied widely [2], two principal types of policies can be identified: (1) health policies aimed at strengthening the capacity of the hospital system; and (2) policies aimed at reducing the probability of people contracting the virus, such as lockdowns and social distancing measures.

Lockdown has fostered a debate about the need for such measures. This resistance on the part of stakeholders and policymakers is likely because lockdown comes with a very high economic price, characterized by the necessary halting of many productive activities. Although both the WHO and previous literature focusing on the Chinese case [3, 4] have highlighted the importance and centrality of such measures in reducing the probability of contagion (and thus the related diffusion of the virus), the political debate appears to have been greatly influenced by the negative impact of those measures on national economies. The debate has thus focused on the potential inefficiency of this policy, and also on the estimation of a good trade-off between safeguarding citizens’ health and avoiding damage to the economy.

Some countries have apparently managed to contain the outbreak without imposing a lockdown, such as Taiwan1; some in which lockdown played a major role in reducing the contagion, such as China; and others that claim a lockdown is unnecessary, such as Sweden, or that it has to be lifted very soon, such as the US.

For all these reasons, it is important to empirically test the efficiency of lockdown in reducing the contagion. While various contributions address this issue, to the best of our knowledge the principal empirical papers that focus specifically on the efficacy of lockdown have been carried out at national level, often adopting susceptible, infectious, recovered (SIR) models, and focusing especially on the Indian and Chinese cases. This literature includes the work of Lau et al. [4], who conclude that thanks to lockdown, a significantly decreased growth in new COVID-19 cases was observed in China, and Sardar et al. [5], who, in a study that incorporates lockdown measures for India, conclude that positive effects of the lockdown are only observed in some provinces. A recent study from the Istituto Superiore di Sanità and Bruno Kessler Foundation of Trento, analysing the reproduction trend of the virus, “underlines the importance of non-pharmaceutical control measures” [6].

Piguillem and Shi [2] study the topic theoretically, adapting an SIR model to include lockdown and virus testing. Their finding was that lockdown is a government’s second best option, after testing. As regards a cross-country perspective, there are comparisons between different patterns of the virus [7], but, to the best of our knowledge, no empirical evidence on the impact of lockdown measures has been provided. Using a qualitative approach, Cruz and Dias [8] investigate COVID-19 in China, Italy, Brazil, and the US, suggesting that “not all relevant actions were taken, in a timely manner, to efficiently address the spread of COVID-19”.

The aim of this manuscript is to provide empirical evidence on the efficacy of lockdown measures by means of quantitative analysis, namely a panel data approach. We address two different research questions. First, is there cross-country empirical evidence regarding the capability of lockdown measures? Second, how long does it take for lockdown measures to become effective?

This kind of approach allows us to observe and take into account heterogeneity within different countries. These types of results, less useful for the detection of a precise estimation at country-level, allow us to generalize a complex phenomenon and to benefit from a higher number of observations able to add robustness to the results.

Data and Methods

To pursue our objectives, we utilized a panel dataset, with daily data from 202 countries around the world used as the basic statistical unit of observation. In formal terms, we estimated the following equation (Eq. 1):

$$\mathrm{\Delta }{i}_{\mathit{ct}}=\alpha +{\beta }_1{i}_{ct-1}+{\beta }_2{\mathit{DLD}}_{\mathit{ct}}+\epsilon$$ 1

where $\mathrm{\Delta }i$ is the new COVID-19 cases at time t with respect to t-1 in country c. This is modeled as a function of the infections in country c the previous day ($i_{t-1}$). Furthermore, Eq. 1 includes DLD, a dummy that signals whether or not on day t there was a lockdown in effect in country c. DLD may also signal which country had a lockdown in place for x days (more details on this further below), in order to control for the time efficiency of the policy.

To estimate our equation, we needed (1) the daily number of COVID-19 cases; and (2) the lockdown measures put in place. We gathered the former from the ‘Novel Coronavirus Cases’ dataset compiled by the Johns Hopkins University Center for Systems Science and Engineering [9] in its latest version available on 11 May 2020. It offers a daily estimation of COVID-19 cases from 22 January to 10 May 2020; 202 countries were included in our final sample, given the list wise deletion of some minor Pacific Island countries due to the lack of data for the datasets of the other variables. From this source, we computed our dependent variable New cases, the operationalization of $\mathrm{\Delta }i$, as the first difference between the cases of today and those of yesterday, and also one of the independent variables, YCases, the operationalization of $i_{t-1}$, which is, for each day, the absolute value of cases found yesterday.

For the lockdown measures, we relied on ACAPS data from the ‘#COVID-19: Government Measures Dataset’ [10].2 This allowed us to distinguish between countries that applied lockdown measures and countries that did not. We used the latest version available on 11 May 2020 (which had been compiled on 5 May 2020), and built the dummy variable Lockdown (operationalization of DLD), which assumes the value of 1 in the first date that a country implemented a partial or complete lockdown measure for the entire population, and also for all subsequent days in which the lockdown is in place. The choice to include policies aimed at the entire population only is justified to avoid having biased estimations due to policy interventions that were referred to a small share of the population. This strategy resulted in a total of 272 measures captured by the DLD dummy, in 100 different countries, in many different times.

We also computed DLD for the number of days elapsed since implementation of the policy. Indeed, 97.5% of those who develop symptoms do so within 11.5 days of infection, with a 95% confidence interval of between 8.2 and 15.6 days [11]. In other words, this means that if a certain delay is in place between infection and the possibility of being tested positive, the lockdown may have greater benefits in terms of a reduction in new cases only after the elapse of a certain time period after the implementation of the policy.

Considering that data have several observations for each c and t, the best estimators are either a feasible generalized least square (FGLS) [12, 13] or generalized estimating equation (GEE) model [14, 15], which have been proposed to extend the generalized linear model to allow for correlated observations. Considering that the spread of the virus may be due to factors specific to each country, from a theoretical perspective we consider it more appropriate to employ a fixed effects (FE) estimator, which captures the heterogeneity between countries. In other words, in this way it is possible to estimate the average effects for single countries, assuming that the heterogeneity among them does not change in the 110 days of our timespan. A Hausman test (reported in Table 1) also suggests that an FE estimator is preferred to a random effects (RE) estimator.

Table 1.

Hausman test for fixed versus random effects, baseline model (dummy lockdown), worldwide and European-only samples

Worldwide sample	European subsample
Ho: difference in coefficients not systematic	Ho: difference in coefficients not systematic
Chi2(1) = (b-B)'[(V_b-V_B)^(-1)](b-B) = 45.67	chi2(1) = (b-B)'[(V_b-V_B)^(-1)](b-B) = 60.83
Prob > chi2 = 0.0000	Prob > chi2 = 0.0000

Moreover, it is possible to imagine that, other than the number of cases on the day before, there are regional differences that influence the evolution of the pandemic. While in an FE estimation all these country-level peculiarities are controlled for, some of these characteristics may be due to the world region to which the country belongs, i.e. its continent. It is also important because, after originating in Asia, the virus took some time to reach Europe, and arrived in America and Africa even later. Thus, the continents may be at different stages of development of the infection. For these reasons, a hierarchical linear model [16] could help to highlight differences and peculiarities within the different world regions by determining the degree of variance in the diffusion of COVID-19 due to cross-regional differences (rather than country-level differences).

Our final dataset is composed of 109 daily observations (for 110 days, i.e. from 22 January to 10 May 2020) in 202 countries, giving a total of 22,018 observations. We also computed estimates for the 47 countries in Europe (with a total of 5123 observations included in this subsample).

Results

Results of the estimates through an FGLS-FE on the complete sample are reported in Table 2 and Fig. 1. YCases is the operationalization of $i_{ct-1}$ and is the total number of COVID-19 cases registered in country c yesterday (on t-1). It has, as expected, a positive and statistically significant coefficient, suggesting that the more cases reported yesterday, the more New Cases of COVID-19 there will be today.

Table 2.

Feasible generalised least squares fixed-effect estimation of the worldwide (complete) sample

New cases
YCases	0.0244***	0.0245***	0.0245***	0.0246***	0.0246***	0.0246***
	(149.82)	(150.27)	(150.48)	(150.68)	(151.15)	(151.35)
Dummy lockdown	21.42
	(1.28)
After 10 days of lockdown		− 73.34***
		(− 3.99)
After 12 days of lockdown			− 102.2***
			(− 5.42)
After 14 days of lockdown				− 129.6***
				(− 6.68)
After 18 days of lockdown					− 191.3***
					(− 9.26)
After 20 days of lockdown						− 220.0***
						(− 10.27)
Constant	64.62***	76.28***	78.70***	80.52***	83.54***	84.24***
	(10.97)	(13.44)	(13.96)	(14.38)	(15.10)	(15.31)
Observations	22,018	22,018	22,018	22,018	22,018	22,018

t statistics are shown in parentheses

*** p < 0.01

Fig. 1.

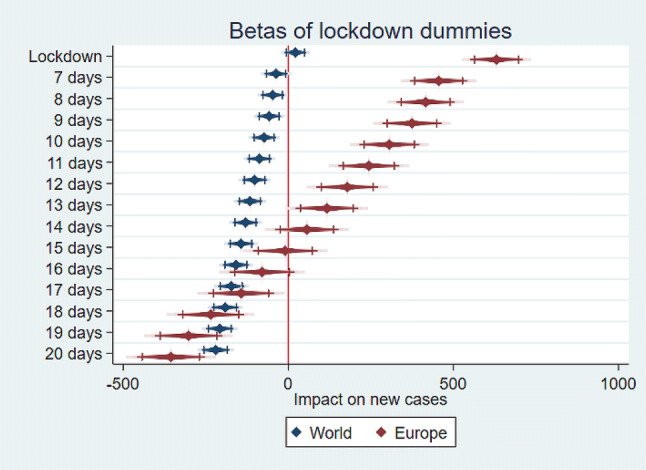
Betas of several lockdown dummies, computed at the date of implementation, 7 days after, 8 days after, etc., up to 20 days after. Lines and lighter colours represent the 95% and 90% confidence intervals. Betas are estimated through the FGLS-FE model. FGLS-FE feasible generalized least square–fixed effects

Lockdown has a negative and statistically significant coefficient, suggesting that countries that implemented the lockdown have fewer New Cases than countries that did not. We can also see that the benefits of lockdown increase exponentially with the passing of time.

When looking at the European subsample (Table 3), the situation is slightly different. It is worth noting that Europe has been affected by COVID-19 severely and diffusely, and that compared with other continents, it is densely inhabited. This, combined with the existence of several different countries in a relatively small space, has possibly increased the speed of the contagion. Here Lockdown is positive, suggesting that countries that implemented the lockdown have, on average, more New Cases than in countries that did not. This is possibly due to the fact that in the countries that implemented lockdown, the spread of COVID-19 was already advanced compared with other European countries. The positive coefficient thus signals a presence in the same continent of countries at different stages of the spread of the virus. In Europe, this difference became statistically non-significant 13 days after the start of lockdown; after 17 days the coefficient become negative, suggesting a net benefit in having implemented the measure; its magnitude and statistical significance keep growing after 20 days, with an apparently exponential trend.

Table 3.

Feasible generalised least squares fixed-effect estimation of the European subsample

New cases
YCases	0.0101***	0.0119***	0.0127***	0.0135***	0.0152***	0.0159***
	(20.80)	(22.92)	(24.20)	(25.46)	(28.68)	(30.02)
Dummy lockdown	630.4***
	(15.56)
After 10 days of lockdown		305.8***
		(6.61)
After 12 days of lockdown			178.4***
			(3.74)
After 14 days of lockdown				56.08
				(1.14)
After 18 days of lockdown					− 234.9***
					(− 4.56)
After 20 days of lockdown						− 355.7***
						(− 6.75)
Constant	99.05***	148.7***	159.1***	167.3***	180.7***	184.1***
	(7.93)	(12.11)	(12.99)	(13.71)	(14.96)	(15.33)
Observations	5123	5123	5123	5123	5123	5123

t statistics are shown in parentheses

***p < 0.01

While both theory and a Hausman test suggested that FE would be a better estimator for testing the model, we cannot assume that all lockdown measures are equal among the 202 different countries included in this analysis. Furthermore, lockdown measures may have happened at different times, and thus could be considerably different between countries or geographical regions. For these reasons, we also estimated Eq. 1 (for both the whole sample and the European subsample) through an FGLS RE estimator. The results are reported in Tables 4 and 5 and are perfectly compatible with the previous finding, suggesting some robustness in the results. Moreover, we also replicated the analysis employing GEE estimators. The results, included in Tables 6 and 7, once again confirm the principal findings, suggesting, if possible, even more stability in the estimates.

Table 4.

Feasible generalised least squares random-effect estimation of the worldwide (complete) sample

New cases
YCases	0.0254***	0.0255***	0.0255***	0.0255***	0.0256***	0.0256***
	(159.23)	(159.76)	(159.98)	(160.19)	(160.68)	(160.90)
Dummy lockdown	3.424
	(0.21)
After 10 days of lockdown		− 89.82***
		(− 4.92)
After 12 days of lockdown			− 118.3***
			(− 6.31)
After 14 days of lockdown				− 145.6***
				(− 7.54)
After 18 days of lockdown					− 207.0***
					(− 10.05)
After 20 days of lockdown						− 235.8***
						(− 11.04)
Constant	62.77***	73.48***	75.72***	77.39***	80.14***	80.73***
	(4.35)	(5.14)	(5.30)	(5.43)	(5.65)	(5.70)
Observations	22,018	22,018	22,018	22,018	22,018	22,018

t statistics are shown in parentheses

***p < 0.01

Table 5.

Feasible generalised least squares random-effect estimation of the European subsample

New cases
YCases	0.0136***	0.0154***	0.0162***	0.0168***	0.0184***	0.0189***
	(29.58)	(31.91)	(33.16)	(34.38)	(37.47)	(38.76)
Dummy lockdown	533.1***
	(13.83)
After 10 days of lockdown		222.0***
		(4.99)
After 12 days of lockdown			102.9**
			(2.24)
After 14 days of lockdown				− 12.35
				(− 0.26)
After 18 days of lockdown					− 286.5***
					(− 5.74)
After 20 days of lockdown						− 402.8***
						(− 7.87)
Constant	84.35***	127.7***	137.0***	144.5***	157.3***	160.7***
	(4.47)	(6.86)	(7.39)	(7.81)	(8.54)	(8.75)
Observations	5123	5123	5123	5123	5123	5123

t statistics are shown in parentheses

**p < 0.05, ***p < 0.01

Table 6.

Generalized estimating equation of the worldwide (complete) sample

New cases
YCases	0.0246***	0.0248***	0.0248***	0.0248***	0.0249***	0.0249***
	(152.85)	(153.34)	(153.55)	(153.76)	(154.24)	(154.45)
Dummy lockdown	16.50
	(0.99)
After 10 days of lockdown		− 77.86***
		(− 4.26)
After 12 days of lockdown			− 106.6***
			(− 5.68)
After 14 days of lockdown				− 134.0***
				(− 6.94)
After 18 days of lockdown					− 195.6***
					(− 9.51)
After 20 days of lockdown						− 224.3***
						(− 10.52)
Constant	64.11**	75.50***	77.87***	79.65***	82.60***	83.27***
	(2.33)	(2.76)	(2.85)	(2.92)	(3.04)	(3.07)
Observations	22,018	22,018	22,018	22,018	22,018	22,018

t statistics are shown in parentheses

^**p < 0.05, ***p < 0.01

Table 7.

Generalized estimating equation of the European subsample

New cases
YCases	0.0106***	0.0125***	0.0133***	0.0141***	0.0158***	0.0189***
	(22.07)	(24.31)	(25.63)	(26.93)	(30.22)	(38.76)
Dummy lockdown	616.8***
	(15.38)
After 10 days of lockdown		292.4***
		(6.38)
After 12 days of lockdown			165.7***
			(3.51)
After 14 days of lockdown				43.96
				(0.90)
After 18 days of lockdown					− 245.2***
					(− 4.80)
After 20 days of lockdown						− 402.8***
						(− 7.87)
Constant	96.89*	145.5***	155.6***	163.6***	176.7***	160.7***
	(1.92)	(2.99)	(3.25)	(3.46)	(3.85)	(8.75)
Observations	5123	5123	5123	5123	5123	5123

t statistics are shown in parentheses

*p < 0.1, ***p < 0.01

Furthermore, a hierarchical linear RE analysis of variance (ANOVA) is presented in Table 8, for the whole dataset, and Table 9, for the European subsample. This model allows us to analyse the degree of variance due to cross-regional differences. As regards the whole dataset (Table 8), the regions identified as a level of aggregation of the countries were Africa (27.23% of the sample), the Americas (23.76%), Asia (22.77%), Europe (23.27%), and the Pacific (2.97%). On the other hand, for the European subsample, following the distinction adopted by the United Nations Statistical Department,3 the regions identified were Eastern Europe (22.92% of this subsample), Northern Europe (22.92%), Southern Europe (35.42%), and Western Europe (18.75%). As expected, the likelihood ratio test statistics for the null hypothesis that there is no cross-regional variation in New Cases have a p-value of 0.00, suggesting that there is indeed variation between the regions identified, both in the complete sample and in the European subsample. Looking at the coefficients, these results are also in line with the previous estimates, suggesting once again some robustness in our findings.

Table 8.

Hierarchical linear model, ANOVA random effects of the worldwide (complete) sample

New cases
YCases	0.0293***	0.0294***	0.0294***	0.0294***	0.0294***	0.0295***
	(201.53)	(202.10)	(202.30)	(202.50)	(202.95)	(203.13)
Days	0.729***	1.105***	1.188***	1.248***	1.351***	1.368***
	(3.56)	(5.49)	(5.93)	(6.26)	(6.86)	(7.00)
Dummy lockdown	− 98.17***
	(− 5.62)
After 10 days of lockdown		− 203.5***
		(− 10.42)
After 12 days of lockdown			− 234.4***
			(− 11.68)
After 14 days of lockdown				− 263.9***
				(− 12.78)
After 18 days of lockdown					− 330.2***
					(− 15.02)
After 20 days of lockdown						− 361.3***
						(− 15.85)
Constant	− 15,967.6***	− 24,239.1***	− 26,055.7***	− 27,366.0***	− 29,648.0***	− 30,024.8***
	(− 3.55)	(− 5.47)	(− 5.92)	(− 6.25)	(− 6.85)	(− 6.98)
lns1_1_1	3.728***	3.712***	3.709***	3.705***	3.705***	3.706***
	(10.54)	(10.52)	(10.52)	(10.52)	(10.54)	(10.56)
lnsig_e	6.736***	6.735***	6.734***	6.733***	6.732***	6.731***
	(1413.43)	(1413.07)	(1412.94)	(1412.81)	(1412.52)	(1412.40)
Observations	22,018	22,018	22,018	22,018	22,018	22,018

t statistics are shown in parentheses

***p < 0.01

ANOVA analysis of variance

Table 9.

Hierarchical linear model, ANOVA random effects of the European subsample

New cases
YCases	0.0172***	0.0187***	0.0192***	0.0198***	0.0210***	0.0214***
	(40.37)	(41.86)	(42.86)	(43.88)	(46.61)	(47.80)
Days	− 1.065**	0.268	0.653	0.988**	1.658***	1.877***
	(− 2.56)	(0.64)	(1.56)	(2.37)	(4.02)	(4.58)
Dummy lockdown	463.0***
	(12.02)
After 10 days of lockdown		136.6***
		(3.05)
After 12 days of lockdown			13.27
			(0.29)
After 14 days of lockdown				− 106.9**
				(− 2.24)
After 18 days of lockdown					− 391.3***
					(− 7.76)
After 20 days of lockdown						− 512.5***
						(− 9.90)
Constant	23,495.3**	− 5777.8	− 14,238.0	− 21,584.3**	− 36,304.3***	− 41,123.8***
	(2.56)	(− 0.63)	(− 1.55)	(− 2.35)	(− 4.00)	(− 4.56)
lns1_1_1	2.576**	2.906***	3.154***	3.361***	3.716***	3.819***
	(1.98)	(3.24)	(4.43)	(5.55)	(7.63)	(8.25)
lnsig_e	6.724***	6.737***	6.738***	6.737***	6.732***	6.728***
	(680.44)	(681.72)	(681.78)	(681.71)	(681.14)	(680.77)
Observations	5123	5123	5123	5123	5123	5123

t statistics are shown in parentheses

**p < 0.05, ***p < 0.01

ANOVA analysis of variance

Moreover, estimates of an alternative model, with an interaction term, are included in the electronic supplementary material.

Discussion

This article provides the first empirical evidence, from a cross-country perspective, regarding the efficacy of lockdown measures. Our results confirm that lockdown policies have had a positive impact on the pandemic, and that they have been able to reduce the number of COVID-19 cases in the countries that implemented them.

It is worth noting that, as previously pointed out, our results are robust to different kinds of estimators (namely FGLS, both with fixed effects and random effects, and GEE), and also when considering the possible existence of differences depending on the world region or European region to which a specific country belongs (through an hierarchical linear model).

All these results contribute to the current debate regarding the need for this kind of policy. Specifically, we believe that our results may contribute to the debate on defining both ‘mitigation measures’ and ‘exit strategy’. Indeed, we have proven that lockdown is effective, on average and worldwide, in reducing COVID-19 contagion. More specifically, looking at the European case, its efficiency begins approximately 3 weeks after the lockdown and continues to reduce the number of COVID-19 infections up to 20 days later. While Sarwal and Sarwal [17] suggest that a ‘localization’ strategy is efficient after 14 days of lockdown, a point at which no further gains can be expected by extending the lockdown, our results seem to contradict this finding from a cross-country perspective, since we detect an increase in benefits and a reduction in contagion even 20 days after the start of lockdown. Accordingly, it seems that any decision to loosen lockdown should be considered very carefully if the full benefits of the measure in terms of reducing new cases are to be enjoyed. More importantly, a rushed removal of lockdown measures may condemn hard-won results to waste.

Limitations

It is important to highlight that we have presented a cross-country analysis. This means it should be considered as an estimate measuring the average effects, worldwide or for European countries. While this has many benefits in terms of generalization of the results and the statistical power of the model, there are also serious limitations in deriving precise estimates, since standard errors can of course increase. Caution is thus suggested in reading these results, which are necessarily also driven by the timing of the measures taken in Europe and the rest of the world, as well as by the spread of the pandemic (it is important to highlight that while we partially controlled this bias in the multilevel analysis, there is still an important heterogeneity within the regions, which are continents for the estimations on the entire dataset, and agglomerates of a dozen countries in the case of the European subsample).

For these reasons, we highlight the importance of and need for further investigations on this topic, which may focus on more specific territorial or climatic subsamples, or on how governments have implemented lockdown policies.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

VA and SE conceived the presented idea. Both authors developed the theoretical framework and performed the computations together, discussed the results, and contributed equally to the final version of the manuscript.

Data Availability Statement

The datasets generated and/or analyzed during the current study are derived from a public dataset, namely the #COVID-19: Government Measures Dataset from ACAPS (available at https://www.acaps.org/covid19-government-measures-dataset) and the Novel Coronavirus Cases from the John Hopkins University Center for Systems Science and Engineering (available at https://coronavirus.jhu.edu/). These datasets are available from the corresponding author upon reasonable request.

Compliance with ethical standards

Funding

No funding was received in order to pursue this research.

Conflict of interest

Vincenzo Alfano and Salvatore Ercolano declare no conflicts of interest.