Understanding Transmission Dynamics of COVID-19-Type Infections by Direct Numerical Simulations of Cough/Sneeze Flows

Abstract

The transmission dynamics of highly contagious respiratory diseases like COVID-19 (through coughing/sneezing) is an open problem in the epidemiological studies of such diseases (Bourouiba, JAMA. https://doi.org/10.1001/jama.2020.4756. 2020). The problem is basically the fluid dynamics of a transient turbulent jet/puff with buoyancy, laden with evaporating droplets carrying the pathogen. A turbulent flow of this nature does not lend itself to reliable estimates through modeling approaches such as RANS (Reynolds-Averaged Navier–Stokes equations) or other droplet-based models. However, direct numerical simulations (DNS) of what may be called “cough/sneeze flows” can play an important role in understanding the spread of the contagion. The objective of this work is to develop a DNS code for studying cough/sneeze flows by a suitable combination of the DNS codes available with the authors (developed to study cumulus cloud flows including thermodynamics of phase change and the dynamics of small water droplets) and to generate useful data on these flows. Recent results from the cumulus cloud simulations are included to highlight the effect of turbulent entrainment (which is one of the key processes in determining the spread of the expiratory flows) on the distribution of liquid water content in a moist plume. Furthermore, preliminary results on the temperature distribution in a “dry cough” (i.e., without inclusion of liquid droplets) are reported to illustrate the large spatial extent and time duration over which the cough flow can persist after the coughing has stopped. We believe that simulations of this kind can help to devise more accurate guidelines for separation distances between neighbors in a group, design better masks, and minimize the spread of respiratory diseases of the COVID-19 type.

Introduction

The continuing COVID-19 pandemic is wreaking havoc in the world affecting more than 180 countries, including India, and resulting in large-scale infections and deaths. The primary cause of the COVID-19 infections is believed to be droplet transmission from an infected person (due to coughing, sneezing or even talking loudly) to a susceptible neighbor (see https://www.who.int/news-room/q-a-detail/q-a-coronaviruses). WHO has recommended maintaining a distance of 1–2 m from an infected person to minimize transmission to a neighbor. However, in a recent article, Bourouiba (2020) has argued that coughing/sneezing produces a turbulent expiratory “cloud” and that small-size droplets can continue to remain suspended in the cloud for over a distance of 7–8 m (especially, for sneezing). This suggests that the WHO prescription of a 1–2-m separation distance could be an under-estimate (Bourouiba 2020). This issue is of critical importance in determining social distancing norms, especially in India, where people often live in close proximity to each other. It is also relevant to healthcare workers treating/testing COVID patients who may get accidentally exposed to the expiratory flows from patients not wearing masks. Moreover, the N95-type masks worn by health-workers are typically not tested for the sneeze/cough clouds impinging on them (Bourouiba 2020). Another important factor is that the droplets, upon complete evaporation, turn into aerosols on which the virus can continue to live, and can remain suspended in the air for a long time. It can also invade ventilation and air-conditioning systems, potentially affecting a large number of people (e.g., in a hospital or a shopping mall).

The above discussion suggests that understanding the fluid dynamics of the cough/sneeze events is crucial in framing more accurate guidelines on the minimum separation distance from an infected person required to mitigate the spread of COVID-19 and other similar viral diseases. This problem has been receiving considerable attention in the news media in the last few weeks (for example, see https://www.sciencenews.org/article/coronavirus-covid-19-why-6-feet-may-not-be-enough-social-distance and https://science.thewire.in/the-sciences/fluid-dynamics-coronavirus-droplets-six-feet-physical-distancing/). Despite its importance, there have been only a few fluid dynamical studies of this problem. Notable among these is the work of Bourouiba et al. (2014), who carried out video-graphic observations of the expiratory flows from human subjects (Fig. 1) and conducted a lab experiment on an idealized set-up. They proposed buoyant turbulent jets and puffs laden with liquid droplets to be the appropriate fluid dynamical model for studying cough/sneeze events. Some other recent studies on this topic are due to Gupta et al. (2009) and Wei and Li (2017). Although these studies have provided useful inputs, much needs to be done to arrive at accurate estimates for the spread of the infectious flows generated by coughing/sneezing. For example, a direct numerical simulation (DNS) of the transient cough/sneeze events, using realistic flow rates and including the thermodynamics of phase change and the dynamics of small water droplets, has not been reported so far to the best of our knowledge. The objective of the present work is to develop a DNS code suitable for studying what may be called “cough/sneeze flows”, by integrating the codes/methods available with the authors, and to carry out simulations on these flows to understand their dynamics. Preliminary results from the simulation of a “dry cough” flow are reported. The simulations of this kind can help to devise more accurate guidelines for separation distances between neighbors in a group to minimize spread of the contagion. Our investigation is in consonance with the WHO Co-ordinated Global Research Roadmap (March 2020), which has identified transmission dynamics of COVID-19-type infections as a key knowledge gap in current epidemiological studies.

Fig. 1.

The “cough cloud” captured from a human subject by superposing instantaneous images. The left picture shows droplet trajectories and the right picture shows a visualization of the cough cloud. Reprinted with permission from Cambridge University Press (Fig. 3e, f in Bourouiba et al. 2014)

Two Closely Related Fluid Flow Problems

In the following, we describe two flow problems which are relevant for understanding the fluid dynamics of the cough/sneeze flows.

Cumulus Cloud Flows

A key parameter that determines the spread rate and trajectory of the cough/sneeze flows, and affects the evaporation rate of suspended droplets, is the turbulent entrainment of ambient fluid into the core of the flow. This bears a strong similarity to atmospheric clouds, in particular cumulus clouds, where water droplets mingle in a turbulent plume generated on the earth’s surface. The authors have extensive experience of studying, experimentally, numerically and theoretically, the dynamics of turbulent entrainment in cloud flows (e.g., Bhat and Narasimha 1996; Narasimha et al. 2011; Diwan et al. 2014; Govindarajan 2002). Diwan et al. (2014) reported numerical simulations based on Boussinesq equations, with external heat addition to mimic latent heat release in cumulus clouds that successfully reproduced typical cumulus cloud forms (see Fig. 2). In this context, our recently developed equations incorporating a field of liquid water and water vapor (including the thermodynamics of phase change), and the MEGHA-5 code developed by Ravichandran (one of the present authors) and others, for solving the dynamical equations governing cloud flows, are ideally suited to carry out the work on cough/sneeze flows (Ravichandran and Narasimha 2020). MEGHA-5 is an MPI-parallelised code and is known to scale to 4000 cores. The domain is pencil-decomposed and the PFFT library is used for solving the pressure Poisson equation. The governing equations are discretized using second-order central differences in space and a second-order time-stepping scheme. The code has recently been used for computing the vorticity dynamics in steady turbulent jet and plumes without phase change (Singhal et al. 2019).

Fig. 2.

Comparison of natural clouds (left) with similar computed cumulus clouds (right)

(Reprinted from Diwan et al. (2014); © American Meteorological Society. Used with permission)

Dynamics of Small Water Droplets

Other key ingredients in the problem of cough/sneeze flows are the inertia of the droplets, and the effect of phase change on the droplets and on the turbulence. We have studied the dynamics of droplets in turbulent flow (e.g., Ravichandran and Govindarajan 2015, 2017; Deepu et al. 2017; Agasthya et al. 2019; Picardo et al. 2019; Ravichandran et al. 2020), and the ejection from a cough is precisely such a flow. Droplet inertia and gravity bring new physics to this problem, and we plan to handle these effects in two ways:

1. In MEGHA-5, the liquid phase will be treated as a field, with appropriate accounting for droplet inertia effects, for the dependence of evaporation on a given droplet size distribution, and effect on the buoyancy due to evaporative cooling, etc. (The size distributions of expired droplets during coughing/sneezing are available in the literature; for example, see Bourouiba et al. 2014 for the size distribution during a typical cough event—it shows maximum number of droplets at a diameter of 16 µm and relatively small number of droplets beyond 100 µm.) The treatment of the liquid phase as a field results from writing an expansion of droplet inertial effects as a power series in the Stokes number (St), and retaining all effects up to first order in St. For cough droplets less than 10 µm in size, St is expected to be far lower than 1, which makes our treatment appropriate. Since droplet sizes are widely dispersed in typical coughing/sneezing, we extend this approach to include three classes of droplets: (a) very small droplets (< 10 µm) that follow fluid streamlines, and take part in thermodynamics by evaporating; (b) moderate-sized droplets (10–100 µm) for which droplet inertia and gravitational settling are both relevant, and which also evaporate; and (c) large droplets (> 100 µm) which settle under gravity, and for which thermodynamic effects can be ignored. Classes (a) and (c) are already available in MEGHA-5. Class (b) can be easily incorporated into the solver.

2. We also plan (on a longer term) an alternative and computationally more involved approach, which is to track each evaporating droplet and couple its dynamics to the flow equations.

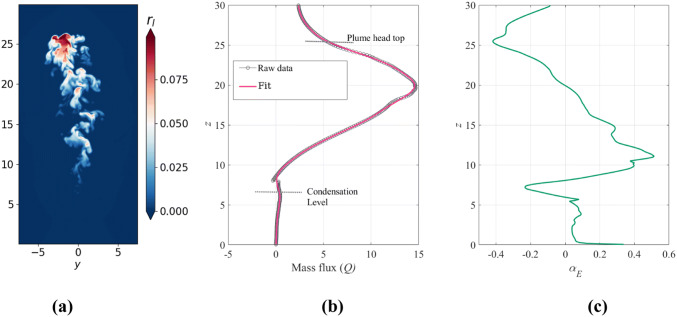
To highlight the capability of MEGHA-5 in handling the thermodynamics of phase change and computing turbulent entrainment (which are key processes governing the spread of droplets during coughing/sneezing), we first present some new results from cumulus cloud computations obtained using this code. Figure 3 shows simulation results on a moist plume in which water vapor undergoes condensation at a certain height (z ≈ 6.5; Fig. 3b) above the hot patch located at z = 0 that generates the plume. The distribution of liquid water content (r_l) in the plume is shown Fig. 3a and the corresponding profiles of the mass flux, Q (integrated over the cross section at a given z), and the entrainment coefficient, ${\alpha }_E$, are shown in Fig. 3b and c. The entrainment coefficient is defined as:

$${\alpha }_E=\frac{\mathit{dQ}/\mathit{dz}}{2\pi \rho bU},$$ 1

where $\rho$ is density, $b$ is a typical length scale representing the width of the plume and $U$ is a typical vertical velocity scale. As can be seen from Fig. 3c, the entrainment coefficient first increases above the condensation level, reaches a maximum and starts decaying further above until the plume head is reached. This trend is qualitatively similar to that reported in Narasimha et al. (2011) for cumulus cloud flows, implying that the code is able to realistically capture the macro-scale dynamics of cumulus flows. Furthermore, the effect of entrainment on the distribution of liquid water content, in the form of large-scale inhomogeneity and highly convoluted edges, is evident in Fig. 3a.

Fig. 3.

a Distribution of liquid water content in a moist plume computed using MEGHA-5 at a certain time instant, t*. b, c Respectively show the distribution of mass flux and entrainment coefficient with height (z) at t*. The mass flux profile is smoothed using the third-order Savitzky–Golay filter

An Integrated DNS Code for Computing Cough/Sneeze Flows

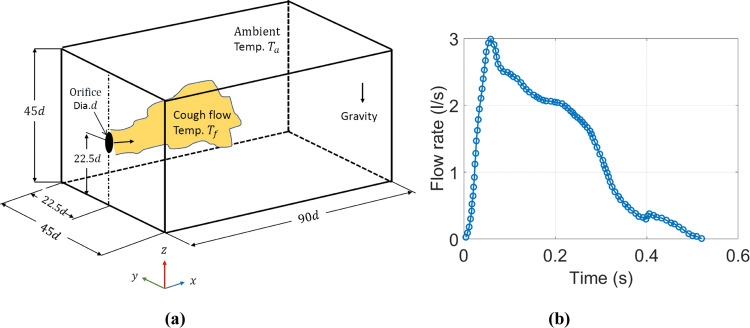
We aim to develop a DNS code suitable for studying cough/sneeze flows, by integrating the codes/methods outlined in “Cumulus Cloud Flows” and “Dynamics of Small Water Droplets”. The typical fluid dynamical parameters for the cough and sneeze events have been reported (e.g., duration: 200–500 ms, Reynolds numbers: O(10⁴), expelled volume: 0.25–1.6 l; see Bourouiba et al. 2014). We first focus on the coughing problem as it is more relevant for the COVID-19 pandemic. The simulations will be carried out in a cuboidal domain that may be made to simulate a room, or a part of it (Fig. 4a), with appropriate boundary conditions specified. A puff ejected from an opening (‘orifice’) on a wall, with parameters obtained from Gupta et al. (2009), will simulate the cough (Fig. 4b). The temperature of the cough fluid can be different from the ambient temperature and, therefore, the effect of buoyancy needs to be included. The inlet temperature difference and the ambient humidity will be treated as parameters. The use of a DNS code for studying the cough flow will enable important advances to be made, over and above the results reported in the literature (Bourouiba et al. 2014; Wei and Li 2017). Table 1 highlights the differences in the conditions and methods used in Bourouiba et al. (2014) and those to be used in the present work.

Fig. 4.

a Schematic of the computational domain for present simulations with typical dimensions specified. b Variation of flow rate during a typical single-cough event; data extracted from Gupta et al. (2009)

Table 1.

Comparison of the conditions and methods used in Bourouiba et al. (2014) and those to be used in our work

Sr	Bourouiba et al. (2014)	Present work
1	Approximate integral model is proposed, using ordinary differential equations, to calculate cloud trajectory and particle fall-out distances	DNS of partial differential equations will be used to directly compute the cloud trajectory (using a physics-based model for incorporating droplet fall-out effects)
2	The cloud trajectories for a cough were calculated for typical winter indoor conditions	Ambient conditions of temperature and humidity, relevant for Indian summer/monsoon conditions, will be specified
3	The experiments in this work use a constant inlet velocity (which is an idealization) over a finite duration to simulate a cough	The use of a DNS will enable specifying realistic inlet velocity variation during a single cough (Fig. 4b), as well as a sequential cough, without difficulty
4	The experiments or the mathematical model proposed do not involve phase changes and effects of evaporative cooling	The thermodynamics of phase change will be included in the DNS computations, which will be much closer to the dynamics of a real cough

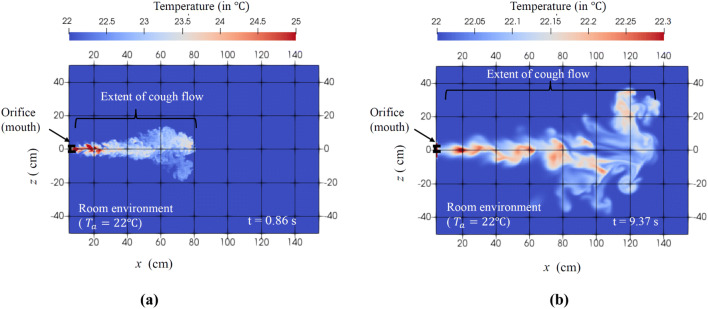
Here, we report preliminary results from simulation on a “dry cough” (i.e., in the absence of liquid droplets), as a first step towards making more realistic simulations using the integrated DNS code mentioned above. The domain size is as shown in Fig. 4a. The number of grid points used is $2048\left(x\right)\times 1024\left(y\right)\times 1024\left(z\right)$, amounting to a total of 2.15 billion. The cough flow-rate variation shown in Fig. 4b is used as the orifice inlet condition, with the total cough duration equal to 0.53 s. Convective boundary conditions are used for the lateral and exit planes (Singhal et al. 2019), to simulate a part of a room. The Reynolds number based on peak inlet velocity and orifice diameter is 11,318. The temperature of the cough fluid ($T_f$) is taken to be 34 °C and the ambient temperature ($T_a$) to be 22 °C (Bourouiba et al. 2014). The simulation was run on the CRAY XC40 (SahasraT) supercomputer housed at IISc Bangalore. The total flow time was 14.6 s, i.e., 27.5 times the cough duration and nearly 400,000 core hours on the CRAY were utilized for completing this run. Note that this is a highly resolved simulation and coarser simulations will take smaller number of core hours. Figure 5a and b shows the temperature distribution in this cough flow for two time-instants marked on the figure. The figure shows a rapid drop in the cough-fluid temperature and considerable lateral spreading of the flow, both caused by the turbulent entrainment of the ambient fluid into the core of the flow. Furthermore, the cough flow persists for a much longer time compared to the duration of the cough as seen in Fig. 5b, which can be a useful input for epidemiological studies. Note that the flow simulated in Fig. 5 corresponds to a relatively “mild” cough (Gupta et al. 2009) and therefore, the streamwise spread of this flow is also relatively small (~ 1.4 m). A more detailed analysis of this flow is being carried out at present.

Fig. 5.

Temperature distribution in a simulated “dry cough” flow at two time-instants from the start of the simulations. Note that the total duration of the cough is 0.53 s. The section corresponds to y = 0

The above example illustrates the kind of results we can expect from the cough-flow simulations. In particular, the use of the integrated DNS code (involving dynamics of water droplets) will help us to study, in sufficient detail, the rate of entrainment of ambient air into the cough flow, its effect on flow buoyancy (including evaporative cooling), the resulting flow trajectory and the droplet fall-out distances. DNS has the potential to provide much more accurate estimates of these quantities than obtained from the CFD (computational fluid dynamics) simulations based on flow/droplet models. Furthermore, the physical insights derived from such a study can guide development of mathematical models for a safe separation distance to be maintained from an infected person for COVID-19 and other infectious diseases.

The timeline for this work is 2 years; code development will take about 6–8 months and the first results are expected in a year. The computational resource needed for this work is estimated to be about 6 million core hours per year and the CRAY supercomputer at IISc Bangalore will be utilized for running the simulations. A medical-practitioner/epidemiologist will be consulted, to fine-tune the simulations and interpret the results. Once basic understanding of the cough flow is developed, a detailed parametric study involving the effect of room size, position of the infected person within the room, ventilation, etc. on the dynamics can be carried out as a future follow-on study. Simulations can be also made on the sneeze flows under similar conditions.

Summary

The objective of the present work is to investigate the fluid dynamics of cough/sneeze events to understand the transmission dynamics of respiratory infections. The MEGHA-5 code developed in-house to study cumulus cloud flows has the capability of tackling the thermodynamics of phase change in a turbulent jet/plume. This is illustrated by presenting a distribution of liquid water content (obtained after condensation of water vapor) in a moist plume, simulated using MEGHA-5, and the associated profile of the entrainment coefficient. A suitable modification of this code should enable incorporating the dynamics of different droplet sizes into the solver, including inertia effects. The resulting DNS code will be used to develop a basic understanding of the spread and trajectories of the cough/sneeze flows, including the droplet fall-out distances. Preliminary results from a “dry cough” simulation, indicating the spread of the cough flow, have been reported as a first step towards more realistic simulations on the cough flow including liquid droplets. The insights gained from these simulations should help devise a methodology or “technique” (in the form of a mathematical model) to determine separation distances from an infected person to minimize respiratory transmission. The work is of direct relevance to the studies on the spread of COVID-19 and to any such outbreaks in the future.