On Negative Heritability and Negative Estimates of Heritability

Abstract

We consider the problem of interpreting negative maximum likelihood estimates of heritability that sometimes arise from popular statistical models of additive genetic variation. These may result from random noise acting on estimates of genuinely positive heritability, but we argue that they may also arise from misspecification of the standard additive mechanism that is supposed to justify the statistical procedure. Researchers should be open to the possibility that negative heritability estimates could reflect a real physical feature of the biological process from which the data were sampled.

THE past decade has seen a proliferation of statistical methods for estimating heritability from large genome-wide genetic data sets. In particular, genomic-relatedness-based restricted maximum-likelihood (GREML; Visscher et al. 2006; Yang et al. 2010) has emerged as a standard tool in statistical genetics, along with related procedures such as Haseman–Elston (HE) and LD score regression (Bulik-Sullivan et al. 2015 preprint; Wu and Sankararaman 2018) that are constructed on the same statistical foundation. In many settings, these approaches can be invaluable for demonstrating the existence and approximate level of heritability by aggregating small genetic effects distributed across the genome. This is practically useful for complex traits given that mapping most causal genetic variants remains difficult (Manolio et al. 2009).

Despite its widespread and often indiscriminate application, GREML depends on very strong assumptions that are impossible to verify in detail, are not believed to be literally true, and are rarely subjected to any formal diagnostic or even qualitative critical consideration. In particular, the underlying statistical model assumes strictly additive causal genetic effects. Even if the additive model is accepted as a sensible foundation, nongenetic effects may reshape the appearance of genetic influences. In this paper we take an instrumental approach to GREML and related procedures: heritability measures arise from these calculations regardless of any connection to the additive model, and these need to be interpreted. In particular, we focus on a phenomenon that is typically dismissed as impossible or meaningless: negative heritability.

While the heritability parameter in the GREML model is mathematically compelled to be nonnegative, we explain how a broader view—not a new view, but one close to the root conception of heritability—implies that values of heritability meaningfully extend into the negative range, and hence that negative estimates of heritability can be taken seriously. It is only the extraneous (and not strictly credible) assumptions of GREML’s motivating model that would exclude negative estimates. We buttress this intuition with a biologically plausible story linked to a mathematically coherent model, where negative heritability estimates arising from the standard GREML procedure are meaningful indicators of causal biological processes.

Operational Definitions of Heritability

As Albert Jacquard pointed out decades ago (Jacquard 1983), the narrow-sense heritability of a phenotype, commonly denoted h², has two distinct conventional meanings:

1. The proportion of total variance attributable to additive genetic effects.

2. The slope of the linear regression of children’s phenotypes on the mean parental phenotypes.

Both meanings appear in the earliest works to give a quantitative operational definition to heritability, in particular Lush (1940). For more on the history of the notion of heritability, see Bell (1977).

The nexus between these two meanings is an additive model, where genetic and nongenetic effects are independent and sum together to produce the phenotype. When we have general genetic relatedness (rather than parental relations with fixed 50% expected relatedness), heritability is analogous to a regression coefficient that relates phenotypic similarity to genotypic similarity.

We are particularly concerned here with the interpretation of negative estimates of heritability. The appearance of negative estimates for a parameter of crucial scientific interest that is prima facie positive is unusual, as has often been noted. Negative estimates of the heritability parameter are often dismissed as a mathematical abstraction, values in a range that arises purely formally and that may only be reported for formal purposes. For example, Johnston et al. (2010) obtain a point estimate of −0.109 for the heritability of horn length in Soay sheep, which is immediately dismissed with the statement that “it is impossible to have negative heritability.” The inference is drawn that the true heritability must actually be a small positive number toward the upper end of the confidence interval.

One case where negative heritability estimates have been used in practice is for estimating the average heritability across a group of exchangeable phenotypic measurements, like gene expression. In this case, negative estimates are reported under the presumption that this yields a complete ensemble of estimates that are collectively unbiased. We illustrate one such analysis using RNA-sequencing data from the Genetic European Variation in Health and Disease (GEUVADIS) consortium (Lappalainen et al. 2013). One significant contribution of our work is our calculation of the bias imparted to the heritability estimate when negative estimates are suppressed, helping to elucidate the conditions under which this bias may be presumed negligible.

Our fundamental argument is that negative heritability estimates need to be taken more seriously. The confusion, we contend, comes from the overlap between statistical models that operationalize the two different interpretations of heritability described above. The argument for rejecting negative estimates appears compelling just so long as the focus is only on the additive random-effects model in Equation 1 that often motivates definition 1 of heritability. Variance is nonnegative, hence the ratio of two variances cannot be negative.

While “variance attributable to additive genetic effects” is a basic element of the genetic model in (1), it has no place in the statistical algorithms commonly used to fit the model to real data, including GREML. As our later discussion of (1) will make clear, the GREML estimate of heritability is defined to serve as an estimator of a ratio of two variances, where the numerator is a component of the denominator. The ratio is constrained to lie between 0 and 1, so the estimate seems intended to lie between 0 and 1. However, as we shall explain, the GREML estimate is realized under a more general multivariate normal model, where the natural constraint on h² is weaker: $h^2\ge -1/\left(\max \left\{s_i^2\right\}-1\right)$, where ${\left(s_i\right)}_{i=1}^n$ are the singular values of the genotype matrix. If the phenotypes were derived from summing independent additive genetic effects, then the true h² would have to be nonnegative, but that must be recognized as an additional assumption that would need to be scientifically warranted, as it is not compelled on strictly logical or mathematical grounds.

This discordance between common practice and formal probability theory manifests itself in two distinct roles in modern genetic analyses. First, alleles can exercise actual causal influences on traits, or can tag causal genetic influences through linkage, and such contributions cannot generate negative heritability. However, second, alleles also serve as markers of family and ancestry, markers of relatedness among individuals that may structure historical, behavioral, social, and environmental influences on traits. We argue that there is no reason to assume nonnegative heritability in this latter, more general class of models. As attention expands beyond basic additive genetic models to more complex characterizations of genome-wide genetic architecture, it is important to understand the behavior of h² beyond its intuitive definition grounded in classical quantitative genetics.

The meaning of negative heritability

Heritability is not a natural, measurable quantity. Heritability is defined only by its role in a model, and the model is inevitably misspecified. The normally distributed random genetic effects have no physical reality, and function instead primarily to justify a model of convenience. In general, the heritability of a trait will vary across populations, measurement devices, choice of scale, and countless environmental factors.

The term “negative heritability” appeared for the first time, so far as we are aware, in a paper by J. B. S. Haldane, written around 1960, but first published posthumously in 1996 (Haldane 1996). Haldane described how the maternal-effect trait of neonatal jaundice could be said to display negative heritability: Because the disease results from maternal antibodies against a fetal antigen, it will not arise in a fetus whose mother herself experienced neonatal jaundice (we thank Jonathan Marchini for pointing out this reference to us). Haldane then calculates a negative heritability from a model that is specialized to the peculiar inheritance structure of this condition.

Once we have accepted the GREML multivariate normal framework, which we will define precisely, we must admit the possibility that the joint distribution of phenotypes and genotypes in a given data set may be best described by an h² value that is negative. The question this raises is, can such a negative heritability estimate be biologically sensible? The heritability parameter may be identified, in a precise way, with a correlation between genotypic similarity and phenotypic similarity. The model invites us to select an estimate of h² that best matches the genetic covariance between individuals to the similarity in their traits. Even if we want heritability to be interpreted as a partition of variance, in the sense of definition 1, this will not always be correct. All we have access to from the data are an estimate of something like heritability in the sense of definition 2. High heritability means that individuals with similar genotypes tend to have similar trait values. Zero heritability means that genotypes tell us nothing about similarities in trait values. Negative heritability, then, could be a perfectly sensible description of data where individuals with similar genotypes tend to have more discordant traits than random pairs. In the special case of twin studies, for example, negative heritability simply means that monozygotic twins are less phenotypically similar than dizygotic twins.

Saying that a given set of data might be best described by a negative heritability estimate goes only part of the way toward answering the biological plausibility of negative true heritability. We cannot assume that a small sample of data pairs that are known (for scientific reasons) to be positively correlated will indeed yield a positive empirical correlation. Negative heritability could arise in the same way, as a spurious effect of random fluctuations in data from a system with zero or small positive heritability. The essential question is, could there be a plausible stochastic mechanism that would produce genuine negative heritability, so that as the amount of data generated by the model goes to infinity, the estimate converges to a negative quantity?

GREML is an optimization procedure derived under a Gaussian model, with a heritability parameter that makes good mathematical sense in the negative range. It would be perfectly straightforward to generate data from this model, but it might be difficult to interpret such a procedure in biologically meaningful terms. We seek, then, a negative heritability mechanism that has a similar form to the random-genetic-effects model, but is misspecified in a way that suggests a plausible story. We propose one such mechanism, based on the phenomenon of “phenotypic repulsion.” As with Haldane’s model (which may be understood as a special case), this mechanism has implications that may be implausible or even obviously false in a given real data set. It involves interactions between individuals that are not primarily genetic. However, the point we want to suggest is that as an abstract physical mechanism that could be producing our data it is as mathematically plausible as the linear random-effects model that undergirds GREML. This is only one example of such a mechanism, and the conclusion we advocate is that negative heritability must be acknowledged as a genuine phenomenon for genotype–phenotype data, even if it may be reasonably excluded by the context of some studies. Speculation about the biological settings that could yield negative heritability can also prove an effective guide to understanding when negative heritability estimates may be reliably truncated or ignored.

Our position parallels the advice on “interpretation of negative components of variance” propounded in a very different context by J. A. Nelder in 1954 (Nelder 1954). Nelder considered the problem of ANOVA testing on split-plot experiments, where the error for main plots was found to be smaller than the error for subplots, producing a negative estimate for the residual subplot error. As we have done here, Nelder showed how the apparently negative “variance component” could arise either from sampling error on a positive variance component or from a misspecification of the model, where correlations between measurements have been neglected. “In any particular situation,” Nelder concludes, “it is the statistician’s responsibility to decide which model is more appropriate.”

The GREML model as linear regression

For the remainder of this paper we follow Steinsaltz et al. (2018) in using the letter ψ to represent heritability, to avoid the confusing implication built into the nomenclature h² that this parameter formally cannot be negative. Our derivations draw on the analysis in that paper, which also discusses criticisms of GREML, such as those in Krishna Kumar et al. (2016).

Underlying GREML, as well as alternative approaches to heritability estimation such as LD score and HE regression, is a random-effects model. Our basic object is a data set consisting of an n × p matrix Z, taken to represent the genotypes of n individuals, measured at p different loci. There is a vector y, representing a scalar trait observation for each of the n individuals. The raw genotypes are counts of alleles taking the values 0, 1, or 2, but the genotype matrix is centered to have mean zero in each column and normalized to have mean square over the whole matrix equal to 1. (Often columns are further standardized to variance 1, but we do not make this assumption.) The model posits the existence of a random vector $u\in {\mathrm{ℝ}}^p$ of genetic influences from the individual SNPs such that

$$y=Zu+\epsilon .$$ (1)

The vectors u and ε are assumed to have independent Gaussian entries with zero means and equal variances. The variances are determined by two parameters, which are to be estimated: θ represents the precision (reciprocal variance) of the nongenetic noise and ψ represents the heritability, entering the model as the ratio of genetic variance to total variance. We also use the notation $\phi =\psi /\left(1-\psi \right)$ in some places, for concision.

The GREML model has been formulated as a random-effects model, but it is equivalent to a multivariate normal model corresponding to the covariance matrix

$$C^2:={\theta }_0^{-1}\left({\phi }_{0}A+I_n\right),$$ (2)

where $A=ZZ\text{*}/p$ is the genetic relatedness matrix (GRM), and θ₀ and Ψ₀ are the true values of the parameters. In this section we describe how the model may also be understood as a linear regression model.

The initial GCTA paper (Yang et al. 2010) spelled out an analogy between GCTA and a different form of linear regression, regressing squared trait differences between pairs of individuals on corresponding off-diagonal elements of the GRM, with $n\left(n-1\right)/2$ points and correlated errors. This is essentially HE regression, which has recently become a popular heritability estimation method due to its speed and robustness to some degree of model misspecification (Chen 2014; Golan et al. 2014). Instead, we draw an approximate comparison between GREML and regression with n points and independent errors.

Let $Z/\sqrt{p}=U\mathrm{diag}\left(s_i\right)V*$ be the singular-value decomposition of $Z/\sqrt{p}$, where $X\text{*}$ indicates the transpose of a matrix X. We rotate the observations to diagonalize the covariance matrix, obtaining

$$z:=U\text{*}y.$$

Because the columns of Z have zero means, one of the singular values is zero and the corresponding column of U is proportional to a vector with all elements equal to 1. Thus every other column of U sums to zero (because its columns are orthogonal), and hence each column defines a contrast between weighted groupings of individuals.

The elements of z are independent centered normal random variables, and z_i has variance $\left(1+\left({\psi }_0/\left(1-{\psi }_0\right)\right)s_i^2\right)/{\theta }_0$. It follows that $z_i^2{\theta }_0\left(1-{\psi }_0\right)/\left(1+{\psi }_0\left(s_i^2-1\right)\right)$ are independent chi-square random variables each on one degree of freedom and

$$\log z_i^2=-\log \left({\theta }_0\right)-\log \left(1-{\psi }_0\right)+\log \left(1+{\psi }_0\left(s_i^2-1\right)\right)+{\mathit{ϵ}}_i^{\text{*}},$$

where the ${\mathit{ϵ}}_i^{\text{*}}$ are distributed as the logarithms of the independent chi-square variables, long-tailed to the left, with mean ≈ −1.302, SD ≈ 2.266, and skewness ≈ −1.643.

The mean of $s_i^2$ is 1, and when ${\psi }_0\left(s_i^2-1\right)$ are uniformly small we may approximate our equation by

$$\log z_i^2\approx -\log \left({\theta }_0\right)-\left[{\psi }_0+\log \left(1-{\psi }_0\right)\right]+{\psi }_0{s}_i^2+{\mathit{ϵ}}_i^{\text{*}}.$$ (3)

Here, Ψ₀ takes on the role of the true slope for a regression of $\text{log}{z}_i^2$ on $s_i^2$. It can be estimated by least squares, bearing in mind that the skew of the ${\mathit{ϵ}}_i^{\text{*}}$ affects SE of estimation.

Practitioners instead usually estimate ψ via (restricted) maximum likelihood. Obviously, the maximum likelihood estimate (MLE) is optimal when the underlying model assumptions hold. However, formally characterizing the behavior of the MLE is nontrivial, especially under nonindependent genotypes (cf. Jiang et al. 2016) or sparse, nonpolygenic architectures. For this reason, most theoretical mixed model analyses focus on regression-based approaches with simple analytic solutions, like HE regression or the eigenvalue regression in (3). In contrast, we derived an analytic approximation to the GREML estimate in Steinsaltz et al. (2018), which we used to demonstrate several important theoretical properties. First, the MLE has a small negative bias on the order of 1/n, which is negligible in many settings. Second, if only k SNPs are causal, the MLE additionally suffers a nonrandom, nonasymptotically vanishing bias of order 1/k. Finally, population structure tends to make GREML more efficient, at the cost of exposure to potential confounding. In this paper, we apply the same analytical framework to a different question: Are there plausible forms of model misspecification that yield truly negative MLE heritability?

Formally, Steinsaltz et al. (2018) shows how the MLEs can be expressed in terms of quantities $w_i\left(\psi \right):=\left(1-\psi \right)/\left(1+\psi \left(s_i^2-1\right)\right)$ and $v_i\left(\psi \right):=w_i\left(\psi \right)z_i^2.$ They satisfy

$$\text{0}=\mathrm{Cov}\left(w\left(\widehat{\psi }\right),v\left(\widehat{\psi }\right)\right)$$

$$\widehat{\theta }=n/{\displaystyle \sum _{i=1}^n{v}_i\left(\widehat{\psi }\right)}$$ (4)

Here, Cov is the empirical covariance of vector elements, an operation on vectors defined by $\mathrm{Cov}\left(x,y\right):=n^{-1}{\displaystyle \sum \left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}$, and Var is similarly defined. We also set ${\tau }_2\left(\psi \right)={\psi }^{-2}\mathrm{Var}\left(w\left(\psi \right)\right)$, and omit the dependence on ψ when helpful. When Ψ₀ is not too close to 1 and the variance of the squared singular values is small, the least-squares and MLEs are close to each other.

Suppose, however, that the true variances of the z_i include a phenotypic contribution that varies inversely with the singular values of Z. In the phenotypic repulsion model to be specified shortly, to first order in $s_i^2-1$ the true slope is $\left({\psi }_0-\alpha -{\psi }_0^2\right)/{\left(1-{\psi }_0\right)}^2$ as a function of a repulsion parameter α. When α exceeds Ψ₀, the true slope turns negative and estimated slopes correctly include negative values. From this regression-based perspective, there is no reason prima facie to assume heritability must be nonnegative.

Bias from rejecting negative heritability estimates

The common practice of truncating the maximum likelihood calculation to nonnegative values introduces bias that is well-known and may be serious for samples of moderate size, both when estimates are truncated at zero and when negative estimates are simply suppressed.

The problem of estimating the probability of negative heritability estimates was studied 50 years ago by Gill and Jensen (1968). We add here a few comments about how the framework described in Steinsaltz et al. (2018) may contribute to understanding the magnitude of the negative heritability estimate problem that arises from sampling noise in settings where the true heritability is understood to be nonnegative, hence where truncation at zero (or rejection of negative estimates) is warranted and guarantees improved estimates in, say, mean squared error. We gain a rough idea of the effect of rejecting negative estimates from a normal approximation $\widehat{\psi }-{\psi }_0\approx {\sigma }_{0}X,$ where ${\sigma }_0=\sqrt{2}\left(1-{\psi }_0\right)/\sqrt{n{\tau }_2}$ and X has standard normal distribution [see Steinsaltz et al. (2018) for derivation]. Here, ≈ means that the difference between the left-hand and right-hand sides is bounded (in probability) by a constant times ${\left(n{\tau }_2\right)}^{-1}$, where the constant may depend on Ψ₀.

Truncating estimates where $\widehat{\psi }<0$ by setting them equal to 0 imposes the truncation bias

$$\begin{array}{l}\mathcal{E}\left[\widehat{\psi }\right]-{\psi }_0\approx -{\psi }_0+\mathcal{E}\left[\left({\psi }_0+{\sigma }_{0}X\right)1\left\{X>-\frac{{\psi }_0}{{\sigma }_0}\right\}\right]\\ =-{\psi }_0\text{Φ}\left(-\frac{{\psi }_0}{{\sigma }_0}\right)+{\sigma }_0{\displaystyle {\int }_{-{\psi }_0/{\sigma }_0}^{\mathrm{\infty }}x\frac{e^{-x^2/2}}{\sqrt{2\pi }}\text{d}x}\\ =-{\psi }_0\text{Φ}\left(-\frac{{\psi }_0}{{\sigma }_0}\right)+\frac{{\sigma }_0}{\sqrt{2\pi }}{e}^{-{\psi }_0^2/2{\sigma }_0^2},\end{array}$$ (5)

where Φ is the standard normal cumulative distribution function (c.d.f.) Note that by standard inequalities for Φ (Feller 1968) this is positive and bounded by $\frac{{\sigma }_0^3}{\sqrt{2\pi }{\psi }_0^2}{\text{e}}^{-{\psi }_0^2/2{\sigma }_0^2}$ when Ψ₀ > 0. This will be very small when nτ₂ is even moderately large compared with $1/{\psi }_0^2$, which is to be expected except when Ψ₀ is zero, or nearly zero. When Ψ₀ = 0 we have a nonnegligible positive bias of approximately the same size as the SE σ₀, and will thus be highly relevant for any statistical tests of the null hypothesis Ψ₀ = 0.

Truncation at zero will at least be recognizable, whereas tacit rejection of negative estimates may leave no trace due to publication bias. If we have an ensemble of $\widehat{\psi }$ estimates that have been selected to be nonnegative, the average has a conditioning bias that is identical to the expression in (5) divided by $\text{Φ}\left({\psi }_0/{\sigma }_0\right):=\mathrm{\mathbb{P}}\left\{X>-{\psi }_0/{\sigma }_0\right\}$. In the special case Ψ₀ = 0, this doubles the bias relative to truncation.

The phenotypic repulsion model

The notion that new species force their way into phenotypic gaps in the existing ecological community was termed by Darwin as the “principle of divergence” and has been further developed by ecologists under the name “phenotypic repulsion” or “phylogenetic repulsion” (Webb et al. 2002). Species living in close proximity, which are often closely related phylogenetically, coexist by separating from each other phenotypically. A similar kind of competitive exclusion has been proposed (Sulloway 2011) on the individual level to explain observed patterns of developmental variation within human families. Social niche formation within families has also been proposed by Conley et al. (2013), without an explicit mathematical model, as the basis for an evaluation of gene–environment interaction based on misclassified twin types.

Phenotypic repulsion has been more commonly described on the level of species differences than within species. Cardillo (2012) has described negative correlation between phylogenetic distance and flowering period difference among fire-killed but not fire-resistant Banksia species in southwestern Australia. A study of Florida oak species found that many traits differed more, between closely related species, than would be expected by chance (Cavender-Bares et al. 2004). We have not found quantitative studies of phenotypic repulsion between individuals within a species, but it seems plausible that local competition for sunlight combined with range-limited seed dispersion would yield an effective phenotypic repulsion between related plants in a forest setting. In human populations anecdotal evidence suggests that monozygotic twins seek to differentiate themselves from their sibling, which may be a stronger force than genetic similarity for traits with a negligible causal genetic basis.

While our focus is on biologically meaningful phenotypic repulsion, as in the examples above, the repulsion may also result from pure experimental artifacts. For example, in mega-analyses across institutes or laboratories, similarity between analytical or experimental procedures may correlate negatively with similarity in genetic ancestry. This induces repulsion in the sense that genetic similarity predicts experimental dissimilarity. Nonetheless, in this situation the resulting repulsion is not connected to a biologically meaningful process and, rather, would disappear under proper experimental protocols and/or correcting for potential technical confounders like laboratory and batch.

The model we propose here is novel, so may be criticized for failing to provide an example of negative heritability in an established ecological model already in use. We would argue that this model does describe a phenomenon of interest in ecology that has not yet been formalized, and so either the behavior it describes should be taken seriously, or it should provoke a better model of the phenomenon.

We propose a model of phenotypic repulsion where individuals that are most closely related genetically strive to avoid each other phenotypically. This starts with a model like the GREML model described above, where individuals have phenotypes determined by normally distributed effect sizes acting on their individual genotypes. We introduce a penalty term to the probability, of the form

$$\exp \left\{-\alpha {\theta }_0\left({\displaystyle \sum _{1\le i<j\le n}{A}_{ij}{y}_i{y}_j+\frac{1}{2}}{\displaystyle \sum _{1\le i\le n}\left(A_{ii}-1\right)y_i^2}\right)\right\},$$

where $A_{ij}=\frac{1}{p}{\displaystyle {\sum }_{k=1}^p{Z}_{ik}{Z}_{jk}}$ is the (i, j) entry of the GRM, and α ≤ 1 is a parameter measuring the extent to which genetically similar individuals are pushed to have differing phenotypes. Of course, this setup could be generalized to higher-dimensional phenotypes, with y_iy_j replaced by an arbitrary inner product. The penalty term is inspired by the statistical mechanics models that have been applied to geographically structured population dynamics, such as the Contact Process (Liggett 1999), used to model the spread of epidemics.

Combining this specification with (2), we see that the phenotypes will now be multivariate normal with mean zero and covariance matrix

$${\theta }_0^{-1}{\left[{\left({\phi }_{0}A+I_n\right)}^{-1}+\alpha \left(A-I_n\right)\right]}^{-1}.$$ (6)

It follows that the transformed phenotypes z = U* y are independent normal with mean zero and variance

$$\mathrm{Var}\left(z_i\right)={\theta }_0^{-1}\frac{1+{\phi }_0{s}_i^2}{1-\alpha +\alpha s_i^2\left(1-{\phi }_0\right)+\alpha {\phi }_0{s}_i^4}.$$

Suppose the data have come from this phenotypic–repulsion model, and we analyze them using the misspecified random-effects model. While it is always possible to get $\widehat{\psi }<0$ because of random fluctuations, we would like to show that the heritability implied by this model is “really” negative, in the sense that the distribution of $\widehat{\psi }$ converges to a strictly negative value as the number of subjects goes to infinity. This will follow from Proposition 1 (below), when we take the function f in that result to be

$$f\left(t\right)=\frac{1+{\phi }_{0}t}{1-\alpha +\alpha \left(1-{\phi }_0\right)t+\alpha {\phi }_0{t}^2},$$ (7)

as long as ${\phi }_0<\alpha$, since

$$f\prime \left(t\right)=\frac{{\phi }_0-\alpha {\left(1+{\phi }_{0}t\right)}^2}{{\left(1-\alpha +\alpha \left(1-{\phi }_0\right)t+\alpha {\phi }_0{t}^2\right)}^2},$$

which is less than 0 for all t ≥ 0.

In other words, to the extent that we say that heritability is defined by the linear model, heritability can be negative if genotypes and phenotypes interact through the environment in a manner like the phenotypic repulsion model. We prove that this is the case—that the heritability to which the estimates converge with increasing population size is negative—in the following Proposition, which is proved in Appendix A.

Proposition 1:

Suppose we have a family of n × n GRMs A_n for $n\to \mathrm{\infty }$, with eigenvalues $s_{n,i}^2$, with

$$s_{\max }^2:=\underset{n\to \mathrm{\infty }}{\lim \sup }\underset{1\le i\le n}{\max }{s}_{n,i}^2<\mathrm{\infty },$$ (8)

$$\underset{n}{\sup }{n}^{-1}{\displaystyle \sum s_{n,i}^{-12}<\mathrm{\infty },\mathit{and}}$$ (9)

$$1<C_2+1:=\underset{n\to \mathrm{\infty }}{\lim \mathrm{ inf}}{n}^{-1}{\displaystyle \sum _{i=1}^n{s}_{n,i}^4}.$$ (10)

We also write $C_3:=\lim \mathrm{su}{\mathrm{p}}_{n\to \mathrm{\infty }}{n}^{-1}{\displaystyle {\sum }_{i=1}^n{s}_{n,i}^4}$.

Let U⁽ⁿ⁾ be the corresponding eigenvector matrix. For each n we have a multivariate normal random vector y⁽ⁿ⁾ with covariance matrix $U^{\left(n\right)}\mathrm{diag}\left(f\left(s_{n,i}^2\right)\right)U^{\left(n\right)\text{*}}$, where $f:{\mathrm{ℝ}}^{+}\to {\mathrm{ℝ}}^{+}$ is a positive, strictly decreasing, continuously differentiable function. We assume that

$$C_1:=\underset{0\le t\le s_{\max }^2}{\inf }\left(-f\prime \left(t\right)\right)>0.$$ (11)

(We maintain the normalization assumption that ${\displaystyle {\sum }_i{s}_{n,i}^2=n}$.)

Let ${\widehat{\psi }}_n$ be the MLE for an observation y⁽ⁿ⁾, calculated from the random-effects model with GRM A_n. Then defining

$$\delta :=\frac{1}{6}{\left(\frac{C_{3}f\left(0\right)}{C_1{C}_2}+s_{\max }^2-1\right)}^{-1},$$ (12)

$\widehat{\psi }$ is bounded above in probability by the strictly negative quantity −δ as $n\to \mathrm{\infty }$. That is, the probability of ${\widehat{\psi }}_n>-\delta$ goes to 0 as $n\to \mathrm{\infty }$.

Although we focus on GREML in this paper, two other prominent approaches to estimate heritability in unrelated samples are HE regression and LD score regression. In Appendix B, we show that HE regression also converges to a negative heritability estimate under the phenotypic repulsion model. While it is simpler to analyze HE, the proof is similar to the proof of Proposition 1: in both cases the key fact is that larger eigenvalues of the kinship matrix are actually associated with lower phenotypic variance under phenotypic repulsion (Equation A3), which is the essence of negative heritability. Moreover, based on established approximate equivalences between HE regression and LD score regression (Bulik-Sullivan 2015; Zhou 2017), LD score regression likely also converges to negative heritability estimates under phenotypic repulsion.

Broadly, these and other estimates of heritability may be understood as approximations for the same parameter as in the GREML model, and hence may be expected to target a negative value for large n, as the various estimates converge. The key point is that none of these procedures is directly estimating a variance component. Each of them is estimating a covariance, and it is easy to see how these covariances can be negative.

Finally, we note that the ordinary asymptotic SE for GREML are no longer accurate under the phenotypic repulsion model. In Appendix C, we derive the asymptotic behavior of the SE under repulsion using the sandwich estimator. However, there seems to be no simple interpretation of the relationship between the genotype distribution and the SE as there is for the well-specified model.

Transcriptome-wide gene expression heritability

We conclude with a brief example that illustrates the practical significance of negative heritability estimates. Although negative estimates of heritability for a single fixed trait are rarely published, it is common to include negative estimates when profiling heritability across a large number of roughly exchangeable traits (Yang et al. 2013; Wright et al. 2014; Bhatia et al. 2015 preprint; Finucane et al. 2015; Zhu et al. 2015; Gusev et al. 2016; Gymrek et al. 2016; Hernandez et al. 2019). Characterizing such -omic-wide heritability is common in functional genomics, where high-throughput measurements of some genomic feature are made at thousands of genomic positions. The most common measurement is (RNA) gene expression, but other prominent examples include methylation levels, chromatin accessibility, expression response to stimuli, or protein expression.

We analyzed an RNA-sequencing data set from the GEUVADIS consortium (Lappalainen et al. 2013). We aligned the raw transcript reads from the European individuals to the reference hg19 transcriptome with the RSEM software package (Li and Dewey 2011). We removed perfectly correlated genes and genes with low expression mean or variance.

For each i in 375 people and j in 4154 genes, we define the phenotype $y_i^{\left(j\right)}$ as $\log \left(1+n_{ij}\right)$ where n_ij is the number of observed RNA reads for gene j measured in person i. We centered and scaled each gene to mean zero and variance one.

Separately for each gene y^(j), we estimate its cis-heritability, that is, the heritability in expression levels explained by SNPs near to the gene. We do so by fitting our standard model (1) with a genotype matrix Z^(j) whose columns correspond to SNPs located up to 1 megabase upstream or downstream of gene j’s transcription start site. Restricting to SNPs near a gene is a common way to enrich for causal SNPs. We discard rare SNPs, which we define as SNPs with minor allele frequencies below 2.5%. Finally, we remove genes with fewer than 1000 corresponding SNPs, which excludes 35 genes.

The column dimensions (p) of the cis genotype matrices range from 1000 to 20,523 across genes, with a mean of 3027 and median of 2754. We fit each $\widehat{\psi }$ with the maximum likelihood routine from Hernandez et al. (2019), yielding 4119 values reflecting systematic variation across genes in their cis-heritability, within the limits imposed by sampling error.

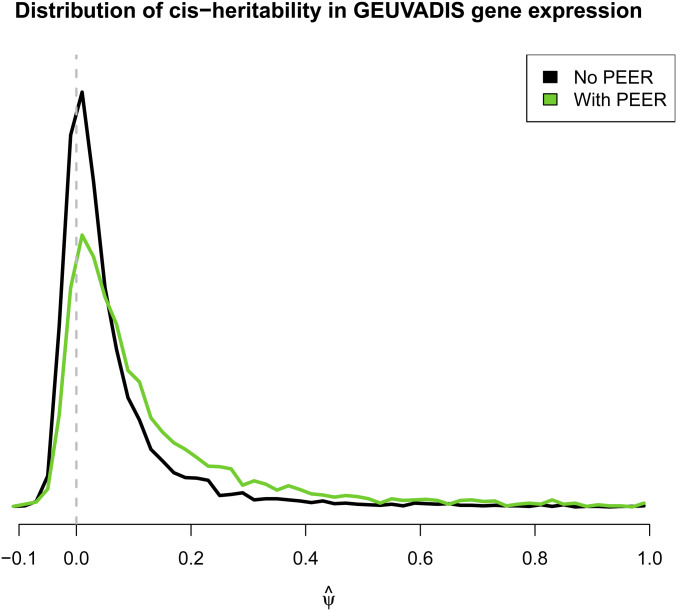
The distribution of the resulting transcriptome-wide cis-heritability estimates is shown in Figure 1 in the form of a smoothed histogram. Clearly, many of the estimates are negative. The mode is close to zero. Removing negative heritability estimates increases the transcriptome-wide average heritability from 6.2 to 9.0%, and truncating at zero increases it from 6.2 to 6.6%.

Figure 1.

Transcriptome-wide density of gene expression cis-heritability estimates in the GEUVADIS data. For each gene, we estimate using GREML and a kinship based only on nearby SNPs.

We repeated the analysis after adjusting for unobserved confounding estimated by 10 probabilistic estimation of expression residuals factors (Stegle et al. 2010). This practice, or variants based on gene expression principal components (Alter et al. 2000) or surrogate variables (Leek and Storey 2007), is standard practice in functional genomics (Stegle et al. 2012). The common aim of these approaches is to approximate latent confounding variation, like experimental batch effects, which can often be partially captured by dimensionality reduction. The confounder estimates are treated as known covariates and residualized from the phenotype and genotype data.

Correcting for 10 probabilistic estimation of expression residuals factors increases many of the $\widehat{\psi }$ values and reduces the incidence of negative $\widehat{\psi }$ as shown in the green curve in Figure 1. However, it is clear that many negative estimates remain. Negative estimates are bound to be part of the picture whenever Ψ₀ is small and estimated with low precision, both conditions that will likely hold in most functional genomic analyses for at least the near future.

On the question of whether some negative estimates may be meaningful reflections of nongenetic phenotypic structure, it is best to keep an open mind.

Data availability

GEUVADIS data were obtained from the GEUVADIS consortium. We fit GREML heritability estimates using the LMM implementation in the singher R package (Hernandez et al. 2019), available at https://github.com/andywdahl/SingHer.

Discussion

Negative heritability estimates are common results of standard statistical procedures. Linear random-effects models of genetic causality make negative heritability impossible, inviting us to treat the negative parameter estimates as spurious results produced by statistical noise that should be truncated back to zero, the closest meaningful value. However, these generative linear models are not physically validated: it is not in any sense literally true that phenotypes are produced by additive contributions of alleles and independent noise. We have shown here that other biologically plausible stochastic models would indeed generate data in the negative range of heritability parameters. These are misspecified from the point of view of the linear random-effects models, but they are correctly specified from the point of view of the Gaussian likelihood that is used to estimate the heritability parameter. Our phenotypic repulsion example demonstrates that truly negative heritability can convey a biological fact when individuals tend to differentiate themselves from their relatives. Meaningfully negative heritability should not always be ruled out.

There has long been some dispute about whether these “spurious” negative estimates ought to be included for the sake of unbiasedness, so that the whole ensemble of estimates from multiple studies might be properly centered. We use an approximation for the GREML heritability estimate that we previously derived (Steinsaltz et al. 2018) to formally support this argument as well as to quantify the bias from truncation.

More importantly, we also suggest that the problem should be considered with more nuance: The very possibility of negative heritability depends strongly on the nature of the trait, of the population, and of the sampling procedure. True, asymptotically persistent negative heritability requires strong nonlinear contributions, increasingly strong as the negative parameter approaches the true negative lower bound. This suggests that it may be reasonable to replace truncation at zero by an appropriate shrinkage of negative estimates toward zero, perhaps based on context. This would affect not only negative point estimates, but also confidence intervals centered at small positive values. In a Bayesian framework this would correspond, of course, to assigning heritability a prior distribution with small, nonzero weight on negative values. Statistical models of convenience, such as the variance-component model that underlies GREML and many other heritability estimation approaches, should never drive substantive scientific conclusions, such as declaring that negative heritability is impossible.

Appendix A: Proof of Proposition 1

We wish to show that $\lim \mathrm{su}{\mathrm{p}}_{n\to \mathrm{\infty }}{\widehat{\psi }}_n\le -\delta$. This will follow if every increasing sequence n_i has a subsequence $n_{i_j}$ such that $\lim \mathrm{su}{\mathrm{p}}_{j\to \mathrm{\infty }}{\widehat{\psi }}_{n_{i_j}}\le -\delta$. Define the empirical measure ${\sigma }_n:={\displaystyle {\sum }_{i=1}^n{\delta }_{s_{n,i}}}$, where δ_x represents unit point mass at x. Since the space of probability measures on $\left[0,\sup s_{n,i}\right]$ is compact, given an increasing sequence n_i we may find a subsequence $n_{i_j}$ such that ${\widehat{\sigma }}_{n_{i_j}}$ converges weakly to a measure σ on $\left[0,s_{\max }\right]$. Thus, it will suffice to prove the proposition under the assumption that ${\sigma }_n{\stackrel{n\to \mathrm{\infty }}{\to }}_w\sigma$.

We follow the general principle, enunciated by White (1982), that the MLE for the misspecified model will converge to the closest fit in the Kullback–Leibler sense. In other words, the parameter estimate converges in probability to the location of the maximum expected value of the log-likelihood function. The arguments of White (1982) do not apply directly here, because we are not sampling identically and independently (i.i.d.) random variables; however, by Equation (22) of Steinsaltz et al. (2018), the score function may be written

$$\frac{1}{2\overline{v}\left(\psi \right)}\cdot G_n\left(\psi ;x\right):=\frac{1}{2n\overline{v}\left(\psi \right)}{\displaystyle \sum _{i=1}^n{a}_{n,i}\left(\psi \right)X_i},$$ (A1)

for $-1/\left(s_{\max }^2-1\right)<\psi \le 1$, where (X_i) are i.i.d. ${\chi }_1^2$ random variables and

$$a_{n,i}\left(\psi \right):=a\left(s_{n,i}^2,\psi \right)$$

$$:=\frac{f\left(s_{n,i}^2\right)}{\left(1-\psi \right)\left(1-\psi +\psi s_{n,i}^2\right)}\left(\frac{s_{n,i}^2}{1-\psi +\psi s_{n,i}^2}-\frac{1}{n}{\displaystyle \sum _{j=1}^n\frac{s_{n,j}^2}{1-\psi +\psi s_{n,j}^2}}\right)$$

$$=\frac{f\left(s_{n,i}^2\right)}{1-\psi +\psi s_{n,i}^2}\left(\frac{s_{n,i}^2-1}{1-\psi +\psi s_{n,i}^2}-n^{-1}{\displaystyle \sum _{j=1}^n\frac{s_{n,j}^2-1}{1-\psi +\psi s_{n,j}^2}}\right).$$

Since ${\left(\max \left\{s_{n\prime ,i}^2:1\le i\le n\prime ,n\prime \ge n\right\}-1\right)}^{-1}>\delta$ for n sufficiently large, we may assume without loss of generality that this holds for all n, perhaps after truncating an initial portion of the sequence. It follows that $a_{n,i}\left(\psi \right)$ is defined for any $\psi \in \left[-\delta ,1\right]$, and by (9) that

$$n^{-1}{\displaystyle \sum _{i=1}^n\left|a_{n,i}\left(\psi \right)\right|}\text{and }{n}^{-1}{\displaystyle \sum _{i=1}^n\left|a_{n,i}^{\prime }\left(\psi \right)\right|}$$

are both uniformly bounded over all n, and $\psi \in \left[-\delta ,1\right]$. By a variant of the central result of Yuan (1997), $G_n\left(\psi ;x\right)$ converges uniformly in ψ to the function that is the limit of the expected values

$$G\left(\psi \right)=\underset{n\to \mathrm{\infty }}{\lim }{G}_n\left(\psi ;1\right)={\mathrm{Cov}}_{\sigma }\left(\frac{f\left(S^2\right)}{1-\psi +\psi S^2},\frac{S^2-1}{1-\psi +\psi S^2}\right).$$

The covariance is understood here to be with respect to S having distribution σ. [This result does not satisfy exactly the conditions of Yuan (1997), so we provide a proof of the result, stated as Lemma 1.]

We need to show that

$$G\left(\psi \right)<0\text{ for }\psi \ge -\delta .$$ (A2)

From this it will follow that $\mathrm{in}{\mathrm{f}}_{\psi \in \left[-\delta ,1\right]}G\left(\psi \right)<0$, hence

$$\underset{n\to \mathrm{\infty }}{\lim \sup }\mathrm{\mathbb{P}}\left\{{\widehat{\psi }}_n\ge -\delta \right\}\le$$

$$\underset{n\to \mathrm{\infty }}{\lim \sup }\mathrm{\mathbb{P}}\left\{\underset{\psi \in \left[-\delta ,1\right]}{\sup }\left|G_n\left(\psi \right)-G\left(\psi \right)\right|\ge \underset{\psi \in \left[-\delta ,1\right]}{\inf }\left|G\left(\psi \right)\right|\right\}=0.$$

It remains to verify (A2). We note that the definition of δ makes

$$\frac{C_1{C}_2}{\delta }\ge 3f\left(0\right)C_3{\left(1+\psi \left(S^2-1\right)\right)}^{-3}$$

for any $\psi \in \left[-\delta ,0\right]$ and $S\in \left[0,s_{\max }\right]$. Since $f\left(t\right)+C_{1}t$ is a decreasing function of t, for $t\in \left[0,s_{\max }^2\right]$, we have by Harris’s inequality (Boucheron et al. 2013, Theorem 2.15)

$$G\left(0\right)={\mathrm{Cov}}_{\sigma }\left(f\left(S^2\right)+C_1{S}^2,S^2\right)-C_1{\mathrm{Var}}_{\sigma }\left(S^2\right)$$

$$\le -C_1{C}_2$$

$$<0.$$ (A3)

We also have

$$\left(1-\psi \right)G\prime \left(\psi \right)=-{\mathrm{Cov}}_{\sigma }\left(\frac{f\left(S^2\right)}{1-\psi +\psi S^2},\frac{S^2\left(S^2-1\right)}{{\left(1-\psi +\psi S^2\right)}^2}\right)$$

$$-{\mathrm{Cov}}_{\sigma }\left(\frac{\left(S^2-1\right)f\left(S^2\right)}{{\left(1-\psi +\psi S^2\right)}^2},\frac{S^2}{1-\psi +\psi S^2}\right)$$

$$+{\left(1-\psi \right)}^{-1}{\mathrm{Cov}}_{\sigma }\left(\frac{f\left(S^2\right)}{1-\psi +\psi S^2},\frac{S^2}{1-\psi +\psi S^2}\right).$$

For $\psi \in \left[-\delta ,0\right]$ and $0\le S\le s_{\max }$ we have

$${\left(1-\psi +\psi S^2\right)}^{-3}\le {\left(1-\delta \left(s_{\max }^2-1\right)\right)}^{-3}.$$

Since f is decreasing, we have for $-\delta \le \psi \le 0$ the bound

$$\left|G\prime \left(\psi \right)\right|\le 3f\left(0\right)C_3{\left(1-\delta \left(s_{\max }^2-1\right)\right)}^{-3}$$

$$\le \frac{C_1{C}_2}{\delta }.$$

This proves that $G\left(\psi \right)<0$ for $-\delta \le \psi \le 0$.

For $\psi \in \left[0,1\right]$ $f\left(t\right)/\left(1-\psi +\psi t\right)$ is a decreasing function of t, and $t/\left(1-\psi +\psi t\right)$ is increasing, so (again by Harris’s Inequality) $G\left(\psi \right)<0$, which completes the proof.

We now prove the key uniform convergence result for G_n. The range of s and of ψ in this result may be rescaled arbitrarily, so for convenience of notation we will denote these by [0,1].

Lemma 1.

Let $a:{\left[0,1\right]}^2\to \mathrm{ℝ}$ be a continuous function such that for all $s\in \left(0,1\right]$

$$K_s:=\underset{\psi \in \left[0,1\right]}{\sup }\left|a\left(s,\psi \right)\right|and{L}_s:=\underset{\psi \ne \psi \prime \in \left[0,1\right]}{\sup }\frac{\left|a\left(s,\psi \prime \right)-a\left(s,\psi \right)\right|}{\left|\psi -\psi \prime \right|}$$

are both finite. Let ${\sigma }_n=n^{-1}{\displaystyle {\sum }_{i=1}^n{\delta }_{s_{n,i}}}$ be atomic probability measures on $\left(0,1\right]$ concentrated at n points $0<s_{n,1}\le \cdots \le s_{n,n}\le 1$. We suppose that the measures σ_n converge weakly to a probability measure $\sigma ={\sigma }_{\mathrm{\infty }}$ on $\left(0,s_{\text{*}}\right)$, and that there is a $\delta \in \left(0,1\right]$ such that

$$K_{\text{*}}^2:=\underset{n}{\sup }{\displaystyle \int {\left(1\vee K_S\right)}^2\mathrm{d}{\sigma }_n\left(S\right)<\mathrm{\infty }and}$$ (A4)

$$L_{\text{*}}^2:=\underset{n}{\sup }{\displaystyle \int {\left(1\vee L_S\right)}^2\mathrm{d}{\sigma }_n\left(S\right)<\mathrm{\infty }}.$$ (A5)

Let $\left\{X_{n,i}:1\le i\le n,n\in \mathrm{\mathbb{N}}\right\}$ be independent random variables with $\mathcal{E}\left[X_{n,i}\right]=1$ and $V:=\sup \mathrm{Var}\left(X_{n,i}\right)<\mathrm{\infty }$. Define for $\psi \in \left(0,1\right]$

$$G_n\left(\psi \right):=n^{-1}{\displaystyle \sum _{i=1}^n{X}_{n,i}a\left(s_{n,i},\psi \right)}.$$

Then $G_n$ converges uniformly in probability to the function $G:\to \mathrm{ℝ}$ defined by

$$G\left(\psi \right):={\displaystyle \int a\left(s,\psi \right)\mathrm{d}\sigma \left(s\right)}.$$

That is,

$$\sup \left\{\left|G\left(\psi \right)-G_n\left(\psi \right)\right|:\psi \in \left[0,1\right]\right\}{\stackrel{n\to \mathrm{\infty }}{\to }}_{P}0.$$

The condition (A4) may be weakened by replacing ${\left(1+K_S\right)}^2$ by ${\left(1+K_S\right)}^{1+\delta }$, for δ positive, and equivalently for L_S, as long as we have correspondingly stronger moment bounds on X_n,i. We have stated it in this form for simplicity.

Proof.

The sublinearity of the Lipschitz constant implies that the Lipschitz constant of G_n is a random variable bounded by

$$L_{\left(n\right)}:=n^{-1}{\displaystyle \sum _{i=1}^n{X}_{n,i}{L}_{s_{n,i}}}.$$

We have

$$\mathcal{E}\left[L_{\left(n\right)}\right]={\displaystyle \int L_S\text{d}{\sigma }_n\left(S\right)\le L_{\text{*}}}$$

by the Cauchy–Schwarz Inequality. Also by the Cauchy–Schwarz Inequality, we have

$$\mathrm{Var}\left(L_{\left(n\right)}\right)=n^{-2}{\displaystyle \sum _{i=1}^n{L}_{s_{n,i}}^2\mathrm{Var}\left(X_{n,i}\right)}$$

$$\le \frac{V{L}_{\text{*}}^2}{n}.$$

Thus $\mathrm{\mathbb{P}}\left\{\text{Lip}\left(G_n\right)\le 2L_{\text{*}}\right\}\stackrel{n\to \mathrm{\infty }}{\to }1$.

We have

$$\underset{\psi \in \left[0,1\right]}{\sup }\left|G\left(\psi \right)-G_n\left(\psi \right)\right|\le \underset{\psi \in \left[0,1\right]}{\sup }\left|n^{-1}{\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)a\left(s_{n,i},\psi \right)}\right|$$

$$+\underset{\psi \in \left[0,1\right]}{\sup }\left|{\displaystyle \int a\left(s,\psi \right)\text{d}{\sigma }_n\left(s\right)}-{\displaystyle \int a\left(s,\psi \right)\text{d}\sigma \left(s\right)}\right|.$$ (A6)

Fix any positive integer k. Because of the bounds on the Lipschitz constants of G and G_n, the second term is bounded by

$$\frac{3L_{\text{*}}}{k}+\underset{1\le j\le k}{\max }\left|{\displaystyle \int a\left(s,j/k\right)\text{d}{\sigma }_n\left(s\right)}-{\displaystyle \int a\left(s,j/k\right)\text{d}{\sigma }_n\left(s\right)}\right|.$$ (A7)

Because of the assumed weak convergence ${\sigma }_n\to \sigma$, this converges to $3L_{\text{*}}/k$ as $n\to \mathrm{\infty }$ for each fixed k. Since k is arbitrary, the second term in fact converges to 0 as $n\to \mathrm{\infty }$.

To deal with the first term we use the standard method of chaining (cf. Pollard 1990, chapter 3): we define finite skeletons of [0,1], subsets $D_0\subset D_1\subset \cdots$ with $\left|D_j\right|=2^j$, defined by

$$D_j:=\left\{\frac{2\ell +1}{2^{j+1}}:\ell =0,\cdots ,2^j-1\right\}.$$

We then proceed by approximating any point $\psi \in \left[0,1\right]$ by a sequence of nearest neighbors ${\psi }_j\in D_j$, so that $\left|{\psi }_j-{\psi }_{j-1}\right|=2^{-j-1}$. Since for any continuous function f

$$f\left(\psi \right)=f\left(0\right)+{\displaystyle \sum _{j=1}^{\mathrm{\infty }}\left(f\left({\psi }_j\right)-f\left({\psi }_{j-1}\right)\right)},$$

we have the basic chaining inequality

$$\underset{\psi \in \left[0,1\right]}{\sup }\left|n^{-1}{\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)a\left(s_{n,i},\psi \right)}\right|\le n^{-1/2}\left(R_0+{\displaystyle \sum _{j=1}^{\mathrm{\infty }}{R}_j}\right),$$ (A8)

where

$$R_0:=n^{-1/2}\left|{\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)a\left(s_{n,i},1/2\right)}\right|,$$

$$R_j:=\underset{{\psi }_j\in D_j}{\max }{n}^{-1/2}|{\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)a\left(s_{n,i},{\psi }_j\right)-}$$

$${\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)a\left(s_{n,i},{\psi }_{j-1}\right)}|.$$

We have

$$\mathcal{E}\left[R_0^2\right]\le n^{-1}V{\displaystyle \sum _{i=1}^{n}a{\left(s_{n,i}^2,0\right)}^2\le K_{\text{*}}^{2}V}.$$

Now note that

$$\mathcal{E}\left[{\left|n^{-1/2}{\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)\left(a\left(s_{n,i},{\psi }_j\right)-a\left(s_{n,i},{\psi }_{j-1}\right)\right)}\right|}^2\right]$$

$$\le 2^{-2j-2}\mathcal{E}\left[n^{-1}{\left|{\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)L_{s_{n,i}}}\right|}^2\right]$$

$$\le 2^{-2j-2}V{L}_{\text{*}}^2.$$

For any collection of random variables ${\xi }_1,\dots ,{\xi }_m$ we know that

$$\mathcal{E}\left[\max {\xi }_k^2\right]\le m\max \mathcal{E}\left[{\xi }_k^2\right].$$

so for $j\ge 1$

$$\mathcal{E}\left[R_j^2\right]\le 2^j\cdot 2^{-2j-2}V{L}_{\text{*}}^2=2^{-j-2}V{L}_{\text{*}}^2$$

By Minkowski’s Inequality, we have

$$\mathcal{E}\left[{\left(R_0+\cdots +R_k\right)}^2\right]\le {\left({\displaystyle \sum _{j=0}^k\mathcal{E}{\left[R_j^2\right]}^{1/2}}\right)}^2\le {\left(K_{\text{*}}+2L_{\text{*}}\right)}^{2}V.$$

So finally, by (A8), we have

$$\mathcal{E}\left[\underset{\psi \in \left[0,1\right]}{\sup }{\left|n^{-1}{\displaystyle \sum _{i=1}^n\left(X_{n,i}-1\right)a\left(s_{n,i},\psi \right)}\right|}^2\right]\le \frac{{\left(K_{\text{*}}+2L_{\text{*}}\right)}^{2}V}{n}.$$ (A9)

Applying Markov’s inequality, and combining this with (A7), completes the proof.

Appendix B: HE Regression Under Phenotypic Repulsion

According to Equation (8) of Wu and Sankararaman (2018) the HE regression estimate of genetic variance may be defined by

$${\widehat{\sigma }}_g^2=\frac{y^{\text{*}}\left(A-I_n\right)y/n}{\text{tr}\left(A^2\right)/n-1}.$$

where tr (·) is the trace of a matrix. As the heritability is the ratio of ${\widehat{\sigma }}_g^2$ to a positive estimate of phenotypic variance, the estimated heritability will be negative whenever ${\widehat{\sigma }}_g^2$ is negative.

Under our model, y = UTx is the vector of phenotypes, with U an orthogonal matrix, x a vector of i.i.d. standard normal random variables, and T the diagonal matrix with $\sqrt{t_i}$ on the diagonal, with

$$t_i=\frac{1+{\phi }_0{s}_i^2}{1-\alpha +\alpha s_i^2\left(1-{\phi }_0\right)+\alpha {\phi }_0{s}_i^4}.$$

These $t_i$ are the same as $f\left(s_i^2\right)$, where f is given in Equation 7.

The denominator in the HE estimator of ${\widehat{\sigma }}_g^2$ is $n^{-1}{\displaystyle {\sum }_{i=1}^n\left(s_i^4-1\right)}$, which converges to the constant we have called C₃−1. The numerator is

$$n^{-1}{x}^{\text{*}}T\left(S^2-I_n\right)Tx=n^{-1}{\displaystyle \sum _{i=1}^n{t}_i\left(s_i^2-1\right)x_i^2,}$$

where S is the diagonal matrix with s_i on the diagonal. By the same argument as in the proof of Proposition 1, where we apply Harris’s inequality to show that $\text{Cov}\left(t_i,s_i^2\right)<0$ (Equation A3), we see that $\lim \mathrm{su}{\mathrm{p}}_{n\to \mathrm{\infty }}{n}^{-1}{\displaystyle {\sum }_{i=1}^n{t}_i\left(s_i^2-1\right)<-C_1{C}_2}$. The Weak Law of Large Numbers implies that the numerator remains bounded above (in probability) as $n\to \mathrm{\infty }$ by −C₁C₂. Hence the HE regression estimate targets a negative number smaller than $-C_1{C}_2/C_3$ for large n.

Appendix C: SE Under Repulsion

Asymptotically correct SE for the standard genotypic random-effects model may be calculated from the Fisher information. We carry out the calculations here for the parametrization in terms of θ and $\phi =\psi /\left(1-\psi \right)$, to simplify the notation. In the region of ψ negative or close to 0 the variance and covariance of ψ hardly differs from that of ϕ, and in any case the transformation is straightforward.

Starting from the transformed phenotypes $z=U\text{*}y$, and using the definitions of v_i and w_i provided above Equation 4, we have the log likelihood

$$\ell \left(\theta ,\phi \right)=\frac{n}{2}\log \theta -\frac{1}{2}{\displaystyle \sum \log \left(1+\phi s_i^2\right)-\frac{\theta }{2}{\displaystyle \sum v_i\left(\phi \right)}}.$$

The first two derivatives may be written as

$$D\ell \left(\theta ,\phi \right)=\frac{n}{2}\left(\begin{array}{c}\frac{1}{\theta }-\langle v\rangle \\ -\langle s^{2}w\rangle +\theta \langle s^{2}vw\rangle \end{array}\right)$$

and

$$D^2\ell \left(\theta ,\phi \right)=-\frac{n}{2}\left(\begin{array}{cc}\frac{1}{{\theta }^2}& \langle s^{2}vw\rangle \\ \langle s^{2}vw\rangle & -\langle s^2{w}^2\rangle +2\theta \langle s^{4}v{w}^2\rangle \end{array}\right),$$

where $\langle a\rangle$ is used to denote the mean of a sequence (a_i). Thus $\langle s^{4}v{w}^2\rangle =n^{-1}{\displaystyle {\sum }_{i=1}^n{s}_i^4{v}_i{w}_i^2}$.

We immediately have $\widehat{\theta }=1/\langle v\rangle$. When samples are drawn from the true model with parameters $\left({\theta }_0,{\phi }_0\right)$ we have that ${\theta }_0{v}_i\left({\phi }_0\right)$ are independent chi-squared random variables with 1 degree of freedom. Thus, the expected Fisher information is

$$\mathrm{ℐ}\left({\theta }_0,{\phi }_0\right)=\frac{n}{2}\left(\begin{array}{cc}1/{\theta }_0^2& \left(1-\langle w\rangle \right)/\left({\phi }_0{\theta }_0\right)\\ \left(1-\langle w\rangle \right)/\left({\phi }_0{\theta }_0\right)& \langle {\left(1-w\right)}^2\rangle /{\phi }_0^2\end{array}\right).$$

The covariance matrix for $\left(\widehat{\theta },\widehat{\phi }\right)$ is the inverse

$$\mathrm{ℐ}{\left({\theta }_0,{\phi }_0\right)}^{-1}=\frac{2}{n\mathrm{Var}\left(w\right)}\left(\begin{array}{cc}{\theta }_0^2\langle {\left(w-1\right)}^2\rangle & {\phi }_0{\theta }_0\left(\langle w\rangle -1\right)\\ {\phi }_0{\theta }_0\left(\langle w\rangle -1\right)& {\phi }_0^2\end{array}\right).$$

In particular, the asymptotic variance of $\widehat{\phi }$ is $2{\phi }_0^2/\left(n\mathrm{Var}\left(w\right)\right)$. It follows immediately that the asymptotic variance of $\widehat{\psi }$ is $2{\psi }_0^2{\left(1-{\psi }_0\right)}^2/\left(n\mathrm{Var}\left(w\right)\right)=2{\left(1-{\psi }_0\right)}^2/\left(n{\tau }_2\right)$.

For the (misspecified) phenotypic repulsion model three changes are needed: First, the expected value of $v_i\left(\phi \right)$ is no longer $\left(1+{\phi }_0{s}_i^2\right)/\left(\left(1+\phi s_i^2\right){\theta }_0\right)$, but

$${\beta }_i\left(\phi \right):={\theta }_0^{-1}\frac{1+{\phi }_0{s}_i^2}{1+\phi s_i^2}\frac{1}{1-\alpha +\alpha s_i^2\left(1-{\phi }_0\right)+\alpha {\phi }_0{s}_i^4}.$$

Second, the Fisher information is evaluated not at the parameters $\left({\theta }_0,{\phi }_0\right),$which no longer define the distribution from which the data are sampled, but rather at the best-fit parameters $\left({\theta }_{\text{*}},{\phi }_{\text{*}}\right)$. We still have ${\theta }_{\text{*}}=1/\langle v\left({\phi }_{\text{*}}\right)\rangle$, but there is no simple representation for ${\phi }_{\text{*}}$, which will solve the equation $\mathrm{Cov}\left(w\left({\phi }_{\text{*}}\right),\beta \left({\phi }_{\text{*}}\right)\right)=0$. The expected Fisher information is

$$\mathrm{ℐ}\left({\theta }_{\text{*}},{\phi }_{\text{*}}\right)=\frac{n}{2}\left(\begin{array}{cc}{\langle \beta \rangle }^2& \frac{\langle \beta \rangle -\langle \beta w\rangle }{{\phi }_{\text{*}}}\\ \frac{\langle \beta \rangle -\langle \beta w\rangle }{{\phi }_{\text{*}}}& \frac{2\langle \beta {\left(1-w\right)}^2\rangle }{\langle \beta \rangle {\phi }_{\text{*}}^2}-\frac{\langle {\left(1-w\right)}^2\rangle }{{\phi }_{\text{*}}^2}\end{array}\right).$$

Here and below β and w are evaluated at ${\phi }_{\text{*}}$.) The inverse is

$$\mathrm{ℐ}{\left({\theta }_{\text{*}},{\phi }_{\text{*}}\right)}^{-1}=\frac{2}{n}{\left(2\langle \beta \rangle \cdot \langle \beta {\left(1-w\right)}^2\rangle -{\langle \beta \rangle }^2\langle {\left(1-w\right)}^2\rangle -{\left(\langle \beta \rangle -\langle \beta w\rangle \right)}^2\right)}^{-1}$$

$$\times \left(\begin{array}{cc}\frac{2\langle \beta {\left(1-w\right)}^2\rangle }{\langle \beta \rangle }-\langle {\left(1-w\right)}^2\rangle & {\phi }_{\text{*}}\left(\langle \beta w\rangle -\langle \beta \rangle \right)\\ {\phi }_{\text{*}}\left(\langle \beta w\rangle -\langle \beta \rangle \right)& {\phi }_{\text{*}}^2{\langle \beta \rangle }^2\end{array}\right).$$

The third change is that the asymptotic variance for a misspecified model is not given by ${\mathrm{ℐ}}^{-1}$, but by the sandwich estimator White (1982) ${\mathrm{ℐ}}^{-1}V{\mathrm{ℐ}}^{-1}$, where V is the covariance matrix of $D\ell$, which is

$$V=\left(\begin{array}{cc}2\langle {\beta }^2\rangle & \frac{\langle {\beta }^2\left(1-w\right)\rangle }{{\phi }_{\text{*}}\langle \beta \rangle }\\ \frac{\langle {\beta }^2\left(1-w\right)\rangle }{{\phi }_{\text{*}}\langle \beta \rangle }& \frac{\langle {\beta }^2{\left(1-w\right)}^2\rangle }{{\phi }_{\text{*}}^2{\langle \beta \rangle }^2}\end{array}\right).$$