Computing PROPr utility scores for PROMIS® Profile instruments

Abstract

Objectives:

The Patient-Reported Outcomes Measurement Information System® (PROMIS®) Profile instruments measure health status on 8 PROMIS domains. The PROMIS-Preference (PROPr) score provides a preference-based summary score for health states defined by 7 PROMIS domains. The Profile and PROPr share 6 domains, PROPr has 1 unique domain (Cognitive Function-Abilities), and the Profile has 2 unique domains (Anxiety, Pain Intensity). We produce an equation for calculating PROPr utility scores with Profile data.

Methods:

We used data from 3,982 members of US online survey panels who have scores on all 9 PROMIS domains. We used a 70%/30% split for model fit/validation. Using root-mean-square-error and mean-error on the utility scale, we compared models for predicting the missing Cognitive Function score via (A) the population average; (B) a score representing excellent cognitive function; (C) a score representing poor cognitive function; (D) a score predicted from linear regression of the 8 Profile domains; and, (E) a score predicted from a Bayesian neural network of the 8 Profile domains.

Results:

The mean-errors in the validation sample on the PROPr scale (which ranges from −0.022 to 1.00) for the models were: (A) 0.025, (B) 0.067, (C) −0.23, (D) 0.018, and (E) 0.018. The root-mean-square-errors were: (A) 0.097, (B) 0.12, (C) 0.29, (D) 0.095, and (E) 0.094.

Conclusion:

Although the Bayesian neural network had the best root-mean-square-error for producing PROPr utility scores from Profile instruments, linear regression performs almost as well and is easier to use. We recommend the linear model for producing PROPr utility scores for PROMIS Profiles.

Précis:

We develop a method to produce a utility score for the widely-used Patient-Reported Outcomes Measurement Information System (PROMIS) Profile instruments.

Introduction

Health-related quality of life (HRQL) measurement usually follows one of two approaches. The psychometric approach describes health states using psychometric testing theories. The econometric approach combines a rudimentary descriptive system for health states with a scoring function to attach utilities to those states. Although both are used for population health studies and clinical trials, only the econometric approach can be used for cost-utility analyses.

The Patient-Reported Outcomes Measurement Information System® (PROMIS®) is an initiative supported by the National Institutes of Health (NIH) that produces scales for various domains of HRQL, such as cognitive function, depression, and physical function, using psychometric methodology from item response theory (IRT).^1,2 PROMIS measures are freely available and used widely.^3–6

The PROMIS-Preference (PROPr) scoring system is based on multi-attribute utility theory, taking health states described by PROMIS and attaching utilities to them so that they can be easily compared⁷. By using PROMIS as its descriptive system for health states, PROPr combines the advantages of psychometric systems – increased reliability and validity of health state measurements – with the usefulness of a value-based econometric system.

The PROPr scoring system is a societal preference-based measure of HRQL based on 7 PROMIS domains: Cognitive Function—Abilities, Depression, Fatigue, Pain Interference, Physical Function, Sleep Disturbance, and Ability to Participate in Social Roles and Activities. PROPr allows for the calculation of preference-based summary scores for any study that collects measurements on its 7 PROMIS domains. The PROPr scoring system connects the psychometrically advanced measurement system represented by PROMIS with best practices in utility-based scoring system construction. PROPr allows PROMIS data to be used to produce health utilities, be incorporated in economic and decision analyses, and be used to construct quality-adjusted life years (QALYs). PROPr was developed as a generic societal-preference based HRQL instrument. Its development, including the choice of its PROMIS domains, are described elsewhere^7–12. Briefly, it was produced using preference elicitations of a US sample representative of the general population (n=983), via the standard gamble technique. Its minimum score is −0.022, dead has a score of 0, and the maximum score is 1.

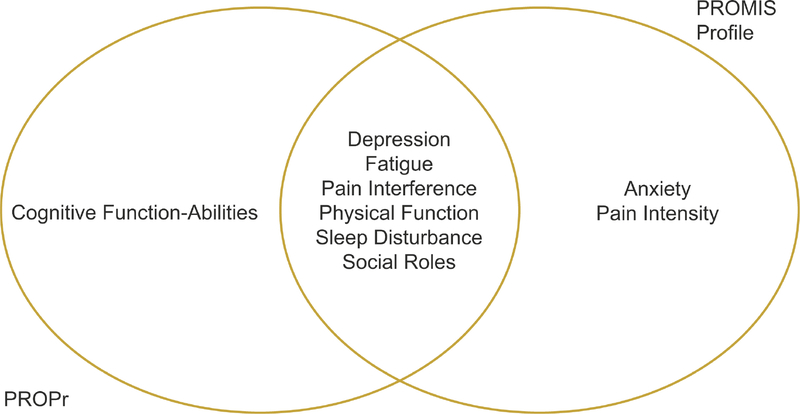
PROMIS Profile instruments are widely-used standardized short-form questionnaires.⁶ Our own scoping review of the literature found that over 20,000 PROMIS Profile survey administrations have been reported. All PROMIS Profile instruments produce measurements on 8 PROMIS domains, 6 of which are used in PROPr, and 2 of which are not included in PROPr (Anxiety and Pain Intensity) (see Figure 1). Studies that use PROMIS Profile instruments cannot calculate a PROPr summary score with their data unless they have a way to predict the missing Cognitive Function score. Here, we compare various methods for predicting a Cognitive Function score from PROMIS Profile data, with the goal of producing a summary PROPr score for those data. Our goal is to find a model that allows those with PROMIS Profile data to produce a PROPr score with a high level of confidence, while also presenting the user with a model that is straightforward to implement, lest it be misapplied or misunderstood.

Figure 1.

Venn diagram showing the PROMIS domains included in the PROMIS profile instruments and those required to generate a Q3 PROPr utility score.

Methods

We begin with a detailed overview of the measures used in the study, and the data we used to select a model for calculating PROPr scores for PROMIS Profile data. We then describe the candidate models.

PROMIS measures

PROMIS is an NIH-funded initiative for producing psychometrically-advanced patient-reported outcomes that are free to use and available for dozens of health domains.^1,13 Every PROMIS domain produces a measurement on a latent unidimensional scale called “theta”. For example, responses to any set of items (questions) from the PROMIS Depression domain would produce a depression score. The underlying IRT calibration is on theta with a population mean of 0 and a standard deviation of 1. PROMIS scores are usually reported on the T-score metric which is a transformation so that the population mean is 50 with a standard deviation of 10.

One advantage of IRT-based measures is that scores produced by different sets of items from a domain are commensurable.¹⁴ This feature makes PROMIS suitable for a variety of data-collecting contexts ranging from population surveys to clinical encounters, as the set of questions can be tailored to the scenario at hand. PROMIS can be administered with computer adaptive testing, that presents an individual with the most informative set of questions available and can use stopping rules to produce a theta estimate with a given level of uncertainty. Standardized short-forms are also commonly used, which give the same set of questions to all participants. Because PROMIS is based on IRT, a score from a computer adaptive test and a score from a short form on the same PROMIS domain can be compared.

PROMIS Profile instruments are widely-used standardized sets of short forms, intended to provide a general HRQL measure. There are a variety in use, such as the PROMIS-29, the PROMIS-43, and the PROMIS-57 (see http://www.healthmeasures.net/). They all measure 8 PROMIS domains: Anxiety, Depression, Fatigue, Pain Intensity, Pain Interference, Physical Function, Sleep Disturbance, and Ability to Participate in Social Roles and Activities.

The PROMIS-Preference (PROPr) Scoring System

The PROMIS-Preference (PROPr) scoring system allows preference-based scores to be estimated from health states described by 7 PROMIS domains. The 7 domains are used to generate single-attribute utility scores – one for each domain – using 7 single-attribute utility functions. These are then combined using multi-attribute utility theory to produce a summary score. Six of the PROPr domains are shared with the PROMIS Profile instruments: Depression, Fatigue, Pain Interference, Physical Function, Sleep Disturbance, and Ability to Participate in Social Roles and Activities. The seventh is Cognitive Function-Abilities.

Without a Cognitive Function score, those with PROMIS Profile data cannot produce a single-attribute Cognitive Function utility score and thus a PROPr summary score.

Data Source

We used data from 3,982 members of US online survey panels who responded to items from 9 PROMIS domains: the 8 included in the PROMIS Profile instruments, plus Cognitive Function—Abilities. The data came from two sources. Of the 3,982 participants, 983 came from the PROPr estimation survey, which was used to produce the PROPr summary scoring function.^7,9 The other 2,999 come from the Profiles-HUI survey.¹⁵ Both surveys have been described in detail elsewhere.^7,15

Scores for each PROMIS domain were calculated using the scoring service from the HealthMeasures Assessment Center (https://www.assessmentcenter.net/ac_scoringservice), with the default adult calibration sample consistent with the Profile v2.0 scoring. PROPr scores were calculated using a freely available scoring algorithm (https://github.com/janelhanmer/PROPr).

Modeling

Model Descriptions

The range of Cognitive Function theta scores captured by PROPr is −2.052 to 1.124. We chose to compare 5 models for producing PROPr scores when Cognitive Function scores are missing:

1. The zero model which uses the population average Cognitive Function score (θ_cognition = 0).

2. The ceiling model, which uses a score representing excellent cognitive function, θ_cognition = 1.124, the lowest Cognitive Function score to produce a utility of 1 in the single-attribute Cognitive Function utility scale.

3. The floor model, which uses a score representing poor cognitive function, θ_cognition = −2.052, which is the highest Cognitive Function score to produce a utility of 0 in the single-attribute Cognitive Function utility scale.

4. A linear regression model, which predicts the Cognitive Function score as a function of the 8 PROMIS Profile domains. The selection of a functional form is described below.

5. A Bayesian neural network, which predicts the Cognitive Function score and where the feature data are the 8 PROMIS Profile domain scores.

These models predict the missing Cognitive Function score, which is then used to produce a single-attribute Cognitive Function utility that is combined with the other 6 single-attribute utilities to produce the PROPr summary score.

Models (A)-(C) are constant models – predicting the same PROMIS Cognitive Function theta score for every participant. The population average theta value (zero model (A)) is 0, by construction, and receives a utility value of 0.858 on the single-attribute Cognitive Function utility scale. A value of 1.124 was used as a score representing excellent Cognitive Function (ceiling model (B)), as it is the lowest theta value receiving a utility of 1 in the PROPr Cognitive Function utility scale, which is the highest possible utility. Similarly, a value of −2.052 was used as a score representing poor Cognitive Function (floor model (C)), because it the highest theta value receiving a utility of 0 in the PROPr Cognitive Function utility scale, which is the lowest possible utility of the scale. These three constant models were chosen to represent naïve approaches to adding a Cognitive Function score to PROMIS Profile data.

Model (D) uses forward and backward stepwise regression without interactions to choose a candidate linear model, where the smallest model is the intercept-only model and the largest is expressed below in Equation 1:

$${\theta }_{\mathit{\text{cognition}}}={\beta }_0+{\beta }_1{\theta }_{\mathit{\text{anxiety}}}+{\beta }_2{\theta }_{\mathit{\text{depression}}}+{\beta }_3{\theta }_{\mathit{\text{fatigue}}}+{\beta }_4{\theta }_{\mathit{\text{physical}}}+{\beta }_5{\theta }_{\mathit{\text{pain}}}+{\beta }_6{S}_{\mathit{\text{pain}}}+{\beta }_7{\theta }_{\mathit{\text{sleep}}}+{\beta }_8{\theta }_{\mathit{\text{social}}}+ϵ.$$ Equation 1: Predicting Cognitive Function scores in a linear model, with the PROMIS Profile domains as independent variables.

Here, θ_domain is the theta score on the given domain, S_pain is the Pain Intensity score (θ_pain is the Pain Interference score), and ϵ is an error term. The θs are unbounded, and the pain intensity score (S_pain) is on a 0–10 scale with unit intervals.

Model (E) implements a machine learning procedure called a multi-layer perceptron neural network. The neural network is particularly suited to discovering nonlinear relationships between the independent variables (8 PROMIS domain scores) and the dependent variable (the Cognitive Function scores). It is a Bayesian neural network because it uses a Bayesian regularization backpropagation process to choose the hyperparameters of the model.^16,17 All analyses were run in R (version 3.4.4). The Bayesian neural network was estimated using the keras package (version 2.2.4) using the TensorFlow backend and rstan (version 2.18.2). We varied the number of layers in the neural network (from 2 to 100) and the number of nodes in each layer (from 5 to 100).

Model comparison procedure

The dataset described above includes the required information to calculate a PROPr score for all participants. Therefore, we used the dataset to predict Cognitive Function thetas using the models from the previous section, using those predicted thetas to produce PROPr scores, and compared the predicted PROPr scores with true PROPr scores. We evaluated model fit using mean-error (ME) and root-mean-squared-error (rMSE). We split the data randomly into 70% training/30% validation (n_training = 2786 and n_validation = 1196) sets for cross-validation, fitting the models on the training set and calculating MEs and rMSEs on the validation set. That split was chosen because the machine-learning method is data-dependent in a way that usual parametric regression is not. Although the parameter estimates of the latter are obviously data-dependent, the actual functional form of the machine-learning model depends on the dataset as well – not just its (hyper)parameters values. In addition, to compared model performance among the competing models, one needs to have a common group for out-of-sample validation. The rMSEs calculated on the validation set provided an unbiased estimate of generalization error.

We calculated ME and rMSE on both the Cognitive Function theta scores as well as the resulting PROPr scores. The former refers to comparing predicted Cognitive Function theta scores with the true Cognitive Function theta scores. The latter refers to using the predicted Cognitive Function theta score along with the 6 other (true) PROMIS domain scores included in the PROPr scoring system to generate a predicted PROPr score and comparing it with the true PROPr score.

As a robustness check, we repeated the above procedure stratifying the validation set by the number of chronic conditions reported by the participants,^7,15 as well as by binning the Cognitive Function theta scores, based on the quartiles of those scores across the whole dataset. These procedures were intended to stress each model’s performance by adjusting the health of the validation sample. We also computed correlations between observed and predicted scores, prediction bias, as well as the means and standard deviations of observed and predicted scores by age and gender, all on the validation set.

Results

Table 1 shows the demographic characteristics of the sample, including the number of chronic conditions reported by the participants.

Table 1:

Demographic information of the study sample, which is comprised of two surveys, the PROPr and Profiles-HUI Survey. The last column compares the makeup of those surveys with the 2010 US Census for the demographic variables and the National Health Interview Survey 2016 for the health-related variables.

	PROPr Estimation Survey	Profiles-HUI Survey	2010 US Census
Gender (%)
Female	54	51	51
Race (%)
White	77	71	64
Black	12	17	12
Asian	4	10	5
Ethnicity (%)
Hispanic	16	17	16
Education (%)
< High School	12	14	11
High School Grad or Equivalent	25	31	30
> High School	63	55	59
Age (%)
18–24 Years	11	13	12
25–34 Years	17	18	17
35–44 Years	10	18	18
45–54 Years	17	19	20
55–64 Years	19	16	16
65–74 Years	13	9	10
75–84 Years	7	6	6
85+ Years	6	2	3
Chronic Health Conditions (%)			National Health Interview Survey 2016
Coronary Heart Disease	2	Not asked	5
Angina (Angina Pectoris)	1	Not asked	2
Heart Attack (Myocardial Infarction)	1	5	4
Chest Pain (Angina)	Not asked	10	Not asked
Hardening of the Arteries (Coronary Artery Disease)	Not asked	4	Not asked
Heart Failure or Congestive Heart Failure	Not asked	4	Not asked
Stroke	6	Not asked	4
Stroke or Transient Ischemic Attack (TIA)	Not asked	3	Not asked
Emphysema	1	Not asked	2
Chronic Obstructive Pulmonary Disease (COPD)	4	5	4
Asthma	14	17	14
Cancer or Malignancy of any Kind	16	5	11
Arthritis/Gout/Lupus/Fibromyalgia	26	Not asked	28
Arthritis or Rheumatism	Not asked	20	Not asked
Seizure Disorder or Epilepsy	6	Not asked	Not asked
Diabetes or Sugar Diabetes	19	11	11
High Blood Pressure (Hypertension)	Not asked	34	35
Liver Disease/Hepatitis/Cirrhosis	Not asked	4	Not asked
Kidney Disease	Not asked	3	Not asked
Migraines or Severe Headaches	Not asked	16	Not asked
Depression	Not asked	24	Not asked
Anxiety	Not asked	21	Not asked
Alcohol or Drug Problem	Not asked	5	Not asked
Sleep Disorder	Not asked	13	Not asked
HIV or AIDS	Not asked	1	Not asked
Spinal Cord Injury	Not asked	3	Not asked
Multiple Sclerosis	Not asked	2	Not asked

The results of both stepwise regression procedures selected the largest model (Equation 1) as the candidate linear model. We observed suppression effects on Fatigue and Pain Interference (i.e., negative zero-order correlations of around −0.3 for each with the dependent variable, but positive coefficients in the model). We re-estimated the model, removing those two domains. That yielded a model with no suppression effects, and similar model fit (the difference in variance-explained occurred at the thousandths decimal place). As worse fatigue or worse pain should not predict better utilities – by predicting better cognitive function – we continued our analyses with the model that omits Pain Interference and Fatigue.

The neural network’s performance plateaued quickly with the increase in the number of hidden layers, and hidden nodes. We relied on using the validation dataset to avoid overfitting the neural network, and we limited the number of nodes to 10 and 2 hidden layers at which the performance of the neural net started to plateau. As expected, the larger models had better fitting scores to the training dataset, but lower scores for the validation dataset.

Table 2 shows the results of calculating rMSE and ME on the PROPr scale (columns 1 and 2), and the rMSE and ME on the Cognitive Function theta scale (columns 3 and 4). The PROPr scale ranges from −0.022 to 1 and the Cognitive Function theta scale is unbounded, though the observed range in these data is −2.70 to 1.67.

Table 2.

Root-mean-squared error and mean error of the models, calculated on the validation data set. The second and third columns show the results on the PROPr utility scale, and the fourth and fifth columns show the results on the Cognitive Function-Abilities scale.

Model	RMSE (PROPr)	ME (PROPr)	RMSE (cog)	ME (cog)
Linear model	0.0946	0.0175	0.954	0.0399
Bayesian neural network	0.0938	0.0175	0.9357	0.0300
Floor	0.2860	−0.2308	2.0958	−1.8085
Ceiling	0.1178	0.0673	1.7296	1.3675
Zero	0.0966	0.0251	1.0867	0.2435

In terms of rMSE on both the PROPr scale and the Cognitive Function scale, the Bayesian neural network performed best, followed by the linear model, the zero model, the ceiling model, and the floor model.

Except for the low score constant model, the other models tended to overpredict the Cognitive Function score (and hence the PROPr score).

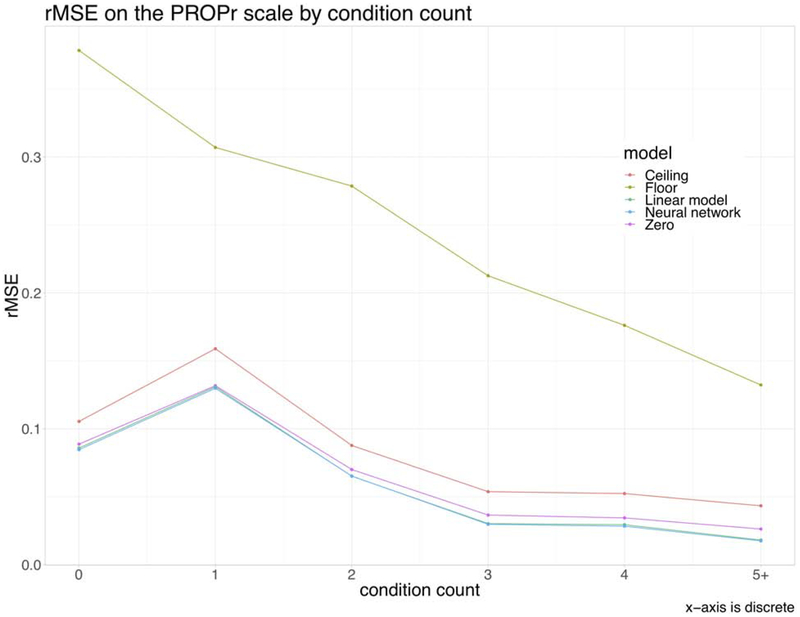
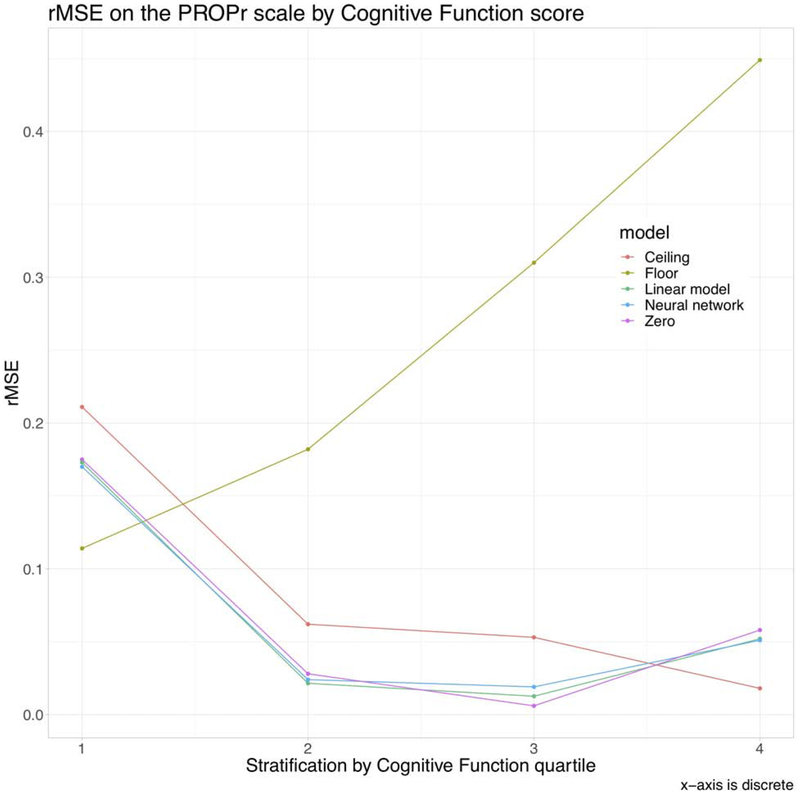
Figure 2 shows the rMSE on the PROPr scale when the validation set is split into those who reported 0, 1, 2, 3, 4, and 5+ chronic conditions (see Table 1). The Bayesian neural network performed best, followed by the linear model, the zero model, the ceiling model, and the floor model. Figure 3 shows model performance when the validation set is divided by the sample quantiles of Cognitive Function scores. Here, the linear model, neural network, and zero model performed best in the middle two quartiles, with the floor and ceiling unsurprisingly producing the best predictions for the lowest and highest cognitive function scores, respectively.

Figure 2.

Root-mean-square error on the PROPr scale, dividing the validation set by self-reported chronic conditions.

Figure 3.

Root-mean-squared error on the PROPr scale, dividing the validation set by sample quartile on Cognitive Function-Abilities. The “1” indicates the group whose cognitive function score fell within the minimum to the first quartile; “2,” the group whose score fell within the first quartile to the median; “3,” the group whose score fell within the median to the third quartile, and “4,” the group whose score fell within the third quartile to the maximum.

Prediction bias and correlations between observed and predicted scores are in Table 3, showing high correlations and a tendency for overprediction (except for the floor model). Table 4 shows the mean actual and predicted scores by age and gender for each of the models.

Table 3.

Prediction bias (mean of predictions minus mean of observed scores) as well as Pearson correlation between predictions and observed scores for each model, all on the PROPr scale.

Model	Prediction bias	Correlation
Linear model	0.0176	0.932
Bayesian neural network	0.0175	0.933
Floor	−0.231	0.930
Ceiling	0.0672	0.930
Zero	0.0251	0.930

Table 4.

Mean and standard deviations of observed scores and predicted scores, by age and gender. Two participants were removed from these calculations: one, who reported an impossible age, and another, who was the only person in the PROPr survey dataset to respond “other” when asked to self-report their gender.

Age	Gender	n	Observed	LM	NN	Floor	Ceiling	Zero
18–24	M	62	0.387 (0.257)	0.452 (0.255)	0.451 (0.257)	0.170 (0.0975)	0.504 (0.267)	0.457 (0.243)
	F	69	0.395 (0.277)	0.419 (0.269)	0.417 (0.270)	0.158 (0.103)	0.471 (0.283)	0.426 (0.257)
25–34	M	107	0.308 (0.209)	0.350 (0.219)	0.348 (0.221)	0.132 (0.0844)	0.399 (0.231)	0.362 (0.210)
	F	117	0.383 (0.233)	0.413 (0.235)	0.411 (0.237)	0.155 (0.0909)	0.464 (0.249)	0.421 (0.226)
35–44	M	96	0.314 (0.2229)	0.352 (0.254)	0.351 (0.256)	0.131 (0.0982)	0.399 (0.269)	0.361 (0.245)
	F	105	0.383 (0.272)	0.400 (0.257)	0.400 (0.259)	0.150 (0.0998)	0.450 (0.273)	0.407 (0.248)
45–54	M	111	0.376 (0.256)	0.386 (0.240)	0.386 (0.243)	0.145 (0.0919)	0.437 (0.252)	0.396 (0.229)
	F	115	0.364 (0.276)	0.371 (0.260)	0.371 (0.263)	0.138 (0.101)	0.418 (0.276)	0.378 (0.251)
55–64	M	82	0.408 (0.267)	0.423 (0.270)	0.425 (0.274)	0.158 (0.103)	0.473 (0.283)	0.428 (0.258)
	F	104	0.467 (0.261)	0.463 (0.246)	0.465 (0.250)	0.174 (0.0950)	0.516 (0.260)	0.468 (0.237)
65–74	M	63	0.460 (0.272)	0.451 (0.262)	0.450 (0.264)	0.169 (0.100)	0.501 (0.275)	0.454 (0.250)
	F	56	0.447 (0.221)	0.435 (0.209)	0.436 (0.211)	0.163 (0.0808)	0.487 (0.221)	0.441 (0.201)
75–84	M	30	0.371 (0.269)	0.385 (0.263)	0.388 (0.272)	0.143 (0.0989)	0.432 (0.271)	0.391 (0.247)
	F	34	0.326 (0.215)	0.324 (0.212)	0.324 (0.217)	0.121 (0.0821)	0.370 (0.224)	0.335 (0.204)
85+	M	24	0.303 (0.251)	0.308 (0.260)	0.312 (0.266)	0.114 (0.100)	0.351 (0.275)	0.317 (0.250)
	F	19	0.260 (0.146)	0.268 (0.132)	0.297 (0.145)	0.0941 (0.0533)	0.256 (0.136)	0.255 (0.137)

Discussion

We compared five models for producing PROPr preference scores using PROMIS Profile data. PROMIS Profile instruments are widely-used standardized questionnaires for measuring HRQL, and provide PROMIS scores for 8 domains: Anxiety, Depression, Fatigue, Pain Intensity, Pain Interference, Physical Function, Sleep Disturbance, and Ability to Participate in Social Roles and Activities. In order to generate PROPr scores, measurements on 7 PROMIS domains are required, which include 6 of the PROMIS Profile domains (all except Anxiety and Pain Intensity), as well as a measurement on the Cognitive Function—Abilities domain. Thus, without true Cognitive Function scores it is necessary to predict them for PROMIS Profile datasets so that those data can be used to inform economic, decision, and public-health analyses via utility values generated from PROPr. Our analyses have produced models with generalization error less than 10% of the PROPr scale, allowing the generation of a PROPr score for datasets with only PROMIS Profile data.

We found that a linear model is nearly as good at predicting Cognitive Function scores as a Bayesian neural network. Our results, we believe, are largely driven by the way that the PROMIS domains in PROPr were chosen: they were selected to be structurally independent, meaning that, given a pair of domains, any combination of theta values could conceivably occur¹¹. Structural and statistical independence are related, but neither one is necessary nor sufficient for the other. The fact that a linear model with no interactions or transformations performs almost as well as the Bayesian neural network can be a seen as an additional empirical validation of the domain selection method. That is, the PROMIS domains in PROPr contain only so much information about each other, and about Cognitive Function in particular: including more complicated terms in the model – the Bayesian neural network excels at discovering nonlinear relationships – only improves prediction by a small amount. The good performance overall of the zero model further demonstrates the difficulty of the prediction task. Thus, although we believe the out-of-sample performance demonstrates that one can estimate a PROPr score with the PROMIS Profile, we do not endorse the use of these models for the prediction of Cognitive Function scores for other purposes. In addition, we recommend that any researcher designing a new data collection with PROMIS measures who also wants to compute health utility scores include the 7 domains from PROPr so that their data set has complete measurements. In the case where a researcher is considering a PROMIS Profile, that can be accomplished by adding only two additional Cognitive Function-Abilities items.

Thus, our analyses suggest that the linear model is sufficient for the task at hand, performing almost as well as a neural network with many more parameters. The linear model is easy to implement as it requires knowing only the 6 coefficients and the intercept value. It is also a method that should be familiar to policy analysts as well as researchers across public health, health and pharmaco-economics, and decision analysis. Table 5 shows the regression coefficients of the linear model estimated from the entire dataset. The entries in Table 5 can be used to predict the missing Cognitive Function score, and then the complete vector of 7 PROMIS scores can be used as input to the PROPr summary scoring function to obtain a PROPr score. An appendix provides example code showing an implementation of the model in Table 5 as well as the computation of a confidence interval for an estimate of a conditional mean Cognitive Function score.

Table 5.

Regression table for the recommended linear model, estimated on the entire data set.

	Dependent variable:
	cognitive function
depression	−0.0370
	(0.025)
physical functioning	0.118***
	(0.023)
sleep	−0.223***
	(0.021)
social roles	0.0505**
	(0.025)
anxiety	−0.168***
	(0.027)
pain intensity	−0.00599
	(0.007)
Constant	0.00943
	(0.030)
Observations	3,982
R2	0.209
Adjusted R2	0.208
Residual Std. Error	0.931 (df = 3975)
F Statistic	175.082*** (df = 6; 3975)

Note:

^*p<0.1;

^**p<0.05;

^***p<0.01

During the course of the study, we also investigated the candidate models under linear equating, a common practice in health-utility mapping studies, where predicted scores are linearly transformed to have the same mean and standard deviation as the observed scores, in order to counteract regression to the mean.^15,18,19 However, unlike mapping studies, the dependent variable in our models was a health domain, not utility, which would then be used as input together with other health domain measurements to estimate a health utility score. As such, we are attempting to best predict cognitive function in order to produce PROPr scores and thus should be minimizing rMSE, rather than scale-aligning, as in the mapping literature.

As PROPr was estimated using a sample whose demographics match the general population, it is not surprising that the unconditional population mean is a small amount worse in terms of rMSE than the non-constant models, but it would not perform as well in samples with Cognitive Function scores very different from the mean (e.g., in those with excellent health or with conditions affecting cognition). As with other generic societal preference-based scores, PROPr is relevant in analyses using patient data when a societal perspective is required. However, in a PROMIS Profile dataset with vastly different participant characteristics than the data we used in our study, our recommended model might not perform as well as it would for datasets from other community samples. Care should be taken in such instances to consider whether, and if so, how, relationships among the PROMIS domains could differ in those contexts, and whether the results of our study are still appropriate.

The Profiles-HUI sample had more unhealthy participants than would be expected from a probability sample of the US general population. Depending on the true relationships among the PROMIS domains, it could be the case that the model selection procedure is sensitive to the health of the sample. Operationalizing health by the number of chronic conditions (Figure 2), the models perform in the same order and with better rMSE values with increasing number of chronic conditions. That could be because of the small negative correlation (−0.20) between condition count and Cognitive Function score – perhaps because those with conditions that would affect cognitive function would be less likely to participate in a survey – and the high leverage of the unhealthy participants. Dividing the validation sample by Cognitive Function score (Figure 3), the floor and ceiling models perform best in the lower and upper quartiles, respectively, because those constant models always predict Cognitive Function theta scores in the correct quartile; the same goes with the zero model for the third quartile (which contained 0).

Both the PROPr survey data and Profiles-HUI survey data are publicly available.^20,21 Our goal was to produce a method that could work for anyone who collected PROMIS Profile data. The two surveys we used both share variables beyond the 8 PROMIS domains used in our models, such as age and sex and common chronic conditions. A researcher whose data shares these variables could use our approach to build a better model. Furthermore, a researcher with a sample of the general population that is missing the Cognitive Function score for other reasons – i.e., who truly has missing data in the sense of Little and Rubin’s seminal work – could combine their data with the PROPr and Profiles-HUI surveys and use multiple imputation to complete their analyses.^22,23

We aimed to produce a recommendation that could be used with individual-level data coming from any PROMIS Profile instrument, and thus we restricted our set of independent variables to the PROMIS domains used in the PROMIS Profile. As PROPr’s summary scoring function is multiplicative, and thus nonlinear, individual-level PROMIS data is required to produce PROPr values. Sample statistics, such as the mean PROMIS domain scores of a sample cannot be used to generate a mean PROPr score for the sample; instead, the individual PROMIS scores of the sample are required.

Conclusion

With the model presented in Table 5, any researcher or analyst with a dataset that administered a PROMIS Profile instrument can now use that data to produce utility-based summary scores using the PROPr scoring system. Many more datasets can now be used for health valuation, and thus be incorporated in analyses that require those numbers, such as cost-effectiveness analyses. The linear model we recommend is easily implementable in any statistical programming language (see the Appendix), and the PROPr scoring system is free to use, with freely available code in R and SAS which can be translated to other programming languages.

Highlights.

• The Patient Reported Outcomes Measurement Information System (PROMIS) is a set of widely-used patient-reported outcomes measures. The PROMIS-Preference (PROPr) Scoring System provides summary utility scores for PROMIS measurements. However, it requires measurements from 7 PROMIS scales; without all of those measurements, it has not been possible to produce a utility score.

• We produce a method for computing a PROPr utility score for a set of standardized PROMIS questionnaires, the PROMIS Profile instruments, which are missing one of PROPr’s seven required PROMIS domains, Cognitive Function-Abilities.