3D-GLCM CNN: A 3-dimensional gray-level co-occurrence matrix based CNN model for polyp classification via CT colonography

Abstract

Accurately classifying colorectal polyps, or differentiating malignant from benign ones, has a significant clinical impact on early detection and identifying optimal treatment of colorectal cancer. Convolution neural network (CNN) has shown great potential in recognizing different objects (e.g. human faces) from multiple slice (or color) images, a task similar to the polyp differentiation, given a large learning database. This study explores the potential of CNN learning from multiple slice (or feature) images to differentiate malignant from benign polyps from a relatively small database with pathological ground truth, including 32 malignant and 31 benign polyps represented by volumetric computed tomographic (CT) images. The feature image in this investigation is the gray-level co-occurrence matrix (GLCM). For each volumetric polyp, there are 13 GLCMs, computed from each of the 13 directions through the polyp volume. For comparison purpose, the CNN learning is also applied to the multi-slice CT images of the volumetric polyps. The comparison study is further extended to include Random Forest (RF) classification of the Haralick texture features (derived from the GLCMs). From the relatively small database, this study achieved scores of 0.91/0.93 (two-fold/leave-one-out evaluations) AUC (area under curve of the receiver operating characteristics) by using the CNN on the GLCMs, while the RF reached 0.84/0.86 AUC on the Haralick features and the CNN rendered 0.79/0.80 AUC on the multiple-slice CT images. The presented CNN learning from the GLCMs can relieve the challenge associated with relatively small database, improve the classification performance over the CNN on the raw CT images and the RF on the Haralick features, and have the potential to perform the clinical task of differentiating malignant from benign polyps with pathological ground truth.

I. Introduction

BASED on the newest report of the international agency for research on cancer, colorectal cancer (CRC), which is the tenn that is commonly used for the cancer of colon and rectum, ranks third for total cancer deaths in the world since 2012 [1]. As reported by the national center for health statistics, centers for disease control and prevention in USA, CRC is the second most common cancer in men (more than 8.4%) and third in women (more than 8.1%) based on the US mortality data from 2001 to 2015. An annual estimation of 140,250 new cases were diagnosed during 2000 to 2014 from 48 states with about 50,630 deaths from this disease [2]. Early detection, accurate diagnosis and optimal treatment of the early detected malignant polyps can effectively decrease the incidence rate before malignant polyp transformation [3,4], where computed tomographic colonography (CTC) is recommended as a polyp screening option [5], which can detect polyps through a minimally invasive procedure. As a screening option, CTC provides fully three-dimensional (3D) image data for volumetric-based polyp detection by either radiologist experts or computer-aided detection (CADe) [6-10]. Previous investigations for volumetric-based polyp diagnosis by either radiologist experts or computer-aided diagnosis (CADx) have shown promising results [11-13]. The volumetric-based CADe and CADx technologies will not only speed up the radiologist’s examination, but also increase their confidence in decision making with the fully 3D information. Some related information processing methodologies for colon polyps are reported in [14-19].

Recently, machine learning-based artificial intelligent (AI) information processing methodology, especially convolution neural network (CNN), has shown great potential in many applications due to its feature learning power. In addition to its success in computer vision including image recognition [20-22], image segmentation [23,24] and image reconstruction [25,26], CNN has rendered good results in the medical imaging applications, such as Lumbar Surgery [27] and gland segmentation [28]. In the area of cancer detection and diagnosis, several CNN based methods have been proposed, e.g. for lung cancer [29-32]. In these cancer detection and diagnosis reports, their CNN models mainly focus on learning from multiple-slice 2D images, without considering the fact that the lesion itself is a volumetric 3D object so that the 3D spatial intrinsic information is ignored.

In an effort to consider the 3D spatial information, Thomas et al. [33] performed pre-training on natural images and fine-tuning on medical target slice images. Similar work can also be seen in references [34,35]. Though some efforts have been made on fine-tuning medical target slice images by using natural images [36, 37], no 3D based solution has been proposed. To implement a 3D CNN model requires large-scale annotated medical image datasets, which has been a challenge not only in data acquisition, but also data annotation. Therefore, given a limited dataset, how to consider the 3D information for the differentiation task remains a challenging task. Several attempts have been reported to mitigate this challenge. Setio et al. [29] designed a model that fuses features learned from differently oriented planes extracted from each candidate for final decision making, which converted the 3D volumetric data into 2D multi-channel representations as inputs to 2D CNN. The 2D CNN strategy has much fewer parameters to train compared to directly using a 3D CNN model in general, where the 3D convolution will increase the kernel numbers significantly [30]. Therefore, extracting the 3D information as multi-channel 2D feature images could be a possible approach to consider the lesion as a volumetric 3D object when given only limited number of datasets.

To address difficulty, this study aims to explore the potential of CNN learning from multiple slice (or feature) images extracted from the raw volumetric CTC data for the clinical task of differentiating malignant from benign polyps by a relatively small database with pathological ground truth, including 32 malignant and 31 benign polyps. To the best of our knowledge, we are the first to propose using GLCM image in the CNN model to encode the 3D texture information of polyps, even though GLCM has been developed decades ago.

The extracted feature images can effectively relieve the requirement for large scale training datasets and further serve as useful supplement to the supervised learning CNN architecture. For example, Wang et al. [31] used one hybrid model to fuse the features maps of Histogram of Oriented Gradient (HOG) and Local Binary Patterns (LBP) with the original intensity images for the CNN training to enrich the information of the limited data. Tan et al. [32] further explored strategies to infuse expert knowledge into machine learning. In addition to infusing expert knowledge, Hu et al. [38] had extended the traditional 2D Haralick texture features/measures [39] to 3D space through the 3D sampled gray-level co-occurrence matrices (GLCMs), where each GLCM is a 2D image and represents a texture mapping of the 3D object from a particular direction. Inspired by these efforts above, in this study we propose a 3D GLCM based CNN (3D-GLCM CNN) model for the clinical task of polyp classification, i.e. differentiating malignant polyps from benign ones. The multiple GLCM texture images, each from the particular 13 sampling directions through the object volume [38] are used to represent the object’s 3D spatial temporal information.

Additionally, the proposed 3D-GLCM CNN model can avoid the resizing operation and its corresponding artifacts in the general CNN models, which learn on the raw CT images. The general CNN models require a fixed size for the 2D input images [29,30]. Since a lesion has large variance in size, the requirement of a fixed size is a potential problem for the general CNN models. Generally speaking, the input size should be chosen as the largest cross section of the lesion volume [31]. For many tasks of early detection, the largest cross section is usually a few millimeters size in diameter. Such a small size is usually problematic for the general CNN models. In an attempt to mitigate this problem, Tan et al. [32] proposed to resize the small lesions’ sizes to an appropriate scale comparable to other lesions in the database. This resizing operation is suboptimal because the size of a lesion is frequently an important indicator of its malignant degree. Although some attempts have been made to utilize 3D convolution to perform 3D based CNN models to relive the difficulty of detecting small lesions [40,41], the challenge of requiring fixed input image size remains. The GLCM texture images count for the frequency of a specific pair of gray-level values, whose size would be determined by the largest gray-level value. That means the GLCM has a fixed size once the CT images are scaled to the same gray-level images.

Evaluation of the proposed 3D-GLCM CNN model is performed based on the quantitative measures of the area under the receiver operating characteristics curve (AUC) with comparison to (i) the 2D, 2.5D and 3D raw CT image-based CNN models, (ii) the 2D and 2.5D image derived GLCM CNN models, and (iii) the well-known Random Forest (RF) classification of the Haralick texture features of the polyp volumes. The corresponding results of accuracy, sensitivity and specificity are also reported for comparison.

Partial results of this work were presented and recorded at [42]. Comparing to the conference record, this paper adds ten 2D and 2.5D models to make a comprehensive study comparing the raw CT image based model and the proposed the GLCM based model through different dimensions and implementations. Moreover, we only report the leave-one-out cross validation result in [42]. In this paper, we include the two-fold cross validation results as well as its statistical analysis with supplement of leave-one-out results to further validate our proposed model.

The rest of this paper is organized as follows. In section II, the proposed 3D-GLCM CNN model is presented in detail with comparison to other models mentioned above. In section III, experimental design is described, and comparison results are reported. In section IV, conclusion is drawn, followed by discussion of the remaining challenges and future researches.

II. Method

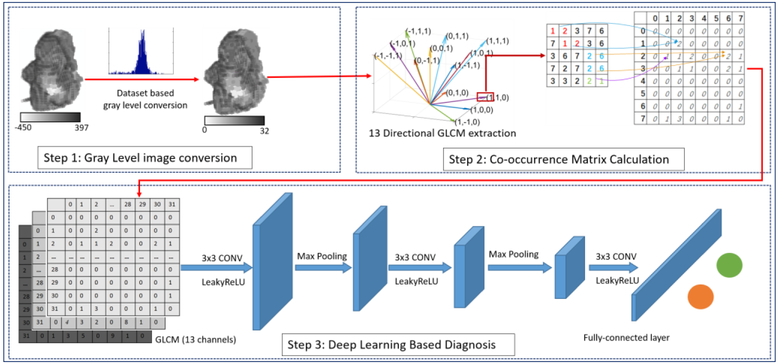
The workflow of the proposed 3D-GLCM CNN model is shown in Fig. 1. Our proposed model contains three steps. The first step is to convert the original Hounsfield unit CT value of the 3D polyp into gray-level value based on the CT value distribution of the whole dataset. The second step is to generate multiple 3D-GLCM feature images from the gray-level images obtained from step 1. At step 3, a multi-channel CNN model is used to perform the polyp classification using the GLCM feature images. More details about these three steps are presented below.

Fig. 1:

Illustration of our 3D-GLCM CNN model, which contains gray level image conversion step, co-occurrence matrix calculation step and CNN based classification step.

A. Gray Level Image Conversion

The goal of step 1 is to perform gray level scaling on the original CT image pixel values (or Hounsfield units) to an appropriate value range. Because of the wide range of Hounsfield units that CT images take on, gray level scaling acts as a filter to smooth the image noise or reduce the sparsity of GLCM. However, if the image is scaled down to too few gray levels, too much information may be filtered out. The gray level scaling is a trade-off between reducing sparsity and preserving sufficient information to classify the polyp types. Therefore, finding an appropriate scaling method to reduce sparsity and while maintaining the important information for improved CADx classification performance is needed.

In this study, we adapted our previously proposed histogram based adaptive scaling method to scale the CT images [43]. Using the histogram from all the polyp’s regions of interest (ROIs) in the CT image database, we generate the gray level bins such that each bin contains roughly the same number of voxels. Compared to the linear scaling method [38], this adaptive method can enhance the contrast between the voxels with similar CT values, which is the case for the voxels inside the polyps. By experimental trials on the number of gray levels in powers of two from 8 to 256, the gray level 32 with bin values from 0 to 31 is a good trade-off between reducing GLCM sparsity and preserving enough information according to [38]. An example of the 3D polyp in Hounsfield unit (−450~397) is shown along with the quantized gray level 3D image (0~31) in Fig. 1 (Step 1).

In summary, the input of this step is the 3D CT images of the polyp volumes containing the polyp voxels and the output is the quantized image voxels with only 32 discrete values.

B. 3D-GLCM Generation

Based on the gray level images from step 1, we calculated the GLCMs by counting the frequency of the pair of voxels with specific gray-level (or bin) values. In a 2D digital image, co-occurrence matrix (CM) is defined by the frequency of pixel-pairs in one image as the following [42]:

$$C_{i,j}(d,\theta )=\sum \begin{array}{c}\hfill \\ p\in V\hfill \end{array}\{\begin{array}{c}1ifI(p)=i\&I\left(p+d(cos\theta ,sin\theta )\right)=j\hfill \\ 0otherwise\hfill \end{array}\phantom{\}}$$ (1)

where I is the image data, p is a point within the slice domain (V),I(p) is a pixel value at point p in the image, i and j represent a pair of image pixel values, d is a displacement between p and another point along the direction θ.

For the 3D volumetric image data, the direction is determined by the three variables of the basis vectors in the 3D space. Following the philosophy of the 2D GLCM used in the classical Haralick model [39], we only sampled along the direction linking the center voxel with its nearest 26 neighbors considering up to second nearest neighbors. Due to the redundant information collected from opposite directions, only half of the directions are considered. Considering more neighbors may bring in extra information, it remains a challenging task to integrate the information without redundancy. The sampling direction of the GLCMs in 3D space is demonstrated in Fig.1 (Step 2). More illustration can be found in the reference [38].

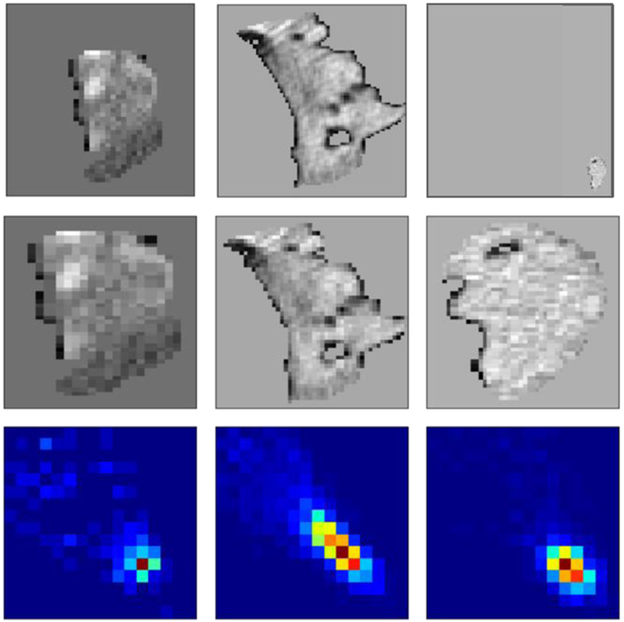
According to Eq. (1), GLCM is a square matrix whose size is determined by the maximum number of discrete gray-level values. This natural property makes the GLCM perfect to avoid the resizing problem when using the CNN. Figure 2 (top) presents a set of typical polyps with various sizes. The large polyp (middle) can be around 60mm, while the small one (right) can be ~1mm. When we fed them into CNN, all the polyps should be resized to the same size using either interpolation (Fig. 2 middle) or zero padding. This may introduce artificial information or make the image too sparse. The proposed GLCM method (Fig. 2 bottom) can enrich the information of the small polyp without bringing in any artificial information. In summary, the input of this phase is the gray level image with k unique values (k=32, as discussed in A). The output is 13×32×32 GLCMs.

Fig. 2:

A typical set of three polyps with various sizes. The top row are the original images. The middle row are the corresponding resized polyps using an interpolation method. The bottom row are the corresponding GLCMs extracted in the direction (1, 1, 1).

C. CNN Based Polyp Classification

The last step in Fig. 1 is to perform CNN based polyp classification using the generated 3D level (13 directional) GLCM volume image, which has the dimension (32, 32, 13). A multi-channel network structure was designed, which takes each directional GLCM (a 2D image) as one input channel as shown in Fig.1 (Step 3). At the late fusion stage in CNN architecture, each direction will be weighted by the trained kernel weights. Therefore, the proposed 3D-GLCM CNN considered the unevenly distributed sampling direction, which is also one advantage of the proposed method. To further improve the model performance, one possible way is to incorporate prior knowledge of the sampling direction into the CNN architecture design but beyond the scope of this paper.

The model consists of seven layers including three convolution layers, two max-pooling layers and two fully connected layers. In each convolution layer, batch normalization and activation function are performed. The model uses the ReLu as the activation function, the cross-entropy loss as the training loss and softmax function at the last fully connected layer. The kernel size, neuro numbers and the stride for each layer are summarized in Table I. The network depth and kernel size were optimized to achieve the best AUC score.

TABLE I.

CONVOVOLUTIONAL NETWORK DESIGN FOR SETP 2.

Layer	Type	Kernel	Number	Stride
1	Convolution	3× 3	32	1
2	Max-pooling	2× 2	-	2
3	Convolution	3× 3	64	1
4	Max-pooling	2× 2	-	2
5	Convolution	3× 3	64	1
6	Fully connected	-	700	-
7	Fully connected	-	2	-

For comparison purposes, the conventional raw CT image-based CNN models and RF classification on Haralick texture features are reviewed below, followed by presentation of our evaluation strategy.

D. Models for Comparison

For comparison study and exploring effective approaches using multiple slice images for classifying polyps from benign to malignant, this study performed the classification task by implementing other strategies, which can be categorized as raw CT image based CNN and 2D/2.5D-GLCM based CNN as well as image texture feature based RF classification models. The proposed model and all the learning models for comparison study are summarized in Table II.

TABLE II.

SUMMARY OF ALL THE MODELS USSED IN THIS STUDY.

No.	Classifier	Input Type	Input	Model Name
1	CNN	CT image based	Random selected slice image	R-IMG
2			Center slice image	C-IMG
3			Random selected slice image with its HOG and LBP feature map	R-Hybrid
4			Center slice image with its HOG and LBP feature map	C-Hybrid
5			Multiple slices image	M-IMG
6			Multiple slices image with their HOG and LBP feature maps	M-Hybrid
7			Volumetric 3D images	3D-IMG
8		GLCM based	GLCM from random selected slice image	R-GLCM
9			GLCM from center slice image	C-GLCM
10			GLCM from multiple slices image	M-GLCM
11			GLCM from 3D image	3D-GLCM
12	Random Forest	Texture Feature based	Haralick features	HF
13			Extend Haralick features	eHF

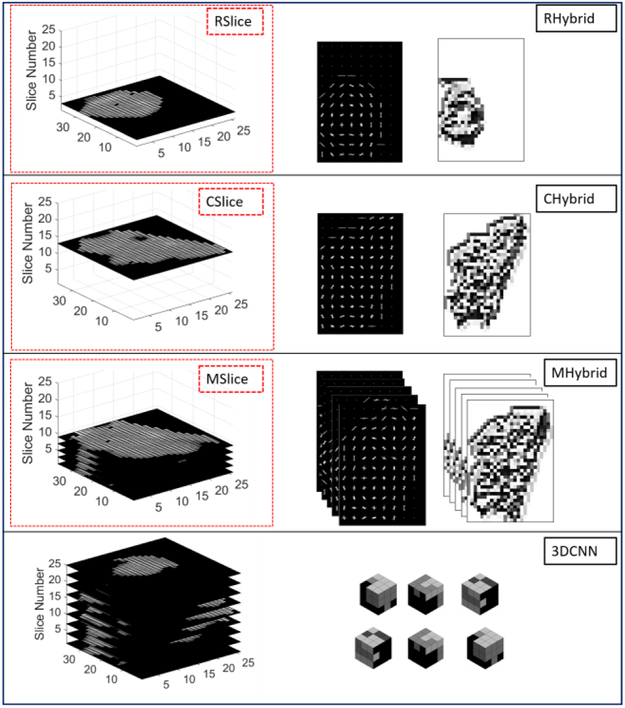
For raw CT image-based CNN model, three schemes were used to deal with the multi-slice 3D data. One way is to randomly select one slice from multiple slices of each polyp volume, called R-IMG. Another way is to take the largest-area slice as input, called C-IMG. To utilize the multi-slice data, we use the multi-channel CNN architecture to treat each slice as one channel input and fuse all channel features early in the network to learn the combined features from the multiple slices, we refer to this multi-slice model as M-IMG. Since M-IMG takes the multiple slices as input but does not consider the spatial relationship between each slice, this scheme is also called 2.5D model.

To add more information to the raw CT image based CNN model, we also implemented the hybrid model proposed in [30], which supplemented the intensity images with extra shape and texture information by adding HOG and LBP features as additional channels of the input. In other words, the input of the hybrid model contains three types of channels: CT images, HOG feature image (which accounts for the border information) and LBP feature image (which accounts for the internal region information). For the hybrid model, we also implemented the three schemes to manipulate the multi-slice data similar with the raw CT image based CNN model. We denoted the random slice-based hybrid model as R-Hybrid, the largest slice based hybrid model as C-Hybrid and multi-slice based hybrid model as M-Hybrid.

We further apply the 3D CNN model [45] to our database with limited sample size. A 3×3×3 cubic kernel was used in each convolution layer. Similar with the model design for 2D CNN, the batch normalization and non-linear filter was used afterwards. Three convolution layers are used before the fully connected layer. Softmax is used at the last layer to make the categorical prediction.

The four CT images based strategies above are illustrated in Fig. 3, where each box contained the data used for the model and the corresponding model name. All the annotations in the figure are the same with that described above. For the hybrid model, the three images from left to right are CT images, HOG images and LBP images respectively. For the 3D CNN, only the CT images (all slices) were used. More details on the implementation will be presented in the next section.

Fig. 3:

Illustration of the raw CT image based CNN model.

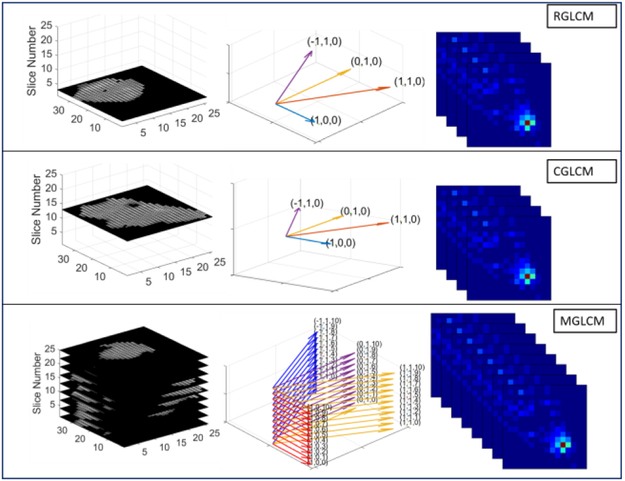
In addition to including the three 2D/2.5D raw CT image-based CNN models above into our comparison experiments, we also included their corresponding 2D image slice-derived GLCM CNN model, called R-GLCM, C-GLCM and M-GLCM, respectively. The R-GLCM refers to the extraction of GCLMs from the four directions [39] from the random selected CT image and these four GLCMs are then used as the four channel inputs for the CNN model. The C-GLCM refers to the extraction of the four GLCMs from the largest-area slice CT image. The M-GLCM refers to the extraction of the GCLMs from the four directions [39] from each of the multiple CT image slices and the summation of all slices-derived GLCMs along one direction, called 2.5D approach. These three 2D image slice-derived GLCM models are called 2D/2.5D-GLCM based CNN and share the same architecture as the 2D image slice based CNN, but different input. This 2D/2.5D-GLCM based CNN model is illustrated in Fig.4. For each model, from left to right, the pictures show the original image, the sampling direction of GLCM and the extracted GLCM respectively.

Fig. 4:

Illustration of the 2D/2.5D-GLCM based CNN model.

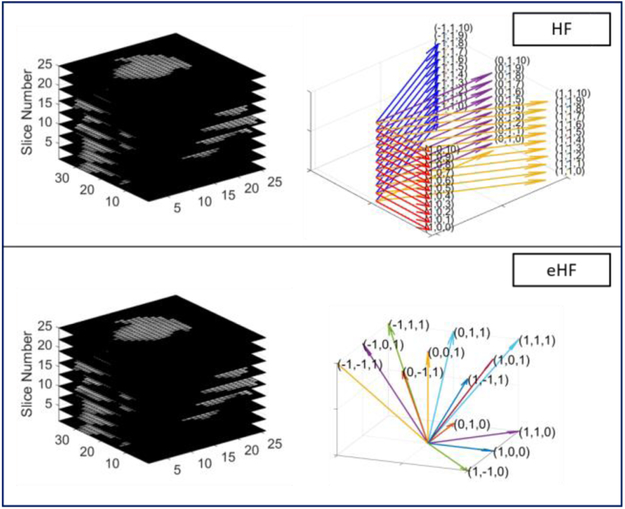
For image texture feature-based RF classification model, we used the Haralick texture features as the input to RF classifier for the comparison study. We used two schemes of input for the RF classifier: The traditional Haralick features (HF) [39] and the extended Haralick features based random forest model (eHF) [38]. The HF model is corresponding with the multiple slices of the 2D image slice-derived GLCM case (M-GLCM), whose features are defined based on the 2D image slice-derived GLCMs (sampling in the four directions as shown in Fig. 4. The eHF model is corresponding with the 3D GLCMs model (3D-GLCM CNN), whose features are defined based on the thirteen directional GLCMs (shown in Fig. 1). The two schemes of features are also presented in Fig. 5.

Fig. 5:

Illustration of the two-feature based Random Forest model.

All the models are summarized in Table II with its classifier name, input type, input description and model name. We also optimized the model parameters during their implementations, for instance the input slice number for the M-IMG, M-Hybrid model to consider the polyp size variation issue. More details will be described in the experiment section. All the model descriptions in the following sections follow the same name convention in Table II.

E. Evaluation Strategy

For the database with limited sample size, we utilized the cross-validation [46] strategy to evaluate the model performance. The leave-one-out and two-fold methods are adopted in this study to provide as the two bounds of the classification performance, where the two methods are two extremes of the k-fold cross validation. In general, a learning model from more data performs better than a model from fewer data. The leave-one-out method tests only on one subject and trains on all the other subjects, which means it trains the model with the most data. The two-fold method trains on half the subjects and tests on the other half, which trains the model with the least data samples. Results from both methods together will provide a fairer evaluation to consider the overfitting that might happen in the leave-one-out method and less training that might happen in the two-fold method. Due to the paper length limit, we will mainly use the two-fold testing results to show the advantage of the proposed model under the toughest condition. The leave-one-out testing results will be summarized in the Appendix I to provide supplementary information. Comparison of these testing results between the two methods will be presented in the discussion section.

III. Experiments and Results

The experiments were designed to explore the potential of CNN learning from multiple slice (or feature) images for polyp classification on a relatively small database with pathological reports as the ground truth. We first extracted the 3D GLCMs from a dataset of 63 volumetric polyps and input these 3D GLCMs into the CNN model of Fig. 1 (Step 3) for polyp classification. Then we compared the performance of this model with the performances of the other twelve models listed in Table II.

A. Datasets

This study focuses on the clinical task of differentiation of high risk polyps from low risk polyps for surgical purposes. All the polyps in this study are massive, or larger than 3cm. If the polyp is malignant, larger neighboring tissue will also be removed during the surgery. If the polyp is less malignant, less neighboring tissue will need to be removed. In this study, the dataset consists of 63 polyp masses found through CTC and confirmed by optical colonoscopy. All the patients were scheduled for surgical removal intervention after the detection and confirmation. When the polyp masses were removed, the follow-up pathology study verified the type of each polyp among five established types, i.e. serrated adenoma, tubular adenoma, tubulovillous adenoma, villous adenoma and adenocarcinoma, where the four adenoma types are labeled as benign (0) and adenocarcinoma is labeled as malignant (1). The pathology report provides us the ground truth for the classification. The dataset is summarized in Table III. It has a relatively even number of the benign (31) and malignant (32) polyps. In total, 51% subjects are male and 49% are female, whose average age is 66.5 years old. While the dataset is relatively small, we note the significance of using a dataset with pathologically proven ground truth. Related CADx studies have shown that setting the classification based on experts’ opinions can have highly variable AUC results depending on what score defines malignancy, and are therefore less reliable than the pathology ground truth. [47, 48]

TABLE III.

POLYP DATASET USED FOR EXPERIMENTS

Category	Pathology	Count	Male: Female
Benign (0)	Serrated Adenoma	3	2:1
	Tubular Adenoma	2	2:0
	Tubulovillous Adenoma	21	11:10
	Villous Adenoma	5	4:1
Malignant (1)	Adenocarcinoma	32	12:20

The scanned CT images for each polyp consist of multiple slices ranging from 17 to 103 depending on the polyp size. On each slice, the contour of polyp was drawn by an experienced radiologist using a semi-automated segmentation algorithm and confirmed by another radiologist. The transverse contour size varies from 10 to 80 mm. For the image-based models, the polyp image was first converted to a square image using zero padding. Then we rescale all the images to the same array size 64×64. For the GLCM-based models, the irregular polyp images can be used directly without any data formatting. The size of the square GLCM is determined by the selection of the gray levels. For presentation purpose, all the GLCMs were extracted by 32 gray levels as an image of the same array size 32 ×32. More studies on the gray levels are reported in [43].

B. 3D-GLCM CNN Optimization

The proposed 3D-GLCM CNN model uses representative feature images or GLCMs to relieve the requirement of a large training datasets for most current CNN classification models. Even though a typical CNN model contains similar network design, like convolution layer, fully connected layer and so on, the network should always be customized for one specific application, for instance, adjusting the learning rate, number of the convolution layers, etc. A deeper network design, i.e. with more convolution layers, is able to extract higher order features that have shown advantages in object detection. However, a deeper network means more weights to train and requires larger training data. Therefore, we started from a shallow network design and added one layer each time to find the optimal network depth for the dataset with limited sample size.

We used the cross-validation result introduced in the method section as criteria for the GLCM-CNN model optimization. We generated 100 runs by the following sampling method. We first randomly select around half samples (16 malignant, 15 benign) as the training data. The remaining 32 samples are testing data. Therefore, the training data and testing data will not have any overlap in one experimental run. Then we put the training and testing data back to generate another group by repeating the procedure above. When all the runs are finished, the AUC and accuracy are obtained and used to evaluate the model performance. The CNN model was trained with Adam optimizer [49] with a batch size of 10. The learning rate was set to be 1e-5, momentum to be 0.9, and weight decay to be 5e-4. The kernel weights were initialized with a Gaussian distribution.

The performance of the model selections with ablation layer numbers is summarized in Table IV. The performance increased first and then decreased when the layer numbers increased one by one. We observed that a 3-layer design, which has 32, 64 and 64 kernels in each layer and max-pooling operations on the first 2 layers gives the best results of accuracy 0.87 and AUC 0.93. This agrees with our expectation that a relatively shallow network performs better than a deep network for a given small dataset. For all the CNN models for comparison, we follow the same exploration step as shown in table IV on network depth, kernel size and number of kernels each layer. Starting from single layer, we found the best setting for it and then searched on the settings for the next layer. It is observed that three-layer is also the optimal network depth for other models. When adding more layer, we also explore on smaller kernel size or fewer kernels of the previous layer as inception field increases. The search is done until more layers or more kernels will decrease the model performance.

TABLE IV.

EXPERIMENT ON THE EFFECT OF DEPTH (NUMBER OF LAYERS). THE FORMAT IS “KERNEL NUMBER (DOWN-SAMPLING FACTOR)”.

Model	Layer Num.	Accuracy	AUC
32(2)	1	0.33	0.13
32(2)-64(2)	2	0.66	0.74
32(2)-64(2)-64(1)	3	0.87	0.93
32(2)-64(2)-64(1)-64(1)	4	0.80	0.88

C. Comparison with Other CNN-based Models

One main idea of this study is the use of the GLCM representative feature images to mitigate the challenge of classifying a small pathologically proven dataset by CNN learning. To validate this idea, we implemented similar schemes in all experiments for both of the CT raw image domain and the GLCM texture image domain, which are introduced in the method section or Table II as: R-IMG, R-Hybrid and R-GLCM, C-IMG, C-Hybrid and C-GLCM, M-IMG, M-Hybrid and M-GLCM, 3D-IMG and 3D-GLCM. Additionally, we designed the experiments to explore the performance of the models from 2D to 2.5D and then to fully 3D. The details of the implementation and comparison results will be presented and discussed in the following.

Implementation of the CT raw image based CNN models:

As shown in Fig. 3, one random single slice, the largest single slice and multiple slices are selected and fed into the corresponding CNN models, all of which have three layers and use max-pooling, batch normalization and ReLu in each layer. At the last fully connected layer, they use the softmax function to predict the categorical results, 0 for benign and 1 for malignant.

For multiple slices, we studied three strategies to manipulate the data. One strategy used the 20 center slices of the polyps (M-IMG (20)), another strategy used all 80-slice volume including the true polyp (M-IMG (80)) (where some small polyps may have zero padding slices), and the third strategy used the true (variable) slices of the polyp (M-IMG (vote)). The 20 center slices contain the most information in the polyps and are used to reduce the noise introduced by those slices covered too little by the polyps. Since the polyps have different slice numbers depending on their sizes, we used the maximum of 80 slice volume including the all polyps with zero-padding for those polyps less than 80 slices. To avoid the noise introduced by zero-padding, we also tried the voting-based CNN inspired by multiple instance learning in [50-52]. Traditionally, the loss of a CNN model is calculated by a summation of loss for each single instance (slice) by comparing the model score with its real label. In the voting CNN model, we calculated the loss as the difference between average model score and the ground truth label, which can be expressed as:

$$L_{vote}=BCE\left(\frac{1}{N}\sum \begin{array}{c}N\hfill \\ i=1\hfill \end{array}CNN(x_i),y\right),$$ (2)

where BCE(·, ·) is the binary cross-entropy loss, N is the total number of slices of a polyp and x_i is slice i of the given polyp. The voting CNN model could utilize multiple slice information without introducing zero-padding due to slice variance. In addition, it can also leverage the situation that some of the slice contains little information to make decision since it is an average prediction of each slice.

The hybrid model was similarly implemented with the single slice model. The only difference is the input images are 3 channels of the CT image, HOG image and LBP image. We also used the 20 center slices and 80-slices volume for the hybrid model of the multiple slices (M-Hybrid (20), M-Hybrid (80), respectively). Both of the multiple slice manipulations were also implemented in the 3D-IMG model, which are denoted as 3D-IMG (20) and 3D-IMG (80) accordingly.

As a comparison to the models pretrained with natural image and tuned on CT image, we adapted pretrained Resnet-18 [18], which is one of the current state-of-the-art in computer vision. We replace its last layer to contain only 2 neurons denoting two classes, malignant and benign. Then it is finetuned on our CT image for 15 iterations and batch size 20. We use SGD as optimization method with learning rate set to 0.001 and momentum 0.9. Since ResNet-18 is originally trained for natural color image (3 channels) and requires the input size to be 224×224, we first convert our CT image into 3 channels and then resize it to 224×224. To convert a CT image, we used HU values of [−450, 200], [−160, 400] and [−1000, −300] for each channel considering different information. For example, [−450 200] contains most polyp including partial volume. Three ranges include certain overlap to make the model more robust.

Implementation of the GLCM based CNN model:

As shown in Fig. 4, the GLCM feature images extracted from one random single slice, the largest single slice, and the multiple slices are selected and fed into the corresponding CNN models with similar network structure to the CT based CNN. One main difference is that the input size for each channel is 64×64 for the CT based models, but 32×32 for the GLCM based models. Another difference is there are only one channel for one slice of CT image but four channels for one slice of four GLCM feature images because there are four sampling directions in the 2D case (as shown in Fig. 3).

Results:

For all the two-fold cross-validation tests, we randomly generated 100 runs by using the fore-mentioned sampling method. At each run, we split the dataset into two parts, 31 training data and 32 testing data. Then we swap the training and testing data. When all the runs are finished, the mean and standard deviation of the AUC scores are obtained and used to evaluate the model performance and its stability. We also applied t-test statistical analysis to calculate the p-value of AUC scores between the proposed 3D-GLCM CNN model and the other models. Our null hypothesis is the AUC score of other methods and of the proposed methods do not perform differently. In other words, the score difference is due to the random effect. This p-value is used to show the performance difference among different methods.

The experiment results of all the CNN based schemes are presented in Table V. All the model annotations in the table are the same as what we introduced above. It can be seen that the proposed 3D-GLCM CNN prominently improved the AUC from [0.55~0.80] of the raw CT image based models and [0.68~0.85] of the 2D/2.5D-GLCM based model to the highest AUC of 0.91 with all p-values smaller than 0.0001, indicating statistically significant gain. The 3D-GLCM CNN improved the AUC by 18% over the best among all the CT raw image based models. The relative results of ACC for all models are the same with AUC. The 3D-GLCM CNN also achieves the best ACC of 0.87. It shows the effectiveness of the GLCM feature images for the 3D CNN diagnosis in the limited datasets.

TABLE V.

COMPARSION BETWEEN THE PROPOSED 3D-GLCM MODEL WITH OTHER CNN BASED STRATAGIES. THE EVALUATION RESULTS ARE TWO-FOLD CROSS-VALIDATION METHOD.

Methods	Model	AUC	ACC	SEN	SPE	p-value
CT images based CNN	R-IMG	0.60±0.11	0.60	0.66	0.54	<0.0001
	C-IMG	0.67±0.07	0.64	0.69	0.59	<0.0001
	ResNet-18	0.63±0.06	0.57	0.68	0.46	<0.0001
	R-Hybrid	0.67±0.08	0.64	0.56	0.73	<0.0001
	C-Hybrid	0.70±0.07	0.66	0.73	0.59	<0.0001
	M-IMG (20)	0.81±0.06	0.74	0.87	0.60	<0.0001
	M-Hybrid (20)	0.83±0.06	0.76	0.76	0.76	<0.0001
	M-IMG (80)	0.68±0.10	0.63	0.76	0.50	<0.0001
	M-Hybrid (80)	0.73±0.06	0.68	0.79	0.55	<0.0001
	M-IMG (vote)	0.73±0.07	0.68	0.83	0.52	<0.0001
	3D-IMG (20)	0.84±0.05	0.77	0.82	0.72	<0.0001
	3D-IMG (80)	0.80±0.06	0.77	0.69	0.87	<0.0001
GLCM based CNN	R-GLCM	0.68±0.08	0.69	0.63	0.75	<0.0001
	C-GLCM	0.79±0.07	0.72	0.76	0.68	<0.0001
	M-GLCM	0.85±0.06	0.77	0.78	0.77	<0.0001
	3D-GLCM	0.91±0.05	0.87	0.90	0.71	1.0000

ACC, SEN and SPE are short for accuracy, sensitivity and specificity.

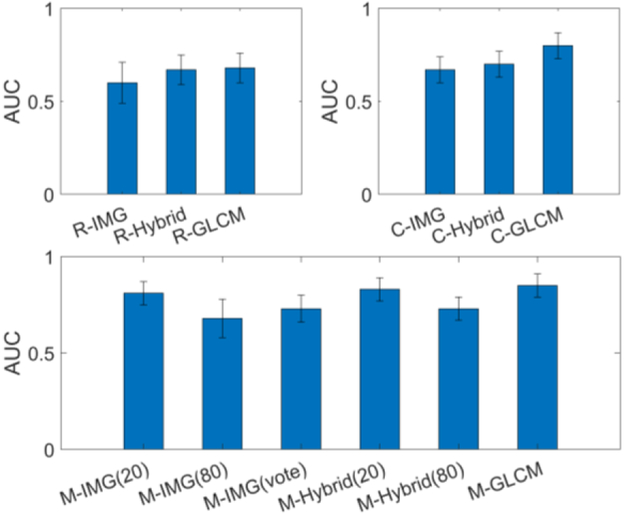
To compare the effectiveness of GLCM image- with the CT image-based models, we plotted the results of AUC scores along with the raw CT image model, the hybrid model and the GLCM-based model in three groups, i.e. the random slice group, the largest slice group and the multiple slices group in Fig. 6. The results are consistent across the three groups. In each group, the GLCM based model outperformed both the raw CT image based model and the hybrid model. An improved AUC of 0.08, 0.13 and 0.04 is observed with respective to each group. This shows that the GLCM feature image could provide more effective information than the CT image for the CNN learning. This agrees with our expectation that for the limited datasets with pathological ground truth, GLCM based learning is more efficient than CT image based learning since the GLCM is extracted from the raw image as a texture descriptor to reflect the lesion heterogeneity, which is known as a footprint of lesion evolution and ecology and an indicator of lesion progress and response to intervention [53].

Fig. 6:

Comparison between the raw CT image based models and the GLCM based models.

Comparing the Hybrid model and the CT image based model, we observe that the HOG and LBP features can improve the AUC by around 0.02~0.03, which also agree with the results in [29]. Comparing the results of multiple slice models, we found the 20 slice model performed better than the 80 slice model. It indicates that the extra slices may bring more noise than useful information. One possible reason could be the small polyps are padded with 0 due to size difference among slices, which makes the input data very sparse and information was washed out during the convolution. If the noise effect dominates, the performance will be dropped. The similar phenomena can also be observed in the 3D-IMG model, where the 3D-IMG (20) has a higher AUC of 0.04 than the 3D-IMG (80). This can also be explained why the vote-based method performed better than the 80 slices model. Therefore, a greed study of adding the slice one by one until achieving the best performance may be a better way to extract most useful information and decrease the noise effect. This is an interesting research topic but is beyond the scope of this study.

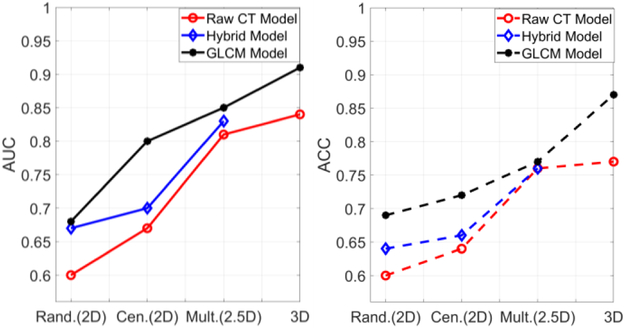
To explore the effect of the dimension of input data, we plotted the results of AUC and ACC in Fig.7, where the CT image model result is in red, the hybrid model result is in blue and the GLCM model result is in black. For both AUC and ACC scores, the three curves have the same trend when the input data varies from low dimension to high dimension. The performance (by AUC scores) increases monotonically with the data dimension from 2D to 2.5D and 3D. This agrees with our convention that 3D data considers the spatial information in all directions and should perform better than the 2D or 2.5D model. The C-IMG model performed better than R-IMG model, indicating that the more pixels the more information. For the CT image based model, we can see the 3D-IMG performs better than the single slice model, which indicates that the large number of weights can still be trained well to learn useful 3D information under a limited dataset. However, the 3D-IMG cannot go deeper or cannot have more convolutional layers due to the limitation of the datasets. It may not be able to learn enough effective features for the classification task, while the presented 3D-GLCM CNN can perform significantly better than the 3D image CNN model.

Fig. 7:

Comparison results of AUC (left) and ACC (right) among models with various input dimensions. Rand., Cen. and Mult. stand for random, center and multiple slices.

D. Comparison with RF Classification on Image Features

We further compared our proposed 3D-GLCM CNN model with the well-known RF classification on image features. We compared with the traditional Haralick features (HF) based RF model and the extended Haralick features based RF model (eHF). The two sampling ways of extracting the Haralick features have been illustrated in Fig. 5, of which the input data dimension is 2.5D with respect to HF model and 3D with respect to eHF model. We also performed the RF classification using features of polyp size, elongation, intensity in Hounsfield units (mean, max, median, histogram with 128 bins).

For RF methods, we also perform optimized structure. 5000 trees are created in our random forest classifier. At initial point, we varied the tree numbers from ~1000 to ~1000,000. It is found the results are very stable. To reduce calculation time, 5000 trees are used. The node size is empirically set as 5 considering we only have 63 samples. Once node size is set, the tree depth is determined.

The results are shown in Table VI. The proposed GLCM-CNN model outperformed the feature-based RF classification model (where the highest AUC is 0.86 among all RF results) in the task of polyp diagnosis. It indicates that the GLCM based CNN model can automatically learn more effective and efficient features from the GLCM images comparing to the hand crafted Haralick features. Since the 3D-GLCM CNN model starts from the GLCM images instead of the CT images, it can relieve the difficulty in classifying relatively small but pathologically proven datasets. We can also see the benefit from 2.5D to 3D, which agrees with the previous observations.

TABLE VI.

COMPARISION WITH THE STATE-OF-ARTS METHODS.

Model	Data Dim.	AUC	ACC	SEN	SPE	p-value
HF	2.5D	0.85 (±0.06)	0.81	0.8.3	0.79	<0.0001
eHF	3D	0.86 (±0.05)	0.80	0.87	0.73	<0.0001
Geometry + Intensity	-	0.83 (±0.073)	0.80	0.80	0.80	<0.0001
3D-GLCMCNN	3D	0.91 (±0.05)	0.87	0.90	0.71	1.0000

ACC, SEN and SPE are short for accuracy, sensitivity and specificity.

IV. Discussion and Conclusion

In this study, we proposed a three-dimensional GLCM based CNN model, called 3D-GLCM CNN, to perform the task of 3D polyp classification by a relatively small but pathologically proven dataset. Constrained by the limited dataset, it is hard for a CNN based model to learn effective features directly from the small number of CT raw images to differentiate benign polyps from malignant. The proposed model takes advantage of the GLCM feature images as the representation of the tissue texture information (prior knowledge [53]) of the polyp heterogeneity. The heterogeneity is a footprint of lesion evolution and ecology, and an indicator of lesion progress and response to intervention, which is reflected by the image contrast distribution across the FOV (field-of-view). An image texture is a pattern consisting of image pixels with the same image contrast relative to a uniform background. As a result, in this work, we take the co-occurrence matrix (CM) as an effective example of texture descriptor.

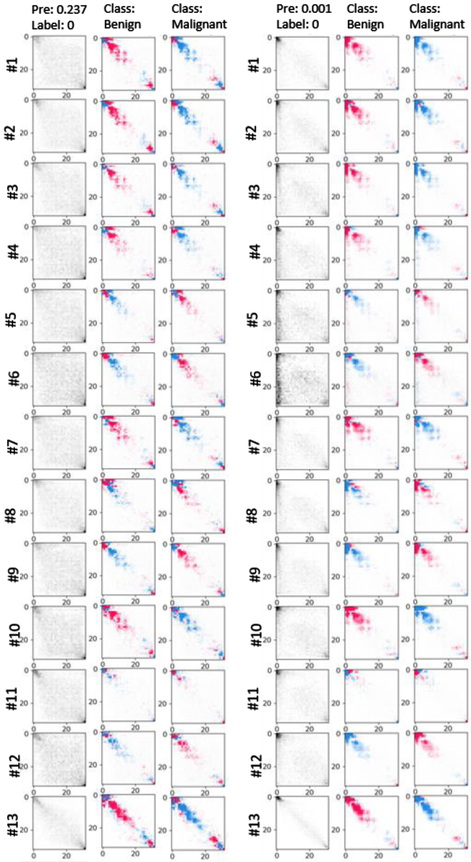
Benefiting from the prior knowledge, the 3D-GLCM CNN can learn effective abstract features for classification with a relatively shallow CNN architecture, which relieves the requirement of a large-scale training data for the heavy, deep CNN learning. The proposed model outperforms the CT raw image based 3D-IMG model and the feature based RF classification models. Experimental results showed the benefit of using the GLCM feature images comparing to the use of the CT raw images across all the CNN based models. To explore the critical GLCM features for classification, we visualize the learnt feature by the CNN model using Shapley additive explanations (SHAP) [54] approach. A typical set of polyps (2 malignant, 2 benign) are shown in the APPENDIX II. The first column is the original GLCMs in thirteen directions. The rest two columns show the interpretation of model prediction on the two classes. Given a class, the red cells showed the entries push the model’s decision to that class while blue pixels pull the prediction results away. The GLCM is only one effective example of feature images extracted based on our understanding on tissue texture of polyps. It demonstrated that our prior knowledge can be used to make better use of the CNN technique with limited dataset in the medical imaging field.

In this study, we have demonstrated the feasibility of the connection between the image textures and the pathologically proven ground truth through the first proposed CNN model to incorporate the GLCM images. The proposed GLCM feature based model naturally overcame the problem of the various lesion sizes existing in all the CNN based models, which may shift the current CNN-raw image paradigm to a CNN-texture image (GLCM) paradigm. In this study, we empirically chose the 32 gray levels according to [38], where gray level 32 gives the best performance. The optimal gray level depends on a variety of factors like the lesion types, for instance colon polyps or lung nodules. Data source is also an important factor. For example, optimal gray level of intensity, gradient or curvature may vary and should be optimized respectively. It would be important to study the most appropriate gray levels across different datasets with different image information, which is one of our further research interests. In the comparison study on the CT image models, we tried two different strategies to reformat the CT image data. One way is to make the multiple slices of one polyp as being a square format with zero padding and then resize each slice to the desired input size for CNN learning. The other way is the use of a minimum square to crop the area of polyp or ROI on each individual slice. The latter strategy enriches the information of each slice most but may lose the spatial information among the multiple slices. The former strategy may improve the 2D model and the latter may be more suitable for the 3D model. Even though we tried those optimizations to boost the performance of the CT image-based models, it seems the best AUC cannot exceed 0.85, which is significantly below the proposed GLCM-CNN model.

In this study, we utilized the leave-one-out and two-fold cross validation methods to evaluate the model performances, which are two extremes of the k-fold cross validation. Overall, the experimental results of both methods agree well with each other. Our conclusion discussed above is quite consistent across both methods. Generally, the leave-one-out performs better due to larger training samples. Comparing the paired results of both methods, the leave-one-out achieves 0.01~0.09 higher AUC than the two-fold in most experiments (Tables V and VI). However, when the model is complex for the given data, i.e. the training data is not enough for the designed model, the leave-one-out may perform worse. LOOCV is usually better than two-folds but some assumptions must be met. One main assumption is that the data should be representative. In other words, we must have enough data in the whole space where we are learning. This may not be met in the medical field, and this point is also one of our motivations to propose the GLCM texture images instead of the raw images for the polyp classification. Given limited datasets, the LOOCV may or may not give better performance, because if the model is complex, increasing samples with LOOCV can produce increased errors since the model learned a lot of various things instead of useful information due to not enough learning data. The phenomenon that two-folds performed better than LOOCV can also happen if the data is biased. We also observed this in our lung nodule datasets [55]. In our experiments, the AUC of 3D-IMG (20/80) model is 0.84/0.80 by two-fold over 0.70/0.74 by leave-one-out. This observation indicates the 3D-IMG requires more CT image data for training. However, for the GLCM based 3D classification model, the leave-one-out performs better than the two-fold, which shows the lesser data requirement for the proposed 3D-GLCM method.

The deliberately designed ablation study showed that the 3D based classification outperforms the 2.5D and 2D based ones across various type inputs, indicating that extraction of meaningful and useful 3D features is critical. The proposed 3D-GLCM CNN model considers the second neighboring voxels in the 3D space, resulting in thirteen sampling directions. When the number of sampling directions increases, the performance of the proposed GLCM CNN might be further improved. This is another interest research topic of our future development of the 3D-GLCM CNN model. Additionally, this work only uses the intensity GLCM feature images, integrating other modality data, like gradient and curvature is another way to improve the performance. Moreover, the success of GLCM-CNN cast light on incorporating more feature descriptors, such as other texture descriptors (e.g. Gabor), geometry, etc., to further improve CNN performance. Last but not least, it is very interesting to design how to make pretrained CNN models adapted using GLCM as inputs, especially given GLCM with more than three channels.

There is another remaining issue to be addressed in our future research efforts. We only used one label to differentiate the malignant polyps from the benign polyps instead of classifying the five pathologies listed in Table III. This task of non-binary classification of small but pathologically proven datasets is much more difficult than this presented binary classification. Conducting the multi-category classification of the pathology proven datasets will be another one of our future research topics. Extending the GLCM-CNN from diagnosis to other applications like detection is also under the way in our lab.

Appendix

Appendix I: Leave-one-out Cross Validation

Table VII.

SUMMARY OF LEAVE-ONE-OUT CROSS-VALIDATION RESULTS.

Methods	Model	AUC	ACC	SEN	SPE
CT images based CNN	R-IMG	0.61	0.58	0.88	0.28
	C-IMG	0.68	0.68	0.71	0.65
	R-Hybrid	0.71	0.73	0.62	0.84
	C-Hybrid	0.74	0.73	0.78	0.68
	M-IMG (20)	0.83	0.80	0.69	0.84
	M-Hybrid (20)	0.84	0.83	0.93	0.73
	M-IMG (80)	0.78	0.77	0.68	0.87
	M-Hybrid (80)	0.78	0.79	0.65	0.93
	M-IMG (vote)	0.82	0.77	0.94	0.60
	3D-IMG (20)	0.70	0.73	0.61	0.84
	3D-IMG (80)	0.79	0.72	0.78	0.65
GLCM based CNN	R-GLCM	0.74	0.73	0.69	0.77
	C-GLCM	0.80	0.79	0.78	0.81
	M-GLCM	0.89	0.82	0.72	0.94
	3D-GLCM	0.93	0.90	0.90	0.90

ACC, SEN and SPE are short for accuracy, sensitivity and specificity.

Appendix II: SHAP of Learnt Features for a Set of Typical Polyps

Fig. 8:

SHAP of learnt features for a set of typical polyps including two malignant (top) and two benign ones. The first column is the original GLCMs in thirteen directions. # refers to channel and directions. The rest two columns show the interpretation of model prediction on the two classes. Given a class, the red cells showed the entries push the model’s decision to that class while blue pixels pull the prediction results away.