Highlights
-
•
Since January 23 2020, stringent measures for controlling novel coronavirus epidemics have been enforced and strengthened in mainland China.
-
•
Most infected cases have been quarantined or put in suspected class, which had been ignored in existing models.
-
•
Results of our model show that the trend of the epidemics mainly depends on quarantined and suspected cases.
-
•
It is important to continue enhancing the quarantine and isolation strategy and improving the detection rate in mainland China.
Keywords: Coronavirus, Multisource data, Mathematical model, SEIR model
Abstract
Objectives
Since January 23, 2020, stringent measures for controlling the novel coronavirus epidemic have been gradually enforced and strengthened in mainland China. The detection and diagnosis have been improved, as well. However, the daily reported cases remaining at a high level make the epidemic trend prediction difficult.
Methods
Since the traditional SEIR model does not evaluate the effectiveness of control strategies, a novel model in line with the current epidemic's process and control measures was proposed, utilizing multisource datasets including the cumulative number of reported, deceased, quarantined and suspected cases.
Results
Results show that the trend of the epidemic mainly depends on quarantined and suspected cases. The predicted cumulative numbers of quarantined and suspected cases nearly reached static states, and their inflection points have already been achieved, with the epidemic's peak coming soon. The estimated effective reproduction numbers using model-free and model-based methods are decreasing, as well as new infections, while newly reported cases are increasing. Most infected cases have been quarantined or put in the suspected class, which has been ignored in existing models.
Conclusions
The uncertainty analyses reveal that the epidemic is still uncertain, and it is important to continue enhancing the quarantine and isolation strategy and improving the detection rate in mainland China.
Introduction
Early identifying signature features of an outbreak can provide policy- and decision-makers with timely information to implement effective interventions (Viboud et al., 2016, Chowell et al., 2016). Recently, a novel coronavirus (COVID-19) outbreak has occurred in Wuhan, Hubei, China, and has spread out to neighboring countries (Cohen and Normile, 2020, Lu et al., 2020, Parry, 2020).
During the early stages, the prediction of the COVID-19 epidemic employing transmission dynamics models relies on the cumulative number of reported cases or the number of newly reported ones. The dynamic impact of the increasingly strong measures of the Chinese government has not been fully captured. Unprecedented interventions, including strict contact tracing, quarantine of entire towns/cities, and travel restrictions, have added and will add further uncertainty to the analysis of the epidemic.
When enforcing such measures to a sample of 100 people, at least nine of these may be found infected. Nearly 50% of infected people are confirmed from suspected cases (HB CHINA, 2020). It is unfeasible to predict the impact of the COVID-19 epidemic without taking into account the effects of the recently implemented control measures. Estimates based on transmission dynamics models not including quarantined/suspected cases, as well as the cumulative reported cases from these compartments, cannot be used for informing public health policies (Tang et al., 2020a).
Since January 23, 2020, after the implementation of the lock-down strategy in Wuhan, all other Chinese provinces have adopted similar measures. Nevertheless, the number of recently reported cases has increased faster than before, because of the incubation period of the virus, or the introduction of new screening/testing measures. Moreover, the diagnosis and treatment procedures have been simplified, and the detection effort has been strengthened (NHCPRC, 2020a).
As such, the classic SEIR model cannot be used to depict and fit the data. The evolutionary trend of the epidemic depends on the strength of interventions, especially on the scale of quarantined and suspected populations (Tang et al., 2020a). It is necessary to devise a dynamic model with suspected compartments incorporating prevention and control strategies to predict the trend of the COVID-19 epidemic based on multiple data sources and assess the efficacy of control strategies. We also include the model-free method to estimate the actual number and to verify the declining trend of new infections.
Methods
Data
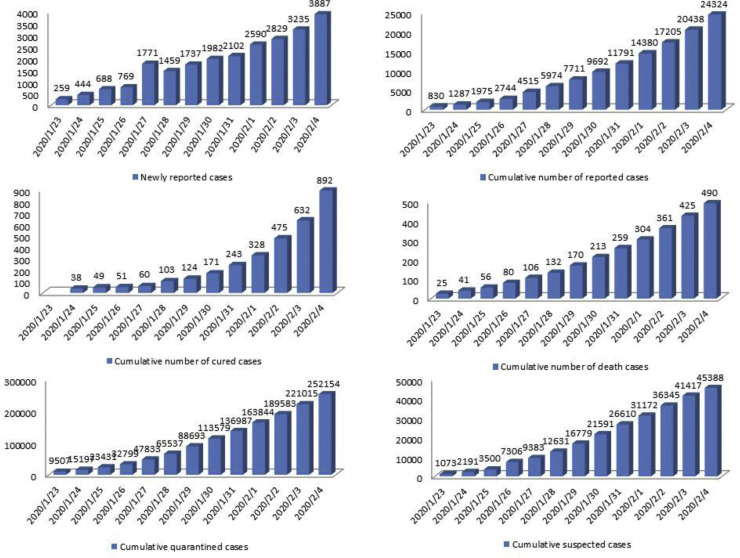
We obtained data of laboratory-confirmed COVID-19 cases in China from the “National Health Commission” of the People's Republic of China and the Hubei's “Health Commission” (Tang et al., 2020b, HCHP, 2020, NHCPRC, 2020b). Data information includes the newly reported cases, the cumulative number of reported confirmed cases, the cumulative number of cured cases, the number of death cases, and the cumulative numbers of quarantined/suspected cases (Figure 1 ). The number of quarantined cases does not include the number of suspected cases, although the suspected cases have been isolated. Except for Hubei, the mean duration of hospital stays was around nine days, with the shortest hospitalization duration of five days (in Hainan) and the longest hospitalization duration of 12.75 days (in Guangdong). The length of hospital stays in Hubei was around 20 days, because, on the one hand, more severe patients were found in Hubei, and on the other hand, Wuhan has set stricter discharge standards. In addition to the usual standards of two nucleic acid tests being negative within 24 h, Wuhan requires 10–12 days more of observation in the hospital (HCHP, 2020, NHCPRC, 2020b, Guanchazhe News, 2020, NHCPRC, 2020c). Since the number of daily cases in hospital is not suitable to identify the model/estimate the parameters, we use cumulative data.
Figure 1.
The datasets related to the COVID-19 epidemic, including newly reported cases, cumulative number of reported cases, cumulative number of cured cases, cumulative number of death cases, cumulative quarantined cases, and cumulative suspected cases.
Data used in the present study is reported in Appendix 1.
The model
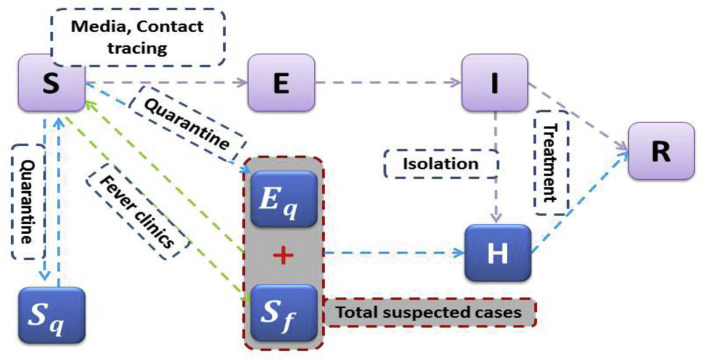
A deterministic SEIR model based on the clinical progression of the disease, epidemiological status of the individuals, and intervention measures was proposed (Figure 2 ). We stratify the populations as susceptible (S), exposed (E), infected (I), hospitalized (H), and recovered (R) compartments, and we further stratify the population to quarantined susceptible (S q) and quarantined suspected individuals (B). We extend our model structure including the quarantined suspected compartment, which consists of exposed infectious individuals resulting from contact tracing and individuals with common fever needing clinical medication.
Figure 2.
Diagram of the model adopted in the study for simulating the COVID-19 infection. Interventions, including intensive contact tracing, followed by quarantine and isolation, are indicated. The gray compartment means a suspected case compartment consisting of contact tracing Eq and fever clinics.
By enforcing contact tracing, a proportion, q, of individuals exposed to the virus is quarantined, and can either move to the compartment B or S q, depending on whether they are actually infected or not (Castillo-Chavez et al., 2003; Keeling and Rohnai, 2008). In contrast, the other proportion, 1 − q, consists of individuals exposed to the virus who are missed from contact tracing and move to the exposed compartment E once actually infected or stay in compartment S otherwise.
Let the transmission probability be β, and the contact rate be c. Then, the quarantined individuals, if infected (or uninfected), move to the compartment B (or S q) at a rate of βcq (or (1 – β)(cq)). Those who are not quarantined, if infected, will move to the compartment E at a rate of βc(1 – q). Let constant m be the transition rate from susceptible class to the suspected compartment via general clinical medication due to fever or illness-like symptoms.
Data includes suspected individuals while most of the confirmed cases come from this compartment. The suspected individuals leave this compartment at a rate of b, with a proportion, f, if they have been confirmed to be infected by COVID-19, going to the hospitalized compartment; the other proportion, 1 − f, has been proven to be not infected by COVID-19 and goes back to the susceptible class once recovery (Table 1 ).
Table 1.
Parameter estimates for the COVID-19 epidemic in Wuhan, China.
| Parameter | Definitions | Estimated values |
Source | |
|---|---|---|---|---|
| Hubei (Std) | China (Std) | |||
| c0 | Contact rate at the initial time | 14.781 | 14.781 | Tang et al. (2020b) |
| cb | Minimum contact rate under the current control strategies | 5.00 (0.0039) | 8.00 (0.066) | Estimated |
| r1 | Exponential decreasing rate of contact rate | 0.20 (0.0067) | 0.15 (0.0352) | Estimated |
| β | Probability of transmission per contact | 0.2068 (0.0048) | 0.1911 (0.0175) | Estimated |
| q0 | Quarantined rate of exposed individuals at the initial time | 0.0051 (0.0052) | 1.00 × 10−4 (0.0037) | Estimated |
| qm | Maximum quarantined rate of exposed individuals under the current control strategies | 0.6297 (0.0134) | 0.98 (0.0087) | Estimated |
| r2 | Exponential increasing rate of quarantined rate of exposed individuals | 0.10 (0.00062) | 0.1531 (0.004) | Estimated |
| m | Transition rate of susceptible individuals to the suspected class | 1.00 × 10−6(1.21 × 10−8) | 1.0002 × 10−7(1.58 × 10−8) | Estimated |
| b | Detection rate of the suspected class | 0.09 (0.0000066) | 0.07 (0.0078) | Estimated |
| f | Confirmation ratio: Transition rate of exposed individuals in the suspected class to the quarantined infected class | 0.80 (0.0032) | 0.50 (0.0541) | Estimated |
| σ | Transition rate of exposed individuals to the infected class | 1/7 | 1/7 | Tang et al. (2020b) |
| λ | Rate at which the quarantined uninfected contacts were released into the wider community | 1/14 | 1/14 | Tang et al. (2020b) |
| δI0 | Initial transition rate of symptomatic infected individuals to the quarantined infected class | 0.1326 | 0.1326 | Tang et al. (2020b) |
| δIf | Fastest diagnosis rate | 2.5 (0.0009) | 2.5 (0.006) | Estimated |
| r3 | Exponential decreasing rate of diagnosis rate | 0.20 (0.000139) | 0.20 (0.093) | Estimated |
| γI | Recovery rate of infected individuals | 0.33 | 0.33 | Tang et al. (2020b) |
| γH | Recovery rate of quarantined infected individuals | 0.20 (0.0045) | 0.15 (0.0132) | Estimated |
| α | Disease-induced death rate | 0.013 (0.00036) | 0.008 (0.00017) | Estimated |
| Initial values | Definitions | Estimated values |
Source | |
|---|---|---|---|---|
| Hubei (Std) | China (Std) | |||
| S(0) | Initial susceptible population | 9.00 × 106 (3.52 × 107) | 2.00 × 107 (1.23 × 107) | Estimated |
| E(0) | Initial exposed population | 4.00 × 103 (390) | 9.00 × 103 (2.11 × 103) | Estimated |
| I(0) | Initial infected population | 935 (60) | 1.2405 × 103 (642) | Estimated |
| B(0) | Initial suspected population | 800 (13) | 1072 | Data |
| Sq(0) | Initial quarantined susceptible population | 2132 | 7347 | Data |
| H(0) | Initial quarantined infected population | 494 | 771 | Data |
| R(0) | Initial recovered population | 34 | 34 | Data |
The contact rate c(t) is a decreasing function with respect to time t:
where c 0 denotes the contact rate on January 23, 2020 with c(0) = c 0, c b denotes the minimum contact rate under the current control strategies with , where c b < c 0, r 1 denotes the contact rate modeled as an exponential decreasing rate, assuming that the contacts are decreasing gradually due to the implementation of interventions.
q(t) is an increasing function with respect to time t:
where q 0 is the initial quarantined rate of exposed individuals with q(0) = q 0, q m is the maximum quarantined rate under the current control strategies with and q m > q 0, and r 2 is the quarantined rate modeled as an exponential increasing rate. This function reflects the gradually enhanced contact tracing.
The transition rate δ I(t) is an increasing function with respect to time t, correspondingly, the period of diagnosis 1/δ I(t) is a decreasing function of t:
where δ I0 is the initial diagnosis rate, δ If is the fastest diagnosis rate, and r 3 is the exponential decreasing rate of the detection period. Here, and with δ If > δ I0. Then, we define the effective reproduction number as
Model-free estimation for R0 and Rt
Taking one day as a time unit and assuming December 31, 2019 to be the time start point, i.e., t = 0 let and be the number of confirmed cases at time t in Wuhan and in China, respectively. Let and be the number of patients eventually confirmed and with illness onset at time t in Wuhan and in China. T represents the duration from onset to confirmation for a patient who is eventually confirmed with P T as a probability distribution.
For k different days , is assumed to follow the Poisson distribution with mean λ j, which is the parameters to be estimated, given the number of confirmed cases on days and the probability that a patient with illness onset on day j will be confirmed on day i. For each j, is positive, with at least a fraction of patients with illness onset on day j and confirmed during the period . Parameters can be estimated by and p ij through the deconvolution method (the Richardson–Lucy iterative algorithm): (Richardson, 1972, Lucy, 1974, Goldstein et al., 2009)
| (1) |
| (2) |
where and are fitted values of and λ j in the nth iteration, respectively. We stop the iteration when the error of fitting
| (3) |
becomes small, and the values of are reasonable.
Because the method above requires at least a fraction of patients with illness onset on day j and confirmed during the period , we can determine the proper t 1 and t 2 such that for in terms of the distribution T.
for is estimated as follows: let T 0 and T c be the dates of a patient with illness onset and confirmed. Let and be the number of patients who are confirmed on or before time S and with illness onset at time t in Wuhan and in China and let be the probability that a patient was confirmed at time s and h days after illness onset, which is the probability that a patient was confirmed at time s and with illness onset being the interval . Let be the probability that a patient was confirmed h days after the illness onset on time s. Then
| (4) |
| (5) |
We use Eqs. (4) and (5) to estimate for . To estimate the daily number of cases with illness onset in the period December 8, 2019–February 2, 2020 in China, , (Figure 1(B)), we performed two steps: 1) we used the daily number of confirmed cases from January 17, 2020 to February 3, 2020 in China and the distribution P T to estimate the daily number of patients with illness onset from January 4–February 2, 2020 ; 2) we used the daily number of confirmed cases before or on January 22, 2020 in China and in Wuhan ( and ), the daily number of cases with illness onset before January 22 and confirmed before January 22 in Wuhan and the distribution and to estimate the daily number of cases with illness onset from December 8, 2019 to January 3, 2020. We use the method based on the following renewal equation to estimate R 0 and R t (Nishiura and Chowell, 2009, Nishiura, 2010). Let j t be the number of new cases on day t, and let be the discretized distribution of the serial interval with G(τ) being the cumulative distribution function:
| (6) |
The number of new cases follows the Poisson distribution. The distribution of the serial interval is modeled as a gamma distribution with a mean of 7.5 days and a standard deviation of 3.4 days (Li et al., 2020).
For R t we have
| (7) |
We estimate R 0 and R t based on the illness onset data per day (which is used to replace j t).
Results
Model-free estimation of the basic/actual reproduction numbers
To estimate the onset-to-confirmation distribution P T, we have collected detailed information of some patients confirmed before January 30, 2020, from the Health Commissions of different cities, including dates of illness onset and dates of confirmation. We use the data of these patients with illness onset before January 20 (10 days prior to the latest onset date of the patients in the data) to avoid underestimating T.
By fitting a Weibull distribution on the illness onset data before January 30th, we estimate P T to be Weibull distributed (mean 7.67, standard deviation 2.88). By fitting a Weibull distribution on the data of cases confirmed on day s, we estimate to be Weibull distributed with mean 5.29 and standard deviation 3.48 for s = 20,21,22. From the literature (Li et al., 2020) was assumed to follow a Weibull distribution with mean 12.5 and standard deviation 7.5 for and a Weibull distribution with mean 9.1 and standard deviation 4.18 for .
We chose (January 17–February 3) to estimate . According to P T, we calculate that for and for other j. Then we can determine (January 4–February 2) and estimate . We got from the literature (Li et al., 2020), we chose s = 22 in formula (4). We obtain for (Figure 3 ), and hence we only need to estimate the distribution for . Therefore, then can be estimated by formula (4) and formula (5).
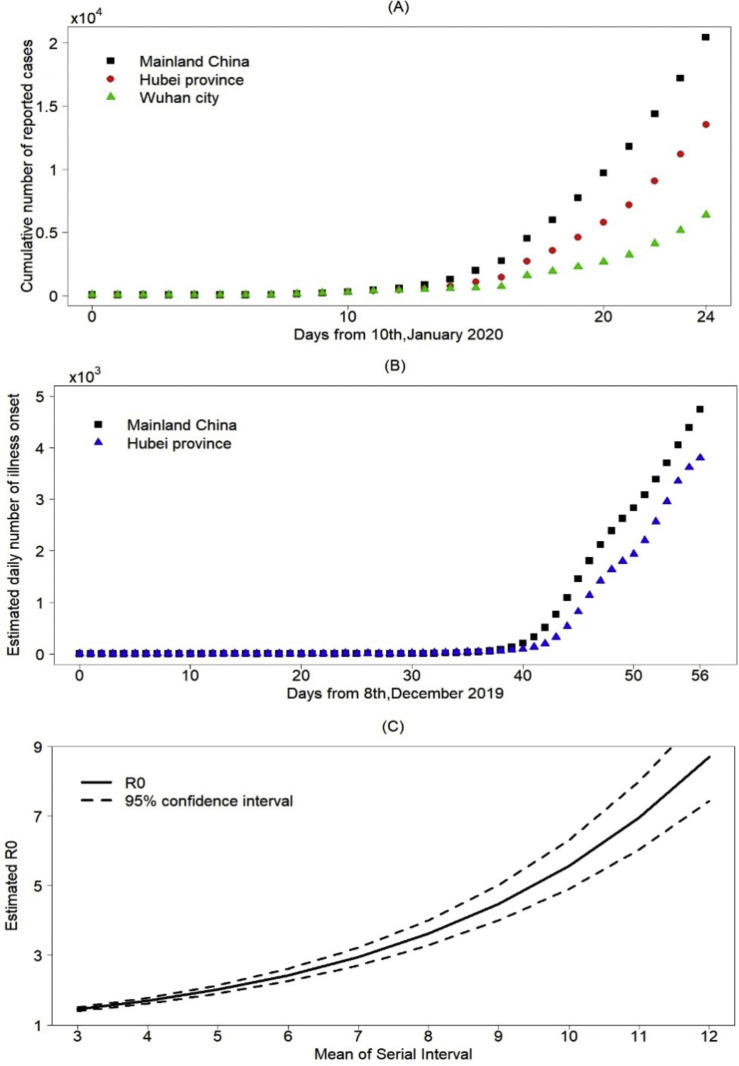
Figure 3.
(A) Cumulative number of confirmed reported cases for mainland China, Hubei province and Wuhan city, (B) Estimated number of illness onset cases for mainland China, Hubei province and Wuhan city, (C) Estimated basic reproduction number R0.
We estimate the daily number of cases with illness onset on the day from December 8, 2019 to February 2, 2020 in China, , (Figure 3(B)). The number of daily illness onset cases grew exponentially before January 20, 2020, and continued to grow but with a lower rate after January 20, 2020. Then it increased with a constant rate since the growth looks like a straight line (Figure 3(B)). We used the data on cases with illness onset before January 4, , to estimate the basic reproduction number R 0 (Li et al., 2020), which was 3.27 (95% confidence interval [2.98, 3.58]). To investigate the variation of the basic reproduction number and its relationship with the serial interval, sensitivity analysis is carried out by changing the mean of the serial interval from three to 12 days. We examine the variation in R 0 with the serial interval (Figure 3(C)). The basic reproduction number R 0 increases in parallel with the serial interval. According to recent papers (Hiroshi Nishiura, 2020, Zhanwei et al., 2020), the serial interval may be shorter than that estimated in the previous references. The mean of the median serial interval was estimated to range from three to six days; the corresponding value of the estimated R 0 is between 1.45 and 2.43 (Figure 3(C)).
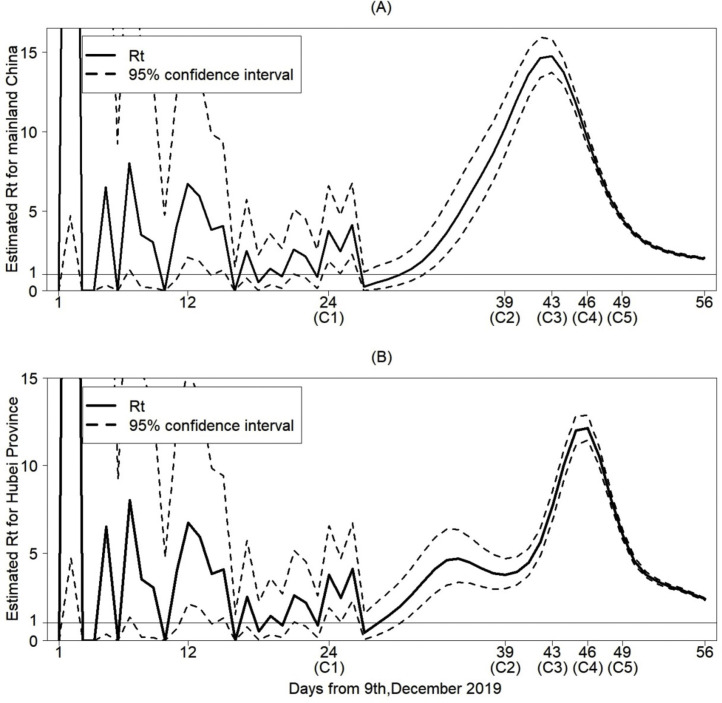
Furthermore, we use the number of cases with illness onset on day t in China, , to estimate the effective reproduction number R t (Figure 4(A)). It has a peak around January 20 and begins to decrease after January 20. It is worth noting that R t started to be stable from late January and was still above 1. By repeating the above process, we also estimated the data on cases with illness onset in Hubei Province between December 8-February 2, and based on that, we further estimated the effective reproduction number R t for Hubei (Figure 4(B)). It follows from Figure 3(B) that the data on cases with illness onset for Hubei is quite similar to that for China before mid-January. From Figure 4(B), the effective reproduction number R t for Hubei shows a declining trend, which decreases quicker than that for mainland China, compared with Figure 4(A). The number of cases with illness onset in Hubei may peak earlier than in mainland China. From Figure 4(B), there was a small peak around January 12, 2020, which induces a relatively small and late main peak in Hubei, compared to Figure 4(A) (Table 2 ).
Figure 4.
Estimated effective reproduction number Rt for mainland China in (A) and for Hubei province in (B). The timing of strategies implemented are as follows: (C1) Huanan Seafood Wholesale Market closed on January 1, 2020; (C2) Detection kits for COVID-19 first used on January 16, 2020; (C3) The Chinese government amended the Law on the Prevention and Treatment of Infectious Diseases to include COVID-19 as a class-B infection but manage it as a class-A infection due to its severity on January 20, 2020; (C4) Lock-down strategy in Wuhan implemented on January 23, 2020; (C5) Spring festival holiday extended and self-quarantine measures kept on January 26, 2020.
Table 2.
Control daily reproduction ratio R(t) for the COVID-19 epidemic in Wuhan, China.
| Date | Jan 23rd | Jan. 24 | Jan. 25 | Jan. 26 | Jan. 27 | Jan. 28 | Jan. 29 | Jan. 30 | Jan. 31 | |
|---|---|---|---|---|---|---|---|---|---|---|
| R(t) | Hubei | 6.3947 | 5.0024 | 3.9330 | 3.1090 | 2.4722 | 1.9784 | 1.5943 | 1.2946 | 1.0599 |
| China | 6.0033 | 4.5709 | 3.4774 | 2.6431 | 2.0076 | 1.5243 | 1.1577 | 0.8803 | 0.6709 | |
| Date | February 1st | Feb. 2 | Feb. 3 | Feb. 4 | Feb. 5 | Feb. 6 | Feb. 7 | Feb. 8 | Feb. 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| R(t) | Hubei | 0.8755 | 0.7302 | 0.6153 | 0.5241 | 0.4515 | 0.3935 | 0.3470 | 0.3096 | 0.2794 |
| China | 0.5131 | 0.3943 | 0.3048 | 0.2375 | 0.1867 | 0.1482 | 0.1189 | 0.0965 | 0.0792 | |
Prediction from the dynamic model
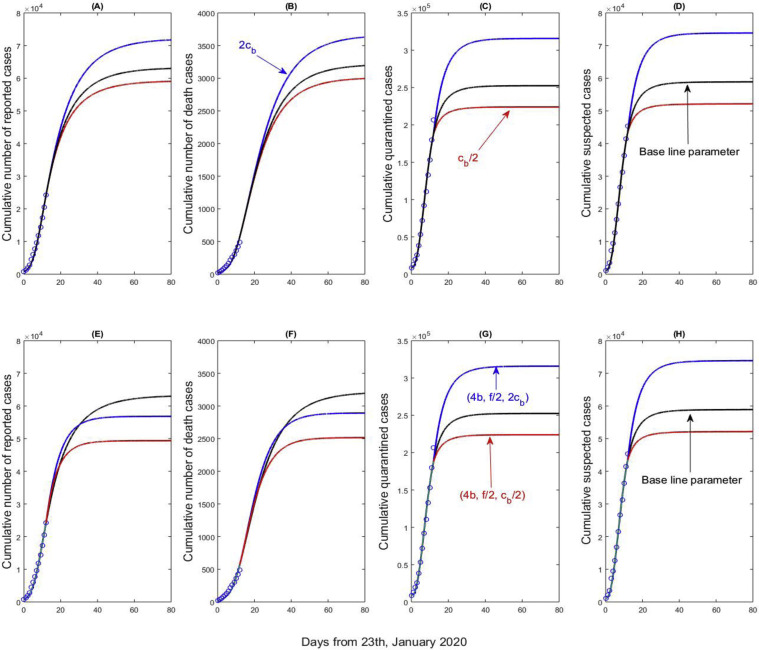
By simultaneously fitting the proposed model to the four columns of data of cumulative reported, death, quarantined, and suspected cases, we obtain the estimations for the unknown parameters and initial conditions. The best-fitting result is shown in Figure 5 (black curves). From Figure 5, the inflection points of cumulative quarantined and suspected population have been basically reached, while the cumulative number of reported cases nearly reaches its inflection point, which implies that the COVID-19 epidemic will nearly peak. Comparing the results in Figure 5(A–D), the number of quarantined/suspected cases peak earlier than the number of reported cases. Increasing the minimum contact rate c b leads to an increase in the cumulative number of reported cases, the cumulative numbers of quarantined, and suspected cases. An increase in individuals’ movement and/or weakening intervention measures (i.e., c b becomes larger) results in more cumulative reported, quarantined, suspected cases and postpones the epidemic peak (Figure 5(A–D)). From Figure 5(C–D, G–H), increasing the detection rate by three times while halving the confirmation ratio will result in more cumulative numbers of quarantined and suspected cases. In such a scenario, the number of cumulative reported cases exhibits a considerable decline, by comparing Figure 5(A) and (E), Figure 5 (B) and (F)), i.e., the blue curves in Figure 5(E–F) stabilize at lower values than the black curves do, which means that increasing the detection rate by four times, even decreasing the confirmation ratio by half, can reduce the final cumulative reported cases and bring forward the epidemic peak. Continuing to enhance the quarantine and isolation strategy, improving the detection rate, and decreasing the confirmation ratio, are beneficial in mitigating the burden of the infection.
Figure 5.
Best model fitting results (black curves) and variation in cumulative number of reported cases, cumulative number of death cases, cumulative quarantined cases, and cumulative suspected cases with the minimum contact rate (cb), detection rate (b), and the confirmation ratio (f).
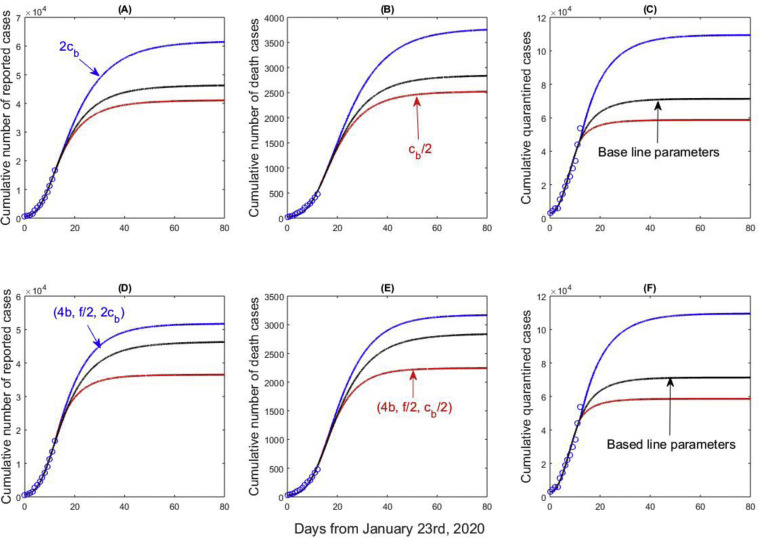
Repeating the above process based on real and generated data for Hubei gives similar results reported in Figure 6 (there is no data on suspected cases in Hubei). From Figure 6(A–C), doubling the minimum contact rate c b leads to an increase in the cumulative number of reported, quarantined, and suspected cases. Similar to Figure 5(A–C), increasing the minimum contact rate c b induces a significant increase in the number of quarantined cases, comparing Figure 6(C) to Figure 5(C). More people may be quarantined if the contact rate becomes greater in Hubei.
Figure 6.
Best model fitting results (black curves) and variation in cumulative number of reported cases, cumulative number of death cases, and cumulative quarantined cases with the minimum contact rate (cb), detection rate (b), and the confirmation ratio (f) for Hubei Province.
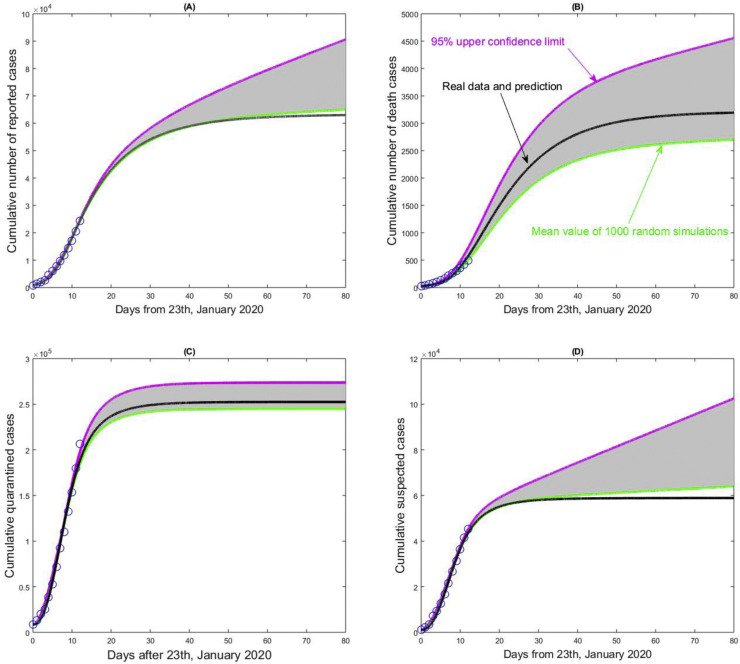
The critical factors making the prediction difficult are the lag in case reporting and the randomness of the monitoring data. To examine the influence of the randomness of multisource data on model prediction, we assume the cumulative reported, death, suspected, and cumulative quarantined cases follow a Poisson distribution with the intraday cumulative number as the key parameter. We randomly generate 1000 columns of datasets for fitting. We then obtain the mean value and the 95% confidence interval of key indicators, including epidemic situation, daily reproduction ratio, peak time, or inflection point (Figure 7 ). Due to the characteristics of the cumulative data, we here only show the 95% of the unilateral upper confidence limit and interval in Figure 7. The number of cumulative quarantined cases tends to be stable.
Figure 7.
The impact of the randomness of the cumulative reporting data sets, including cumulative number of reported cases, cumulative number of death cases, cumulative quarantined cases and cumulative suspected cases on the 2019nCov epidemic in mainland China. The unilateral 95% confidence intervals (here 95% upper confidence limits) have been given, and the mean curve and estimated curve based on the real data sets are marked in each subplot.
In contrast, the other three types of cumulative population sizes exhibit great randomness, implying that a random event (such as a sudden cluster infection) may lead to a rapid increase in the numbers of cumulative reported cases, deaths, and suspected cases. Moreover, the fitting curve of the cumulative death cases with the real data is located in the middle of the 95% unilateral upper confidence interval. The number of cumulative death cases due to the COVID-19 infection is highly uncertain, where the improvement of treatment level may significantly reduce the fatality rate.
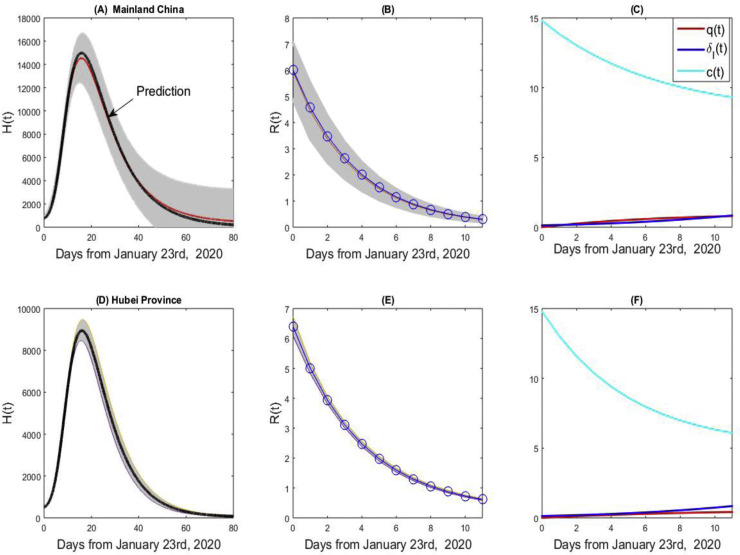
Similarly, based on real data and 1000 columns of generated data, we plot the curve of hospital notifications (Figure 8(A) for China and (D) for Hubei). The hospital notifications will peak around February 8, 2020, and the peak time for Hubei province may be one day early. The values of the hospital notifications in Figure 8(A) and (D) are much smaller than those reported by the National Health Commission of China (NHCPRC, 2020b), due to the very restrictive discharge conditions in Hubei. From Figure 8(B) and (E), the estimated effective reproduction number based on the real data almost coincides with the mean values for both China and Hubei, while the effective reproduction number in Hubei province is always larger than the value for mainland China. From Figure 8(A) and (B), the COVID-19 epidemic in China is highly uncertain. Figure 8(C) and (F) give the estimated contact rate c(t), quarantined rate q(t), and diagnosis rate δ I(t), showing that the contact rate curve for Hubei decreases faster than that for mainland China with a smaller c b. The quick decrease of the contact rate and the gradual increase of quarantined diagnosed cases rate indicate that the restrictive measures in China have been strengthened since January 23, 2020.
Figure 8.
The hospital notifications, effective reproduction numbers, and estimated contact rate, quarantined rate and diagnose rate curves for mainland China (A–C) and the Hubei province (D–F).
Discussion
Since January 23, 2020, the Chinese government has implemented several measures in controling the COVID-19 epidemic. Recent data show that most reported cases come from suspected individuals. This implies that the changing trends of cumulative quarantined and suspected cases greatly influence the pattern of the COVID-19 epidemic. The cumulative numbers of quarantined and suspected cases tend to stabilize since their inflection points have already been achieved. The COVID-19 epidemic will peak in the near future.
The existing models either use the data of only confirmed cases or data of both confirmed and death cases, with most model predictions ignoring the effects of quarantine and isolation. Here we extend a previously developed model (Tang et al., 2020b) by including new compartments, and utilizing more data of quarantined and suspected cases, to make predictions and perform assessment and risk analysis. Based on our predictions, the number of cumulative confirmed cases is near to its inflection point, and the COVID-19 infection will peak soon. The trends of the COVID-19 epidemics in Hubei and China depend on cumulative quarantined and suspected cases, in terms of variations of detection rate and the confirmation ratio for these two compartments.
Therefore, our model is consistent with the current epidemic development and in line with the prevention measures implemented in mainland China. The actual reproduction numbers are quite large before January 24, 2020, suggesting that the population movement before the Spring Festival, especially the outflow of the population before the lock-down of Wuhan, is a key factor resulting in the COVID-19 epidemic. The actual reproduction numbers show a declining trend, indicating that new infections have been decreasing, while newly reported cases have been increasing significantly from February 3 to February 7, 2020.
The strong measures implemented have reduced the actual reproduction number. These interventions may take a longer time to be effective as the second and third generations of infected people are exposed in succession. After the first wave of the Spring Festival, the flow of people increased the risk of spreading the novel coronavirus. The uncertainty of the national epidemic is higher than that of Hubei, so the evolutionary trend of the epidemic still needs attention in the future in terms of population migration or possible infection clusters on the way.
Conflict of interest
None.
Funding source
This research was funded by the National Natural Science Foundation of China (grant numbers: 11631012 (YX, ST), 61772017 (ST)), and by the Canada Research Chair Program (grant number: 230720 (JW) and the Natural Sciences and Engineering Research Council of Canada (Grant number: 105588-2011 (JW).
Ethical Approval
Waived, since all data utilized are publicly available.
Appendix A. Data information
| Date | Cumulative confirmed cases |
Cumulative death cases |
Cumulative quarantined population |
Cumulative suspected cases | |||
|---|---|---|---|---|---|---|---|
| China | Hubei | China | Hubei | China | Hubei | China | |
| 01/23 | 830 | 549 | 25 | 24 | 9507 | 3653 | 1073 |
| 01/24 | 1287 | 729 | 41 | 39 | 15197 | 5682 | 2191 |
| 01/25 | 1975 | 1052 | 56 | 52 | 23431 | 7989 | 3500 |
| 01/26 | 2744 | 1423 | 80 | 76 | 32799 | 10394 | 7306 |
| 01/27 | 4515 | 2714 | 106 | 100 | 47833 | 16904 | 9383 |
| 01/28 | 5974 | 3554 | 132 | 125 | 65537 | 22095 | 12631 |
| 01/29 | 7711 | 4586 | 170 | 162 | 88693 | 28780 | 16779 |
| 01/30 | 9692 | 5806 | 213 | 204 | 113579 | 35144 | 21591 |
| 01/31 | 11791 | 7153 | 259 | 249 | 136987 | 41075 | 26610 |
| 02/01 | 14380 | 9074 | 304 | 294 | 163844 | 48571 | 31172 |
| 02/02 | 17205 | 11177 | 361 | 350 | 189583 | 56088 | 36345 |
| 02/03 | 20438 | 13522 | 425 | 414 | 221015 | 68988 | 41417 |
| 02/04 | 24324 | 16678 | 490 | 479 | 252154 | 81039 | 45388 |
References
- Castillo-Chavez C., Castillo-Garsow C.W., Yakubu A. Mathematical models of isolation and quarantine. JAMA. 2003;290:2876–2877. doi: 10.1001/jama.290.21.2876. [DOI] [PubMed] [Google Scholar]
- Chowell G., Viboud C., Simonsen L., Moghadas S.M. Characterizing the reproduction number of epidemic with early subexponential growth dynamics. J R Soc Interface. 2016;13(123) doi: 10.1098/rsif.2016.0659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J., Normile D. New SARS-like virus in China triggers alarm. Science. 2020;367:234–235. doi: 10.1126/science.367.6475.234. [DOI] [PubMed] [Google Scholar]
- Goldstein E., Dushoff J., Ma J., Plotkin J.B., Earn D.J., Lipsitch M. Reconstructing influenza incidence by deconvolution of daily mortality time series. Proc Natl Acad Sci. 2009;106(51):21825–21829. doi: 10.1073/pnas.0902958106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guanchazhe News. https://baijiahao.baidu.com/s?id=1657591560934072148&wfr=spider&for=pc [Accessed 6 Feb 2020].
- HB.CHINA.COM.CN. http://hb.china.com.cn/2020-01/27/content_41043813.htm?f=pad&a=true [Accessed 4 Feb 2020].
- Health Commission of Hubei Province. Available at http://wjw.hubei.gov.cn/bmdt/ztzl/fkxxgzbdgrfyyq/[Accessed February 6th, 2020].
- Nishiura H., Linton N.M., Akhmetzhanov A.R., Serial interval of novel coronavirus (COVID-19) infections, medRxiv preprint 10.1101/2020.02.03.20019497. [DOI] [PMC free article] [PubMed]
- Keeling M.J., Rohnai P. Princeton University Press; 2008. Modeling infectious diseases in humans and animals. p. 313-320. [Google Scholar]
- Li Q., Guan X., Wu P. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 2020 doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu H., Stratton C.W., Tang Y.W. Outbreak of Pneumonia of unknown etiology in Wuhan China: the mystery and the miracle. J Med Virol. 2020 doi: 10.1002/jmv.25678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucy L.B. An iterative technique for the rectification of observed distributions. Astronomical J. 1974;79(6):745–754. [Google Scholar]
- National Health Commission of the People's Republic of China. http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml [Accessed 9 Feb 2020]. [DOI] [PMC free article] [PubMed]
- National Health Commission of the People's Republic of China. http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml [Accessed 6 Feb 2020]. [DOI] [PMC free article] [PubMed]
- National Health Commission of the People's Republic of China. http://www.nhc.gov.cn/xcs/xwbd/202002/35990d56cfcb43f4a70d7f9703b113c0.shtml [Accessed February 4th, 2020]. [DOI] [PMC free article] [PubMed]
- Nishiura H. Correcting the actual reproduction number: a simple method to estimate R0 from early epidemic growth data. Int J Environ Res Public Health. 2010;7(1):291–302. doi: 10.3390/ijerph7010291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H., Chowell G. Mathematical and statistical estimation approaches in epidemiology. Springer; Dordrecht: 2009. The effective reproduction number as a prelude to statistical estimation of time-dependent epidemic trends. (pp. 103-121) [Google Scholar]
- Parry J. China coronavirus: cases surge as official admits human to human transmission. BMJ. 2020;368:m236. doi: 10.1136/bmj.m236. [DOI] [PubMed] [Google Scholar]
- Richardson W.H. Bayesian-based iterative method of image restoration. JOSA. 1972;62(1):55–59. [Google Scholar]
- Tang B., Bragazzi N.L., Li Q., Tang S., Xiao Y., Wu J. An updated estimation of the risk of transmission of the novel coronavirus (COVID-19) Infect Dis Model. 2020;5:248–255. doi: 10.1016/j.idm.2020.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang B., Wang X., Li Q. Estimation of the transmission risk of the COVID-19 and its implication for public health interventions. J Clin Med. 2020;9:462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viboud C., Simonsen L., Chowell G. A generalized-growth model to characterize the early ascending phase of infectious disease outbreaks. Epidemic. 2016;15:27–37. doi: 10.1016/j.epidem.2016.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Z.W., Wang L., Xu X.K., Wu Y., Cowling B.J., Meyers L.A., The serial interval of COVID-19 from publicly reported confirmed cases, medRxiv preprint. 10.1101/2020.02.19.20025452. [DOI] [PMC free article] [PubMed]