Rapid Chlorophyll a Fluorescence Light Response Curves Mechanistically Inform Photosynthesis Modeling^,

Chlorophyll a fluorescence rapid light response curves improve mechanistic models of drought limitations to photosynthetic electron transport.

Abstract

Crop improvement is crucial to ensuring global food security under climate change, and hence there is a pressing need for phenotypic observations that are both high throughput and improve mechanistic understanding of plant responses to environmental cues and limitations. In this study, chlorophyll a fluorescence light response curves and gas-exchange observations are combined to test the photosynthetic response to moderate drought in four genotypes of Brassica rapa. The quantum yield of PSII (ϕ_PSII) is here analyzed as an exponential decline under changing light intensity and soil moisture. Both the maximum ϕ_PSII and the rate of ϕ_PSII decline across a large range of light intensities (0–1,000 μmol photons m⁻² s⁻¹; β_PSII) are negatively affected by drought. We introduce an alternative photosynthesis model (β_PSII model) incorporating parameters from rapid fluorescence response curves. Specifically, the model uses β_PSII as an input for estimating the photosynthetic electron transport rate, which agrees well with two existing photosynthesis models (Farquhar-von Caemmerer-Berry and Yin). The β_PSII model represents a major improvement in photosynthesis modeling through the integration of high-throughput fluorescence phenotyping data, resulting in gained parameters of high mechanistic value.

Increasing global populations and environmental change require greater mechanistic understanding of plant responses to fluctuating environmental factors along with meaningful phenotyping for tolerance to stress such as drought (Sheffield and Wood, 2008; Jin et al., 2018). Improved phenotyping technologies can also advance our ability to link physiological mechanisms to rapidly improving genetic information. Among the challenges toward this goal is the genetic complexity behind drought tolerance traits of interest to breeders (Holland, 2007; Shi et al., 2009). Hence, model-assisted phenotyping has been advocated to separate complex traits such as quantum yield of photosynthesis, stomatal conductance, and water use efficiency into manageable mechanistic components (Tardieu, 2003). Mechanistic modeling formalizes plant physiology using interconnected mathematical equations, which describe primary biochemical and first-principles biophysical processes. Improving predictive understanding of crop responses to changing environments will require that mechanistic models directly use phenotypic and environmental data to simulate outcomes sensitive enough to capture possible variation in the expressed traits among unknown genotypes. When these requirements are met, mechanistic models can assist in unraveling the genetic architecture underlying the complex quantitative traits of drought physiology (Reymond et al., 2003; Hammer et al., 2006; Chenu et al., 2009).

Although mechanistic models have evolved to capture the expression of complex plant traits in a changing environment, no current model can dependably capture the impact of drought on photosynthesis (Drake et al., 2017). Photosynthesis models focus on those environmental factors considered critical to net assimilation rates (A_n; de Witt, 1966; Farquhar et al., 1980; Patrick et al., 2009; Yin et al., 2009). Observations of A_n and available CO₂ (A/C_i) are combined in mechanistic models, such as the Farquhar, von Caemmerer, and Berry (FvCB) model (Farquhar et al., 1980), to reveal biochemical mechanisms underpinning photosynthesis. FvCB estimates A_n as limited by two primary factors. First, Rubisco-limited A_n (A_c) is dominated by the response of the maximum rate of carboxylation (V_cmax). Second, light-limited A_n (A_J) is constrained by the electron transport rate (ETR) across PSII and PSI, which ultimately produces ATP and NADPH needed for the Calvin carboxylation cycle (Farquhar et al., 1980; Von Caemmerer, 2000). Although the FvCB model captures the phenomenological link between ETR and A_n, it omits mechanistic details of the photosynthetic electron transport chain (Horton et al., 1994; Allen and Pfannschmidt, 2000; Laisk et al., 2002; Yin et al., 2004). Whereas the conceptual power of a reduced complexity model (FvCB) yields crucial insights under nonstressed conditions, it lacks additional mechanistic detail for plants exposed to environmental stress (Urban et al., 2017).

Drought stress impacts both A_c and A_J via interactive mechanisms (Flexas and Medrano, 2002; Bota et al., 2004; Fini et al., 2012). The initial response to water stress is often a decline in stomatal conductance (g_s), which impacts CO₂ availability for photosynthesis (Medrano et al., 2002; Grassi and Magnani, 2005). Additional CO₂ constraints on A_c are possible via mesophyll conductance (g_m), limiting CO₂ at the site of carboxylation (Flexas et al., 2002, 2018; Niinemets et al., 2009; Pons et al., 2009). Prolonged CO₂ limitation can result in overreduction of the photosynthetic electron transport chain (Miller et al., 2010), triggering the production of reactive oxygen species at different sites of the photosynthetic pathway with the potential for photooxidative damage (Krieger-Liszkay et al., 2008; Miller et al., 2010; Sharma et al., 2012). PSII is highly susceptible to oxidative stress, and a variety of mechanisms, collectively called photoprotection, preserve it from irreversible photodamage that causes sustained declines in the overall efficiency of PSII (Murata et al., 2007; Takahashi and Badger, 2011). Heat energy dissipation, state transitions, augmented PSI energy utilization, and changes in leaf absorbance using alternate pigments or chloroplast avoidance are all known mechanisms of photoprotection (Müller et al., 2001; Kasahara et al., 2002; Takahashi and Badger, 2011).

Photosynthesis models must now progress to reflect these stress-induced mechanisms while using high-throughput phenotyping data, including noninvasive measures of leaf spectral reflectance, absorbance, and chlorophyll a fluorescence (Cruz et al., 2016; Kuhlgert et al., 2016; Silva-Perez et al., 2018). Fast and informative techniques provide fine temporal resolution of mechanistic responses to external stressors from mild to lethal stress (Guadagno et al., 2017), which are necessary to improve predictive understanding of photosynthesis responses to drought.

In particular, pulse amplitude modulated (PAM) chlorophyll a fluorescence analysis quantifies PSII activity in response to observed photosynthetically active radiation (Q) and is informative of the status of the photosynthetic electron transport (Maxwell and Johnson, 2000; Kramer et al., 2004a; Baker, 2008). PAM measurements, using the signal of the excitation energy reemitted by the chlorophyll a molecule as fluorescence, are used to define the fate of the absorbed light in the leaf and are currently one of the fastest and most reliable phenotyping tools in photosynthetic measurements (Filek et al., 2015; Gullì et al., 2015; Flood et al., 2016; Guadagno et al., 2017; Gómez et al., 2018). The operating efficiency of PSII (ϕ_PSII) is a fluorescence parameter calculated from the relative difference in light conditions between the steady-state fluorescence (F_s) and the maximum fluorescence emitted after a saturating flash that closes (reduces) all PSII reaction centers [F_m′; i.e. ϕ_PSII = (F_m′ − F_s)/F_m′; Genty et al., 1989]. A large fraction of the excitation energy not used in PSII photochemistry or reemitted as fluorescence is dissipated as heat via regulated (e.g. nonphotochemical quenching [NPQ]) and nonregulated energy dissipation (e.g. ϕ_NO) mechanisms (Müller et al., 2001; Kramer et al., 2004a). Recently, the original derivation of NPQ has been extended, allowing for high-throughput estimates of quantum yield NPQ (ϕ_NPQt; Tietz et al., 2017). ϕ_NPQt can be measured in a few seconds, allowing for high-throughput and field applications, and its calculation does not require full relaxation of quenching processes as for the classic NPQ parameter. The combination of fluorescence observations with leaf gas-exchange data has been shown as a powerful way to inform and test models of photosynthesis (Laisk et al., 2002; Yin et al., 2009; Bellasio et al., 2016).

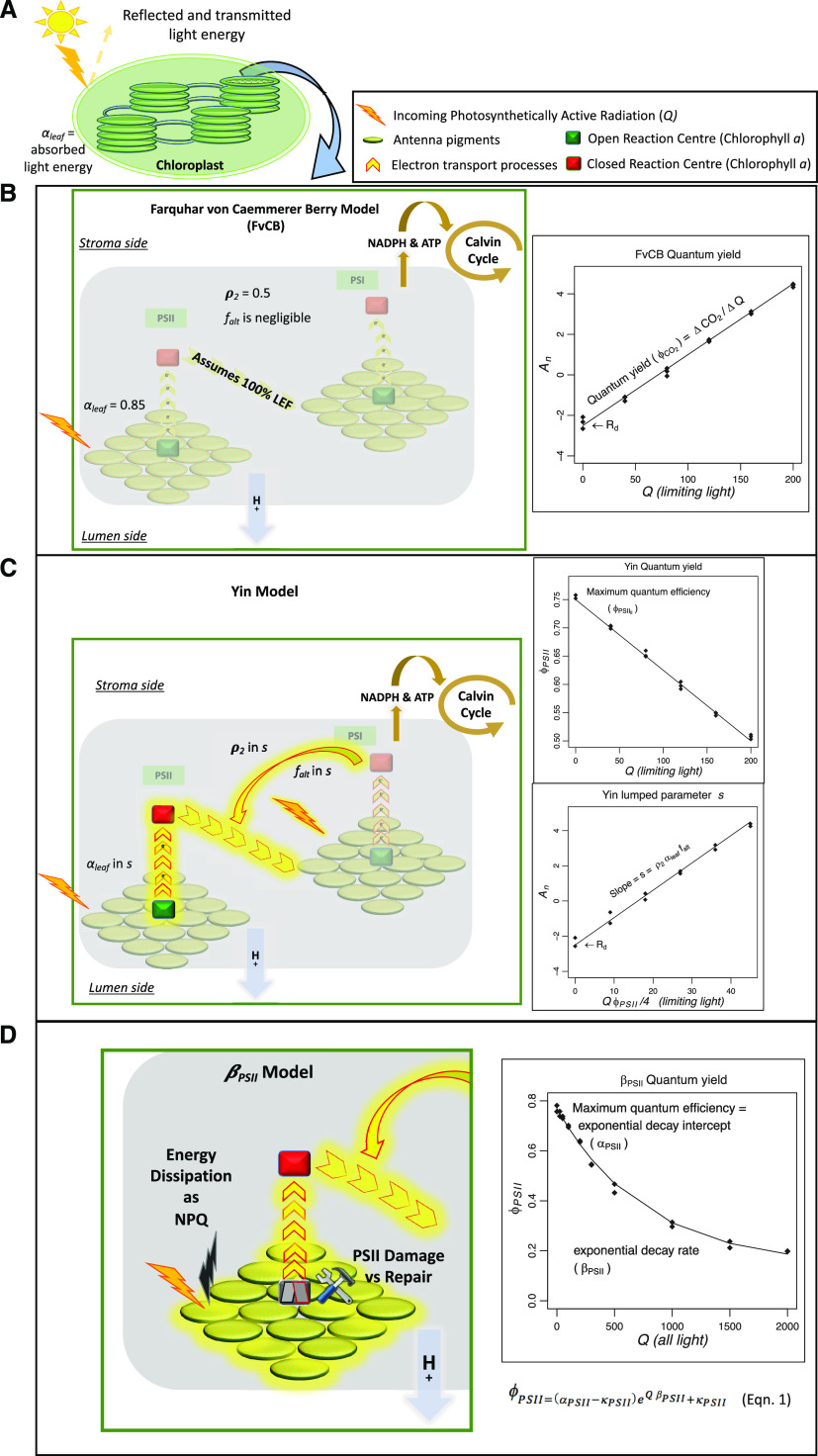
Alternative models of photosynthetic electron transport have been developed using an increasing number of mechanistic details of the Z-scheme for the electron transport (Fig. 1). Within chloroplasts, photosynthetic electron transport occurs across the thylakoid membranes (Fig. 1A), where a hydrogen ion gradient builds up upon the transfer of excited e^- to ultimately produce ATP and NADPH, which are used as substrates in the Calvin cycle. Figure 1B summarizes the ETR derivation of the FvCB model. This model assumes that the electron flow is entirely linear (LEF) from PSII to NADP⁺ reduction, with the CO₂ fixation rate from the A/C_i response used to parametrize the maximum ETR (J_max). Data from the linear portion of a light response curve can be used to parameterize quantum yield on a ΔCO₂/ΔQ basis (ϕ_CO2; Fig. 1B, inset graph). Although the significance of the correlation between the quantum yield of assimilation and the PSII quantum yield has been previously studied (Oberhuber and Edwards, 1993; Pietrini and Massacci, 1998; Singsaas et al., 2001), to the best of our knowledge, the effect of drought on its linearity is still unclear. The FvCB model has been recently implemented to include proportional changes between ETR and A_n using observations of A_n and ϕ_PSII under low-light conditions (Q < 200 μmol photons m⁻² s⁻¹) to estimate ETR and A_J (Fig. 1C; Yin et al., 2004, 2009; Bellasio et al., 2016). Quantum yield is estimated on a Δe^-/ΔQ basis using the linear portion of the ϕ_PSII light response (Fig. 1C, top inset graph), but the use of only low-light conditions to characterize PSII quantum yield is limiting. In the Yin model, a lumped parameter, s, is estimated to account for the energy partitioning between photosystems (ρ₂), leaf absorbance in the antenna complex (α_leaf), and the potential use of electron pathways other than LEF (f_alt). However, neither FvCB nor the Yin model explicitly addresses the influence of environmental stress on ETR and A_n, and they are not well equipped to capture the A_J responses of the PSII antenna complex to stressors (Govindjee, 2002; Asada, 2006; Murata et al., 2007; Urban et al., 2017).

Figure 1.

Simplified illustration of the light reactions of photosynthesis representing how three conceptual models account for the photosynthetic electron transport. A, Upon light energy absorption, energy in the form of excited electrons (e⁻) is transferred from light-harvesting antennae to the reaction centers of PSI and PSII in the chloroplastic thylakoid membranes. This energy transport has been described as a Z-scheme (Hill and Bendall, 1960) whereby e⁻ from PSII produce a transmembrane H⁺ gradient (used for ATP production) while e⁻ downstream of PSI produce NADPH; both ATP and NADPH are then used for Calvin cycle CO₂ fixation. For modeling applications (inset graphs of B, C, and D), photosynthetic quantum yield describes how light energy relates to CO₂ fixation (Genty et al., 1989; Martre et al., 2015) and assumptions are made about the processes of electron transfer more or less obscuring (gray boxes in B, C, and D) the actual physiological mechanisms. B, In the traditional FvCB conceptualization, quantum yield is calculated on a photon-to-CO₂ basis (ϕ_CO2; inset graph). Here, ETR processes are ignored, assuming 100% LEF from PSII to NADPH production, leaf absorbance (α_leaf) is fixed (0.85), and an implicit 50:50 fractionalization of Q exists between PSII and PSI (ρ₂). C, The Yin conceptualization improved the use of PSII physiology by calculating quantum yield on a photon-to-e⁻ basis, using the relationship between ϕ_PSII and Q under light-limiting conditions (ϕ_{PSII_ll}; top inset graph). Yin also used a lumped s parameter defined by the slope of a linear regression of A_n against (Q ϕ_PSII)/4 using light < 200 μmol m⁻² s⁻¹, where 4 is the number of protons needed to synthesize one ATP. This regression was used to calibrate for three factors, the unknown fraction of nonlinear electron flow around PSI (f_alt), α_leaf, and ρ₂ (collectively s; bottom inset graph). D, Our alternative β_PSII conceptualization captures the behavior of energy transfer from the antennae complex to the PSII reaction complex. Here, quantum yield is modeled using an exponential decay function (Eq. 1) across all relevant Q conditions, on a photon-to-e⁻ basis, providing estimates of both maximum light-acclimated quantum yield (α_PSII) and the decay rate in ϕ_PSII under increasing Q (β_PSII; inset graph). The β_PSII model maintains the use of the s parameter to address f_alt, α_leaf, and ρ₂. Implementations of modeling photosynthetic electron transport in the Yin and β_PSII approaches are represented as incrementing highlighted yellow in C and D.

Here, we introduce an alternative approach (β_PSII model) that considers PSII activity across a wide range of light conditions and that can better accommodate the role of stress-related mechanisms (Fig. 1D). We observe that data from the ϕ_PSII/Q response can be modeled as an exponential decline (Fig. 1D, inset graph). This new parameter as the rate of decline (β_PSII) can be used to calculate ETR, A_J, and A_n under stress conditions such as drought. Using a more complete characterization of quantum yield via the ϕ_PSII light response, the β_PSII model approach accommodates mechanisms of photoprotection including NPQ, chloroplast avoidance, and pigment alterations as well as PSII damage relative to repair (Fig. 1D). Our integration of the ϕ_PSII decline provides a link between gas conductance-based limitations on A_c and photoprotective limitations impacting A_J, representing a further step in the mechanistic understanding of the electron transport under stress (incremental yellow shadow in Fig. 1). All model parameters (observed and predicted) for the FvCB, Yin, and β_PSII models are compared in Table 1, whereas Table 2 describes the equations used in the three photosynthesis models.

Table 1. List of abbreviations used for models (observations, predictions, and parameters).

Abbreviation	Definition	Units
An	CO2 assimilation rate observed	μmol m−2 s−1
Ci	Intercellular CO2 partial pressure observed	Pa
Tleaf	Leaf temperature observed	°C
gs	Conductance to CO2 from atmosphere to intercellular space observed	μmol m−2 s−1
O	Ambient O2 (assumed 21% atmosphere)	Pa
Q	Photosynthetically active radiation observed	μmol m−2 s−1
ϕPSII	Operating efficiency of PSII (Fm′ − Fs′/Fm′) observed	e− photon−1
Ac	Predicted Rubisco limited rate of CO2 assimilation	μmol m−2 s−1
Aj	Predicted electron transport limited rate of CO2 assimilation	μmol m−2 s−1
Jm	Predicted rate of electron transport following FvCB	μmol m−2 s−1
Jf	Predicted rate of electron transport following Yin	μmol m−2 s−1
Jl	Predicted rate of electron transport following beta decay model	μmol m−2 s−1
R	Universal gas constant (8.314 J K−1 mol−1)	J K−1 mol−1
αleaf	Absorptance of leaf photosynthetic pigments	%
ρ2	Partitioning of energy between PSII and PSI	%
falt	Fraction of electron not using LEF (1 − fpseudo(b)/(1 − fcyc) in Yin et al. (2009)	%
s	Lumped parameter (ρ2 αleaf falt; Yin et al., 2009)	%
Γ*25	CO2 photocompensation point (standardized to 25°C)	Pa
Kc25	Michaelis-Menten constant for Rubisco for CO2 (standardized to 25°C)	Pa
Ko25	Michaelis-Menten constant for Rubisco for O2 (standardized to 25°C)	kPa
Ei's (Kc, Ko, Rd, Vcmax, Γ*, Jmax, gm)	Activation energy used in Arrhenius function	KJ mol−1
Rd25	Respiration rate in the dark (standardized to 25°C)	μmol m−2 s−1
gm25	Mesophyll conductance (standardized to 25°C)	μmol m−2 s−1 Pa−1
Vcmax25	Maximum rate of carboxylation (standardized to 25°C)	μmol m−2 s−1
Jmax25	Maximum rate of electron transport (standardized to 25°C)	μmol m−2 s−1
ϕCO2	Quantum yield of CO2 using Equation 2.6	mol CO2 mol−1 photon
θJ	Curvature factor on electron transport rate predictions Jm and Jf	unitless
ϕPSII_ll	Maximum quantum efficiency following Yin using Equation 2.6	mol e− mol−1 photon
βPSII	Decay rate in ϕPSII under increasing Q using Equation 1	Q -1
αPSII	Modeled ϕPSII as Q approaches zero using Equation 1	unitless
κPSII	Modeled ϕPSII as Q approaches ∞ using Equation 1	unitless

Table 2. List of equations used in three photosynthesis models (FvCB, Yin, and β_PSII decay).

Equation No.	Equation	Description
2.1		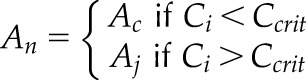An depending on two limiting factors and the critical Ci (Ccrit)
2.2		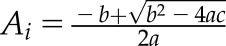General quadratic form for solving Ac, Aj, Jm, and Jf
2.3		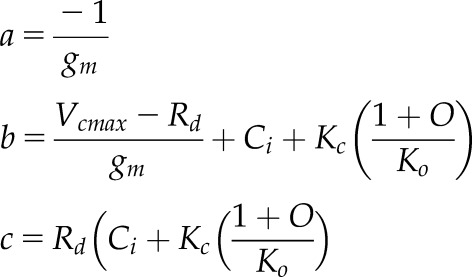Quadratic roots using intercellular CO2 (Ci) and a gm term for describing Ac
2.4		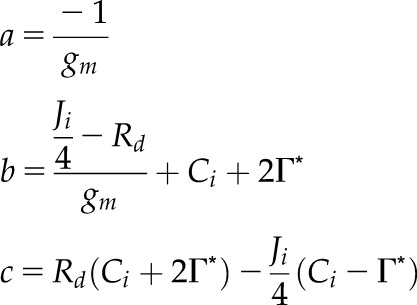Quadratic roots for Aj using Jm, Jf, or Jl
2.5		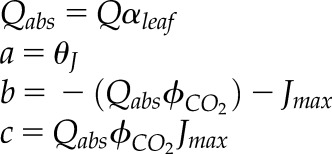Quadratic roots for whole-chain ETR (Jm) as described by Von Caemmerer (2000) assumes αleaf = 0.85
2.6		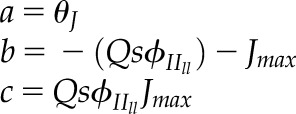Quadratic roots for combined gas-exchange and chlorophyll fluorescence ETR (Jf) as described by Yin et al. (2009),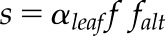
2.7		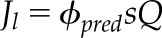βPSII model for full ϕPSII versus Q derivation of ETR (Jl) using Equation 1 to predict ϕII from decay with Q

We tested the β_PSII approach in an effort to analyze physiological responses of A_n under different soil moisture conditions from full watering to moderate drought in the species Brassica rapa (Supplemental Figs. S1 and S2). High intraspecific physiological diversity with respect to complex quantitative traits such as A_n and water use efficiency has previously been shown for Brassica species (Edwards et al., 2011, 2012; Franks, 2011; Baker et al., 2015), making it a perfect model to investigate photosynthesis phenotyping tools. Specifically, we tested a turnip crop type (VT), a cultivated oilseed (R500), and two experimental genotypes (recombinant inbred lines [RILs]) developed from a cross between a rapid-cycling genotype (Imb211) and an oilseed crop (R500), thus ensuring a broad range of both photosynthetic and biomass allocation diversity (Edwards et al., 2011; Yarkhunova et al., 2016; Pleban et al., 2018).

We developed a ϕ_PSII light response curve using a three-parameter exponential function,

where the exponential rate of decline for ϕ_PSII (β_PSII) under increasing light (Q) and the intercept of ϕ_PSII as Q approaches zero (α_PSII) are used to model the responses. Importantly, α_PSII derives from measurements taken in light conditions and is different that the classic F_v/F_m parameter derived from dark-adapted measurements (Table 1). The κ_PSII term represents a non-zero minimum of ϕ_PSII as Q approaches ∞. To evaluate potential differences in photoprotection strategies due to ETR, we validated the ϕ_PSII light response parameters (β_PSII and α_PSII) at different soil moisture conditions. Then, we incorporated these parameters in an alternative photosynthesis model that directly incorporates ϕ_PSII light response traits into the estimation of ETR, and we assessed how the derived parameters relate to known traits, including V_cmax and g_m.

Using rapid measurements with high mechanistic significance, our approach innovatively connects high-throughput phenotyping and biophysical modeling to better predict plant photoprotective strategies. Gained knowledge will help to clarify the complexity of photosynthetic traits, such as drought tolerance, thus improving breeding and management strategies toward more drought-resistant crops with increased final yield.

RESULTS

Establishing Drought Treatments

After sowing, plants were immediately randomized and put into different treatment groups (Supplemental Fig. S1). On experimental day 0 (28 d after sowing), drought was applied via complete water withholding for the droughted cohort. Control pots (well watered [WW]) were watered daily throughout the experiment, and WW plants were measured on experimental days 1, 4, 5, 6, and 9. Droughted plants were assigned to three different groups, and replicate plants were observed on experimental days 4 to 7 (treatment group D1), 9 to 12 (treatment group D2), and 15 (treatment group D3). On experimental day 9, water was reapplied to a subset of droughted plants (R1), and they were observed on experimental days 9 to 12. On experimental day 15, a second subset of droughted plants (R2) was rewatered and observed 6 h after rewatering. Finally, on day 16, the last subset of droughted plants was rewatered and assessed at 30 h after rewatering (R3). For each experimental day, volumetric soil water content (VWC) was measured across all cohorts of plants for the duration of the experiment (Supplemental Fig. S2).

Impact of Drought on Leaf Traits and Genotypic Difference

The progressive drought and recovery (Supplemental Fig. S1) application inevitably impacted the photosynthetic performance of all genotypes. Table 3 summarizes 14 photosynthetic leaf traits assessed on three different experimental days for each B. rapa genotype. As expected, D1 plants were the least impacted by water scarcity for the measured physiological traits. However, early signs of drought stress were already detected. g_s was reduced in D1 plants of all genotypes by a mean of 0.16 ± 0.1 mmol m⁻² s⁻¹, with the biggest decline for R500 (0.29 mmol m⁻² s⁻¹). In VT, the electrochromic shift (ECSt; Δ absorbance 530 nm), which reflects the transthylakoidal ∆H⁺ gradient, at 300 and 1,000 μmol photon m⁻² s⁻¹, increased in D1 plants relative to WW plants. More sustained drought (D2 and D3 plants) results in pronounced changes across all genotypes (Table 3). g_s showed further reduction in all genotypes but r46 in D3 plants. LEF was decreased across genotypes, with R500 showing the greatest loss at both 300 and 1,000 μmol photon m⁻² s⁻¹.ϕ_NPQt and ECSt at both 300 and 1,000 μmol m⁻² s⁻¹ increased overall in D3 plants. Pigments content as SPAD at 530 nm units and relative chlorophyll content increased in all four genotypes of the D3 cohort. The changes in ECSt, LEF, and SPAD are reflected in a decreased lumped s parameter in D3 plants, which accounts for potential changes in f_alt, ρ₂, and α_leaf (Supplemental Fig. S3). These results validate the robustness of high-throughput measurements of fluorescence to pick up early signs of drought stress. The drought treatments applied here can be considered as mild to moderate for B. rapa, with an overall recorded VWC never lower than 3% and plants still capable of recovery upon rewatering for all genotypes (Supplemental Fig. S1). Changes in physiological traits reflect the expected behavior of the four genotypes under drought (Edwards et al., 2011, 2012; Baker et al., 2015; Greenham et al., 2017). Genotypes with high biomass accumulation (R500, r301, and VT) were more impacted at an earlier stage by changes in soil moisture, whereas the small, highly water use-efficient r46 was able to tolerate drought and maintain a stable level of gas exchange despite the decreased LEF. These genotypic differences in drought behavior were confirmed when looking at the onset of NPQt at increased LEF (Supplemental Fig. S4), where R500 and VT showed earlier changes in NPQt values already at lower LEF in comparison with the inbred lines r46 and r301.

Table 3. Genotype × treatment trait estimates.

Modeled traits show median of posterior distribution (95% credible interval range), while observed traits show mean values (sd). Boldface indicates significance relative to well-watered conditions at P < 0.05 or for 95% confidence interval (CI). HDI interval difference not intersecting with zero was used to describe a credible trait variance (A_max and s).

Trait	Treatment	r301	r46	R500	VT
Amax	Well watered	27.70 (25.47, 30.26)	17.12 (14.99, 19.57)	25.42 (22.86, 28.13)	18.25 (15.94, 20.64)
(μmol m−2 s−1)	Early drought	28.70 (26.02, 31.22)	14.54 (12.73, 16.43)	25.62 (23.33, 27.74)	14.71 (12.91, 16.45)
(95% CI range)	Late drought	9.70 (7.63, 11.76)	8.75 (6.65, 10.71)	4.75 (2.17, 7.21)	3.30 (−0.74, 6.83)
s	Well watered	0.33 (0.3, 0.37)	0.29 (0.25, 0.32)	0.32 (0.29, 0.34)	0.31 (0.27, 0.35)
unitless	Early drought	0.36 (0.33, 0.38)	0.28 (0.25, 0.31)	0.32 (0.3, 0.34)	0.29 (0.25, 0.32)
(95% CI range)	Late drought	0.16 (0.12, 0.2)	0.19 (0.15, 0.22)	0.26 (0.02, 0.53)	0.11 (0.05, 0.17)
ESCt_300 × 1000	Well watered	1.7 (0.35)	1.7 (0.34)	1.4 (0.32)	1.2 (0.42)
Δ absorbance 530 nm	Early drought	1.4 (0.10)	1.7 (0.49)	1.8 (0.48)	1.9 (0.32)
(sd)	Late drought	3.0 (0.44)	2.4 (0.13)	2.7 (0.24)	2.7 (0.21)
ESCt_1000 × 1,000	Well watered	2.7 (0.15)	2.6 (0.27)	2.5 (0.29)	1.9 (0.78)
Δ absorbance 530 nm	Early drought	2.5 (0.18)	2.3 (0.35)	2.3 (0.65)	2.4 (0.22)
(sd)	Late drought	3.7 (0.43)	3.1 (0.27)	3.6 (0.57)	3.7 (0.07)
LEF_300	Well watered	61.07 (2.90)	57.37 (0.26)	70.25 (4.43)	64.06 (3.39)
(μmol m−2 s−1)	Early drought	68.72 (0.18	57.46 (7.59)	63.27 (4.34)	61.23 (3.05
(sd)	Late drought	34.48 (11.38)	43.06 (7.59)	36.21 (5.70)	42.39 (1.53)
LEF_1000	Well watered	93.00 (6.78)	79.14 (8.03)	106.17 (6.76)	92.48 (7.64)
(μmol m−2 s−1)	Early drought	105.18 (0.30)	76.93 (2.65)	98.07 (17.36)	88.93 (9.63)
(sd)	Late drought	49.22 (13.29)	54.62 (10.92)	51.74 (8.27)	59.93 (3.61)
φNPQt_300	Well watered	0.31 (0.03)	0.33 (0.04)	0.21 (0.03)	0.24 (0.04)
(%)	Early drought	0.24 (0.02)	0.32 (0.01)	0.27 (0.06)	0.28 (0.03)
(sd)	Late drought	0.55 (0.05)	0.49 (0.07)	0.52 (0.08)	0.49 (0.03)
φNPQt_1000	Well watered	0.64 (0.02)	0.66 (0.02)	0.57 (0.03)	0.59 (0.04)
(%)	Early drought	0.6 (0.01)	0.67 (0.01)	0.60 (0.06)	0.62 (0.03)
(sd)	Late drought	0.73 (0.01)	0.73 (0.02)	0.69 (0.05)	0.69 (0.01)
φNO_300	Well watered	0.21 (0.019)	0.22 (0.009)	0.24 (0.011)	0.25 (0.028)
(%)	Early drought	0.22 (0.018)	0.23 (0.01)	0.23 (0.032)	0.24 (0.011)
(sd)	Late drought	0.18 (0.045)	0.17 (0.015)	0.20 (0.036)	0.18 (0.019)
φNO_1000	Well watered	0.15 (0.022)	0.15 (0.006)	0.18 (0.018)	0.20 (0.029)
(%)	Early drought	0.15 (0.005)	0.15 (0.011)	0.17 (0.021)	0.17 (0.008)
(sd)	Late drought	0.15 (0.026)	0.14 (0.007)	0.19 (0.035)	0.16 (0.005)
SPAD 530	Well watered	58.66 (3.93)	52.42 (6.57)	58.53 (5.8)	41.54 (8.2)
	Early drought	53.06 (7.57)	45.61 (7.39)	56.86 (17.02)	43.19 (9.4)
(sd)	Late drought	98.91 (10.11)	72.59 (11.91)	102.86 (8.66)	84.86 (27.68)
gs	Well watered	0.48 (0.07)	0.21 (0.06)	0.44 (0.12)	0.23 (0.11)
(mmol m−2 s−1)	Early drought	0.30 (0.15)	0.17 (0.07)	0.15 (0.15)	0.09 (0.11)
(sd)	Late drought	0.19 (0.14)	0.17 (0.12)	0.04 (0.06)	0.06 (0.06)
Leaf temperature	Well watered	−1.2 (1.57)	−0.68 (1.02)	−0.58 (1.19)	−1.03 (0.94)
Differential (°C)	Early drought	−0.17 (0.81)	0.51 (1.32)	0.45 (1.48)	1.76 (0.7)
(sd)	Late drought	−0.1 (1.41)	0.53 (0.57)	0.33 (0.24)	−0.24 (0.35)
Relative	Well watered	45.75 (3.58)	42.46 (5.91)	45.72 (3.03)	29.57 (10.98)
Chlorophyll	Early drought	47.13 (3.18)	38.12 (2.41)	41.29 (14.02)	39.00 (4.99)
(sd)	Late drought	73.52 (2.04)	56.82 (5.37)	77.85 (3.67)	67.44 (10.18)

Analysis of Rapid Light Response Curves of Fluorescence

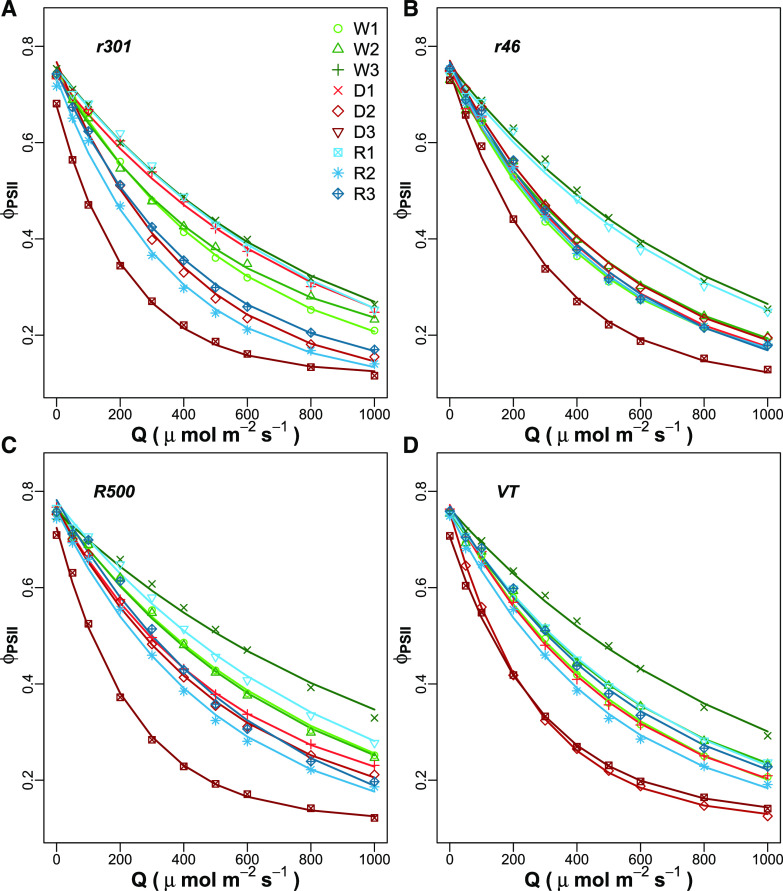
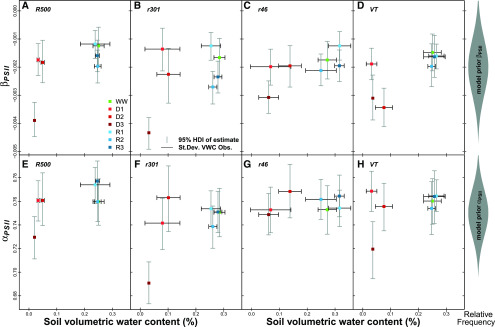
Rapid chlorophyll a fluorescence light response curves were taken on 119 replicate leaves during six different experimental days, with each genotype × treatment replicated one to seven times (mean replication rate of 3.3; Supplemental Fig. S1). The variation in sample size was due to time constraints and destructive measurements occurring during the experiment. First, the rapid light response curves for all genotypes and treatments were pooled together with the mean of observed ϕ_PSII at each Q estimated using the median value of the posterior distributions of the parameter from Equation 1. The decline was then fitted with an exponential model for each genotype and treatment (Fig. 2). All genotypes show a decline in ϕ_PSII under drought, more pronounced after 15 d (D3), but all plants recovered to prestressed values after rewatering (R1, R2, and R3). The partial increase of ϕ_PSII can be found in the rapid leaf development of the utilized genotypes, typical of the Brassicaceae. Since the youngest fully developed leaf was utilized at each measuring point, leaf growth and display changed over the course of 15 d, causing different leaf angles, changes in the photosynthetic complex stoichiometry, and different responses to incoming radiation and absorbance. Then, to utilize a more rigorous and probabilistic approach to signify differences (Kruschke, 2014), we used the 95% posterior high-density intervals (HDIs) as a Bayesian probabilistic estimator of difference. Figure 3 summarizes the changes in β_PSII and α_PSII, estimated following Equation 1, at varying VWC. Genotypes VT and r301 showed credible interval differences at 95% HDI in β_PSII for D2 and D3 relative to the WW treatment, whereas r46 and R500 showed a credible interval difference (95% HDI) only for D3 relative to the WW treatment (Fig. 3, A–D).

Figure 2.

ϕ_PSII across photosynthetically active radiation (Q) of 0 to 1,000 μmol photons m⁻² s⁻¹ for four B. rapa genotypes. Observations of r301 (A), r46 (B), R500 (C), and VT (D) occurred over a range of water regimes from well-watered (W1, W2, and W3) to increasing drought (D1, D2, and D3) conditions and different levels of rewatering (R1, R2, and R3). Points are mean values of replicates (n curves = 119, average n curves per replicate = 3.3), and fitted lines use median posterior estimates of a three-parameter exponential decline model (Eq. 1) by genotype × treatment.

Figure 3.

PSII dynamics in response to different water regimes. Decline rate in ϕ_PSII under increasing light intensity (β_PSII [Q⁻¹]; A–D) and maximum light-acclimated PSII efficiency (α_PSII; E–H) are shown for the four B. rapa genotypes R500 (A and E), r301 (B and F), r46 (C and G), and VT (D and H) over a range of water regimes, as defined in Figure 2, described by VWC. Points represent median posterior estimates of β_PSII and α_PSII from a three-parameter exponential decline model (Eq. 1; β_PSII and α_PSII are derived from n curves = 119, average n curves per replicate = 3.3), vertical bars are 95% high-density intervals of posterior estimates, and horizontal bars are sd values on observations of VWC (n = 153, average n per replicate = 4.25). At right are Bayesian prior distributions of β_PSII and α_PSII.

All genotypes demonstrated similar recovery patterns in β_PSII, with credible differences at 95% HDI for the R2 and R3 treatments relative to D3. For R plants, a less negative β_PSII was observed at 30 h after rewatering (R3) with respect to the 6-h period (R2), demonstrating ongoing recovery during that time period. Figure 3, E to H, displays the change of slope in ϕ_PSII as Q approaches zero, α_PSII, with 95% posterior HDI. r301, R500, and VT all show credible interval differences at 95% HDI in α_PSII for D3 relative to WW treatment, whereas r46 remains stable in α_PSII. The α_PSII parameter shows a recovery response similar to β_PSII, with r301, R500, and VT all showing credible interval differences at 95% HDI for the R3 treatment with respect to prestressed values.

Comparison of Photosynthesis Models

All three photosynthesis models (FvCB, Yin, and β_PSII) performed well across genotypes and treatments when comparing observations of leaf gas exchange with simulated results, using the medians of the posterior (i.e. a more rigorous Bayesian estimator that incorporates uncertainty in both measurements and models; Kruschke, 2014; McElreath, 2016) parameter distributions. For the β_PSII model, a comparison of simulated A_n versus observed A_n from light response and A/C_i curves results in 0.66 < R < 0.98 across genotypes and treatments (Supplemental Fig. S5).

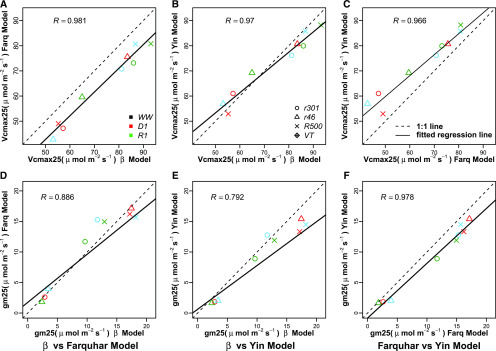
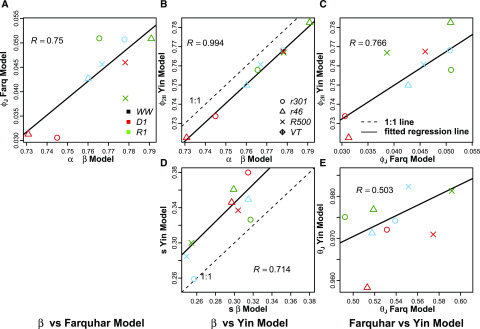
The β_PSII parameter, describing the slope of decline of ϕ_PSII versus Q, was integrated into the ETR derivation for estimating light-limited photosynthesis, A_J, and the updated ETR description was compared with both the FvCB and Yin photosynthesis models. To quantitatively evaluate the alternate modeling approaches estimating ETR, posterior parameter distributions were compared between the FvCB, Yin, and β_PSII decline models (Figs. 4 and 5). The correlation (R) of the medians of these posterior distributions was chosen to evaluate the strength and direction of a linear relationship among alternative parameterizations. For the parameter V_cmax, all models showed close agreement in estimates, with R values of 0.97 to 0.98 (Fig. 4, A–C). For g_m, the R value between the FvCB model and the β_PSII model was 0.9, between the Yin model and the β_PSII model it was 0.9, and between the FvCB model and the Yin model it was 0.99 (Fig. 4, D–F). Additional posterior parameters not common to all three models were compared with factors with similar biophysical meaning, such as quantum yield terms (ϕ_CO2, ϕ_2ll, and α_PSII; Fig. 5, A–C). Agreement between the quantum yield terms is particularly strong between ϕ_2ll (Yin model) and α_PSII (β_PSII model; Fig. 5B). The κ_PSII estimates show little correlation with J_max in the FvCB or Yin model (Fig. 5, D and E), whereas J_max estimates in FvCB and Yin are highly correlated. The Yin model and the β_PSII model were highly correlated in the lumped s parameter (R = 0.83). The convexity factor, θ, used in the FvCB and Yin models shows a correlation of 0.57, with the Yin estimates closer to the maximum of 1. Finally, a comparison was made between β_PSII as described in Equation 1 and the V_cmax and J_max estimates from the FvCB and Yin models. β_PSII showed an R value of 0.81 with V_cmax as described by the FvCB model and 0.83 with V_cmax as described by Yin. β_PSII showed R = 0.69 with J_max estimates of the FvCB model and R = 0.68 with Yin (Supplemental Fig. S6).

Figure 4.

Comparison of posterior median estimates of parameters common to the FvCB, Yin, and β_PSII photosynthesis models. A to C, Comparison of V_cmax estimates between β_PSII and FvCB, β_PSII and Yin, and FvCB and Yin with R for each relationship. D to F, Comparison of g_m estimates between β_PSII and FvCB, β_PSII and Yin, and FvCB and Yin with R for each relationship. Genotypes and water regimes are as defined in Figure 2.

Figure 5.

Comparison of posterior median estimates of parameters in the FvCB, Yin, and β_PSII models. A to C, Comparison of quantum yield terms for each model: α_PSII (mol photon mol⁻¹ e⁻) of the β_PSII model with ϕ_CO2 (mol CO₂ mol⁻¹ e⁻) of the FvCB model (A), α_PSII with ϕ_{PSII_ll} (mol photon mol⁻¹ e⁻) of the Yin model (B), and ϕ_J with ϕ_{PSII_ll} (C) with correlation coefficient (R) for each. D and E, Comparison of the s parameter between the Yin model and the β_PSII model (D) and comparison of θ_J between the Yin model and the FvCB model (E). Genotypes and water regimes are as defined in Figure 2.

Comparison of High- and Low-Throughput Fluorescence Measurements

Full gas-exchange light response curves coupled with fluorescence were taken on 34 leaves on four experimental days with each genotype × treatment replicated one to four times (mean replication rate of 2.3 ± 0.9; Supplemental Fig. S1). The variation in sample size was once again due to time constraints and destructive measurements occurring during the experiment. Specifically, the assessment of gas-exchange light response curves was done at experimental days 1 and 6 for WW plants, at days 5 and 7 for D1 plants, and at days 9 and 13 for D2 plants. Rewatered plants in the cohort R2 were observed at experimental day 10 (Supplemental Fig. S1). The assessment of rapid ϕ_PSII versus Q curves was done at experimental days 1, 5, and 9 for WW plants, at day 5 for D1 plants, at days 9 and 12 for D2 plants, and at day 13 for D3 plants. Rewatered plants had rapid ϕ_PSII versus Q observations for cohort R1 on experimental day 9, for cohort R2 on experimental day 13 (6 h after watering was restored), and for cohort R3 on experimental day 14 (30 h after watering was restored). The comparable posterior parameter estimates were matched with posterior parameter estimates from classic gas-exchange light response curves following Equation 1 and shown in Supplemental Figure S7. The median posterior estimates of β_PSII show an R value of 0.72, whereas median posterior estimates of α_PSII show R = 0.67 (Supplemental Fig. S7, A and C). Next, the correlation between the posterior estimates for both β_PSII and α_PSII derived using the full β_PSII photosynthesis model and the rapid fluorescence curves was tested (Supplemental Fig. S7, B and D). The full β_PSII photosynthesis model utilizes coupled gas-exchange and fluorescence observations from a low-throughput infrared gas analyzer (LiCOR 6400XT), whereas the rapid fluorescence curves of ϕ_PSII versus Q curves are obtained using the high-throughput spectrophotometer MultispeQ. Despite the different times of collection, the two methods agree, with correlations of 0.66 for β_PSII and 0.69 for α_PSII (Supplemental Fig. S7, B and D).

DISCUSSION

Here, we tested how applying alternative descriptions of quantum yield (ϕ_CO2, ϕ_PSII, and β_PSII) in photosynthesis models (Fig. 1) can improve the mechanistic realism of electron transport processes and their potential changes under drought. Our β_PSII photosynthesis model utilized the full ϕ_PSII versus Q response, accounting for possible photoprotective mechanisms (i.e. NPQ, changes in absorbance, etc.). All these mechanisms decrease photosynthetic ETR and play crucial roles in the A_n magnitude under stress, and we have to consider and quantify them to mechanistically improve simulated responses to drought and other environmental changes.

β_PSII Dynamics

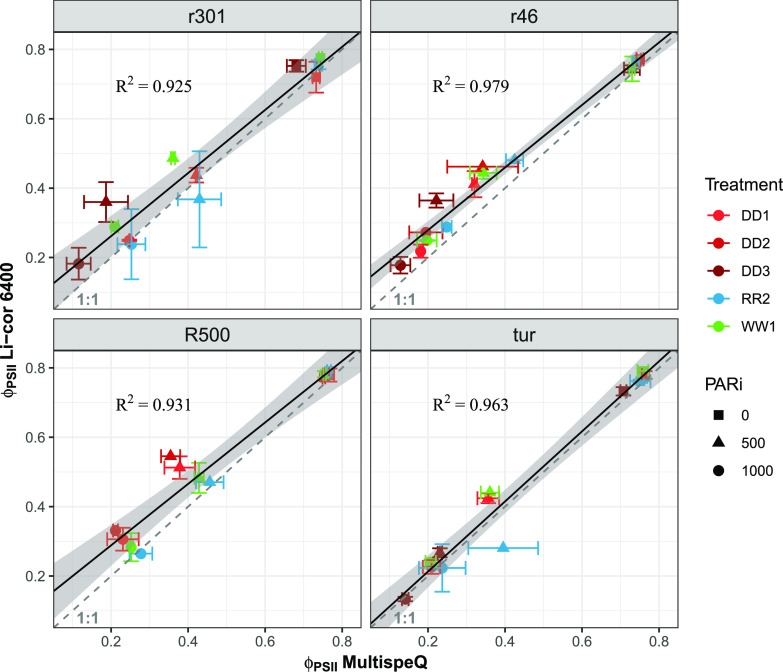
Our main goal was to explore the use of chlorophyll a fluorescence parameters derived from rapid light curves, collected with a dynamic high-throughput tool, to develop a photosynthesis model for estimating photosynthetic ETR. The major design improvement of the MultispeQ is the quick capture of fluorescence parameters precisely during steady-state illumination (Kuhlgert et al., 2016), and we tested the relationship between rapid fluorescence data from the MultispeQ and the LiCOR 6400-40 fluorimeter (Fig. 6). Single-measurement comparisons grouped by genotype show linear relationships across different light levels and water treatment, with R² > 0.9 despite the variations in time of day, duration of the actinic light, etc., between the low- and high-throughput measurements due to the fact that the LiCOR instrument is primarily utilized to take simultaneous measurements of gas exchange. Our results build on previous work by Meacham et al. (2017), who posed the question about the use of rapid fluorescence analysis for photosynthesis modeling. However, we experimented beyond their results, using the high-throughput MultispeQ instead of a monitoring PAM device from Walz, thus avoiding the use of aluminum foil to cover the leaves during the measurements and the possible increases in temperature with consequent changes in water vapor exchange (Giorio, 2011; Bücher et al., 2018). Rapid light curves are complex to interpret due to the presence of several components in the photosynthetic apparatus characterized by different time constants (i.e. the time to reach ∼63% of the full response) involved (Pearcy, 1990; Way and Pearcy, 2012). We acknowledge that light harvesting and energy transfer respond nearly instantaneously to changes in the light environment, whereas adjustments in the carbon cycle metabolites can take up to several seconds (Powles, 1984; Geiger and Servaites, 1994). However, the use of a fast analysis is necessary to capture the true light conditions of plants in the field, where they rarely photosynthesize at full capacity (Ort and Melis, 2011). Fast changes in incoming radiation, such as that used during the collection of rapid light curves, can be thought to have similar consequences as for leaves exposed to sunflecks. After an initial uncoupling of the electron transport from CO₂ fixation, the metabolite pool has been shown to refill within a few seconds in healthy leaves (Parry et al., 2008; McClain and Sharkey, 2019). The fluorescence calculated parameters have already been shown to have a very dynamic behavior (Porcar-Castell et al., 2012), which leaves room to accommodate for stress-related mechanisms.

Figure 6.

PSII efficiency instrumentation correlation. Comparison of ϕ_PSII across two instruments, LiCOR 6400 and MultispeQ, and three light intensities (0, 500, and 1,000 μmol photons m⁻² s⁻¹ photosynthetically active radiation [PARi]) for the four B. rapa genotypes r301 (A), r46 (B), R500 (C), and VT (D). Each set of observations occurred over a range of water regimes from well-watered (W1) to increasing drought (D1–D3) and rewatering (R2). Points are means of replicates, and error bars represent sd (total n LiCOR 6400 = 162, average n per replicate = 2.7; total n MultispeQ = 213, average n per replicate = 3.6).

The exponential decline of ϕ_PSII versus Q (Eq. 1) takes into account changes occurring at PSII antenna reaction center complexes and is extremely relevant under stress conditions. These changes are not included in current photosynthesis models (Fig. 1). Identifying the parameter β_PSII, meaning the rate of decline of ϕ_PSII at Q increase, and its dynamics at the onset of water stress is highly valuable to mechanistically elucidate processes of photoprotection and increased photorespiration, which are relevant for the overall reduction of assimilation under stress (Ort and Baker, 2002; Souza et al., 2004). The ϕ_PSII and Q relationship has been previously used to assess photosynthetic responses using the ETR maximum, showing declines under water stress (Rascher et al., 2004; Li et al., 2008; Batra et al., 2014).

Our results depict a more complete picture of the changes in ϕ_PSII versus Q under drought, and the parameter β_PSII seems to be better suited to explain a range of stress responses (Figs. 2 and 3). The observed declines in β_PSII, here observed under drought, may in fact be the result of more or less regulated processes, such as NPQ (Table 3), chloroplast light avoidance, and nonregulated energy dissipation (Müller et al., 2001; Kasahara et al., 2002; Takahashi and Badger, 2011). Furthermore, the modest recovery after a 6-h period in both β_PSII and α_PSII suggests that these parameters account for more than just fast-regulated photoprotective mechanisms (Dall’Osto et al., 2005; Lambrev et al., 2012). Nearly full recovery by 30 h after the start of rewatering may be due to slow-relaxing and/or unregulated processes, along with protein turnover and repair processes that require a longer time to return to prestress conditions (Nishiyama et al., 2006; Brooks et al., 2013; Malnoë, 2018). Indeed, both slow and rapid light curves are able to trigger slow-relaxing NPQ mechanisms (qI), with qI having lifetime changes similar to those observed during qE (rapid relaxing mechanisms; Müller et al., 2001; Lazár, 2015; Ruban, 2016).

Both β_PSII and α_PSII depicted genotypic variation relative to drought severity, with r301 showing greatest declines (i.e. transgressive segregation with respect to the RIL parents), followed by R500 and VT, which accumulate the highest amount of aboveground biomass (Fig. 3, B and F). Future work should consider how the slope of variation in the ϕ_PSII versus Q response relates to previous findings of root-shoot allocation differences occurring under drought (Edwards et al., 2016) as well as explore how variance in β_PSII may influence reactive oxygen species production and, when more pronounced declines occur, cellular damage (Reddy et al., 2004).

Implementing Photosynthesis Modeling

Using direct observations of ϕ_PSII versus Q data as parameters in a leaf photosynthesis model provided a means of quantifying the impacts of PSII photoprotective mechanisms on ETR. Although these protective processes are critical to final net photosynthesis, they are abstracted out of all FvCB-based modeling efforts (Horton et al., 1994; Allen and Pfannschmidt, 2000; Laisk et al., 2002); therefore, current parameterization approaches may be biased by tuning parameters without mechanistic insight. Our β_PSII approach extends the development of FvCB-based models using both A/C_i and light response curves in analysis (Holland, 2007; Patrick et al., 2009) to integrate both gas-exchange and fast chlorophyll a fluorescence observations into models (Laisk and Loreto, 1996; Laisk et al., 2002; Yin et al., 2006, 2009). The β_PSII photosynthesis model maintains the use of commonly employed parameters, such as V_cmax, R_d, and g_m, while shifting away from others, such as J_max and θ_J, that do not fully incorporate stress impacts on ETR, for describing ETR and associated processes. Estimates of the common parameters including V_cmax show strong similarity across the three considered photosynthetic models (Fig. 4). The correlations between the β_PSII with V_cmax and J_max estimates of the FvCB and Yin models is promising for model parameterization. The throughput of ϕ_PSII versus Q measurements will also increase the number of genotypes used in models and thus better incorporate mechanistically rigorous, genotype-level informed parameters for crop simulation (Boote et al., 2001; Bertin et al., 2010; Archontoulis et al., 2012; Pleban et al., 2018).

The lumped s parameter has a valuable role in accommodating a number of mechanisms affecting the final ETR and showed declines after 13 d of drought (Supplemental Fig. S3). Our photosynthesis model is able to assess the extent of the mechanisms slowing down ETR as a whole. However, the same MultispeQ collects fluorescence values at each recorded pulse. All components of NPQ (qE, qT, and qI) could then be calculated from values of F_m′ and F_m over time, allowing for a detailed energy partitioning analysis. These results could benefit the model and separate physiological (feedback mechanisms) and damage consequences of the stress. Future work, including the use of knockout mutants, such as those for genes involved in NPQ mechanisms, will be needed to disentangle the three factors lumped in s (f_alt, α_leaf, and ρ₂). Changes in relative chlorophyll and SPAD at 540 nm affect the overall leaf absorbance (α_leaf) and are partially responsible for changes in s (Table 3). Future work evaluating the light-harvesting properties of photosynthetic pigment molecules will help clarify the importance of this component on the lumped s. Isolating changes in α_leaf might also use statistical methods to identify dominant shifts in absorption from spectrophotometric data (Baker et al., 2018). It appears likely that the other two factors, f_alt and ρ₂, changed during drought progression, based on the decline in LEF relative to increases in ECS_t (Table 3). We speculate that the altered relationship between LEF and ECS_t may relate to energetic spillover and changes in cross-membrane ∆H⁺ triggering unbalanced activity in the PSII-PSI duo, ultimately leading to an increased cyclic electron flow around PSI (Livingston et al., 2010; Strand et al., 2015). Future data-model integration could consider saturation pulse estimation of PSI yield parameters to quantify the specific contribution of f_alt and ρ₂ (Klughammer and Schreiber, 1994). Integration with ECS_t data could also assist in understanding the potential for change in how transthylakoidal ∆H⁺ might be coordinated by the use of cyclic and other nonlinear electron transport pathways (Kramer et al., 2004b).

Our framework offers opportunities to better evaluate stress limitations on quantum yield and ETR. The coupling of s and β_PSII as described here is critical for future efforts to model individual photoprotective, photoinhibitory, and photodamaging mechanisms, which are encompassed in these two parameters, albeit in a lumped way. Further implementation of current instrumentation and further modeling approaches may allow for itemizing specific physiological or genetic mechanisms underlining s and β_PSII responses to drought (Noctor et al., 2002; Miller et al., 2010; Guadagno et al., 2017).

β_PSII Photosynthesis Model Limitations

Our approach needs additional tests under natural and/or higher intensity light conditions to investigate details of photoprotective mechanisms and their behavior under extreme environmental conditions. For instance, the ratio of carotenoids in the PSII antenna complex responsible for NPQ can vary with growing conditions (Kato et al., 2003). Furthermore, photodamage has been shown to be more severe in the UV range and at 500 to 600 nm, and the ratio of photodamage to repair is higher as light intensity increases (Nogués and Baker, 2000; Murata et al., 2007; Zavafer et al., 2015). Also, dynamic fluctuations in light, such as those in natural settings, can have relevant effects on photosynthetic rate (Vialet-Chabrand et al., 2016, 2017), which we expect are more severe under drought, with subsequent recovery processes possibly delayed (Fig. 3). The repair of PSII damage can also be compromised by temperature stress (Murata et al., 2007). Consequently, how β_PSII, α_PSII, and s respond to field conditions, drought, and other stresses should be further investigated.

The difficult estimation of g_m may also affect further implementation of our framework, and alternative methods of g_m assessment should be considered. The g_m estimation in all three photosynthesis models used the combined fluorometry/gas-exchange approach (Harley et al., 1992; Pons et al., 2009; Archontoulis et al., 2012). Two of the three models (Yin and β_PSII) included the s parameter to consider alternative electron pathways influencing the g_m estimation (Fig. 4, D–F). State-of-the-art photosynthesis models include a dynamic g_m responding to variations in both internal leaf status and external environments (Tazoe et al., 2009; Moualeu-Ngangue et al., 2017). Coupling online isotope discrimination data to the linear and total electron flow, gathered from gas-exchange and fluorometry observations, may help resolve concerns related to g_m estimation and allow for the integration of a dynamic g_m model into the β_PSII method (Pons et al., 2009; Tazoe et al., 2009; Gu and Sun, 2014; Moualeu-Ngangue et al., 2017; Flexas et al., 2018).

Predictive understanding of both photoprotective and g_m mechanisms is still in its infancy; the alternative approach we have successfully tested provides a crucial transfer of high-throughput empirical measurements and analyses to mechanistic simulations that are likely to improve predictive understanding of drought and other stress responses across a range of plant species and genotypes. Our β_PSII model will further the improvements of current whole-plant crop modeling by the incorporation of first-principles mechanisms (Hammer et al., 2006; Chenu et al., 2009; Wang et al., 2019) through the incorporation of more genetic and omic information into the parameters of biophysical-based models.

MATERIALS AND METHODS

Plant Material

Four genotypes of Brassica rapa were utilized for our analysis: two crop accessions, R500 (oilseed crop, B. rapa ssp. trilocularis [‘Yellow Sarson’]) and VT (VT-089, D’Auvergne Hative); and two RILs (r46 and r301). The RILs are part of a population developed from a cross between the R500 × Imb211 genotypes. The R500 genotype is an oilseed cultivar planted in India for approximately 3,000 years (Prakash and Hinata, 1980) with large allocation to seed production (Baker et al., 2015). The Imb211 genotype is a rapid-cycling line derived from the Wisconsin Fast Plant (Williams and Hill, 1986). The extremely divergent selection history suggests that genetic variation segregating in the RILs may resemble that segregating in crop × wild hybrids found commonly in nature (Adler et al., 1993). The RIL population has been previously described, and the two RILs of interest were chosen based on their transgressively segregating drought stress phenotypes identified in earlier research (Iniguez-Luy et al., 2009; Edwards et al., 2011, 2012; Pleban et al., 2018). Seeds of R500, r46, and r301 were obtained from a single-seed collection bulked at the University of Wyoming in 2011. VT was obtained from the Wageningen University and Research Center for Genetic Resources (CGN#10995).

Growth Conditions

Seeds were germinated and grown in pots (500 mL) filled with a soil mixture (Miracle-Gro Moisture Control Potting Mix [20%, v/v] and Profile Porous Ceramic Greens Grade [80%, v/v]) with the addition of 2 mL of Osmocote 18-6-12 fertilizer (Scotts). Experiments occurred during July and August 2017 at the University at Wyoming in three growth chambers (PGC-9/2; Percival Scientific). Growth chamber conditions were set at a 14-h photoperiod of approximately 250 to 300 μmol photons m⁻² s⁻¹ Q, with a 25°C to 30°C/18°C to 22°C day/night cycle, and relative humidity maintained at 45% to 65%. Soil moisture content was monitored daily for all treatment groups (ECH₂O/EC5 probe; Decagon). Plants were randomized in three growth chamber compartments with blocks of each treatment, with a randomized mix of four genotypes present in each compartment.

For 4 weeks, all plants were regularly watered to maintain VWC at 0.3 ± 5. At 28 d after sowing, watering was withheld from treatment plants in the droughted and rewatered cohorts (Supplemental Fig. S1). On experimental day 0, drought was applied via complete water withholding for the droughted cohort. Droughted plants were assigned to three different groups and replicate plants observed on experimental days 4 to 7 (treatment group D1), 9 to 12 (treatment group D2), and 15 (treatment group D3). On experimental day 9, water was reapplied to a subset of droughted plants (R1), and they were observed on experimental days 9 to 12. On experimental day 15, a second subset of droughted plants (R2) was rewatered and observed 6 h after rewatering. Finally, on day 16, the last subset of droughted plants was rewatered and assessed at 30 h after rewatering (R3). Soil moisture observations in this study were comparable to those from Guadagno et al. (2017), where the mean VWC was 0.06 ± 0.01 after 14 d of drought; here, the mean VWC after 13 d of drought was 0.05 ± 0.03.

Plant Physiological Observations

Physiological data collection followed the temporal frequency in Supplemental Figure S1. For evaluation of photosynthesis traits throughout the treatment period, A/C_i curves and photosynthetic light response curves were taken (LiCOR 6400XT; LI-COR Biosciences) following established methods (Long and Bernacchi, 2003). Both response curves were measured between 10 am and 4 pm on fully expanded leaves (between fifth and eighth leaves) with cuvette settings at a flow rate of 300 μmol s⁻¹, relative humidity maintained at 50% ± 8%, and temperature maintained at 20°C. A/C_i curves set sample chamber CO₂ concentrations to 50, 100, 200, 300, 400, 500, 600, 800, 1,000, 1,250, 1,500, and 2,000 µmol CO₂ mol⁻¹ air. A/C_i curves were taken on WW, D1, and R1 plants. Light response curves were measured across 10 light conditions (Q = 2,000, 1,500, 1,000, 500, 250, 125, 60, 30, 15, and 0 µmol photons m⁻² s⁻¹). Light response curves were taken on WW, D1, and R1 as well as D2 and D3 plants. For both response curves, PAM fluorescence was measured immediately after gas exchange using a leaf chamber fluorimeter (LiCOR 6400-40; LI-COR Biosciences). With actinic light maintained at setting of curve protocol (λ = 470 nm, 10% blue to obtain values of F_s), a short saturating pulse (0.8 s; ∼8,000 µmol photons m^–2 s^–1) was applied to measure F_m′ with a short far-red pulse to record the F_o′ value at the end of induction (Baker, 2008). These were used to determine the operating efficiency of PSII photochemistry, (F_m′ − F_s)/ F_m′ = ϕ_PSII, for light-acclimated conditions (Genty et al., 1989). Fluorescence measurements were taken in conjunction with all changes in C_i or Q for each A/C_i and light response curve.

Further chlorophyll fluorescence observations used a rapid PAM light response protocol developed for the MultispeQ spectrophotometer (PhotosynQ). The protocol is available on the PhotosynQ platform under project title: B. rapa drought and recovery Chl Fl evaluation (https://photosynq.org/projects/b-rapa-drought-and-recovery-chl-fl-evaluation). In a single 5-min clamping with a fully expanded leaf (between fifth and eighth leaves), actinic light (655 nm [Lumileds; LXZ1-PA01]) was incremented at 10 light intensities (1,000, 800, 600, 500, 400, 300, 200, 100, 50, and 0 µmol photons m^–2 s^–1) for 30 s before a PAM fluorometry sequence was initiated following established methods (Rascher et al., 2000; Datko et al., 2008). After each light acclimation period, the PAM sequences used the classic multiphase flash technique with four rectangular saturation flashes of 4,500, 4,050, 3,600, and 3,150. A linear regression of each maximum fluorescence ramp versus 1/Q was made to determine expected F_m′, used for calculating fluorescence parameters. Recently, the original derivation of NPQ was extended to NPQ_t, allowing for high-throughput (under 1 min each) yet mechanistically relevant measurements (Tietz et al., 2017). Therefore, this protocol assessed ϕ_PSII, the fraction of Q dissipated safely as heat (ϕ_NPQt), and the fraction of Q quenched via unregulated excitation dissipation (ϕ_NO) at each light intensity. ϕ_NPQt assumes a constant theoretical maximum dark-adapted fluorescence yield, and ϕ_NO represents the fraction of light use remaining after accounting for ϕ_NPQt and ϕ_PSII [ϕ_NO = 1 − (ϕ_NPQt + ϕ_PSII); Tietz et al., 2017]. From these response curves, LEF was calculated for each Q following LEF = ϕ_PSII Q α_leaf ρ₂, where α_leaf is assumed to be 0.85 and ρ₂ is assumed to be 0.5. Rapid PAM light response curves were taken on plants from each watering cohort (Supplemental Fig. S1).

Total ECSt measurements were obtained at two Q intensities (300 and 1,000 µmol photons m⁻² s⁻¹ at 650 nm) using the MutlispeQ (Kuhlgert et al., 2016). ECSt monitors the proton flow into the thylakoid lumen by evaluating shifts in the absorbance of cross-membrane carotenoid pigments (Fig. 1, blue H⁺ arrows). The carotenoid absorbance spectrum is dependent on the changing electrical gradient produced by proton flow across the thylakoid membrane (Sacksteder et al., 2000). The protocol for these ECSt observations is available on the PhotosynQ platform (https://photosynq.org/projects/b-rapa-drought-and-recovery-ecs-evaluation). ECSt observations were taken on plants of all watering cohorts (Supplemental Fig. S1). Observations of relative chlorophyll content were also measured with a hand-held MultispeQ spectrophotometer on plants of all watering cohorts (Supplemental Fig. S1).

Exponential Decline of ϕ_PSII Versus Q

Light response data, ϕ_PSII, from both the LiCOR fluorimeter and the MultispeQ rapid fluorescence protocol were used to model the decline in ϕ_PSII under increasing Q. A hierarchical Bayesian framework generated genotype × treatment posterior trait distributions of exponential decline parameters. A three-parameter exponential decline function was used following Equation 1:

where α_PSII (y intercept) represents the maximum light-adapted ϕ_PSII, β_PSII represents the exponential decline rate in ϕ_PSII under increasing Q, and κ_PSII represents a non-zero minimum of ϕ_PSII as Q approaches ∞. Equation 1 was modeled using rjags (Plummer, 2014), with samples from the posterior parameter distributions generated from a Gibbs sampling method (Plummer, 2003). Model parameters (α_PSII, β_PSII, and κ_PSII) were estimated using a three-level hierarchical structure with global, genotype × treatment, and individual plant levels. Priors for the means of the exponential decline parameters followed wide informed normal distributions broadly informed with wide variances. Priors for the precision terms used weakly informed normal distributions (Gelman, 2006). The credible interval divergence at 95% HDI was used to evaluate posterior parameter differences for each treatment time. This comparison metric used in Bayesian analysis allows the identification of definitive portions of the posterior distributions characterized by higher probability density than the regions outside those intervals (Kruschke, 2014, 2018; Kruschke and Liddell, 2018), with more rigorous results and higher predictive power.

Photosynthesis Modeling

Utilizing Bayesian statistics, all photosynthesis models describe how quantum yield and underpinning mechanisms are related to CO₂ assimilation under changing light conditions and water availability. The three model formulations are similar to those found in photosynthesis process models while hierarchically incorporating uncertainty and providing probabilistic quantification of parameters. Tables 1 and 2 outline the three modeling approaches used to test the utility of ϕ_PSII light response data for characterizing ETR and light-limited A_n. All three approaches estimate A_n following Equation 2.1 with the estimation of the critical C_i (C_crit), where A_c shifts to A_J, following methods detailed below. All three approaches estimate A_c using Equations 2.2 and 2.3 (Table 2). The approaches vary in the derivation of photosynthetic ETR. The first approach followed the FvCB model, estimating ETR using information from leaf gas exchange (Eq. 2.5; Farquhar et al., 1980; Farquhar and Wong, 1984; Fig. 1A). This FvCB derivation of ETR for A_J (J_m) requires estimation of three parameters: J_max, the maximum rate of electron transport; ϕ_CO2, the quantum yield on a CO₂-to-photon basis; and θ_J, the convexity factor for the response of ETR to Q. Two other parameters are fixed a priori in FvCB: an equal fractionation of light between PSI and PSII (ρ₂ = 0.5), and leaf absorbance (α_leaf) is set at 0.85. The second approach, described by Yin et al. (2009), used a combined gas-exchange and fluorescence approach for modeling ETR (J_f; Fig. 1B). The Yin model used ϕ_PSII data to parameterize PSII efficiency under limiting light (ϕ_{PSII_ll}) as well as the lumped parameter, s, which lumps α_leaf differences, differences in ρ₂, as well as utilization of alternate electron paths, f_alt, along the Z-scheme (Eq. 2.6). Low-light (0 < Q < 200 μmol photon m⁻² s⁻¹) response data (A_n, Q, and ϕ_PSII) were subset to estimate R_d, s, and ϕ_{PSII_ll} in the Yin model. R_d is estimated as the y intercept of linear regression of A_n against 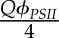. The slope of this regression is used to estimate s. The quantum yield parameter for the Yin model, ϕ_{PSII_ll}, was estimated as the y intercept of a linear regression of A_n against ϕ_PSII under low Q. Finally, for the third approach, the β_PSII photosynthesis model derivation ETR (J_l), the full light response ϕ_PSII data set was passed in the β_PSII model for the estimation of α_PSII, β_PSII, or κ_PSII needed to describe ETR (J_l; Fig. 1C). Following Equation 1, the α_PSII, β_PSII, and κ_PSII estimates were used to predict ϕ_PSII at each Q, next J_l was solved following Equation 2.7. β_PSII implementation used the same R_d and s estimation as Yin.

All models used a temperature response following an Arrhenius function for K_c, K_o, V_cmax, J_max, g_m, R_d, and Γ*. Each parameter was normalized with respect to 25°C following:

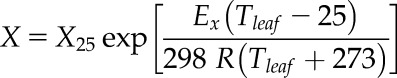where T_leaf is leaf temperature (°C), X₂₅ is the parameter normalized with respect to 25°C, E_X is the activation energy of each parameter, and R is the universal gas constant (8.314 J K⁻¹ mol⁻¹). Other temperature response functions were considered, but given the limited variability in T_leaf (mean = 20 ± 0.2), a simple one-parameter equation was selected for analysis.

C_crit, the C_i at which A_n transitions from A_c to A_J, was fixed at 285 ppm in all models based on an analysis of F_v′F_m′ under increasing C_i. F_v′F_m′ increases when C_i < C_crit and remains constant when C_i > C_crit (Sharkey et al., 2007; Gu et al., 2010; Moualeu-Ngangue et al., 2017). A Bayesian model was employed using a single change point method (Dose and Menzel, 2004) to estimate individual and population-level C_crit. Results of the change point model found that the posterior population level estimate had a mean of 287.3 with a 95% HDI of 265.1 to 318.7 ppm (Supplemental Fig. S8).

All C_i, A_n, Q, and T_leaf data from A/C_i and light response curves were used to estimate A_n traits, an approached used previously (Patrick et al., 2009; Archontoulis et al., 2012), with ϕ_PSII data supplied to the Yin and β_PSII models as described above. Parameter priors for FvCB and shared parameters among the three models were selected based on a recent implementation (Pleban et al., 2018). The code for all three photosynthesis models as well as the simple β_PSII decline model are available at https://github.com/jrpleban/.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Experimental design and observation schedule.

• Supplemental Figure S2. Volumetric soil water content dynamics.

• Supplemental Figure S3. Changes in lumped s parameter estimates.

• Supplemental Figure S4. Onset of the NPQt parameter.

• Supplemental Figure S5. Simulated A_n versus observed A_n for three photosynthesis models.

• Supplemental Figure S6. Correlations of β_PSII with classic photosynthetic model parameters.

• Supplemental Figure S7. Decline rates of PSII efficiency under changing light conditions.

• Supplemental Figure S8. Identification of the transition point between A_c and A_J (C_crit).