Accelerating membrane simulations with Hydrogen Mass Repartitioning

Abstract

The time step of atomistic molecular dynamics (MD) simulations is determined by the fastest motions in the system and is typically limited to 2 fs. An increasingly popular solution is to increase the mass of the hydrogen atoms to ~3 amu and decrease the mass of the parent atom by an equivalent amount. This approach, known as hydrogen-mass repartitioning (HMR), permits time steps up to 4 fs with reasonable simulation stability. While HMR has been applied in many published studies to date, it has not been extensively tested for membrane-containing systems. Here, we compare the results of simulations of a variety of membranes and membrane-protein systems run using a 2-fs time step and a 4-fs time step with HMR. For pure membrane systems, we find almost no difference in structural properties, such as area-per-lipid, electron density profiles, and order parameters, although there are differences in kinetic properties such as the diffusion constant. Conductance through a porin in an applied field, partitioning of a small peptide, hydrogen-bond dynamics, and membrane mixing show very little dependence on HMR and the time step. We also tested a 9-Å cutoff compared to the standard CHARMM cutoff of 12 Å, finding significant deviations in many properties tested. We conclude that HMR is a valid approach for membrane systems but a 9-Å cutoff is not.

Graphical Abstarct

Introduction

Biological membranes are an essential component of all living cells.¹ They serve as a barrier between the cell and the outside world, preventing entry of many potentially harmful compounds, as well as regulating cellular import and export through membrane proteins. Cell membranes are typically composed of a phospholipid bilayer with embedded and/or associated proteins.¹ Phospholipids are amphiphilic molecules that are characterized by a hydrophilic head group containing a phosphate, which is glycerol-linked to one or more hydrophobic fatty-acid tails (Fig. 1A).¹

Figure 1:

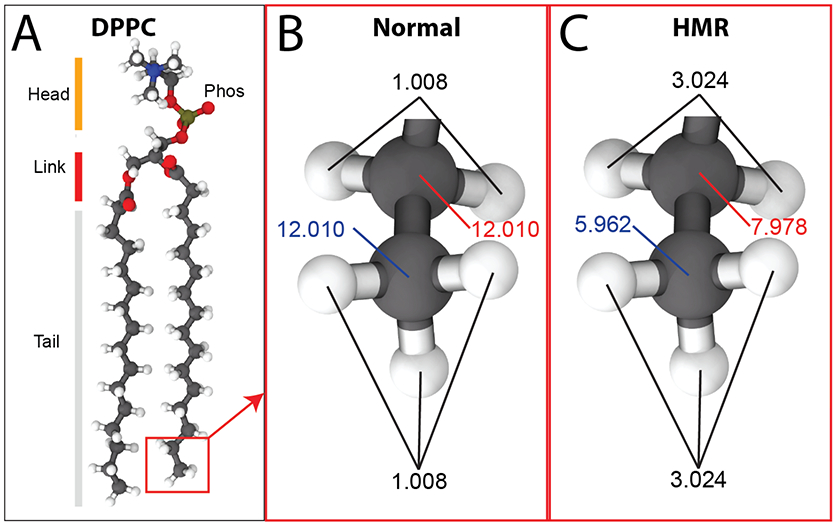
(A) Structure of DPPC lipid. Carbons are colored in dark grey, hydrogens in white, oxygens in red, nitrogen in blue, and phosphorus in tan. “phos” and “link” denote phosphate and ester linkages, respectively. (B) Normal mass distribution for the atoms in the acyl-chain tail. (C) Mass distribution for the same atoms with HMR.

Membrane models are frequently used in molecular dynamics (MD) studies because of their biological relevance. As such, MD simulations can be used to study membrane properties and provide an atomistic description of membrane structure and dynamics.^2-8 Additionally, membrane permeability and small molecule interactions are often of interest in drug design, which can be investigated computationally using membrane models.^9,10

A major challenge in membrane simulations is the need for accurate lipid force fields.^11,12 To date, multiple force field models have been developed: AMBER14,¹³ SLIPIDS,¹⁴ CHARMM36,¹⁵ and multiple GROMACS united-atom models;^16-18 several studies have compared lipid models and improved upon existing ones.^2,9,11,12,18 Force-field parameters are typically evaluated based on their ability to reproduce experimentally known structural and dynamic properties of pure-lipid bilayers, e.g., lipid area, bilayer thickness, compressibility modulus, deuterium order parameters, and diffusion coefficients.^2,8,11,12 In some cases partition coefficients have been calculated to validate lipid:small-molecule interactions.⁷ Furthermore, compatibility with water and protein force fields should be considered when choosing a lipid force field.^19,20

The CHARMM36 (C36) lipid force field is frequently used in MD simulations because it can accurately reproduce a number of physical properties of lipids, as well as its compatibility with the C36 protein and general small-molecule force field. ^{2,7,8,12,15,19,20} The most recent C36 lipid force field update resulted in improved agreement with experimental order parameters, compressibility modulus, and area per lipid.¹⁵ Furthermore, the recently launched CHARMM-GUI web interface, which supports several MD software packages, has greatly facilitated the construction of membrane systems for MD simulations, specifically utilizing the C36 force field.^21-24 CHARMM-GUI automatically generates structures, coordinates, parameters and input files for pure membrane and membrane-protein systems, supporting numerous phospholipid molecules.

In order to study properties of a membrane system, multiple simulations of sufficiently long time scales are typically required.^9,25 As such, there is significant benefit to improving simulation efficiency, particularly for membrane-containing systems, which can be much larger than protein-only systems. Previously suggested approaches to speed up MD simulations include using a longer time step.^26,27 Implementing a longer time step decreases the accuracy when integrating the equations of motion in MD; however, it has been shown that the introduced errors are typically much smaller than the statistical errors due to limited sampling.²⁸ Additionally, the increased energy drift introduced by a longer time step can be dampened by using a thermostat.^27,28 Currently, the magnitude of the time step in atomistic MD is limited by the fastest-moving atoms in the simulation, which are the vibrational motions of the hydrogen atoms.²⁶ Therefore, increases in time step can be achieved by slowing down or restricting the movement of the hydrogens.²⁶ Common practice in MD simulation has been an increased time step from 1 to 2 fs by keeping the covalent bonds involving hydrogen atoms rigid using SETTLE and SHAKE algorithms for water and other molecules, respectively.^29,30 The implementation of these algorithms nearly doubles the achievable simulation time at fixed computational cost; however, the SHAKE algorithm is likely to fail at time steps beyond 2 fs for conventional MD.^27,29

Recently, MD simulation studies have shown that time steps of up to 4 or 5 fs can be achieved by altering hydrogen masses.^26,27,31 It is important to note that when implementing mass modifications, it is requisite that the total mass of the system does not change.^26,27 As described by Feenstra et al., increasing the total mass of the system will result in a slower time scale for various events of interest, e. g., diffusion.²⁶ Similarly, in the virtual site technique (VST), the hydrogens' masses are assigned to the adjacent heavy atoms and their positions are calculated and updated based upon the positions of the heavy atoms.^31,32 However, implementing VST requires re-optimization of force field parameters, such that when applied to the C36 force field, VST was shown to alter several lipid properties, leading to thinner and more disordered bilayers.³¹ Recently, it was found that the combination of VST with HMR on every fourth methyl group in the lipid tails resulted in excellent agreement with measured lipid properties in standard MD simulations.³³

To clarify, HMR modifies the atomic input by repartitioning mass from each heavy atom to its covalently bonded hydrogens, while conserving the overall molecular mass.^26,27 Thus, when applying HMR, the reweighted hydrogen mass should not be greater than 3 amu because a larger mass transfer would make methyl carbons lighter than their bonded hydrogens. While in theory, such an increase in hydrogen mass only allows the time step to be increased by approximately a factor of $\sqrt{3}$, a 4-fs timestep has routinely been used. For instance, Hopkins et al. illustrated this method for both a small peptide as well as a large protein in explicit solvent.²⁷ They found that the protein/peptide with HMR applied, using a hydrogen mass of 3 amu and a time step of 4 fs, consistently reproduced conformations observed without HMR. However, when HMR was applied to both protein and water molecules, there was an increase in the viscosity of water and, consequently, slower transition rates between different protein conformations. Therefore, HMR should not be applied to water. Since its inception, HMR has been used in several software packages such as NAMD,³⁴ AMBER³⁵ and ACEMD,³⁶ in order to speed up MD simulation output.

It has also been shown that additional speed up can be obtained by decreasing the cutoff for non-bonded interactions. Although C36 lipids were parameterized and validated using a 12-A cutoff with a force-based switching function applied at 8 Å,¹⁵ most HMR studies employing lipids to date have used the C36 lipid force field with a 9-Å cutoff (default setting) in ACEMD or AMBER.^37-39 Previous MD simulations have shown that membrane properties are highly sensitive to the cutoff value and Lennard-Jones (LJ) switching functions because lipid dynamics are primarily driven by LJ interactions.^15,24 Additionally, lipids are more hydrogen rich than proteins, for which HMR was previously validated.²⁷ However, to date, the effects of HMR and a shorter 9-Å cutoff with the C36 lipid force field have not been systematically investigated.

In this paper we test the application of HMR with a 4-fs time step to membrane systems by comparing membrane properties and lipid-protein interactions. Additionally, the effects of 9-Å cutoff are examined. Several single-lipid, mixed-lipid, and protein-embedded membrane systems were studied. It is found that applying HMR with a 12-Å cutoff provides consistent results in comparison to conventional 2-fs time step and 12-Å cutoff MD across all studied systems. However, employing a 9-Å cutoff altered several structural and kinetic properties for lipid bilayers, as well as protein dynamics in some, but not all, cases.

Methods

Construction and analysis of pure membrane systems

All-atom lipid bilayers were generated for pure-membrane systems using CHARMM-GUI.²³ Three pure-membrane models (DPPC, POPE, and DOPC) were generated, as well as a fourth, multiple-lipid “Top6” model.⁴⁰ Each system contained 480 lipids (240/leaflet) and was solvated and ionized to a concentration of 150mM NaCl. Although smaller (60 lipids/leaflet) membranes were attempted initially, it was found that many of the properties measured either did not converge well in 100-ns simulations or disagreed with previously reported simulation results (data not shown). Further details about each system and constitutive components can be found in Table S1. Upon completion of the simulations, trajectories were analyzed to measure structural and kinetic properties such as area per lipid (APL), membrane thickness, deuterium order parameters, electron density profile, compressibility modulus (K_A), diffusion coefficient, dihedral trans-gauche transition rates, and hydrogen-bond lifetimes.

In the present work, the APL for all lipid membranes was computed from the area of the simulation box in the x-y plane divided by the number of lipids in each leaflet (240). Since we employed anisotropic pressure coupling, the simulation box was allowed to fluctuate during the simulation; APL was used to monitor simulation equilibrium. Membrane thickness is reported as the head-to-head average distance as measured in the electron density profiles, which was calculated using a simple binning procedure, as opposed to more precise methods designed for larger membranes.⁴¹ K_A is a measure of the stiffness of the membrane and was calculated as

$$K_{\mathrm{A}}=k_{\mathrm{B}}T\left(\frac{A}{{\sigma }_A^2}\right)$$ (1)

where k_B is Boltzmann’s constant, T is the temperature, A is the area, and σ_A² is the variance of the area during the simulation.

Diffusion values (D) are measured from the mean-squared displacement of lipids in the x-y plane according to

$$<\Delta r(\tau {)}^2>=\frac{1}{N}\sum _{i=1}^N\langle \Vert {\overrightarrow{r}}_i(t+\tau )-{\overrightarrow{r}}_i(t){\Vert }^2\rangle =4D\tau .$$ (2)

The sum occurs over all lipids and is averaged over all time separations τ. The first 1 ns of time lag is discarded. The diffusion coefficient is then obtained from the slope of the linear regime of mean-squared displacement versus time-separation. All diffusion values are measured over the last 50 ns of simulation with τ up to 20 ns. Any center-of-mass drift of each monolayer was removed prior to calculating the mean-squared displacement.

Deuterium order-parameters (S_CD) are used to compare lipid simulations to experimental results of membrane systems for each acyl carbon in the aliphatic tail, which are given by

$$S_{\text{CD}}=<\frac{1}{2}(3{\cos }^2\theta -1)>$$ (3)

where θ is the angle measured between the carbon-hydrogen bond vector and the membrane normal. The pure membrane systems simulated here are small enough to not exhibit largescale undulations, such that the normal vector to a membrane can be assumed to be parallel to the z-axis.

Construction and analysis of mixed membrane and large POPC systems

System construction and Anton simulation details of the mixed POPC:cholesterol membrane (POPC:CHL, see Table S1) were described in Hong et al.⁴² A POPC bilayer with 680 lipids was constructed by replicating an equilibrated bilayer with 170 POPC lipids four times.⁴² All simulation conditions of this large POPC bilayer as well as HMR simulations using a 4-fs timestep and 12-Å or 9-Å cutoff of the mixed POPC:CHL membrane were identical to those of the pure lipid bilayers described above.

Radial pair distribution function and clustering analysis of the mixed POPC:CHL membrane were performed following Hong et al.⁴² Undulation analysis of the 680-lipid POPC bilayer was performed using the MDAnalysis package.⁴³ Error estimation of the bending modulus k_c was performed as the following: A simulation trajectory was divided into M blocks, each of length τ_b. The average of u²(q), the square amplitude of undulation at a given wavenumber q, from each block was determined and then used to compute a standard deviation σ_ηb, based on which we obtained the blocked standard error (BSE):⁴⁴

$$BSE=\frac{{\sigma }_{{\tau }_b}}{\sqrt{M}}.$$ (4)

The error in k_c was then determined by assuming a ‘worst-case-scenario combination’ of errors from the four wavenumbers analyzed here: we subtracted the BSE from 〈u²(q)〉 for the lowest wavenumber and added the corresponding the BSEs to 〈u²(q)〉 for the remaining three wavenumbers, followed by re-fitting of a first-order polynomial. This procedure resulted in the upper-bound error in k_c. Conversely, a lower-bound error was obtained by adding the BSE to 〈u²(q)〉 for the lowest wavenumber and subtracting it from 〈u²(q)〉 for the remaining three wavenumbers. We note that the thus obtained errors were asymmetric.

Applied electric field simulations

An OmpF membrane-protein system was created using the crystal structure reported by Yamashita et al.⁴⁵ (PDB: 2ZFG) and embedded in a POPE phospholipid bilayer to replicate the systems used in Pezeshki et al.⁴⁶ The CHARMM36 protein force field was used.²⁰ The system contained 99,157 atoms with 176 POPE lipids, 19,421 water molecules, and 420 potassium (K⁺) and 396 chloride (Cl⁻) ions, giving a 1.12MKCl concentration. Three replica simulations of 10 ns each were carried out at 0 V, ±0.2 V, ±0.5 V, and ±1V mirroring a previous OmpF conductance study.⁴⁶ We report the average and standard deviation of the current at each applied voltage by summing up the movement of the charges in the z direction.^46-48

Construction and analysis of a G-protein coupled receptor (GPCR) system

The model of a GPCR was taken from the study by Hurst et al.⁴⁹, in which the cannabinoid type 2 (CB2) receptor was simulated in a POPC bilayer. The receptor was extracted and rebuilt in a slightly larger simulation cell with 83/75 phospholipids and 53/53 2-arachidonoyl glycerol molecules (2-AG, an endogenous ligand for CB2) in the upper/lower leaflets. Three separate 100-ns simulations utilizing each of the three protocols were performed. Trajectories were saved at a 10-ps time interval. Additional 1-ns simulations with trajectories saved every 100 fs were also performed to provide a more accurate measure of the short-lived water hydrogen-bonding autocorrelation functions.

The hydrogen bonding analysis and autocorrelation functions were computed using the LOOS ver 2.3.2 toolset.^50,51 For each frame, a hydrogen bond is defined as present (1) or absent (0) using a given geometric criterion between pairs of donors and acceptors. The autocorrelation function is subsequently computed using half of the trajectory and averaged over all pairs. Distance/angle cutoffs of 2.5 Å between the polar hydrogen and acceptor and a maximum deviation from linearity of 35 degrees were employed. In addition, an alternate approach to computing hydrogen bond dynamics is given by a procedure introduced by Rapaport⁵². Here the hydrogen bond between an acceptor/donor pair, h_ij, is again defined as 1 or 0 based on the above geometric criterion. The intermittent hydrogen bond autocorrelation function is given by:

$$C_I(t)=\langle \frac{\sum h_{ij}(t_0)h_{ij}(t_0+t)}{\sum h_{ij}(t_0{)}^2}\rangle .$$ (5)

The sum in the above equation is over all hydrogen bonds that exist at time t₀. Intermittent refers to a definition where a given hydrogen bond pair is allowed to break and subsequently reform. Finally an averaging over multiple start times is performed. This approach produces an autocorrelation function that represents the hydrogen bond population. In this work the hydrogen bond autocorrelation module of MDAnalysis⁴³ was used to compute the above correlation function.

Construction and analysis of L8 peptide system

An ac-L₈-nme (L8) peptide was constructed and embedded into the water phase of a box containing a pre-formed POPC lipid bilayer with a upper leaflet of 53 lipids and a lower leaflet of 52 lipids. The initial conformation was an ideal α-helix, placed 10 Å from the bilayer surface. The CHARMM36 protein force field was used to match previous simulations.^20,53 Dihedral restraints were applied to the peptide backbone to maintain the helicity due to the high temperature used (423 K), which has been validated previously for the same system.^53,54 The 200 kcal/(mol·deg.²) dihedral force constant used previously in a non-HMR system produced instabilities in the HMR system due to the smaller masses of the heavy backbone atoms, which are reduced by ~15%. Therefore, in order to maintain roughly the same mass-to-force-constant ratio, we similarly reduced the dihedral force constant to 175 kcal/(mol·deg.²) in the HMR system.

The insertion propensity, p_TM, of the L8 peptide was calculated as the probability of the peptide being in the TM state. To distinguish the TM state from the S state, a criterion of ∣z∣ < 8 Å was found to be optimal. The free energy of S→TM partitioning was then calculated as

$$\Delta G_{\mathrm{S}\to \text{TM}}=+k_{\mathrm{B}}T\log (1∕p_{\text{TM}}-1).$$ (6)

Construction of the glycophorin A dimer system

Simulations of glycophorin A (GpA) were started from the NMR structure in PDB 1AFO. The transmembrane (TM) helix dimer was placed in a POPC bilayer containing 60 lipids in each leaflet using CHARMM-GUI.²³ The flexible termini of each protein were removed as done previously,⁵⁵ leaving residues 69 to 97. The system was solvated with water, and Na⁺ and Cl⁻ ions were added at a concentration of 150 mM (12 ions of each species).

MD simulations

After construction, HMR was applied to each unique system using a VMD⁵⁶ script provided in the supplement (hmr.tcl), which created two copies, standard and modified, with the difference being the repartitioned mass in the latter. For the standard copy, MD was performed with a 2-fs time step, a 12-Å cutoff (2-12) for the Lennard-Jones interactions, and a force-based switching function starting at 11 Å to match that used for NAMD simulations in Klauda et al. 2010.¹⁵ The modified copy was simulated using a 4-fs time step and either a 12-Å cutoff with switching starting at 11 Å (4-12) or a 9-Å cutoff with no switching (4-9). In all simulations, long-range electrostatic interactions were evaluated every 4 fs using the particle-mesh Ewald method.⁵⁷ Unless otherwise stated, constant temperature was enforced using Langevin dynamics with a damping constant of 1.0 ps⁻¹ and constant pressure was enforced using a Langevin piston at 1 atm.⁵⁸ All simulations used NAMD2.12,³⁴ TIP3P water⁵⁹ and, unless otherwise noted, the CHARMM36m force field for proteins^20,60 and CHARMM36 for lipids.¹⁵ System visualization and analysis was performed with VMD.⁵⁶ An example NAMD configuration file with the recommended settings for an HMR membrane simulation is provided in the supplement.

Free-energy calculations for the glycophorin A dimer system

Potentials of mean force (PMFs) for GpA separation were calculated for 2-12, 4-12, and 4-9 simulation protocols. When used, forced-based switching of the LJ interactions started at 10 Å instead of 11 Å used in other simulations. The PMFs are a function of the distance between the centers-of-mass of the C_α atoms of residues 72 to 96 of each helix. Replica-exchange umbrella sampling (REUS) was used. A total of 26 windows separated by 0.5-1 Å were distributed along the range 7 Å to 24 Å; the force constant in each window was between 2.5 and 4 kcal/mol·Å². Typical exchange rates between windows were between 0.1 and 0.5. For each of the three protocols, 100 ns/window was used (2.6 μs/protocol); the first 10 ns was discarded with the weighted histogram analysis method (WHAM) performed on the last 90 ns.⁶¹ Although the PMFs are likely not yet fully converged,⁵⁵ the root mean-square difference between 70 ns and 100 ns is 0.3 (2-12; 0.1 for 90 vs. 100 ns), 0.9 (4-12; 0.2 for 90 vs. 100 ns), and 1.4 kcal/mol (4-9; 0.5 for 90 vs. 100 ns).

Results and Discussion

To determine the effects of HMR, time step, and cutoff on structural and kinetic properties, we performed all-atom MD simulations employing three different simulation protocols. As a reference, we first simulated each system using a 2-fs time step and a 12-Å cutoff with a force-based switching function (referred to as 2-12 throughout the text). The other two protocols implement HMR along with a 4-fs time step and either a 12-Å cutoff (referred to as 4-12) or a truncated 9-Å cutoff with no switching (referred to as 4-9). Results of lipid membrane simulations are compared with observations from X-ray, neutron scattering, or NMR experiments by considering temporal and spatial averages of various observables, e.g., bilayer thickness (D_HH) or APL.^62,63

Pure membranes

DPPC membrane

Dipalmitoylphosphatidylcholine (DPPC) is a common lipid that has been widely utilized in both experiments and simulation and, thus, has ample data for comparison.^15,64-66 We examined multiple static and kinetic properties of a DPPC membrane based on 100-ns simulations, including electron density, APL, K_A, S_CD, D, and dihedral trans-gauche transition rates.

First, static properties of the pure DPPC membrane were measured to compare with previous experimental and MD results. The APL for DPPC at 323 K in the 2-12 and 4-12 simulations is around 60-61 Ų (Table 1). Experimental values are slightly larger at 63.3-64.3 Ų.^64,65 Our numbers are in good agreement with those using HMR and a stochastic velocity rescaling thermostat and optimal temperature evaluation.⁶⁷ However, Venable et al. found slightly larger simulated areas (62.9 - 63.0 Ų) when using a switching function for the LJ interactions that began at 8 Å instead of 10 Å, the latter being the default for the C36/C36m protein force field.⁵ In our 4-9 simulation, the APL increases substantially, to 65.1 Ų. This increase is due to a reduction in the dispersion interactions, which are dominant in the aliphatic tails region (Fig. S1), and is also reflected in the decreased tail order (Fig. 2C) and thinning of the electron density profile (Fig. 2B). Fluctuations in the APL contribute to the area expansion modulus, K_A (see Eq. 1). K_A values from each of the DPPC systems (Table 1) are in reasonable agreement with the experimentally observed value (231 mN/m⁶²), with no observable pattern between the different simulation protocols.

Table 1:

Average properties of lipid bilayer; Area per lipid (APL), membrane thickness (D_HH), area compressibility modulus (K_A), and diffusion coefficient (D). The values of temperature in the parentheses indicate that the property was measured at that specific temperature. We note that for all simulations presented in this table, temperature was controlled using Langevin dynamics with a damping constant of 1.0 ps⁻¹.

System	Setting	APL (Å2)	DHH (Å)	KA (mN/m)	D (Å2/ns)
DPPC (323 K)	2fs-12Å	60.4 ± 0.7	39.1	249	1.32
	2fs-12Å HMR	60.4 ± 0.7	39.0	228	1.04
	2fs-9Å	64.0 ± 0.7	38.0	196	1.96
	4fs-12Å	61.6 ± 0.7	38.7	253	1.37
	4fs-9Å	65.1 ± 0.7	38.0	251	2.27
	Exp.	63.1 – 64.264,65,68	37.8-38.065,68	231 62 (318K)	1.78 69
POPE (310 K)	2fs-12Å	57.4 ± 0.6	40.4	282	0.57
	4fs-12Å	58.0 ± 0.7	40.3	222	0.86
	4fs-9Å	61.1 ± 0.6	39.5	280	1.11
	Exp.	59.8 – 60.870	40.070 (303K)	233 71	–
DOPC (295 K)	2fs-12Å	67.0 ± 0.6	38.7	350	0.59
	4fs-12Å	67.0 ± 0.6	38.7	289	0.56
	4fs-9Å	70.3 ± 0.7	38.0	241	1.04
	Exp.	67.468 (303K)	36.772 (303K)	30073 (303K)	1.074 (296.5K)
Top6 (310 K)	2fs-12Å	61.5 ± 0.6	37.2	327	0.71
	4fs-12Å	62.5 ± 0.6	37.0	269	0.84
	4fs-9Å	64.8 ± 0.6	36.9	290	1.35
	Exp.	63.0 ± 0.275	–	24075 (310K)	–

Figure 2:

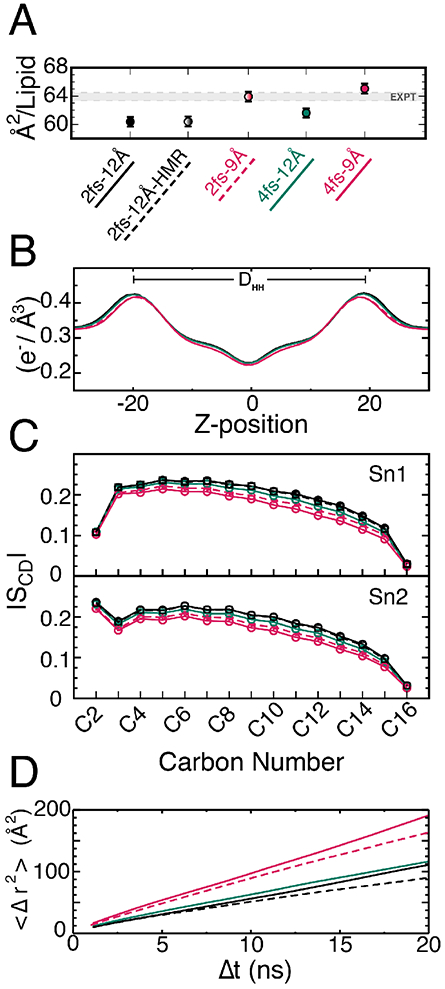
DPPC membrane properties. For each panel, results from 2-12 simulation is colored in black, 4-12 in green, and 4-9 in red. An additional 2-12 simulation with HMR is shown as a dashed black line and an additional 2-9 simulation with a shorter cutoff is shown as a dashed red line. (A) Area per lipid with standard deviation bars taken from last 50 ns of production. (B) Plot of electron density; membrane thickness is measured from left peak to right peak of each distribution. (C) Plot of sn1 (top) and sn2 (bottom) lipid order parameters (circles). (D) Mean-squared displacement vs. time averaged over all lipids and times for each simulation.

Next, we looked at order parameters (Fig. 2C), finding that the values from our 2-12 simulation agree well with previous experimental⁶⁴ and simulation^15,76-78 results. When comparing the 4-12 simulation to the 2-12 simulation, there is a small decrease in lipid order resulting in a 5.7 ± 2.8% difference on average over all the carbon positions; when comparing 2-12 and 4-9 simulations, the decrease is much larger (17.4 ± 6.4%), suggesting that the cutoff has a significant effect on tail order. To decipher the individual roles of HMR and the 4-fs time step, we performed an additional simulation with 2-fs time step, 12-Å cutoff and HMR (2-12-HMR), which showed a decrease of 1.0±0.8% on average in the order parameters (Fig. 2C), similar to the 2-12 simulation. This result suggests that HMR has little to no effect on order parameters, a 4-fs time step causes a slight but measurable decrease, and a reduced cutoff causes a substantial decrease in lipid tail order. The decrease in tail order parameters is also evident from an increased interdigitation of the aliphatic tails in the 4-9 simulation (Fig. S1, bottom) compared to 2-12 (Fig. S1, top) and 4*12 (Fig. S1, middle) simulations. Furthermore, aliphatic interdigitation between membrane leaflets results in membrane thinning by 1 Å in the 4-9 simulation compared ⁷⁹to the 2-12 simulation (Fig. 2B).

Diffusion in the DPPC membrane

We examined the rate of lipid diffusion as a function of HMR, time step, and cutoff. The diffusion constant is known to be sensitive to a number of simulation parameters, including box size⁷⁹ and thermostat.⁸⁰ A high sensitivity was observed here as well. Diffusion constants were calculated from the slope of the mean-square displacement vs. time, averaged over lipids and time (Fig. 2D). We found that the 2-12 and 4-12 simulations produced similar values at 1.32 and 1.37 Ų/ns, respectively, both smaller than the experimental value of 1.78 Ų/ns.^69,81 For the 4-9 simulations, D was much larger at 2.27 Ų/ns. All values of D described in this section can also be found in Table S2.

To further disentangle the roles of cutoff, time step, and HMR, we carried three additional simulations: one with a 2-fs time step but with HMR applied (2-12-HMR), one with a 2-fs time step and a 9-Šcutoff (2-9), and one with a 2-fs time step and 12-Šcutoff as well as an area fixed to match that of 4-9 simulation (2-12-CA; 65.1 Ų/lipid). The 2-12-HMR simulation produced a value of D at 1.04 Ų/ns, even smaller than 2-12 (1.32 Ų/ns), indicating that mass repartitioning is not a source of increased diffusion observed in the 4-9 simulation. The 2-9 simulation gave a value of D at 1.96 Ų/ns, close to 4-9 and much greater than 2-12 and 4-12. This suggests that the decreased cutoff, which results in an increase in APL, is responsible for a large fraction of the increase in D. Finally, the 2-12-CA simulation resulted in a value of D of 1.54 Ų/ns, closer to 2-12 than to 4-9, suggesting that the increase in D observed in the 4-9 simulation is primarily a direct result of the reduced cutoff, as opposed to an indirect result due to the increased APL.

The previously described simulations all used Langevin dynamics with a damping constant of γ = 1.0 ps⁻¹. However, although it is one of the most common thermostats used in NAMD simulations, Langevin dynamics has been demonstrated to reduce diffusion constants by up to 35%.⁸⁰ We decided to investigate the role of the thermostat by first lowering the Langevin damping constant from 1.0 to 0.1 ps⁻¹. Unsurprisingly, D became larger for all systems at 1.55 Ų/ns for 2-12, 2.30 Ų/ns for 4-12, and 3.59 Ų/ns for 4-9. We also tested the Lowe-Andersen thermostat, which is designed to minimize suppression of diffusion.⁸² Interestingly, the 2-12 simulation gave a similar value of D at 1.23 Ų/ns (Fig. S2). However, D was much greater for 4-12 at 2.33 Ų/ns and 4-9 at 3.89 Ų/ns, similar to Langevin dynamics with a very small damping constant. The increase in D when going from a 2- to a 4-fs time step, which was minimal previously (see Table 1), is significant here. Increasing the time step is expected to contribute a very small additional “numerical damping” when using Langevin dynamics,⁸³ counter to what is observed. Alternatively, it has been found previously in simulations of a generic van der Waals fluid that increasing the time step (in increments of 10 fs) leads to enhanced diffusion, due to harder collisions.⁸⁴ This is also borne out by looking at the average temperatures, which are consistently higher for a 4-fs time step vs. a 2-fs one (see Fig. S3 and Table S3).

To investigate another possible source for the different diffusion constants related to the altered masses, the trans-gauche (t-g) transition rate for the aliphatic dihedral angles were measured. It has been suggested that intramolecular conformation of the lipid molecule is closely related to the intermolecular structure of the membrane, such that the t-g transition time in dihedral angles may provide a good estimate for the equilibration time needed.⁸⁵ Here, we measured the rate of transition between the trans, gauche+ and gauche- conformations of sequential carbons on the lipid tails of DPPC. It was found that the transition rates between trans, gauche+, and gauche- were nearly identical for all simulation protocols over a 1-ns simulation (see Tables S4 and S5). Therefore, the variation in diffusion constants among the three simulation protocols described above did not correlate with their trans-gauche transition rates.

Other membranes

After measuring the effects of HMR, longer time step, and a shorter cutoff on an unsaturated membrane, we proceeded to simulate three additional membranes to determine if varying lipid composition would alter our initial observations. We performed simulations of 1-palmitoyl,2-oleoyl-sn-glycero-phosphatidylethanolamine (POPE, one unsaturated tail), 1,2-oleoyl-sn-glycero-phosphotidylcholine (DOPC, two unsaturated tails), as well as the socalled “Top6” membrane, which is a mixture of saturated, unsaturated, and cyclic-containing lipids.⁴⁰ In order to expand upon the same measurements as the DPPC simulations, each of these membranes were simulated using the 2-12 protocol as a control, as well as the additional 4-12 and 4-9 protocols applying HMR. We report the various physical properties of the membranes in Table 1. These properties were calculated over the last 50 ns of each 100-ns simulation.

For each system, APL values in the 2-12 and 4-12 systems are in a good agreement with experimental measurements (see Fig. S4 for graphs of APL fluctuation over the entire simulation period). It was also observed that the 4-9 systems have the largest APL values in each of the systems, demonstrating again that APL increases with a shorter cutoff (12 Å vs. 9 Å). One particular result of interest is the difference in diffusion coefficients observed in each of the membrane-only systems. For the POPE membrane, we observe a 50% increase going from 2-12 to 4-12, although both DOPC and Top6 membranes are closer (5-18% difference between 2-12 and 4-12); however, as was observed for the DPPC membrane, damping from the Langevin thermostat may be suppressing larger differences between them. All 4-9 systems have diffusion values nearly twice as large as their respective 2-12 system. This is due in part to the increased fluidity of the membrane as is also seen in the lipid order parameters (Figs. S5-S8). Unlike other properties, the values of K_A showed no consistent pattern between simulation protocols, although almost all numbers were within a range of ~200-300 mN/m.

Lipid mixing and membrane bending modulus

To examine the impact of time step, HMR and cutoff on lipid mixing, we turn to the POPC:CHL mixture previously investigated by microsecond Anton simulations.⁴² Each leaflet of the mixture was composed of 70 POPC and 35 cholesterol, with the latter initially placed at the center of the bilayer. This mixed membrane was simulated for 1 μs with either the 4-9 or the 4-12 protocol (the Anton simulation reported previously⁴² provides the reference for 2-12). Unless otherwise noted, we analyzed the trajectory from the first microsecond of the 2-μs Anton simulation for a fair comparison with the 1-μs runs performed in this work.

As shown in Fig. 3, regardless of the protocol used, the final structures of the mixtures are similar to each other, as reflected by the ratios of unlike-to-like (UL) neighbors (Fig. 3A,B) and the size distribution of cholesterol clusters (Fig. 3C). Therefore, the equilibrium distribution of the lipids is unaffected by the choice of time step, use of HMR, or cutoff. The APL of the mixtures, however, is clearly affected: averaging over all POPC and cholesterol yields an APL of 46.4 Ų, 47.1 Ų and 49.4 Ų for the 2-12, 4-12, and 4-9 simulations, respectively, reflecting a trend consistent to that observed in our DPPC simulations (Table 1). Comparison of the three simulations also reveals a clear difference in the speed of mixing. Semi-quantitatively, this can be seen from Fig. 3D-F and Fig. S9, which show the evolution of the radial pair distribution function g(r) over the course of the 4-9 and the 4-12 simulations as well as the first 1 μs of the previously performed 2-12 simulation. The g(r) curves, drawn every 100 ns, suggest that the 4-9 run converges much faster than the other two simulations. Quantitatively, the lateral diffusion coefficient of cholesterol in the 4-9 simulation (0.65 Ų/ns) is over 2× larger than that in the 2-12 simulation (0.25 Ų/ns). Similarly, POPC diffuses significantly faster in the former system, with a diffusion coefficient of 0.61 Ų/ns (0.22 Ų/ns in the 2-12 run). In the 4-12 simulation, diffusion of cholesterol (0.44 Ų/ns) and POPC (0.30 Ų/ns) is also accelerated compared with the 2-12 simulation, although to a much smaller degree than in the 4-9 simulation.

Figure 3:

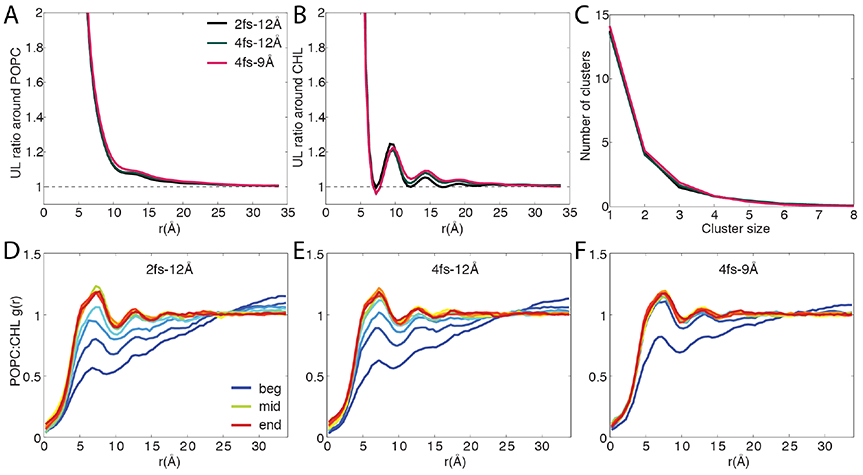
Impact of HMR, time step and cutoff on lipid mixing. (A-B) Average ratio of unlike neighbors to like neighbors (UL) around a given lipid species. The expected values based on mixing ratio are indicated by dashed lines. (C) Clustering analysis results of the POPC:CHL mixture. (D-F) Time evolution of the radial pair distribution functions g(r) for POPC:CHL. g(r) is averaged in 100-ns blocks and colored by simulation time, with blue, green and red indicating the beginning, the middle and the end of a simulation, respectively.

Apart from lipid lateral diffusion, it is worth noting that a cholesterol flip-flop event was recorded in both the 4-9 and the 4-12 simulation, in contrast to zero flip-flop events recorded throughout the 2-μs 2-12 simulation. The larger APL in the 4-12 and 4-9 simulations may have contributed to their increased cholesterol flip-flop events, as the APL is linked to the free energy barrier of defect formation in a membrane.⁸⁶ Taken together, the choice of time step, cutoff and use of HMR has a negligible effect on the distribution of lipids in an equilibrated mixture, although other equilibrium properties, such as the APL, are evidently affected. On the speed of lipid mixing, while increasing the simulation time step from 2 fs to 4fs and applying HMR has a rather moderate effect, decreasing the cutoff from 12 Å to 9 Å significantly accelerates mixing. Overall, our results indicate that mixing simulations designed to investigate the equilibrium distribution of various lipid components can safely employ HMR.

Following our investigation on lipid mixing, we went on to evaluate how HMR may affect one of the most important material moduli of a membrane, namely, its bending modulus. Using a bilayer with 680 POPC lipids, we performed three 1-μs simulations with the 2-12, 4-12, and 4-9 protocol, respectively. The ~150 Å × 150 Å bilayer supported relatively long-wavelength undulation modes, thereby, allowing us to determine k_c from 〈u²(q)〉, the average square amplitude of undulation at a given wavenumber q. More specifically, k_c was calculated from the last 900 ns of the 1-μs trajectories according to 〈u²(q)〉 = k_ck_BTA⁻¹q⁻⁴ using the MDAnalysis package⁴³ and methods presented in Refs.^87,88. As shown in Fig. S10, k_c was found to be 30.9 k_BT (12.9 × 10⁻²⁰ J) in the 2-12 simulation, which is comparable to the experimental value (9.0 × 10⁻²⁰ J) reported for a similar lipid bilayer (1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine).⁸⁹

To estimate the uncertainty in k_c, we first examined the blocked standard error in 〈u²(q)〉. The undulation mode with the smallest wavenumber (longest wavelength) was found to have the largest error, calculated from the last 900 ns (Fig. S10). The error is approximately an order of magnitude greater if only the last 50 ns of trajectories are used in the analysis instead of the last 900ns (data not shown). This behavior supports the need for microsecond-long trajectories in reliable analysis of k_c. Here, the uncertainty in our k_c values was found to be approximately 2 k_BT. Compared with the 2-12 run, k_c decreased slightly to 28.6 k_BT in the 4-12 simulation. In the 4-9 simulation, a further decrease was seen, with k_c reaching 25.4 k_BT. We note that the difference between the 2-12 and the 4-9-simulations is well beyond the estimated uncertainty in k_c, indicating that the comparison is statistically meaningful. The average projected APL was found to be 64.2, 64.9, and 67.3 Ų in the 2-12, 4-12, and 4-9 simulations, respectively. Taken together, these results again reflect the weakened lipid interactions when a short cutoff (9 Å) is adopted. Such weakened interactions not only produce an increased area per lipid, but also reduce the energetic cost of bending the membrane and, thereby, resulting in a decreased k_c.

Membrane-protein systems

Electric Field Simulations of OmpF

One important function of membrane proteins is to regulate the flow of ions into and out of the cell. OmpF is a well-characterized trimeric protein that acts as a nonspecific ion channel in the outer membrane of Gram-negative bacteria.^90,91 To continue the investigation into the effect of timestep, cutoff, and HMR on properties like conductance, we performed simulations with an applied electric field on the outer membrane ion channel OmpF. We note here again that HMR was never applied to water molecules. Scaling by molarity, our results across all simulation protocols compare favorably to those reported by Pezeshki et al.,⁴⁶ including the higher current for positive voltages due to a slight cation selectivity of the channel. At low voltages we observe a near exact agreement between all three simulation protocols (Fig. 4). At higher voltages, the 4-9 simulation underestimates the current, while the 4-12 simulation slightly overestimates the current with respect to the conventional 2-12 simulation. However, the deviation for each of the HMR systems is within, or very nearly within the standard deviation of the conventional 2-12 system indicating that HMR, longer timestep, and shorter cutoff do not significantly affect the conductance of OmpF. Interestingly, however, the root mean-square deviation (RMSD) of the proteins is notably higher in most cases for the 4-9 simulations, especially at higher voltages, while the 2-12 and 4-12 simulations are practically the same (Fig. S11). This suggests that the shorter cutoff may perturb the structure of proteins under applied forces.

Figure 4:

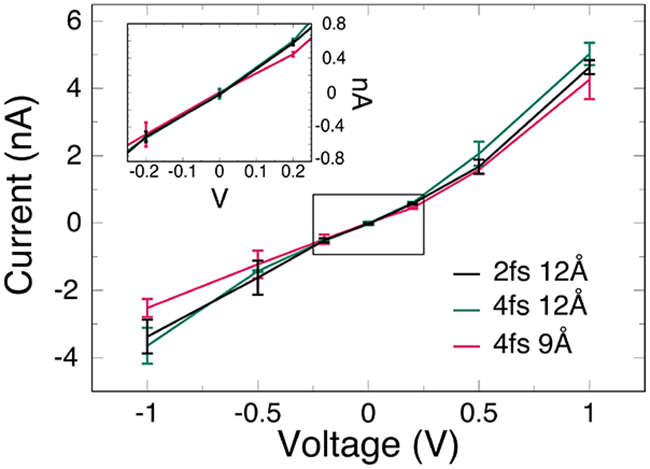
Current vs. voltage for OmpF membrane protein systems (2-12 in black, 4-12 in green, and 4-9 in red). Inset graph shows the low-potential regime and the little distinguishable difference in the measured current of each system.

CB2 Simulations

GPCRs are integral membrane proteins that share a common architecture of seven transmembrane helices (TMHs) connected by intracellular (IC) and extracellular (EC) loops. These membrane-bound proteins are central among the classes of proteins involved in signal transduction. Ligand binding to, and subsequent conformational changes of, GPCRs leads to activation of intracellular heterotrimeric G-proteins and ultimately cellular response. To a large degree, this functionality is achieved by the inherent flexibility of GPCRs.⁹² As a result functional outcomes can and are modulated by their lipid environment.⁹³ Therefore one should anticipate that the structure and function of these membrane bound systems would be coupled to the details of the treatment of the membrane environment. Given the importance of hydrogen bonding in maintaining the structure of GPCRs in a membrane environment, we have explored the effects of HMR, as well as potential energy truncation, on the initial equilibration of the receptor to a lipid environment as well as the occurrence and lifetime of intra- and inter-molecular hydrogen bonding for the CB2/POPC systems.

Using the CB2 model of Hurst et al.⁴⁹ we have run three 100-ns simulations for each of the 2-12, 4-12, and 4-9 protocols. The RMSD of the transmembrane portion of the receptors is reported in Fig. 5. The use of the transmembrane region for analysis is motivated by the work of Grossfield et al.⁹⁴ where they have shown that sampling on the time scale of 100 ns for the extracellular and intracellular loops of rhodopsin are not converged. In fact further analysis indicates that convergence can be expected to be much longer.⁹⁵ Here we are interested primarily in the initial equilibration of the starting structure. For each trajectory the first 20 ns was discarded and all further analysis was performed on the last 80 ns. Subsequently, time averaging for each trajectory was performed. This resulted in an average RMSD of 1.41 (±0.22) Å, 1.40 (±0.23) Å, and 1.53 (±0.14) Å for the 2-12, 4-12, and 4-9 simulation protocols, respectively (standard deviation in parentheses). From these data, it appears the choice of HMR and time step produces results that are nearly identical on the 100-ns time scale. The 4-9 simulation has a slightly larger RMSD; however, given the standard deviations these differences appear minimal.

Figure 5:

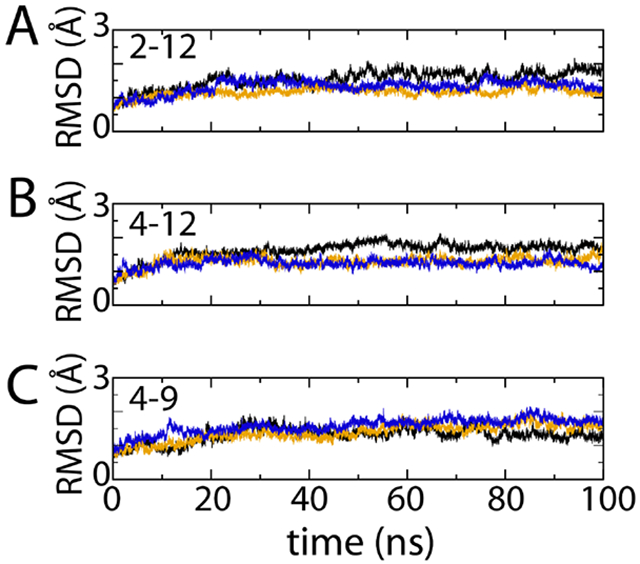
Root mean-square deviation (RMSD) for the three 100-ns trajectories using (A) the 2-12, (B) the 4-12, and (C) the 4-9 protocols. The colors for the traces represent independent runs.

We examined the hydrogen bonding capacity of the transmembrane helices as a function of HMR, time step, and cutoff. In Fig. S12, the fraction of hydrogen bonds is plotted for each transmembrane helix in each protocol. Overall, given the overlap of the error bars, the three simulation protocols produce essentially the same helical hydrogen bonding patterns. Lastly, the functionally important “ionic lock”, a salt bridge between the intracellular ends of TMH3-TMH6 keeping the receptor in the inactive state, is maintained, and the toggle switch residue W6.48 remains in the g+ conformation for all three sets of simulations.^92,96

We also examined the intra- and inter-molecular hydrogen bonding autocorrelation functions. Given that water was not subjected to HMR and polar hydrogens are not present in POPC, hydrogen bonding between CB2 donors (polar hydrogens) and the available acceptors in the simulation, including CB2, water, and lipid acceptors, have been considered. Due to the short lifetime of a typical water hydrogen bond, we ran and analyzed separate 1-ns simulations with a high trajectory output rate. The averaged autocorrelation functions obtained using LOOS are reported in Fig. 6A-C. These individual correlation functions appear to give similar results, with all three protocols agreeing to within their standard deviations.

Figure 6:

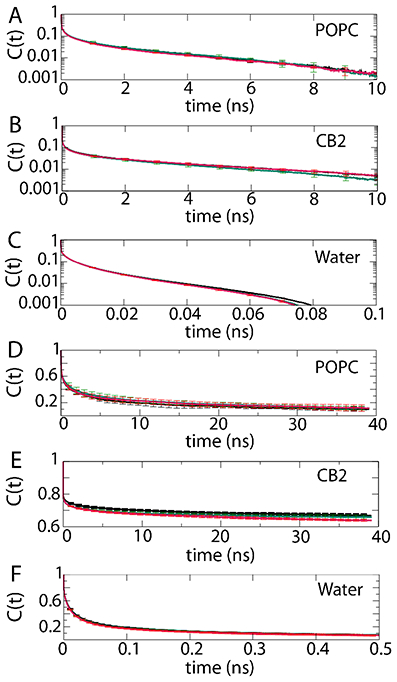
Hydrogen bonding auto-correlation functions. 2-12 data is shown in black, 4-12 in green, and 4-9 in red. Values reported are averaged over three separate runs with the standard deviations reported. (A-C) Hydrogen bonding correlation functions generated with LOOS for the indicated interactions, plotted using a logarithmic scale on the y-axis. (D-F) Hydrogen bonding correlation functions generated with MDAnalysis.

In addition to the LOOS-based hydrogen-bond autocorrelation functions, MDAnalysis⁴³ was used to generate population autocorrelation functions⁵² which are plotted in Fig. 6D-F. Analogous to the LOOS results, and given the standard deviations, there is very little apparent difference in the autocorrelation functions indicating that the hydrogen bonding dynamics for these 100-ns trajectories are not particularly sensitive to the mass repartitioning/cutoff treatment.

Peptide partitioning in POPC

To further investigate how membrane-protein kinetics are affected by HMR, we performed long equilibrium simulations of an octoleucine (L8) helix embedded within a POPC bilayer (see Methods) using the 4-12 and 4-9 protocol for comparison to a previous simulation on Anton.⁵³ With the peptide starting in a transmembrane (TM) state and using a high temperature (423 K), we measured the number of transitions between the TM and surface-associated (S) states over the course of a 1.3- and 1.5-μs production run for the 4-12 and 4-9 protocol, respectively. The TM state was defined as ∣z∣ < 8 Å, where z is the distance between the center of mass of the peptide backbone and the center of the membrane, consistent with previous studies of L8 insertion into a lipid bilayer.⁵³ The high temperature was necessary for sufficient sampling of the two states, and backbone dihedral restraints were added to ensure the peptide did not unfold (see Methods).⁵³ We observed 14 transitions in 1.3 μs (10.7 transitions/ μs) in the 4-12 simulation, while we only observed 10 transitions in 1.5 μs (6.7 transitions/ μs) in the 4-9 simulation (see Fig. 7A). In addition, the peptide spent far less time in the S state for the latter, with ΔG_S→TM = −2.8 kcal/mol for the 4-9 simulation compared to −0.9 kcal/mol for the 4-12 simulation (see Fig. 7B and Methods for calculation of ΔG_S→TM). Previous multi-μs-scale simulations of L8 at 423 K run on the Anton supercomputer with a 2.5-fs timestep and a 13-14-Å cutoff without HMR produced roughly 12 transitions/ μs, with a temperature-independent ΔG_S→TM = −0.9 ± 0.2 kcal/mol.⁵³ Results from the 4-12 simulation are in good agreement with these values, reproducing the free energy difference and only slightly underestimating the S→TM transition rate. The 4-9 simulation, however, significantly overestimates the free energy difference and underestimates the transition rate. This difference is likely due to the increase in area (6% on average for the 4-9 vs. the 4-12 simulation), which may stabilize the TM state.

Figure 7:

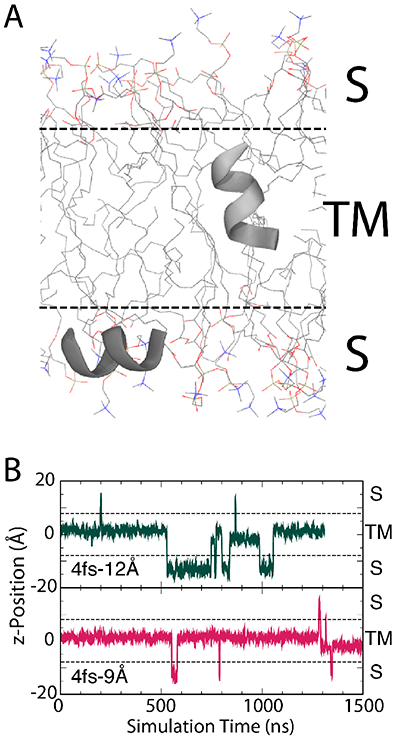
Transmembrane to surface-associated transitions of L8 helix in a POPC bilayer with HMR. (A) Position and orientations of L8 in surface-associated (S) and transmembrane (TM) states. The peptide is shown in cartoon representation and colored grey. Lipid molecules are shown in line representation and colored by atom name (hydrogen atoms omitted). (B) Position of helix within the membrane for the (top) 4-12 simulation and (bottom) 4-9 simulation. The center of the membrane is defined as z = 0 Å and TM states are defined as ∣z∣ < 8 Å.

Free-energy calculations of transmembrane helix dimerization

The transmembrane domain of glycophorin A (GpA), a single helix, forms a dimer in the membrane through the interactions of matched GxxxG sequences in each copy. It has long been a model system for both experimental and computational investigations into helix-helix packing in the membrane.^55,97-107 A number of these studies focused on the energetics of dimerization, calculating potentials of mean force (PMFs) in multiple environments and using different reaction coordinates. The most straightforward choice is a center-of-mass distance between the two helices, although it has been recognized recently that this coor-dinate becomes degenerate at close (< 15 Å) separation.¹⁰⁷ Nonetheless, for simplicity of comparison to previous PMFs, we used the center-of-mass distance between the two helices to calculate the PMF here for each of the 2-12, 4-12, and 4-9 protocols.

PMFs were determined using replica-exchange MD with 26 windows covering a range of 7 to 24 Å (see Methods). All PMFs exhibit a minimum at 7.5 Å with a well depth of ~6 kcal/mol, similar to at least one of the previously determined PMFs (Fig. 8).¹⁰³ While the 2-12 and 4-12 PMFs are broadly similar (root mean-square difference of 0.5 kcal/mol), the 4-9 PMF stands out, reaching its maximum roughly 5-10 Å closer than the other two (root mean-square difference between 4-9 and 2-12 PMFs of 1.0 kcal/mol). Thus, we see here that the shorter cutoff has a more dramatic effect on the free energy of interaction than the longer timestep and HMR.

Figure 8:

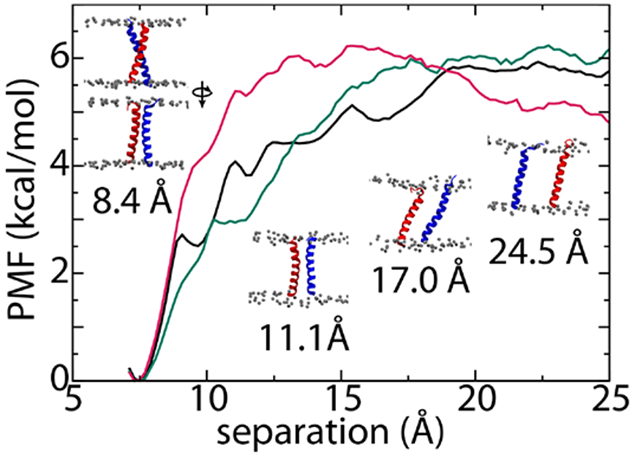
Potentials of mean force for glycophorin A separation as a function of distance between the centers-of-mass of the transmembrane helices (100 ns/window REMD calculation). Black is the 2-12, green is the 4-12, and red is the 4-9 simulation.

Benchmarks

Benchmarking simulations were carried out for the 240-lipid DPPC membrane (113,064 atoms) and the large, 680-lipid POPC membrane (170,844 atoms). Each system was run on 1, 2, 4, 8, 12, 16, and, for the larger system, 24 CPU-only nodes of (1) Stampede2 at Texas Advanced Computing Center (Intel Xeon Skylake CPUs; 48 cores/node) and (2) Bridges at Pittsburgh Supercomputing Center (Intel Haswell CPUs; 28 cores/node). Each simulation system was run using (1) the 2-12 protocol, (2) the 4-12 protocol, (3) the 4-12 protocol and PME evaluated every 8 fs, (4) the 4-9 protocol, and (5) the 4-9 protocol and PME evaluated every 8 fs.

As expected, the 4-9/8-fs-PME simulations had the greatest simulation output (ns/day) at practically all node counts (Fig. S13). However, the benefits accruing from each approximation were not equal. The 4-12 simulations are consistently ~75% faster than the 2-12 simulations on CPUs (Fig. S14). However, employing a 9-Å cutoff only speeds up simulations by an additional 20-45%. Evaluating PME electrostatics every 8 fs instead of 4 fs is of mixed benefit at either cutoff, giving at most 40% improvement in speed at high node counts; at reasonable node counts (efficiency > 75%), the speedup is 20% at most (Fig. S15).

Although no production simulations in this paper used GPUs, we also benchmarked on 1-4 NVIDIA GTX 980 cards on a single node with two Intel Xeon Haswell CPUs (24 cores, using 6 cores/GPU). Going from 2-fs to 4-fs time steps gives a consistent speedup of 40%. No improvement was seen when shortening the cutoff; short-range interactions are evaluated on the GPU(s), but these simulations are CPU-limited. Additionally, no benefit was seen when evaluating PME every 8 fs instead of 4 fs (Fig. S13E,F). For comparison, we tested the DPPC membrane with Amber16 on a single P100 GPU. As with NAMD on CPUs, going from a 2-fs to a 4-fs time step gave a speedup of 85-90%. In contrast, however, the 9-Å cutoff with no switching gave an additional 60% speedup.

Conclusions

MD simulations of membranes and membrane proteins have become increasingly common over the last two decades, and the need for longer trajectories has grown concomitantly. Thus, methods to improve the efficiency of these simulations are highly desirable. One approach, although at least two decades old,²⁶ has gained prominence recently: HMR. HMR accelerates the simulation by redistributing the mass from a parent atom onto its bonded hydrogens, thus slowing their motions and permitting a larger time step, typically 4 fs instead of 1-2 fs.²⁷ We applied HMR to a variety of membrane-only and membrane-protein systems using NAMD³⁴ along with the C36/C36m^15,20,60 force field. Our results show only marginal differences between the standard masses with a 2-fs time step and the repartitioned masses with a 4-fs time step for almost all properties tested, namely, the electron density profiles, order parameters, and compressibility modulus. APL and diffusion constants, which showed some differences, are discussed below. The overall robustness of MD simulations to such system alterations is supported by the modified virtual interaction sites method in Gromacs, which also found excellent agreement for most structural properties of modified C36 lipids using a time step as large as 5 fs.³³

Diffusion constants were found to be larger in many cases with a 4-fs time step compared to a 2-fs one. Specifically, D was as much as 50-90% greater in the 4-12 DPPC simulation compared to the 2-12 simulation when Langevin dynamics with a damping constant of 0.1 ps⁻¹ or a Lowe-Andersen thermostat is used (see Fig. S2); however, this difference was nonexistent in most cases with Langevin dynamics with a damping constant of 1.0 ps⁻¹. Such an increase is expected due to harder collisions that occur when atoms are allowed to move closer to one another in a single time step.⁸⁴ The effect of harder collisions is also manifest in the temperature (see Fig. S3 and Table S2) and the APL, which was slightly larger (by 1-2%) in most systems with a 4-fs time step, similar to the increase in area observed when going from 1-fs to 2-fs time steps.⁵ While to obtain precise kinetic properties, it is recommended to first test the simulation parameters selected against experimental data, a general approach of using Langevin dynamics with a very small damping constant, e.g., 0.5 ps⁻¹, may be a reasonable compromise. A similar recommendation was made based upon a thorough analysis of different thermostats, although caution was still advised when using Langevin dynamics and related approaches.¹⁰⁸

We also investigated another common approach used to speed up simulations, namely reducing the Lennard-Jones potential cutoff. Although C36 is parameterized for membranes based on a 12-Å cutoff with a force-based switching function starting at 8 Å (although typically set to 10 Å to match the protein force field),⁵ a number of studies have pushed the cutoff to 9 Å with no switching function.^37-39 However, our results here show that there are trade-offs involved with this approximation, such as increased APL, disorder, and rate of diffusion (Fig. 2). While these altered properties do not necessarily invalidate a simulation’s results, their effects should be carefully considered. Looking ahead, approaches such as Lennard-Jones PME, ^109,110 which obviates the need for a cutoff, is likely to overcome the