Abstract
Cardiac-coronary interaction and the effects of its pathophysiological variations on spatial heterogeneity of coronary perfusion and myocardial work are still poorly understood. This hypothesis-generating study predicts spatial heterogeneities in both regional cardiac work and perfusion that offer a new paradigm on the vulnerability of the subendocardium to ischemia, particularly at the apex. We propose a mathematical and computational modeling framework to simulate the interaction of left ventricular mechanics, systemic circulation, and coronary microcirculation. The computational simulations revealed that the relaxation rate of the myocardium has a significant effect whereas the contractility has a marginal effect on both the magnitude and transmural distribution of coronary perfusion. The ratio of subendocardial to subepicardial perfusion density (Qendo/Qepi) changed by −12 to +6% from a baseline value of 1.16 when myocardial contractility was varied by +25 and −10%, respectively; Qendo/Qepi changed by 37% when sarcomere relaxation rate, b, was faster and increased by 10% from the baseline value. The model predicts axial differences in regional myocardial work and perfusion density across the wall thickness. Regional myofiber work done at the apex is 30–50% lower than at the center region, whereas perfusion density in the apex is lower by only 18% compared with the center. There are large axial differences in coronary flow and myocardial work at the subendocardial locations, with the highest differences located at the apex region. A mismatch exists between perfusion density and regional work done at the subendocardium. This mismatch is speculated to be compensated by coronary autoregulation.
NEW & NOTEWORTHY We present a model of left ventricle perfusion based on an anatomically realistic coronary tree structure that includes its interaction with the systemic circulation. Left ventricular relaxation rate has a significant effect on the regional distribution of coronary flow and myocardial work.
Keywords: cardiac-coronary coupling, coronary flow analysis, flow dispersion, heart failure, left ventricular mechanics, regional myocardial work, subendocardial ischemia
INTRODUCTION
Coronary flow provides nutrients and oxygen to the myocardium and is spatially heterogeneous (6, 7). The spatial heterogeneity in perfusion occurs at both the macroscale (45) and the microscale (53). The contraction and relaxation of the left ventricle (LV) have a significant influence on the coronary microcirculation (43), and coronary flow dispersion in a beating heart is significantly lower than in an arrested heart (7). Spatial dispersion of coronary flow is well documented in the LV’s transmural direction and significantly increases with coronary artery disease, leading to subendocardial hypoperfusion and ischemia (35). A few studies have also reported spatial heterogeneity of flow in the axial (base to apex) direction of the LV (7, 45, 49) with a lower value of coronary flow around the apex (26, 75). The effect of the LV’s dynamics on spatial heterogeneity of coronary flow is underscored by the increase in subendocardial vulnerability to ischemia from either a longer systolic contraction or a slower LV relaxation during ischemic heart disease (12). Furthermore, spatial heterogeneity of coronary flow is highly sensitive to changes in the myocardial contractility (22), the diastolic time (12, 56), and the LV’s afterload and preload (35). Quantification of the effect of these variables on both the organ-scale LV mechanics and coronary microcirculation can help identify factors causing the global and regional balance (or imbalance) between demand and supply of oxygen to the myocardium, which is physiologically relevant for preventing myocardial ischemia.
The global mechanical work done by the LV, characterized by the pressure-volume (PV) loop area, is linearly correlated to the LV’s oxygen consumption (80). Regional work done by the LV, characterized by the myofiber stress-strain area, has been a realistic measure of local oxygen demand (20). A linear correlation between the work done and oxygen consumption of the LV is valid even when the LV’s contractility, preload, and afterload were varied (13, 80, 87). Therefore, a similar relationship between myocardial work and oxygen consumption can be hypothesized at the local or regional level. Because the myocardium extracts a major portion of oxygen from coronary flow (23), it is likely that the regional coronary flow also scales linearly with regional oxygen consumption. Changes in either the coronary flow (supply) because of coronary disease or the oxygen consumption (demand) due to remodeling of a diseased LV could result in the uncoupling of coronary flow from cardiac work. Furthermore, measuring the regional myocardial work (myofiber stress-strain curve) is not feasible (20), thereby confounding the evaluation of clinical therapies that redistribute regional cardiac work (64, 65). An additional complexity in determining a relationship between LV’s energetics and its perfusion is the ventricular-vascular coupling (88) and the regulation of coronary flow based on the myocardial metabolic demand (23, 35). The above quantitative description between global cardiac work and oxygen consumption has not shed light on the effect of the LV’s intrinsic properties of contractility, relaxation rate, passive properties, and myofiber orientation, nor its extrinsic characteristics of preload and afterload on the spatial distribution of coronary flow and regional cardiac work.
Computational models of the mechanical interaction between the LV and the coronary tree are viable options for quantitative understanding of cardiac and coronary pathophysiology (1, 5, 54, 60, 61, 74, 84). Existing computational approaches for coronary flow are either lumped parameter models (21, 35, 48) or distributive network flow models (9, 37, 50, 62). Some distributive models for coronary flow consider the entire arterial tree (9, 37) but do not model the cardiac-coronary interaction (2, 61). Existing simulations consider the LV as a lumped model (58, 60) or as a time-varying elastance model (25, 69, 71), both of which cannot capture the transmural and base-apex differences in myocardial-vessel interaction. Three-dimensional finite element (FE) models (5, 72, 74, 85), unlike the lumped models of the LV, can incorporate patient specific geometries, inhomogeneous material properties, complex boundary conditions, myofiber orientation, large deformation, and electromechanics. Computational models have shown the important role of coronary vessel properties and myocardial vessel interaction (MVI) in the subendocardium on transmural heterogeneity of myocardial ischemia (2). Integrating this MVI model (2) with a high-resolution integrated cardiac-vascular FE model (72) will yield novel predictions on the effect of the LV’s intrinsic and extrinsic characteristics on the regional distribution of coronary flow and myocardial work that are not yet available.
Therefore, a multiscale computational cardiac-coronary model that accounts for the spatial mechanical effect of the LV on coronary microcirculation is presented here. This model provides a unique opportunity to quantify macro- to microscale changes in the LV on the alteration of regional cardiac work and coronary flow in both the transmural and axial directions. It also offers insight into the regional vulnerability of the LV to ischemia under a wide range of pathophysiological conditions, from abnormal coronary microvascular function (15) to reduced cardiac function and exercise intolerance leading to heart failure (19).
METHODS
A model of the LV is constructed from an idealized geometry (Fig. A1) with anisotropic material properties that account for the myofiber orientation. A high-resolution finite element (FE) model of the LV (72) is coupled to a lumped model of the systemic circulation (Fig. 1), and the model details are presented in appendix a, Left Ventricular Finite Element Model and Systemic Circulation Model. The second aspect of the platform is the coronary flow model that is presented in a later section and in appendix b. The baseline input parameters for the LV model (Table A1) are adopted from the Guccione model (29, 30), the LV circulatory system (Table A2) from Shavik et al. (72), and the coronary flow model (Table A3) from Namani et al. (61). Model assumptions for the LV, systemic, and coronary circulation are listed in Table 1. Interaction between the myocardium and coronary vessels is defined below.
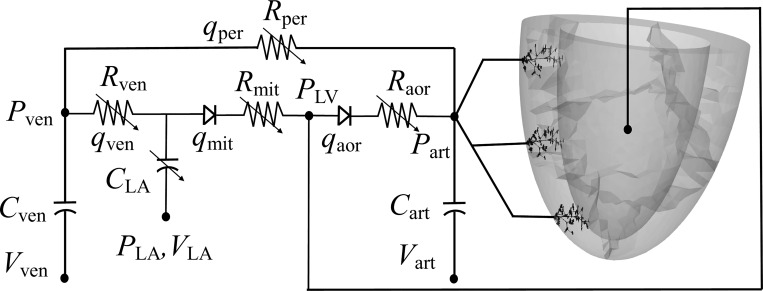
Fig. 1.
Schematic of the cardiac-coronary modeling framework. Left ventricle (LV) and coronary tree were connected to a closed-loop lumped circulatory system. Pressure (P), volume (V), resistance (R), and compliance (C) are the properties in each compartment. LV, left atrium (LA), arterial (art), venous (ven), and peripheral (per) vessel compartments and aortic (aor) and mitral (mit) valves are denoted by subscripts. All the variables in the lumped circulatory system are time-dependent functions.
Table 1.
List of model assumptions
| Model Features | Assumption | Reference |
|---|---|---|
| LV’s geometry | Ellipsoidal | 11 |
| LV’s passive properties | Anisotropic hyperelastic and incompressible | 29 |
| LV’s active properties | Modified Hill type | 30 |
| LV’s boundary conditions | Zero mean translation and rotation | 72 |
| Left atrium | Time varying elastance model | 73 |
| Resistances and compliances of systemic circulation | Windkessel model | 72 |
| Coronary tree geometry | Anatomically realistic tree reconstructed from morphometric measurements of a swine LCX | 44 |
| Coronary vessel passive properties | Sigmoidal shape of pressure versus diameter; Tethering of vessels to myocardium | 52 |
| Outflow pressure boundary condition | Transmural depth dependent | 1 |
| Target precapillary flow rate | Constant value in all terminal order 1 vessels. Flow rate is estimated from microvascular velocity under maximum dilation | 76 |
| Transmural precapillary density | Subendocardium is higher than in the subepicardium | 41 |
LCX, left circumflex; LV, left ventricle.
Myocardial Vessel Interaction
Tissue deformation as well as myocyte contraction and thickening were assumed to generate intramyocardial pressure (IMP) and cause cardiac-coronary coupling (67). A time-varying elastance mechanism was proposed to cause systolic flow impediment, and IMP was not considered to be due to the LV pressure (47). Later experiments (46), however, proved that elastance has a limited effect but LV pressure plays a major role in the cardiac-coronary interaction. IMP was previously defined as the average of the LV wall stresses normal to the fiber direction (54, 74). Recent theoretical and computational models have shown the importance of specifying IMP as a sum of two components: one from cavity pressure and the other from myocyte shortening-induced pressure (1, 60, 61). A recent model showed the importance of myocardial vessel interaction on coronary flow regulation by increasing the pressure range of autoregulation (61). The present model extends this approach of coupling IMP and coronary flow by incorporating the spatial and transmural variation of IMP from an LV mechanics model and coupling it to the coronary network flow analysis. The coronary capillaries were assumed to be oriented in the same direction as the myofibers (16, 55). Similar to Algranti et al. (1), the local IMP (PIMP) imposed on the coronary vessels is composed of the cavity-induced extravascular pressure, which is defined as the sum of the Cauchy stress components in the deformed sheet direction, es, and the sheet-normal direction, en (Fig. 2), and the shortening-induced intramyocyte pressure, PSIP (34, 66); i.e.:
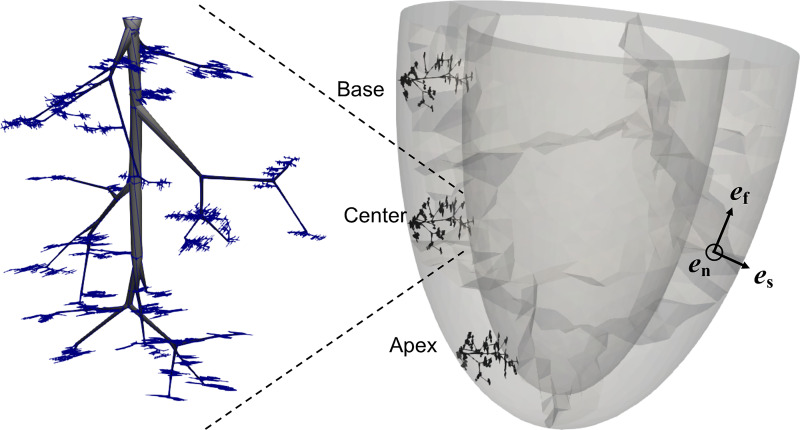
Fig. 2.
Left circumflex (LCX) subtree of 8,634 vessels implanted at 3 axial left ventricle positions, with a magnified view of the tree shown in the inset. The taper in the vessels is only for visualization purposes. In the lumped model for coronary flow, each vessel has a uniform diameter. The unit vectors, ef, es, and en, define a local coordinate system of the fiber, sheet, and sheet-normal directions, respectively.
| (1) |
In the above equation, σ is the total Cauchy stress tensor, and
| (2) |
The constant α was prescribed a value of 0.14 mmHg per percent shortening (1), and the shortening was taken to be the local myofiber stretch (λf) at the location of each coronary vessel in the subtree.
Coronary Flow Model
An anatomically realistic left circumflex (LCX) subtree of a coronary network (41) consisting of 8,634 vessels from an order 8 vessel to order 0 capillaries was used to model regional coronary flow. To do so, the same coronary tree was implanted in the basal, mid-LV, and apical regions such that each vessel has a unique spatial position and all the vessels are within the endocardial and epicardial surfaces of the LV (Fig. 2).
Flow analysis was performed on each subtree implanted at these three different locations with prescribed vessel properties and pressure boundary conditions. Pressure and flow rate of each vessel in all the vessels of the coronary tree were determined from network flow analysis (61, 62). The network flow solution comprises five components: 1) reassign diameter of the coronary tree (appendix b, Diameter Reassignment of the Coronary Tree), 2) lumped model of a single vessel (appendix b, Single Vessel Model), 3) prescribe passive and active vessel constitutive properties (appendix b, Vessel Wall Constitutive Properties), 4) construct the network flow model (appendix b, Network Flow Model), and 5) impose network flow boundary conditions, as described below.
Coronary network flow boundary conditions.
Outlet pressure waveform (Pout) is transmural depth dependent and was assigned for each terminal precapillary vessel to be between the previously predicted subepicardium and subendocardium waveforms, and (61, 62). Inlet pressure waveform to the coronary tree, Pin, was obtained from the aortic pressure output, Paor, of the circulatory model (Fig. 1) and reduced by 20 mmHg to account for the average pressure drop from the aorta to an order 8 vessel and provide for a sufficient flow perfusion in the terminal order 1 vessels (0.4 × 10−3 mm3/s) (76, 81). The pressure induced by myofiber shortening, PSIP, given by Eq. 2, was directly obtained from the myofiber stretch (λf) determined from the LV FE model. Hence, the total intramyocardial tissue pressure, PIMP, defined in Eq. 1, acts locally on each coronary vessel.
Terminal precapillary flow rate and coronary perfusion density.
Terminal precapillary flow rate, qterm, is the volume flow rate of order 1 terminal vessels of the subtree. Mean and SD values of qterm are analyzed in three regions with transmural depth range of 80–100% (subendocardium), 40–60% (midwall), and 0–20% (subepicardium). To obtain the perfusion density (Q) in the three transmural layers of the subepicardium, midwall, and subendocardium, the mean value of the terminal vessel flow (qterm) from each transmural layer was multiplied by the number of terminal precapillary vessels of the respective layer.
Global and Regional Myocardial Work
The area under the pressure-volume loop is indicative of the global work done by the LV. Regional myocardial work (J) is obtained from the area under the stress-strain curve in the myofiber direction. Sampling of the regional myocardial work is done at three transmural locations of the LV’s subendocardium, midwall, and subepicardium for three different axial locations, namely the base, center, and apex. Regional myocardial work (J) is in milliwatts per milliliter (mW/mL) of tissue.
Baseline Model Parameters
The baseline model parameters for the coupled cardiac-circulatory model were chosen based on a previous modeling study (29, 30, 72) so that the predicted PV loop is physiological with a normal ejection fraction (EF) that is greater than 50%. The model parameter values are listed in Tables A1–A3.
Sensitivity Analysis of the Cardiac-Coronary Model Parameters
The relative contribution of the LV’s geometric factors versus its material properties and the contribution of the systemic circulation parameters can only be elucidated by independently varying each factor and observing its effect on the global and regional cardiac work as well as regional flow perfusion.
Sensitivity analysis of the cardiac-coronary model was performed on a subset of the model parameters that were observed to cause large changes in the PV loop from preliminary runs using a coarse FE mesh. Because there are many model parameters, we focused on the LV parameters that include the sarcomere relaxation rate, b; the contractility parameter that defines isometric tension under maximal activation, Tmax; and the passive material parameter of the myocardium, A. Systemic circulatory parameters that were tested are Cart, the aortic compliance; Rper, the peripheral vascular resistance that defines the ventricular afterload; and Vven0, the resting venous volume that defines the preload (73). Note that a change in Vven0 (Eq. A21) alters the preload in the opposite direction. Each sensitivity run was a ± 25% perturbation of the selected parameter from its baseline value, with the other model parameters fixed at their values in Tables A1 and A2. If the FE model for a specific parameter perturbation did not converge, the parameter perturbation was reduced to 10% of its baseline value. After each sensitivity run, PIMP was calculated with Eq. 1 from the FE model solution and input to the coronary flow model to determine the effect of these parameters on terminal precapillary flow rate, regional distribution of coronary flow, and regional cardiac work. Because there is inherent variability in the LV wall thickness for the same species, the effect of this geometric variability on IMP and coronary flow is an essential parameter for perturbation in the model. With a goal of predicting the effect of axial thickness variation on regional changes in myocardial work and coronary flow, a uniformly thick LV wall geometry was created, and the model coupled to the coronary network flow was solved for the same set of baseline model parameters.
Perfusion density (Q), an indicator of the energy supply, and myocardial work (J), an indicator of energy demand, were both calculated for each parameter perturbation. Changes in the ratio of the perfusion densities (Qendo/Qepi) and the ratio of the myocardial work (Jendo/Jepi) for each sensitivity run from the baseline value are indicative of alterations in both the coronary flow and myocardial work in the transmural direction. The difference between the changes in these two quantities as a percentage of their baseline values (ΔQ–ΔJ) for each parameter perturbation is an estimate of the spatial distribution of the energy imbalance.
RESULTS
Numerical Solutions of the LV Mechanics, Systemic Circulation, and Coronary Circulation Model
The model outputs are the time-dependent changes in LV cavity volume and pressure, LV mechanics (strains, stresses, and intramyocardial pressure), aortic pressure, and work done by the myofibers in a cardiac cycle. The coronary flow model outputs are the time-dependent changes in flow and diameters in each coronary vessel of the tree, transmural and axial variation in perfusion density, endo-to-epi perfusion ratio, and flow dispersion. The relevant model outcomes are the LV’s pressure-volume loop in a cardiac cycle, aortic pressure waveform, spatial distribution of both the coronary flow and myocardial work, and their sensitivity to the LV and the systemic circulation (appendix c).
Global and Regional LV Mechanics and their Interaction with the Systemic Circulation
Pressure-volume loop.
Converged FE solutions exhibit typical characteristics of a continuous PV loop with four distinct phases of the cardiac cycle; i.e., the isovolumic contraction, ejection, isovolumic relaxation, and diastolic filling phases (Fig. 3). The baseline model parameters selected from other models (Tables A1 and A2) produced a stroke volume (SV), peak systolic pressure, and peak aortic pressure that are typical of a healthy heart (11, 51). The FE solution produced a peak systolic cavity pressure () of 134.9 mmHg, an end-diastolic pressure () of 1.5 mmHg, an end-diastolic volume () of 112 mL, an end-systolic volume () of 54.5 mL, and a PV loop area of 0.97 Pa·m3.
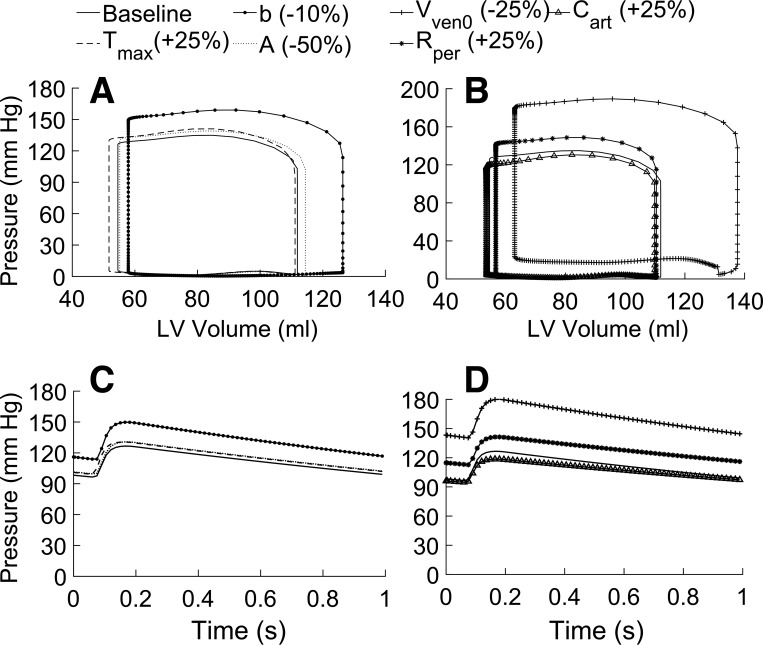
Fig. 3.
Pressure-volume (PV) loop and aortic pressure changes during the cardiac cycle are outputs from the closed-loop left ventricle (LV) model and systemic circulation. Sensitivity of the model to changes in the myocardial properties on the LV’s PV loop (A) and the aortic pressure waveform (C) and the effect of changes in systemic circulation parameters on the LV’s PV loop (B) and the aortic pressure waveform (D) are shown. The following model parameters are independently varied from their baseline values (values in brackets show % change): myocardial contractility, Tmax (+25%); relaxation time constant, b (+10%); passive modulus, A (−50%); preload, Vven0 (−25%); afterload, Rper (+25%); and aortic compliance, Cart (+25%).
Aortic pressure waveform.
The FE model predicted a mean aortic pressure () of 112 mmHg and a pulse pressure (ΔPaor) of 30 mmHg, as shown by the baseline curve (Fig. 3, C and D). The PV loop and the aortic pressure waveform are sensitive to both the myocardial properties (Fig. 3, A and C) and systemic circulation parameters external to the LV (Fig. 3, B and D).
Parametric studies on the PV loop and the dynamic aortic pressure.
Both the passive and active LV properties affect the PV loop and the aortic pressure with varying degree (Fig. 3, A and C; Table 2). Elastic modulus, A, has a marginal effect on the PV loop and aortic pressure during diastolic filling (Fig. 3, A and C). However, when modified from the baseline (Table A1) to a nearly circumferential orientation with a small transmural difference (i.e., ef0 varied from −100 at the epicardium to 100 in the endocardium), the myofiber orientation produced large changes in both the PV loop and aortic pressure waveform (Table 2). The active LV parameter, b, has a significant effect on the systolic and diastolic phases of the PV loop and the aortic pressure waveform (Fig. 3, A and C). Parameters Vven0 and Cart have a strong effect on the PV loop and aortic pressure, whereas Rper (which defines the afterload) has a marginal effect (Fig. 3, B and D; Table 2).
Table 2.
Parametric variation of the left ventricle-systemic circulation model parameters
| Parameter | % Variation | %SV | % | % | % | %ΔPaor | %PVA |
|---|---|---|---|---|---|---|---|
| Tmax | +25/−10 | +4/−2 | −1/0 | +5/−2 | +3/−2 | +4/−1 | +8/−4 |
| b | +10 | +19 | +13 | +18 | +18 | +19 | +43 |
| A | +50/−50 | −3/+3 | −2/+2 | −3/+3 | −3/+3 | −3/+3 | −6/+7 |
| ef0 | +83 | −37 | +10 | −36 | −34 | −38 | −61 |
| Rper | +25/−10 | −6/+3 | −1/1 | +10/−5 | +14/−7 | −5/+3 | +5/−3 |
| Vven0 | +10/−25 | −44/+30 | −28/+23 | −44/+40 | −45/+44 | −44/+32 | −68/+69 |
| Cart | +25/−25 | −2/+1 | −2/+2 | −3/+3 | −4/+3 | −21/+34 | −5/+3 |
LEGEND; . Parametric variation of the left ventricle (LV)-systemic circulation model parameters from their baseline values (Tables A1 and A2) and their effect on the percentage change in stroke volume (SV), end-diastolic volume (), systolic pressure (), mean aortic pressure (), pulse pressure (ΔPaor), and pressure volume loop area (PVA) from their baseline values of 57 mL, 112 mL, 135 mmHg, 112 mmHg, 30 mmHg, and 0.97 Pa·m3, respectively. A, elastic modulus; b, sarcomere relaxation rate; Cart, aortic compliance; ef0, fiber orientation; LV, left ventricle; Rper, peripheral vascular resistance; Tmax, isometric tension under maximal activation; Vven0, resting venous volume
Spatial distribution of IMP.
Fiber strain obtained from the LV’s deformation (stretch), which is a contributing factor of IMP (Eq. 2), is different in systole and early diastole between the three transmural regions, whereas transmural fiber strains are similar at the three axial locations during diastole (Fig. 4). Transmural fiber strain profiles also show that midwall strains are different from the outer two layers in systole, and these differences decreased during diastole in all the three axial regions (Fig. 4). These regional differences in fiber strains enhance the differences in PSIP (Eq. 2).
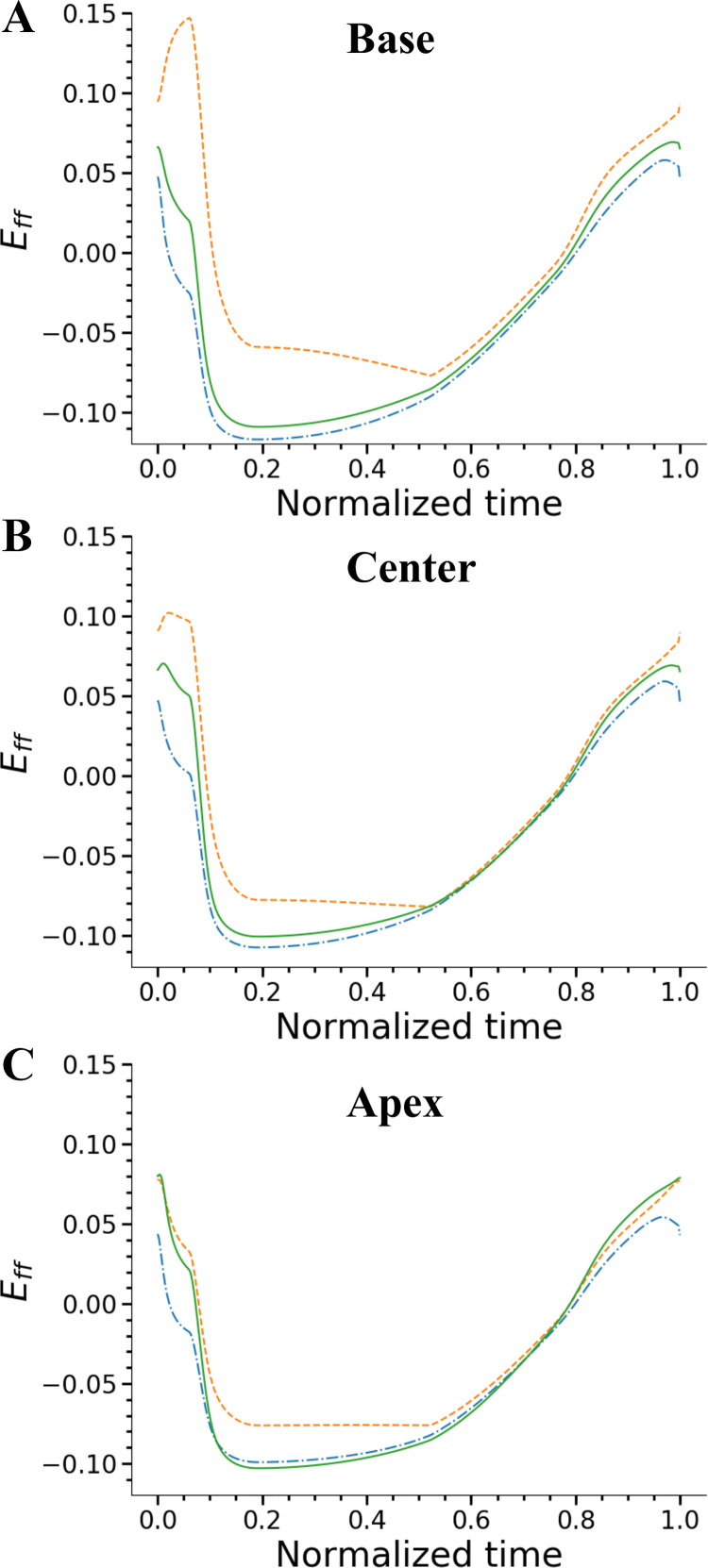
Fig. 4.
Fiber strains in the left ventricle (LV) as a function of the cardiac cycle time at 3 transmural locations of base (A), center (B), and apex (C) of the LV. At each axial location, 3 transmural regions of subendocardium (solid line), midwall (dashed line), and subepicardium (dash-dotted line) regions were sampled. In all the axial regions, transmural difference is significantly higher at peak systole. Eff, myofiber strain.
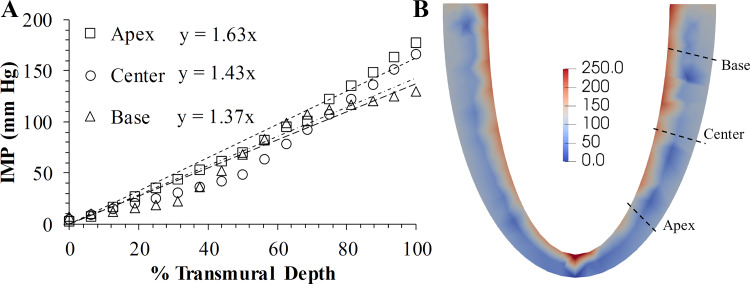
The model predicts an IMP (Eq. 2) whose peak value varied approximately linearly across the transmural thickness (Fig. 5). Base-apex differences in the transmural distribution of IMP exist as seen from the different slopes of the linear fits of 1.63 (R2 = 0.985) in the apex, 1.43 (R2 = 0.95) in the center, and 1.37 (R2 = 0.96) in the base of the LV (Fig. 5A). In the base, center, and apex regions, IMP is the highest in the endocardium, followed by the midwall and the epicardium. During the cardiac cycle, IMP is highest at peak systole and reduces to a minimum at the end of diastole. The highest value of IMP during a cardiac cycle is found in the endocardium of the apex, followed by that in the center and base regions (Fig. 6).
Fig. 5.
A: variation in peak intramyocardial pressure (IMP) across the transmural wall thickness in the base, center, and apex regions of the left ventricle (LV). Start of the x-axis is the epicardium and the end is the endocardium. B: contour plot of IMP distribution in the LV at peak systole has the highest negative (compressive) values in the subendocardium, which decays to nearly zero in the subepicardium. Units of the color bar are in mmHg.
Fig. 6.
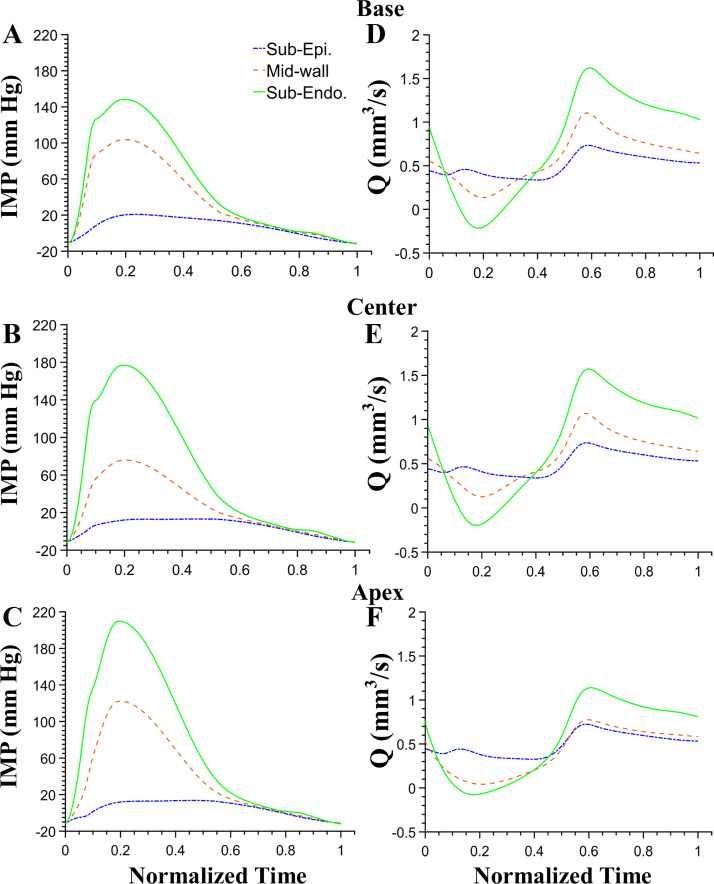
Regional differences in intramyocardial pressures (IMPs) at axial locations of the base (A), center (B), and apex (C) of the left ventricle. At each axial location, IMP at 3 transmural regions of subendocardium (solid line), midwall (dotted line), and subepicardium (dash-dotted line) is shown. The highest values of IMP at an axial location are in the subendocardium and the lowest in the subepicardium. Transmural perfusion density differences at different axial locations of the base (D), center (E), and apex (F) locations show higher values in the subendocardium in diastole.
Regional Coronary Flow
Spatial distribution of coronary flow.
The regional variation in IMP (Fig. 5B) translated to regional differences in coronary flow (Fig. 6). Simulations revealed the presence of a transmural difference in terminal precapillary flow rate, qterm, that decreased from the subepicardium to the subendocardium (Tables 3 and 4). An axial (base to apex) difference in qterm and perfusion density (Q) is also present. In general, the coronary flow is largest at the base and lowest at the apex in each of the three transmural locations (subepicardium, midwall, and subendocardium). This axial difference in coronary flow is largest in the subendocardial layer. The endo-to-epi flow ratio (Qendo/Qepi) also follows the same pattern as qterm. Regional flow dispersion in the LV is in the range of 50–120%, with the lowest value in the midwall of the LV apex (Table 3).
Table 3.
Spatial distribution of terminal precapillary flow rate and perfusion density for a coronary subtree
| Axial Position | Subepicardium | Midwall | Subendocardium | Qendo/Qepi | |||
|---|---|---|---|---|---|---|---|
| Base | 1.42 ± 1.08 | 0.50 | 1.27 ± 1.31 | 0.61 | 1.02 ± 0.79 | 0.62 | 1.22 |
| Center | 1.40 ± 1.03 | 0.50 | 1.27 ± 1.31 | 0.61 | 0.96 ± 0.77 | 0.58 | 1.16 |
| Apex | 1.40 ± 1.14 | 0.50 | 1.27 ± 0.63 | 0.61 | 0.79 ± 0.95 | 0.48 | 0.96 |
The table lists the mean ± SD values of terminal precapillary flow rate (qterm) (qterm × 10−3 mm3/s), perfusion density (Q) (Q × mm3/s), and the ratio of perfusion densities in the subendocardium and subepicardium (Qendo/Qepi); n = 8,634 vessels. Q in different transmural regions is calculated from qterm multiplied by the terminal arteriole density of 355 in subepicardium, 480 in the midwall, and 603 in the subendocardium, respectively. The ratio of arteriolar densities in the subendocardium vs. subepicardium is 1.7 and 1.35 in the midwall vs. subepicardium, which are close to the measured arterial volumes in these regions (42, 89).
Table 4.
Sensitivity of terminal precapillary flows from the central-LV region to the LV-systemic circulation model parameters
| % Variation | Subepicardium | Midwall | Subendocardium | Qendo/Qepi |
|---|---|---|---|---|
| Baseline | 1.40 ± 1.03 | 1.27 ± 1.31 | 0.96 ± 0.77 | 1.16 |
| Myocardial contractility (Eqs. A4, A8) | ||||
| Tmax | ||||
| +25 | 1.43 ± 1.09 (+2) | 1.27 ± 1.35 (0) | 0.86 ± 0.73 (−10) | 1.02 |
| −10 | 1.31 ± 0.9 (−6) | 1.21 ± 1.29 (−5) | 0.95 ± 0.80 (−1) | 1.23 |
| b | ||||
| +10 | 1.75 ± 1.62 (+25) | 1.82 ± 2.15 (+39) | 1.64 ± 1.34 (+71) | 1.59 |
| Passive myocardial modulus (Eq. A3) (A) | ||||
| +50 | 1.34 ± 0.96 (−4) | 1.18 ± 1.20 (−7) | 0.84 ± 0.69 (−13) | 1.06 |
| −50 | 1.61 ± 1.14 (+15) | 1.46 ± 1.15 (+15) | 1.15 ± 0.94 (+20) | 1.21 |
| Afterload (Eq. A18) (Rper) | ||||
| +25 | 1.59 ± 1.34 (+14) | 1.51 ± 1.73 (+19) | 1.18 ± 0.96 (+19) | 1.26 |
| −10 | 1.30 ± 0.90 (−7) | 1.15 ± 1.13 (−9) | 0.86 ± 0.68 (−10) | 1.12 |
| Preload (Eq. A21) (Vven0) | ||||
| −25 | 2.13 ± 2.33 (+52) | 2.01 ± 2.65 (+57) | 1.5 ± 1.38 (+56) | 1.20 |
| Aorta compliance (Eq. A20) (Cart) | ||||
| +25 | 1.23 ± 0.83 (−12) | 1.07 ± 1.04 (−16) | 0.82 ± 0.65 (−15) | 1.13 |
| −25 | 1.54 ± 1.26 (+10) | 1.42 ± 1.59 (+12) | 1.08 ± 0.87 (+13) | 1.19 |
The number in parenthesis is the percentage change in the mean value of flow rate in the precapillary vessels from its baseline value [qterm × 10−3 mm3/s (Mean ± SD)]. A, elastic modulus; b, sarcomere relaxation rate; Cart, aortic compliance; LV, left ventricle; Qendo/Qepi, ratio of the perfusion densities; qterm, terminal precapillary flow rate; Rper, peripheral vascular resistance; Tmax, isometric tension under maximal activation; Vven0, resting venous volume.
Regional coronary flow and its relation to regional myocardial work.
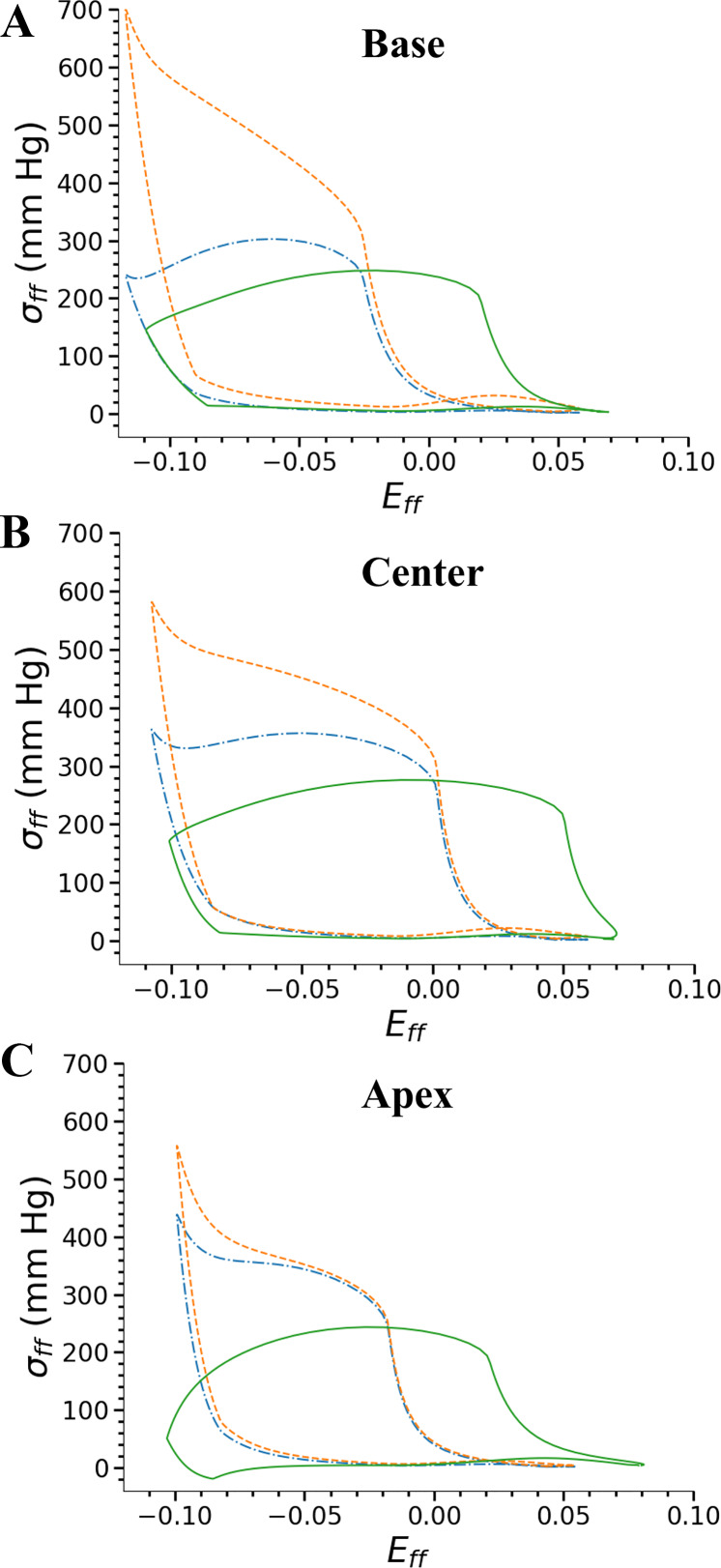
Stresses are higher in the midwall compared with the outer layers of the LV in all axial regions (Fig. 7). Regional work done by the myocardium, J, is largest at the midwall of the base of the LV (Fig. 7, Table 5). In the three LV regions sampled, work done in the subendocardial region is similar to the work done by the subepicardium (Table 5). At the apex, work done by the tissue in all transmural locations is lower than their corresponding transmural locations at the center of the LV. The ratio of myocardial work in the subendocardium versus the subepicardium (Jendo/Jepi) is 1.14 at the base and 1.10 in the center and apex regions. These differences between Jendo and Jepi at the base and the center are close to the differences between Qendo and Qepi of the corresponding LV regions. The differences in work done and coronary perfusion density between the center and the apex have a similar trend in their corresponding three transmural LV regions (Tables 3 and 6).
Fig. 7.
Myofiber stress-strain plots at 3 axial left ventricle (LV) positions and 3 transmural regions of base (A), center (B), and apex (C) of the LV and 3 transmural locations of subendocardium (solid line), midwall (dashed line), and subepicardium (dash-dotted line). Regional work done by the myofibers is from the area under the stress-strain curve. Area of the curves in the 3 transmural regions of the apex are lower than that in the base or center region. Eff,, myofiber strain; σff, myofiber stress.
Table 5.
Regional work done by the myofibers
| Axial LV Location | Subepicardium | Midwall | Subendocardium |
|---|---|---|---|
| Base | 4.1 | 18.3 | 4.6 |
| Center | 5.6 | 13.2 | 6.2 |
| Apex | 4.3 | 6.9 | 4.7 |
Regional work done by the myofibers, J (in mW/mL of tissue) is the area under the fiber stress vs. strain curve (Fig. 7) at 3 axial locations and 3 transmural regions of the left ventricle (LV).
Table 6.
Changes in the regional work and coronary perfusion density
| Subepicardium | Midwall | Subendocardium | ||||
|---|---|---|---|---|---|---|
| % Variation | ΔJ/ΔQ | ΔQ–ΔJ | ΔJ/ΔQ | ΔQ–ΔJ | ΔJ/ΔQ | ΔQ–ΔJ |
| Tmax | ||||||
| +25 | +4.2/+2.1 | −2.0 | +8.8/+0.0 | −8.8 | +4.3/−10.4 | −14.8 |
| −10 | −2.4/−6.4 | −4.0 | −4.5/−4.7 | −0.2 | −2.4/−1.0 | +1.4 |
| b | ||||||
| +10 | +56.9/+25.0 | −31.9 | +39.4/+43.3 | +3.9 | +59.1/+70.8 | +11.8 |
| A | ||||||
| +50 | −6.6/−4.3 | +2.3 | −5.4/−7.1 | −1.7 | −6.0/−12.5 | −6.5 |
| −50 | +7.8/+15.0 | +7.2 | +6.0/+15.0 | +8.9 | +6.5/+19.8 | +13.3 |
| Rper | ||||||
| +25 | +5.1/+13.6 | +8.5 | +4.3/+18.9 | +14.6 | +5.1/+22.9 | +17.8 |
| −10 | −2.7/−7.1 | −4.4 | −2.4/−9.4 | −7.1 | −3.0/−10.4 | −7.4 |
| Vven0 | ||||||
| −25 | +94.9/+52.1 | −42.8 | +49.6/+58.3 | +8.6 | +91.3/+56.3 | −35.2 |
| Cart | ||||||
| +25 | −7.2/−12.1 | −5.0 | −5.4/−15.7 | −10.3 | −7.3/−14.6 | −7.3 |
| −25 | +6.9/+10.0 | +3.1 | +4.8/+11.8 | +7.0 | +7.0/+12.5 | +5.5 |
Changes in the regional work (J) and coronary perfusion density (Q) as a % of their baseline values to perturbations in the left ventricle-systemic circulation model parameters from the central-LV region. The difference between the % change in perfusion density (ΔQ) and the % change in work done (ΔJ) is the energy imbalance that needs to be reduced by coronary flow regulation. Note that a change in Vven0 (Eq. A21) causes the preload to change in the opposite direction. A, elastic modulus; b, sarcomere relaxation rate; Cart, aortic compliance; Rper, peripheral vascular resistance; Tmax, isometric tension under maximal activation; Vven0, resting venous volume.
Sensitivity of the Coronary Flow and Myocardial Work due to the LV and the Systemic Circulation
Myocardial contractility, LV relaxation rate, and passive mechanical properties.
Alteration in the myocardial contractility effects both the coronary flow and myocardial work. The perturbation of Tmax from its baseline value produced a marginal effect on both Q and J, with a larger change in subendocardial Q and a larger change in the midwall J (Table 6). For an increase in Tmax, the sensitivities of Q and J in the subendocardium are in the opposite direction; hence, a much greater difference (−14.8%) between regional flow and work done (ΔQ–ΔJ) is present in the subendocardium compared with the −2.0% in the subepicardium and −8.8% in the midwall at the center of the LV (Table 6). Altering the sarcomere relaxation rate, b, has a major effect on the precapillary flow rates and the transmural distributions of both Q and J. An increase in b by 10% from its baseline value of −1,429 ms (Table 4) increased the diastolic filling time by ~100 ms (data not shown), which caused the perfusion ratio (Qendo/Qepi) to increase by 37%. Sensitivity of Q is highest in the subendocardium for a perturbation in the LV relaxation rate. In the subendocardium, Q is most sensitive to the relaxation rate compared with either the contractility or the passive modulus (Table 6). Perturbation of the parameter, A (Eq. A1), has a marginal effect on both qterm and J (Table 6).
Preload, afterload, and aortic compliance.
An increase in the LV’s preload (Eq. A19) has a significant effect on qterm, which increased by >50% in both the subepicardium and the subendocardium; however, the change in Qendo/Qepi is negligible (< 5%) from their baseline values. The sensitivity of J is much higher than Q in the subendocardium and subepicardium when LV’s preload is increased, whereas the sensitivities (ΔJ and ΔQ) are similar in the midwall (Table 6). The substantially higher sensitivity of J compared with that of Q in the subendocardium could drastically alter the supply-demand balance for an increase in the cardiac preload. Perturbation of the peripheral vascular resistance, Rper (Eq. A16), to assess the sensitivity of afterload produced only a moderate effect on qterm. An increase in Rper by 25% from its baseline value increased qterm by 14% (to 1.6 × 10−3 mm3/s) in the subepicardium and by 23% (to 1.2 × 10−3 mm3/s) in the subendocardium. For both the perturbations in afterload, the changes in both the global LV work and the regional work in the three transmural regions are less than 5% from their baseline values. Perturbation of the aortic compliance, Cart (Eq. A18), has a marginal effect on both the precapillary flow rates and regional myocardial work (Tables 4 and 6).
Effect of wall thickness on coronary flow.
Compared with an LV wall with variable thickness, an LV wall with a uniform thickness of 12.3 mm produced a higher magnitude of coronary flow in all the transmural regions (Table 7). The mean terminal precapillary flow rate (qterm) in the subendocardial layer has the highest change of 25–35%. The axial difference in qterm in the subendocardium of a uniformly thick LV increased by 7% (Table 7) compared with a nonuniformly thick LV (Table 3). Ratio of the subendocardial to subepicardial perfusion densities (Qendo/Qepi) changed by 18% in the base and 25% in the apex region.
Table 7.
Spatial distribution of coronary flow for a large subtree implanted at three axial locations in an LV with a uniform thickness of 12.3 mm
| Axial Position | Subepicardium | Midwall | Subendocardium | Qendo/Qepi |
|---|---|---|---|---|
| Base | 1.51 (+6.3) | 1.45 (+14.2) | 1.28 (+25.5) | 1.44 (+18.0) |
| Center | 1.53 (+9.3) | 1.47 (+12.2) | 1.27 (+32.3) | 1.41 (+21.1) |
| Apex | 1.52 (+8.6) | 1.36 (+7.1) | 1.07 (+35.4) | 1.2 (+25.0) |
The table lists the mean values of terminal precapillary flows (qterm) at 3 transmural regions and the ratio of perfusion densities (Qendo/Qepi) in outer layers of the left ventricle (LV). Value in brackets is the % change in the mean value of qterm or Q in a uniformly thick LV from the corresponding value in a nonuniformly thick LV (Table 3). n = 8,634 vessels.
DISCUSSION
We developed an integrated cardiac-vascular model and found an effect of the LV’s intrinsic and extrinsic characteristics on regional distribution of both the coronary flow and the myocardial work. This computational model produced some novel findings that include the following: 1) presence of an axial difference in IMP and coronary flow perfusion that marginally decreased with a higher apical LV thickness; 2) LV’s contractility affects the magnitude and distribution of both the regional coronary flows and myocardial work—an increase in the LV’s contractility produced a higher regional myocardial work in all the transmural regions but produced a higher coronary flow only in the midwall and the subepicardium; 3) a faster relaxation rate of the LV increased the diastolic filling time and produced a higher change in both the regional myocardial work and the coronary flow in all the transmural regions, with the largest increase in the subendocardial coronary flow; 4) LV’s passive mechanical properties affected both the regional myocardial work and the coronary flows, with the highest effect on the subendocardial coronary flows; 5) afterload changes uniformly altered the myocardial work in all transmural regions, whereas it has a higher effect on coronary flow in the midwall and the subendocardium; 6) preload and aortic compliance changes altered coronary flow nearly uniformly in all the transmural regions, whereas changes in the myocardial work is nonuniform across the transmural regions with the lowest change in the midwall of the LV; and 7) local mechanical work done by the subendocardium is marginally higher than the subepicardium and is similar to the trend in coronary flow between these two regions under maximum vasodilation of the coronary vessels.
The model simulations reproduced PV loops, aortic pressure waveforms, wall strains, transmural distribution of IMP in the LV, and coronary flow characteristics similar to the measurements. The PV loop for the baseline parameters (Fig. 3) is similar to data from a healthy subject under resting state physiological conditions (14), and bidirectional perturbations of the model parameters produced consistent changes to the PV loop similar to measurements. For instance, a decrease in the aortic compliance, Cart, increased the LV pressures during the ejection phase of the cardiac cycle (Fig. 3) by ~10% (68). The decrease in Psys, Paor, SV, and EF (Table 2) when the peripheral vascular resistance, Rper, is reduced agrees with established results (70, 77). Second, the model predicts a transmural distribution of IMP that compares favorably with micropipette measurements (32, 57, 67). The predicted IMP (Fig. 5) in the transmural direction is similar to experimental data (32); i.e., a monotonic increase in the peak IMP from near zero at the epicardium to a maximum value at the endocardium. Our model predicted that the maximum value of IMP (Fig. 5) is higher than the maximum PLV (Fig. 3) and agrees with the experimental data (48, 57). Transmural variation in peak IMP is approximately linear in the three LV regions (Fig. 5). Linear regression of the peak IMP as a function of the transmural depth (Fig. 5) has an R2 > 0.95, and the linear slope is 20% higher in the apex than the base, which was not previously reported either from models or experiments. Third, our model predictions of regional LV strain profiles (Fig. 4) are comparable to those predicted by other models (86). Transmural differences in fiber strains (Figs. 4 and 7) show an increase in the operating range of fiber strains from the base to the apex regions and are similar to trends found by Wang et al. (86). In all the LV regions, fiber strains were similar in the subendocardium and subepicardium (Fig. 4) during the entire cardiac cycle, whereas the fiber strains in the midwall were different during systole. The higher midwall strains can be ascribed to the myofiber orientation, which is the primary differentiator between the three transmural regions (Fig. 4). Previous FE models (11, 28) and experiments (90) have observed differences in strains in the axial direction but did not report any transmural differences to compare with our model (Fig. 4).
In our model, maximal fiber stresses for the central LV region are 26 kPa in the subendocardium, 40 kPa in the subepicardium, and 66 kPa in the midwall for the baseline model parameters. The maximal stress of 30 kPa in the central LV region reported by another FE model (28) at end systole is close to our stress value in the subendocardium. However, Guccione et al. (28) report lower stresses in the midwall than in the subendocardium. This could be due to different assumptions, such as an axi-symmetric LV geometry and a linear variation of the sarcomere length across the LV wall (28), which are not present in our model. Another model (83) predicted that the midwall does the most work, similar to our model predictions. Other models (30, 38) have predicted different distributions of the wall stresses and have varying assumptions on the LV geometry, constitutive relationships, and theoretical formulation.
The regional perfusion in Fig. 6 is compared with the model from Smolich’s group (59) and shows that the peaks of subendocardial flow in diastole from our model are similar to those of Fig. 5 in Mynard et al.’s study (59). The modeling study (1) that compared subepicardial and subendocardial flow velocities with data (82) found good agreement and reported peak flow velocity in diastole in the subepicardium. The ratio of subendocardial perfusion density in the apex versus the base of ~0.8 (Table 3) is comparable to the measured ratio of myocardial perfusion in the apex versus base of ~0.9 found under hyperemic conditions (33). A decrease of 11% in the ratio of subendocardial perfusion between the apex and the base when contractility was increased by 25% suggests that the subendocardium of the LV apex could be more vulnerable to ischemia. Regional coronary flow from microsphere deposition in canine hearts (7) has indicated a decreasing coronary flow in the axial direction and a higher flow dispersion (18) toward the apex. However, there is scant data on the transmural distribution of coronary flow in the apical LV region. Flow dispersion of 0.5–1.2 from our model is higher than measured values of 0.3 (7), as our existing methodology of diameter reassignment of a reconstructed coronary tree (62) could not reduce flow dispersion any further. Our model predicts the ratio of Qendo versus Qepi in the range of 0.96–1.22, which compares well with data in healthy subjects that vary between 1.0 and 1.5 (23). The axial difference in subendocardial flow predicted by our model would likely make the bottom half of the LV more vulnerable to subendocardial ischemia than the top half. Clinical imaging studies (26) have found an axial difference in perfusion during stress perfusion testing with adenosine that maximally dilates the coronary tree, providing a validation to our model and potentially a new tool for the diagnosis of microvascular disease.
The effect of increasing the diastolic time (faster relaxation rate of the LV) on greater subendocardial flows (Table 4) is supported by data on higher subendocardial perfusion due to an increase in diastolic time fraction without changes to perfusion pressure and heart rate (24, 56). A slower sarcomere relaxation time, a characteristic feature observed in hypertensive heart disease, was hypothesized to be a mechanism in diastolic heart failure (10). Our model reveals that a slower sarcomere relaxation time caused a major alteration in the transmural distribution of coronary flow with a lower value of Qendo and revealed a hitherto unknown connection between a loss of organ-level relaxation behavior during diastole and subendocardial hypoperfusion. Seminal work was done by Hoffman et al. (12, 36), who coined the term ‘diastolic pressure-time index (DTPI),’ which is the area under the aortic pressure and LV pressure waveforms in diastole. This index, together with the systolic pressure-time index, was considered as a surrogate of supply-to-demand ratio in the LV and is sensitive to endo-to-epi flow. DTPI is sensitive to subendocardial flow under maximally vasodilated conditions similar to the flow under passive vessel conditions used in the current work. Others (8) have also observed that when coronary flow reserve is exhausted, endo-to-epi flow ratio is very sensitive to the diastolic time fraction (DTF). LV relaxation rate affects DTF and is an important mechanism behind diastolic dysfunction in heart failure (10). To our knowledge, there is no published study that links the effect of the LV’s relaxation rate on coronary flow. The outcome of this study points to an important physiological process that not only impacts organ level mechanics (LV’s relaxation rate) but could also impact the organ level energetics via altering coronary flow specifically in the endocardium. The large sensitivity of the LV relaxation rate modeled by the sarcomere relaxation rate in our active LV contraction model on the multiscale behavior of coronary flow and its spatial distribution is a novel outcome of this model. This can be the focus of therapeutic interventions, either by pharmaceuticals such as β-blockers or neurohormonal antagonists or implantation of cardiac-assist devices or any surgical procedures for heart failure that can improve isovolumic relaxation and increase diastolic filling time, thereby improving subendocardial perfusion. Additionally, our model quantifies the magnitude of change in Q due to a change in b, which could motivate the design of experiments that provide mechanistic insights into how the loss in cellular scale properties such as titin’s elasticity (27) and cross-bridge relaxation rate changes could make the myocardium more vulnerable to ischemia in heart failure with preserved ejection fraction.
A significant aspect of the sensitivity analysis is the change in terminal arteriole flow rate to perturbation in the model parameters. The reference model parameters of the LV in Table A1 (29, 30) and the LV circulatory system in Table A2 (73) are from models validated with data. The coronary flow model parameters (Table A3) are based on data (1, 61). The observed sensitivities for flow rates (Table 6) are primarily due to changes in both the aortic pressure (Paor) and intramyocardial pressure (PIMP) and their nonlinear effect on coronary arteriole dilation for each parameter perturbation. The effect of an increase in contractility (Tmax) on the attenuation of subendocardial flow can be explained from the higher increase in subendocardial PIMP, which restricts the dilation of subendocardial arterioles versus only a 2% increase in Paor that nominally increases flow. The amplification of subendocardial flow to an increase in the LV relaxation rate, b, is because of an increase in both the Paor, which drives coronary flow, and the magnitude and duration of dilation of the subendocardial vessels caused by a reduced PIMP at a faster relaxation rate of the LV. The sensitivity of the terminal arteriole flow rate, qterm, for an increase in afterload, Rperf, is due to a greater dilation of the subendocardial vessels at a lower PIMP and a higher Paor (Table 4) causing a moderate transmural redistribution of coronary flow. In hypertension studies, pharmacological treatment is prescribed to reduce both a higher afterload and a higher contractility, which then increases the subendocardial flow (39). Direct comparison between data and simulations for assessing the independent effect of afterload on the transmural distribution of coronary flow cannot be made because changes in afterload typically accompany changes in contractility, and vice versa, in experiments. For an increase in preload (modeled by a decrease in Vven0), it is well observed that the subendocardium is vulnerable to ischemia, and this has been attributed to a higher IMP (4), a higher coronary sinus pressure, and a higher zero flow pressure (35). An increase in the passive elastic modulus produced a nonuniform change in Q, with a higher change in the subendocardium for a more compliant LV (Table 2). Q in the subendocardium is more sensitive to the LV’s afterload than in the other transmural regions.
A second outcome of the sensitivity analysis is that for most perturbations of the model parameters, changes in the LV’s global work (PV loop area in Table 2) have a similar magnitude and direction with that of the regional work, J (Table 6). The sensitivity (ΔJ) in the subendocardium is greater than that in the subepicardium. The exception to this is the sensitivity (ΔJ) in the midwall to contractility, which is markedly different from that of the global LV work and nearly twice the sensitivity of the subendocardium or the subepicardium (Tables 2 and 6). This is the highest increase in J compared with the effect of the other model parameters. The analysis also points to an additional hypothesis that at higher preloads, the greater difference between the sensitivities of regional work and coronary flow (Table 6) can lead to a greater increase in regional work that is not met by the increase in coronary flow in the subendocardium. The spatial nonuniformity in the sensitivity of J is partly because of the circumferential orientation of myofibers in the midwall, which is markedly different from the myofiber orientation in the subendocardium and subepicardium (79). For all model parameter perturbations, the subendocardium performs more mechanical work than the subepicardium (Jendo > Jepi) at all axial locations (Table 6), suggesting that this transmural region always has a higher oxygen demand.
Another significant model outcome is the ability to compare regional myocardial work, J, and perfusion, Q, which are surrogates for oxygen demand and supply, respectively. The mismatch between the sensitivities of myocardial work (ΔJ) and perfusion density (ΔQ) for a particular LV region (Table 6) suggests that a mechanism should exist to bridge the difference between supply (Q) and demand (J), which could perhaps be achieved by the coronary flow regulation mechanisms (61). A correlation between regional perfusion density and work in the midwall (Table 6) could not be made because the regional work done in the midwall is ~2 times higher than the other transmural regions in the LV’s center, whereas the perfusion density is similar across the three transmural regions (Table 3). Regional perfusion from experiments in swine has measured a ratio of 1:1.15:1.19 in the subepicardium versus the midwall and versus the subendocardium (37). The flow rate of a single terminal arteriole located in the midwall lies between the flow rates of a terminal arteriole located in the subepicardium and subendocardium. If autoregulation is considered in the present coronary flow model (61), regional perfusion could be better matched with regional work. However, because the regional work in the midwall is ~2 times higher than in the subendocardium, the midwall’s autoregulation should be nearly at maximal strength and the subendocardial and subepicardial autoregulation should be significantly attenuated. A previous model (74) has not been able to obtain a correlation between regional myocardial work and coronary perfusion and argued that this could be due to the lack of flow regulation and a lack of closed-loop feedback between the coronary flow and myocardial contractility. We are currently working on incorporating both these aspects in our model.
There is a fundamental issue that needs to be addressed in future studies as the FE model predicts a much higher regional work in the midwall. There is some evidence from ex vivo data on permeabilized myocytes (31) that the power output is highest in the midwall. The ratio of the maximum power output is 1.8:2.4:1 in the epicardium versus the midwall and versus the endocardium. The ratio of 2.4 from this data (31) is close to the ratio of the work done in the midwall versus the subendocardium at the LV center from our model. Several FE models predict different transmural stress and strain distributions, both of which yield a different amount of regional work. Reliable data on the transmural distribution of myocardial work in vivo are required but are currently not available. An alternative theory for a mismatch between regional work and perfusion is that the midwall’s myocytes may require a different amount of oxygen to contract and relax compared with the other regions. Future modeling and experimental works are necessary to definitively answer this issue.
Limitations of the study.
The current model is limited to the LV but in the future can be extended to a biventricular model and subject-specific geometries to more accurately predict stress distributions in the entire organ. In our model, the same coronary subtree was implanted in the three axial locations; hence, there is a mismatch in the orientation of coronary vessels with the myofiber orientation in the three regions. A full-scale coronary tree for the flow analysis will overcome this limitation and provide a more accurate determination of IMP. Because we considered a uniphasic material model, the fluid-filled nature of the myocardium is not accounted for and may produce deviations in IMP. Additional diameter reassignment rules for the reconstructed coronary tree are required to reduce the high-flow dispersion values from this model to be comparable with data. Sensitivity analysis was performed on a single model parameter of the LV system, whereas a pathological state may need a multiparameter sensitivity analysis to accurately characterize the effects of the cardiac model on coronary circulation. For instance, stiffening of the aorta not only reduces its compliance but may also cause LV hypertrophy. As a result, diastolic time may be reduced (due to slower relaxation rate of the LV) and aortic pulse pressure may increase simultaneously, which can result in a larger change in the spatial distribution of coronary flow compared to considering only the effect of reduced aortic compliance. Although our analysis is restricted to a single heart rate, the cardiac-coronary coupled framework provides a strong theoretical basis to explore physiological pathways that alter subendocardial perfusion under exercise conditions.
Conclusions
The cardiac-coronary modeling framework predicts an axial (apex to base) difference in the coronary flow that decreases toward the apex, which was corroborated by coronary perfusion measurements in the base and apex regions. Myocardial contractility has a significant effect on the transmural and axial distribution of coronary flow and produced a larger change in myocardial work done by the midwall compared with other transmural regions. An increase in the contractility increased the axial difference in subendocardial flow. Systemic circulation characteristics, namely the preload, afterload, aortic compliance, and myocardial passive elastic modulus, all affect the coronary flow magnitude but have a negligible influence on the transmural coronary flow distribution. Preload and aortic compliance have a significant influence on the distribution of the regional myocardial work. Relaxation rate of the LV has a major effect on the transmural distribution of coronary flow and regional myocardial work. The relaxation rate is a promising target for pharmaceutical therapies, such as inotropic agents that are specifically targeted to improve sarcomere relaxation at the cellular scale or the design of mechanical devices or procedures that improve organ level relaxation behavior, which can mitigate subendocardial ischemia.
GRANTS
This work is supported by NIH Grants HL134841 and HL133359 and American Heart Association Scientist Development Grant 17SDG33370110.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
R.N., L.C.L., Y.L., B.K., and G.S.K. conceived and designed research; R.N., B.K., and S.M.S. performed experiments; R.N., L.C.L., B.K., and S.M.S. analyzed data; R.N., L.C.L., Y.L., S.M.S., and G.S.K. interpreted results of experiments; R.N. prepared figures; R.N. and L.C.L. drafted manuscript; R.N., L.C.L., Y.L., and G.S.K. edited and revised manuscript; R.N., L.C.L., Y.L., B.K., S.M.S., and G.S.K. approved final version of manuscript.
ACKNOWLEDGMENTS
The software codes used to obtain the results are available upon request to the corresponding author.
APPENDIX A: CARDIAC-SYSTEMIC CIRCULATION MODEL
The cardiac mechanics model is coupled with the systemic circulation and the coronary microcirculation model as follows:
Left Ventricular Finite Element Model
Geometry and Mesh.
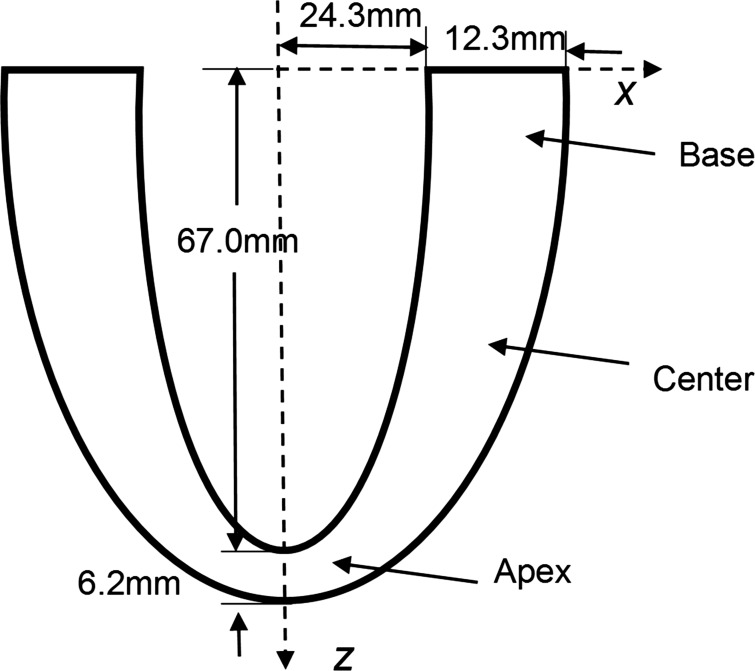
The LV geometry was idealized as a half-truncated ellipsoidal geometry with a nonuniform wall thickness based on the dimensions obtained from Bovendeerd et al. (11) and Streeter and Hanna (78). The axisymmetric geometry of the LV was meshed with 11,394 quadratic tetrahedral elements.
Material model.
The prescribed LV material constitutive model comprises cardiac passive mechanical properties and the active mechanical properties of myofibers. Passive mechanical behavior was described by an incompressible transversely isotropic Fung-type hyperplastic material model that has the following strain energy function:
| (A3) |
where
In Eq. A3, Eij are the components of the Green–Lagrange strain tensor, and i, j = (f, s, n) defines the local material coordinates consisting of the fiber , sheet , and sheet-normal directions , respectively. There are four material parameters: A defines a material constant that scales the stresses and passive stiffness; bff defines the fiber stiffness; bxx defines the shear properties in a plane normal to the fibers, and bfx defines the shear properties in the f-n and f-s planes. Values of these parameters are listed in Table A1.
Active myofiber stress in the LV was determined from an active phenomenological contraction model (17, 30), which is a modified Hill equation scaled by a time-dependent function, Ct (t). The active 2nd Piola–Kirchhoff stress tensor is given as:
| (A4) |
where is the local vector of myofibers in the reference configuration. In Eq. A4, Tmax is a parameter defining the isometric tension achieved at the longest sarcomere length and Ca0 defines the peak intracellular calcium concentration. Sarcomere length-dependent calcium sensitivity, ECa0 and Ct (t), is given by:
| (A5) |
| (A6) |
In Eq. A5, the parameter B is a constant, (Ca0)max is the maximum peak intracellular calcium concentration, and l0 is the sarcomere length at which no active tension develops. The variable ω(t) in Eq. A6 is given by:
| (A7) |
The time taken to reach peak tension by the sarcomere, t0, and the duration of relaxation, tr, depend linearly on sarcomere length, l, as:
| (A8) |
where m and b are constants. Sarcomere length l can be obtained from the myofiber stretch λ, which was obtained from the Cauchy–Green deformation tensor E as:
| (A9) |
Myofiber orientation was prescribed to be helical, with a transmural linear variation starting from a helix angle of 60° at the endocardium to −60° at the epicardium (79). It was assumed that myofiber contraction occurs at the same time homogenously in the LV. Parameters of the passive material properties and active contraction model were assumed to be homogeneous in the LV, and their values are listed in Table A1.
Finite element formulation.
The weak form of the governing equations for the nonlinear elasticity problem of finite deformation of the LV was previously derived (72) based on the Lagrangian functional as:
| (A10) |
where u is the displacement vector, p is the Lagrange multiplier for enforcing tissue incompressibility of the LV, PLV is the cavity pressure, (u) is the cavity volume function, VLV is the prescribed cavity volume, c1 and c2 are Lagrange multipliers for enforcing zero mean displacement and rotation of the LV, respectively, X is a vector in the reference configuration, and W is the strain energy function of the tissue. If we take the first variational of L, this leads to the following expression:
| (A11) |
The LV base was constrained to move only in plane. Linearized equations of the weak form were solved using an open source finite element library (3).
Systemic Circulation Model
The circulatory system was described by the following ordinary differential equations (ODEs) (72, 73):
LA volume:
| (A12) |
LV volume:
| (A13) |
Systemic circulation volumes:
| (A14) |
and
| (A15) |
Flow rates, q, in the different segments are given as:
| (A16) |
| (A17) |
| (A18) |
| (A19) |
Pressures in different compartments, Part, Pven, PLA, and PLV, are given by
Arterial pressure:
| (A20) |
Venular pressure:
| (A21) |
where Vart,0 and Vven,0 are constants that define resting arterial and venous volumes and Cart and Cven are the arterial and venous compliances.
Left atrium pressure:
| (A22) |
| (A23) |
| (A24) |
In Eq. A23, Ees,LA is the end-systolic elastance of the left atrium and V0,LA is the volume axis intercept of the end-systolic pressure volume relationship (ESPVR). In Eq. A24, both ALA and BLA are parameters of the end-diastolic pressure volume relationship (EDPVR) of the left atrium and the driving function e(t) in Eq. A22 is given as:
| (A25) |
The circulatory model parameters and the dynamic LV elastance parameters are listed in Table A2. The pressure-volume relationship of the LV; i.e., PLV (VLV), was calculated from the finite element model.
APPENDIX B: CORONARY FLOW MODEL
Diameter Reassignment of the Coronary Tree
The rationale for diameter reassignment of the reconstructed large subtree of 8,634 vessels (41, 42) is based on a previous work (62) that showed how to produce realistic flow dispersions in small subtrees. For the coronary flow model, vessel diameters were reassigned for a given set of qtarget, IMP, and perfusion pressure boundary conditions obtained from the finite element solution such that a target terminal precapillary flow rate and dispersion are prescribed.
Single Vessel Model
A nonlinear resistor-capacitor element (40) was used as the basic unit of the network flow analysis. Detailed descriptions of the equations and solution methodology can be found in Namani et al. (61, 62). Briefly, flow in an anatomically realistic structure of the network was solved with lumped models based on a resistor-capacitor analogy of electrical circuits. The junction common to the resistors and the capacitor has an unknown pressure, Pmid. The junction of a vessel bifurcation has an unknown nodal pressure (Pnode). Based on the conservation of fluid mass, the net flow at both the junctions is zero. Assumptions in the model are: 1) uniform vessel geometry, 2) laminar flow in the vessels, 3) blood viscosity in all the vessels is a nonlinear function of its diameter (63), 4) spatially homogeneous active and passive mechanical properties within each vessel, 5) uniform dynamic extravascular pressure PIMP in each vessel (but varies in each vessel depending on its transmural location).
Vessel Wall Constitutive Properties
Similar to the myocardium, vascular mechanical properties of each coronary vessel can be separated into passive and active components. The current model only accounts for vessel passive mechanical properties. Passive mechanical properties were characterized by the pressure-diameter relationship from inflation tests. Vascular mechanical properties were prescribed to depend on the vessel size. Following previous formulation, the passive radius (rp) is prescribed as follows (91):
| (B1) |
Parameters Ap and Bp, are asymptotic values of the maximum and minimum vessel radii at their corresponding maximum and minimum transvascular pressure (ΔP); ϕp is the pressure at a radius of (Ap + Bp)/2; and Cp is the bandwidth of the passive vessel response. Order-dependent values of the above passive parameters have been experimentally determined for some microvessel orders (52) and interpolated for other orders (61). A detailed description of the procedure to determine the vessel wall tension and stiffness is given in Namani et al. (61).
Network Flow Model
A system of ordinary differential equations (ODEs) was derived based on the conservation of mass for all network junctions. Equations for the nodal pressures were obtained by applying mass conservation at each node. The governing equations were assembled for the network into a system of ODEs describing the time evolution of the nodal pressures Pmid. The coupled ODEs are nonlinear and time dependent and can be represented in matrix form as:
| (B2) |
For a coronary tree with n number of vessels, A(t) is a square matrix of size n × n and B(t) is an n × 1 vector. Coefficient matrices in Eq. B2 were built with nonzero elements of A(t) and B(t) based on the pattern of the connectivity matrix indicating the neighboring vessel’s number and the column index in direct contact (61).
Building the A and B matrices.
A network structure matrix (61) for the coronary subtree (n = 8,634) yielded the coefficient matrices A (n × n) and B (n × 1). The nonzero elements of the sparse matrix A are dependent on the conductivities of the vessel’s neighbors in direct contact with either its proximal or distal ends. For a bifurcating node, the vessel’s neighbors, , , , and , represent the conductance of the daughter, sister, first daughter, and second daughter, respectively. For a trifurcating node, two additional elements, and , are the conductance of the third daughter vessel. A vessel with a trifurcating vessel at its origin has an additional sister with index (i, n−21). For a vessel, i, connected to bifurcations at both its ends, the elements of matrices A are
| (B3) |
| (B4) |
| (B5) |
For a vessel, i, connected to a bifurcation at its origin and a trifurcation at its end, the elements of matrices A are
| (B6) |
| (B7) |
| (B8) |
For a vessel, i, connected to a trifurcation at its origin and a bifurcation at its end, the elements of matrices A are
| (B9) |
| (B10) |
For an ith vessel, which is a terminating arteriole, the elements at each row in A are
| (B11) |
| (B12) |
For the source vessel, the elements of A are
| (B13) |
For all interior vessels, the elements of B are
| (B14) |
For an ith vessel, which is a terminal arteriole, the elements at each row in B are
| (B15) |
For the source vessel, the elements of B are
| (B16) |
The boundary conditions at the inlet vessel and at the outlet vessels are
| (B17) |
APPENDIX C: NUMERICAL SOLUTION OF THE COUPLED FE MODEL AND CORONARY NETWORK FLOW
Mesh Convergence Study
The effects of mesh size on the finite element solution were analyzed by calculating differences in stroke volume, peak cavity pressure, and transmural distribution of PIMP obtained between three levels of mesh discretizations of the LV geometry, namely coarse (330 quadratic elements), medium (4,897 quadratic elements), and fine (11,394 quadratic elements). We found that the differences in stroke volume, peak cavity pressure, and transmural IMP distributions were all within 5% between the coarse and medium level of mesh discretization. Fiber stress-strain curves in different transmural regions showed large differences between the coarse and medium meshes. Dynamic fiber strains during different phases of the cardiac cycle have a similar magnitude for medium and fine mesh discretization, with minor deviations seen in their pattern during isovolumic contraction. As such, the fine level of mesh discretization was applied for all simulations here.
Numerical Solution of Network Flow
The system of time-dependent ODEs in Eq. B2 was integrated over the entire cardiac cycle for every vessel in the tree. Vessel hydraulic properties (i.e., conductance and capacitance), which are the elements of A(t) in Eq. B2, were updated at each time point. The time span of integration for the system of ODEs was the time taken for one entire cardiac cycle. The system of ODEs was iteratively solved until the periodicity condition between successive cardiac cycles was satisfied. Periodicity condition was deemed to be satisfied when the difference in Pmid between the start and end of the cardiac cycle for each vessel did not vary by more than 0.005 Pa. Numerical accuracy of the solution was deemed to be acceptable when the net flow at the midpoint in all the vessels and at the network bifurcating or trifurcating nodes was < 0.1%. More details of the numerical solution are discussed in Namani et al. (61).
Fig. A1.
Frontal view of the idealized axisymmetric left ventricle (LV) ellipsoidal geometry with a varying thickness that decreases in the axial direction, from the base to the apex.
Table A1.
Passive and active material properties: inputs to the LV model
| Parameter | Parameter | Value | Units | Reference |
|---|---|---|---|---|
| A – scaling parameter for LV’s passive stiffness | A | 0.1 | kPa | 29 |
| bff – stiffness in fiber direction | bff | 29.9 | 29 | |
| bxx – shear stiffness normal to fiber direction | bxx | 13.3 | 29 | |
| bfx – shear stiffness in fiber direction | bfx | 26.6 | 29 | |
| ef0epi – fiber orientation in the epicardium | ef0epi | −60 | deg | 29 |
| ef0endo – fiber orientation in the endocardium | ef0endo | +60 | deg | 29 |
| Tmax – isometric tension under maximal activation | Tmax | 200.0 | kPa | 30 |
| Ca0 – peak intracellular calcium concentration | Ca0 | 4.35 | μm | 30 |
| (Ca0)max – maximum peak intracellular calcium concentration | (Ca0)max | 4.35 | μm | 30 |
| B – shape of peak isometric tension-sarcomere length relation | B | 4.75 | μm−1 | 30 |
| l0 – sarcomere length at which there is no active force | l0 | 1.58 | μm | 30 |
| t0 – time to peak tension | t0 | 151 | ms | 30 |
| m – slope of linear relaxation duration-sarcomere length relation | M | 1,048 | ms/μm | 30 |
| b – relaxation rate | b | −1,429 | ms | 30 |
| lr – relaxed sarcomere length | lr | 1.85 | μm | 30 |
LV, left ventricle.
Table A2.
Model parameters that are inputs to the closed loop LV circulatory system and time varying elastance model of the LA
| Parameter | Value | Units |
|---|---|---|
| Cart – Arterial compliance | 0.0125 | mL/Pa |
| Cven – Venous compliance | 0.3 | mL/Pa |
| Vart0 – Resting volume of artery | 680.0 | mL |
| Vven0 – Resting volume of vein | 3,300.0 | mL |
| Raor – Aortic valve resistance | 2.0 | kPa·ms−1·mL−1 |
| Rven – Venous network resistance | 2.0 | kPa·ms−1·mL−1 |
| Rmv – Mitral valve resistance | 2.0 | kPa·ms−1·mL−1 |
| Rper – Peripheral network resistance | 200 | kPa·ms−1·mL−1 |
| Vven – Venous network volume | 3,700 | mL |
| Vart – Arterial network volume | 740 | mL |
| VLA – LA volume | 12 | mL |
| Ees,LA – Endo systolic elastance of LA | 60.0 | Pa/mL |
| ALA – Scaling factor of EDPVR | 58.67 | Pa |
| BLA – Exponent of EDPVR | 0.049 | mL |
| V0,LA – Volume axis intercept | 10.0 | mL |
| tmax,LA – Time to end-systole | 120 | ms |
| τLA − Time constant of relaxation | 25 | ms |
LA, left atrium; LV, left ventricle.
Table A3.
Parameters as inputs to the coronary flow model
| Parameter | Value | Units |
|---|---|---|
| n – Number of network vessels | 8,634 | |
| r – Number of network terminal precapillaries | 1,786 | |
| HD – hematocrit | 0.45 | |
| η – Blood viscosity | Diameter dependent | |
| Ap, ϕp, Cp (Eq. B1) | As in Table A1A of (61) | |
| qtarget – Target flow rate in the terminal arterioles | 1.5 × 10−3 | mm3/s |
| – Mean value of the outlet pressure waveform at the terminal arterioles | 41.7 | mmHg |
REFERENCES
- 1.Algranati D, Kassab GS, Lanir Y. Mechanisms of myocardium-coronary vessel interaction. Am J Physiol Heart Circ Physiol 298: H861–H873, 2010. doi: 10.1152/ajpheart.00925.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Algranati D, Kassab GS, Lanir Y. Why is the subendocardium more vulnerable to ischemia? A new paradigm. Am J Physiol Heart Circ Physiol 300: H1090–H1100, 2011. doi: 10.1152/ajpheart.00473.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alnæs MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN. The FEniCS Project Version 1.5. Arch Numer Softw 3: 9–23, 2015. doi: 10.11588/ans.2015.100.20553. [DOI] [Google Scholar]
- 4.Archie JP., Jr Intramyocardial pressure: effect of preload on transmural distribution of systolic coronary blood flow. Am J Cardiol 35: 904–911, 1975. doi: 10.1016/0002-9149(75)90127-7. [DOI] [PubMed] [Google Scholar]
- 5.Arts T, Reneman RS. Interaction between intramyocardial pressure (IMP) and myocardial circulation. J Biomech Eng 107: 51–56, 1985. doi: 10.1115/1.3138520. [DOI] [PubMed] [Google Scholar]
- 6.Austin RE Jr, Aldea GS, Coggins DL, Flynn AE, Hoffman JI. Profound spatial heterogeneity of coronary reserve. Discordance between patterns of resting and maximal myocardial blood flow. Circ Res 67: 319–331, 1990. doi: 10.1161/01.RES.67.2.319. [DOI] [PubMed] [Google Scholar]
- 7.Austin RE Jr, Smedira NG, Squiers TM, Hoffman JIE. Influence of cardiac contraction and coronary vasomotor tone on regional myocardial blood flow. Am J Physiol Heart Circ Physiol 266: H2542–H2553, 1994. doi: 10.1152/ajpheart.1994.266.6.H2542. [DOI] [PubMed] [Google Scholar]
- 8.Bache RJ, Cobb FR. Effect of maximal coronary vasodilation on transmural myocardial perfusion during tachycardia in the awake dog. Circ Res 41: 648–653, 1977. doi: 10.1161/01.RES.41.5.648. [DOI] [PubMed] [Google Scholar]
- 9.Beard DA, Bassingthwaighte JB. The fractal nature of myocardial blood flow emerges from a whole-organ model of arterial network. J Vasc Res 37: 282–296, 2000. doi: 10.1159/000025742. [DOI] [PubMed] [Google Scholar]
- 10.Borlaug BA, Kass DA. Mechanisms of diastolic dysfunction in heart failure. Trends Cardiovasc Med 16: 273–279, 2006. doi: 10.1016/j.tcm.2006.05.003. [DOI] [PubMed] [Google Scholar]
- 11.Bovendeerd PH, Arts T, Delhaas T, Huyghe JM, van Campen DH, Reneman RS. Regional wall mechanics in the ischemic left ventricle: numerical modeling and dog experiments. Am J Physiol Heart Circ Physiol 270: H398–H410, 1996. doi: 10.1152/ajpheart.1996.270.1.H398. [DOI] [PubMed] [Google Scholar]
- 12.Buckberg GD, Fixler DE, Archie JP, Hoffman JI. Experimental subendocardial ischemia in dogs with normal coronary arteries. Circ Res 30: 67–81, 1972. doi: 10.1161/01.RES.30.1.67. [DOI] [PubMed] [Google Scholar]
- 13.Burkhoff D, de Tombe PP, Hunter WC, Kass DA. Contractile strength and mechanical efficiency of left ventricle are enhanced by physiological afterload. Am J Physiol Heart Circ Physiol 260: H569–H578, 1991. doi: 10.1152/ajpheart.1991.260.2.H569. [DOI] [PubMed] [Google Scholar]
- 14.Burkhoff D, Mirsky I, Suga H. Assessment of systolic and diastolic ventricular properties via pressure-volume analysis: a guide for clinical, translational, and basic researchers. Am J Physiol Heart Circ Physiol 289: H501–H512, 2005. doi: 10.1152/ajpheart.00138.2005. [DOI] [PubMed] [Google Scholar]
- 15.Camici PG, d’Amati G, Rimoldi O. Coronary microvascular dysfunction: mechanisms and functional assessment. Nat Rev Cardiol 12: 48–62, 2015. doi: 10.1038/nrcardio.2014.160. [DOI] [PubMed] [Google Scholar]
- 16.Caulfield JB, Borg TK. The collagen network of the heart. Lab Invest 40: 364–372, 1979. [PubMed] [Google Scholar]
- 17.Dang AB, Guccione JM, Mishell JM, Zhang P, Wallace AW, Gorman RC, Gorman JH III, Ratcliffe MB. Akinetic myocardial infarcts must contain contracting myocytes: finite-element model study. Am J Physiol Heart Circ Physiol 288: H1844–H1850, 2005. doi: 10.1152/ajpheart.00961.2003. [DOI] [PubMed] [Google Scholar]
- 18.Decking UK. Spatial heterogeneity in the heart: recent insights and open questions. News Physiol Sci 17: 246–250, 2002. doi: 10.1152/nips.01393.2002. [DOI] [PubMed] [Google Scholar]
- 19.Del Buono MG, Arena R, Borlaug BA, Carbone S, Canada JM, Kirkman DL, Garten R, Rodriguez-Miguelez P, Guazzi M, Lavie CJ, Abbate A. Exercise intolerance in patients with heart failure: JACC state-of-the-art review. J Am Coll Cardiol 73: 2209–2225, 2019. doi: 10.1016/j.jacc.2019.01.072. [DOI] [PubMed] [Google Scholar]
- 20.Delhaas T, Arts T, Prinzen FW, Reneman RS. Regional fibre stress-fibre strain area as an estimate of regional blood flow and oxygen demand in the canine heart. J Physiol 477: 481–496, 1994. doi: 10.1113/jphysiol.1994.sp020209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Downey JM, Kirk ES. Inhibition of coronary blood flow by a vascular waterfall mechanism. Circ Res 36: 753–760, 1975. doi: 10.1161/01.RES.36.6.753. [DOI] [PubMed] [Google Scholar]
- 22.Duncker DJ, Bache RJ. Regulation of coronary blood flow during exercise. Physiol Rev 88: 1009–1086, 2008. doi: 10.1152/physrev.00045.2006. [DOI] [PubMed] [Google Scholar]
- 23.Feigl EO. Coronary physiology. Physiol Rev 63: 1–205, 1983. doi: 10.1152/physrev.1983.63.1.1. [DOI] [PubMed] [Google Scholar]
- 24.Fokkema DS, VanTeeffelen JWGE, Dekker S, Vergroesen I, Reitsma JB, Spaan JA. Diastolic time fraction as a determinant of subendocardial perfusion. Am J Physiol Heart Circ Physiol 288: H2450–H2456, 2005. doi: 10.1152/ajpheart.00790.2004. [DOI] [PubMed] [Google Scholar]
- 25.Formaggia L, Lamponi D, Tuveri M, Veneziani A. Numerical modeling of 1D arterial networks coupled with a lumped parameters description of the heart. Comput Methods Biomech Biomed Engin 9: 273–288, 2006. doi: 10.1080/10255840600857767. [DOI] [PubMed] [Google Scholar]
- 26.Gould KL, Johnson NP. Coronary physiology beyond coronary flow reserve in microvascular angina: JACC state-of-the-art review. J Am Coll Cardiol 72: 2642–2662, 2018. doi: 10.1016/j.jacc.2018.07.106. [DOI] [PubMed] [Google Scholar]
- 27.Granzier H, Labeit S. Cardiac titin: an adjustable multi-functional spring. J Physiol 541: 335–342, 2002. doi: 10.1113/jphysiol.2001.014381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Guccione JM, Costa KD, McCulloch AD. Finite element stress analysis of left ventricular mechanics in the beating dog heart. J Biomech 28: 1167–1177, 1995. doi: 10.1016/0021-9290(94)00174-3. [DOI] [PubMed] [Google Scholar]
- 29.Guccione JM, McCulloch AD, Waldman LK. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J Biomech Eng 113: 42–55, 1991. doi: 10.1115/1.2894084. [DOI] [PubMed] [Google Scholar]
- 30.Guccione JM, Waldman LK, McCulloch AD. Mechanics of active contraction in cardiac muscle: part II—cylindrical models of the systolic left ventricle. J Biomech Eng 115: 82–90, 1993. doi: 10.1115/1.2895474. [DOI] [PubMed] [Google Scholar]
- 31.Haynes P, Nava KE, Lawson BA, Chung CS, Mitov MI, Campbell SG, Stromberg AJ, Sadayappan S, Bonnell MR, Hoopes CW, Campbell KS. Transmural heterogeneity of cellular level power output is reduced in human heart failure. J Mol Cell Cardiol 72: 1–8, 2014. doi: 10.1016/j.yjmcc.2014.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Heineman FW, Grayson J. Transmural distribution of intramyocardial pressure measured by micropipette technique. Am J Physiol Heart Circ Physiol 249: H1216–H1223, 1985. doi: 10.1152/ajpheart.1985.249.6.H1216. [DOI] [PubMed] [Google Scholar]
- 33.Hernandez-Pampaloni M, Keng FY, Kudo T, Sayre JS, Schelbert HR. Abnormal longitudinal, base-to-apex myocardial perfusion gradient by quantitative blood flow measurements in patients with coronary risk factors. Circulation 104: 527–532, 2001. doi: 10.1161/hc3001.093503. [DOI] [PubMed] [Google Scholar]
- 34.Heslinga JW, Allaart CP, Yin FC, Westerhof N. Effects of contraction, perfusion pressure, and length on intramyocardial pressure in rat papillary muscle. Am J Physiol Heart Circ Physiol 272: H2320–H2326, 1997. doi: 10.1152/ajpheart.1997.272.5.H2320. [DOI] [PubMed] [Google Scholar]
- 35.Hoffman JI, Spaan JA. Pressure-flow relations in coronary circulation. Physiol Rev 70: 331–390, 1990. doi: 10.1152/physrev.1990.70.2.331. [DOI] [PubMed] [Google Scholar]
- 36.Hoffman JIE, Buckberg GD. The myocardial supply:demand ratio—a critical review. Am J Cardiol 41: 327–332, 1978. doi: 10.1016/0002-9149(78)90174-1. [DOI] [PubMed] [Google Scholar]
- 37.Huo Y, Kaimovitz B, Lanir Y, Wischgoll T, Hoffman JIE, Kassab GS. Biophysical model of the spatial heterogeneity of myocardial flow. Biophys J 96: 4035–4043, 2009. doi: 10.1016/j.bpj.2009.02.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Huyghe JM, Arts T, van Campen DH, Reneman RS. Porous medium finite element model of the beating left ventricle. Am J Physiol Heart Circ Physiol 262: H1256–H1267, 1992. doi: 10.1152/ajpheart.1992.262.4.H1256. [DOI] [PubMed] [Google Scholar]
- 39.Iwanaga S, Ewing SG, Husseini WK, Hoffman JIE. Changes in contractility and afterload have only slight effects on subendocardial systolic flow impediment. Am J Physiol Heart Circ Physiol 269: H1202–H1212, 1995. doi: 10.1152/ajpheart.1995.269.4.H1202. [DOI] [PubMed] [Google Scholar]
- 40.Jacobs J, Algranati D, Lanir Y. Lumped flow modeling in dynamically loaded coronary vessels. J Biomech Eng 130: 054504, 2008. doi: 10.1115/1.2979877. [DOI] [PubMed] [Google Scholar]
- 41.Kaimovitz B, Lanir Y, Kassab GS. Large-scale 3-D geometric reconstruction of the porcine coronary arterial vasculature based on detailed anatomical data. Ann Biomed Eng 33: 1517–1535, 2005. doi: 10.1007/s10439-005-7544-3. [DOI] [PubMed] [Google Scholar]
- 42.Kaimovitz B, Lanir Y, Kassab GS. A full 3-D reconstruction of the entire porcine coronary vasculature. Am J Physiol Heart Circ Physiol 299: H1064–H1076, 2010. doi: 10.1152/ajpheart.00151.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kajiya F, Yada T, Hiramatsu O, Ogasawara Y, Inai Y, Kajiya M. Coronary microcirculation in the beating heart. Med Biol Eng Comput 46: 411–419, 2008. doi: 10.1007/s11517-008-0335-x. [DOI] [PubMed] [Google Scholar]
- 44.Kassab GS, Rider CA, Tang NJ, Fung YC. Morphometry of pig coronary arterial trees. Am J Physiol Heart Circ Physiol 265: H350–H365, 1993. doi: 10.1152/ajpheart.1993.265.1.H350. [DOI] [PubMed] [Google Scholar]
- 45.King RB, Bassingthwaighte JB, Hales JRS, Rowell LB. Stability of heterogeneity of myocardial blood flow in normal awake baboons. Circ Res 57: 285–295, 1985. doi: 10.1161/01.RES.57.2.285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kouwenhoven E, Vergroesen I, Han Y, Spaan JA. Retrograde coronary flow is limited by time-varying elastance. Am J Physiol Heart Circ Physiol 263: H484–H490, 1992. doi: 10.1152/ajpheart.1992.263.2.H484. [DOI] [PubMed] [Google Scholar]
- 47.Krams R, Sipkema P, Zegers J, Westerhof N. Contractility is the main determinant of coronary systolic flow impediment. Am J Physiol Heart Circ Physiol 257: H1936–H1944, 1989. doi: 10.1152/ajpheart.1989.257.6.H1936. [DOI] [PubMed] [Google Scholar]
- 48.Kresh JY, Cobanoglu MA, Brockman SK. The intramyocardial pressure: a parameter of heart contractility. J Heart Transplant 4: 241–246, 1985. [PubMed] [Google Scholar]
- 49.Laussmann T, Janosi RA, Fingas CD, Schlieper GR, Schlack W, Schrader J, Decking UK. Myocardial proteome analysis reveals reduced NOS inhibition and enhanced glycolytic capacity in areas of low local blood flow. FASEB J 16: 628–630, 2002. doi: 10.1096/fj.01-0574fje. [DOI] [PubMed] [Google Scholar]
- 50.Lee J, Niederer S, Nordsletten D, Le Grice I, Smaill B, Kay D, Smith N. Coupling contraction, excitation, ventricular and coronary blood flow across scale and physics in the heart. Philos Trans A Math Phys Eng Sci 367: 2311–2331, 2009. [Erratum in Philos Trans A Math Phys Eng Sci 367: 3331, 2009]. doi: 10.1098/rsta.2008.0311. [DOI] [PubMed] [Google Scholar]
- 51.Lee WS, Nakayama M, Huang WP, Chiou KR, Wu CC, Nevo E, Fetics B, Kass DA, Ding PY, Chen CH. Assessment of left ventricular end-systolic elastance from aortic pressure-left ventricular volume relations. Heart Vessels 16: 99–104, 2002. doi: 10.1007/s003800200003. [DOI] [PubMed] [Google Scholar]
- 52.Liao JC, Kuo L. Interaction between adenosine and flow-induced dilation in coronary microvascular network. Am J Physiol Heart Circ Physiol 272: H1571–H1581, 1997. doi: 10.1152/ajpheart.1997.272.4.H1571. [DOI] [PubMed] [Google Scholar]
- 53.Matsumoto T, Ebata J, Tachibana H, Goto M, Kajiya F. Transmural microcirculatory blood flow distribution in right and left ventricular free walls of rabbits. Am J Physiol Heart Circ Physiol 277: H183–H191, 1999. doi: 10.1152/ajpheart.1999.277.1.H183. [DOI] [PubMed] [Google Scholar]
- 54.May-Newman K, McCulloch AD. Homogenization modeling for the mechanics of perfused myocardium. Prog Biophys Mol Biol 69: 463–481, 1998. doi: 10.1016/S0079-6107(98)00020-0. [DOI] [PubMed] [Google Scholar]
- 55.May-Newman K, Omens JH, Pavelec RS, McCulloch AD. Three-dimensional transmural mechanical interaction between the coronary vasculature and passive myocardium in the dog. Circ Res 74: 1166–1178, 1994. doi: 10.1161/01.RES.74.6.1166. [DOI] [PubMed] [Google Scholar]
- 56.Merkus D, Kajiya F, Vink H, Vergroesen I, Dankelman J, Goto M, Spaan JA. Prolonged diastolic time fraction protects myocardial perfusion when coronary blood flow is reduced. Circulation 100: 75–81, 1999. doi: 10.1161/01.CIR.100.1.75. [DOI] [PubMed] [Google Scholar]
- 57.Mihailescu LS, Abel FL. Intramyocardial pressure gradients in working and nonworking isolated cat hearts. Am J Physiol Heart Circ Physiol 266: H1233–H1241, 1994. doi: 10.1152/ajpheart.1994.266.3.H1233. [DOI] [PubMed] [Google Scholar]
- 58.Mynard JP, Nithiarasu P. A 1D arterial blood flow model incorporating ventricular pressure, aortic valve and regional coronary flow using the locally conservative Galerkin (LCG) method. Commun Numer Methods Eng 24: 367–417, 2008. doi: 10.1002/cnm.1117. [DOI] [Google Scholar]
- 59.Mynard JP, Penny DJ, Smolich JJ. Scalability and in vivo validation of a multiscale numerical model of the left coronary circulation. Am J Physiol Heart Circ Physiol 306: H517–H528, 2014. doi: 10.1152/ajpheart.00603.2013. [DOI] [PubMed] [Google Scholar]
- 60.Mynard JP, Smolich JJ. Influence of anatomical dominance and hypertension on coronary conduit arterial and microcirculatory flow patterns: a multiscale modeling study. Am J Physiol Heart Circ Physiol 311: H11–H23, 2016. doi: 10.1152/ajpheart.00997.2015. [DOI] [PubMed] [Google Scholar]
- 61.Namani R, Kassab GS, Lanir Y. Integrative model of coronary flow in anatomically based vasculature under myogenic, shear, and metabolic regulation. J Gen Physiol 150: 145–168, 2018. doi: 10.1085/jgp.201711795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Namani R, Kassab GS, Lanir Y. Morphometric reconstruction of coronary vasculature incorporating uniformity of flow dispersion. Front Physiol 9: 1069, 2018. doi: 10.3389/fphys.2018.01069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pries AR, Secomb TW, Gessner T, Sperandio MB, Gross JF, Gaehtgens P. Resistance to blood flow in microvessels in vivo. Circ Res 75: 904–915, 1994. doi: 10.1161/01.RES.75.5.904. [DOI] [PubMed] [Google Scholar]
- 64.Prinzen FW, Augustijn CH, Arts T, Allessie MA, Reneman RS. Redistribution of myocardial fiber strain and blood flow by asynchronous activation. Am J Physiol Heart Circ Physiol 259: H300–H308, 1990. doi: 10.1152/ajpheart.1990.259.2.H300. [DOI] [PubMed] [Google Scholar]
- 65.Prinzen FW, Hunter WC, Wyman BT, McVeigh ER. Mapping of regional myocardial strain and work during ventricular pacing: experimental study using magnetic resonance imaging tagging. J Am Coll Cardiol 33: 1735–1742, 1999. doi: 10.1016/S0735-1097(99)00068-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Rabbany SY, Funai JT, Noordergraaf A. Pressure generation in a contracting myocyte. Heart Vessels 9: 169–174, 1994. doi: 10.1007/BF01746060. [DOI] [PubMed] [Google Scholar]
- 67.Rabbany SY, Kresh JY, Noordergraaf A. Intramyocardial pressure: interaction of myocardial fluid pressure and fiber stress. Am J Physiol Heart Circ Physiol 257: H357–H364, 1989. doi: 10.1152/ajpheart.1989.257.2.H357. [DOI] [PubMed] [Google Scholar]
- 68.Randall OS, van den Bos GC, Westerhof N, Pot FOM. Systemic compliance: does it play a role in the genesis of essential hypertension? Cardiovasc Res 18: 455–462, 1984. doi: 10.1093/cvr/18.8.455. [DOI] [PubMed] [Google Scholar]
- 69.Reymond P, Merenda F, Perren F, Rüfenacht D, Stergiopulos N. Validation of a one-dimensional model of the systemic arterial tree. Am J Physiol Heart Circ Physiol 297: H208–H222, 2009. doi: 10.1152/ajpheart.00037.2009. [DOI] [PubMed] [Google Scholar]
- 70.Santamore WP, Burkhoff D. Hemodynamic consequences of ventricular interaction as assessed by model analysis. Am J Physiol Heart Circ Physiol 260: H146–H157, 1991. doi: 10.1152/ajpheart.1991.260.1.H146. [DOI] [PubMed] [Google Scholar]
- 71.Segers P, Stergiopulos N, Westerhof N, Wouters P, Kolh P, Verdonck P. Systematic and pulmonary hemodynamics assessed with a lumped-parameter heart-arterial interaction model. J Eng Math 47: 185–199, 2003. doi: 10.1023/B:ENGI.0000007975.27377.9c. [DOI] [Google Scholar]
- 72.Shavik SM, Jiang Z, Baek S, Lee LC. High spatial resolution multi-organ finite element modeling of ventricular-arterial coupling. Front Physiol 9: 119, 2018. doi: 10.3389/fphys.2018.00119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Shavik SM, Wall ST, Sundnes J, Burkhoff D, Lee LC. Organ-level validation of a cross-bridge cycling descriptor in a left ventricular finite element model: effects of ventricular loading on myocardial strains. Physiol Rep 5: e13392, 2017. doi: 10.14814/phy2.13392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Smith N, Stevens C, Hunter P. Computational modeling of ventricular mechanics and energetics. Appl Mech Rev 58: 77–90, 2005. doi: 10.1115/1.1859794. [DOI] [Google Scholar]
- 75.Steffen DA, Giannopoulos AA, Grossmann M, Messerli M, Schwyzer M, Gräni C, Gebhard C, Pazhenkottil AP, Kaufmann PA, Buechel RR. “Apical thinning”: Relations between myocardial wall thickness and apical left ventricular tracer uptake as assessed with positron emission tomography myocardial perfusion imaging. J Nucl Cardiol, 2018. doi: 10.1007/s12350-018-1397-2. [DOI] [PubMed] [Google Scholar]
- 76.Stepp DW, Nishikawa Y, Chilian WM. Regulation of shear stress in the canine coronary microcirculation. Circulation 100: 1555–1561, 1999. doi: 10.1161/01.CIR.100.14.1555. [DOI] [PubMed] [Google Scholar]
- 77.Stergiopulos N, Meister JJ, Westerhof N. Determinants of stroke volume and systolic and diastolic aortic pressure. Am J Physiol Heart Circ Physiol 270: H2050–H2059, 1996. doi: 10.1152/ajpheart.1996.270.6.H2050. [DOI] [PubMed] [Google Scholar]
- 78.Streeter DD Jr, Hanna WT. Engineering mechanics for successive states in canine left ventricular myocardium. I. Cavity and wall geometry. Circ Res 33: 639–655, 1973. doi: 10.1161/01.RES.33.6.639. [DOI] [PubMed] [Google Scholar]
- 79.Streeter DD Jr, Spotnitz HM, Patel DP, Ross J Jr, Sonnenblick EH. Fiber orientation in the canine left ventricle during diastole and systole. Circ Res 24: 339–347, 1969. doi: 10.1161/01.RES.24.3.339. [DOI] [PubMed] [Google Scholar]
- 80.Suga H, Hayashi T, Shirahata M. Ventricular systolic pressure-volume area as predictor of cardiac oxygen consumption. Am J Physiol Heart Circ Physiol 240: H39–H44, 1981. doi: 10.1152/ajpheart.1981.240.1.H39. [DOI] [PubMed] [Google Scholar]
- 81.Tillmanns H, Ikeda S, Hansen H, Sarma JS, Fauvel JM, Bing RJ. Microcirculation in the ventricle of the dog and turtle. Circ Res 34: 561–569, 1974. doi: 10.1161/01.RES.34.4.561. [DOI] [PubMed] [Google Scholar]
- 82.Toyota E, Ogasawara Y, Hiramatsu O, Tachibana H, Kajiya F, Yamamori S, Chilian WM. Dynamics of flow velocities in endocardial and epicardial coronary arterioles. Am J Physiol Heart Circ Physiol 288: H1598–H1603, 2005. doi: 10.1152/ajpheart.01103.2003. [DOI] [PubMed] [Google Scholar]
- 83.Vendelin M, Bovendeerd PH, Engelbrecht J, Arts T. Optimizing ventricular fibers: uniform strain or stress, but not ATP consumption, leads to high efficiency. Am J Physiol Heart Circ Physiol 283: H1072–H1081, 2002. doi: 10.1152/ajpheart.00874.2001. [DOI] [PubMed] [Google Scholar]
- 84.Vis MA, Bovendeerd PH, Sipkema P, Westerhof N. Effect of ventricular contraction, pressure, and wall stretch on vessels at different locations in the wall. Am J Physiol Heart Circ Physiol 272: H2963–H2975, 1997. doi: 10.1152/ajpheart.1997.272.6.H2963. [DOI] [PubMed] [Google Scholar]
- 85.Vis MA, Sipkema P, Westerhof N. Modeling pressure-flow relations in cardiac muscle in diastole and systole. Am J Physiol Heart Circ Physiol 272: H1516–H1526, 1997. doi: 10.1152/ajpheart.1997.272.3.H1516. [DOI] [PubMed] [Google Scholar]
- 86.Wang VY, Ennis DB, Cowan BR, Young AA, Nash MP. Myocardial contractility and regional work throughout the cardiac cycle using FEM and MRI. In: Statistical Atlases and Computational Models of the Heart. Imaging and Modelling Challenges. STACOM 2011. Lecture Notes in Computer Science, edited by Camara O, Konukoglu E, Pop M, Rhode K, Sermesant M, Young A. Berlin, Heidelberg: Springer, 2012, p. 149–159. [Google Scholar]
- 87.Wannenburg T, Schulman SP, Burkhoff D. End-systolic pressure-volume and MVO2-pressure-volume area relations of isolated rat hearts. Am J Physiol Heart Circ Physiol 262: H1287–H1293, 1992. doi: 10.1152/ajpheart.1992.262.4.H1287. [DOI] [PubMed] [Google Scholar]
- 88.Westerhof N, Stergiopulos N, Noble MIM, Westerhof BE. Snapshots of Hemodynamics: an Aid for Clinical Research and Graduate Education. New York: Springer, 2018. doi: 10.1007/978-1-4419-6363-5. [DOI] [Google Scholar]
- 89.Wüsten B, Buss DD, Deist H, Schaper W. Dilatory capacity of the coronary circulation and its correlation to the arterial vasculature in the canine left ventricle. Basic Res Cardiol 72: 636–650, 1977. doi: 10.1007/BF01907044. [DOI] [PubMed] [Google Scholar]
- 90.Young AA, Kramer CM, Ferrari VA, Axel L, Reichek N. Three-dimensional left ventricular deformation in hypertrophic cardiomyopathy. Circulation 90: 854–867, 1994. doi: 10.1161/01.CIR.90.2.854. [DOI] [PubMed] [Google Scholar]
- 91.Young JM, Choy JS, Kassab GS, Lanir Y. Slackness between vessel and myocardium is necessary for coronary flow reserve. Am J Physiol Heart Circ Physiol 302: H2230–H2242, 2012. doi: 10.1152/ajpheart.01184.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]