Investigación clínica XXIII

Resumen

Las revisiones sistemáticas (RS) son estudios que intentan contestar una pregunta clínica por medio del uso de artículos originales. Los metaanálisis (MTA) son el análisis matemático de las revisiones sistemáticas. Estos análisis se dividen en dos grandes grupos: aquellos que evalúan los resultados medidos como variables cuantitativas (por ejemplo, el índice de masa corporal —IMC—) y aquellos que evalúan variables cualitativas (por ejemplo, si un paciente está vivo o muerto, o si ha mejorado o no de su enfermedad). Los primeros utilizan en general la diferencia de medias. Para los segundos se puede utilizar el cálculo de razón de momios (RM) u odds ratio (OR), riesgo relativo (RR), reducción absoluta del riesgo (RAR), hazard ratio (HR), etcétera. Estos análisis se grafican por medio de forest plots que permiten tanto la evaluación individual de los estudios como la del resultado final, así como la heterogenidad de estas comparaciones. Asimismo, estos análisis se basan en análisis estadísticos básicos como la t de Student y la χ². Para la toma de decisiones basadas en las RS y en los MTA, es importante evaluar cuidadosamente los posibles sesgos y los apartados estadísticos con el fin evitar malas interpretaciones.

Yo sabía que no había ninguna evidencia real en el tratamiento que ofrecíamos para la tuberculosis. Me temo que yo acorté la vida de algunos de mis amigos gracias a intervenciones innecesarias.

Archie Cochrane (1909–1988)

Antecedentes

En las últimas décadas, el avance vertiginoso en las técnicas diagnósticas y en el tratamiento ha llevado a buscar estrategias que ayuden a organizar, revisar, analizar y gestionar de manera eficiente el conocimiento científico, principalmente en beneficio de los pacientes. Este tipo de estrategias han contribuido en los profesionales de la salud (PROSUD) a continuar con su proceso de aprendizaje a lo largo de la vida además de fortalecer su juicio clínico, ya que en muchas ocasiones estos pueden acceder a información de dudosa calidad, a pesar de estar publicada en revistas de prestigio, con un mensaje tan “contundente” que hasta el mejor de los clínicos podría caer en la interpretación incorrecta de los hallazgos.

Usted en este momento podría estarse preguntando si aspectos como la intuición del clínico, las emociones y las motivaciones en la consulta que pueden despertarse en el proceso de la relación médico-paciente, el contexto en el cual se realiza la práctica clínica, la propia experiencia empírica son importantes en los procesos llamados juicio clínico y aprendizaje; sin duda lo son. Sin embargo, para fines del presente artículo el enfoque se dará a una estrategia basada en evidencia científica que tiene que ver con la búsqueda y evaluación sistematizada además del análisis clínico y la toma de decisiones que va de la mano del quehacer del PROSUD. Esta misma estrategia, aplicada de manera correcta, ayudaría a mejorar la comunicación entre el PROSUD y el paciente para saber los alcances de cada opción de diagnóstico y tratamiento, además del pronóstico de cada entidad de acuerdo con las circunstancias para cada caso en particular. Por ejemplo, si se tratase de la fase diagnóstica, el PROSUD podría llegar a recomendar o no la realización de alguna prueba diagnóstica dependiendo de la utilidad o el costo-beneficio que ha mostrado dicha prueba en distintos reportes científicos o en el caso de la fase de tratamiento, o la elección de una u otra opción terapéutica dependiendo de los resultados de estudios que mostrasen su real magnitud de efecto. Finalmente, en el caso del pronóstico se podría emitir una estimación sobre la probabilidad de éxito del tratamiento o la duración de la enfermedad con base en lo que se muestre en estudios clínicos.

Ya desde mediados del siglo XIX Bichat y Magendi proponían un cambio sustancial en la manera de establecer las bases clínicas del diagnóstico precoz, el pronóstico y el tratamiento de las enfermedades que podemos considerar como la base de lo que hoy conocemos como la medicina basada en la evidencia (MBE). El término metaanálisis fue empleado por primera vez en 1976 por Gene V. Glass, de la Universidad del Estado de Arizona, para referirse al análisis estadístico del conjunto de resultados obtenidos en diferentes ensayos clínicos sobre una misma pregunta de investigación. Sin embargo, las bases matemáticas se conocían desde el final del siglo XVII cuando Gauss y Laplace lo usaron y describieron estos métodos en el área de la astronomía para disminuir el error.

Las revisiones sistemáticas (RS) y/o metaanálisis (MTA) son compilaciones organizadas y de análisis sistematizado de todos los estudios que hasta ese momento se han realizado sobre algún tema específico, y que tratan de contestar una pregunta de investigación clínica en común. Las RS y MTA han tomado un gran auge en los últimos años, ya que han aparecido como una buena alternativa para los PROSUD, cuyo tiempo para la obtención y el análisis de la evidencia científica suele ser limitado. Sin embargo, estos estudios no están exentos de sesgos que lleven a los clínicos a terminar con una mala interpretación de la información.

Por todos estos motivos, es que consideramos de gran trascendencia el revisar en este número los análisis estadísticos más usados en las RS para realizar MTA y explicaremos el significado de los estadísticos, desde su fundamento hasta los gráficos que se han popularizado en las publicaciones de la colaboración Cochrane y que han permeado incluso en revistas de alto impacto como el New England Journal of Medicine.

Empezaremos con un poco de historia. Ya desde mediados del siglo XIX Bichat y Magendi proponían entusiastamente un cambio sustancial en la manera de establecer las bases clínicas del diagnóstico precoz, el pronóstico y el tratamiento de las enfermedades que podemos considerar como la base de lo que hoy conocemos como la medicina basada en la evidencia (MBE).

Hoy en día, los conceptos han cambiado y se conciben las RS y los MTA como estudios secundarios. Esto significa que compilan los resultados de otros estudios con diversos fines. Entre los más destacados tenemos:

1. Ponderar los resultados obtenidos en distintos artículos del mismo tema. A esta circunstancia también se le ha llamado validez externa, pues se trata de una evaluación de los artículos realizada por otros autores diferentes a los autores que hicieron los artículos originales. Esto supone una revisión de los posibles sesgos que concluya en un resultado final con mayor credibilidad, que sea transparente y directo al resolver una pregunta clínica específica en un solo documento, a fin de que el clínico, tras usar su juicio, logre tomar la mejor decisión ante el paciente que tiene delante de él.

2. Evaluar la consistencia entre los ensayos clínicos de similares intervenciones inherentes al tema y generar un estimador del efecto más eficiente.

3. Mejorar el poder estadístico, es decir, la precisión de los resultados arrojados por artículos vistos de manera individual que por tener un tamaño de muestra pequeño no logren tener resultados estadísticamente significativos.

4. Obtener información para el cálculo del tamaño de muestra para estudios futuros.

Cuando las RS tienen valores cuantitativos (como la media del índice de masa corporal —IMC—) o cualitativos dicotómicos (vivo o muerto) y estos son susceptibles de ser comparados y sumados, a estos análisis se les llama metaanálisis. Es decir los MTA son la parte matemática de las RS. Es común que se piense que es mejor un MTA que una RS, cuando en la realidad el mecanismo de búsqueda de la información es el mismo y solo difieren en la parte matemática; de hecho, muchas veces cuando el clínico no está adiestrado en la lectura de los MTA puede ser fácilmente manipulado por autores que se valen de herramientas estadísticas para mostrar resultados que no son necesariamente ciertos o que no tienen una relevancia clínica.

En general, tanto las RS como los MTA requieren de una metodología llamada sistema PICO o PICOST,¹ la cual permite hacer explícitos los métodos que llevaron a localizar los artículos.

En este sentido las revisiones sistemáticas con MTA usan distintas técnicas estadísticas para intentar analizar cada uno de los resultados de un artículo y luego compilarlos y resumirlos para dar un resultado final. En específico, en los MTA se pretende contestar preguntas en las que tenemos un estado basal similar entre estudios. Este se verifica mediante criterios de inclusión de los artículos. Casi siempre se comparan únicamente dos intervenciones, lo que se denomina como “cara a cara”. Estos estudios son analizados de manera individual (para reproducir los resultados de los autores) y finalmente son compilados en un resultado final (en un rombo final).

El gráfico más popular de los metaanálisis es el llamado forest plot, que recibe ese nombre por su apariencia similar a la de un bosque. En los forest plots la línea vertical del gráfico señala la ausencia de efecto y se despliega el efecto para favorecer a una u otra maniobra. Esta siempre se muestra en los gráficos, en el área de las columnas. El resultado se muestra en el área del gráfico (figuras 1a y 1b).

Figura 1a.

Ejemplo de las partes de la arquitectura de la investigación cuyas equivalencias las encontrará resaltadas el lector con colores en la figura 1b

Figura 1b.

Partes de un forest plot

En este ejemplo, el gráfico muestra que el efecto del tratamiento favorece el uso de la aspirina al compararlo con el placebo para el manejo de una cefalea. En el ejemplo de consumo de café frente al del placebo no hay diferencias como antioxidante y en el ejemplo del grupo de sujetos con dislipidemias se favorece al grupo de los sanos (sin dislipidemia) para la prevención de infartos agudos al miocardio.

Estos gráficos son usados para evaluar tanto resultados cualitativos dicotómicos (como puede ser el estar vivo o muerto, o el estar infartado o sin infarto en pacientes usuarios de aspirina profiláctica) como resultados cuantitativos (horas de sueño posteriores a la ingesta de café o placebo). Cada uno de los artículos se representa con su comparación real (tal cual está publicada), que se basa en los números crudos y se representa gráficamente como un cuadrado, que es la media del efecto, y por intervalos de confianza (en general del 95 %) que se representan con una línea horizontal que atraviesa el cuadrado.

Diferencia de medias

Cuando el desenlace es cuantitativo, el gráfico se llama forest plot de diferencia de medias. Este análisis se basa en los estadísticos de la t de Student para grupos independientes, con la diferencia de que en este caso el MTA es la suma de todos los resultados de cada uno de los artículos que forman parte de la revisión sistemática.

A continuación presentamos la fórmula general del MTA de la diferencia de medias, donde δ es igual al resultado final del diamante final (del forest plot) de los MTA. Y este resultado es igual a la suma de la media de cada uno de los estudios del grupo de tratamiento activo y se le resta la misma medida de los del grupo control o de comparación, todo lo anterior divido entre la desviación estándar:

$$\delta =\frac{{\mu }_t-{\mu }_c}{\sigma }$$

El análisis de cada uno de los artículos se realiza de modo similar a la t de Student. En un ejemplo hipotético (figura 2) en el que se estudian dos grupos de veinte pacientes y en el que se compara un medicamento para bajar de peso (A) con un placebo (B), el primer análisis consistiría en la comparación del IMC entre los grupos por medio de la prueba t de Student para grupos independientes (como vimos en Investigación clínica XV).²

Figura 2.

Análisis de la maniobra A frente a la B mediante la prueba t de Student

En la figura 3 podemos ver que el análisis individual de los artículos es similar al que se realiza con la t de Student. Sin embargo, el forest plot tiene la ventaja de mostrar la diferencia de medias (en verde) y los intervalos de confianza del 95 % (IC 95 %).

Figura 3.

Forest plot del análisis individual de la comparación hipotética de A frente a B

Como vimos en el artículo de Investigación clínica VI (cuyo tema es la relevancia clínica),³ en el que mencionamos la importancia del uso de los IC del 95 %, en especial se puede obviar el valor de p, ya que si los intervalos de confianza atraviesan la unidad, esta comparación no es estadísticamente significativa.³ En este ejemplo podemos ver las partes de un forest plot. En la columna donde dice Weight se hace referencia al peso de cada artículo sobre el resultado final que se aprecia en forma de rombo negro. En este caso hipotético solo hay un artículo, por lo que se infiere que el resultado final se debe en un 100 % al artículo de Rivas-Ruiz del 2013. En las filas podemos observar además los valores crudos del estudio con su media y su desviación estándar; una fila más abajo, la sumatoria total con su resultado. Y más abajo se presenta el análisis de heterogeneidad entre los estudios. Como solo se trata de un estudio, no es aplicable llevar a cabo este análisis. El tema de la heterogeneidad lo vamos a abordar más adelante.

En la línea final se encuentra el análisis estadístico para obtener el valor de p (la probabilidad de que el efecto final del metaanálisis —rombo negro— se deba al azar). Al igual que todos los análisis, este valor de p debe ser < 0.05 para considerarse significativo. En este caso el valor es de 0.06, lo que refiere que los tratamientos de A y B no son distintos en la efectividad para disminuir el IMC.

Ahora realizaremos combinaciones hipotéticas para ejemplificar con los componentes de las RS y los MTA.

Siguiendo el ejemplo hipotético, si combináramos los resultados de un estudio con otro estudio con menor tamaño de muestra, para incrementar el poder estadístico, pero con resultados similares (figura 4), lo que se encontraría es que el resultado final (rombo negro) tendría ya un resultado estadísticamente significativo; en este caso a favor del tratamiento B para la reducción del IMC.

Figura 4.

Forest plot del análisis de dos artículos de la comparación hipotética de A frente a B

Siguiendo el orden anterior, tendríamos el resultado de la t de Student del segundo estudio hipotético (Pérez-Rodríguez, 2014), el cual no resultó significativo p = 0.08. Sin embargo, al combinar los dos estudios el resultado final (rombo negro) resulta a favor del tratamiento B (p = 0.02).

Como ya se había mencionado, la columna del apartado de peso (Weight) hace referencia al peso quetiene cada artículo a partir de la cantidad de pacientes que tiene cada estudio. La prueba de heterogeneidad de χ² que se observa en la figura evalúa si los resultados son homogéneos o heterogéneos: cuando el valor de p de la prueba es < 0.05 se dice que los resultados son heterogéneos y cuando el valor de p es ≥ 0.05 la prueba resulta no significativa, lo que quiere decir que los estudios tienen resultados homogéneos (es decir, similares, en este caso idénticos). Las siglas df de la prueba de heterogeneidad hacen referencia a los grados de libertad que se calculan restando una unidad al número de estudios incluidos en el análisis; en este caso, en el que son dos estudios los incluidos, se tiene 1 grado de libertad (2 estudios − 1 = 1).

Siguiendo con el ejemplo hipotético, si añadiéramos otro estudio publicado con anterioridad con resultados completamente contrarios, el efecto final estadísticamente significativo desaparecería y refutaría los hallazgos de los otros dos artículos, lo cual nos daría como resultado que no hay diferencia entre ambos tratamientos (p = 1.00). En la figura 5, podemos observar que al incorporar un artículo más con mayor número de pacientes la columna de peso vuelve a cambiar y le da mayor peso (50 %) al grupo con más pacientes. Además, en el análisis de heterogeneidad la χ² con dos grados de libertad (df) por tener tres estudios tiene un valor de p = 0.005, lo cual significa que alguno de los estudios tiene resultados heterogéneos (en este ejemplo el heterogéneo es el estudio del doctor Talavera, el cual es completamente contrario a los dos artículos publicados tiempo después).

Figura 5.

Forest plot de la comparación de tres artículos con dos maniobras con un resultado cuantitativo, con heterogenidad, analizado por métodos fijos

Cuando los resultados de los estudios son heterogéneos se recomienda hacer el análisis de forma más robusta con efectos aleatorios, lo cual se explicará con más detalle más adelante. Con esto en mente encontramos que debido a que el estudio del doctor Talavera incorporó más pacientes y tiene un mayor peso, la heterogeneidad medida con I2 es del 81 %.

Debido a que la comparación presentó esta heterogeneidad alta, el MTA debe ser analizado por efectos aleatorios (random), lo cual vemos en la parte superior de la figura 6.

Figura 6.

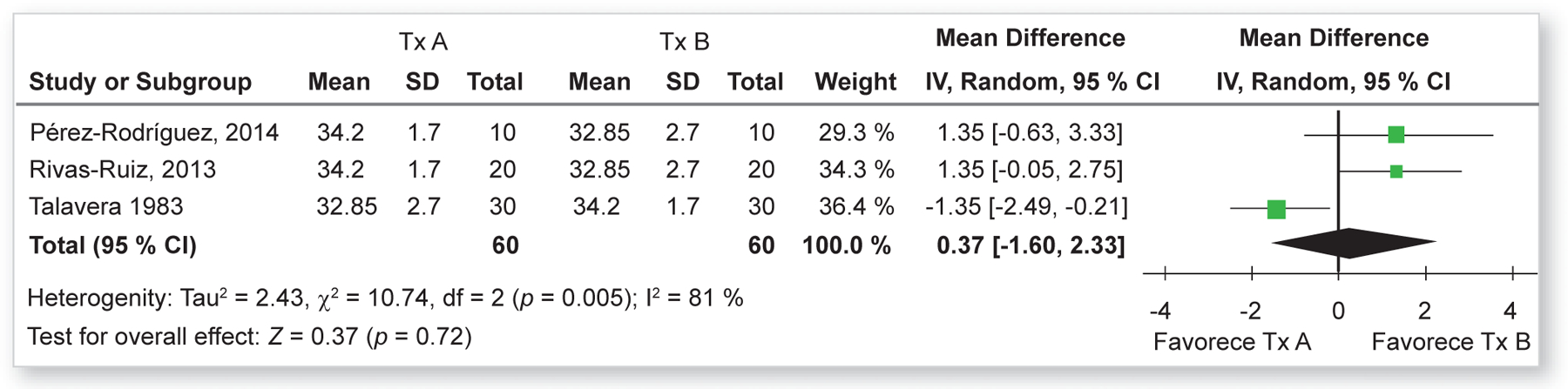
Forest plot de la comparación de dos maniobras con un resultado cuantitativo, con heterogenidad, analizado por métodos aleatorios

Cuando se analiza por métodos aleatorios, no se toma en cuenta solo el peso de cada uno de los artículos, sino el del efecto y el de los intervalos de confianza. Este análisis cambia el resultado final, como podemos ver en la fila del total (95 % CI), el cual a diferencia de la figura 5, donde la diferencia era de 0, ahora al cambiar el criterio de ponderación, presenta una tendencia ligeramente a favor del Tx B con una diferencia de 0.37 de IMC, sin ser estos estadísticamente significativos (p = 0.72).

Diferencia de proporciones

Este es uno de los análisis más populares, ya que en la práctica clínica la pregunta directa de los pacientes es: “¿Qué medicamento es mejor A o B?”, por lo que este análisis es uno de los más utilizados.

Se utiliza el forest plot para la diferencia de proporciones cuando el resultado del estudio es dicotómico (por ejemplo, enfermo o no enfermo). Hoy en día el software Rev Man (disponible en http://tech.cochrane.org/revman/download) permite realizar distintos análisis y se puede calcular razón de momios (RM) o odds ratio (OR) cuando se comparan estudios transversales y casos y controles. En el caso de cohortes y ensayos clínicos, se calculan los riesgos relativos (RR). También se pueden hacer cálculos usando la reducción absoluta del riesgo (RAR). Recientemente se han incorporado análisis para estudios de seguimiento, en los que la medida de asociación es el hazard ratio (HR), el cual es producto de estudios de supervivencia.

El método estadístico que usan estos análisis tiene su base estadística en la χ², por medio de la cual se considera lo observado frente a lo esperado.⁴

Estos forest plots tienen las mismas características que las enunciadas previamente, en las que a cada uno de los estudios se le analiza de manera individual en cada renglón con la fórmula que le corresponda (RM, RR o HR).³

Siguiendo con el ejemplo hipotético, en el cual se busca cuál es la eficacia de un tratamiento A al compararlo con un tratamiento B, y en el que ahora el resultado es que los pacientes lleguen a un peso adecuado, tendríamos lo que se muestra en la figura 7.

Figura 7.

En el forest plot (A) se hace un análisis de los tres estudios con RM (B), después con RR (C) y finalmente con reducción absoluta del riesgo (RAR)

En estos ejemplos encontramos que los estudios de Pérez-Rodríguez y Rivas-Ruiz muestran que un mayor número de pacientes en el tratamiento B llegan a un peso adecuado en mayor porcentaje que los pacientes que tomaron el tratamiento A, a diferencia del estudio de Talavera, el cual refiere que no hay diferencias significativas entre los dos grupos y se representa gráficamente con los IC 95 % que tocan la unidad.

Sin embargo, el resultado final (rombo negro) nos hace referencia a que el efecto general de la comparación A frente a B favorece a la administración del tratamiento B y además esto resulta estadísticamente significativo (p = 0.009).

En la figura 7, presentamos todas las posibilidades de análisis. Sin embargo, lo correcto sería un análisis con RR (B), debido a que los estudios fueron ensayos clínicos.

Heterogeneidad

Como vimos en los ejemplos anteriores, se utilizan dos métodos para demostrar la homogeneidad o la heterogeneidad de los resultados que se incorporan en un MTA. El primero consiste en una prueba de hipótesis, con la cual se busca conocer si existe o no heterogeneidad. Esa prueba se basa en la siguiente prueba de hipótesis:

$$\text{H}0=\text{E}1=\text{E}2\left(\text{los resultados de los estudios}\left[\text{E}\right]\text{son homogéneos}\right)$$

$$\text{Ha}=\text{E}1\ne \text{E}2\left(\text{los resultados de los estudios}\left[\text{E}\right]\text{son homogéneos}\right)$$

Para realizar esta prueba, se utiliza en general la prueba de χ². El valor crítico para desechar la hipótesis nula es un valor de p < 0.05.

Sin embargo, si queremos conocer el grado de heterogeneidad, se requiere de otro estadístico llamado I², el cual se describe en forma de porcentaje, y va del 0 al 100 %, donde el 0 es la heterogeneidad nula (total homogeneidad) y el 100 % es completamente heterogéneo. En general el punto crítico de la I² es el 50 %. Sin embargo este valor puede ser modificado a consideración de los investigadores. En los ejemplos anteriores de la figura 7 encontramos que en todos los casos la I² demostraba que los resultados eran heterogéneos, es decir, dos artículos refieren que el fármaco B es mejor que el A y un artículo lo contrario, por lo que los resultados son contradictorios.

Con estas pruebas se pueden tomar decisiones para realizar los análisis del MTA, ya sea por métodos fijos (en caso de que los estudios sean homogéneos) o por métodos aleatorios (en caso de que los estudios sean heterogéneos).

Los métodos aleatorios son más robustos que los métodos fijos, por lo que se recomiendan cuando los resultados no van a la misma dirección.

Regresando a nuestro caso hipotético, encontramos que la heterogeneidad es significativa (p < 0.001) y que la I² siempre es > 50 %, por lo que el análisis más conveniente debe de ser por efectos aleatorios (figura 8).

Figura 8.

Forest plot de la comparación de A frente a B mediante efectos aleatorios

Como se puede apreciar, ahora el resultado del MTA es no significativo (p = 0.42) a pesar de que parece favorecer al tratamiento B.

Por lo anterior, es muy importante seleccionar la prueba adecuada para el análisis de estos datos, ya que a partir de la selección del análisis los resultados pueden resultar contrarios.

A pesar de que las fórmulas para los MTA son muy sencillas, hoy en día se requiere que estos análisis se realicen con software especializado. El software que nosotros recomendamos es el que distribuye de manera gratuita la colaboración Cochrane, el cual se llama Rev Man y, como mencionamos antes, puede ser descargado directamente de su página de Internet. También se pueden utilizar otros programas estadísticos como STATA.

Conclusiones

Los MTA son la ponderación matemática de los estudios cuantitativos. Cuando la variable dependiente es una variable cuantitativa (como peso, talla o IMC), entonces se utiliza la diferencia de medias.

Cuando la variable dependiente es dicotómica (variable cualitativa, como vivo o muerto, mejoría o no mejoría), se pueden utilizar distintos modelos dependiendo del tipo de diseño de los artículos originales (puede ser RM, RR o HR).

Los MTA son de utilidad por compilar la información de una revisión sistemática. Los estadísticos pretenden ser sencillos y son graficados para que puedan ser leídos a primera vista. Sin embargo, se debe tener cuidado en la interpretación y el uso adecuado de los modelos estadísticos.

Algunos investigadores y personal de la salud están en contra de este tipo de estudios, al referir que al juntar basura solo se obtiene más basura. Existe controversia también sobre el peso de los MTA en los niveles de evidencia que utilizan las guías de práctica clínica. Esta controversia radica en que es preferible usar la información de un solo ensayo clínico aleatorizado multicéntrico, la cual otorga una información mas robusta al venir de un solo protocolo.

Sin embargo, el principio de las RS y los MTA es tener un protocolo lo suficientemente limitado que permita combinar pacientes y maniobras similares. Esto se consigue cuando elaboramos la pregunta de investigación utilizando la palabra PICO o PICOST, con lo cual delimitamos la población blanco, la intervención, el comparador, los resultados, y otras características particulares, como el tipo de estudio que nos permitirá elegir aquellas publicaciones que respondan de forma clara y específica la pregunta planteada. Por eso creemos que entender la estadística de este tipo de estudios ayudará sin duda a modular el juicio clínico y a mejorar la toma de decisiones en la práctica cotidiana.

También consideramos que todos los estudios están sujetos a distintos sesgos y por lo tanto entenderlos y analizarlos mejor ayuda a desmitificar este tipo de controversias y a valorar los estudios en su justa dimensión.