Effects of ambient temperature and humidity on droplet lifetime – A perspective of exhalation sneeze droplets with COVID-19 virus transmission

Abstract

A one-dimensional droplet evaporation model is used to estimate the droplet lifetime from evaporation in air. The mathematical model invokes assumptions of spherical symmetry, ideal gas mixture, binary diffusion, no re-condensation on droplet surface, and constant properties. Four initial droplet diameters (0.001, 0.01, 0.1, and 1 mm), two ambient temperatures (20 and 30 ^oC) and a range of ambient relative humidity are considered. For the conditions studied, the results show that the ambient relative humidity plays an important role in the droplet lifetime calculation. Increasing the ambient temperature does not necessarily decrease the droplet lifetime; it occurs only when the ambient relative humidity is set below 37%. When the ambient relative humidity is higher than 37%, the higher ambient temperature (30 ^oC) results in a longer droplet lifetime for the same initial droplet diameter considered. The results also suggest that there may exist a critical ambient relative humidity; beyond which, the droplet lifetime will increase exponentially. For ambient temperature at 30 ^oC, the critical ambient relative humidity is around 55.7%. It must be mentioned that the results of this study do not imply that the COVID-19 virus will be deactivated at the end of the droplet lifetime. The study simply shows the potential effects resulting from the ambient temperature and ambient relative humidity on virus carrying drops.

Nomenclature

B

mass transfer number, Equation (6)

d_o

initial droplet diameter

D

binary diffusion coefficient, water vapor diffusion into ambient air

m_f

mass of liquid drop

${\dot{m}}_s^{"}$

evaporation mass flux at droplet surface

M_k

molecular weight of species k

p

pressure

p_w,sat

saturation vapor pressure of water

r

radial direction

RH

relative humidity

r_o

initial droplet radius

r_s

droplet radius

t

time

T

temperature

$t^{\ast }$

droplet lifetime

$v$

mixture radial velocity

X_k

mole fraction of species k

Y_k

mass fraction of species k

Greek

ρ

density

Subscript

da

dry air

f

liquid water

s

droplet surface condition

w

water

w,s

water at droplet surface

w,∞

ambient water

∞

ambient condition

1. Introduction

The COVID-19 virus pandemic has gravely impacted the world and is changing the way we live. The U.S. CDC reported, as of April 7, 2020, there were 374,329 confirmed cases and 12,064 deaths in the U.S. The numbers appeared to continue to increase. The WHO (World Health Organization) Scientific Brief (WHO, 2020) reviewed available data of COVID-19 virus transmission (Liu et al., 2020; Chan et al., 2020; Li et al., 2020; Huang et al., 2020; Burke et al., 2020; World Health Organization, 2020) and concluded that the transmission was primarily through respiratory droplets (e.g., from exhalation sneeze) and contact routes. There were no reports of transmission through the droplet nuclei (defined to be the drops smaller than 5 μm). As given in national and international guidelines, personal protective equipment and social distancing are important measures to contain the spread of COVID-19 virus. A better understanding on how exhalation sneeze drops transport in air may provide insight that contributes to effective measures to contain the virus spread.

Bourouiba (2020) showed that droplets from human exhalation sneeze could travel up to 7–8 m when the peak exhalation speed was in the range 10–30 ms⁻¹. It further pointed out that COVID-19 virus was found in hospital ventilation systems in hospital rooms of patients infected with COVID-19 in China (Ong et al., 2020). Bourouiba suggested (Bourouiba, 2020) that the interactions of virus particles/droplets from a human sneeze with ambient flow turbulence (e.g., the turbulent transport of, and interaction with, virus droplets) may play an important role in the virus spread. One of the transport phenomena is the mass transport between the droplets and the surrounding air – a topic of current study.

The objective of current study is to examine the droplet lifetime in different ambient conditions, namely, the ambient temperature and the ambient relative humidity.

1.1. Theoretical condensation

Formulation of evaporating drops are well documented in science and engineering literature (Spalding, 1953; Faeth, 1977, 1983; Law, 1982, Kuo, 2005). The mathematical model of the gas-phase transport of mass and species of an evaporating drop shown in Fig. 1 can be written as follows:

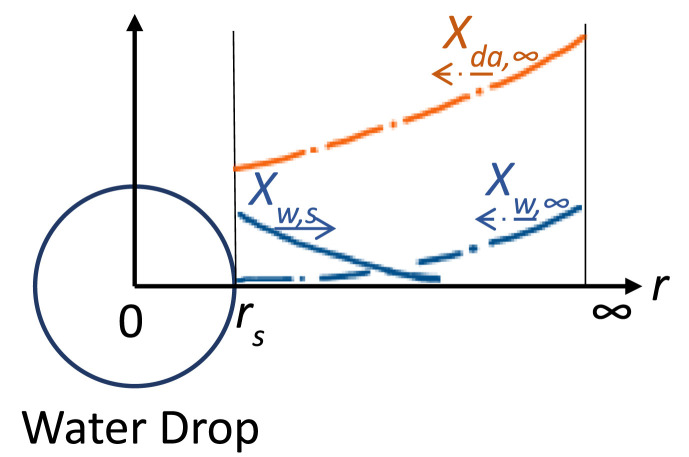
Fig. 1.

Schematic of the coordinate system and illustration of water vapor (mole faction, X_w,s) diffusion away from the droplet surface(r_s) and ambient dry air (mole fraction, X_da) and ambient moisture (water vapor, X_w,∞) diffusion toward the droplet surface.

Mass

$$\frac{d\left(r^2\rho v\right)}{dr}=0$$ (1)

Species

$$\frac{1}{r^2}\frac{d\left(r^2\rho v{Y}_w\right)}{dr}=\frac{1}{r^2}\frac{d}{dr}\left(r^2\rho D\frac{d{Y}_w}{dr}\right)$$ (2)

Boundary Conditions

$$\text{r }={\text{r}}_{\text{s}}{\rho }_s{v}_s={\rho }_s{v}_s{Y}_w+\left(-\rho D\right){\left(\frac{d{Y}_w}{dr}\right)}_s$$ (3)

$$r\to \infty Y_w=Y_{w,\infty }$$ (4)

Assumptions invoked in deriving the above transport equations are (a) one-dimensional transport in r-direction (i.e., spherical symmetry), (b) ideal gas mixture of the gas phase, (c) binary diffusion of water vapor from the droplet surface into surrounding air, (d) no re-condensation on droplet surface, and (e) ρD = constant.

Solution of Equation (1) states that $\rho v{r}^2$ = constant. Integrating Equation (2) and applying the solution of Equation (1) along with the boundary conditions, one obtains the mass flux at the droplet surface

$${\dot{m}}_s^{"}={\rho }_s{D}_s\frac{\ln (1+B)}{r_s}$$ (5)

where B is the Spalding mass transfer number,

$$B=\frac{Y_{w,s}-Y_{w,\infty }}{1-Y_{w,s}}$$ (6)

The mass fraction of water vapor at the droplet surface,$Y_{w,s}$ , is calculated from the mole fractions, X _k, and molecular weights, M _k, by

$$Y_{w,s}=\frac{X_s{M}_w+\left(1-X_s\right)X_{w,\infty }{M}_w}{X_s{M}_w+\left(1-X_s\right)\left(\left(1-X_{w,\infty }\right)M_{da}+X_{w,\infty }{M}_w\right)}$$ (7)

where subscript w,∞ denotes the ambient water vapor and subscript da denotes the dry air.

The droplet lifetime can be obtained by solving the mass balance equation of the droplet:

$$\frac{d{m}_f}{dt}=-4\pi r_s^2{\dot{m}}_s^{"}$$ (8)

where subscript f denotes the liquid-phase (water droplet) property. Assuming constant liquid water density, the droplet lifetime, t*, can be obtained from solving Equation (8) with an initial condition, $d_f\left(0\right)=d_o$.

$$t^{\ast }=\frac{{\rho }_f{d}_o^2}{8{\rho }_w{D}_w\left(\ln \left(1+B\right)\right)}$$ (9)

2. Results

To calculate the droplet lifetime, the needed thermodynamic and transport properties are summarized in Table 1 . The ambient pressure was set to 1 atm. The initial droplet size (d _o) was set to 0.001, 0.01, 0.1 and 1 mm, which was based on the droplet size distribution from exhalation sneeze reported in (Han et al., 2013). Two ambient temperatures, T _∞ = 20 °C and T _∞ = 30 °C were considered. For T _∞ = 20 °C, RH _∞ was set to vary from 0 to 100% and for T _∞ = 30 °C, 0–55.7%. The 55.7% relative humidity corresponds to the condition that $Y_{w,\infty }=0.95Y_{w,s}$ at T _∞ = 30 °C. When $Y_{w,\infty }$ approaches $Y_{w,s}$, B approaches zero, cf., Equation (6), and t* approaches infinity, cf., Equation (9).

Table 1.

Summary of property values used in computation.

T (0C)	ρf (kg m−3) (Moran and Shapiro, 2004)	ρw (kg m−3)	pw,sat (atm)	D (m2 s−1) (Engineering ToolBox, 2018)	Mw	Mda
20	9.982 × 102	1.730 × 10−2	2.31 × 10−2	2.42 × 10−5	18.01	28.97
30			4.19 × 10−2	2.42 × 10−5	18.01	28.97

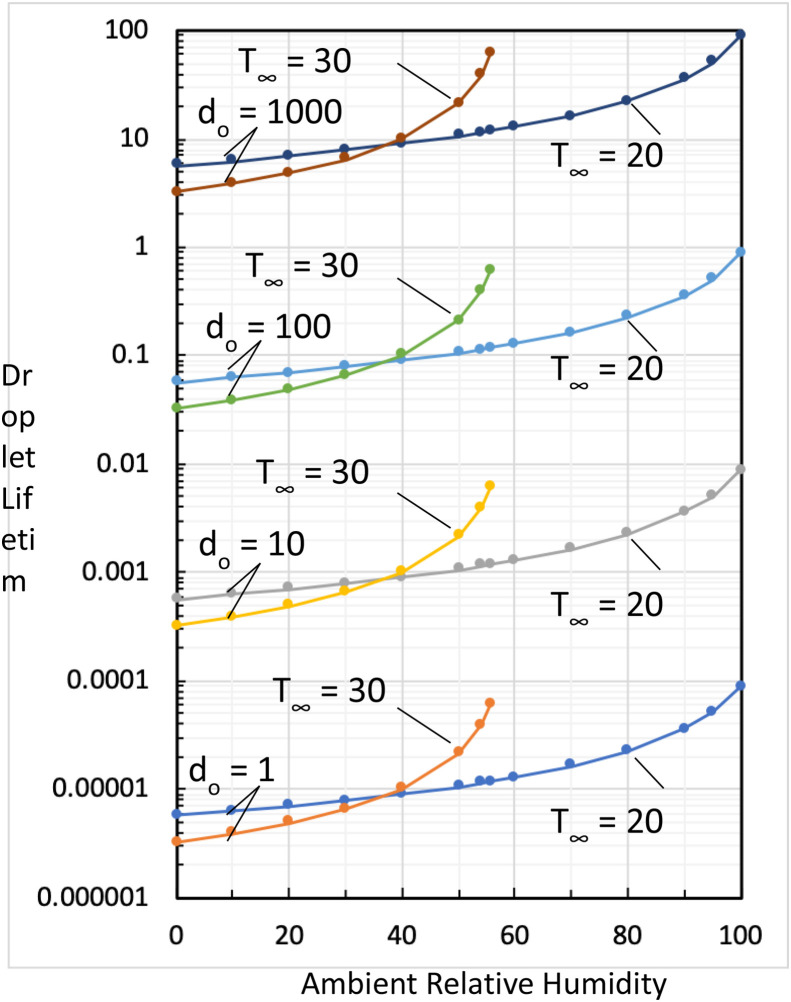
The calculated droplet lifetime (t*) in hours (h) versus ambient relative humidity (RH _∞) in percentage (%) is summarized in Fig. 2 . Four sets of results are presented; representing four different initial droplet diameters, d _o = 1, 10, 100, and 1000 μm, respectively. Two ambient temperatures are considered for each initial droplet diameters, T _∞ = 20 and 30 °C. As expected, the droplet lifetime increases with increasing ambient relative humidity and it increases with increasing initial droplet size, e.g., $t^{\ast }\propto d_o^2$, cf., Equation (9). The results also show that a higher ambient temperature does not necessarily decrease the droplet lifetime. It decreases the droplet lifetime only for RH _∞ < 40% (or 37.1% for the condition considered). Conversely, a higher ambient temperature with low relative humidity can decrease the droplet lifetime but it depends on the ambient relative humidity.

Fig. 2.

Summary of droplet lifetime (t*) versus ambient relative humidity (RH_∞); results of 4 droplet initial diameters (d_o) and two ambient temperatures (T_∞) are considered.

To illustrate the importance of ambient humidity, Fig. 3 summarizes the ratio of droplet lifetime with T _∞ set to 30 °C to that with T _∞ set to 20 °C. For an ambient relative humidity below 37.1%, the droplet lifetime is shorter when the ambient temperature is set to 30 °C. Specifically, the ratio is 0.56 for RH _∞ = 0%; 1 for RH _∞ = 37.1%; 5.13 for RH _∞ = 55.7%.

Fig. 3.

Summary of the ratio of droplet lifetime with T_∞ set at 30 °C $\left(t_{T_{\infty }={30}^{o}C}^{\ast }\right)$ to that with T_∞ set at 20 °C $\left(t_{T_{\infty }={20}^{o}C}^{\ast }\right)$ as a function of ambient relative humidity (RH_∞).

3. Discussion

The computation shows that the droplet size has the major effect on the droplet lifetime. For an initial droplet diameter of 100 μm and the droplet surface temperature T _w,s of 20 °C, the calculated droplet lifetime ranges from 0.056 h (at RH _∞ = 0%) to 0.887 h (at RH _∞ = 100%) when T _∞ is set to 20 °C. For T _∞ set to 30 °C and T _w,s set to 20 °C, the droplet lifetime ranges from 0.032 h (at RH _∞ = 0%) to 0.606 h (at RH _∞ = 55.7%). However, for an initial droplet diameter of 1000 μm, the droplet lifetime can be in hours for both ambient temperatures and ambient relative humidity examined in the study.

When the ambient relative humidity is high, it can lead to drastic increases of droplet lifetime. An example is that when T _∞ is set to 30 °C and RH _∞ to 55.7%, an exponential increase of droplet lifetime is shown in Fig. 3, which can be seen from Equation (9). When B approaches 0, the droplet lifetime approaches infinity. A higher ambient temperature can lead to a shorter droplet lifetime provided a low ambient relative humidity is maintained; as shown by Fig. 3, RH _∞ < 37.1% is needed for the conditions examined in this paper.

Uncertainty in estimating the droplet lifetime reported in this paper includes the assumptions and the properties used in the analysis. The binary diffusion and constant property assumption can be relaxed when a multi-component system is adopted. The temperature effects on estimated droplet lifetime due to the assumption of constant binary diffusion coefficient will result in an overestimate of the droplet lifetime at a level of 2.5–5.1% as D is proportional to T ^7/4 based on Chapman-Enskog equation of binary diffusion coefficient (Reid et al., 1987). The coupling of droplet and flow turbulence can be accounted for by the well-established Lagrangian-Eulerian formulation such as that reported in (Faeth, 1983; Shuen et al., 1983). These are the topics for further studies.

4. Conclusion

A one-dimensional droplet evaporation model was used to estimate the droplet lifetime from evaporation in air. The mathematical model invokes assumptions of spherical symmetry, ideal gas mixture, binary diffusion, no re-condensation on droplet surface, and constant properties. Four initial droplet diameters (1, 10, 100, and 1000 μm), two ambient temperatures (T _w,∞ = 20 and 30 °C) and a range of ambient relative humidity were considered. The results show that the ambient relative humidity plays an important role in the droplet lifetime calculation. Increasing the ambient temperature does not necessarily decrease the droplet lifetime; it occurs only when the ambient relative humidity is set below 37%. When the ambient relative humidity is above 37%, the higher ambient temperature results in a longer droplet lifetime for the same initial droplet diameter considered. The results also suggest that there may exist a critical ambient relative humidity; beyond which, the droplet lifetime will increase exponentially. For T _∞ = 30 °C, the critical ambient relative humidity is around 55.7%.

It must be mentioned that the results of this study do not imply that the COVID-19 virus will be deactivated at the end of the droplet lifetime. The results simply show the potential effects resulting from the ambient temperature and ambient relative humidity on virus carrying drops. The findings of this paper might be helpful when considering the indoor air quality and setting the dehumidifier operating conditions of the HVAC systems of hospitals, schools, apartment buildings, and shopping malls alike places, as we are combating to contain the COVID-19 virus transmission.