Analysis of the mitigation strategies for COVID-19: From mathematical modelling perspective

highlights

• •A deterministic mathematical model for the transmission dynamics of COVID-19 is formulated, analysed and validated with real data.
• •It is shown that model exhibit a backward bifurcation phenomenon if people recover without permanent immunity.
• •Recent history of similar outbreaks plays an important role in delaying the outbreak at the initial stage provided the average effectiveness of self-protection measures is high enough.
• •It is necessary to detect and isolate at least 30% of the asymptomatic cases and 50% of the symptomatic individuals if the disease is to be contained.

Abstract

In this article, a mathematical model for the transmission of COVID-19 disease is formulated and analysed. It is shown that the model exhibits a backward bifurcation at ${\mathcal{R}}_0=1$ when recovered individuals do not develop a permanent immunity for the disease. In the absence of reinfection, it is proved that the model is without backward bifurcation and the disease free equilibrium is globally asymptotically stable for ${\mathcal{R}}_0<1$. By using available data, the model is validated and parameter values are estimated. The sensitivity of the value of ${\mathcal{R}}_0$ to changes in any of the parameter values involved in its formula is analysed. Moreover, various mitigation strategies are investigated using the proposed model and it is observed that the asymptomatic infectious group of individuals may play the major role in the re-emergence of the disease in the future. Therefore, it is recommended that in the absence of vaccination, countries need to develop capacities to detect and isolate at least 30% of the asymptomatic infectious group of individuals while treating in isolation at least 50% of symptomatic patients to control the disease.

1. Introduction

A novel coronavirus, named a severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2; previously known as 2019-nCoV), was identified as the infectious agent causing an outbreak of viral pneumonia in Wuhan, China, in December 2019 [1]. The World Health Organization (WHO) medical team codenamed the new outbreak caused by SARS-CoV-2 as “coronavirus disease 2019 (COVID-19)”. The infection is in the same category as the Severe Acute Respiratory Syndrome (SARS) which emerged in Southern China in 2002, spreading to up to 30 Countries, with a total of 8098 cases and claiming 774 lives [2]. COVID-19 is also in the same category as the Middle East Respiratory Syndrome (MERS) which was first identified in Saudi Arabia in 2012, and ended up spreading to 27 countries around the world, reaching a total of 2519 cases confirmed and claiming up to 866 lives [3].

Since January 2020, an increasing number of cases confirmed to be infected with COVID-19 have been detected outside Wuhan, and currently the infection has spread all over the world. As of May 28, 2020, (09:09 GMT), COVID-19 had affected all continents including island nations (213 countries and territories as well as 2 international conveyances), with the total number of cumulative infections globally standing at 5,807,012 cases and 357,800 deaths [4], and the numbers still increasing.

The major portal of entry of the virus into the body is the tissue lining the T-zones of the face (including the nose, eyes and mouth). The infection is characterised by loss of the sense of smell (a condition referred to as hyposmia/anosmia), taste and poor appetite. Although, such conditions have been observed in COVID-19 patients, many carriers of the infection may not show any severe symptoms like fever and cough but have hyposmia, loss of taste and loss of appetite.

Whereas knowledge of the virus dynamics and host response are essential for formulating strategies for antiviral treatment, vaccination, and epidemiological control of COVID-19, estimation of changes in transmission over time can provide insights into the epidemiological situation and help to identify whether public health control measures are having a measurable effect [5], [6]. The analysis from mathematical models may assist decision makers to estimate the risk and forecast the potential spread of the disease in the population. Understanding the transmission dynamics of the infection is crucial in designing alternative intervention strategies [7]. In general, by approaching infectious diseases from a mathematical perspective, we can identify patterns and common systems in disease function, which would enable us to find some of the underlying structures that govern outbreaks and epidemics.

Mathematical models that analyse the spread of COVID-19 have began to appear in few published papers and online resources [7], [8], [9], [10], [11], [12], [13]. However, there are several challenges to the use of mathematical models in providing nearly accurate predictions at an early stage of the outbreak, particularly in real time as it is difficult to determine many of the pathogen-based parameters through mathematical models. The estimation of such parameters will require clinical observations and “shoe-leather” epidemiology [14]. It is also possible for some of the parameters to be verified through observation only at a later stage in the course of the epidemic. To get better predictions and to design and analyse various alternative intervention strategies in the absence of such parameter values, one needs to estimate them from existing epidemiological data.

Like many respiratory viruses, the novel coronavirus SARS-CoV-2 can be spread in tiny droplets released from the nose and mouth of an infected individual. As soon as the virus enters the body (either through the mouth, nose or membrane of the eyes), it finds its way to the windpipe and then the lungs. This viral attack is characterised by flu like symptoms, fever (body temperatures more than 38.3 ^∘C) and dry cough at the initial stage of the infection. Once the virus gets into the lungs, it causes fibrosis of the lungs leading to shortness of breath (or difficulty to breathe) and severe pneumonia followed by impaired functioning of the liver and acute kidney injury [15]. The virus is then released from the infected individual when they cough, sneeze and when they touch their own nose or mouth. Some particles that are released through coughing or sneezing may land on clothing of other people in close proximity, and surfaces around them while some of the smaller particles can remain in the air for some time. In addition, some scientific evidence shows that the virus can also be shed for a longer time in faecal matter [16]. The virus survives on surfaces, fabrics, metals, plastics for variable times. Recent reports indicate that the virus can survive from a shorter time (in the air) up to 2–3 days long on plastic and stainless-steel surfaces [17]. This implies that an uninfected individual can also acquire the virus through contact with infected surfaces. That means, there is a possibility for COVID-19 infection to spread from such contaminated surfaces and objects to uninfected humans. Hence, including the proportion of indirect transmission from the environment in the mathematical model structure is important to address this situation. We note that the impact of environmental contamination and its role in the transmission of the disease is not well studied in mathematical models developed so far.

Reinfection by the family of coronavirus is possible as it is indicated in Isaacs et al. [18], Wu et al. [19]. Even if it is not yet well known how long it takes for a person who recovered from COVID-19 to lose immunity, we can not overlook its impact at this stage. Therefore, when formulating a mathematical model for COVID-19 dynamics, it is reasonable to consider a kind of Susceptible-Infected-Recovered-Susceptible (SIRS) type of epidemiological model formulation.

So far there is no known curing medicine nor vaccine to combat the COVID-19 pandemic. The available prevention mechanisms that are recommended by the WHO so far are also limited and their effectiveness is not yet fully tested. The level of the population’s understanding and application of these preventive mechanisms varies from region to region and from country to country. In some places, the protective measures are employed voluntarily by individuals and in some other places, governments impose some kind of rules on the population to use strict social distancing and wearing face masks in public places. However, the adherence to these rules is not uniform.

In the past, it has been witnessed that during the outbreak of infectious diseases, the human population has been taking precautionary actions such that wearing masks, abstinence from risky contacts, avoiding public transport means and increasing the uptake of vaccination (when available) [20], [21], [22]. Behaviour change towards using preventive mechanisms by the population to protect themselves from an infectious disease is assumed to be dependent on the way the disease is transmitted and its fatality rate. Individuals who have awareness about the disease and who decided to use preventive mechanisms have less susceptibility than those without awareness and demonstrating the usual risky behaviour.

A number of mathematical models have been proposed to analyse the effects of human behaviour in the dynamics of infectious diseases (see [22], [23], [24], [25], [26], [27], [28], [29], [30], and the references therein). In this paper, we follow the diffusion of innovation approach, which was proposed by Kassa and Ouiniho [21]. In models of this approach, it is assumed that the perceived threat for the population is the level of prevalence of the disease. However, for diseases with short time cycles, the prevalence dependent awareness function may be unrealistic. Therefore, in this work we assume that awareness is driven by the magnitude of the incidence rate reported each day. That means, based on the diffusion of innovation method, one may consider the perceived threat for the population to be the incidence of the disease.

At the beginning of the COVID-19 outbreak, a huge disparity has been observed in the use of self-protective mechanisms and adherence to the advice given by public health agencies. In particular, the people in some parts of Asia have fully embraced the measures while many in other parts of the world were very much hesitant to use them. For example, wearing a face mask everyday in public appearances is like a ritual in most of the countries in Southeast Asia, while the same is considered as a bad gesture in many of the other parts of the world [31] (even if it is now becoming a “new normal” also everywhere in the globe). One key difference between these societies and the people in the West is that, the communities in the Southeast Asia have experienced similar disease outbreaks before and the memories are still fresh and painful [31]. That means, recent history of a similar event plays a role in behavioural change of the population especially at the beginning of the outbreak in addition to the perceived threat from the disease.

Therefore, in this paper, we consider a mathematical model that takes into account

• 1.the transmission dynamics of COVID-19 similar to the SIRS model,
• 2.the contribution of the asymptomatic infectious individuals in the transmission dynamics of the disease in the population,
• 3.the effect of indirect transmission of the disease through the environment,
• 4.behavioural change of individuals in the society to apply self-protective measures, and
• 5.the intensity of historical events from recent similar outbreaks.

By analysing the proposed basic mathematical model, the effect of each of these factors is investigated in terms of their contribution to the control strategies of the disease. Moreover, the use of isolation or quarantining and strict social distancing measures are also considered as mitigation strategies, and a comparative study is made for different scenarios.

The layout of this paper is as follows: The model is described and formulated in the next section. Its qualitative analysis is presented in Section 3. Estimation of the parameters and the sensitivity analysis of the reproduction number of the model with respect to involved parameters are discussed in Section 4. Numerical simulations of the model with some assumed intervention scenarios are also presented and analysed in this same section. Concluding remarks of the study are given in Sections 5.

2. Model formulation

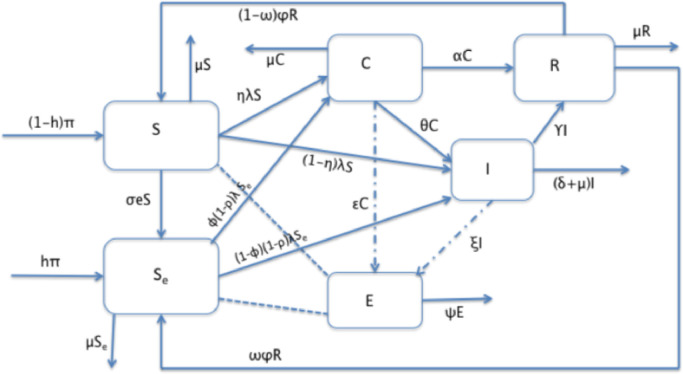
In this section, we present a mathematical model for the transmission dynamics of COVID-19 which spreads in a population. The susceptible individuals can be infected through either direct contact with infectious individuals or indirect contact with the novel coronavirus infected environment. The population under consideration is grouped into disjoint compartments. Individuals who are susceptible to the disease and without formal awareness about the prevention mechanisms or who did not decide to use any protective mechanisms are grouped in the S class. Individuals who are susceptible but are aware of and decide to apply any of the existing protective mechanisms after receiving public health information on how to protect themselves from the novel coronavirus infection are placed in the S_e class. COVID-19 infected individuals who are asymptomatic and symptomatic are grouped in classes C and I, respectively. Some studies consider the asymptomatic class as the “exposed” class (see for instance [9]). But since the individuals in this group are known to be infectious and some of them also recover from the disease without going through the I group [32], we used a name “carrier” to avoid confusion. The R class contains the recovered individuals from COVID-19. Finally, E denotes the amount of the novel coronavirus pathogen that contaminates the environment due to shedding by COVID-19 infectious individuals. In the analysis of the model, we intentionally excluded the actual exposed class for mathematical simplicity. However, a 5 days incubation period is taken into consideration in the numerical simulation part of this paper.

By combining the direct and indirect ways of transmission, the force of infection will have the form

$$\lambda ={\beta }_1\frac{I+\nu C}{N}+{\beta }_2\frac{E}{E+K},$$ (1)

where $N=S+S_e+C+I+R$ and K is the concentration of the novel coronavirus in the environment which increases 50% chance of triggering the disease transmission.

The proposed flow diagram for the transmission dynamics of COVID-19 is depicted in Fig. 1 while the description of each of the state variables is given in Table 1 .

Fig. 1.

Schematic diagram of the proposed model.

Table 1.

Description of the model variables.

Variables	Description
S	Susceptible population.
Se	Susceptible individuals who are educated to prevent the disease.
C	Carrier individuals (infected & infectious but asymptomatic).
I	Infected individuals (symptomatic).
R	Recovered individuals.
E	Pathogen concentration on contaminated surfaces or objects in the environment.

The dynamics of the pandemic is described by using the following system of differential equations (see Table 2 for the description of the involved parameters):

$$\begin{array}{cc}{S}^{\prime }\hfill & =(1-h)\pi -(\lambda +\sigma e+\mu )S+(1-\omega )\phi R,\hfill \\ S_e^{\prime }\hfill & =h\pi +\sigma eS-((1-\rho )\lambda +\mu )S_e+\omega \phi R,\hfill \\ C^{\prime }\hfill & =\eta \lambda S+\varphi (1-\rho )\lambda S_e-(\theta +\alpha +\mu )C,\hfill \\ I^{\prime }\hfill & =(1-\eta )\lambda S+(1-\varphi )(1-\rho )\lambda S_e+\theta C-(\gamma +\mu +\delta )I,\hfill \\ R^{\prime }\hfill & =\alpha C+\gamma I-(\phi +\mu )R,\hfill \\ E^{\prime }\hfill & =ϵC+\xi I-\psi E,\hfill \end{array}$$ (2)

where

$$e\left(\lambda \right)=\frac{{\lambda }^n}{{\lambda }_0^n+{\lambda }^n},$$ (3)

with λ ₀ is the value of the force of infection corresponding to the threshold infectivity in which individuals start reacting swiftly (that means, the point at which the behaviour change function changes its concavity). We append the following nonnegative initial conditions to the system (2):

$$\begin{array}{ccc}\hfill S\left(0\right)& =& S_0,S_e\left(0\right)=S_{e_0},C\left(0\right)=C_0,I\left(0\right)=I_0,R\left(0\right)=R_0,\hfill \\ & & \text{and}E\left(0\right)=E_0.\hfill \end{array}$$

Table 2.

Description of the model parameters.

Parameters	Description
Π	Rate of recruitment to the susceptible individuals
h	Fraction of recruitment to the Se class because of past disease history
σ	Rate of dissemination of information about the disease in the population
η	Fraction of infected susceptible individuals who become carriers
ϕ	Fraction of ‘educated’ individuals who get infected and become carriers
ρ	Average effectiveness of existing self-preventive measures
α	Rate of recovery for carrier individuals
θ	Rate of transfer of carrier individuals to the sick class
ϵ	Shedding rate from the C class to the environment
γ	Rate of recovery for the sick class
δ	Death rate due to coronavirus
ξ	Shedding rate from the I class to the environment
ψ	Virus decay rate from the environment
β1	Rate of disease transmission directly from humans
β2	Rate of disease transmission from the environment
K	The pathogen concentration in the environment that yields 50% of chance
	for a susceptible individual to catch the viral infection from the environment
ν	Modification parameter (transmission of C relative to I)
φ	Rate of loosing immunity after recovery
μ	Natural death rate
ω	Fraction of recovered individuals moving into the Se class after loosing immunity

3. Analysis of the model

In this section, we study the quantitative and qualitative analysis of the model system Eq. (2).

3.1. Well-posedness

We begin by determining the biologically feasible set for the model (2). The following theorem implies that the solutions of (2) are nonnegative and bounded from above, provided that the initial conditions are nonnegative.

Theorem 3.1

Equation (2) defines a dynamical system on Ω, where

$$\begin{array}{ccc}\hfill \Omega & =& \{(S,S_e,C,I,R,E)\in {\mathbb{R}}_{+}^6:0\le S+S_e+C+I+R\hfill \\ & & =N\le \frac{\pi }{\mu },0\le E\le \frac{(ϵ+\xi )\pi }{\mu \psi }\}.\hfill \end{array}$$ (4)

Proof: The proof of this Theorem is outlined in Appendix A.

3.2. Asymptomatic stability of the disease-free equilibrium

To determine the equilibrium solutions, we set the right-hand-side of Eq. (2) equal to zero and obtain

$$\begin{array}{c}(1-h)\pi -(\lambda +\sigma e+\mu )S+(1-\omega )\phi R=0,\hfill \\ h\pi +\sigma eS-\left(\right(1-\rho )\lambda +\mu )Se+\omega \phi R=0,\hfill \\ \eta \lambda S+\varphi (1-\rho )\lambda S_e-(\theta +\alpha +\mu )C=0,\hfill \\ (1-\eta )\lambda S+(1-\varphi )(1-\rho )\lambda S_e+\theta C-(\gamma +\mu +\delta )I=0,\hfill \\ \alpha C+\gamma I-(\phi +\mu )R=0,\hfill \\ ϵC+\xi I-\psi E=0.\hfill \end{array}$$ (5)

Then, the disease-free equilibrium (DFE) is found to be

$${\mathcal{E}}_0=(\frac{(1-h)\pi }{\mu },\frac{h\pi }{\mu },0,0,0,0,0).$$ (6)

The basic reproduction number, which is very important for the qualitative analysis of the model, is determined here below by using the method of the next generation matrix used in Diekmann and Heesterbeek [33], van den Driessche and Watmough [34]. For the model under consideration, using the notation $X=(C,I,E),$ we have the vector functions

$$\mathcal{F}\left(X\right)=\left(\begin{array}{c}\eta \lambda S+\varphi (1-\rho )\lambda S_e\\ (1-\eta )\lambda S+(1-\varphi )(1-\rho )\lambda S_e\\ 0\end{array}\right),$$

and

$$\mathcal{V}\left(X\right)=\left(\begin{array}{c}{k}_{1}C\\ -\theta C+k_{2}I\\ -(ϵC+\xi I)+\psi E\end{array}\right),$$

with $k_1=\theta +\alpha +\mu$ and $k_2=\gamma +\mu +\delta$ represent the rates at which the disease compartments increase and decrease in size due to the infection, respectively. Then the next generation matrix is

$$\mathbf{B}=J_{\mathcal{F}}{\left(J_{\mathcal{V}}\right)}^{-1},$$ (7)

where

$$J_{\mathcal{F}}\left({\mathcal{E}}_0\right)=\left(\begin{array}{ccc}\nu {\beta }_{1}p& {\beta }_{1}p& \frac{{\beta }_2\pi }{\mu K}p\\ \nu {\beta }_{1}q& {\beta }_{1}q& \frac{{\beta }_2\pi }{\mu K}q\\ 0& 0& 0\end{array}\right),$$

and

$$J_{\mathcal{V}}\left({\mathcal{E}}_0\right)=\left(\begin{array}{ccc}{k}_1& 0& 0\\ -\theta & k_2& 0\\ -ϵ& -\xi & \psi \end{array}\right),$$

with $p=\eta (1-h)+\varphi (1-\rho )h$ and $q=(1-\eta )(1-h)+(1-\varphi )(1-\rho )h$. Here, it is not difficult to show that

$$J_{\mathcal{V}}^{-1}\left({\mathcal{E}}_0\right)=\left(\begin{array}{ccc}{\displaystyle \frac{1}{k_1}}& 0& 0\\ {\displaystyle \frac{\theta }{k_1{k}_2}}& {\displaystyle \frac{1}{k_2}}& 0\\ {\displaystyle \frac{1}{k_1\psi }(ϵ+\frac{\theta \xi }{k_2})}& {\displaystyle \frac{\xi }{k_2\psi }}& {\displaystyle \frac{1}{\psi }}\end{array}\right).$$

The basic reproduction number denoted by ${\mathcal{R}}_0$ is defined as the average number of secondary cases produced in a completely susceptible population by a typical infected individual during its entire period of being infectious [33], [34]. Mathematically, ${\mathcal{R}}_0$ is the spectral radius of B in Eq. (7) and after further simplification, we obtain

$${\mathcal{R}}_0={\beta }_1[\frac{p}{k_1}(\nu +\frac{\theta }{k_2})+\frac{q}{k_2}]+\frac{{\beta }_2\pi }{\mu \psi K}[\frac{p}{k_1}(ϵ+\frac{\theta \xi }{k_2})+\frac{q\xi }{k_2}].$$ (8)

The next result is a direct application of Theorem 2 in van den Driessche and Watmough [34].

Theorem 3.2

The DFE ${\mathcal{E}}_0$ of the model (2) is locally asymptotically stable whenever ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$ .

The epidemiological implication of Theorem 3.2 is that the transmission of COVID-19 can be controlled by forcing the dynamics through its parameter values so that ${\mathcal{R}}_0<1$ if the initial total numbers in each of the subpopulation involved in Eq. (2) are in the basin of attraction of ${\mathcal{E}}_0$. To ensure that elimination of the disease is independent of the initial size of the subpopulation, the disease-free equilibrium must be globally asymptotically stable when ${\mathcal{R}}_0<1$. This is what we present here below.

Theorem 3.3

The model (2) undergoes a backward bifurcation at ${\mathcal{R}}_0=1$ when the parameters satisfy the condition

$$\frac{DH+GJ}{(p+qF)L}\ge 1,$$ (9)

where

$$\begin{array}{ccc}\hfill A& =& \frac{\mu \psi k_{1}K\left[{\beta }_1\right(\frac{p\theta }{k_1{k}_2}+\frac{q}{k_2})+\frac{{\beta }_2\pi }{\mu \psi K}(\frac{p\theta \xi }{k_1{k}_2}+\frac{q\xi }{k_2}\left)\right]}{p(\mu \psi {\beta }_{1}K+\xi {\beta }_2\pi )},\hfill \\ \hfill D& =& \frac{1}{\mu }[\frac{(1-\omega )\phi (\alpha +\gamma A)}{k_3}\hfill \\ & & -(1-h)({\beta }_1(\nu +A)+\frac{{\beta }_2\pi }{\mu \psi K}(ϵ+\xi A))],\hfill \\ \hfill F& =& \frac{p(\mu \psi {\beta }_{1}K+\xi {\beta }_2\pi )}{q(\nu \mu \psi {\beta }_{1}K+ϵ{\beta }_2\pi )+\mu \psi \theta K}A\hfill \\ \hfill G& =& \frac{1}{\mu }[\frac{\omega \phi }{k_3}(\alpha +\gamma A)-(1-\rho )h({\beta }_1(\nu +A)+\frac{{\beta }_2\pi }{\mu \psi K}(ϵ+\xi A)\left)\right]\hfill \\ \hfill H& =& \frac{\mu {\beta }_1}{\pi }(\nu +A)(\eta -p+F(1-\eta -q))\hfill \\ & & +\frac{{\beta }_2(ϵ+\xi A)}{\psi K}(\eta +F(1-\eta ))\hfill \\ \hfill J& =& \frac{\mu {\beta }_1}{\pi }(\nu +A)(1-h)\left[\right(-\eta +\varphi (1-\rho ))\hfill \\ & & +F(-(1-\eta )+(1-\varphi \left)\right(1-\rho \left)\right)]\hfill \\ & & +\frac{(1-\rho ){\beta }_2(ϵ+\xi A)}{\psi K}(\varphi +F(1-\varphi ))\hfill \\ \hfill L& =& \frac{\mu {\beta }_1}{\pi }(\nu +A(1+\nu +A)+\frac{\alpha +\gamma A}{k_3}(\nu +A))\hfill \\ & & +\frac{{\beta }_2\pi }{\mu }{\left(\frac{ϵ+\xi A}{\psi K}\right)}^2.\hfill \end{array}$$

The proof of Theorem 3.3 is carried out using the center manifold theory in Castilo-Chavez and Song [35] and is given in Appendix B.

In the above theorem (Theorem 3.3), if the parameter describing the waning of immunity, φ, is zero, we can observe that both D and G are negative. Hence, Eq. (9) fails to be true. In this case, we give below a Theorem which asserts the global stability of the DFE of the model.

Theorem 3.4

The disease-free equilibrium of system (2) in the case when $\phi =0$ is globally asymptotically stable for ${\mathcal{R}}_0<1$ .

Proof

To prove the theorem for the case $\phi =0,$ we use Kamgang-Sallet Stability Theorem stated in Kamgang and Sallet [36]. Let $X=(X_1,X_2)$ with $X_1=(S,S_e,R)\in {\mathbb{R}}^3$ and $X_2=(C,I,E)\in {\mathbb{R}}^3$. Then the system (2) can be written as

$${\dot{X}}_1=A_1\left(X\right)(X_1-X_1^{*})+A_{12}\left(X\right)X_2,$$ (10)

$${\dot{X}}_2=A_2\left(X\right)X_2,$$ (11)

where $X_1^{*}=(\frac{(1-h)\pi }{\mu },\frac{h\pi }{\mu },0),$

$$A_1\left(X\right)=\left(\begin{array}{ccc}-\mu & 0& 0\\ 0& -\mu & 0\\ 0& 0& -\mu \end{array}\right),$$

$$A_{12}\left(X\right)=\left(\begin{array}{ccc}{\displaystyle -k_4\frac{\nu {\beta }_1}{N}S}& {\displaystyle -k_4\frac{{\beta }_1}{N}S}& {\displaystyle -k_4\frac{{\beta }_2}{E+K}S}\\ {\displaystyle k_5\frac{\nu {\beta }_1}{N}}& {\displaystyle k_5\frac{{\beta }_1}{N}}& {\displaystyle k_5\frac{{\beta }_2}{E+K}}\\ \alpha & \gamma & 0\end{array}\right),$$

and

$$A_2\left(X\right)=\left(\begin{array}{ccc}{\displaystyle \frac{\nu {\beta }_1}{N}{k}_6-k_1}& {\displaystyle \frac{{\beta }_1}{N}{k}_6}& {\displaystyle k_6\frac{{\beta }_2}{E+K}}\\ {\displaystyle \frac{\nu {\beta }_1}{N}{k}_7+\theta }& {\displaystyle \frac{{\beta }_1}{N}{k}_7-k_2}& {\displaystyle \frac{{\beta }_2}{E+K}{k}_7}\\ ϵ& \xi & -\psi \end{array}\right).$$

with $k_4=1+\frac{\sigma {\lambda }^{n-1}}{{\lambda }^n+{\lambda }_0^n},k_5=\frac{\sigma {\lambda }^{n-1}}{{\lambda }^n+{\lambda }_0^n}S-S_e,k_6=\eta S+\varphi S_e$ and $k_7=(1-\eta )S+(1-\varphi )S_e$. □

We show that the five sufficient conditions of Kamgang-Sallet Theorem (in Kamgang and Sallet [36]) are satisfied as follows.

• 1.The system (2) is a dynamical system on Ω. This is proved in Theorem 3.1.
• 2.The equilibrium $X_1^{*}$ is GAS for the subsystem ${\dot{X}}_1=A_1(X_1,0)(X_1-X_1^{*})$. This is obvious from the structure of the involved matrix.
• 3.The matrix A ₂(X) is Metzler (i.e., all the off-diagonal elements are nonnegative) and irreducible for any given X ∈ Ω. Again this is straight forward from the formulation of matrix A ₂(X).
• 4.
  There exists an upper-bound matrix ${\overline{A}}_2$ for the set

  $$\mathcal{M}=\{A_2\left(X\right):X\in \Omega \}.$$

  Indeed,

  $${\overline{A}}_2=\left(\begin{array}{ccc}\nu {\beta }_{1}p-k_1& {\beta }_{1}p& {\displaystyle \frac{{\beta }_2}{K}p}\\ \nu {\beta }_{1}q+\theta & {\beta }_{1}q-k_2& {\displaystyle \frac{{\beta }_2}{K}q}\\ ϵ& \xi & -\psi \end{array}\right)$$

  with $p=(1-h)\eta +h\varphi$ and $q=(1-h)(1-\eta )+h(1-\varphi )$ is an upper-bound for $\mathcal{M}$.
• 5.
  For ${\mathcal{R}}_0\le 1$ in Eq. (8)

  $$\alpha \left({\overline{A}}_2\right)=\max \{Re\left(\lambda \right):\lambda \text{eigenvalue}\text{of}{\overline{A}}_2\}\le 0.$$

  This can also be verified by checking the eigenvalues of ${\overline{A}}_2$ under the condition of ${\mathcal{R}}_0<1$.

Hence, by the Kamgang-Sallet Stability Theorem [36], the disease-free equilibrium is globally asymptotically stable for ${\mathcal{R}}_0<1$. □

The reality behind Theorem 3.4 is that, if immunity is permanent ($\phi =0$), coronavirus will be effectively controlled in the community by reducing ${\mathcal{R}}_0$ effectively to a value less than unity.

4. Numerical simulations and discussion

4.1. Estimation of parameters from data and literature

The novel coronavirus being a new strain of coronaviruses, information about the dynamics of the infection is still evolving. Biological studies of parameter values describing the vital dynamics of the infection are still ongoing as more laboratory tests become available. Although some studies have been done on the early dynamics of the disease most especially on data from Wuhan, extensive reading reveals that some of the disease dynamics parameters are highly variable and some processes are not fully explored. In this work, we use new cases data from Hubei Province of China extracted from WHO situation reports 1–57 [1], i.e. for the period January 21, 2020 to March 17, 2020. We ought to fit the proposed model to the extracted data and estimate the unknown parameters.

The total population of Hubei province was estimated as 59.2 million. The life expectancy of Hubei province varies depending on the area of dwelling (i.e urban or rural) as well as gender [37]. For urban dwellers, the average life expectancy is estimated to be 75.68 years (with an average being 73.72 years for men and 77.79 years for women). The life expectancy of China of the year 2019 was estimated to be 76.79 years whereas that for the year 2020 is estimated as 76.96 years [38]. Owing to the negligible difference in the provincial and Countrywide value, we use the Country life expectancy for the year 2019 which gives an average mortality rate of $\mu =3.57\times {10}^{-5}$ per day. The recruitment rate is thus given as $\pi =\mu \times N_0,$ where N ₀ is taken to be the total population size, 59.2 million.

The average time period taken for symptoms to appear after exposure is observed to vary considerably, with ranges between 2–14 days [39], 2–24 days [40], and some outliers going to up to 27 days. The observed median incubation period was nearly 5 days [41].

The time to recovery from the onset of symptoms varies depending on the seriousness of the infection. Individuals presenting mild illness were observed to recover in an average period of 2 weeks while those presenting serious/critical illness recovering in about 3 to 6 weeks. For our parameter estimation and simulations, we consider a nominal value of $0.0476{\text{day}}^{-1}$ (corresponding to 3 weeks) estimated from an interval (0.0238, 0.0714). We note that a patient is considered recovered: (1) if two swab tests taken in a time interval of at least 24 h both test negative, (2) if the time taken after the end of respiratory symptoms and fever is at least 72 h.

The waning of the immunity after recovery is estimated to range between 4 months to 1 year, which gives an interval for φ as $(0.00274,0.00824){\text{day}}^{-1}$. For our simulation, we consider a nominal value of $\phi =0.00274{\text{day}}^{-1}$ (approximately one year). We propose that at the end of the epidemic, at least 20–65% of the recovering population will learn from the experiences during the infection and even when the acquired immunity wanes, such individuals will become susceptible individuals with past history/knowledge of the disease.

The rate of recovery for the symptomatic individuals (γ) in Wuhan varied considerably but majority of individuals who recovered from the virus were discharged from hospital after $2\frac{1}{2}$ weeks [42]. However, the patients in Wenzhou-China stayed in hospital for 27 days (0.037 per day) on average. In the model fitted on the early trends data from Wuhan-China [43], the recovery rate obtained for symptomatic cases was 0.0897 per day (accounting for 10 days to recovery). The rate of recovery (α) for carrier individuals is expected to be higher [9].

According to the WHO situation report [44], it is estimated that up to 80% of COVID-19 cases are asymptomatic or show mild symptoms, 15% show severe symptoms and up-to 5% end up with critical infection and require oxygen or a ventilator. The proportion of individuals who do not show symptoms or have mild symptoms can be as high as 94% [45]. For our model fitting, we use a range of (0.65,0.86) for both η and ϕ with selected initial values within the prescribed interval.

Although Hubei province was put on a lockdown on January 23, 2020, the first major decline in the number of new confirmed cases was only observed on February 20, 2020 (Situation report 31 [1]), approximately 1 month after the lockdown was imposed. From February 14, 2020, the method of identification of new cases was revised to include both cases confirmed through laboratory tests and clinical observations. As such, there was an observed spike in the number of new cases on February 14, 2020 to 4823 compared to 1508 cases (reported on February 13, 2020) and 2420 cases (reported February 15, 2020).

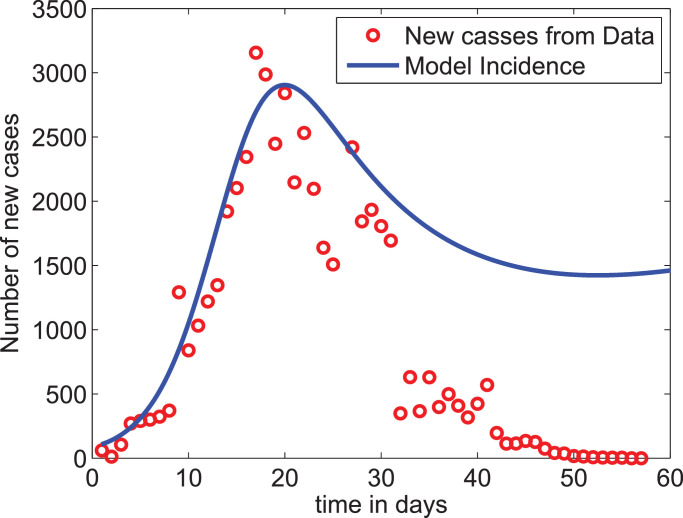
Applying the above described set of assumptions in the bounds for some of the parameters, we optimized the model output to fit the daily new cases data reported from the Hubei province, China. The parameter values for which the model best fits to the incidence data are given in Table 3. Fig. 2 shows the plot of the reported new-cases data together with the incidence of the disease obtained from the model. As we can observe from the graph, the model slightly overestimates the reported data except for the two highest points. In addition, since our model does not assume any control measure at this stage while the reported data after the 31st day may represent the effect of the strict lockdown measure taken by the authorities, the parameters estimated give a good result. We note however that, in some recent work [46], [47], the use of fractional-order calculus is recommended to get better data fit. When we calculate the value of ${\mathcal{R}}_0$ from Eq. (8) using the estimated parameters given in Table 3, we obtain ${\mathcal{R}}_0\approx 2.91,$ which is within the range of values reported in China-CDC [48], Wu et al. [49].

Table 3.

Nominal values and ranges of parameters values.

Parameter	Description	Range	Nominal Value	Source
Π	Persons ${\text{day}}^{-1}$		μ × N0	Assumed
β1	Contacts ${\text{day}}^{-1}$	(0.24, 0.275)	0.270	Fitted
β2	Contacts ${\text{day}}^{-1}$	(0.001, 0.028)	0.001006082	Fitted
h	proportion	(0.1, 0.65)	0.59996	Fitted
ν	Relative value	(1.1, 3)	2.662830741	Fitted
K	No. of pathogens	(100, 107)	2091775	Fitted
σ	Intensity ${\text{day}}^{-1}$	(0.2, 0.65)	0.649996150	Fitted
ϕ	Proportion	(0.65, 0.867)	0.866999986	Fitted
η	Proportion	(0.65, 0.86)	0.650286467	Fitted
ρ	Proportion	(0.10, 0.15)	0.149999732	Fitted
α	${\text{day}}^{-1}$	(0.04, 0.075)	0.074999946	Fitted
θ	${\text{day}}^{-1}$	(0.1, 0.25)	0.249999979	Fitted
ε	Pathogens ${\text{person}}^{-1}$${\text{day}}^{-1}$	(0.098, 0.33)	0.101989917	Fitted
γ	${\text{day}}^{-1}$	(0.025, 0.05)	0.049999999	Fitted
ξ	Pathogens ${\text{person}}^{-1}$${\text{day}}^{-1}$	(0.135, 0.673)	0.431477395	Fitted
δ	${\text{day}}^{-1}$	(0.006, 0.11)	0.11	Fitted
ψ	${\text{day}}^{-1}$	(0.14, 1)	0.75248	Fitted
μ	${\text{day}}^{-1}$		$3.57\times {10}^{-5}$	[37]
φ	${\text{day}}^{-1}$	(0.00000273, 0.00824)	0.000002740	Fitted
ω	Proportion	(0.2, 0.65)	0.633695	Fitted

Fig. 2.

Model fit to the data. The very low data values after day 32 account for the effects of the strict lockdown measure taken by the authorities while the proposed model does not account for such measures.

4.2. Sensitivity analysis

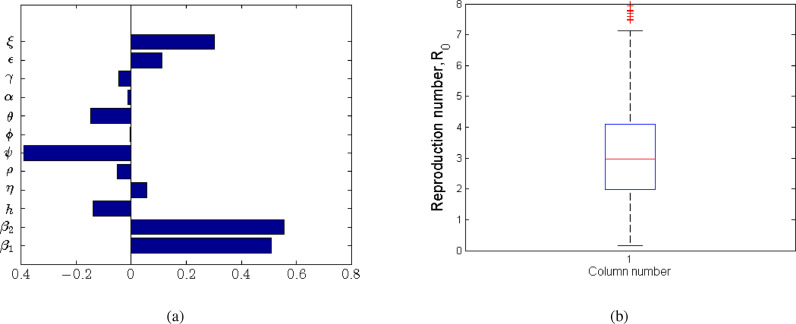
We examine the sensitivity of ${\mathcal{R}}_0$ to variations in parameter values and establish the significance of the sensitivity indices. We used the Latin hypercube Sampling (LHS) scheme, which is an efficient stratified Monte Carlo sampling that allows for simultaneous sampling of the multi-dimensional parameter space [50]. For each run, 1000 simulations were done and Partial Rank Correlation Coefficients (PRCCs) [51] calculated between each of the selected input parameters and the disease threshold. The PRCCs indicate the degree of effect each parameter has on the outcome, which in this case is the disease threshold. The sign of the PRCC identifies the specific qualitative relationship between the input parameter and the output variable. The positive value of the PRCC of the variables implies that when the value of the input parameter increases, the future number of cases will also increase. On the other hand, processes underlying the parameters with negative PRCCs have a potential to contain of the number of cases when enhanced. The results of sensitivity analysis are indicated in Fig. 3 a and the box plot (Fig. 3b) gives the five-number summary for the computed disease threshold value from the sampled parameter space.

Fig. 3.

Partial Rank Correlation Coefficients (PRCCs) for a selected range of model parameters in Table 3. The processes underlying the parameters β₁, β₂, ε and ξ have the greatest potential of making the epidemic worse if increased, whereas processes described by ψ and h have the greatest potential of containing the epidemic when enhanced.

The processes described by parameters β ₁, β ₂, ε and ξ with the greatest positive PRCCs have the greatest potential of worsening pandemic when increased. On the other hand, parameters (h and ψ) with negative PRCCs have the greatest potential in helping contain the infection when maximised. In this respect, we note that increasing social/physical distancing directly reduces β ₁ as this lowers the likelihood of a susceptible individual getting in contact with a potentially infected individual. In addition, practising good hygiene (such as regularly washing hands, using sanitisers to disinfect the infected environment and avoiding touching the T-zones of the face) is associated with lowering the likelihood of contracting the virus from infected surfaces. Anything contrary to the above increases the likelihood of getting the infection through the two aforementioned routes. We further note that practising good hygiene also involves the infected individuals reducing the shedding of the virus into the environment. It is evident from the results in Fig. 3 and Table 4 that reducing the rate at which the virus is shed into the environment is significant in reducing the severity of the problem.

Table 4.

Parameter PRCC significance (FDR Adjusted p-values).

Variable	PRCC	p-value	Significance?
β1	0.108132611	$1.566\times {10}^{-3}$	TRUE
β2	0.706803546	0.0000000	TRUE
h	$-0.081725771$	$2.022\times {10}^{-2}$	TRUE
η	0.003556638	0.9110	FALSE
ρ	$-0.037485329$	0.3186	FALSE
ψ	$-0.4787134264$	0.00000	TRUE
ϕ	0.004377062	0.9110	FALSE
θ	$-0.060636753$	0.09703	FALSE
α	$-0.021180254$	0.607	FALSE
γ	$-0.045896543$	0.223	FALSE
ε	0.159616950	$1.289132\times {10}^{-06}$	TRUE
ξ	0.359785405	0.000000	TRUE

From the five number summary of the results in Fig. 3b, the lower quartile of the computed values of ${\mathcal{R}}_0$ is about 2, the median around 2.9 and the upper quartile of about 4. The obtained value of ${\mathcal{R}}_0$ is within the range of 3.11 (95%CI, 2.39–4.13) obtained in the early studies in Read et al. [52]. We note that for a selected combination of underlying processes much higher values of ${\mathcal{R}}_0$ can be obtained, which is an indication of possible worsening of the situation. In a similar way, we observe that for particular underlying processes (a selected combination of parameters) the value of ${\mathcal{R}}_0$ can be reduced to values below one.

As indicated in Blower and Dowlatabadi [51], we note that although some parameters in the model may have very small magnitudes of PRCCs (non-monotonically related to the disease threshold output), they may still produce sizeable changes in the disease burden. To identify the most important parameters in containing or aggravating the epidemic, we computed p-values for the simulated parameters using Fisher’s Transformation [51]. We note that the computed PRCCs are bounded between the interval $[-1,1]$. For this matter, some sampling distribution of variables that are highly correlated is skewed. The Fisher’s Transformation $\rho \left(r\right)=0.5\log \left(\frac{1+r}{1-r}\right)$ is used to transform the skew distribution to a normal distribution and then compute p-values for each of the parameters based on the PRCCs [51]. The PRCCs for the parameters together with their corresponding p-values are indicated in Table 4.

We carry out pairwise comparison of the significant parameters (whose p-values are less than 0.05, see Table 4) to ascertain whether the processes described by the compared parameters are different. We computed the p-values for the different pairs of significant parameters while accounting for the false discovery rate (FDR) adjustment and the results are given in Table 5 .

Table 5.

Pairwise PRCC Comparisons (FDR Adjusted p-values).

	β1	β2	h	ψ	ε	ξ
β1		0	$2.347\times {10}^{-5}$	0	0.2443	$2.642\times {10}^{-9}$
β2			0	0	0	0
h				0	$8.647\times {10}^{-8}$	0
ψ					0	0
ε						$1.942\times {10}^{-6}$
ξ

The major question posed at this point is: Are the different pairs of significant parameters different after FDR adjustment? Based on the FDR adjusted p-values in Table 5, the compared pair of parameters are rendered to be different if their p-value is less than 0.05 and not different otherwise. We summarise our results in Table 6 , where “TRUE” indicates that the compared parameters are significantly different and “FALSE” indicating otherwise.

Table 6.

Are the parameters different after FDR adjustment?.

	β1	β2	h	ψ	ε	ξ
β1		TRUE	TRUE	TRUE	FALSE	TRUE
β2			TRUE	TRUE	TRUE	TRUE
h				TRUE	TRUE	TRUE
ψ					TRUE	TRUE
ε						TRUE
ξ

We observe that the more sensitive parameters are also significantly different (see Table 6) except for the ${\beta }_1-\epsilon$ pair which may not necessarily be related.

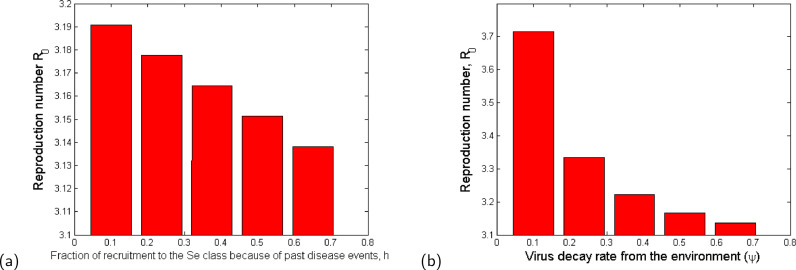
We examine effect of variation of the sensitive parameters on the reproduction number (${\mathcal{R}}_0$). The results of the variation of parameters with more negative PRCCs are indicated in the bar graphs in Fig. 4 .

Fig. 4.

Bar plots showing the effect of the most sensitive parameters to ${\mathcal{R}}_0$: (a) Fraction of recruitment to the Se class because of past disease events; (b) Virus decay rate from the environment. The values of the parameter values used are given in Table 3.

From Fig. 4, it is evident that the decay of the virus from the environment (Fig. 4b) which can be accelerated by disinfecting surfaces reduces the value of ${\mathcal{R}}_0$ and consequently the disease burden. In addition, we observe that an increased proportion of individuals with knowledge of similar infections from the past that are practising self-protection and preventive measures (see Fig. 4a) is important in slowing down the infection at the initial stage. Such proportions of individuals would normally have knowledge about prevention and control mechanisms of the infection just at the onset of the disease.

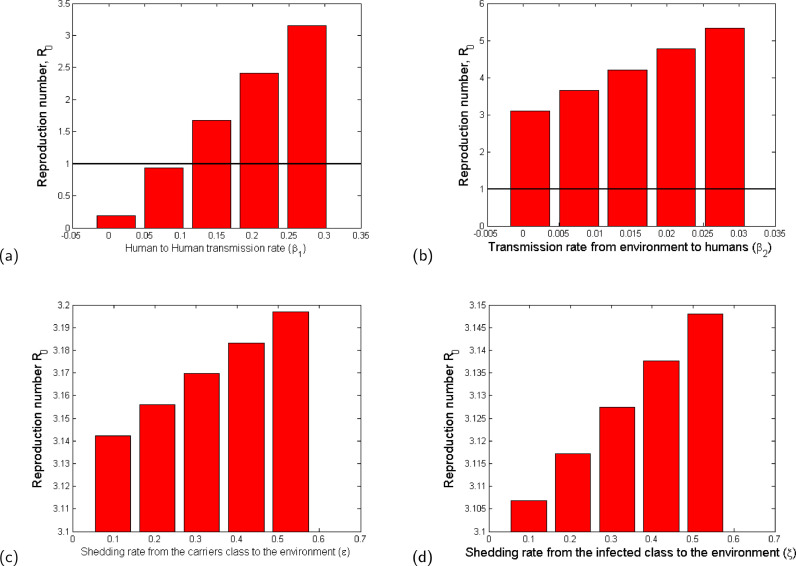
We observe in Fig. 5 that the increase in person-to-person contact, β ₁ (Fig. 5a), poor personal hygiene, β ₂ (Fig. 5b), and the rate of shedding of the virus into the environment by both carriers (Fig. 5c) and symptomatic individuals (Fig. 5d) increase the value of ${\mathcal{R}}_0$ and therefore the disease burden. It is evident that the most effective way of containing the infection is by minimizing contact, which is why in most cases imposing a lockdown becomes an effective way of slowing the spread of the infection. In addition, good hygiene practices by all individuals are two-fold: (1) avoiding touching surfaces, always washing hands with soap and water, or using alcohol based hand sanitizer, which reduced the likelihood of contracting the pathogen from the environment; (2) those who are sick with symptoms like cough and flu, ought to use masks, when they cough or sneeze, must do so in a sanitary tissue which must then be properly disposed off. We also note that hygienic practices without social/physical distancing may not significantly slow down the infection.

Fig. 5.

Bar plot showing the effect of the most sensitive parameters to ${\mathcal{R}}_0$: (a) Rate of disease transmission directly from human to human; (b) Rate of disease transmission from the environment; (c) Shedding rate from the carriers class to the environment (ε); (d) Shedding rate from the infected class to the environment (ξ). The values of the parameter values used are given in Table 3.

In summary, we observe that it is possible to reduce the value of ${\mathcal{R}}_0$ to a value less than unity by reducing only the value of β ₁ below 0.1 (see Fig. 5a). This observation is in direct agreement with mitigation approaches that are aimed at minimising human-to-human contact (such as social distancing and imposing a lockdown). Therefore, the paremeter β ₁ is more influential in the model and can also play a significant role in eradication of the disease. The other parameters (see Figs. 4 and 5 b–d) may reduce the value of ${\mathcal{R}}_0$ significantly when applied in combination but not as independent mitigation processes.

4.3. Numerical simulations and analysis of mitigation strategies

There are various intervention mechanisms for COVID-19 that are being implemented in different parts of the world. The strategies differ from country to country depending on the scientific information available to decision makers. To investigate the outcomes of the mitigation strategies, we include the isolated and/or quarantined classes to the model system (2). We assume that the individuals in the asymptomatic class (C) are detected at a rate of κ and placed in isolation Q ₁ class, while the individuals in the symptomatic class (I) are identified at a rate of ℓ and quarantined in Q ₂ class. Moreover, the system is formulated as a mixed-delay system of differential equations, where the time delay d is assumed to account for the incubation period of the disease. Then the system becomes

$$\begin{array}{ccc}\hfill S^{\prime }& =& (1-h)\pi -\left[\lambda \right(t-d)+\sigma e(t-d\left)\right]S(t-d)-\mu S\hfill \\ & & +(1-\omega )\phi R,\hfill \\ \hfill S_e^{\prime }& =& h\pi +\sigma e(t-d)S-(1-\rho )\lambda (t-d)S_e(t-d)-\mu S_e+\omega \phi R,\hfill \\ \hfill C^{\prime }& =& \eta \lambda (t-d)S(t-d)+\varphi (1-\rho )\lambda (t-d)S_e(t-d)-(\kappa +\theta \hfill \\ & & +\alpha +\mu )C,\hfill \\ \hfill Q_1^{\prime }& =& \kappa C-(n_1+\mu )Q_1,\hfill \\ \hfill I^{\prime }& =& (1-\eta )\lambda (t-d)S(t-d)+(1-\varphi )(1-\rho )\lambda (t-d)S_e(t-d)\hfill \\ & & +\theta C-(\ell +\gamma +\mu +\delta )I,\hfill \\ \hfill Q_2^{\prime }& =& \ell I-(n_2+\mu +\delta )Q_2,\hfill \\ \hfill R^{\prime }& =& \alpha C+\gamma I+n_1{Q}_1+n_2{Q}_2-(\phi +\mu )R,\hfill \\ \hfill E^{\prime }& =& ϵC+\xi I-(\psi +v)E,\hfill \end{array}$$ (12)

where the force of infection λ is now modified to

$$\lambda =(1-u){\beta }_1\frac{I+\nu C}{N}+(1-v){\beta }_2\frac{E}{E+K},$$

with u representing the average percentage of contacts reduced due to the social distancing measures and v representing the total average rate (or percentage) of disinfecting the environment. In the modified model system (12), the parameters n ₁ and n ₂ represent the reciprocal of the time the individuals stay in Q ₁ and Q ₂ classes, respectively. Here, we assumed that $n_1=n_2=1/21$. Note that, the value $\psi +v$ in the last equation of (12) represents the effective decay rate of the pathogen from the environment and should not be greater than 1.

For the simulation purpose of this study, we considered five different cases or scenarios of how to apply the interventions. The strategies described in each of the cases below are in addition to the awareness creation for voluntary self-protective mechanisms which are widely communicated through various media outlets. Here, we assume that the average effectiveness of the self-protective measures is 15% (as estimated from the data and reported in Table 3), and the individuals who decided to use any one of them are strict in following the appropriate rules. Here below, we consider each of the scenarios for mitigation strategies case by case.

• Case 1:

  In this case, we assume that about 40% of the symptomatic infectious individuals and only 1% of the asymptomatic infectious individuals are detected and quarantined. This scenario is based on the assumption that among the people in the I class only about 40% show “above mild” symptoms and hence visit health care facilities, while the remaining individuals in this class (nearly 60% of them) remain at home or at large in the society. Then, through contact tracing mechanisms corresponding the hospitalized individuals, some people will be traced and tested, thereby about 1% of the total asymptomatic individuals can be detected.

  A similar scenario is being applied currently in some sub-Saharan African countries.

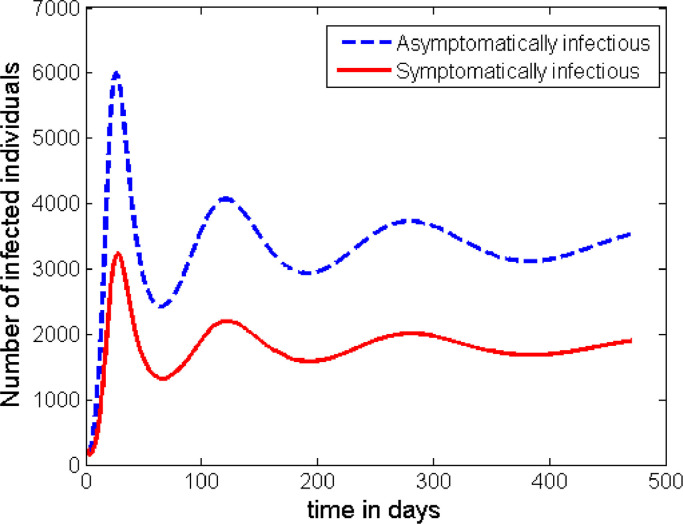
  The time profile in Fig. 6 shows the situation described in Case 1. From this graph we can observe that the infection stabilizes around its endemic equilibrium, which is nearly at 5000 cases. (This number depends on the initial conditions and the demographic variables of the population under study.) This shows that the disease persists in the population.

• Case 2:

  In this case, we assume that strict and longer time (6 weeks) of social distancing rules are enforced by the government nearly 4 weeks after the first positive case of COVID-19 is reported in the community.

  We assume for simulation purpose that the implementation of the intervention strategy is divided into the following 4 time phases.

  • Phase 1:
    The first phase in this case, is 24 days long (measured starting from the time the first positive case of COVID-19 is reported). During this phase, because of lack of information and the nature of the infection, we assume (as in Case 1) that only 40% of symptomatic infectious individuals and 1% of the asymptomatic infectious individuals are detected and quarantined.
  • phase 2:
    The second phase is assumed to last for 6 weeks (42 days). During this period, it is also presumed that;

    • •
      80% of the symptomatic class and 30% of the asymptomatic class are detected and quarantined,
    • •
      a mandatory strict social distancing rule is imposed, which is assumed to have a 70% reduction of effective contacts of individuals in the society,
    • •
      environmental disinfection is widely carried out, which is assumed to result in a 50% reduction in the rate of infection from the environment, and to contribute about the same percent impact in increasing the rate of decay of the pathogen from the environment.
  • Phase 3:
    The third phase is assumed to be 4 weeks (28 days) long, and is characterised by the partial lifting of the ‘lockdown’ imposed in Phase 2. During this period, it is assumed further that;

    • •
      70% of the symptomatic class and 25% of the asymptomatic class are detected and quarantined,
    • •
      a relaxed social distancing rule is exercised, which is assumed to have a 25% reduction of effective contacts of individuals in the society,
    • •
      environmental disinfection is partially carried out, which is assumed to have an impact of reducing the rate of infection from the environment by 30% and increasing the rate of decay of the pathogen from the environment by the same 30%.
  • Phase 4:
    The last and fourth phase is the time when the social distancing rule is fully lifted. Due to the lesson learnt from the previous phases, we assume that the following interventions will continue during this period as well;

    • •
      70% of the I class and 10% of the C class are detected and quarantined,
    • •
      environmental disinfection is partially carried out, which is assumed to have an impact of reducing the rate of infection from the environment by 20% and increasing the rate of decay of the pathogen from the environment by the same 20%.

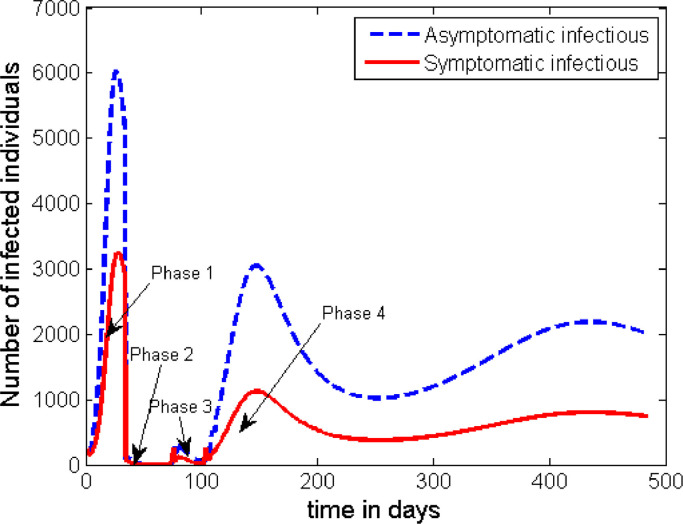
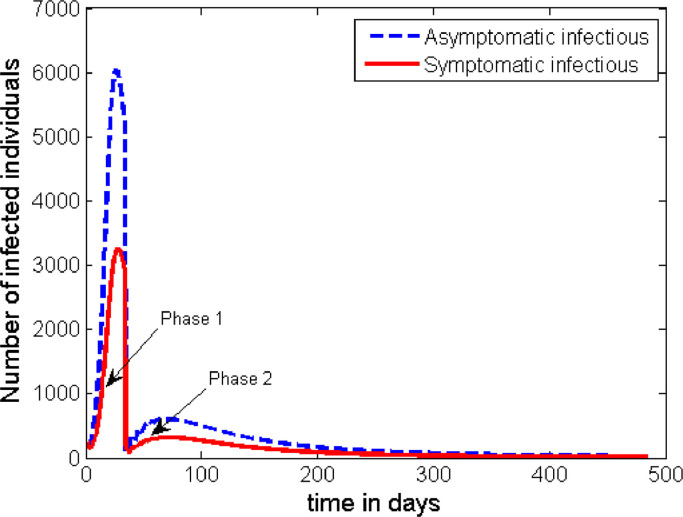
  The time profile of the disease dynamics after implementing the above described interventions strategy is plotted in Fig. 7 . The figure shows that the count of the infected individuals decreases down to nearly zero in Phases 2 and 3, but the disease resurges back into the society soon after. However, the peak of the second wave looks to be much smaller than the first one. That means, the intervention mechanisms described in the above 4 phases of this case are not enough to contain the disease, and unless some additional intervention mechanisms are developed the disease persists in the society.

• Case 3:
  In this case, we assume that early action with shorter time social distancing rule is applied. In this scenario, it is assumed that the interventions described in Case 2 started half way through the time that Phase 2 was implemented in Case 2. That means, the implementation of the interventions described in the four phases of Case 2 is assumed to be followed, but the length of the time in Phases 1 and 2 is reduced as described below.

  • 1.
    Phase 1 lasts only 12 days,
  • 2.
    Phase 2 lasts only 3 weeks, and
  • 3.
    Phase 3 lasts 4 weeks (the same as in Case 2).

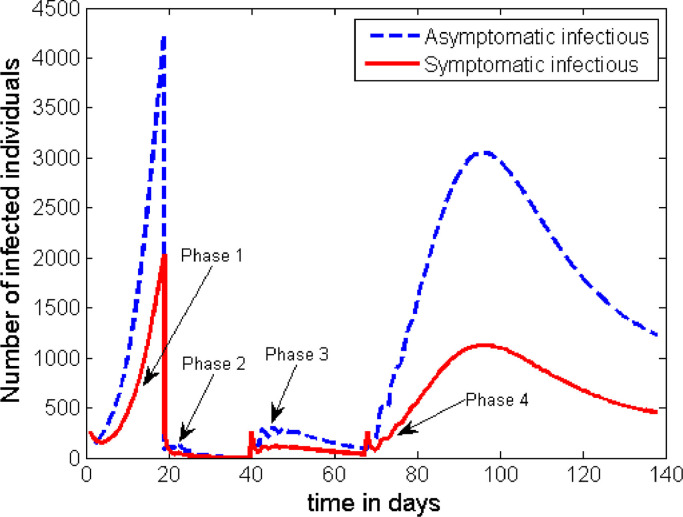
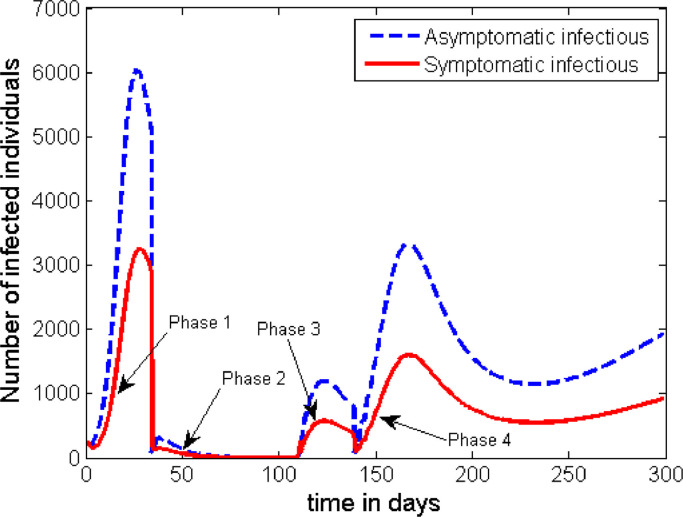
  Otherwise, all the details of the interventions in Case 2 are kept the same. The time profile for this set of interventions is given in Fig. 8 .

  The general behaviour of the graph in Fig. 8 is the same as that of Fig. 7. However, this strategy has an advantage in significantly reducing the height of the first peak. The height of the subsequent peaks are found to be the same unless some additional measures are taken after Phase 3.

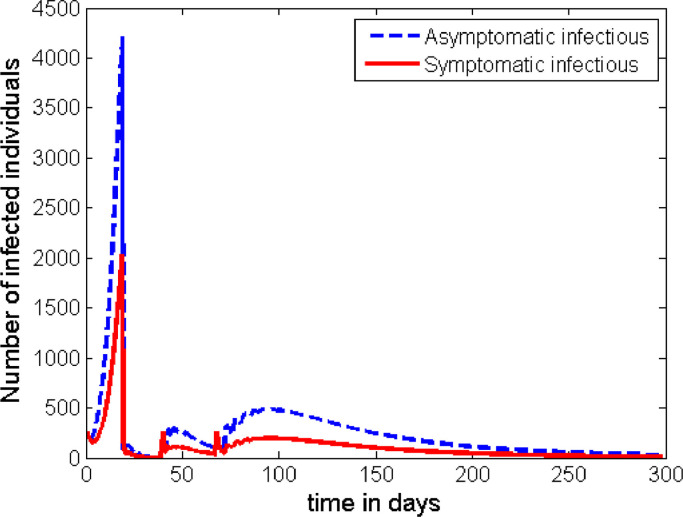
  Unfortunately, the strategies in both of the above two scenarios (Case 2 and Case 3) do not help to fully contain the disease once it spreads in the population. As it can be seen from Figs. 7 and 8, another wave of outbreaks of the disease emerge at a later stage. Here, we can see that the asymptomatic infectious individuals play the greater role in becoming the major source for the second wave. Therefore, if there is a possibility to track and detect people with asymptomatic infection, and if they can be effectively quarantined for the required period of time, then there is a possibility for the disease to be contained. As it can be observed from Fig. 9 , if we can increase the rate of detecting and quarantining the asymptomatic individuals to a proportion of about 30%, it is possible to significantly reduce the infection to a level where it cannot be a public threat. Otherwise, any lower proportion of this effort will imply the resurgence of a second wave of the infection in the community.

  Therefore, to contain COVID-19 in every given community, public health authorities need to work more on the detection and quarantining of the asymptomatic infectious individuals.

• Case 4:

  In this case, we assume that there is no lockdown imposed but only a large number of testing is applied to detect and quarantine a larger proportion of infected cases.

  If it is possible to intensify the effort of tracing the asymptomatic infectious individuals and be able to quarantine at least 35% of them continuously and effectively, our simulation shows that there is a possibility for the disease to be contained without imposing the strict lockdown rule on the total population. The plot in Fig. 10 shows the time profile of the count of the infected groups while about 50% of the individuals from I class are effectively quarantined (for example inside appropriate health facilities).

  We can observe that this intervention strategy can also produce the required result in containing the outbreak as some countries (like South Korea) are currently following this pattern.

• Case 5:
  In this case, we assume that the length of the lockdown period is nearly twice to the scenario in Case 2. However, the effort in detecting the asymptomatic infectious individuals is kept at the minimum level. This scenario is more applicable in highly resource constrained countries as the current cost of testing is high. In this case, it is assumed that the length of the duration of each phase (except for Phase 2) is the same as that given in Case 2. More still, it is supposed that;

  • 1.
    the conditions in Phase 1 remain the same,
  • 2.
    Phase 2 lasts 11 weeks with 50% of the symptomatic individuals and 5% of the asymptomatic individuals detected and quarantined. Moreover, strict social distancing rules are still in place with an effect of reducing 70% of human contacts and 50% of environmental variables,
  • 3.
    Phase 3 lasts 4 weeks (the same as in Case 2), but with 50% of individuals in the I class and 10% of individuals in the C class detected and quarantined, while partial social distancing rules are in place with an effect of reducing 25% of human contacts and 25% of environmental variables,
  • 4.
    Phase 4 continues with detecting and quarantining 50% of members in the I class and 10% of members in the C class, while the other mandatory intervention are lifted.

  The time profile of the infection following the scenario in Case 5 is plotted in Fig. 11 .

  The simulation for this scenario shows that even if we increase the length of lockdown period to 11 weeks (like it was practised in the Hubei province, China) the disease may re-emerge after some period of time. However, the heights of the peaks in the subsequent waves of the disease are much lower than the first peaks. Therefore, once again, unless the authorities apply some kind of strict contact tracing mechanism and conduct enough testing to detect and isolate up to 30% of the asymptomatic infectious individuals, the disease persists in the community with multiple subsequent waves.

In general, from the simulations, we can observe that in all of the above scenarios a transition from one phase to the other intervention phase is characterised by a surge in new cases. However, the number will eventually go down if the intervention in the immediate next phase is effective, or else the disease re-emerges in the population.

Fig. 6.

Dynamics of the disease with no additional intervention is applied.

Fig. 7.

Dynamics of the disease (portraying the scenario in Case 2) with the start of early intervention measures but for half of the time as compared to that of Case 2.

Fig. 8.

Dynamics of the disease with 30% of the C class and at least 70% of the I class are detected and quarantined in Phase 4 (after the interventions described in Case 2 are carried out).

Fig. 9.

Dynamics of the disease with 30% of the population in the C class and at least 50% of the I class are detected and quarantined just after Phase 1 period.

Fig. 10.

Dynamics of the disease with at most 10% of the population in the C class and at least 50% of the I class are detected and quarantined just after Phase 1 period, with strict social distancing rule imposed for 11 weeks.

Fig. 11.

Dynamics of the disease with a mandatory 6-weeks lockdown and a 4-weeks of partial social distancing is imposed as described in Case 2.

5. Conclusions

We presented a mathematical model for the dynamics of COVID-19 whose first cases were reported in December 2019 in Wuhan-China. The model incorporates a behaviour change function to account for the proportion of individuals who decided to use any of the self-protective measures and adhered to them. In addition, it also considers a proportion of individuals with a history/knowledge of similar infections from the past and practice necessary protective measures right from the onset of the epidemic. The model also accounts for asymptomatic carriers of the infection as well as the concentration of the pathogen within the environment. The basic properties of the model including well-posedness, the disease free equilibrium and its stability, model basic reproduction number as well as the existence of backward bifurcation were examined. To estimate the parameter values, the model was fitted to the data on daily new cases reported in WHO situation reports 1–57 [1], which accounts for the period from January 21, 2020 to March 17, 2020. From the nominal values from the data fitting, we obtained a reproduction number, ${\mathcal{R}}_0\approx 2.9$ (2.1–4) which compares well with the values of ${\mathcal{R}}_0$ obtained in other researches, for instance, (2.24–3.58) [53] and 3.11 (95%CI, 2.39–4.13) [52]. From our sensitivity analysis simulations, we observed that for some given parameter combinations, the value of ${\mathcal{R}}_0$ can be reduced to below 1, and similarly for values much higher than 4.

We observed that if the recovering individuals do so with permanent immunity ($\phi =0$), then reducing the reproduction number to a value below unity is enough to contain the infection. On the other hand, if recovering individuals do so with temporary immunity (φ ≠ 0), the proposed model exhibits backward bifurcation, which implies that reducing the value of ${\mathcal{R}}_0$ below 1 is not enough to contain the infection.

By applying the Latin Hypercube sampling scheme, we observed that if the disease is to be easily contained, measures such as; physical/social distancing (which reduces the rate of disease transmission directly from human to human), improved personal hygiene (which reduces the rate of disease transmission from the environment to humans), and minimal shedding of the pathogen into the environment by both asymptomatic and symptomatic individuals, have the greatest potential of slowing the epidemic when enhanced. We further observed that increased decay of the pathogen from the environment (achieved by disinfecting surfaces) alone is less significant in reducing/curbing the number of cases.

We further observed that having high numbers of people with knowledge from previous similar infections, that are practising the prescribed self-protective measures can delay/slow down the otherwise potentially explosive outbreak. Consequently, the daily number of cases is kept at low manageable levels. In addition, increasing the average effectiveness of the self-protective measures and adherence to such measures is vital in realising low peaks of the number of cases. Furthermore, due to the absence of vaccination or any approved medication, developing capacity to detect carrier groups is very important. From our results, it is recommended that countries should develop capacities to identify and quarantine at least 30% of carriers as well as at least 50% of symptomatic cases if the infection is to be controlled. Our model predicts a possible resurgence of the number of cases, if the asymptomatic cases are still many by the time disease spread curbs/lockdown measures are lifted. In addition, we observe from simulations that although disease spread curbs (such as a lockdown measure) may be imposed, their real impact on the number of new cases may only be realised after approximately 21 days, and the reduction (when it appears) could be sharp in the case of a strict lockdown measure with high impact in reducing effective contact between individuals in the population.

When providing the mitigation strategies, we did not account for the delay between the actual incidence and the point when cases have been confirmed since the actual parameters describing such a delay are not known. In health systems where testing of suspected cases is done after individuals show symptoms or on demand, it is likely to have a big gap between the actual incidence and confirmation of new cases. The impact of the delay between actual incidence and confirmation of case can be explored in future work. In addition, we assumed that all individuals who recover, do so with the same level of immunity. However, this may not necessarily be the case since immunity of individuals is affected by a number of factors, including age, cortisol levels and nutrition among others. The impact of differentiated levels of immunity on the disease dynamics and potential resurgence of the epidemic can be explored in the future when relevant data becomes available. Our model did not include the possibility of vaccination or treatment. We, however acknowledge their importance in controlling the infection. Therefore, optimal control of the infection in the presence of these mitigation strategies can be explored in future works when relevant data becomes available. Since the disease has been observed to affect age groups differently, it is plausible to consider age-structured models to better understand the effect of the disease in the respective age groups.

CRediT authorship contribution statement

Semu M. Kassa: Conceptualization, Methodology, Writing - original draft. John B.H. Njagarah: Formal analysis, Writing - original draft. Yibeltal A. Terefe: Conceptualization, Methodology, Formal analysis, Writing - original draft.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Proof of Theorem 3.1

The proof of Theorem 3.1 is outlined here below based on the following two steps.

First, we show that all solutions of Eq. (2) are nonnegative as required in Busenberg and Cooke [54], Stuart and Humphries [55]. To show that the state variables S and S_e of the model are positive for all t ≥ 0, we use proof by contradiction. We suppose that a trajectory crosses one of the positive cones at times t ₁ or t ₂ such that:

• • t ₁: $S\left(t_1\right)=0,S^{\prime }\left(t_1\right)<0,S_e\left(t\right)>0,C\left(t\right)>0,I\left(t\right)>0,R\left(t\right)>0,$ and E(t) > 0 for t ∈ (0, t ₁), or
• • t ₂: $S_e\left(t_2\right)=0,S_e^{\prime }\left(t_2\right)<0,S\left(t\right)>0,C\left(t\right)>0,I\left(t\right)>0,R\left(t\right)>0,$ and E(t) > 0 for t ∈ (0, t ₂),

Using the first equation of Eq. (2), the first assumption leads to

$$S^{\prime }\left(t_1\right)=(1-h)\pi +(1-\omega )\phi R\left(t_1\right)>0,$$

which contradicts the first assumption that S′(t ₁) < 0. Thus, S(t) remains positive for all t ≥ 0. Here, t ₁ is chosen so that our point to be on the positive axis of S(t) so that R(t ₁) is positive.

Using the second equation of Eq. (2),

$$S_e^{\prime }\left(t_2\right)=h\pi +\sigma eS+\omega \phi R>0,$$

which also contradicts the assumption $S_e^{\prime }\left(t_2\right)<0$. Hence, S_e(t) remains positive for all t ≥ 0. Based on the third equation of Eq. (2),

$$C^{\prime }=\eta \lambda S+\varphi (1-\rho )\lambda S_e-(\theta +\alpha +\mu )C\ge -(\theta +\alpha +\mu )C,$$ (13)

because S(t) and S_e(t) are nonnegative for t ≥ 0. Solving Eq. (13) yields

$$C\left(t\right)\ge C\left(0\right)\exp (-(\theta +\alpha +\mu \left)t\right)\ge 0,$$ (14)

Likewise, from the fourth equation of (2), we obtain

$$\begin{array}{ccc}\hfill I^{\prime }& =& (1-\eta )\lambda S+(1-\varphi )(1-\rho )\lambda S_e+\theta C-(\gamma +\mu +\delta )I\hfill \\ & \ge & -(\gamma +\mu +\delta )I.\hfill \end{array}$$ (15)

Solving (15) leads to

$$I\left(t\right)\ge I\left(0\right)\exp (-(\gamma +\mu +\delta \left)\right)\ge 0.$$ (16)

Similarly, using the last two equations of Eq. (2), we have

$$R^{\prime }=\alpha C+\gamma I-(\phi +\mu )R\ge -(\phi +\mu )R,$$ (17)

and

$$E^{\prime }=ϵC+\xi I-\psi E\ge -\psi E,$$ (18)

because S(t), S_e(t), C(t), and I(t) are nonnegative for t ≥ 0. Solving Eqs. (17) and (18) gives

$$R\left(t\right)\ge R\left(0\right)\exp (-(\phi +\mu \left)t\right)\ge 0,$$ (19)

and

$$E\left(t\right)\ge E\left(0\right)\exp (-\psi t)\ge 0,$$ (20)

respectively.

Thus, any solution of Eq. (2) is nonnegative for t ≥ 0 and any initial condition in Ω.

Finally, the total number of the population N(t) at time t is governed by

$$N^{\prime }\left(t\right)=\pi -\mu N\left(t\right)-\delta I\le \pi -\mu N\left(t\right)$$ (21)

Thus, for the initial data $0\le N\left(0\right)\le \frac{\pi }{\mu },$ by Gronwall inequality, we obtain

$$0\le N\left(t\right)\le \frac{\pi }{\mu }.$$ (22)

Moreover, for the environmental variable E, we have

$$E^{\prime }=ϵC+\xi I-\psi E\le (ϵ+\xi )\frac{\pi }{\mu }-\psi E,$$ (23)

because C(t) and I(t) are less than $\frac{\pi }{\mu }$ for all t ≥ 0. Applying again the Gronwall inequality, for $0\le E\left(0\right)\le \frac{(ϵ+\xi )\pi }{\mu \psi },$ leads into

$$0\le E\left(t\right)\le \frac{(ϵ+\xi )\pi }{\mu \psi }.$$ (24)

Combining the above two steps and Theorem 2.1.5 in Diekmann and Heesterbeek [33] for the existence of unique bounded solution, we infer that any solution of Eq. (2) is nonnegative and bounded. Hence, Eq. (2) defines a dynamical system on Ω.

Appendix B. Proof of Theorem 3.3

Proof

The theorem is the direct application of Theorem 4.1 in Castilo-Chavez and Song [35]. To check the existence of backward bifurcation of the model Eq. (2) at ${\mathcal{R}}_0=1,$ we use the center manifold theorem [35]. For this purpose, we introduce the following change of variables.

$$x_1=S,x_2=S_e,x_3=C,x_4=I,x_5=R,x_6=E$$ (25)

so that

$$N=x_1+x_2+x_3+x_4+x_5,\lambda =\frac{{\beta }_1(x_4+\nu x_3)}{N}+\frac{{\beta }_2{x}_6}{x_6+K},\text{and}e\left(\lambda \right)=\frac{{\lambda }^n}{{\lambda }_0^n+{\lambda }^n}.$$

Moreover, by using the vector notation $X={(x_1,x_2,x_3,x_4,x_5,x_6)}^T,$ the model Eq. (2) can be written in the form $X^{\prime }\left(t\right)=F={(f_1,f_2,f_3,f_4,f_5,f_6)}^T$ as follows:

$$\begin{array}{cc}{x}_1^{\prime }\hfill & =(1-h)\pi -(\lambda +\sigma e+\mu )x_1\left(t\right)+(1-\omega )\phi x_6,\hfill \\ x_2^{\prime }\hfill & =h\pi +\sigma e{x}_1-((1-\rho )\lambda +\mu )x_2+\omega \phi x_5,\hfill \\ x_3^{\prime }\hfill & =\eta \lambda x_1+\varphi (1-\rho )\lambda x_2-k_1{x}_3,\hfill \\ x_4^{\prime }\hfill & =(1-\eta )\lambda x_1+(1-\varphi )(1-\rho )\lambda x_2+\theta x_3-k_2{x}_4,\hfill \\ x_5^{\prime }\hfill & =\alpha x_3+\gamma x_4-k_3{x}_5,\hfill \\ x_6^{\prime }\hfill & =ϵx_3+\xi x_4-\psi x_6,\hfill \end{array}$$ (26)

where,

$$k_1=\theta +\alpha +\mu ,k_2=\gamma +\mu +\delta ,\text{and}{k}_3=\phi +\mu .$$

When ${\mathcal{R}}_0=1$ and β ₁ is considered as a bifurcation parameter, from (8) we get

$$1={\beta }_1{T}_1+T_2\text{or}{\beta }_1={\beta }_1^{*}=\frac{1-T_2}{T_1},$$ (27)

where

$$T_1=\frac{p}{k_1}(\nu +\frac{\theta }{k_2})+\frac{q}{k_2}\text{and}{T}_2=\frac{{\beta }_2\pi }{\mu \psi K}\left[\frac{p}{k_1}\right(ϵ+\frac{\theta \xi }{k_2})+\frac{q\xi }{k_2}].$$

Further more, ${\beta }_1<{\beta }_1^{*}$ if and only if ${\mathcal{R}}_0<1$ and ${\beta }_1>{\beta }_1^{*}$ whenever ${\mathcal{R}}_0>1$.

The Jacobian of the system (26) at the associated $DFE\left({\mathcal{E}}_0\right)$ is

$$J\left({\mathcal{E}}_0\right)=\left(\begin{array}{cccccc}-\mu & 0& -\nu {\beta }_1^{*}(1-h)& -{\beta }_1^{*}(1-h)& (1-\omega )\phi & {\displaystyle -\frac{{\beta }_2(1-h)\pi }{\mu K}}\\ 0& -\mu & -(1-\rho )h\nu {\beta }_1^{*}& -(1-\rho )h{\beta }_1^{*}& \omega \phi & {\displaystyle -\frac{(1-\rho )h{\beta }_2\pi }{\mu K}}\\ 0& 0& p\nu {\beta }_1^{*}-k_1& p{\beta }_1^{*}& 0& {\displaystyle \frac{p{\beta }_2\pi }{\mu K}}\\ 0& 0& q\nu {\beta }_1^{*}+\theta & q{\beta }_1^{*}-k_2& 0& {\displaystyle \frac{q{\beta }_2\pi }{\mu K}}\\ 0& 0& \alpha & \gamma & -k_3& 0\\ 0& 0& ϵ& \xi & 0& -\psi \end{array}\right),$$ (28)

where $p=\eta (1-h)+\varphi (1-\rho )h,$ and $q=(1-\eta )(1-h)+(1-\varphi )(1-\rho )h$.

The transformed system Eq. (26), with ${\beta }_1={\beta }_1^{*},$ has a non-hyperbolic equilibrium point such that the linear system has a simple eigenvalue with zero real part and all other eigenvalues have negative real parts. Hence, the centre manifold theory [35] can be used to analyse the dynamics of the model Eq. (26) near ${\beta }_1={\beta }_1^{*}$. By using the notation in Castilo-Chavez and Song [35], the following computations are carried out.

The right-eigenvector

$$w={(w_1,w_2,w_3,w_4,w_5,w_6)}^T$$ (29)

associated with the zero eigenvalue of $J\left({\mathcal{E}}_0\right)$ such that

$$J\left({\mathcal{E}}_0\right).w=0$$

at ${\beta }_1={\beta }_1^{*}$ is given by

$$\begin{array}{ccc}\hfill w_1& =& D{w}_3,w_2=G{w}_3,w_3=w_3>0,\hfill \\ \hfill w_4& =& A{w}_3,w_5=\frac{1}{k_3}(\alpha +\gamma A)w_3,w_6=\frac{1}{\psi }(ϵ+\xi A)w_3,\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill A& =& \frac{\mu \psi k_{1}K\left[{\beta }_1^{*}\right(\frac{p\theta }{k_1{k}_2}+\frac{q}{k_2})+\frac{{\beta }_2\pi }{\mu \psi K}(\frac{p\theta \xi }{k_1{k}_2}+\frac{q\xi }{k_2}\left)\right]}{p(\mu \psi {\beta }_1^{*}K+\xi {\beta }_2\pi )}>0,\hfill \\ \hfill D& =& \frac{1}{\mu }[\frac{(1-\omega )\phi (\alpha +\gamma A)}{k_3}-(1-h)({\beta }_1^{*}(\nu +A)+\frac{{\beta }_2\pi }{\mu \psi K}(ϵ+\xi A)\left)\right],\hfill \\ \hfill G& =& \frac{1}{\mu }[\frac{\omega \phi }{k_3}(\alpha +\gamma A)-(1-\rho )h({\beta }_1^{*}(\nu +A)+\frac{{\beta }_2\pi }{\mu \psi K}(ϵ+\xi A)\left)\right].\hfill \end{array}$$ (30)

Similarly, the left-eigenvector

$$v=(v_1,v_2,v_3,v_4,v_5,v_6),$$ (31)

of J(x*) such that

$$v.J\left({\mathcal{E}}_0\right)=0$$

associated with the zero eigenvalue is given by,

$$\begin{array}{ccc}\hfill v_1& =& o,v_2=0,v_3=v_3>0,\hfill \\ \hfill v_4& =& F{v}_3,v_5=0,v_6=\frac{{\beta }_2\pi }{\mu \psi K}(p+qF)v_3,\hfill \end{array}$$

where

$$F=\frac{p(\mu \psi {\beta }_1^{*}K+\xi {\beta }_2\pi )}{q(\nu \mu \psi {\beta }_1^{*}K+ϵ{\beta }_2\pi )+\mu \psi \theta K}A>0.$$

The right-eigenvector w and the left-eigenvector v need to satisfy the condition $v.w=1$.

The bifurcation coefficient a at the DFE $\left({\mathcal{E}}_0\right)$ is given by

$$\begin{array}{ccc}\hfill a& =& \sum _{k,i,j=1}^6{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j}({\mathcal{E}}_0,{\beta }_1^{*}),\hfill \\ & =& \sum _{i,j=1}^6[v_3{w}_i{w}_j\frac{{\partial }^2{f}_3}{\partial x_i\partial x_j}({\mathcal{E}}_0,{\beta }_1^{*})+v_4{w}_i{w}_j\frac{{\partial }^2{f}_4}{\partial x_i\partial x_j}({\mathcal{E}}_0,{\beta }_1^{*})+v_6{w}_i{w}_j\frac{{\partial }^2{f}_6}{\partial x_i\partial x_j}({\mathcal{E}}_0,{\beta }_1^{*})]\hfill \\ & =& 2\left\{D\right[\frac{\mu {\beta }_1}{\pi }(\nu +A)(\eta -p+F(1-\eta -q))+\frac{{\beta }_2(ϵ+\xi A)}{\psi K}(\eta +F(1-\eta ))]\hfill \\ & & +G\left[\frac{\mu {\beta }_1}{\pi }(\nu +A)(1-h)\right[(-\eta +\varphi (1-\rho ))+F(-(1-\eta )+(1-\varphi )(1-\rho ))]\hfill \\ & & +\frac{(1-\rho ){\beta }_2(ϵ+\xi A)}{\psi K}(\varphi +F(1-\varphi ))]\hfill \\ & & -(p+qF)\left[\frac{\mu {\beta }_1}{\pi }\right(\nu +A(1+\nu +A)+\frac{\alpha +\gamma A}{k_3}(\nu +A))+\frac{{(ϵ+\xi A)}^2}{\mu {\psi }^2{K}^2}{\beta }_2\pi ]\}{v}_3{w}_3^2\hfill \end{array}$$ (32)

Thus, the bifurcation coefficient a, can be positive for the right choice of the parametric values that satisfy the condition in Eq. (9).

The second bifurcation coefficient b is given by

$$b=\sum _{k,j=1}^6{v}_k{w}_j\frac{{\partial }^2{f}_k}{\partial x_j\partial {\beta }_1}({\mathcal{E}}_0,{\beta }_1^{*}),=\sum _{j=1}^6[v_3{w}_j\frac{{\partial }^2{f}_3}{\partial x_j\partial {\beta }_1}({\mathcal{E}}_0,{\beta }_1^{*})+v_4{w}_j\frac{{\partial }^2{f}_4}{\partial x_j\partial {\beta }_1}({\mathcal{E}}_0,{\beta }_1^{*})+v_6{w}_j\frac{{\partial }^2{f}_6}{\partial x_j\partial {\beta }_1}({\mathcal{E}}_0,{\beta }_1^{*})]=(\nu +A)(p+qF)v_3{w}_3$$ (33)

Clearly, b > 0 because A and F are positive.

When $\phi =0,$ D and G in (30) are negative and a in (32) is negative as well. Hence, by Theorem 4.1 in Castilo-Chavez and Song [35], the model will not exhibit a backward bifurcation at ${\mathcal{R}}_0=1$. □