On Compatibility of Two Approaches to Generalization of the Lovász Extension Formula

Abstract

We present a method of generalization of the Lovász extension formula combining two known approaches - the first of them based on the replacement of the product operator by some suitable binary function F and the second one based on the replacement of the minimum operator by a suitable aggregation function A. We propose generalization by simultaneous replacement of both product and minimum operators and investigate pairs (F, A) yielding an aggregation function for all capacities.

Introduction

Aggregation of several values into a single value proves to be useful in many fields, e.g., multicriteria decision making, image processing, deep learning, fuzzy systems etc. Using the Choquet integral [3] as a mean of aggregation process allows to capture relations between aggregated data through so-called fuzzy measures [9]. This is the reason of the nowadays interest in generalizations of the Choquet integral, for a recent state-of-art see, e.g., [4].

In our paper we focus on generalizations of the Choquet integral expressed by means of the so-called Möbius transform, which is also known as Lovász extension formula, see (2) below. Recently, two different approaches occured - in the first one the Lovász extension formula is modified by replacing of the product operator by some suitable binary function F and the second one is based on the replacement of the minimum operator by a suitable aggregation function A. We study the question, when these two approaches can be used simultaneously and we investigate the functional obtained in this way.

The paper is organized as follows. In the next section, some necessary preliminaries are given. In Sect. 3, we propose the new functional and exemplify the instances, when the obtained functional is an aggregation function for all capacities and when it is not. Section 4 contains results concerning the binary case. Finally, some concluding remarks are given.

Preliminaries

In this section we recall some definitions and results which will be used in the sequel. We also fix the notation, mostly according to [5], wherein more information concerning the theory of aggregation functions can be found.

Let 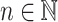and .

Definition 1

A function is an (n-ary) aggregation function if A is monotone and satisfies the boundary conditions and .

We denote the class of all n-ary aggregations functions by .

Definition 2

An aggregation function is

• conjunctive, if for all ,

• disjunctive, if for all .

Definition 3

A set function is a capacity if whenever and m satisfies the boundary conditions , .

We denote the class of all capacities on by .

Definition 4

The set function , defined by

for all , is called Möbius transform corresponding to a capacity m.

Möbius transform is invertible by means of the so-called Zeta transform:

1

for every .

Denote the range of the Möbius transform. The bounds of the Möbius transform have recently been studied by Grabisch et al. in [6].

Definition 5

Let be a capacity and . Then the Choquet integral of with respect to m is given by

where the integral on the right-hand side is the Riemann integral.

Proposition 1

Let and . Then the discrete Choquet integral can be expressed as:

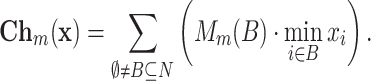2

Formula (2) is also known as the Lovász extension formula [8].

Now we recall two approaches to generalization of the formula (2). The first one is due to Kolesárová et al. [7] and is based on replacing the minimum operator in (2) by some other aggregation function in the following way:

Let 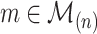be a capacity, be an aggregation function. Define by

3

where whenever and 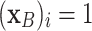otherwise. The authors focused on characterization of aggregation functions A yielding, for all capacities , an aggregation function 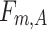extending the capacity m, i.e., on such A that and for all (here stands for the indicator of the set B).

Remark 1

There was shown in [7] that (among others) all copulas are suitable to be taken in rôle of A in (3). For instance, taking , where is the product copula, we obtain the well-known Owen multilinear extension (see [10]).

The second approach occured recently in [2] and is based on replacing the product of and minimum operator in the formula (2) by some function in the following way:

Let , be a function bounded on . Define the function by

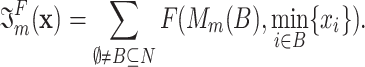4

The authors focused on functions F yielding an aggregation function 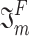for all capacities .

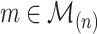Remark 2

It was shown in [2] that all functions F yielding for all 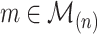aggregation functions with a given diagonal section are exactly those of the form

5

where is a function satisfying

for all such that .

However, there is no full characterization of all functions F yielding an aggregation function for every in [2].

Double Generalization of the Lovász Extension Formula

Let 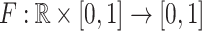be a function bounded on , A be an aggregation function , m be a capacity . We define the function as

6

where whenever and otherwise.

Lemma 1

Let be a function bounded on 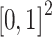and . Let be a function defined by

Then, that for any , it holds for all .

Proof

Since , the result follows.

Consequently, one can consider with no loss of generality (compare with Proposition 3.1 in [2]).

Let us define

Definition 6

A function is I-compatible with an aggregation function iff for all .

Note that, according to Remark 1, the product operator is I-compatible with every copula. Next, according to Remark 2, all binary functions of the form (5) are I-compatible with .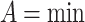

Example 1

Let , be a conjunctive aggregation function. We have

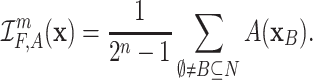Clearly, it is a monotone function and . Moreover, conjunctivity of A gives . Thus, is an aggregation function for all capacities and therefore F is I-compatible with every conjunctive aggregation function .

Example 2

Let be a nondecreasing function such that and , i.e., . Let 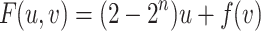. Then F is I-compatible with every disjunctive aggregation function . Indeed, disjunctivity of A implies for all , . Then, using (1), we obtain

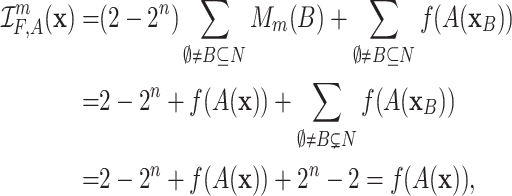which is an aggregation function for all .

On the other hand, for , F is not I-compatible with the minimal aggregation function defined as if and otherwise, since in this case 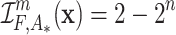for all . Note that for we obtain .

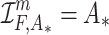For a measure let us denote and .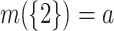

Example 3

Let . Let , 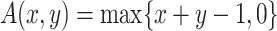. Then

which is an aggregation function for all , thus F is I-compatible with A.

However, taking a disjunctive aggregation function in rôle of A, we obtain

which is not an aggregation function for all capacities up to the minimal one (). Hence, F is not I-compatible with any disjunctive aggregation function.

Binary Case

Let . Then the function defined by (6) can be expressed as

7

Proposition 2

Let , . Then F is I-compatible with A iff the following conditions are satisfied

• (i)There exist constants such that for any it holds

  

  

  

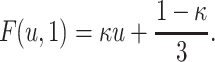
• (ii)
  For all such that and it holds

  

  and

  

  for any .

Proof

It can easily be checked that conditions (i) ensure boundary conditions and . To show necessity, let us consider the following equation:

for all .

Denoting , and , for 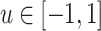, the previous equation takes form

8

for all . Following techniques used for solving Pexider’s equation (see [1]), we can put and 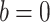respectively, obtaining

Thus, for any , we have

Consequently

9

10

Therefore, formula (8) turns into

for all . Now, denoting , we get

11

which is the Cauchy equation. Taking , we get . Therefore, putting , we get , i.e., is an odd function. Since we suppose F to be bounded on , according to Aczél [1], all solutions of the Eq. (11) on the interval can be expressed as 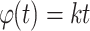, for some . Therefore,

for all , which for gives . Denoting , by (9) and (10) we obtain

Since by assumption 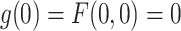, we have and consequently,

12

13

for all as asserted.

The second boundary condition for gives

for all . As A is an aggregation function, it holds . Denoting we obtain

for all . Similarly as above, this equation can be transformed into the Cauchy equation (see also [2]) having all solutions of the form , for and .

The conditions (ii) are equivalent to monotonicity of , which completes the proof.

Considering aggregation functions satisfying (e.g., all conjunctive aggregation functions are involved in this subclass), the conditions in Proposition 2 ensuring the boundary conditions of can be simplified in the following way.

Corollary 1

Let , be an aggregation function with . Then the following holds:

• (i) iff for any ,
• (ii) iff there exist a constant 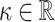such that for any . Moreover, if F is I-compatible with A, then .

Proof

We have for all . The conditions (i) in Proposition 2 yield , and consequently , thus for all as asserted.

Supposing that F is I-compatible with A and considering nondecreasingness of in the first variable, we obtain

for all .

Hence,

for all and consequently , which completes the proof.

Considering aggregation functions satisfying (e.g., all disjunctive aggregation functions are involved in this subclass), the conditions in Proposition 2 ensuring the boundary conditions of 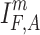can be simplified in the following way.

Corollary 2

Let , be an aggregation function with . Then the following holds:

• (i) iff 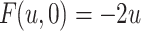for any ,
• (ii) iff 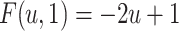for any ,

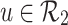Proof

Since , the Eq. (8) takes form

for all . Taking and considering we obtain

for all , and thus . Proposition 2(i) yields

thus , and consequently formulae (12),(13) imply the assertion.

Conclusion

We have introduced a new functional generalizing the Lovász extension formula (or the Choquet integral expressed in terms of Möbius transform) using simultaneously two known approaches. We have investigated when the obtained functional is an aggregation function for all capacities and exemplified positive and negative instances. In case of the binary functional we have found a characterization of all pairs (F, A) which are I-compatible, i.e., yielding an aggregation function for all capacities m. In our future reasearch we will focus on the characterization of all I-compatible pairs (F, A) in general n-ary case. Another interesting unsolved problem is the problem of giving back capacity, i.e., characterization of pairs (F, A) satisfying for all .