Maladaptive Contractility of 3D Human Cardiac Microtissues to Mechanical Nonuniformity

Abstract

Cardiac tissues are able to adjust their contractile behavior to adapt to the local mechanical environment. Nonuniformity of the native tissue mechanical properties contributes to the development of heart dysfunctions, yet the current in vitro cardiac tissue models often fail to recapitulate the mechanical nonuniformity. To address this issue, a 3D cardiac microtissue model was developed with engineered mechanical nonuniformity, enabled by 3D-printed hybrid matrices composed of fibers with different diameters. When escalating the complexity of tissue mechanical environment, cardiac microtissues started to develop maladaptive hyper-contractile phenotypes, demonstrated in both contractile motion analysis and force-power analysis. This novel hybrid system could potentially facilitate the establishment of “pathologically-inspired” cardiac microtissue model for deeper understanding of heart pathology due to nonuniformity of the tissue mechanical environment.

Table of Contents

Native heart tissues adjust their function when experiencing nonuniform mechanical environments caused by heart diseases (e.g. partial fibrosis). A 3D cardiac microtissue model under nonuniform mechanical environment was developed by combining fibers with high or low mechanical resistance. This “pathologically-inspired” 3D in vitro cardiac microtissue model allowed for probing the adaptivity of cardiac microtissues to nonuniform tissue mechanical environments.

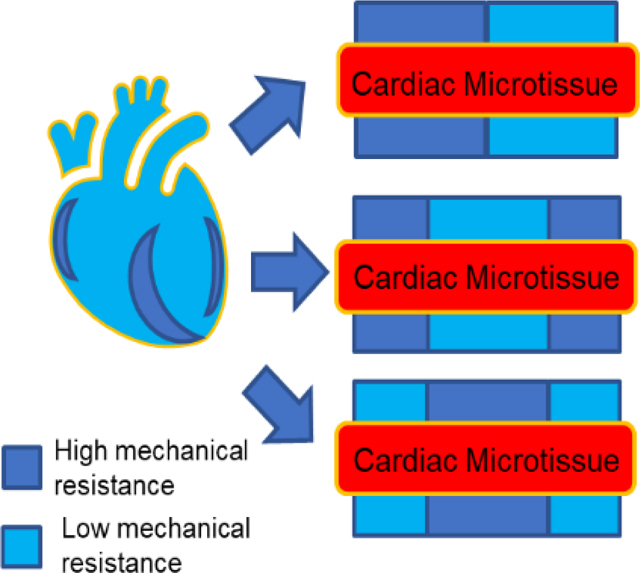
1. Introduction

Engineered in vitro 3D cardiac tissue models based on human induced pluripotent stem cells (hiPSCs) have been extensively developed to achieve physiologically relevant cardiac tissue architecture and contractile function.^[1–6] These model systems provide unique opportunities to understand the development of cardiac dysfunctions due to specific genetic deficiency,^[7–9] and to evaluate the responsiveness of cardiac contractile behavior to a variety of external perturbations (e.g., drug induced cardiotoxicity).^[10–13] In native myocardium, as well as these cardiac tissue models, the mechanical environment plays an important role in either maintenance of physiological functions or inducement of pathological dysfunctions.^[14–18] For example, optimal substrate stiffness based on polyacrylamide has been demonstrated to promote maximal contractile force from micropatterned single hiPSC-derived cardiomyocytes (hiPSC-CMs).^[19] Alternatively, the maturation level of hiPSC-CMs can be improved by gradually increasing stimulation intensity starting at the early stages, rather than constant stimulations.^[20] Recently, manipulation of tissue mechanical environment has been found to alter the disease phenotypes of engineered cardiac microtissues with genetic deficiencies: TTN mutations coupled with high mechanical stress led to more severe dilated cardiomyopathy phenotypes,^[3] while the cardiac microtissues harboring MYBPC3 mutation only exhibited contractile deficits, when they were experienced with mechanical overload.^[21]

How cardiac tissues respond to the complex and nonuniform mechanical environments, either enforcing or restricting the contractile outputs, still remains a question. In spite of the known influence of the mechanical environment on tissue function, the majority of current engineered cardiac models still focus on creating physiological relevant cardiac tissues under uniform mechanical environments.^[22–24] However, nonuniformity of tissue mechanical environment has been long recognized as one of the essential elements that regulate cardiac pathophysiology.^[25,26] The mechanical nonuniformity directly affects the heart’s pumping efficiency, which potentially leads to the heart failure.^[27] Furthermore, spatial mechanical discontinuity and nonuniform distribution of mechanical load can propagate local cardiac dysfunction throughout the entire heart. Heterogeneous fibrosis has been directly related to regional nonuniform elasticity of the heart due to cardiomyopathy or myocardial infarction.^[28,29] Although these studies suggested there was a correlation between mechanical nonuniformity and cardiac structural pathology, the impact of nonuniformity on contractile functions has not been well characterized. The in vivo models used in the aforementioned studies cannot isolate the cardiac dysfunctions attributed to the mechanical nonuniformity, as global biochemical signaling would be directly interwoven with heart pathology.

To create a nonuniform mechanical environment to assess the function of hiPSC-based cardiac microtissues, we took the advantage of two-photon polymerization (TPP) technique to fabricate hybrid filamentous matrices with precise control of spatial mechanical properties.^[30] Instead of “physiologically-relevant” biomimetic design, we established a “pathologically-inspired” 3D cardiac microtissue model based on the synthetic filamentous matrices with fully artificial designs that presented nonuniform mechanical environments. In these filamentous matrices, synthetic fibers served three roles: i) structural backbone to organize 3D cardiac microtissues; ii) physical cues to modulate spatial tissue mechanics; and iii) force sensor to measure the contractile force. Different levels of mechanical load were achieved by fabricating the matrices with different fiber thickness (thin fiber: 5 μm in diameter; thick fiber: 10 μm in diameter). By positioning fibers with different diameters within one matrix, we created different designs of mechanical hybrid matrices (double-hybrid (DH) and triple-hybrid (TH)). By assessing tissue remodeling, contractile motion velocity, contraction force and power, we found that cardiac microtissues growing on the double-hybrid matrices exhibited hyper-contractile behavior for self-compensation over mechanical imbalance. In contrast, cardiac microtissues on the triple-hybrid matrices exhibited maladaptive contractile dysfunctions with inefficient force-energy relationship. This “pathologically-inspired” cardiac microtissue model enabled us to investigate how the nonuniform tissue mechanical environments affected the cardiac contractile functions, potentially leading to hyper-contractile behavior, indicative of acquired hypertrophic cardiomyopathy.^[31]

2. Results

2.1. Tissue morphology of 3D cardiac microtissues on hybrid matrices

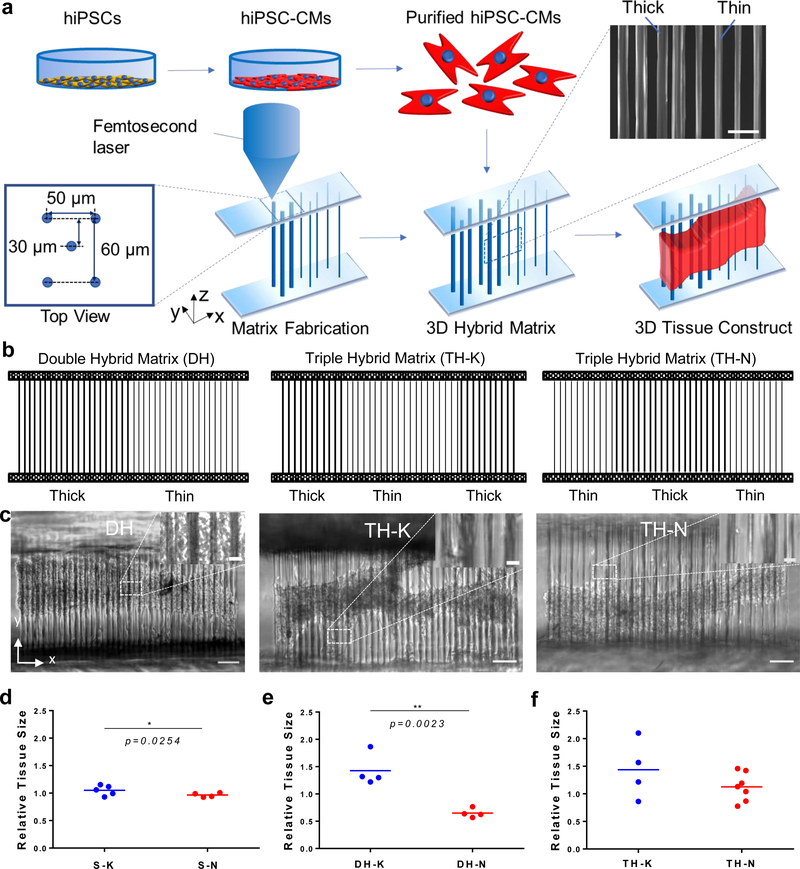
With the TPP technique, we fabricated 3D filamentous matrices composed of three layers of parallel fibers with two diameters (thick fiber: 10 μm and thin fiber: 5 μm).^[32] The layer spacing was 30 μm (matrix width was 60 μm) and fiber spacing within each layer was 50 μm. Different fiber diameters were achieved by controlling the power and exposure time of the femtosecond laser (Figure 1a). Two single matrices (S-K: single thick and S-N: single thin), one double-hybrid matrix (DH: Thick/Thin) and two triple-hybrid matrices (TH-K: Thick/Thin/Thick and TH-N: Thin/Thick/Thin) were fabricated (Figure 1b). With these artificial designs of hybrid matrices, spatial organization of the fibers with different thickness created nonuniform mechanical environments to regulate cardiac contraction.

Figure 1. 3D hybrid matrix designs and cardiac microtissue morphology.

(a) The workflow to grow a 3D cardiac microtissue on a hybrid filamentous matrix. hiPSC-CMs were differentiated, purified, recollected and seeded onto the 3D filamentous hybrid matrices fabricated by TPP technology. hiPSC-CMs self-assembled into 3D beating cardiac microtissues. SEM image shows local fiber structure at mechanical mismatch region in a hybrid matrix. Scale bar, 50 μm. (b) Design schematics of double-hybrid matrix (DH) with half thin and half thick fibers, triple-hybrid matrix (TH) with center thin fibers sandwiched by two sides of thick fibers (TH-K), and triple-hybrid matrix with center thick fibers sandwiched by two sides of thin fibers (TH-N). (c) Representative 3D cardiac microtissues growing on DH (left), TH-K (middle) and TH-N (right) matrices. The mechanical mismatch regions (one for DH matrix design and two for TH matrix designs) are highlighted in the image insertions. Scale bars: 100 μm. Scale bar for insertions: 15 μm. Relative tissue size showed significant difference (d) between S-K and S-N matrices, (e) between thick side and thin side of the DH matrices, (f) but no difference between TH-K and TH-N matrices. Statistical analysis: two-tailed student t-test (*p < 0.05, **p < 0.005). Data is shown as mean value (n ≥ 4).

Purified healthy wild-type (WT) hiPSC-CMs were seeded onto Matrigel-coated 3D fiber matrices and assembled to form condensed 3D cardiac microtissues with stable contractile behavior. Cardiac microtissues on the hybrid matrices condensed to the center of filamentous matrices along the Y direction, but remained elongated as anisotropic tissue shape across entire matrices along X axis (Figure 1c). We also observed that cardiac microtissues tended to form asymmetric tissue shapes across the DH matrices with relative larger and denser tissues on thick fiber regions of the DH matrices than the thin fiber regions (Figure 1c). We determined the relative tissue size by measuring the tissue size (cross-section area of the microtissues) at two edges of the single matrix, and then normalizing to the center tissue size. We found that the cardiac microtissues on S-K matrices had larger tissue size than the ones on S-N matrices, (Figure 1d). The difference of tissue size became more prominent for the microtissues on the DH matrices between thin and thick regions (Figure 1e), while the difference was not significant between the microtissues grown on TH-K and TH-N matrices (Figure 1f). We also showed that cardiac microtissues preserved intact and organized sarcomere structures on these hybrid matrices across the mechanical mismatch regions (Figure S1).

2.2. Contractile velocities of cardiac microtissues on hybrid matrices

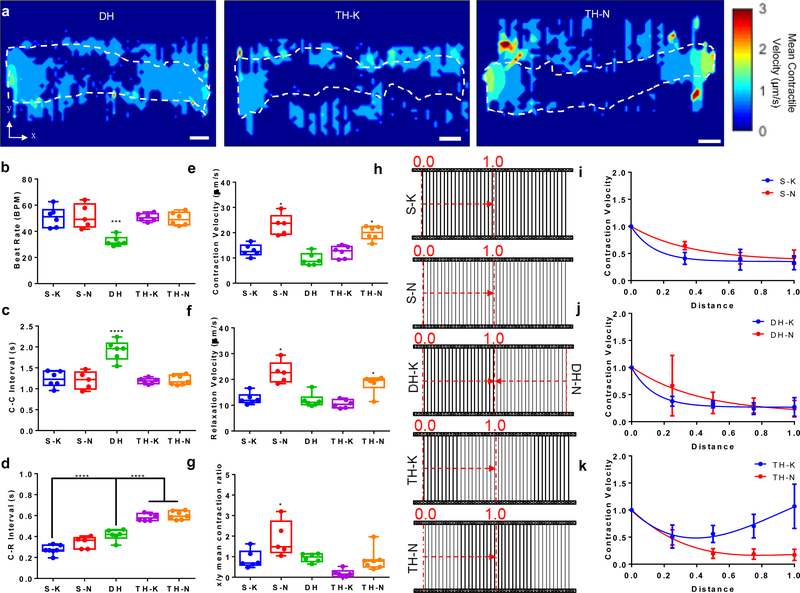
To evaluate the cardiac contractile behavior under nonuniform mechanical environments, we characterized the contractile motions, using an in-house developed open-source motion-tracking algorithm.^[33] Beating videos with motion vectors were outputted from this algorithm (Movie S1-S3, see Supporting Information). The velocity heatmaps showed the contractile motion was coordinated across the entire cardiac microtissues on the DH matrices, while the contractile motion showed discontinuity at two mechanical mismatch regions in the TH matrices, especially TH-N matrices (Figure 2a). We observed that the regions without cardiac microtissues were also detected with motions, which were largely resulted from active cardiac contractions, which pulled the fibers from where the tissues attached to. Then, the motions that initiated by active cardiac contraction would propagate along the fibers to the regions without tissue attachment. The motion velocity waveform for each beating cycle was composed of one contraction peak (first peak) and one relaxation peak (second peak) (Figure S2). The anisotropic contractile functions can also be visualized by plotting the velocity heatmaps for X-direction and Y-direction contractile motion separately (Figure S3).

Figure 2. Contractile motion velocities of cardiac microtissues under mechanical nonuniformity.

(a) Contractile velocity heatmaps of cardiac microtissues on DH, TH-K and TH-N matrices. Most motion occurred at the edge of cardiac microtissues. White dashed lines depicted the contour of cardiac microtissues. Scale bars: 100 μm. Among all the matrix designs, the cardiac microtissues on DH matrices exhibited (b) slower beat rate and (c) longer C-C time intervals (time between two consecutive contraction peaks). (d) The cardiac microtissues on TH matrices manifested significantly longer C-R interval (time between two coupled contraction and relaxation peaks) than the ones from other matrix designs. The cardiac microtissues on the matrices with thick fiber edges (S-K, DH and TH-K) showed significantly (e) lower contraction velocity, and (f) lower relaxation velocity compared to matrices with thin fiber edges (S-N and TH-N). (g) The ratio of mean contraction velocities between X-axis (perpendicular to fiber direction) and Y-axis (parallel to fiber direction) showed that the cardiac microtissues on S-N matrices maintained high anisotropic contraction, compared to the other matrix designs. (h) Contraction velocity decay curves of the cardiac microtissues from edge (segment “0.0”) to center (segment “1.0”), indicated by the red dash arrows, was analyzed for (i) single matrices (S-N versus S-K), (j) DH matrices (DH-N versus DH-K), and (k) TH matrices (TH-N versus TH-K), and showed distinct spatial characteristics between the matrices with thick fiber edges and the matrices with thin fiber edges. Statistical analysis: ANOVA with Tukey’s multiple comparisons test (*p < 0.05, ***p < 0.001, ****p < 0.0001). Data is shown as minimum, maximum, median, and 25th and 75th percentiles for box plots (n ≥ 5).

We found no significant difference on the beat rate of cardiac microtissues grown on the single and TH matrices, in which the mechanical properties were balanced on the two sides of the matrices (Figure 2b). The cardiac microtissues on DH matrices showed a significant decrease of beat rate (Figure 2b) and an increase of in time interval between two consecutive contraction peaks (C-C interval) (Figure 2c), indicating that an imbalanced mechanical environment affected the overall rhythm of cardiac microtissues. However, we found a significantly longer time interval between consecutive contraction and relaxation peaks (C-R Interval) from the cardiac microtissues on the TH matrices, compared to the single and DH matrices (Figure 2d). A long C-R interval suggested that cardiac microtissues took longer time to complete one beating cycle, indicating that an increase of mechanical nonuniformity would prolong the contraction-relaxation, an early sign of hyper-contractile behavior.

We next compared the maximal contraction and relaxation velocities of the entire cardiac microtissues for each matrix design (Figure 2e, f). Overall, cardiac microtissues grown on the matrices with thin fibers had significantly higher contractile velocities than the ones on the matrices with thick fibers, since thin fibers were more compliant and deformable for cardiac contraction. We found that microtissues on TH-K matrices and TH-N matrices showed similar contractile velocities to the ones on S-K and S-N matrices respectively, which indicated that the fiber stiffness at two edges of the matrices had determinant effects on the overall contractile velocities of entire cardiac microtissues. We also found contractile velocities measured from DH matrices were closer to the ones from S-K matrices, rather than S-N matrices. Although DH matrices had thin fibers on one edge and thick fibers on the other edge, the high stiffness of thick fibers had determinant effects on the contractile velocities of the entire cardiac microtissues. We then calculated the contractile velocity ratio between X-axis (perpendicular to fiber direction) and Y-axis (parallel to fiber direction), and found that only S-N matrices maintained a high X/Y velocity ratio (Figure 2g). Once the thick fibers were incorporated into the matrices, there was a significant decrease of X/Y velocity ratio. Especially, cardiac microtissues on the TH-K matrices showed the lowest velocity ratio, which indicated that mechanical overloading and nonuniformity prominently influenced the anisotropic contraction of the cardiac microtissues.

2.3. Effect of mechanical nonuniformity on local contractile behavior of cardiac microtissues

After analyzing the contractile velocities (contraction and relaxation velocities) of entire microtissues, we investigated the spatial characteristics of contractile behavior by dissecting the microtissues from center to edge of both homogenous and heterogenous fiber constructs (Figure 2h). The local velocities measured from each tissue segments were normalized to the velocity at the matrix edges. The cardiac microtissues exhibited a trend of exponential decay on the contraction (Figure 2i-k) and relaxation (Figure S4a-c) velocities from edge to center for all the matrix designs, except for TH-K matrices. For the TH-K matrices, the cardiac microtissues showed a decrease of contraction velocity from the edge to the center as the other matrix designs. However, due to the low resistance to the cardiac contraction from the thin fibers in the center of TH-K matrices, the contraction velocity started to increase after the thick-to-thin transition mechanical mismatch region (Figure 2k). We also found a steeper decrease in contraction and relaxation velocities associated with the matrices with thick fibers, compared to the matrices with thin fibers (Figure 2i, j), suggesting that the spatial decay of contractile velocities was highly depended on the local fiber stiffness.

To better confirm the effect of mechanical nonuniformity on local contractile velocities, we compared the cardiac contractile velocities of the cardiac microtissues between the matrix edges and matrix centers. We found there were significant differences of contractile velocities between edges and centers for all matrices, except for TH-K matrices (Figure S5). Comparing to the single matrices, we found that the differences in motion velocities between edge and center were much larger for the hybrid matrices, indicating that mechanical nonuniformity could induce hypercontractile behavior, but create high resistance to propagate the high contractile motions from edge to the center of the matrices.

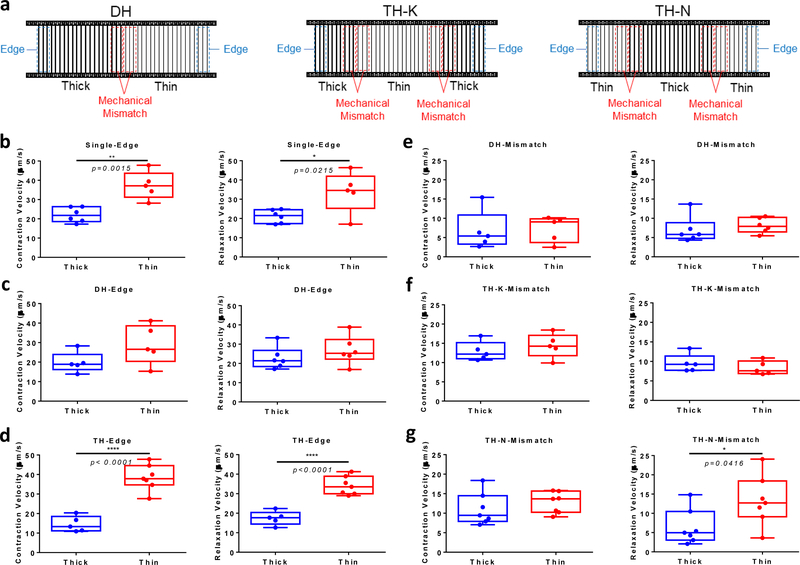
To study how mechanical mismatch would impact local contractile behavior of the cardiac microtissues, we compared local contractile velocities of cardiac microtissues between the matrix edges and mechanical mismatch regions (Figure 3a). We found that the contractile velocities of the cardiac microtissues at the S-N matrix edges were higher than the ones at S-K matrix edges (Figure 3b). Similarly, cardiac contractile velocities at the TH-N matrix edges were higher than the ones at TH-K matrix edges (Figure 3d). For the asymmetric DH matrices, we compared the contractile velocities between two sides (DH-N versus DH-K) of the same cardiac microtissues. The contractile velocities at DH-N edges were slightly higher, but not significant (p = 0.1107), comparing to DH-K edges (Figure 3c), suggesting the microtissues on DH matrices were able to compensate for the disparity in fiber stiffness and generate comparable contraction. We found no significant differences on the contraction velocities between thin side and thick side across the mismatch line for all the hybrid matrices (Figure 3e-g), which suggested that the cardiac microtissues were able to coordinate muscle contraction and maintain the velocity continuity across the mechanical mismatch.

Figure 3. Local contractile behavior of cardiac microtissues at mechanical mismatch regions.

(a) Analysis diagram of local contractile motion velocity on DH, TH-K and TH-N matrices. Blue dash box indicates the region-of-interest (ROI) at the matrix edges, and red dash box indicates the ROI at the mechanical mismatch regions. For TH matrices, the local velocities for two mismatch regions were averaged. Comparison of local contraction and relaxation velocity at matrix edges (b) between S-K and S-N matrices, (c) between thick side and thin side of DH matrices, and (d) between TH-K and TH-N matrices showed higher contractile motion velocity at thin fiber edges than thick fiber edges for single and TH matrices, but not DH matrices. Comparison of local contraction and relaxation velocity at mechanical mismatch regions within (e) DH matrices, (f) TH-K matrices and (g) TH-N matrices showed continuity of contractile motion across the mismatch line, except for the relaxation discontinuity at the TH-N mismatch regions. Statistical analysis: two-tailed student t-test (*p < 0.05, **p < 0.005 ****p < 0.0001). Data is shown as minimum, maximum, median, and 25th and 75th percentiles for box plots (n≥5).

2.4. Contractile force of cardiac microtissues on hybrid matrices

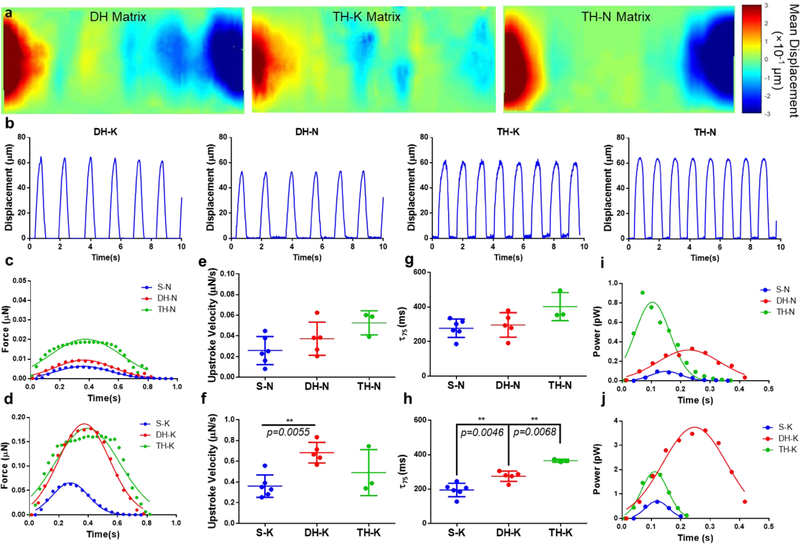
The displacement of the matrices due to cardiac contraction were analyzed to show real-time movement of the matrices (Movie S4-S6, see Supporting Information). Displacement heatmaps were generated to demonstrate the intensity of matrix displacement based on the beating videos of the cardiac microtissues (Figure 4a). In general, the matrix edges exhibited larger displacements compared to the central regions, except for TH-K matrices, which showed relative higher displacements in the matrix center, where the thin fibers were located. We calculated and plotted the contractile force kinetics based on the fiber displacement at the matrix edges (Figure 4b).^[21] For all the matrix configurations, cardiac microtissues grown on thick fibers produced approximately an order of magnitude higher contractile forces than the ones on thin fibers (Figure 4c, d). For the matrices with thin fibers at the edges (S-N, DH-N and TH-N), coined as “thin-dominant matrices”, we found there was an increasing trend of contractile force generated from the microtissues with increasing mechanical nonuniformity, as TH-N matrices produced the highest force (Figure 4c). In contrast, for the matrices with thick fibers at the edges (S-K, DH-K and TH-K), coined as “thick-dominant matrices”, the cardiac microtissues on DH-K and TH-K matrices produced much higher force than the ones on S-K matrices (Figure 4d). We further characterized the force kinetics by calculating the maximal force upstroke velocity (dF/dt_max) as an indicator of systolic function,^[34] and decay time (τ₇₅) as an indicator of diastolic functions.^[35,36] Because the cardiac microtissues on the thick fibers produced much higher force than on the thin fibers, they had a faster force development indicated by high dF/dt_max values. All the microtissues on thin-dominant matrices showed similar dF/dt_max values (Figure 4e), but the microtissues on DH-K matrices showed higher dF/dt_max value than S-K matrices (Figure 4f). According to the force decay, thin-dominant matrices shared a similar τ₇₅, while the cardiac microtissues grown on the thick-dominant matrices showed an increase trend of τ₇₅ with the increase of mechanical nonuniformity from S-K to TH-K matrices (Figure 4h), which suggested that mechanical nonuniformity, especially in TH matrices, prolonged the release of contractile force, indicating abnormal diastolic functions.

Figure 4. Force kinetics and power output of cardiac microtissues under mechanical nonuniformity.

(a) Displacement heatmaps of entire cardiac microtissues on the DH and TH matrices. Positive and negative values indicated the displacement in opposite directions. (b) Displacement waveforms for the cardiac microtissues at matrix edges of DH and TH matrices. The force kinetics of cardiac microtissues (c) on thin-dominant matrices showed a sequential increase of contraction force with the increase of nonuniformity, while (d) on thick-dominant matrices showed comparable contraction forces between DH-K and TH-K matrices. The power output of cardiac microtissues showed (e) the highest power output from TH-N matrices among the thin-dominant matrices, but (f) the highest power output from DH-K matrices among the thick-dominant matrices. The force upstroke velocity of cardiac microtissues showed (g) faster force development on the DH-K matrices compared to S-K matrices, (h) but no differences were observed for the thin-dominant matrices. The force decay of cardiac microtissues showed (i) an increased trend of time decay for S-K compared to TH-K matrices but (j) no significant difference among thin-dominant matrices. Statistical analysis: ANOVA with Tukey’s multiple comparisons test (*p < 0.05, **p < 0.005, ****p < 0.0001). Data is shown as mean ± s.d. (n≥3).

Next, we calculated contraction power output from the cardiac microtissues by multiplying force and velocity. We found that a sequential increase of power output from the cardiac microtissues grown on the thin-dominant matrices, consistently with the sequential increase of contractile forces (Figure 4i). For thick-dominant matrices, the microtissues on DH-K matrices had highest power output, since they needed longer time to overpower the mechanical imbalance during contractions, shown as a right shift of the contraction power peak (Figure 4j). The microtissues on the TH-K matrices had relative lower power output with a high contractile force, indicating an inefficient contraction (Figure 4d, j). Moreover, we also determined the energy of contraction from the microtissues (work done by the contractile forces) by measuring the total area underneath the power curves, and found that microtissues on DH matrices had highest energy of contraction amongst all the hybrid matrix designs (Table S1), possibly due to the mechanical challenges from both overloading and imbalance.

3. Discussion

Heart is a highly adjustable organ that can modify its contractile functions to adapt to undesired environments, especially to high cardiac demands (pressure or volume overload),^[37] which triggers the growth of ventricular volume. The adaptive responses of heart tissues result in physiological hypertrophy with enhanced contractility, while maladaptive responses result in pathological hypertrophy with impaired contractile functions.^[38] In animal models, it is difficult to decouple the cardiac dysfunctions attributed to the mechanical nonuniformity from other inflammatory responses. To address this problem, we created a “pathologically-inspired” 3D in vitro cardiac microtissue model by integrating hiPSCs and two-photon polymerization (TPP) technology to fabricate mechanical-hybrid filamentous matrices that improved the model’s reliability and complexity for disease phenotyping. We analyzed the contractile adaptivity of the cardiac microtissues to the mechanical nonuniformity by characterizing the tissue morphology, contractile motion velocity, motion synchronicity, force generation and kinetics, power output and energy of contraction. We found that cardiac microtissues showed high degree of adaptation to a double-hybrid (DH) mechanical environment, while their self-adjustments for contraction behavior were limited and exhibited pathological phenotypes under triple-hybrid (TH) mechanical environments.

Our cardiac tissue model is critically linked to TPP fabrication based on the ultrafast femtosecond laser, which allows us to precisely control fiber dimensions, spacing and location within our matrices.^[39,40] By changing the power and exposure time of the laser beam for TPP, we were able to change the volume of polymerization for the liquid resins, which resulted in the fiber structures with different thickness.^[32] We generated human cardiac microtissues on TPP-fabricated matrices with different fiber thicknesses. In general, it’s more difficult for the cardiac microtissue to contract against thick fibers compared to the thin fibers, since they experienced higher mechanical resistance from thick fibers as “mechanical overloading”.^[21] By switching the laser power and exposure time during one single fabrication procedure, thin and thick fibers were polymerized at spatially-defined positions within one contiguous matrix, which enabled the fabrication of complex hybrid fiber matrices as “mechanical nonuniformity”.

We created the DH matrices with mechanical mismatch at the center of the matrices. The imbalance of the mechanical environment from two sides of the DH matrices created an asymmetric tissue shape, since the production of sufficient contractile force under mechanical overloading led to the hypertrophic growth of cardiac microtissues on the thick regions of DH matrices (DH-K; Figure 1e). We also found that the mechanical imbalance significantly affected the contraction cycles of the cardiac microtissues, which required longer time intervals between two consecutive heartbeats (C-C interval, Figure 2c) in order to compensate the mechanical imbalance. Despite of the significant difference on beat frequency, we observed no difference on contractile velocities from two unbalanced sides (two matrix edges and mechanical mismatch regions), which demonstrated the ability of the cardiac microtissues to synchronize contractile motion under an unbalanced mechanical environment (Figure 3b, d). Next, we analyzed the cardiac microtissues on the DH matrices separately as DH-N (half thin side) and DH-K (half thick side). The overall contractile behavior of the cardiac microtissues on DH matrices were dominated by the DH-K region, which led to the hyper-contractile functions, shown as high levels of force generation (Figure 4c, d), power output (Figure 4i, j) and energy of contraction (Table S1).

To further escalate the mechanical nonuniformity to the cardiac microtissues, we created TH matrices by alternating three regions of either thick (TH-K) and thin (TH-N) fibers to create two mechanical mismatch interfaces. Different from the DH matrices, with longer time interval between two heartbeats, the cardiac microtissues on the TH matrices showed significant longer time intervals from contraction to relaxation within one heartbeat (C-R interval, Figure 2d), indicating that high nonuniformity impaired the diastolic transition from contraction to relaxation. Such diastolic impairment was further confirmed by the prolongation of force release on the TH-K matrices measured as force decay time (Figure 4h). Two mechanical mismatch regions within one hybrid matrix severely obstructed the contractile motion synchronicity of the cardiac microtissues, shown as discontinuity in TH contractile velocity heatmaps (Figure 2a) and differences on relaxation velocities across the mechanical mismatch regions (Figure 3g). Comparing TH matrices to single matrices (TH-N versus S-N and TH-K versus S-K), we found significantly higher force generation and power output due to mechanical nonuniformity. Although high force generation directly translated into high energy of contraction for the microtissues on the TH-N matrices, such force-work translation was not efficiently converted on the microtissues on the TH-K matrices (Table S1). These results suggested that mechanical nonuniformity, in combination with overloading, induced severe contractile inefficiency, which further confirmed the importance of high mechanical nonuniformity on triggering maladaptive contractile dysfunctions.^[41]

To investigate spatial characteristics of cardiac contractile behavior on the hybrid matrices, we fit the spatial contractile velocities from edge to the center of S-K, S-N, DH and TH-N matrices based on the one-phase decay function, and TH-K matrices based on a cubic function (Figure 2i-k). We compared the decay rate of the velocity curves measured from the microtissues on single, DH and TH-N matrices (Table S2). We found that the thick side of the DH matrices (DH-K) had a comparable decay rate as the S-K matrices, and the thin side of the DH matrices (DH-N) had a comparable decay rate as the S-N matrices. This similarity indicated that tissue mechanical environment (thin fibers versus thick fibers) had an inherent effect on the contractile velocity decay across the cardiac microtissues, despite the differences in the matrix design (single versus double-hybrid). We also found that the cardiac microtissues on TH-N matrices had a median contraction velocity decay rate among these five configurations (S-N ≈ DH-N > TH-N > DH-K ≈ S-K) (Table S2). This was attributed to a mixture of half thin and half thick fibers from edge to the center of TH-N matrices, compared to the other configurations with either pure thin fibers (S-N and DH-N) or pure thick fibers (S-K and DH-K).

Although we successfully engineered nonuniform mechanical environments within the hybrid matrices, there are limitations in the method to modulate mechanical properties by changing fiber thickness. Considering that thick fibers would occupy eight times more volume than thin fibers, less hiPSC-CMs might be compacted within the matrices with thick fibers. Higher contractile force generation due to mechanical overloading from less cells could lead to greater work demand from individual hiPSC-CMs. Fabrication of fibers with same geometry but different bending stiffness could potentially solve this problem. This might be possible by either changing the chemical compositions resin to control the modulus of elasticity of the polymerized materials, or regulating the degree of photo-polymerization by applying trains of laser pulses using an acousto-optic modulator. During culture, the majority of the cardiac microtissues had the tendency to condense to the matrix center, due to the low mechanical resistance to the contraction at the middle of individual fibers, which were fixed at two ends to the glass slides. However, since our cardiac microtissues were generated relying on cell self-assembly on the fiber matrices without additional hydrogel encapsulation, we observed the biological variability in both tissue assembly and local attachment to the fibers among different matrices. To improve the tissue condensation to the matrix centers, we can potentially increase the fiber length without sacrificing the high aspect ratio by pushing the technical limit of TPP-based laser printing method.

As the first example of cardiac tissue model with mechanical nonuniformity, we focused our work on the analysis of contractile phenotypes of the cardiac microtissues in this study, instead of drifting our efforts to the investigation of molecular events and signaling, such as calcium related pathways,^[42] which might underlie the maladaptive responses of cardiac microtissues to the mechanical nonuniformity. In future work, computational modeling of tissue mechanics for the cardiac microtissues on hybrid matrices would also provide a mechanistic understanding of the relationship between cardiac contractile function and complex mechanical environment. Our system could be modeled as an orthotropic material with microtissues as the bulk matrix and the photopolymerized beams as the fibers of a composite, although it would have to take into consideration of the discrepancy between classic linear elastic behavior of the orthotropic materials and experimental observations of nonlinear behavior from cardiac microtissues (e.g. velocity decay curves). Considering the material’s viscoelastic effects, the cardiac microtissues can be modeled with a first order kinematic scheme, combined with a Hill-like relation to calculate the stress distribution on the cardiac microtissues,^[43,44] though these previous studies focused on the mechanical stretching of the tissues, instead of the mechanical bending to the fibers within our tissue model.

4. Conclusion

By combining hiPSCs and TPP technology, we successfully created a “pathologically-inspired” 3D cardiac microtissue model based on hybrid filamentous matrices. The cardiac microtissues grown on DH matrices were able to overpower the mechanical imbalance on two sides of the matrices through hyper-contractile behavior, shown as high cardiac outputs in force, power, and energy of contraction. Although cardiac microtissues on TH matrices also developed hyper-contractile behavior, the increase of mechanical nonuniformity led to severe maladaptive hypertrophic phenotypes with inefficient cardiac outputs of high contraction force but low power output. Nevertheless, engineering a nonuniform mechanical environment offers a new perspective of recapitulating in vivo pathological conditions for understanding cardiac disease progression.

5. Experimental Section

Fabrication of Hybrid Filamentous Matrices:

The details on two-photon initiated polymerization have been described in previous publications.^[21,30,32] Briefly, two glass coverslips with cured thin layers of resin OrmoClear were assembled with a spacer with 500 um thickness. Then uncured OrmoClear was filled within the space, and polymerized by a high-repetition-rate femtosecond laser (pulse duration: ~400 fs, repetition frequency: 1 MHz, wavelength: 1,045 nm; FCPA uJewel D-400; IMRA America). The frequency of laser beam was doubled (wavelength: 522 nm) by a lithium triborate (LBO) second harmonic nonlinear crystal (Newlight Photonics). The laser beam focused at the uncured resin region with a 5× objective (NA=0.14) (M Plan Apo; Mitutoyo). Diameter of fibers was controlled by varying laser power and exposure time. The 5 μm fibers were fabricated by 3.7 mW power for 0.9 seconds exposure, while the 10 μm fibers were fabricated by 5.2 mW power for 2 seconds exposure.

Single matrices were fabricated by navigating the laser beam through the entire resin layer with consistent laser power and exposure time. For hybrid matrices, the laser power and exposure time were switched to polymerize either thin or thick fibers for individual matrix fabrication. To fabricate the DH matrices, thick fibers were polymerized at first for half of the matrix, and then thin fibers were polymerized subsequently for the other half of the matrix. To fabricate the TH-K matrices, thick fibers were polymerized at first till completion of one quarter of the matrix, then thin fibers were polymerized till completion of three quarters of the matrix, and at last thick fibers were polymerized till completion of the entire matrix. To fabricate the TH-N matrices, the laser was operated in an opposite order of fiber polymerization in contrast to the TH-K matrices.

Generation of 3D Cardiac Microtissues:

The differentiation, purification and cryopreservation of hiPSC-CMs have been described in our previous publications.^[21,24,45] To generate the 3D cardiac microtissues, three sets of matrix devices were placed into one well of a six-well plate, rinsed with Dulbecco’s phosphate buffered saline (DPBS, Gibco) three times, and then incubated with diluted Matrigel for 1 hour. After rinsing residual Matrigel, a thin layer of Matrigel coating formed on the surface of matrices. Cryopreserved hiPSC-CMs were thawed in the EB20 media (Knockout DMEM supplemented with 20% FBS, 1% GlutaMAX, 1% MEM NEAA and 4.2 uL β-mercaptoethanol; ThermoFisher Scientific), seeded onto a Matrigel-coated six-well plate, and recovered in RPMI/B27+C media (RPMI 1640 supplemented with B27 complete; ThermoFisher Scientific) supplemented with 10 μM Y-27632. After 4 days, hiPSC-CMs were trypsinized, quenched with EB20, and seeded onto filamentous matrices at a density of 3×10⁶ cell per mL RPMI/B27+C media supplemented with 10 μM Y-27632. After 4 h, another 4 ml RPMI/B27+C media with 10 μM Y-27632 was added to each well to cover the entire set of matrices. The next day, the media was switched to RPMI/B27+C media, and changed every 2 days. After 20 days of culture, the beating videos of assembled cardiac microtissue were recorded for contractile analysis.

Contractile Velocity and Displacement Measurement:

The beating videos of cardiac microtissues on filamentous matrices were analyzed by Motion-Tracking algorithm.^[33] The software is available at https://gladstone.org/46749d811. The positions of pixel macroblocks were tracked in each frame to generate motion vectors between adjacent frames to calculate the velocity. The displacement measurement of the fibers at the matrix edge has been integrated into this software for automation, rather than labor-intensive manual measurement described previously.^[21] An average motion velocity heatmap was generated for each beating video. The contractile motion velocity of region of interest (ROI) can be plotted as waveforms with repeating two coupled peaks of motion velocity. The first peak was contraction, and the second peak was relaxation. Depending on the ROI, contractile motion velocities of entire matrix, matrix edges and mismatch regions can be analyzed and quantified. The displacement of ROI can be also plotted as waveforms with repeating single peaks of displacement.

For the study of spatial characteristics of contractile velocity from matrix edge to matrix center, position of the fibers at the matrix edge and in the center (red fibers) were set as ‘0.0’ and ‘1.0’, respectively (Figure 2i). After evenly dividing the microtissues between ‘0.0’ and ‘1.0’ into a few segments, contractile motion velocity was determined at the boundary fiber of each segment (blue fibers) to plot the spatial velocity curves from matrix edge to the center (red dash arrow). For TH matrices, data from two matrix edges were averaged.

For the study of contractile behavior at mechanical mismatch regions, the mismatch regions were divided into mismatch thick ROI and mismatch thin ROI. The mismatch thick ROI was defined as an area of cardiac microtissues grown on three thick fibers closest to the thin fibers, and vice versa. For example, in a DH matrix (Figure 3a), motion velocity at the DH-K side were analyzed with ROI of three thick fibers at matrix edge (edge velocity-thick) and ROI of three thick fibers adjacent to the thin fibers (mismatch velocity-thick). For TH matrices, data from two matrix edges and two mismatch regions were averaged.

Displacement Heatmap Generation:

A computational algorithm called ‘Brighfield GUI’ was used to generate displacement heatmaps for the beating cardiac microtissues.^[46] The software is available at http://doi.org/10.5281/zenodo.495617. The original beating videos were imported into the software and a ROI that covered the entire matrix was outlined. The motion vectors within the ROI were captured to measure the length of these vectors. The frame that cardiac microtissues showed relaxed state was smart guessed by the software, and then the displacement of this specific frame, set as reference frame, was defined as 0. The displacement of other frames in the video will be calculated based on the relative motion vector length change to the reference frame. Due to difference in the computing methods between Brightfield GUI algorithm and Motion-Tracking algorithm, the absolute displacement values outputted from these two algorithms were slightly different, but the relative displacement for each position within matrices remains the same. The displacement heatmaps can be generated for each frame, and then stacked to create the real-time displacement videos for each sample.

Force and Power Characterization:

The elastic modulus of fibers (E_f) was characterized with atomic force microscope (AFM, XE-100; Park Systems) with tipless AFM cantilevers (TL-CONT-SPL and TL-FM-SPL; Nanosensors). Calculated elastic modulus of fibers for both 5 and 10 um diameters is 183.9 $\pm$ 11.7 MPa.^[21] We made the following assumptions to calculate the contractile forces for the cardiac microtissue: (i) the force vectors were parallel to each other and perpendicular to the aligned directions of fibers; (ii) contractile force was localized at the center of the fiber; (iii) the fiber had a circular cross-section. Based on beam deflection theory, we could calculate the point force generated at the matrix edge using equation (1)

$${\text{F}}^{\prime }=\frac{3\text{π}{E}_f{D}^{4}d}{L^3}$$ (1)

where F^’ is the contractile force, E_f is the elastic modulus of fibers, D is the fiber diameter, L is the fiber length, and d is the average displacement of the fibers at the matrix edge. The contraction power was calculated by multiplying one contraction velocity peak with the corresponding force kinetics. Force delay time (τ75) was defined as the time interval between the time at maximal force and the time at 75% decrease of maximal force. After fitting contractile force with Gaussian distribution curve, the first derivative of the rising portion of force kinetic trace was calculated to obtain the force upstroke velocity. The maximal value of the force upstroke velocity curve was defined as maximal upstroke velocity.

Statistical Analysis:

Data is analyzed using the software GraphPad Prism (version 8.3.0). Data was presented as box plots show the minimum, maximum, median, and 25th and 75th percentiles. One-way ANOVA with multiple t-test was used to compare the difference among different groups. The statistical significance is determined based on p-value < 0.05. Sample size for each experiment is more than 3 (n ≥ 3).