Abstract
This article investigates the fractal contagion effect of the COVID-19 pandemic on the stock markets. The stock market information of the top 32 coronavirus affected economies (as of 31st March 2020) was sampled for ex-ante and ex-post COVID-19 outbreak analysis using the Detrended Moving Cross-Correlation Analysis (DMCA) and Detrended Cross-Correlation Analysis (DCCA) techniques. The results confirm a fractal contagion effect of the COVID-19 pandemic on the stock markets. Furthermore, this fractal contagion effect fizzles out over time (in the middle and long run) for both the stock markets return and volatility. Therefore, this article provides pieces of evidence for the COVID-19 fractal contagion effect on the stock markets.
Keywords: Return, Volatility, Stock markets, Cross-correlation, Contagion
1. Introduction
The COVID-19 pandemic has resulted in panics as well as the temporary closure of businesses in most economies with confirmed positive coronavirus cases. These reactions are bound to affect the performance of the businesses in these economies as well as their stock market dynamics. As long as the coronavirus is contagious and migrations exist, this virus is capable of affecting many economies of the world and their stock markets simultaneously. Therefore, this article seeks to establish a substantial contagion effect of the COVID-19 pandemic on the stock market returns and volatilities. The current coronavirus (COVID-19) pandemic emanated in a wildlife market in the city of Wuhan, China. Due to its rapid spread and threats to humans, the market was closed. Subsequently, the whole city, country, other countries of the world are locked down to strategically separate and quarantine the infected persons from the uninfected persons. This outbreak has rapidly spread from China to many, if not all, countries of the world, and a great number of deaths and confirmed positive results have been declared concurrently. In the absence of a working vaccine, an effective model for curtailing and controlling the effects of the COVID-19 in an economy involves a total lockdown and stay at home strategy. For sustenance, most investors liquidate their positions, this includes stock market positions and thus affects the stock markets.
Contagion effects, as a result of global events that originate from a country or region, have been an interest in economic and financial literature. Park and Shin (2020) investigated the foreign banks' exposure at the regional and national levels during the 2008 global financial crisis and found that the banks in emerging economies are more exposed directly and indirectly, to the global financial crisis and suffered more capital outflow. Even at the local levels of financial institutions (Agosto et al., 2020). However, using conditional correlation methods, there is a regional contagion effect of the financial crisis on the stock markets even though some sectors are relatively less affected than other sectors (Kenourgios and Dimitriou, 2015). Wang et al. (2017) and Jin & An (2016) examined the impact of the global financial crisis on the G7 and BRICS countries and discovered a multifractal contagion which depends on the recipient country and time scale. There is also a significant contagion effect of the global financial crisis on the top 8 largest economies of the world (Dungey and Gajurel, 2014). Others are; Zhang et al. (2020), Scheicher (2001), Wang et al. (2010), Forbes & Rigobon (2002), and Ang & Chen (2002) stock market, Mohti et al. (2019) and Paulo et al. (2008) US subprime and Eurozone debt crisis, Bashir et al. (2016) and Ang & Bekaert (2002) equity market, Hussain et al. (2017) crude oil market, etc.
2. Empirical strategy
The nonlinear process has been a very powerful tool in establishing contagion effects among various markets. Within the existing literature, some of these nonlinear processes that have been adopted to study contagion are the Regime Switching models, Smooth Transition Autoregressive (STAR) model (Terasvirta and Anderson, 1992; Terasvirta, 1994), Nonlinear Error Correction Models (NECMs) (Granger and Terasvirta, 1993), Threshold Autoregressive (TAR) models (Tong and Lim, 1980; Tsay 1989; Tong, 1990), Switching Transition Error Correction and Generalized Autoregressive Conditional Heteroscedasticity (STEC-GARCH) process (Arouri et al., 2011), Exogenous Asymmetric BEKK and DCC processes (Okorie, 2019; Okorie and Lin, 2020), etc. However, among other advantages, the Detrended Moving Cross-Correlation Analysis (DMCA) and the Detrended Cross-Correlation Analysis (DCCA) processes do not require the time series processes to be stationary and they directly use the moment properties of the series to establish the cross-correlation (contagion effects) in both regimes. In other words, no sample reduction (which can be the case when a series is differenced stationary) and the original observations are used. Generally, the cross-correlation techniques and the nonlinear process approach are both capable of identifying a significant switch or periodic switch in a time series over time. The linkage between the nonlinear processes and the cross-correlation techniques is their ability to specify and identify, at least, two different regimes and allow them to depend on the regime's moments & the smooth transition modalities.
The Detrended Moving Cross-Correlation Analysis (DMCA) proposed by Vandewalle & Ausloos (1998) and modified by Kristoufek (2014) as well as the Detrended Cross-Correlation Analysis (DCCA) methods introduced by Peng et al. (1994) and augmented by Podobnik & Stanly (2008) have been used to study contagion or cross-correlation dynamics among various systems. DCCA is a modification of the Detrended Fluctuation Analysis (DFA) proposed by Peng et al. (1994) just as Kristoufek (2014) modified the DMCA by Vandewalle & Ausloos (1998). These approaches have been vastly applied in various areas (Mohti et al., 2019; Kristoufek, 2014; Zebende, 2011; Zebende, et al., 2018), including economics and finance (Zhang et al., 2020; Wang et al., 2010).
| (1) |
Given a set of time series XT and YT of size T, we define the profiles in Eq. (1) where and are the mean of the time series and k = 1, 2, ..., T. Next, each profile is divided into non-overlapping number of segments, s, of length n(λ) for DCCA (DMCA). For each segment, s, we compute and which are the moving averages (local trends) for the DMCA (DCCA) fluctuation functions.
Eqs. (2) and (3) are the fluctuation functions for DMCA and DCCA respectively. where η = n(s − 1) and θ is the type of moving average employed. θ is set to 0 or 0.5 or 1 for forward or centered or backward moving averages respectively. Empirically, the centered moving averages outperforms the rest. Hence, θ = 0.5 (Zhang et al., 2020; Mohti et al., 2019; Kristoufek, 2014) in this analysis.
| (2) |
| (3) |
The cross-correlation is defined in Eq. (4) which ranges from zero to 1 in absolute terms |ρxy(n/λ)| ε [0,1]. When it equals 1, there is a perfect cross-correlation or contagion while there is anti-cross-correlation when it equals − 1. Similarly, when it equals 0, it implies there is no significant cross-correlation. Other properties of the cross-correlation coefficients are detailed in Zhao et al. (2017). The significance hypothesis testing of the cross-correlation coefficient Eq. (4) and for the differenced cross-correlation coefficient Eq. (5) proposed by Podobnik et al. (2009, 2010, 2011) and Guedes et al., 2018a, Guedes et al., 2018b respectively are also applied on the (differenced) cross-correlation coefficients in this study of COVID-19 contagion effect.
| (4) |
| (5) |
Δρxy(n/λ) > 0 confirms that there is a significant contagion or cross-correlation effect in the stock markets during the COVID-19 pandemic while Δρxy(n/λ) < 0 suggests that the cross-correlation or system dependence within the stock markets declined during the COVID-19 period. The stock market returns and unconditional volatility as defined in Eqs. (6) and (7) respectively.
| (6) |
| (7) |
rt is the markets return and Pt is the asset's price at time t. vt is the market volatility at time t. The normalized market properties differences X, Y, and Z are defined as the differences between normalized high, close, and low prices from the normalized open price respectively. Unlike conditional volatility measures of the autoregressive conditional heteroscedastic models (Bollerslev, 1986; Engle and Shepard, 2002; Baba et al., 1995; Okorie, 2019; Okorie and Lin, 2020), the unconditional measures of a market's volatility have taken different forms, for instance, the squared return, the squared conditional mean return residual, even more, sophisticated approaches, etc. This paper adopts the best analytic scale-invariant unconditional volatility estimator model proposed by Garman and Klass (1980). The unconditional volatility equation of each asset market is specified in Eq. (7). I α is a 3 × 3 α − identity matrix.1 and M and N are symmetric matrices of normalized differences.
3. Results and discussions
3.1. Data
Major stock market index information from the top 32 countries that have recorded over 1500 confirmed COVID-19 cases,2 (τ), are sampled from 1st October 2019 to 31st December 2019 (the Calm Period) and from 1st January 2020 to 31st March 2020 (the COVID-19 Period). The closing price series from these major stock exchange indexes are sourced from Investing.com3 platforms. We select a relatively short periods before and after the outbreak of the COVID-19 virus to minimize the occurrences of other exogenous shocks or factors that might affect the stock markets and thus bias the findings of this study. In line with this, MacKinlay (1997) stated in his article entitled, Event studies in Economics and Finance, ” .. thus, a measure of the event's economic impact can be constructed using security prices observed over a relatively short-time period…”. The idea hinges on the fact that there might be other events which may have occurred after the event being studied. As such, the effect of the particular event under study is best captured using a relatively small window around the event's announcement date. Indeed, this is often the case. For instance, after the ICO ban in China, few other economies have proceeded to consider banning ICOs, Okorie (2019) used a piece of relatively small window information around the ICO ban event in China to investigate its effect in the Bitcoin market.
Table 1 shows the basic summary statistic distribution of the stock market return series from the sampled economies. The average, standardized average deviations, minimum, and maximum return values are reported for each economy during the calm period and COVID-19 period. Generally, these distributions are higher in magnitude during the COVID-19 period relative to the calm period. It can also be seen that the Iranian stock market experienced the largest maximum return in both periods followed by the Israeli stock market. Moreover, other stock markets have moderate fluctuations in both periods.
Table 1.
Return data distribution.
| Calm Period |
COVID-19 Period |
|||||||
|---|---|---|---|---|---|---|---|---|
| Statistic | Mean | St. Dev. | Min | Max | Mean | St. Dev. | Min | Max |
| China | 0.024 | 0.663 | −1.846 | 1.767 | −0.133 | 1.751 | −8.039 | 3.098 |
| USA | 0.133 | 0.534 | −1.784 | 1.253 | −0.460 | 3.598 | −12.597 | 9.564 |
| Italy | 0.161 | 0.863 | −2.912 | 1.862 | −0.557 | 3.580 | −18.541 | 8.549 |
| Spain | 0.087 | 0.830 | −2.807 | 1.844 | −0.605 | 3.161 | −15.151 | 7.528 |
| Germany | 0.162 | 0.808 | −2.800 | 2.816 | −0.500 | 2.977 | −13.055 | 10.414 |
| France | 0.119 | 0.767 | −3.174 | 1.717 | −0.519 | 3.033 | −13.098 | 8.056 |
| Iran | 0.234 | 4.891 | −9.431 | 20.544 | 0.076 | 13.102 | −25.131 | 69.315 |
| UK | 0.051 | 0.807 | −3.284 | 2.227 | −0.504 | 2.737 | −11.512 | 8.667 |
| Switzerland | 0.121 | 0.633 | −1.981 | 1.148 | −0.231 | 2.441 | −10.134 | 6.780 |
| Belgium | 0.142 | 0.719 | −2.759 | 1.900 | −0.566 | 3.100 | −15.328 | 7.361 |
| Netherlands | 0.103 | 0.764 | −2.806 | 1.820 | −0.408 | 2.729 | −11.376 | 8.591 |
| Turkey | 0.151 | 1.194 | −5.230 | 3.641 | −0.421 | 2.375 | −8.416 | 5.810 |
| S.Korea | 0.153 | 0.855 | −2.183 | 1.805 | −0.360 | 2.654 | −7.540 | 8.975 |
| Austria | 0.149 | 0.815 | −2.313 | 2.219 | −0.781 | 3.494 | −14.675 | 10.206 |
| Canada | 0.062 | 0.322 | −0.835 | 0.839 | −0.435 | 3.732 | −13.176 | 11.294 |
| Portugal | 0.097 | 0.614 | −1.356 | 1.708 | −0.450 | 2.567 | −10.267 | 7.532 |
| Brazil | 0.200 | 0.923 | −2.947 | 2.047 | −0.719 | 4.840 | −15.994 | 13.023 |
| Isreal | −0.012 | 2.339 | −8.505 | 10.317 | −0.101 | 4.114 | −11.704 | 10.405 |
| Australia | 0.022 | 0.840 | −2.237 | 2.273 | −0.411 | 3.007 | −10.203 | 6.766 |
| Norway | 0.101 | 0.859 | −2.389 | 1.738 | −0.483 | 2.594 | −8.951 | 5.237 |
| Sweden | 0.154 | 0.816 | −2.621 | 1.911 | −0.324 | 2.541 | −11.173 | 6.849 |
| Czechia | 0.096 | 0.606 | −1.846 | 1.779 | −0.657 | 2.384 | −9.501 | 6.216 |
| Ireland | 0.251 | 1.011 | −1.893 | 3.666 | −0.632 | 2.816 | −10.465 | 6.710 |
| Malaysia | 0.020 | 0.538 | −1.680 | 1.395 | −0.288 | 1.683 | −5.405 | 6.626 |
| Denmark | 0.185 | 0.883 | −2.478 | 2.418 | −0.118 | 2.003 | −7.821 | 3.505 |
| Chile | −0.085 | 1.639 | −4.504 | 7.654 | −0.589 | 3.026 | −13.837 | 6.158 |
| Poland | 0.028 | 1.336 | −3.656 | 3.456 | −0.224 | 2.723 | −13.853 | 4.519 |
| Japan | 0.149 | 0.723 | −2.026 | 2.522 | −0.358 | 2.314 | −6.274 | 7.731 |
| Russia | 0.221 | 1.265 | −3.731 | 3.284 | −0.213 | 2.115 | −5.546 | 8.835 |
| Pakistan | 0.365 | 1.131 | −2.492 | 2.584 | −0.603 | 2.196 | −7.102 | 3.398 |
| Philippines | 0.035 | 0.922 | −2.349 | 2.086 | −0.684 | 3.089 | −14.322 | 7.172 |
| Thailand | −0.009 | 0.699 | −1.754 | 2.209 | −0.615 | 3.305 | −12.439 | 8.862 |
In Table 2 , we present the basic summary statistic distribution of the stock market volatility series from the sampled economies. The average, standardized average deviations, minimum, and maximum return values are reported for each economy during the calm period and COVID-19 period. Generally, these volatility distributions are higher in magnitude during the COVID-19 period relative to the calm period. It can also be seen that the Iranian stock market experienced the largest maximum volatility (consistent with the return series) in both periods followed by the Israeli stock market volatility (consistent with the return series). Moreover, other stock market volatility has moderate fluctuations in both periods. The periodic changes in all these stock markets suggest a contagion effect of the COVID-19 pandemic.
Table 2.
Volatility data distribution.
|
Calm Period |
COVID-19 Period |
|||||||
|---|---|---|---|---|---|---|---|---|
| Statistic | Mean | St. Dev. | Min | Max | Mean | St. Dev. | Min | Max |
| China | 0.00003 | 0.00003 | 0.00000 | 0.0001 | 0.0001 | 0.0001 | 0.00001 | 0.001 |
| USA | 0.00002 | 0.00003 | 0.00000 | 0.0001 | 0.0004 | 0.001 | 0.00000 | 0.003 |
| Italy | 0.0001 | 0.00004 | 0.00001 | 0.0002 | 0.001 | 0.002 | 0.00001 | 0.010 |
| Spain | 0.00004 | 0.00003 | 0.00000 | 0.0001 | 0.001 | 0.001 | 0.00001 | 0.005 |
| Germany | 0.00004 | 0.00004 | 0.00001 | 0.0002 | 0.0005 | 0.001 | 0.00000 | 0.004 |
| France | 0.00004 | 0.00004 | 0.00000 | 0.0002 | 0.0004 | 0.001 | 0.00000 | 0.004 |
| Iran | 0.002 | 0.004 | 0.000 | 0.026 | 0.011 | 0.046 | 0.000 | 0.367 |
| UK | 0.00004 | 0.0001 | 0.00001 | 0.0003 | 0.0005 | 0.001 | 0.00001 | 0.004 |
| Switzerland | 0.00003 | 0.00003 | 0.00000 | 0.0001 | 0.0004 | 0.001 | 0.00000 | 0.004 |
| Belgium | 0.00004 | 0.00003 | 0.00000 | 0.0001 | 0.0005 | 0.001 | 0.00000 | 0.004 |
| Netherlands | 0.00003 | 0.00004 | 0.00000 | 0.0002 | 0.0004 | 0.001 | 0.00000 | 0.004 |
| Turkey | 0.0001 | 0.0001 | 0.00001 | 0.001 | 0.0004 | 0.001 | 0.00001 | 0.003 |
| S.Korea | 0.00004 | 0.00003 | 0.00001 | 0.0002 | 0.0003 | 0.001 | 0.00002 | 0.003 |
| Austria | 0.0001 | 0.00004 | 0.00001 | 0.0002 | 0.001 | 0.001 | 0.000 | 0.006 |
| Canada | 0.00001 | 0.00001 | 0.00000 | 0.0001 | 0.0004 | 0.001 | 0.00000 | 0.004 |
| Portugal | 0.00003 | 0.00002 | 0.00001 | 0.0001 | 0.0003 | 0.001 | 0.00001 | 0.003 |
| Brazil | 0.0001 | 0.00005 | 0.00001 | 0.0002 | 0.001 | 0.002 | 0.00002 | 0.014 |
| Isreal | 0.0004 | 0.001 | 0.00002 | 0.004 | 0.001 | 0.001 | 0.00004 | 0.007 |
| Australia | 0.00002 | 0.00002 | 0.00000 | 0.0001 | 0.0005 | 0.001 | 0.00000 | 0.008 |
| Norway | 0.00004 | 0.00003 | 0.00000 | 0.0001 | 0.001 | 0.001 | 0.00001 | 0.007 |
| Sweden | 0.0001 | 0.00005 | 0.00000 | 0.0002 | 0.0004 | 0.001 | 0.00001 | 0.004 |
| Czechia | 0.00002 | 0.00002 | 0.00000 | 0.0001 | 0.0004 | 0.001 | 0.00000 | 0.003 |
| Ireland | 0.0001 | 0.0001 | 0.00001 | 0.001 | 0.001 | 0.001 | 0.00001 | 0.006 |
| Malaysia | 0.00002 | 0.00001 | 0.00000 | 0.0001 | 0.0001 | 0.0002 | 0.00000 | 0.001 |
| Denmark | 0.0001 | 0.00004 | 0.00001 | 0.0002 | 0.0003 | 0.001 | 0.00001 | 0.003 |
| Chile | 0.0001 | 0.0001 | 0.00000 | 0.001 | 0.0004 | 0.001 | 0.00001 | 0.003 |
| Poland | 0.0002 | 0.0002 | 0.00001 | 0.001 | 0.0005 | 0.001 | 0.00001 | 0.003 |
| Japan | 0.00002 | 0.00002 | 0.00000 | 0.0001 | 0.0003 | 0.001 | 0.00000 | 0.003 |
| Russia | 0.0001 | 0.0001 | 0.00001 | 0.001 | 0.001 | 0.001 | 0.00002 | 0.006 |
| Pakistan | 0.0001 | 0.0001 | 0.00002 | 0.0004 | 0.0003 | 0.0004 | 0.00001 | 0.002 |
| Philippines | 0.00005 | 0.0001 | 0.00000 | 0.001 | 0.001 | 0.002 | 0.00001 | 0.013 |
| Thailand | 0.00004 | 0.00002 | 0.00001 | 0.0001 | 0.001 | 0.002 | 0.00002 | 0.015 |
3.2. Analysis of the stock markets’ return
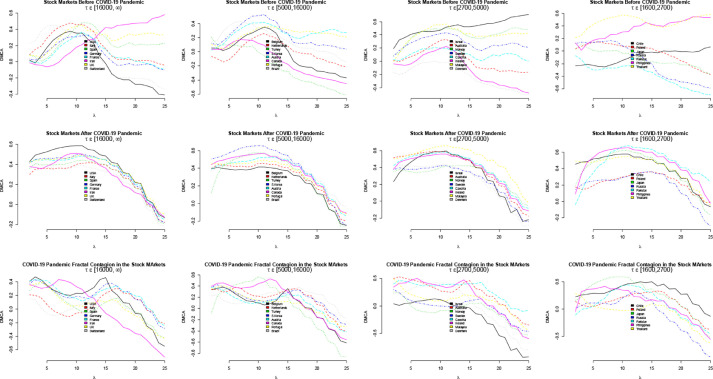
The DMCA and DCCA techniques are applied to the return series from all the sampled stock markets for both the calm period and the COID-19 period. Afterward, the periodic differences where computed. These results are presented in Fig. 1, Fig. 2 .
Fig. 1.
DMCA on return.
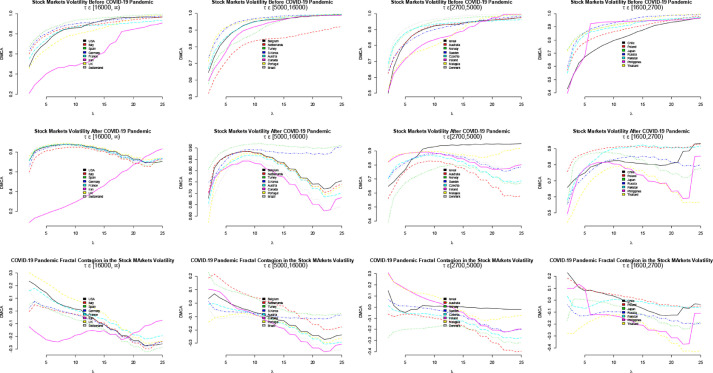
Fig. 2.
DMCA on volatility.
In Fig. 1, the DMCA results for the sampled stock markets are presented. The first-row plots represent the comovement of the sampled stock markets return during the calm periods (ex-ante COVID-19 pandemic). The second-row plots represent the comovement of the sampled stock markets return during the COVID-19 periods (ex-post COVID-19). The third-row plots represent the differences in the sampled stock markets return comovements, thus, the fractal contagion effect of the COVID-19 pandemic in the Stock markets. The total number of confirmed COVID-19 infected persons, τ, is used to group these economies to observe unique patterns and similarities. The first-column plots present the comovement of the stock markets wherein confirmed COVID-19 cases are above 16,000 persons; between 5000 and 16,000 infected persons in column two; between 2700 and 5000 infected persons in column three; and between 1600 and 2700 infected persons in column four (as of 31st March 2020).
Based on these results, it is pertinent to conclude that the COVID-19 pandemic has a contagion effect on the stock markets. This effect is stronger for economies with a relatively higher number of confined virus-infected persons. This is practically intuitive given that the outbreak and presence of the COVID-19 cases in an economy make the populace to panic, businesses are closed down as well as other gatherings like churches, meetings, conferences, etc. Every economy does this because they want to strategically group the populace into virus-infected and uninfected persons by asking (and enforcing) that people stay at their homes. This will help to isolate and quarantine infected persons while the rest of the people can return to their normal lives. However, this panic (coupled with the fear of future market performance and possibly global downturns) makes the stock markets investors to take early non-market based actions. In other words, their decision to take short or long positions was not informed by the traditional alpha rule but mostly to have enough resources to afford staying at home until it is necessary to resume their businesses as usual or due to the rapid fall in the asset prices. This is likely the observed and similar patterns for these sampled economies, hence, the contagion effect of the COVID-19 pandemic on the stock markets.
3.3. Analysis of the stock markets’ volatility
The DMCA and DCCA techniques are applied to the stock markets volatility series from the sampled stock markets for both the calm period and the COID-19 period. Afterward, the periodic differences where computed. These results are presented in Figs. 3 and 4 .
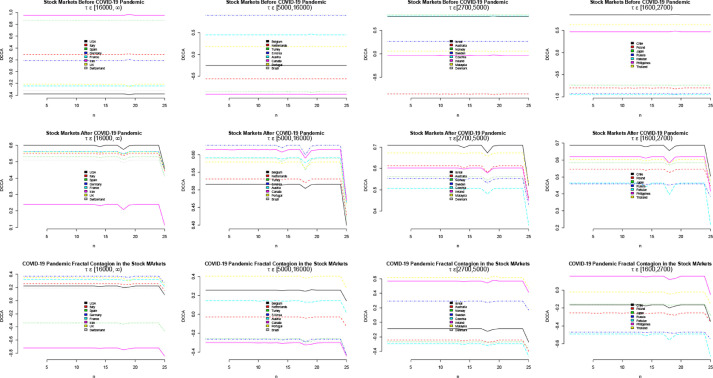
Fig. 3.
DCCA on return.
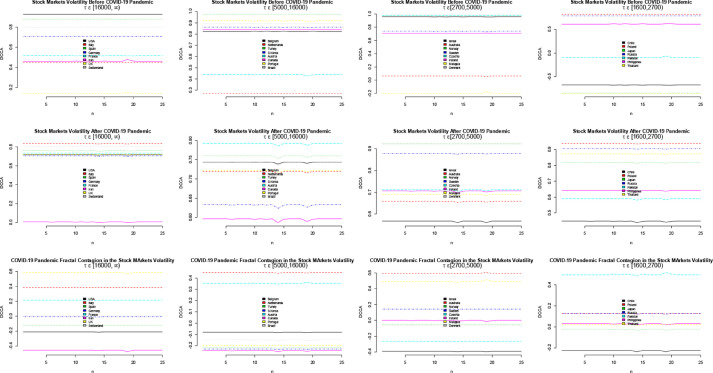
Fig. 4.
DCCM on volatility.
The first row plots show that there are, more or less, strong comovements among these market volatilities before the COVID-19 pandemic. This is mostly true for economies with higher confirmed cases of the virus infection. However, for those with lesser confirmed cases, the association appears to be stronger too. Therefore, the stock market volatilities associate greatly for all these economies during the calm period. After the outbreak of COVID-19, the DMCA results in the second row confirms a significant comovement among these sampled stock market volatilities for all these groups. Besides, it can be observed that this comovement dynamic was increasing strongly during the early stages of the COVID-19 outbreak and started decreasing, jointly, over time. This suggests a fizzling out effect of the virus outbreak in the stock markets’ volatilities. Similarly, these close associations are observed more in the economies with higher confirmed cases relative to those with fewer confirmed cases. The last row plots confirm there exists a significant fractal contagion effect of the COVID-19 pandemic on the stock markets. However, this contagion, in the stock market volatilities, fizzles out in longer horizons or periods just as observed for the stock market returns.
3.4. Robustness check
Figs. 3 and 4, show the DCCA results for the return and volatility of the sampled stock markets. The DCCM results on the stock market returns (Fig. 3) and volatility (Fig. 4) are consistent with that of the DMCA in Fig. 1 and Fig. 2 respectively. In other words, the DCCM results confirm the existence of a contagion effect in the stock markets as a result of the COVID-19 pandemic and this effect fizzles out over time. Generally, The contagion in the stock market is evident in the volatilities, just like the returns. Therefore, there exists a COVID-19 fractal contagion effect in the stock markets.
4. Conclusions
This article provides empirical pieces of evidence on the fractal contagion effect of the COVID-19 on the stock markets. The DMCA and DCCM techniques are used to test the contagion effect hypothesis. The results show that there exists a significant but short-lived contagion effect in the stock markets as a result of the COVID-19 pandemic. These contagion effects are observed both in the stock market returns and volatilities.
Declaration of Competing Interest
I write to confirm that there is no conflict of interest, whatsoever, pertaining to my submission entitled “Stock Markets and the COVID-19 Fractal Contagion Effects”, with the manuscript number FRL_2020_536, and confirm that this paper is not published or under publication consideration by any other journal.
Acknowledgements
This paper is supported by Xiamen University project: Policy and institution of clean, low carban and substainable energy system (Grant No. 0610/ZK1108).
Footnotes
α1 = 0.511, α2 = −0.019, and α3 = −0.383.
See a real time indicators of COVID-19 at https://www.worldometers.info/coronavirus/.
See https://www.investing.com/indices/shanghai-composite-historical-data, These stock markets are the SSE (China), NYSE (U.S.A), FTSE MIB (Italy), IBEX 35 (Spain), DAX (Germany), CAC 40 (France), RAN14 (Iran), FTSE 100 (U.K), SMI (Switzerland), BEL 20 (Belgium), AEX (Netherlands), XU100 (Turkey), KOSPI 50 (South Korea), ATX (Austria), S&P/TSX (Canada), PSI 20 (Portugal), Tel Aviv (Isreal), Bovespa (Brazil), S&P/ASX 200 (Australia), OBX (Norway), OMX (Sweden), MSCI (Czechia), ISEQ (Ireland), FTSE KLCI (Malaysia), OMXC20 (Denmark), S&P/CLX/IGPA (Chile), GPW (Poland), Nikkei 225 (Japan), MOEX (Russia), KSE 100 (Pakistan), PSEi (Philippines), and SET50 (Thailand).
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.frl.2020.101640.
Appendix B. Supplementary materials
References
- Agosto A., Ahelegbey D.F., Giudici P. Tree networks to assess financial contagion. Econ. Model. 2020;85:349–366. [Google Scholar]
- Ang A., Bekaert G. International asset allocation with regime shifts. Rev. Financ. Stud. 2002;15(4):1137–1187. [Google Scholar]
- Ang A., Chen J. Asymmetric correlations of equity portfolios. J. Financ. Econ. 2002;63(3):443–494. [Google Scholar]
- Arouri M.E.H., Jawadi F., Louhichi W., Nguyen D.K. In: Nonlinear Financial Econometrics: Markov Switching Models, Persistence, and Nonlinear Cointegration. Gregoriou G.N., Pascalau R., editors. Palgrave Macmillan; London: 2011. Nonlinear shift contagion modeling: further evidence from high-frequency stock data. [Google Scholar]
- Baba Y., Engle R..., Kraft E., Kroner K.F. Multivariate simultaneous generalized arch. Econ. Theory. 1995;11(1):122–150. [Google Scholar]
- Bashir U., Yu Y., Hussain M., Zebenede G. Do foreign exchange and equity markets co-move in Latin American region? Detrended cross-correlation approach. Physica A. 2016;462:889–897. [Google Scholar]
- Bollerslev T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986;31:307–327. [Google Scholar]
- Dungey M., Gajurel D. Equity market contagion during the global financial crisis: evidence from the world’s eight largest economies. Econ. Syst. 2014;23(2):161–177. [Google Scholar]
- Engle R., Shepard K. Dynamic conditional correlation – a simple classs of multivariate GARCH models. J. Bus. Econ. Stat. 2002;42(1):231–265. [Google Scholar]
- Forbes K.J., Rigobon R. No contagion, only interdependence: measuring stock market comovements. J. Financ. 2002;57(5):1–17. [Google Scholar]
- Garman M.B., Klass M.J. On the estimation of security price volatilities from historical data. J. Bus. 1980;53(1):67–78. [Google Scholar]
- Granger C.W.J., Teräsvirta T. Oxford University Press; New York: 1993. Modeling Nonlinear Economic Relationships. [Google Scholar]
- Guedes E., Brito A., Filho O., Fernandez B.F., de Castro A., Filho d.S., Zebende G. Statistical test for ΔρDCCA: methods and data. Data Brief. 2018;18:795–798. doi: 10.1016/j.dib.2018.03.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guedes E., Brito A., Filho O., Fernandez B.F., de Castro A., Filho D.S., Zebende G. Statistical test for ΔρDCCA cross-correlation coefficient. Physica A: Stat. Mech. Appl. 2018;501:134–140. [Google Scholar]
- Hussain M., Zebende G.F., Bashir U., Donghong D. Oil price and exchange rate co-movements in Asian countries: detrended cross-correlation approach. Physica A. 2017;465:338–346. [Google Scholar]
- Jin X., An X. Global financial crisis and emerging stock market contagion: a volatility impulse response function approach. Res. Int. Bus. Finance. 2016;36:179–195. [Google Scholar]
- Kenourgios D., Dimitriou D. Contagion of the global financial crisis and the real economy: a regional analysis. Econ. Model. 2015;44:283–293. [Google Scholar]
- Kristoufek L. Detrending moving-average cross-correlation coefficient: measuring cross-correlations between non-stationary series. Physica A. 2014;406:169–175. [Google Scholar]
- MacKinlay A. Event studies in economics and finance. J. Econ. Lit. 1997;XXXV(1):13–39. [Google Scholar]
- Mohti W., Dionísio A., Vieira I., Ferreira P. Financial contagion analysis in frontier markets: evidence from the US subprime and the Eurozone debt crises. Physica A. 2019;525:1388–1389. [Google Scholar]
- Okorie D.I. Could stock hedge Bitcoin risk(s) and vice versa? Digit. Finance. 2019:1–20. doi: 10.1007/s42521-019-00011-0. [DOI] [Google Scholar]
- Okorie D.I., Lin B. Crude oil price and cryptocurrencies: evidence of volatility connectedness and hedging strategy. Energy Econ. 2020 doi: 10.1016/j.eneco.2020.104703. [DOI] [Google Scholar]
- Park C.-Y., Shin K. Contagion through National and Regional Exposures to Foreign Banks during the Global Financial Crisis. J. Financ. Stab. 2020;46 [Google Scholar]
- Paulo, H., Carlos, M. & Isabel, V. (2008). Contagion effects of the US subprime crisis on developed countries. CEFAGE-UE Working Papers 2008_08, University of Evora, CEFAGE-UE (Portugal)., 1–22.
- Peng C.-.K., Buldyrev S.V., Havlin S., Simons M., Stanley H.E., Goldberger A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E. 1994;49(2):1685–1689. doi: 10.1103/physreve.49.1685. [DOI] [PubMed] [Google Scholar]
- Podobnik B., Stanly E. Detrended cross-correlation analysis: a new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008:1–11. doi: 10.1103/PhysRevLett.100.084102. [DOI] [PubMed] [Google Scholar]
- Podobnik B., Horvatic D., Petersen A.M., Stanley H.E. Cross-correlations between volume change and price change. Proc. Natl. Acad. Sci. U.S.A. 2009;106(52):22079–22084. doi: 10.1073/pnas.0911983106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podobnik B., Jiang Z.-Q., Zhou W.-X., Stanley H.E. Statistical tests for power-law cross-correlated processes. Phys. Rev. E. 2011;84 doi: 10.1103/PhysRevE.84.066118. [DOI] [PubMed] [Google Scholar]
- Podobnik B., Wang D., Horvatic D., Grosse I., Stanley H.E. Time-lag cross-correlations in collective phenomena. Europhys. Lett. Assoc. 2010;90(6):68001. [Google Scholar]
- Scheicher M. The comovements of stock markets in Hungary, Poland, and the Czech Republic. Int. J. Finance Econ. 2001;6(1):27–39. [Google Scholar]
- Teräsvirta T. Specification, estimation and evaluation of smooth transition autoregressive models. J. Am. Stat. Assoc. 1994;89(425):208–218. [Google Scholar]
- Teräsvirta T., Anderson H.M. Characterizing nonlinearities in business cycles using smooth transition autoregressive models. J. Appl. Econ. 1992;7(S):119–136. [Google Scholar]
- Tong H. Oxford University Press; Oxford: 1990. Nonlinear Time Series: A Dynamical System Approach. [Google Scholar]
- Tong H., Lim K.S. Threshold autoregression, limit cycles, and cyclical data. J. R. Stat. Soc. 1980;42(B):245–292. [Google Scholar]
- Tsay R. Testing and modelling threshold autoregressive processes. J. Am. Stat. Assoc. 1989;84(405):231–240. [Google Scholar]
- Vandewalle N., Ausloos M. Crossing of two mobile averages: a method for measuring the roughness exponent. Phys. Rev. E. 1998;58(5):6832. [Google Scholar]
- Wang G.-J., Xie C., Lin M., Stanley H.E. Stock market contagion during the global financial crisis: a multiscale approach. Finance Res. Lett. 2017;22:163–168. [Google Scholar]
- Wang Y., Wei Y., Wu C. Cross-correlations between Chinese A-share and B-share markets. Physica A. 2010;389:5468–5478. [Google Scholar]
- Zebende G. DCCA cross-correlation coefficient: quantifying level of cross-correlation. Physica A. 2011;390(4):614–618. [Google Scholar]
- Zebende G., Brito A., Filho A., Castroe A. ρDCCA applied between air temperature and relative humidity: an hour/hour view. Physica A. 2018;494:17–26. [Google Scholar]
- Zhang N., Lin A., Yang P. Detrended moving average partial cross-correlation analysis on financial time series. Physica A. 2020;542 [Google Scholar]
- Zhao X., Shang P., Huang J. Several fundamental properties of DCCA cross-correlation coefficient. Fractals. 2017;25(2) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.