Dynamics and functional diversity of the smallest phytoplankton on the Northeast US Shelf

Significance

Approximately half of the world’s primary production is carried out by marine phytoplankton, of which the picoeukaryotes are a diverse and understudied group. Here, we report on a phytoplankton community we have been monitoring over many years to gain insight into factors that drive their dynamics. We found that the picoeukaryotes reproduce and are lost (probably via grazing) much more rapidly than other picophytoplankton. They appear to be a preferred prey item of the micrograzer community and so contribute more to the region’s primary productivity than would be inferred from their abundance alone. This work improves our understanding of the economically important Northeast US Shelf ecosystem and highlights the possible limitations of treating the picoplankton as a single functional group.

Abstract

Picophytoplankton are the most abundant primary producers in the ocean. Knowledge of their community dynamics is key to understanding their role in marine food webs and global biogeochemical cycles. To this end, we analyzed a 16-y time series of observations of a phytoplankton community at a nearshore site on the Northeast US Shelf. We used a size-structured population model to estimate in situ division rates for the picoeukaryote assemblage and compared the dynamics with those of the picocyanobacteria Synechococcus at the same location. We found that the picoeukaryotes divide at roughly twice the rate of the more abundant Synechococcus and are subject to greater loss rates (likely from viral lysis and zooplankton grazing). We describe the dynamics of these groups across short and long timescales and conclude that, despite their taxonomic differences, their populations respond similarly to changes in the biotic and abiotic environment. Both groups appear to be temperature limited in the spring and light limited in the fall and to experience greater mortality during the day than at night. Compared with Synechococcus, the picoeukaryotes are subject to greater top-down control and contribute more to the region’s primary productivity than their standing stocks suggest.

Marine picophytoplankton impact global biogeochemical cycles and form the foundation of many marine food webs (1, 2). While this size class is often treated as a single functional group, it is taxonomically diverse, consisting of the cyanobacteria (Prochlorocococcus and Synechococcus) and the picoeukaryotes (e.g., Micromonas and Ostreococcus). Understanding the ecological significance of this diversity, however, requires knowledge of community dynamics and vital rates. Compared with cyanobacteria, the picoeukaryotes are less numerous, more taxonomically heterogeneous, and consequently less well understood. Despite their lower abundance, picoeukaryotes can dominate primary productivity in some regions because of their capacity for rapid cell growth and division (3, 4). Here, we report on our analysis of a 16-y time series of observations of a coastal phytoplankton community, including estimates of division rates, loss rates, and primary productivity for the picoeukaryote assemblage.

While cells in a laboratory may be contained, counted, and observed, monitoring natural populations of marine phytoplankton presents added challenges. The number of picoeukaryotes produced and grazed in a single day can far exceed the standing stock of the population (4). It is therefore difficult to partition changes in abundance into growth and loss processes. Sosik et al. (5) developed a method for estimating division rate independently of cell number by fitting a size-structured matrix model to frequent observations of cell size distribution. This method has successfully been applied to natural populations of well-defined phytoplankton groups, including Synechococcus (6), Prochlorococcus (7, 8), and some dinoflagellates (9).

We adapted the model described in Hunter-Cevera et al. (6) in order to apply it to the assemblage of small eukaryotes present at the Martha’s Vineyard Coastal Observatory (MVCO; $41^{○}$ 19.500′ N, $70^{○}$ 34.0′ W). These eukaryotes can be identified with flow cytometry based on their individual cell traits, including pigmentation and size. Traditionally, only cells with diameters less than 2 $\mathrm{\mu }$m are considered picoplankton. Imposing this arbitrary threshold on our data, however, would exclude the tail of the observed size distribution at times of day and year when cells tend to be largest (SI Appendix, Figs. S1F and S2). To ensure that we capture the entire distribution, we chose to include in our analysis all eukaryotes with diameters less than approximately 8 $\mathrm{\mu }$m. This is a conservative upper threshold; very few cells approach this size (SI Appendix, Fig. S2). Since more than $80\%$ of these cells ($\sim 87\%$ in the summer) are less than 2 $\mathrm{\mu }$m in diameter, we will refer to this community as the picoeukaryotes throughout this paper.

Our population model allows for transitions between size classes through cell growth and division (Materials and Methods). The probability of a cell growing depends on the light availability, and the probability of a cell dividing depends on the cell’s size. Observations of Synechococcus led Hunter-Cevera et al. (6) to prohibit division in the first 6 h after dawn in their model. In contrast, the picoeukaryote size distribution frequently exhibits decreases in cell size after dawn, suggesting division early in the day. We therefore relaxed the constraint, making the division function in our model independent of time within a day. We evaluated our method against a standard laboratory technique for estimating division rate (Model Validation) and found that the agreement between the two methods was improved by this change.

We then applied our model to observations of picoeukaryotes at MVCO, a dynamic location within the Northeast US Shelf Long-Term Ecological Research (NES-LTER) site. This observatory is open to advection from the broader continental shelf system, which undergoes dramatic seasonal change and has been warming in recent years (10). The region is home to an economically important ecosystem that relies on phytoplankton as the primary producers. It is therefore critical to understand the structure of this plankton community and in particular, how it responds to changes in the physical environment. The environmental variability in this region as well as the scope and resolution of our observations make MVCO a valuable location to study picophytoplankton ecology. Comparative work will be necessary to determine whether our conclusions about the picophytoplankton at MVCO hold throughout their range.

Here, we describe diel, seasonal, and interannual patterns in picoeukaryote dynamics and compare them with those of Synechococcus at the same location. Our analysis reveals similarities in the responses of these populations to their shared environment—but also surprising differences in the ecological roles of these two picoplankton groups.

Results

Model Validation.

To ensure that our method can accurately estimate picoeukaryote division rate, we first applied it to observations from a dilution series experiment. The dilution series is a standard technique for estimating division and grazing rates by comparing phytoplankton growth in a sample of seawater with that in a sample that has been diluted with filtered water (11). Theory suggests that diluting a sample increases the distance between organisms in the bottle and so effectively reduces grazing pressure on the phytoplankton. From the difference in net growth rate across the treatments, one can infer what the growth rate would be in the absence of grazers—approximately the division rate. We applied the model to flow cytometric observations of the picoeukaryote cells within both the undiluted and most diluted seawater samples. We evaluated our method using the concordance correlation coefficient (12). This statistic accounts for both precision and accuracy, with one corresponding to perfect agreement and zero corresponding to no agreement. Application of the model to the undiluted and diluted bottles led to concordance correlation coefficients with the dilution series method of 0.719 and 0.894, respectively. Details of the experimental work are presented in Hunter-Cevera et al. (6). While there is reason to doubt the generality of division rates measured in incubations (13–15), it is reassuring to see that our model produced estimates that agree with those obtained through direct counts of cells in a contained system (SI Appendix, Fig. S3A).

Note that the division rate estimates derived from our model depend on changes in cell size distribution rather than changes in cell counts. Moreover, the model assumes that the size distribution is only altered through cell growth and division. This assumption could be violated if there are size-dependent loss processes, such as size-selective sinking or grazing. With this concern in mind, we compared the division rates estimated for the samples in diluted and undiluted experimental treatments (SI Appendix, Fig. S3B). We found no evidence of a systematic difference in the estimates produced by the model across the two treatments, indicating that grazing does not have a detectable effect on the size distribution. However, we cannot be certain that size-dependent losses do not arise in picoeukaryote populations at other times of year or in situ.

Seasonality.

The assemblage of picoeukaryotes at MVCO exhibits a pronounced seasonal cycle (Fig. 1). Division rate is lowest in February ($\sim$0.1 ${\mathrm{d}}^{-1}$) and increases steadily from April to a peak in August ($\sim$2.1 ${\mathrm{d}}^{-1}$), before declining to winter values again. These striking differences in daily division rate are reflected in the range of diel patterns in community size distribution. On winter days, the size distribution remains relatively constant. In summer, the distribution shifts toward larger cell sizes during daylight hours and then drops back toward the initial distribution before dawn. Our model is able to reproduce the range of distributions and diel dynamics observed in this picoeukaryote community throughout the year (SI Appendix, Fig. S1).

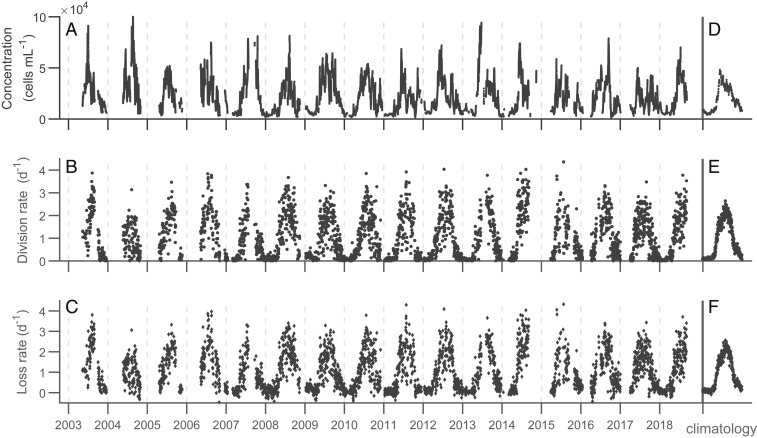
Fig. 1.

Daily measurements between 2003 and 2018. (A) Cell concentration is a 48-h running average. (B) Division rate is computed by comparing initial and final population sizes in each day’s simulation, and (C) loss rate is calculated by subtracting the observed net growth rate from the division rate. (D–F) Climatological values are the averages for each day of the year across all years in the time series. Only dates with at least 23 h of FlowCytobot observations are included in this analysis (n = 3,200).

The concentration of picoeukaryotes at MVCO rises from $\sim$300 cells ${\mathrm{m}\mathrm{L}}^{-1}$ in the winter to $\sim$50,000 cells ${\mathrm{m}\mathrm{L}}^{-1}$ in June. In the climatologies, peak cell concentration precedes peak division rate by 60 d (Fig. 2). Estimated daily division rates typically far exceed the corresponding daily changes in population size. For the entire time series, the daily net growth rate remains near zero with an SD of 0.16 ${\mathrm{d}}^{-1}$. The loss rate, therefore, follows a seasonal cycle as well, remaining tightly coupled to division rate throughout the year (Fig. 1 B and C).

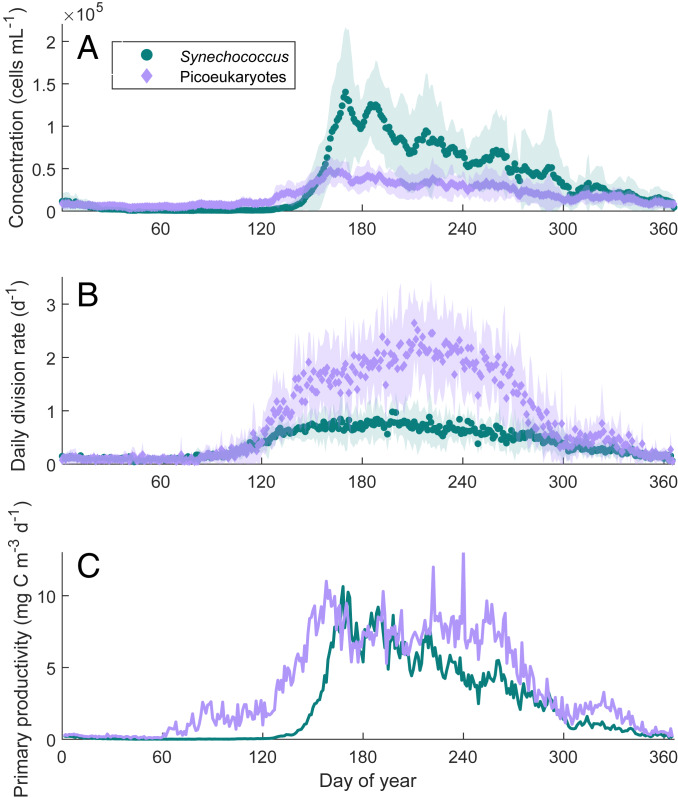
Fig. 2.

Comparison of seasonal cycles in (A) concentration, (B) division rate, and (C) primary productivity for picoeukaryotes and Synechococcus. In the late winter (year days 20 to 130), picoeukaryotes are more abundant on average than Synechococcus, but they become drastically outnumbered in the summer, even as picoeukaryote division rate continues to climb. Values plotted are climatological averages for the 16-y time series. Shaded regions are within 1 SD of the mean. Values of primary productivity for Synechococcus are those reported in ref. 16, with the maximum estimate for carbon-to-volume ratio of 290 fg C $\mathrm{\mu }{\mathrm{m}}^{-3}$. Note that changes in cell concentration govern the pattern in primary productivity for Synechococcus but not for the picoeukaryotes.

We also discovered an annual pattern in cell size distribution (SI Appendix, Fig. S4). Picoeukaryote cells tend to be smaller during the summer months (cell volume $\sim$0.5 $\mathrm{\mu }$m³) and larger in the late fall (cell volume $\sim$1.75 $\mathrm{\mu }$m³). While we cannot determine whether this pattern reflects a physiological response or a change in community composition, there is a negative relationship between mean cell size and daily division rate in the picoeukaryotes. The size distribution of the small eukaryote community is usually unimodal but is frequently bimodal in March to early April (mean cell volumes $\sim$1 and 16 $\mathrm{\mu }$m³) (SI Appendix, Figs. S1A and S2), a feature that our model captures (SI Appendix, Fig. S1D).

From these seasonal patterns in cell size, cell concentration, and division rate, we can estimate the annual pattern in picoeukaryote primary productivity at MVCO. Following Hunter-Cevera et al. (16), we first calculated the product of the climatological division rate, cell concentration, and cell volume (here, we used the minimum value attained by the mode of the population size distribution on any given day). We then multiplied this product by an approximate carbon-to-volume ratio of 238 fg $\mathrm{\mu }{\mathrm{m}}^{-3}$, as measured for Micromonas pusilla by DuRand et al. (17). From values near zero in the winter, picoeukaryote primary productivity rises dramatically in the spring and maintains a roughly steady rate of 8 mg C ${\mathrm{m}}^{-3}\hspace{0.17em}{\mathrm{d}}^{-1}$ between June and August (Fig. 2C). This rate corresponds to 18% of the total primary productivity for the region, based on summer average estimates obtained from the MARMAP program (18, 19). Picoeukaryote productivity is nearly equal to that of Synechococcus when the latter is in bloom but is greater throughout most of a typical year (Fig. 2C).

Diel Patterns.

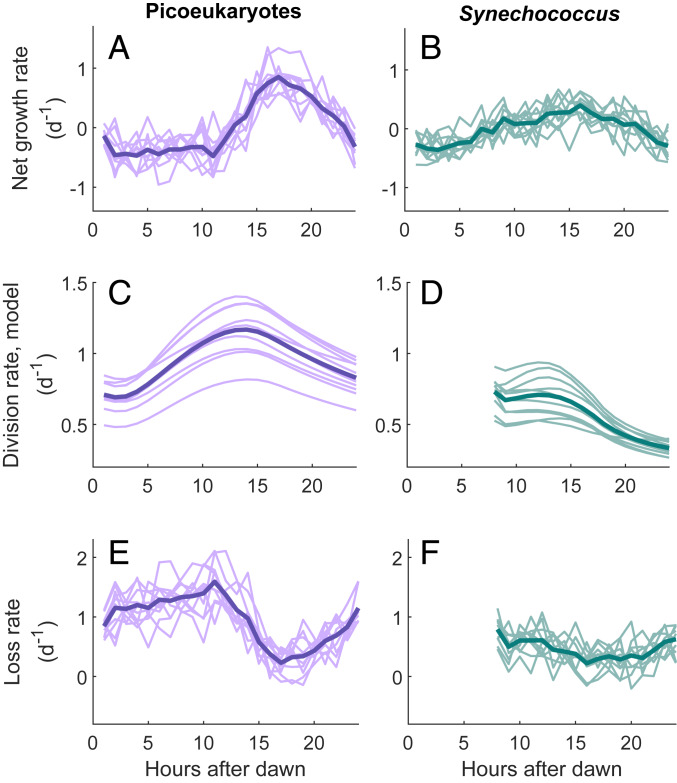
Thanks to the high temporal resolution of our data, we were also able to uncover patterns in vital rates at a subdaily scale. Although our validation process only examined daily division rates for the picoeukaryotes, previous work has shown good correspondence between hourly division rates from the model and cell cycle-based estimates for the picoplankter Prochlorococcus (7). Hourly changes in cell concentration at MVCO indicate that, on average, picoeukaryote concentration decreases during the day and increases at night (Fig. 3A). Comparison with our estimates of hourly division rate suggests that this net population growth at night coincides with a sudden decrease in cell loss rate between 10 and 15 h after dawn (Fig. 3E). The same pattern is observed in the picoeukaryotes for every year examined. In the Synechococcus population, we see a similar although less dramatic pattern whereby net growth rate rises gradually throughout the day to a peak value in the evening (Fig. 3B). For both groups, these patterns are most evident at times of year when daily division and loss rates are highest (summer and fall) (SI Appendix, Fig. S5). In the winter, when daily division rate is low, the hourly rates of picoplankton net growth, division, and loss are all roughly zero throughout the day.

Fig. 3.

Hourly rates of (A and B) net growth, (C and D) division, and (E and F) loss for the picoeukaryote and Synechococcus populations. Each curve represents a distinct year, and hourly values are averaged across all days of the year. Years with fewer than 180 d of data (2003 to 2006, 2014 to 2015) are excluded. Each bold line is the average across all years considered. Picoeukaryotes exhibit consistently higher rates of net growth at night than during the day, corresponding to a decrease in loss rate. A similar pattern with lower amplitude is apparent for Synechococcus. Note that the Synechococcus model from Hunter-Cevera et al. (20) excludes the first 6 h after dawn.

Discussion

Abiotic Controls.

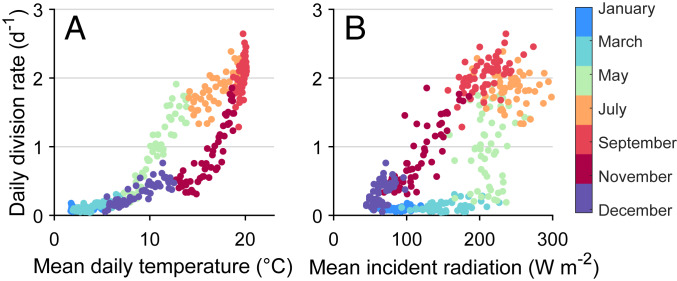
The picoeukaryotes are a complex assemblage of taxonomically diverse plankton, yet we have identified patterns in their community composition and vital rates over a variety of timescales. Most notably, concentration and division rate are highest in the summer and lowest in the winter. Such seasonality is typical of picophytoplankton in temperate climates, as cell division can be limited by low temperatures (6, 21). For the picoeukaryotes, daily division rate increases with increasing temperature between March and July (Fig. 4A). This relationship suggests that the picoeukaryote population growth is temperature limited during that period. Division rate on fall days is noticeably lower than on spring days at the same temperatures, indicating another limiting factor.

Fig. 4.

Relationship between daily picoeukaryote division rate, (A) temperature, and (B) incident solar radiation. Values plotted are climatological averages for each day of the year across all years in our time series.

The relationship between division rate and sunlight availability (Fig. 4B) neatly complements that between division rate and temperature. Between August and December, division rate decreases linearly as daily radiation drops. It is likely that sunlight availability is responsible for the steady decrease in division rate observed in the fall and at least partially responsible for the decline in picoeukaryote concentration observed over the same period (Fig. 2A). It is important to note that because our data cannot identify individual species, changes in division rate may not correspond to physiological responses within a species. Instead, the seasonal changes we observe might reflect seasonal shifts in community composition. It is arguably all the more noteworthy that this diverse assemblage exhibits systematic responses to changes in temperature and sunlight. Moreover, these patterns are very similar to those of the taxonomically distinct Synechococcus observed with the same methods (6, 16). Division in these two picoplankton groups appears to be temperature limited in the spring and light limited in the fall.

If division rate is limited by temperature in the spring, we expect the timing of the annual spring bloom to depend on water temperature. Synechococcus, which can exhibit up to a 1,000-fold increase in concentration during the bloom, blooms earlier during warmer springs and later during cool springs (20). Because the small eukaryotes do not exhibit as dramatic a change in concentration, it is difficult to discern a trend in the timing of their bloom. We have, however, observed an annual change in the cell size distribution. Each spring, the small eukaryotes initially span a wide range of cell sizes, then undergo a transition to an assemblage that is dominated by cells less than 2 $\mathrm{\mu }$m (SI Appendix, Fig. S2). The timing of this transition appears to relate to temperature in the same way that the timing of the Synechococcus bloom does (SI Appendix, Fig. S6). That is, warmer springs correspond to earlier changes in picoeukaryote community composition. We do not yet know what species dominate the assemblage either before or after the transition.

Biotic Controls.

On summer days, the picoeukaryotes at MVCO appear to experience minimal resource limitation. Daily division rate is more variable in the summer than in the winter, but the magnitude of the estimates reported here is bound to surprise some plankton ecologists. The picoeukaryotes at MVCO are dividing at rates comparable with some of the highest rates reported for the group in culture and incubation experiments [1.78 ${\mathrm{d}}^{-1}$ (22), 2.43 ${\mathrm{d}}^{-1}$ (23), 3.36 ${\mathrm{d}}^{-1}$ (24)]. Notably, our estimates of picoeukaryote division rate in the summer are approximately twice those estimated for Synechococcus (20). This difference in division rate is consistent with the results of our dilution series experiments as well, where division rates were on average 2.5 times higher for picoeukaryotes than for Synechococcus in the same bottle (SI Appendix, Table S1). In the climatology, division rates for the two groups are well aligned for the first 120 d of the year, but as the Synechococcus division rate plateaus, the picoeukaryotes continue to divide more rapidly for another 100 d (Fig. 2). Despite these continued high and increasing division rates, the picoeukaryote population is held in check throughout summer, suggesting significant top-down control. Their high division rates and relatively low net growth indicate that the picoeukaryotes contribute more to primary productivity than their standing stock would suggest. In particular, the annual pattern in picoeukaryote primary productivity reflects large changes in division rate and cell size, so it is not as closely aligned with cell concentration as that of Synechococcus (Fig. 2 A and C).

Synechococcus can be up to 10 times more abundant than the picoeukaryotes at MVCO during summer. Given their relative scarcity, the picoeukaryotes seem to be strongly preferred by the grazer community. This hypothesis is supported by the results of our dilution series experiments, where picoeukaryotes suffered higher grazing rates than Synechococcus in all incubations (SI Appendix, Table S1), as well as by laboratory results that suggest that Synechococcus is a poor-quality food source (25).

Since picoeukaryote cell concentration remains relatively constant on short timescales (e.g., days), one would expect daily division and loss rate to be similar in magnitude. Indeed, there is a seasonal change in loss rate that closely tracks the annual pattern in division rate (Fig. 1). This tight coupling is consistent with theory and observations of other picophytoplankton communities (26–28). It also supports our assumption that calculated loss rates can be attributed primarily to biological causes rather than advection or spatial patchiness, since it is unlikely that loss due to physical processes would be correlated with division rate.

The main biological drivers of loss in picoplankton are microzooplankton grazing and viral lysis (29–31). Picoeukaryote mortality from viral lysis has been observed to range widely (0 to 100%), with some evidence that the smallest picoeukaryotes may be more susceptible to viral lysis than other picophytoplankton (31). A meta-analysis of dilution series experiments found that phytoplankton division rate is positively correlated with loss rate from viral lysis (32). It seems likely then that increased loss rate in the summer is at least in part due to an increase in viral lysis. Grazing rates are also generally higher in summer (26, 33). As in the dilution experiments, higher concentrations of phytoplankton can lead to increased contact rates and more grazing per predator. There can be seasonal fluctuations in predator population size and activity (34), and microzooplankton growth rates have been seen to roughly match those of their phytoplankton prey (27). Whether phytoplankton mortality is due to lysis or grazing has important implications for the fate of carbon produced, but our methods cannot distinguish between these two pathways.

Because our dilution experiments were conducted in June and October, they did not include the period during which in situ picoeukaryote division and loss rates are highest. It is interesting to note that, in these experiments, the highest model-derived division rate estimates are from undiluted bottles. One of the assumptions of the dilution series method is that phytoplankton division rate is independent of dilution, while mortality is proportionately affected by dilution. However, recent work suggests that diluting a sample of seawater may inhibit the growth of the phytoplankton, including picoeukaryotes (35). Stoecker et al. (15) found that the preparation of filtrate results in the release of polyunsaturated aldehydes, which negatively affect phytoplankton growth rate. Weinbauer et al. (14) suggested that picophytoplankton may even be stimulated in undiluted bottles due to nutrient cycling through grazing and lysis. Lastly, the work of Morris and colleagues (13, 36) suggests that leakiness in picoplankton’s resource production can result in shared resources and “accidental” mutualisms, the benefits of which would be reduced in a more diluted sample. If dilution does indeed have an effect on the growth of picoeukaryotes, it would mean that previous studies may have underestimated their natural division rate. These findings emphasize the importance of in situ work and the need to continue developing incubation-free approaches like ours.

Timing of Growth and Loss.

One question raised by the high-division rate estimates reported here is that of timing. A continuous division rate of 3 ${\mathrm{d}}^{-1}$ corresponds to approximately four divisions over the course of 24 h. Observations of picoeukaryotes in culture and in the field suggest that division primarily occurs in the first few hours after dark (37). At MVCO, the diel patterns in size distribution can show dramatic decreases in mode cell size (e.g., from 1.74 to 0.57 $\mathrm{\mu }$m³ in SI Appendix, Fig. S1C). Taken together, this information might lead us to believe that individual cells are more than doubling in size during the day and then dividing rapidly in succession in the evening. However, this scenario is unlikely given current knowledge of cell division in eukaryotic phytoplankton, which is that mitosis and DNA synthesis occur in distinct phases separated by gaps (38). Additionally, the model simulations are able to match the observed daily dynamics even though the division function (Eq. 1, Materials and Methods) does not depend on sunlight availability. That is, division in our simulations occurs throughout the day, yet division rate is still highest in the early evening. This is because, by construction, division will peak when the majority of cells are at larger volumes, and in practice, mean cell size is largest after a full day of sunlight. The consistent timing of division in the picoeukaryotes, therefore, may not be the result of any environmental cue or circadian clock, but instead, the picoeukaryotes might divide at sunset simply because that is when the cells are largest. Our work demonstrates that this mechanism could explain the pattern observed across the diversity of picoeukaryotes, but experimental work would be necessary to directly test the hypothesis. Note that our estimates of hourly division rate, as opposed to daily division rate, have not yet been validated with experimental methods.

Several studies have looked for diel patterns in picoplankton abundance (7, 39, 40). Consistent patterns are hard to discern over short periods of time, however, especially in coastal environments or for taxa that are less abundant (41, 42). At MVCO as well, cell concentrations are variable and noisy, such that diel patterns only become clear after we average over many days. The resulting pattern in net growth rate varies surprisingly little from year to year (Fig. 3A).

Changes in abundance are the result of changes in both division and loss rate, and our analysis indicates that loss rate at MVCO is on average higher during the day than at night (Fig. 3E). Many microzooplankton exhibit diel patterns in grazing activity, whether due to light stimulation (43) or internal circadian rhythms (44). This behavior is not consistent across species, however, and different studies have reported increased (45–47) and decreased (48–50) grazing rates during the day. If the majority of grazers at MVCO are more active during the day than at night, it could explain the loss pattern we observe. The fact that the magnitude of the pattern in loss is greater for picoeukaryotes than for Synechococcus would then be consistent with the idea that grazers have a stronger effect on the picoeukaryotes.

Alternatively, the same pattern in loss could arise from viral lysis. Brown et al. (51) found that photosynthetic activity was required for a particular virus to lyse the picoeukaryote M. pusilla. Other viruses, however, are destroyed or rendered less infective by ultraviolet radiation (52, 53), and still others have been shown to not be light dependent (54). The diel patterns in picoplankton net growth rates warrant further investigation to determine their causes and their implications for carbon export.

Conclusions

The abundance, community composition, and vital rates of the picophytoplankton at the NES-LTER MVCO site exhibit systematic changes over periods ranging from hours to many years. Here, we have analyzed 3,200 days of in situ observations, spanning 16 years in a highly variable environment. From this dataset, we are able to discern and describe in detail the behavior of the picoplankton community over short and long timescales. Relative to their standing stock, the picoeukaryotes contribute disproportionately to the region’s primary productivity throughout the time series. Compared with Synechococcus, they are capable of extremely rapid division and seem to be a preferred prey item of the micrograzer community.

Despite these differences, the concentration trajectories of picoeukaryotes and Synechococcus at MVCO share many features throughout our time series (Fig. 2 and SI Appendix, Fig. S7). While there are noticeable periods of time when synchrony is not evident, the picoeukaryote population typically increases and decreases at the same time as that of Synechococcus. We interpret this synchrony to be a result of the two groups’ similar responses to abiotic conditions. Warm sunny days that support the growth of cyanobacteria also support picoeukaryote growth. Conversely, poor environmental conditions lead to less population growth in both groups. Thus, even with different vital rates, grazers, and population sizes, the two communities roughly track one another in terms of their changes in concentration. For this reason, it is reasonable to model the picophytoplankton as a single group in many scenarios. If one is interested, however, in the role that organisms play in their ecosystem or the transfer of carbon through the food web, our work illustrates that the picoeukaryotes and cyanobacteria have striking differences.

Materials and Methods

Data Collection.

The MVCO offshore tower is the inner shelf study site of the NES-LTER. Observations were made by two autonomous submersible flow cytometers, FlowCytobots, which have been alternately deployed at the MVCO offshore tower since 2003. The resulting time series includes hourly records of cell concentrations as well as light scattering and fluorescence of individual cells. These signals can be used in combination to identify Synechococcus and the picoeukaryotes and to estimate cell volumes. Olson et al. (55) has details on FlowCytobot design and operation. FlowCytobot data were processed according to methods described in Sosik et al. (5). Environmental data were also collected from MVCO, including water temperature recorded by MicroCat conductivity, temperature, and pressure sensor and incident short-wave radiation recorded by an Eppley pyranometer at the MVCO meteorological mast ($41^{○}$ 20.996′ N, $70^{○}$ 31.60′ W). Short gaps in the environmental data were filled according to the methods described in Hunter-Cevera et al. (16).

Matrix Model.

We use a model to estimate division rate by following the same steps described in Hunter-Cevera et al. (6). Cells are classified into discrete size classes based on the log of their volumes. The probability of a cell dividing in half is assumed to depend only on cell size, and the probability of a cell growing into the next size class is assumed to depend on the immediate light availability. Any cells that do not grow or divide remain in the same size class until the next time step. The volume bins and the size of the time step (10 min) were chosen so that cells could be expected to undergo only one transition at a time. We use 66 volume bins, ranging from 0.03 to 256 $\mathrm{\mu }$m³, to accommodate the range of small eukaryotes observed at MVCO. The transition matrix is a function of time, $t$, and the model parameters, $\mathbf{\theta }$; its structure is summarized in SI Appendix, Fig. S8.

The model we use here differs from that of Hunter-Cevera et al. (6) in two ways. First, we allow the eukaryotes to divide at any time of day. The transition matrix is therefore only indirectly dependent on time of day through the amount of light present. Second, the division function was modified slightly to prohibit the division of cells in the smallest size classes. Hunter-Cevera et al. (6) assumed that cells smaller than twice the minimum size, $v_{min}$, could divide. The two resulting daughter cells would be placed into the smallest size bin. This produces an increase in biomass through division, which, though very small, is physically unreasonable. To prevent this problem, we prohibit division of cells with volume less than $v*$, the volume of the largest size class that is less than $2v_{min}$:

$$\delta \left(i;\mathbf{\theta }\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hspace{0.17em}{v}_i\le v*,\hfill \\ {\delta }_{max}\frac{{\left(v_i-v*\right)}^b}{1+{\left(v_i-v*\right)}^b}\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$$ [1]

Here, $\delta \left(i;\mathbf{\theta }\right)$ is the proportion of cells in size class $i$ that will divide, and $b$ and ${\delta }_{max}$ are elements of the parameter vector, $\mathbf{\theta }$. The growth function we use is the same as that in Hunter-Cevera et al. (6).

As in Hunter-Cevera et al. (6), the model accommodates two distinct populations, each with its own size distribution and growth and division functions. This choice was made in order to accommodate days when the observed cell size distribution is bimodal. On different occasions at MVCO, we see the fit model describe 1) two relatively distinct populations (SI Appendix, Fig. S9), 2) two populations with overlapping size distributions (SI Appendix, Fig. S10), or 3) one clear population and a second widely distributed population, which may account for background noise (SI Appendix, Fig. S11). While the two-population construct does not represent the actual diversity of the picoeukaryote assemblage, it is sufficient to capture the cell size distributions we observe.

The dynamics of the two populations are simulated simultaneously, and the sum of the two size distributions at each hour is used to define the probability vector in a Dirichlet-multinomial distribution. The model has 14 parameters in total. For each day, we fit the model to the observed size distributions by finding a maximum likelihood estimate for $\mathbf{\theta }$. When fit to simulated data, our model correctly identifies each of the subpopulation’s growth and division functions (SI Appendix, Figs. S9–S11).

Given the vector of most likely parameters and the observed solar radiation, we use the matrix model to project our simulated populations forward for one full day. We then use the simulated cell concentrations at 0 and 24 h to calculate the daily division rate for the assemblage. Daily net growth rates are calculated similarly from smoothed cell concentration observations. We used a 48-h running mean in order to reduce tidal effects and noise. Because our model does not include any cell mortality, we then compare the estimated division rate with the observed net growth rate and take the difference to be the loss rate for the assemblage.

Data and Code Availability.

All MATLAB scripts for the division rate model as well as the data presented in this manuscript are available online (56).