Global increase in major tropical cyclone exceedance probability over the past four decades

Significance

Tropical cyclones (TCs), and particularly major TCs, pose substantial risk to many regions around the globe. Identifying changes in this risk and determining causal factors for the changes is a critical element for taking steps toward adaptation. Theory and numerical models consistently link increasing TC intensity to a warming world, but confidence in this link is compromised by difficulties in detecting significant intensity trends in observations. These difficulties are largely caused by known heterogeneities in the past instrumental records of TCs. Here we address and reduce these heterogeneities and identify significant global trends in TC intensity over the past four decades. The results should serve to increase confidence in projections of increased TC intensity under continued warming.

Abstract

Theoretical understanding of the thermodynamic controls on tropical cyclone (TC) wind intensity, as well as numerical simulations, implies a positive trend in TC intensity in a warming world. The global instrumental record of TC intensity, however, is known to be heterogeneous in both space and time and is generally unsuitable for global trend analysis. To address this, a homogenized data record based on satellite data was previously created for the period 1982–2009. The 28-y homogenized record exhibited increasing global TC intensity trends, but they were not statistically significant at the 95% confidence level. Based on observed trends in the thermodynamic mean state of the tropical environment during this period, however, it was argued that the 28-y period was likely close to, but shorter than, the time required for a statistically significant positive global TC intensity trend to appear. Here the homogenized global TC intensity record is extended to the 39-y period 1979–2017, and statistically significant (at the 95% confidence level) increases are identified. Increases and trends are found in the exceedance probability and proportion of major (Saffir−Simpson categories 3 to 5) TC intensities, which is consistent with expectations based on theoretical understanding and trends identified in numerical simulations in warming scenarios. Major TCs pose, by far, the greatest threat to lives and property. Between the early and latter halves of the time period, the major TC exceedance probability increases by about 8% per decade, with a 95% CI of 2 to 15% per decade.

During the lifetime of a tropical cyclone (TC), intensity (i.e., the magnitude of the surface winds) is modulated by a number of environmental factors. The maximum intensity that a TC can achieve is dictated by its ambient “potential intensity,” which is based on the thermodynamic state of the ambient environment (1). Other factors such as ambient vertical wind shear can inhibit a TC from reaching its potential intensity (2–4), but an increase in mean potential intensity is expected to manifest as an increase in mean measured intensity if these other factors remain unchanged (5, 6). Potential intensity has been increasing, in general, as global mean surface temperatures have increased (1, 7), and there is an expectation that the distribution of TC intensity responds by shifting toward greater intensity (8). In this case, positive trends should manifest in mean TC intensity, but are expected to be proportionally greater at the higher intensity quantiles (7, 9). This expectation is borne out in numerical simulations and projections (10). Testing this expectation with observations, however, is problematic because the instrumental record of TC intensity, known as the “best-track” record, is heterogeneous in time and by region (11–14).

To address the heterogeneities in the best-track data, a new global record of intensity was previously constructed (7) by applying a well-known intensity estimation algorithm (the advanced Dvorak Technique, or ADT) (15, 16) to a globally homogenized record of geostationary satellite imagery (the Hurricane Satellite record, or HURSAT) (17, 18). The original version of the ADT-HURSAT record spanned the 28-y period 1982–2009. Global trend analyses using quantile regression on these data provided two key results: 1) There were positive trends found in most of the quantiles of the intensity distribution, but 2) these trends had not risen to the 95% significance level (figure 6 of ref. 7). During this same 28-y period, positive trends in potential intensity in active TC regions were identified (7), which is consistent with the observed increasing trends in TC intensity (8). To better understand the lack of statistical significance of the observed intensity trends, an idealized experiment was performed (7) based on the expected intensity changes that might occur in the environment of observed increases in potential intensity (8). The experiment suggested that the observed changes in the mean tropical environment should cause an increase in TC intensity at a rate similar to the observed rate, but there was only about a 50 to 60% probability that the increasing intensity trends would rise to a statistically significant level within a 28-y period. The purpose of this paper is to extend the ADT-HURSAT data record to span the 39-y period 1979–2017 and explore these data to determine whether statistically significant positive global trends have yet emerged in this extended period of data.

Results

Development of the ADT-HURSAT Data.

The Dvorak Technique has served as a fundamental operational tool for estimating TC intensity in all TC-prone regions of the globe for more than 40 y (13, 19–21). The technique utilizes satellite imagery to identify and measure specific features in the cloud presentation of a TC, and relates these to the current intensity of the storm. The technique could be considered a statistical regression- and analog-based algorithm, but it is somewhat subjective because it requires the analyst or forecaster to follow a sequence of steps while making expert judgments at many of the steps. Because of the subjective nature of the technique, different forecasters may introduce biases into the intensity estimates based on their personal perception and interpretation of the Dvorak Technique decision flowcharts and rules. To remove this subjectivity, the fully automated ADT was introduced and presently serves as an important tool for TC forecasters around the world (15, 16).

The ADT is largely based on the “Enhanced Infrared” version of the Dvorak Technique (20), which utilizes infrared brightness temperatures to measure TC features such as cloud-top temperature above the eyewall, which is related to convective vigor, and eye temperature, which is related to the strength of the TC transverse circulation, both of which are related to intensity. The ADT is typically applied to geostationary satellite imagery, which has been measured with increasingly better and higher-resolution sensors since the 1970s (17, 18). In order to create a homogeneous global record of TC intensity, a homogeneous collection of global geostationary satellite imagery known as the HURSAT record was created (7, 17, 18). HURSAT imagery has been resampled to a consistent 8-km spatial resolution and 3-hourly temporal resolution and has been further homogenized through recalibration procedures. A final homogenization step was the removal of data from geostationary satellites that were stationed over and near the 60°E meridian (SI Appendix, Fig. S1). This last step addresses the discontinuity in satellite view angle that was introduced in 1998 when satellites were introduced over an area that was previously devoid of geostationary satellites (7). The ADT algorithm is applied to the global HURSAT data to form the ADT-HURSAT homogenized global record of TC intensity.

Over the period 1979–2017 considered here, there are about 225,000 ADT-HURSAT intensity estimates in about 4,000 individual TCs worldwide. The minimum estimated intensity is 25 kt, and the maximum is 170 kt (SI Appendix, Fig. S2). As discussed in ref. 7, the distributions of intensity and lifetime maximum intensity (LMI) estimates (SI Appendix, Fig. S2) are affected by cases where an eye forms under the dense cirrus cloud that overlies the TC central region but is not evident in the infrared imagery because cirrus is opaque at that wavelength. In these cases, the TC is likely to be intensifying as the eye forms, but the ADT will maintain a more constant intensity. This usually occurs near but below about 65 kt (the minimum threshold for Saffir−Simpson category 1), which projects onto the intensity distribution by increasing the frequencies near but below this threshold. In cases where the eye does eventually appear in the infrared imagery, the ADT will identify an “eye scene” and will begin intensifying the TC. As the intensity estimates increase, eye scenes become more frequent. If an eye never appears in the infrared and no eye scene is identified by the ADT during a TC lifetime, the LMI will more likely be underestimated at an intensity near but below 65 kt, which contributes to the jump in LMI frequency around 65 kt evident in SI Appendix, Fig. S2B.

When comparing all ADT-HURSAT and International Best Track Archive for Climate Stewardship (IBTrACS) intensity estimates (Methods) globally, the spread demonstrates a far-from-perfect fit (SI Appendix, Fig. S3), although, given the known issues with global best-track data (e.g., refs. 12–14), it is not always clear which of the two data records is the more accurate for any particular estimate. Regardless, the key point here is that the ADT-HURSAT record is homogenous in time and by region, whereas the best-track data are not. The ADT-HURSAT record, particularly in light of the fact that it necessarily uses coarse (8 km) resolution satellite data, is not designed to be a substitute for the best track, nor is it designed to be used on a point-by-point or storm-by-storm basis. The ADT-HURSAT should be considered a record that sacrifices some measure of absolute accuracy for homogeneity, and which allows more robust trend analysis.

Changes in TC Intensities over the Past Four Decades.

Over the past 40 y (and longer), anthropogenic warming has increased sea surface temperature (SST) in TC-prone regions (22–24), and, in combination with changes in atmospheric conditions, this has increased TC potential intensity in these regions (7). Based on physical understanding and robust support from numerical simulations, an increase in environmental potential intensity is expected to manifest as a shift in the TC intensity distribution toward greater intensity and an increase in mean intensity. More importantly, the shift is further expected to manifest as a more substantial increase in the high tail of the distribution (6, 9, 25), which comprises the range of intensities that are responsible for the great majority of TC-related damage and mortality (26). Consequently, detection and attribution of past and projected TC intensity changes has often focused on metrics that emphasize changes in the stronger TCs (6, 10, 27, 28), and we will follow that emphasis here. As discussed above, the ADT-HURSAT intensities near but below the minimum 65-kt threshold for a minimal Saffir−Simpson category 1 hurricane are generally less reliable, particularly at times when a developing eye is obscured under the TC cirrus cloud canopy.* This can be mitigated by simply focusing only on estimates within Saffir−Simpson categories 1 to 5, which is also appropriate for our emphasis on changes in the stronger TCs. Our metrics of interest in this work are based on the proportions of major hurricane intensities (Saffir−Simpson categories 3 to 5 that have winds equal to or greater than 100 kt) to all hurricane intensities (Saffir−Simpson categories 1 to 5).

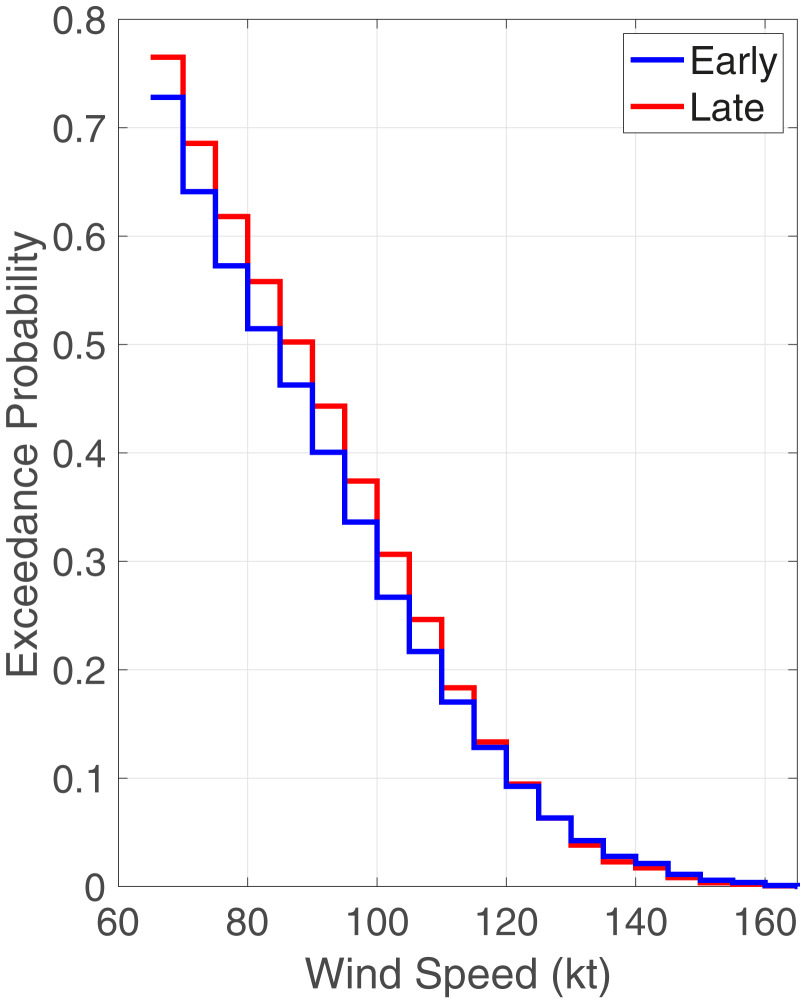
We begin with a broad view of the change in the global distribution of ADT-HURSAT intensity estimates between the early and latter halves of the 39-y period 1979–2017. Fig. 1 shows the change in the exceedance probabilities (complementary cumulative distribution function) among all estimates greater than hurricane intensity (65 kt). There is a clear shift toward greater intensity that manifests as increased probabilities of exceeding major hurricane intensity (100 kt). The probability of major hurricane exceedance increases from 0.27 to 0.31, which represents about a 15% increase. The centroids of the early and latter subperiods are around 1988 and 2007, respectively, with a separation of about 19 y. This represents an increase in probability of major hurricane intensity of about 8% per decade. The probability difference between the early and latter halves of the period is statistically significant after accounting for serial correlation in the two samples (Methods). The CIs for the early and latter halves are [0.25 0.28] and [0.29 0.32], respectively. The range of exceedance probability increases within these 95% CIs is then about 2 to 15% per decade.

Fig. 1.

Comparison of complementary cumulative distribution functions of the global ADT-HURSAT hurricane intensity estimates between the early and latter halves of the 39-y period 1979–2017.

For comparison, the change in best-track intensities over the same period is roughly 17% per decade (Table 1 and SI Appendix, Fig. S4), or about twice the increase in major hurricane intensity exceedance found in the homogenized ADT-HURSAT data. This is consistent with the expectation that the best-track data contain nonphysical technology-based trends in the estimation of TC intensity, particularly at the greater intensities. In this case, it appears that the trends in the best track are about equally split between actual physical trends and spurious technology-based trends.

Table 1.

Differences in major hurricane intensity exceedance probability (P_maj) between the early and later halves of the period of analysis

	ADT-HURSAT							Best-track global
	Global	NA	EP	WP	NI	SI	SP
Early (1979–1997)	Pmaj = 0.27	Pmaj = 0.18	Pmaj = 0.25	Pmaj = 0.35	Pmaj = 0.16	Pmaj = 0.21	Pmaj = 0.24	Pmaj = 0.21
	CI=[0.25,0.28]	CI=[0.13,0.22]	CI=[0.22,0.28]	CI=[0.31,0.37]	CI=[0.08,0.25]	CI=[0.17,0.25]	CI=[0.19,0.28]	CI=[0.20,0.23]
	Ntot = 8,848	Ntot = 777	Ntot = 2,411	Ntot = 3,071	Ntot = 227	Ntot = 1,299	Ntot = 1,063	Ntot = 11,959
	Nmaj = 2,362	Nmaj = 136	Nmaj = 606	Nmaj = 1,060	Nmaj = 37	Nmaj = 271	Nmaj = 252	Nmaj = 2,570
Late (1998–2017)	Pmaj = 0.31	Pmaj = 0.34	Pmaj = 0.27	Pmaj = 0.34	Pmaj = 0.16	Pmaj = 0.28	Pmaj = 0.29	Pmaj = 0.28
	CI=[0.29,0.32]	CI=[0.30,0.38]	CI=[0.24,0.30]	CI=[0.32,0.37]	CI=[0.08,0.24]	CI=[0.24,0.32]	CI=[0.23,0.34]	CI=[0.27,0.30]
	Ntot = 9,275	Ntot = 1,572	Ntot = 2,089	Ntot = 3,236	Ntot = 237	Ntot = 1,331	Ntot = 807	Ntot = 14,463
	Nmaj = 2,842	Nmaj = 529	Nmaj = 565	Nmaj = 1,105	Nmaj = 37	Nmaj = 374	Nmaj = 232	Nmaj = 4,117
Change	8% decade−1	49% decade−1	4% decade−1	−1% decade−1	0% decade−1	18% decade−1	8% decade−1	17% decade−1
Sig. lev.	>95%	>99%	<90%	<90%	<90%	>90%	<90%	>99%
Triad time series	6% decade−1	42% decade−1	7% decade−1	2% decade−1	−15% decade−1	31% decade−1	8% decade−1
	P = 0.02	P = 0.02	P = 0.25	P = 0.58	P = 0.71	P = 0.004	P = 0.13

CI is the pointwise 95% CI on P_maj. The significance level (Sig. lev.) of the difference is also shown. N_tot and N_maj are the total number of hurricane and major hurricane estimates, respectively, in each period. The bottom row shows the Theil−Sen trend amplitudes and Mann−Kendall significance levels (P values) for the triad time series shown in Figs. 2 and 3.

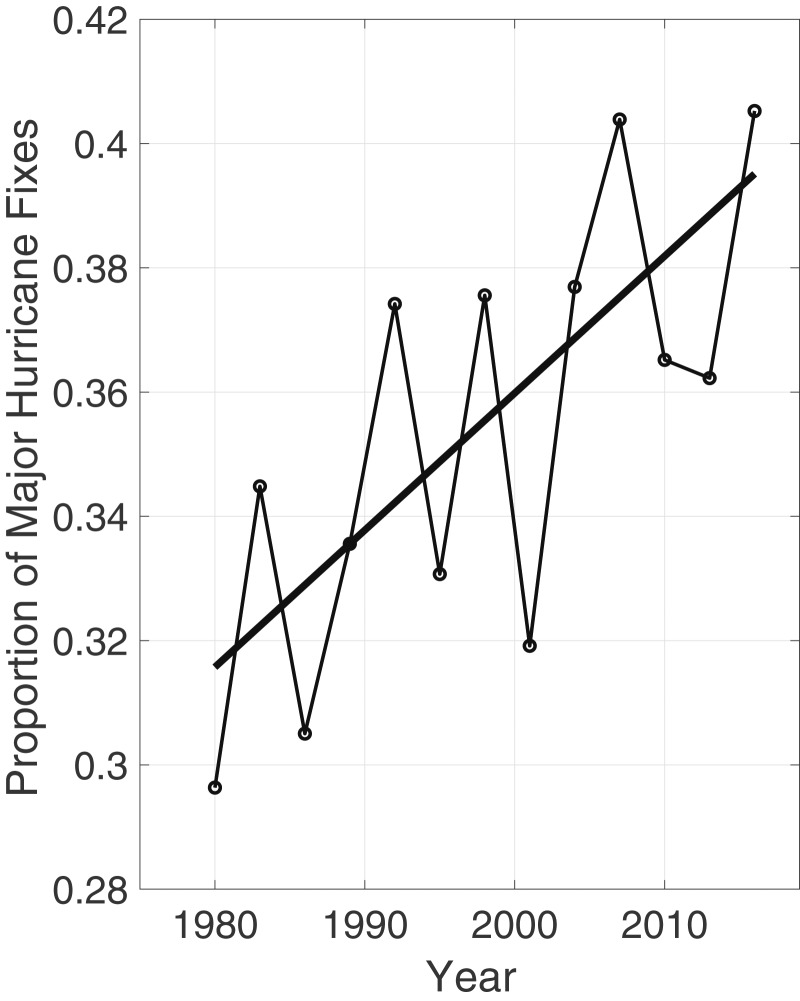
Another way to explore changes in the intensity distribution is to consider time series of the proportion of major hurricane intensities. Fig. 2 shows a triad time series (3-y bins) of the global fractional proportion of major hurricane intensities to all hurricane intensities (Methods). The time series exhibits a statistically significant increasing trend that represents a 25% (about 6% per decade) increase in the likelihood that any estimate of at least hurricane intensity is at or above major hurricane intensity (Table 1).

Fig. 2.

Time series of fractional proportion of global major hurricane estimates to all hurricane estimates for the period 1979–2017. Each point, except the earliest, represents the data in a sequence of 3-y periods. The first data point is based on only 2 y (1979 and 1981) to avoid the years with no eastern hemisphere coverage. The linear Theil−Sen trend (black line) is significant at the 98% confidence level (Mann−Kendall P value = 0.02). The proportion increases by 25% in the 39-y period (about 6% per decade).

Similar to the Dvorak technique, the ADT uses a “scene-typing” strategy to provide intensity estimates (16, 21). In particular, an essential aspect of these routines is the ability to recognize the presence of a TC eye in a satellite image. The appearance of an eye generally signals that a TC has reached hurricane intensity, and major hurricanes, as well as rapidly intensifying hurricanes, generally (almost always) exhibit an eye (29, 30). We can exploit these facts to indirectly identify intensity trends by looking for changes in the proportion of eye scenes (SI Appendix, Fig. S5). Here, again, there is an apparent trend toward increasing likelihood of finding an eye scene, which is consistent with the increasing likelihood of finding a major hurricane intensity. This is a particularly useful result because the identification of an eye scene is largely insensitive to any potential heterogeneities that may still remain in the resampled and recalibrated infrared brightness temperatures in the HURSAT data (15). Additionally, when the ADT identifies an eye scene, it produces an estimate of the eye diameter. Smaller eyes are generally related to greater intensity (31), and there is a shift toward smaller eyes in the ADT data (SI Appendix, Fig. S6). This is consistent with the increasing intensity trends, but also uncovers a potential bias in the ADT-HURSAT intensities. As eye sizes become smaller, and, particularly, as eye diameters smaller than about 20 km become more likely (SI Appendix, Fig. S6), they would be expected to be more difficult to resolve in the 8-km resolution HURSAT data. This could cause the ADT to underestimate the intensity trend, particularly at the smallest-eye/greatest-intensity end of the spectrum, which may also help to explain the absence of a probability shift at the most intense part of the intensity spectrum, as seen in Fig. 1. This is difficult to quantify, however, and is left here as an open question for possible future exploration.

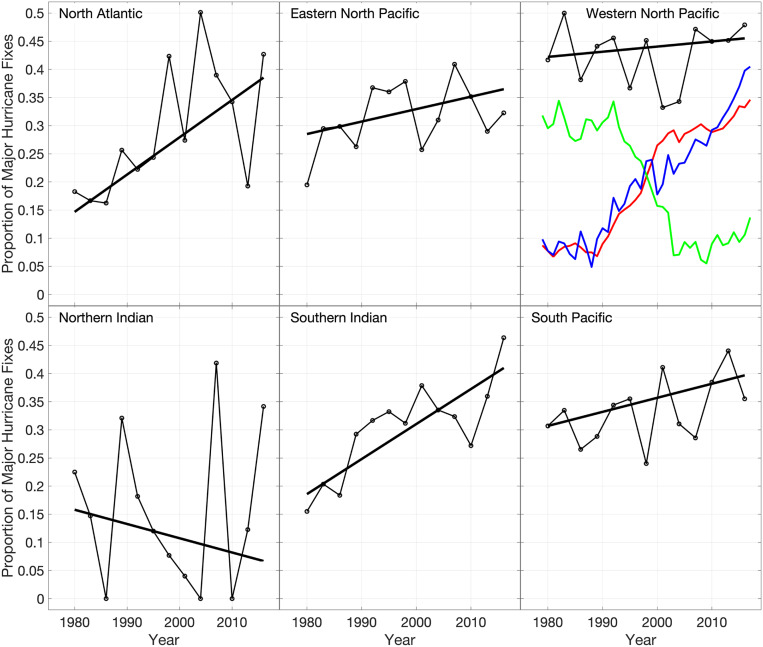
The main focus of this work is the identification of global changes in TC intensity (Figs. 1 and 2). When the global data are parsed into regional subsets, there is an expectation for changes in signal-to-noise ratios and greater sensitivity to known regional modes of variability (e.g., the Interdecadal Pacific Oscillation [IPO], Atlantic Multidecadal Oscillation [AMO], or Indian Ocean Dipole [IOD]). Nonetheless, it is generally informative to identify changes and trends within individual ocean basins, and results of the regional analyses are shown in Table 1 and Fig. 3. The greatest changes are found in the North Atlantic, where the probability of major hurricane exceedance increases by 49% per decade, significant at greater than the 99% confidence level (Table 1). Consistent with this, an increasing trend is found in the triad time series of the proportion of major hurricane intensities (Fig. 3) that represents an increase of 42% per decade, significant with 98% confidence (Table 1). Large and significant increases are also found in the southern Indian Ocean. More modest increases are found in the eastern North Pacific and South Pacific, and there is essentially no change found in the western North Pacific. The northern Indian Ocean exhibits a decreasing trend, but it is highly insignificant and based on a small sample of data (Table 1). With the exception of the northern Indian Ocean, all of the basins are contributing to the increasing global trend shown in Fig. 2.

Fig. 3.

As in Fig. 2, but for individual ocean basins. The red, green, and blue curves shown arbitrarily in the western North Pacific panel are time series of annually averaged indices representing Atlantic, Pacific, and Indian Ocean multidecadal variability, respectively, and represent 11-y centered means that have been normalized and shifted for plotting purposes.

Discussion

The global TC intensity trends identified here are consistent with expectations based on physical process understanding (1) and trends detected in numerical simulations under warming scenarios (10). As the tropics have warmed, SSTs and TC potential intensity have increased in regions where TCs track, and this provides an a priori expectation that TC intensity has increased, all other factors being equal. Detecting increases in the instrumental record has been hindered by heterogeneities in the best-track data, which we have addressed by creating a globally homogenized record of TC intensity based on homogenized satellite data. This record is limited to the geostationary satellite period, however, and is thus limited to the past four decades.

The amplitude and significance of the trends among the individual ocean basins vary considerably, and are very likely influenced by internal and externally forced regional variability, particularly at decadal and interdecadal timescales. For example, the large trends in the North Atlantic are linked to observed regional multidecadal variability, which very likely represents internal quasi-oscillatory factors (e.g., the Atlantic meridional overturning circulation) and/or both natural and anthropogenic nonoscillatory external factors (e.g., mineral aerosols, or African dust, volcanic activity, and anthropogenic aerosols and greenhouse gas) (5, 32–34). Within the period of our homogenized data, this multidecadal variability manifests as a pronounced trend (red curve in Fig. 3), which complicates detection because the climate drivers of the variability are not fully understood (35, 36). Similarly, multidecadal variability within this period in the Indian and Pacific Oceans manifests as a trend in the Indian Ocean (blue curve in Fig. 3) and a change point in the Pacific Ocean (green curve in Fig. 3). All of these regional climate drivers are likely projecting onto the observed changes and trends in TC intensity documented here. These effects are further complicated by the projection of these modes from one region onto another. For example, Pacific multidecadal variability projects onto TC activity in the Atlantic and eastern North Pacific (37), and Atlantic multidecadal variability projects onto TC activity in the western North Pacific (38).

The lack of significant trends in western North Pacific TC intensity, which has been previously documented (e.g., refs. 39 and 40), substantially reduces the global trend, as the western North Pacific contributes the largest number of estimates to the global sample (Table 1). The lack of intensity trends in the western North Pacific may be due to a pronounced poleward migration of TC tracks (6, 41, 42). This moves TCs into regions of lower potential intensity, which counteracts the effects of increasing mean-state potential intensity (43). This highlights an important relationship between TC track and intensity. The variability and trends in track characteristics introduce an additional source of variability in TC intensity and its trends beyond changes in the thermodynamic state of the ocean/atmosphere (43, 44). Track variability is driven largely by atmospheric variability, which introduces substantial shorter timescale noise that is mostly absent in SST and potential intensity variability.

Ultimately, there are many factors that contribute to the characteristics and observed changes in TC intensity, and this work makes no attempt to formally disentangle all of these factors. In particular, the significant trends identified in this empirical study do not constitute a traditional formal detection, and cannot precisely quantify the contribution from anthropogenic factors. From a storyline, balance-of-evidence, or Type-II error avoidance perspective (e.g., refs. 6 and 45), the consistency of the trends identified here with expectations based on physical understanding and greenhouse warming simulations increases confidence that TCs have become substantially stronger, and that there is a likely human fingerprint on this increase. Given the well-understood impacts and risk that increasingly powerful TCs carry with them, strict adherence to Type-I error avoidance could be considered overly conservative.

Methods

Best-Track and ADT-HURSAT Data.

The global best-track intensity data used here are taken from the IBTrACS Version 4.0 data record (46). These data (wind intensity and geographic position) are provided every 6 h on the primary synoptic hours (0, 6, 12, and 18 UTC) during the lifetimes of each TC. The ADT-HURSAT data are provided every 3 h, but only the primary synoptic hour data are used here to match the native temporal resolution of the best-track data. The 6-hourly data from both the ADT-HURSAT and IBTrACS are traditionally referred to as “fixes.” These fixes include the estimated location of the TC center at that time and, when available, the estimated wind intensity. The best-track and ADT-HURSAT intensity data are provided within 5-kt bins.

As shown in SI Appendix, Fig. S1, there is a lack of available geostationary satellite data in the eastern hemisphere in the years 1978 and 1980. The ADT-HURSAT analyses here exclude these 2 y but include 1979, for which global data are available. The time series analyses shown in Figs. 2 and 3 are based on 3-y triads, with the exception of the first data point, which comprises the years 1979 and 1981. The remaining triads comprise the years 1982–1984, 1985–1987, …, 2015–2017. The results are not highly sensitive to this choice. Analyzing annual mean time series or 3-y running mean time series does not change the results in a substantial way.

There are a number of intensity estimates in the IBTrACS data with no corresponding intensity estimate in the ADT-HURSAT, due to missing HURSAT data. These gaps can be due to satellite issues or requirements that occurred in real time, or lost or compromised data that occurred later. Similarly, there are intensity estimates in the ADT-HURSAT with no corresponding intensity estimate (only position) in the IBTrACS, due to various inconsistencies in the collection and reporting of the operational best-track data. The analyses presented here use all of the data available in each of the two datasets, except for the direct comparison shown in SI Appendix, Fig. S3. Using only the matched data does not change the analyses in any substantial way.

The HURSAT data rely on best-track center position estimates. These estimates generally become available from the various regional forecast offices around the globe within a year after the end of their respective TC seasons, and, when all of the data are available, the HURSAT data for that year can be constructed. For the analyses here, 2017 is the extent of the available HURSAT data.

The time series of indices of Atlantic, Pacific, and Indian Ocean multidecadal variability shown in Fig. 3 represent the annual mean AMO, IPO, and IOD indices, respectively. These indices are available at the website listed in Data Availability.

Metrics of Interest.

As noted above, the HURSAT data rely on best-track position estimates, and thus are subject to whatever heterogeneities may exist in the best-track measures of TC frequency and track duration. This also introduces potential heterogeneity into metrics such as accumulated cyclone energy (ACE) and power dissipation, which depend strongly on frequency and track duration. To mitigate the projection of these potential heterogeneities onto the analyses presented here, we focus on intensity metrics that have comparatively minimal dependence of absolute measures of frequency and duration (i.e., intensive, or bulk properties). Actual numbers of estimates are included in Table 1, but changes in these numbers should be interpreted with caution, as they are more likely to be affected by absolute frequency data issues than the probabilities and proportions that are the focus of this work.

Compositing Analysis.

As noted above, the ADT-HURSAT data used here span the years 1979–2017. The two periods considered here comprise all of the estimates in the first half (1979–1997) and last half (1998–2017) of these years. The results are robust to using the first and last 15 y or to shifting the year of separation of the two periods. The centroids of the early and later periods are 1988 and 2007, respectively. The composite difference values are then separated by about 19 y.

Statistical Significance.

In comparison to the methods of refs. 7 and 9, which concentrated only on the LMI of each TC, the analyses presented here are based on all intensity estimates. This choice is based on the argument that a TC poses a threat at any time during its lifetime, and particularly during (possibly prolonged) periods of major hurricane intensity. These periods will also have a substantial effect on integrated hazard metrics such as ACE and power dissipation index, which LMI does not project onto as clearly. However, while LMI data are essentially independent between the individual TCs, there can be substantial serial correlation along individual TC tracks, and this needs to be taken into account when forming CIs for differences in the probability of exceedance (there is no correlation between one track and another). To address this, every track from every TC was tested for serial correlation at progressively greater lags (SI Appendix, Fig. S7). The mean decorrelation timescale (i.e., the time at which the mean lag correlation crosses zero) for the ADT-HURSAT tracks during periods of hurricane intensity is between 12 h and 18 h. For the significance testing on the separation of the cumulative distribution functions shown in Fig. 1, the degrees of freedom in the early and later samples are reduced by a factor of 3, which assumes a decorrelation time of 18 h. The pointwise 95% confidence bounds in Table 1 are given by $F_X\left(x\right)\pm z_{0.025}\sqrt{F_X\left(x\right)\left[1-F_X\left(x\right)\right]/N_{eff}}$, where $F_X\left(x\right)=P(X\ge x)$ is the complementary cumulative distribution function, x = 100 kt, $z_{0.025}$ is the critical z value (∼1.96), and $N_{eff}$ is the reduced (effective) degrees of freedom (one-third of the total number in the sample).

The points in each of the individual triad time series (Figs. 2 and 3) do not show significant temporal autocorrelation (based on a Durbin−Watson test), and none required adjustment of the degrees of freedom to determine significance levels. The significance of the trends is based on the P value of a nonparametric Mann−Kendall test in each time series (Table 1). The slopes of the trend lines are given by Theil−Sen trend lines, which provide a robust nonparametric alternative to ordinary least-squares regression that are insensitive to outliers. The global trend amplitude and significance are essentially unchanged under ordinary least-squares regression and are also robust to the removal of the endpoints of the time series.

Data Availability.

The ADT-HURSAT data are available in Datasets S1–S9 and are described in SI Appendix. IBTrACS data are available at https://www.ncdc.noaa.gov/ibtracs/. The climate indices shown in Fig. 3 are from the National Oceanic and Atmospheric Administration (NOAA) Earth System Research Laboratories (ESRL) Physical Sciences Division website: https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/.