Significance
Protein oligomers are a fundamental component of amyloidogenic disorders such as Alzheimer’s disease, being both critical intermediates in the formation of amyloid fibrils and the most toxic species on the protein aggregation pathway. Here, we derive general analytical expressions for the chemical kinetics of the oligomers generated during amyloid-formation reactions and explain how these may be used to categorize oligomers according to their basic physicochemical properties. By applying this framework to experimental kinetic data on the aggregation of a wide range of amyloidogenic proteins, we are able to determine features common to all amyloid oligomers. In particular, most are not capable of rapid growth by monomer addition, and most dissociate rather than mature into fibrils.
Keywords: amyloid, oligomers, kinetics, modeling, Alzheimer’s
Abstract
The spontaneous assembly of proteins into amyloid fibrils is a phenomenon central to many increasingly common and currently incurable human disorders, including Alzheimer’s and Parkinson’s diseases. Oligomeric species form transiently during this process and not only act as essential intermediates in the assembly of new filaments but also represent major pathogenic agents in these diseases. While amyloid fibrils possess a common, defining set of physicochemical features, oligomers, by contrast, appear much more diverse, and their commonalities and differences have hitherto remained largely unexplored. Here, we use the framework of chemical kinetics to investigate their dynamical properties. By fitting experimental data for several unrelated amyloidogenic systems to newly derived mechanistic models, we find that oligomers present with a remarkably wide range of kinetic and thermodynamic stabilities but that they possess two properties that are generic: they are overwhelmingly nonfibrillar, and they predominantly dissociate back to monomers rather than maturing into fibrillar species. These discoveries change our understanding of the relationship between amyloid oligomers and amyloid fibrils and have important implications for the nature of their cellular toxicity.
Amyloid oligomers are supramolecular structures consisting of several amyloidogenic proteins noncovalently assembled into clusters. They exist in a great diversity of structures and morphologies (1–4) and have been shown to be critical kinetic intermediates in the formation of new filamentous aggregates by a wide range of different amyloidogenic proteins (5–8). Metastable oligomeric intermediates have in fact recently been shown to be expected on physicochemical grounds as a generic feature of amyloid fibril formation (9, 10). Moreover, these species possess cytotoxic properties driving the pathology of human disorders associated with the deposition of amyloid fibrils, such as Alzheimer’s disease and Parkinson’s disease (11–16). As such, they represent important potential targets for the design of new drugs for the treatment of neurodegenerative diseases.
Amyloid fibril formation is typically studied using bulk assays, (17) providing data on the mass concentration of fibrils formed as a function of time. The fundamental kinetic equations describing the formation and growth of amyloid fibrils in bulk, and their analytical solutions, are now well established in the literature (18–26), permitting the analysis of kinetic data to discover the reaction mechanisms underlying well-known aggregation processes. Commonalities in filaments’ physicochemical properties discovered in this way include rapid elongation by monomer addition, explaining the observed high aspect ratios; a single elongation rate constant, explaining their high level of order; and a very slow primary nucleation step. Differences include the sites at which nucleation of new filaments occurs, with widely varying fibril surface properties resulting in a broad range of surface-catalyzed secondary nucleation behavior. Such filamentous growth models do not explicitly consider oligomeric intermediates, with formation of new filaments from monomers instead described in a coarse-grained fashion as a single nonclassical nucleation step; oligomers are therefore treated implicitly but not explicitly in these models. In the absence of experimental time-resolved data on these intermediates, such coarse-graining is crucial for the avoidance of overfitting (27).
Recent advances in single-molecule experimental techniques have allowed the time dependence of the concentration of oligomeric species present during amyloid fibril formation to be recorded (6, 28). To begin exploring both their properties and their precise roles in fibril formation requires a new kinetic theory, generalizing the earlier bulk models to feature explicitly oligomeric intermediates and the generic reactions they undergo (Fig. 1A). Some initial progress has been made in this direction, with the development of bespoke kinetic models designed to analyze specific protein-aggregation reactions (6–8, 28–32). However, although effective in the specific contexts in which they have been used, these models suffer from limitations that prevent their more widespread application. Some are only valid at the earliest stages of the reaction time course, ignoring reaction steps that are crucial at later reaction times (6, 28–31); others do not have analytical solutions, placing limits on the physicochemical insight that can be gained from them (7, 8). A recent work (33) resolves these issues, with its model both being valid over the entire reaction time course and admitting an analytical solution; however, its validity is limited to systems in which the dominant mechanism for new filament formation is surface-catalyzed secondary nucleation. If we wish to directly compare the physicochemical properties of diverse amyloid oligomers, a more general analytical model of oligomer-mediated filament formation, encompassing all known reaction mechanisms, is instead required.
Fig. 1.
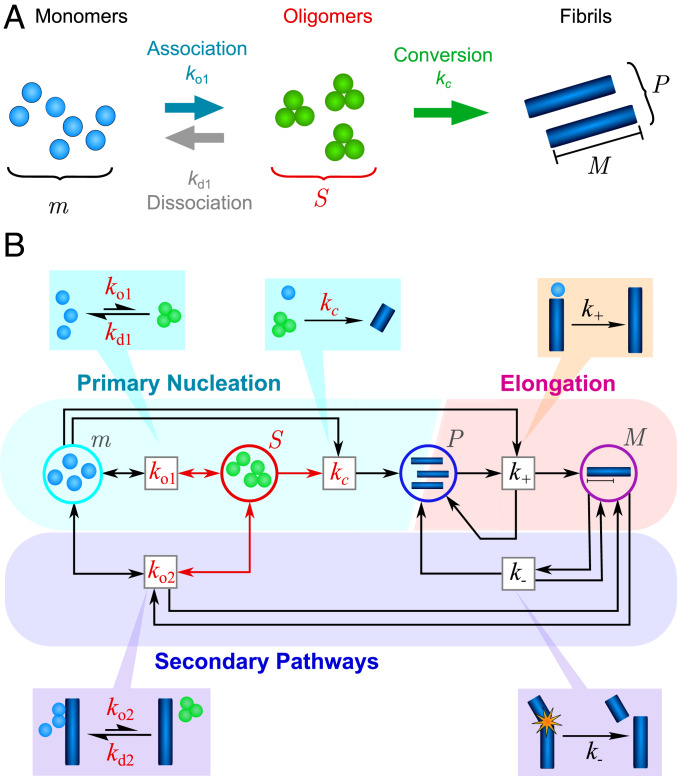
(A) The different possible reactions that can produce and deplete nonfibrillar amyloid oligomers. Oligomers (concentration ) may be generated by free association of monomeric protein (concentration ) with rate constant . Once formed, they may dissociate back to monomers (rate constant ) or undergo a structural conversion process to generate fibrillar species (concentration ) with rate constant . Reverse conversion of fibrils to oligomers is neglected as it is found experimentally that fibrils are far more thermodynamically stable than nonfibrillar oligomers. (B) The coarse-grained reaction network describing oligomer-mediated fibril formation, represented in Petri net form (34), with reactions represented by boxes and chemical species of interest as circles. Oligomers, and reactions involving them, are highlighted in red. Both oligomer formation through monomer association and oligomer dissociation may in some cases be catalyzed by the surfaces of existing fibrils (fibril mass concentration ) with rate constants and , respectively. Once formed, fibrillar species undergo rapid elongation by monomer addition (rate constant ), increasing the fibril mass concentration. They may also fragment to generate new fibrils (rate constant ), increasing .
In this paper, we develop a general chemical kinetic description for the proliferation of amyloid fibrils that explicitly includes metastable oligomeric intermediates, as well as every reaction step that has hitherto been observed in amyloid aggregation. We derive previously undescribed analytical rate laws for oligomer and fibril concentrations and illustrate both their generality and their effectiveness by fitting to kinetic data for Aβ40, Aβ42, tau, Ure2, and αS proteins, each of which forms amyloid according to very different reaction mechanisms. We discover the natural timescales controlling these models, which allow us to classify oligomers according to their kinetic properties. By using our modeling framework to reanalyze experimental data on protein aggregation from a large number of earlier publications, we are able to determine the kinetic commonalities and differences between a wide range of amyloid oligomers. Finally, we determine the conditions under which models based only on bulk data are capable of providing an accurate description of oligomer-mediated filament formation.
Results
Most Amyloid Oligomers Are Nonfibrillar.
The kinetics of filament assembly have hitherto been successfully modeled without explicit consideration of oligomeric intermediates by describing the formation of new filaments using coarse-grained nonclassical nucleation reactions. New fibrils are formed through free association of monomers in solution (primary nucleation) and occur with rate constant and reaction order (18). In some systems, they may additionally be formed by the “secondary nucleation” of monomers at the surfaces of existing fibrils (26, 35) with rate constant and reaction order with respect to monomers. Rate equations can then be written down considering only the quantities , and , representing the concentrations of monomers, fibrils, and the fibril mass, respectively (SI Appendix). Note that, since nucleation of new fibrils is typically nonclassical (10), the reaction orders and do not in general correspond to a critical nucleus size. In the case of primary nucleation, is related to the number of monomers within a nucleating cluster necessary to stabilize its conformational conversion to fibrillar form (36), whereas in secondary nucleation, is related to the surface coverage of fibrils by monomeric protein (37).
As discussed in the Introduction, amyloid oligomers may be detected during the majority of aggregation reactions. We first asked the question whether these can be identified as short growing fibrils, termed fibrillar oligomers (40), or whether they are instead oligomeric intermediates of the various nucleation processes. To determine the precise importance of fibrillar oligomers, we may derive an upper bound on the concentration of fibrillar oligomers observed during an aggregation reaction, in terms of the rate constants entering the bulk reaction network (Materials and Methods). In all amyloid systems studied here, we find that is significantly lower, by up to five orders of magnitude, than the maximum experimentally observed concentrations of oligomers (). The upper bounds we derive are orders of magnitude lower than those computed by earlier, cruder analytical methods (31, 32). Explicit values of for all such systems are given in SI Appendix. In general, therefore, from a kinetic point of view, almost all amyloid oligomers are nonfibrillar and unable to undergo the rapid growth characteristic of mature fibrils.
It may be shown that many of these nonfibrillar oligomers are in fact on-pathway intermediates of the filament nucleation steps (termed prenucleation clusters in nucleation theory). In light of this, we next extend the bulk reaction network to include nonfibrillar oligomeric nucleation intermediates explicitly, as shown in the form of a Petri net in Fig. 1B. We may also easily extend our analysis further to include off-pathway oligomers. Although in reality oligomer populations are likely to be heterogeneous, existing in a range of aggregation numbers and conformations, it is particularly insightful to consider only the total fluxes into and out of the oligomeric state, as described by the network in Fig. 1B. Moreover, in practice, often only the total oligomer concentration is measured, and to avoid overfitting in such cases, it is necessary to model the dynamics at this simpler level, in which all oligomeric species have been coarse-grained into a single population. Modeling all systems at this level, including those for which more detailed data are available, permits direct comparison of the kinetic properties of different protein oligomers.
Kinetic Modeling of Oligomer-Mediated Filament Proliferation.
In general, oligomers (concentration ) may be formed through both primary and secondary processes. As a result, three qualitatively different oligomer-mediated filament-assembly mechanisms can be described by the minimal reaction network represented in Fig. 1B. In all three mechanisms, on-pathway oligomers are produced through the free association of monomers (primary association), occurring with rate ; the inverse of this process is a dissociation reaction occurring with rate . Once formed, oligomers may convert to elongation-competent fibrillar species with rate (since conversion may be a multistep process that includes monomer addition as well as conformational changes). Fibrils may subsequently elongate with rate . In the first kind of filament assembly, there are no further reaction processes. In the second kind, fibrils also break, generating new fibrils with rate (24, 41). In the third kind, oligomers are additionally formed at fibril surfaces with rate (secondary association), and fibril-mediated dissociation occurs with rate (33). Closed sets of rate equations describing this reaction network may then be written down:
| [1] |
| [2] |
| [3] |
These equations may be generalized to include multiple on- and off-pathway oligomeric intermediates; however, this is beyond the scope of the current study. In the early-time limit, before significant monomer depletion has occurred, and these equations become linear and admit exact solutions, provided , which holds under most circumstances, including all those encountered in this paper. These early-time solutions are then used as trial functions in iterative fixed-point schemes, yielding new analytical solutions to the fibril mass concentration and oligomer concentration that are valid over the full time course (SI Appendix).*
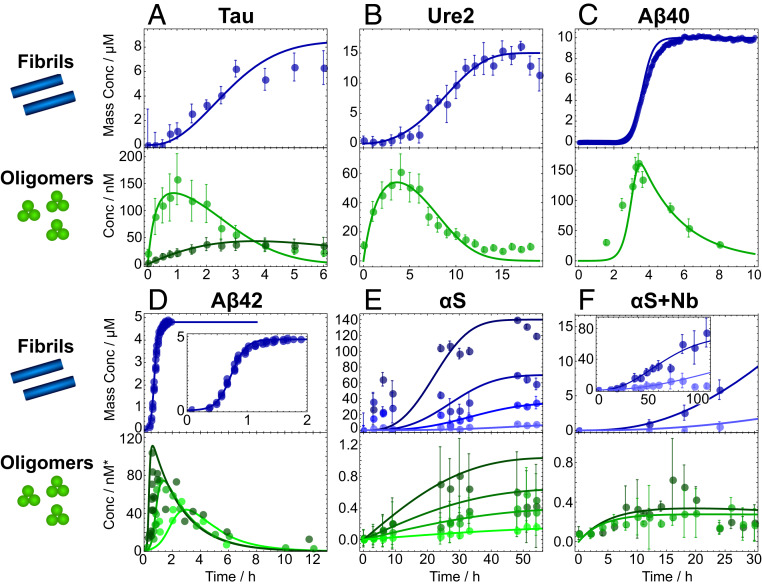
In Fig. 2, we illustrate that these integrated rate laws can successfully describe experimental kinetic data on oligomer-mediated filament formation. Previously published data (8, 31–33, 39) on seven separate aggregating protein systems were analyzed using our models: the repeat region of tau protein, responsible for forming neurofibrillary tangles in the later stages of Alzheimer’s disease (Fig. 2A); the functional yeast prion protein Ure2, whose aggregation helps to regulate yeast metabolism (Fig. 2B); Aβ40 and Aβ42, whose aggregation into amyloid plaques occurs in the early stages of Alzheimer’s disease (Fig. 2 C and D); αS, whose aggregation is associated with Parkinson’s disease (Fig. 2E); and αS aggregated in the presence of either NbSyn2 or NbSyn87 (αS-specific single-domain antibodies known as nanobodies; Fig. 2F). A brief account of the experimental methodology is presented in Materials and Methods.
Fig. 2.
Global fits of experimental kinetic data on aggregating protein systems to the analytical models derived in SI Appendix, using the reaction steps identified in Table 1. Soluble oligomer concentration (measured using single molecule techniques) and fibril mass concentration (usually measured using thioflavin T [ThT] dye fluorescence) are fitted simultaneously, with fitting parameters summarized in SI Appendix, Table S1. See Materials and Methods for summaries of experimental techniques and fitting methodologies. (A) Tau data taken from ref. 32; type-A oligomers (pale green) are on-pathway and type-B oligomers (dark green) off-pathway. (B) Ure2 data from ref. 8. (C and D) Aβ40 and Aβ42 oligomer data from ref. 33. Fibril data are from earlier papers (26, 38); for visual clarity, only one initial monomer concentration of the many available is shown for each. (E) αS data from the first quantitative FRET-based study (ref. 31); experimental accuracy thus lower than more recent studies with optimized protocols, resulting in lower-quality fits. Both oligomer and fibril concentrations measured via FRET. Initial monomer concentrations are 10 (lightest), 35, 70, and 140 M (darkest). (F) Data on αS aggregated in the presence of nanobodies NbSyn2 (darker) and NbSyn87 (lighter). Data are taken from ref. 39. Note that for most proteins, the reaction processes involved in aggregation depend sensitively on the reaction conditions. See SI Appendix, Table S4 for a summary of the conditions under which the data shown here were collected. Oligomer concentrations in E and F were measured in micromoles per liter.
For each system, the data for fibril mass and oligomer concentration were plotted against rate laws featuring the reaction processes identified as relevant in Table 1; the high quality of the fits shown demonstrates that these models are capable of rationalizing the kinetic behavior observed in aggregation reactions. The curves were fitted with three to four parameters, depending on the number of rate constants in the kinetic model, the number of parameters that could be determined by analysis of orthogonal experiments (e.g., by fitting additional bulk fibril formation data), and the number of different initial monomer concentrations available in the combined oligomer and fibril datasets; see Materials and Methods for full fitting details. The rate constants used for the reaction steps involving oligomers are displayed in SI Appendix, Table S1.
Table 1.
The reaction processes responsible for generating the protein aggregation data shown in Fig. 2, identified by diverse methods in the original papers (8, 31–33, 39)
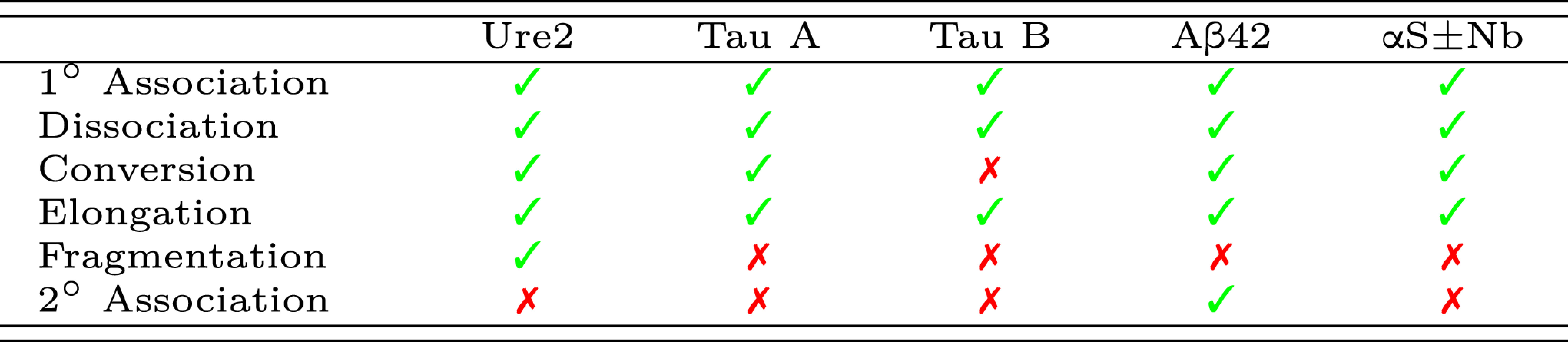 |
The relevant reaction conditions are listed in SI Appendix, Table S4. Types A and B tau oligomers are on- and off-pathway, respectively. αS aggregation data are collected both in the presence and in the absence of camelid nanobodies (Nb). The identities of these reaction processes can depend very sensitively on the reaction conditions. For instance, a drop in pH can induce secondary nucleation in αS (42). Moreover, removing the nucleation inducer used in the tau aggregation experiments causes fibril fragmentation to become a comparatively significant source of new fibrils (43).
Oligomer Depletion Mechanisms.
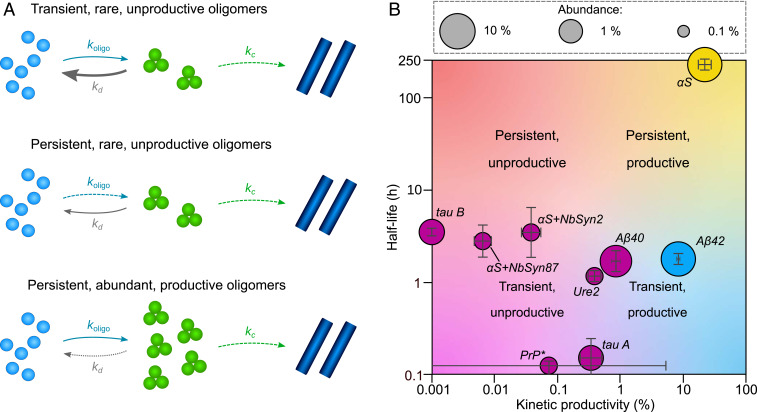
Oligomers are transient species, and their concentrations can decrease by conversion to fibrils, as well as through dissociation to monomers (Fig. 1A). A key kinetic property of oligomers is their productivity, defined as , where and are the maximal pseudo first-order rate constants for oligomer conversion and dissociation, respectively. This ratio encapsulates their propensity to convert into fibrils rather than dissociate to monomers (Fig. 3A). It does not inform on whether oligomers are on- or off-pathway, unless it is exactly zero.
Fig. 3.
(A) Categorizing oligomers from Fig. 2 by their key properties. “Persistence” is the kinetic stability of the oligomers as indicated by their half-life (with ). “Abundance” is the maximal rate of formation divided by the maximal rate of depletion and indicates the maximal steady-state oligomer concentration. “Productivity” indicates the relative contributions of conversion and dissociation to overall oligomer depletion, defined as . (B) Of the systems hitherto studied, in every case, the oligomers dissociate more rapidly than they convert, and only αS oligomers, Aβ42 oligomers, and type-B (off-pathway) tau oligomers persist longer than the corresponding monomeric protein. These oligomers are also relatively abundant, as might be expected. Prion protein PrP data were taken from ref. 44 (proteinase K-sensitive species); abundance was not measured.
Examining our integrated rate laws (given in SI Appendix), we see that the productivity affects the kinetics primarily via the combined parameters and the maximal depletion rate . To decouple these terms, must be determined separately, either from measurements of the fibril size distribution (8) or by fitting fibril mass concentration data from seeded protein aggregation reactions (45). The values for Aβ42, Aβ40, and αS are taken from refs. 26, 38, and 45, respectively; the values for the remaining proteins were determined in the studies from which we have taken the oligomer concentration data. See SI Appendix, Table S3 for explicit values. values for a variety of amyloid-forming systems can then be calculated and are found to be far smaller than 100% (Fig. 3B). This confirms that, under the conditions heretofore encountered, a universal property of amyloid oligomers is that the majority of the reactive flux from monomers to fibrils goes through oligomeric intermediates that have much faster rates of dissociation than of conversion to fibrils. Productivity values approaching 100% can only be consistent with the observed timescales of fibril formation if oligomer concentrations are far lower than those typically observed (SI Appendix, Fig. S3).
The rate constant for unimolecular oligomer dissociation may be measured directly by taking aliquots over time from an aggregation reaction, diluting them greatly to suppress all nonunimolecular processes, and fitting the observed oligomer concentrations to an exponential decay function. This method was necessary to determine for αS, since depletion was too slow on the timescale of fibril formation for it to be determined from fitting our kinetic models to protein aggregation data. Moreover, this method was also used previously to independently verify the value of for Ure2 oligomers calculated from fitting protein aggregation data (8).
The Pattern of Oligomer Kinetic Stabilities.
We next focused on characterising the kinetic stability of oligomers. The parameter enters the integrated laws as a timescale . This timescale governs the average oligomer half-lives, which are given explicitly by and which determine the persistence of these species in solution. Interestingly, examining Fig. 3B, it appears that the majority of amyloid oligomers have half-lives of 1 to 5 h. By contrast, αS oligomers appear uniquely kinetically stable, with a half-life orders of magnitude higher, whereas prion protein PrP and type-A tau oligomers are at least an order of magnitude less stable.
This pattern of persistence may relate to the predominant type of bonding interaction present in each species. The high persistence of αS oligomers is as expected, given that they are known to contain high β-sheet content (6) and that H-bonding between β-sheets are the most stable noncovalent interactions that can arise between proteins (indeed, β-sheet interactions are responsible for the high stability of amyloid fibrils). The much lower persistence of all other oligomer populations examined suggests that weaker kinds of bonding are predominantly responsible for their assembly. The clustering of most of these around half-lives of 1 to 5 h suggests that they may have a common architecture. On structural grounds (9, 10), we expect that most aggregation-prone proteins should be easily capable of forming micellar oligomers held together by hydrophobic interactions; a generic micellar structure is therefore a promising candidate for these oligomers of intermediate persistence. Micellar Aβ40 and Aβ42 oligomers have indeed explicitly been observed in earlier studies (46, 47), with kinetic stabilities broadly consistent with those observed here.† On the other hand, type-A tau oligomers are known to be held together by electrostatic interactions (32); the lack of conformational rearrangement required to assemble or disassemble such oligomers compared with those held together by hydrophobic or β-sheet interactions may explain their significantly lower kinetic stability. Finally, although PrP oligomers are likely held together by hydrophobic interactions, their unusually low persistence is likely due to the partially denaturing conditions under which they are formed (2 M GuHCl), which greatly facilitates the conformational conversion required for their formation or disassembly.
Also of interest is the relative persistence, defined as , where is the observed half-time for monomer depletion. Its significance is to determine the timescale for disappearance of oligomers from solution: where relative persistence is high, oligomers persist longer than monomers, and their removal from solution is thereafter determined purely by the rate of oligomer dissociation (SI Appendix, Fig. S3 D and F). Where it is low, by contrast, oligomers and monomers rapidly approach chemical equilibrium with one another, and the timescale of oligomer disappearance is instead given by that for monomer depletion (SI Appendix, Fig. S3 C and E). Examining SI Appendix, Fig. S4, it appears that most oligomers have low persistence values and are thus less kinetically stable than their monomers; in these cases, the oligomer concentration depends almost solely on the monomer concentration, and the oligomer depletion kinetics are therefore governed by those of monomers. By contrast, observed decay of αS oligomers and Aβ42 oligomers occur over longer timescales than monomer depletion, and hence their survival time must be determined primarily by the rate of oligomer dissociation. Type-B tau oligomers are an intermediate case and persist approximately as long as tau monomers. Note that monomer half-lives are very sensitive to the initial monomer concentration, and so these conclusions cannot be extrapolated meaningfully to different experimental conditions.
Oligomer Abundance.
The oligomer-formation process enters the integrated rate laws as , the maximal rate of oligomer formation via primary nucleation, and , related to the maximal rate of oligomer formation via secondary nucleation . Dividing these terms by , we arrive at an estimate of the maximum concentration oligomers can theoretically attain relative to monomer concentration during an aggregation reaction, which we term “abundance” (Fig. 3A). In practice, this value is only attained in the limit that , i.e., when oligomers equilibrate with monomers rapidly compared with the timescale of monomer depletion.‡ For primary oligomers, this metric is given by , which is simply the steady-state concentration of oligomers attained when is held at . When secondary pathways dominate, it is instead given by . The resulting abundances are 0.3 to 0.4% (Ure2; αS suppressed by camelid nanobody inhibitors), 1.5% (tau), and 8% (αS; Aβ42). In the case of αS and Aβ42, these maximum theoretical relative concentrations are not realized in practice in closed reactions because oligomers cease to form due to monomer depletion long before steady-state conditions are reached.
We finally note that the three metrics we have defined (productivity, half-life, and abundance) are independent combinations of the three rate constants (or four when secondary oligomer formation also occurs) featuring in the rate equations for oligomer concentration. Each metric can therefore be changed without affecting the others, guaranteeing that any correlations observed between them are a consequence of the underlying chemistry, not the mathematics.
Influence of Oligomer Populations on the Bulk Kinetics of Fibril Formation.
When secondary processes are important, the dynamics described by the bulk kinetic models are governed by two timescales: (where ), describing proliferation of filaments through primary processes; and (where ), describing proliferation of filaments through secondary processes. To a good approximation, the corresponding integrated rate laws for are functions solely of and the dimensionless parameters and . When oligomeric intermediates are introduced into these models, the integrated rate laws for retain their functional forms, but the dependence of the timescales on the rate constants changes. This finding explains the remarkable success of the bulk models in describing amyloid filament assembly, despite the nonclassical nature of new filament nucleation.
When secondary processes are negligible and , the picture is more complicated. Now, in addition to being modified, the rate law for gains a term proportional to upon introduction of an oligomeric intermediate into the nucleation step. Its functional form is therefore only retained when , i.e., the oligomers dissociate or convert rapidly compared with the measurement timescale. We do not therefore expect the bulk model to give an accurate representation of systems undergoing nucleated polymerization kinetics in which primary nucleation in fact proceeds via relatively stable intermediates.
When oligomers are introduced into primary nucleation only, is replaced with:
| [4] |
but remains unchanged. This is not surprising, since introducing an oligomeric intermediate into the primary nucleation reaction should not have a direct impact on secondary processes. Equating timescales permits us to resolve the bulk nucleation rate in terms of oligomer formation, conversion and dissociation:
| [5] |
In the absence of secondary processes, this is simply the steady-state oligomer concentration multiplied by the early-time conversion rate, which is as expected since the limit also describes the onset of steady-state conditions () for oligomers.
However, when an oligomeric intermediate is introduced into both primary and secondary processes, both and are replaced, becoming and . Note that these rates are the geometric averages of the individual rates of the single steps; this argument generalizes to arbitrary numbers of intermediate steps through the Hinshelwood cycle (48). Equating old and new timescales, we may interpret the coarse-grained rate constants and in terms of the more fundamental rate constants of the oligomerization model as:
| [6] |
| [7] |
Intriguingly, this result indicates that when secondary nucleation proceeds via oligomers, the coarse-grained “nucleation” rate constants in the bulk model also contain a contribution from the microscopic reaction step of filament elongation. Within the analogy to Hinshelwood cycles, this is a direct consequence of the fact that we are comparing geometric averages of two and three steps.
Conclusions
In summary, we have presented a general chemical kinetic approach to understanding the nature, formation, and disappearance of protein oligomers generated during amyloid filament formation. Our analytical solutions to the time dependence of the oligomer and fibril concentrations reveal that three key parameters control oligomer behavior, termed half-life, productivity, and abundance. Persistence measures the relative kinetic stability of oligomers compared with monomers; productivity is a measure of the propensity of oligomers to convert into fibrils rather than dissociate, and abundance is defined as the maximum possible concentration of oligomers during an aggregation reaction normalized by the starting protein concentration. We were able to use these metrics to categorize the kinetic properties of all amyloid oligomers for which there exist accurate kinetic data. Our methodology can readily be applied to other systems when appropriate data are available.
A striking result from this study is that, despite the fact that the mechanisms producing both oligomers and fibrils differ widely in different systems, the majority of oligomers formed dissociate to monomers rather than proceeding to form fibrils. This revelation as to the nature of the oligomers formed in such systems may have far-reaching implications for the understanding of amyloid diseases and for rational design of drugs to target those oligomers that exert toxicity.
A related result is that oligomer productivity is universally low under experimental conditions hitherto encountered. Since is likely to have a greater dependence on initial monomer concentration than , this result is likely to remain valid at the much lower concentrations typically found in vivo. Conversely, in the case of Aβ42, it is predicted that at concentrations only slightly larger than those previously investigated, productivity becomes . This does not violate the expectation that most oligomers ultimately do not become fibrils, since monomers are depleted as the aggregation reaction progresses, causing the conversion rate, and therefore the fraction of oligomers becoming fibrils, to drop rapidly.
Values of oligomer half-life vary over many orders of magnitude and likely reflect the predominant bonding type within each species. Many half-lives cluster around 1 to 5 h at physiological pH and temperatures and may correspond to hydrophobic structure. Oligomers that are substantially more kinetically stable likely have significant β-sheet content, and those that are substantially less stable may be held together by electrostatic interactions.
It is intriguing to see that some of the oligomers most closely associated with amyloid disease toxicity (Aβ42, αS and tau) possess high abundance, whereas oligomers from the sole functional amyloid system investigated (Ure2) exhibit low abundance, as might be expected given the well-established link between oligomer concentration and pathology in toxicity assays. The ability to determine such values should allow us in the future to derive comparative values of oligomer toxicity, normalized for concentration. Such values have already been computed for oligomers formed at equilibrium between different αS mutants (49).
The three key parameters defined in this paper form a basis for future investigations of oligomer kinetic properties in a wide variety of environments. Given their significance in amyloid diseases, determining how their properties change in vivo is of special interest. The far lower physiological concentrations of monomeric proteins means that oligomer abundance, and also productivity where , is likely decreased in living systems. However, other effects such as specific interactions with membranes and chaperones, molecular crowding, and local heterogeneities in concentration may also be of importance. Rather than speculate on their net impact, we instead provide in SI Appendix, Table S5 a list of key differences between in vitro and in vivo environments and a qualitative assessment of how each of these are likely to affect the parameters, to show what remains to be understood before this question can be fully answered.
Materials and Methods
Upper Bound for Fibrillar Oligomer Concentration.
The maximum possible concentration of a fibrillar oligomer of length monomers produced via primary nucleation is that attained at steady state under a constant monomer concentration. This value is given as a number concentration by the late-time limit of equation 26 in ref. 50: . The maximum possible number concentration of a fibrillar oligomer of length produced via secondary nucleation, on the other hand, is given by equation 30 in ref. 51 as . To calculate an upper bound on the total concentration of fibrillar oligomers, we must first choose a cutoff for the maximum number of monomers a fibrillar species may contain to still be considered oligomeric. Since our upper bounds for the concentrations of both primary and secondary oligomers of length monomers are independent of , we can calculate a generous upper bound on the total number concentration of fibrillar oligomers of all lengths present at any time, , by simply multiplying these expressions by . For simplicity, we instead use , yielding:
| [8] |
where is the rate constant for the fastest fibril-nucleation process present (primary or secondary, i.e., or ), and , or in the absence of secondary nucleation. For all proteins considered in the present study, we find that is far lower than experimentally observed concentrations of oligomers; this indicates that the oligomers observed experimentally are predominantly nonfibrillar and not able to undergo the rapid elongation characteristic of fibrillar species. This conclusion negates the need for explicitly considering the contribution of fibrillar oligomers when modeling experimental data. We illustrate this conclusion with the example of Aβ42. Here, for an of 5 M, , , and (26). Then, choosing a generous , is at most 4 pM, compared with an observed oligomer concentration of around 75 nM. Full details for other systems are given in SI Appendix, Table S3.
Experimental Protocols.
Although the data shown in Fig. 2 are taken from previous works, it is still useful to give a brief account of the experimental techniques used to collect them. Reaction conditions are given in SI Appendix, Table S4. Note that, for each protein studied here, both oligomer and fibril mass concentration measurements were performed on protein-aggregation reactions occurring under the same reaction conditions and in the same apparatus. Aliquots were taken from these reactions as necessary and immediately quenched to prevent any further reaction. This ensured that measurement methods for both oligomers and fibrils were reporting on the same reactions and did not themselves influence the reactions, such that all of the data could be fitted globally to kinetic models.
Oligomer Concentration Measurements.
The tau, Ure2, and αS oligomer concentration data in Fig. 2 were detected by single-molecule fluorescence resonance energy transfer (FRET). The proteins were first labeled with donor and acceptor fluorophores prior to being permitted to aggregate. Oligomer number concentrations were recorded by taking aliquots from the aggregation reaction and performing confocal single-molecule FRET measurements; several repeats were taken at each time point to permit the calculation of error bars. For further details, see refs. 8, 31, 32, and 39. To obtain the Aβ40 and Aβ42 oligomer number concentration data in Fig. 2, by contrast, 3H-labeled recombinant monomeric protein were synthesized, purified, and allowed to aggregate in plate-reader wells. For each time point, samples from 12 wells were combined and centrifuged, with the oligomer fraction isolated from the supernatant by size-exclusion chromatography prior to liquid scintillation counting. No repeats were performed; instead, it was decided to increase the measurement frequency in rapidly changing regions of the curve, to give more useful data for kinetic model fitting. For further details, see ref. 33.
Fibril Mass Concentration Measurements.
Fibril mass concentration data for Ure2 and for αS in the presence of nanobodies were recorded by taking aliquots from aggregation reactions of unlabeled protein performed under the same conditions, at the same concentrations and in the same reaction vessel as that used to generate aliquots for oligomer concentration measurements. These aliquots were quenched by dilution into a ThT solution and fluorescence rapidly measured using a fluorimeter (8, 39). Fibril mass concentration for tau and for αS in the absence of nanobodies was instead inferred from monomer concentration data recorded by single-molecule FRET techniques at the same time as the oligomer concentrations. For further details, see refs. 31 and 32. These data are shown in Fig. 2. For Aβ40 and Aβ42, on the other hand, fibril mass concentration data were taken from earlier studies using the same reaction conditions (26, 38). In these studies, data were collected in situ by ThT assays using a plate reader and unlabeled peptides, with the aggregation reaction occurring in the same plate-reader wells as were used in the oligomer measurements. In situ ThT measurements in a plate reader are continuous; therefore, repeats of the entire aggregation reaction must be taken rather than repeats at specific time points, and calculating error bars would be misleading. Instead, in accordance with with long-established experimental protocol (26, 38, 52), all repeats are displayed.
Data-Fitting Methodology.
Since data for tau and Ure2 oligomer concentration were available at only a single initial monomer concentration, the reaction mechanisms (as well as for tau and for Ure2) were instead inferred from a variety of orthogonal experiments performed in the original studies (8, 32) and earlier studies (43, 53), including bulk concentration-variable ThT assays for fibril formation. The values for were finally determined by fitting the rate equations 1–3 numerically to the combined fibril mass and oligomer concentration data displayed in Fig. 2 A and B (the remaining reaction orders were invisible to the fitting process and so were assigned arbitrary values). These values are used directly in the analytical model derived in this paper and plotted against the data in Fig. 2 A and B.
In the case of Aβ40 and Aβ42 aggregation, the bulk kinetic parameters and were accurately determined by bulk model fitting in earlier works (26, 38), for which multiple initial monomer concentrations were available. The oligomer model parameters were then originally determined in ref. 33 by globally fitting the oligomer concentration data to an analytical solution to Eqs. 1–3 of slightly lower accuracy than the highly accurate model presented here and using Eqs. 6–7 alongside SI Appendix, Eqs. S12 and S16 as additional constraints. Entering these parameters into our model still gives sufficiently accurate fits to the data; these fits are displayed in Fig. 2 C and D.
Finally, the models originally used to fit αS data in refs. 31 and 39 were incomplete, being early-time only and also lacking a dissociation reaction step. This made it necessary to refit the data to our model; the revised fits are shown in Fig. 2E. Both fibril mass and oligomer concentration data are based on multiple initial monomer concentrations, permitting a complete characterization of the rate parameters; however, the data are not accurate enough to determine , which is therefore arbitrarily set to zero. To fit the data with nanobodies, collected at only one initial monomer concentration, requires only that we change (fits shown in Fig. 2F).
Access to Data, Associated Protocols, Code, and Materials.
All data were taken from previously published works; these have been clearly referenced throughout this paper. Full experimental protocols can be found in these references; brief summaries have been reproduced in Materials and Methods. Analysis protocols are outlined in some detail in Materials and Methods. Where necessary, data fitting to analytical models was performed in Mathematica.
Supplementary Material
Acknowledgments
We gratefully acknowledge the contributions of C.M.D., who sadly passed away shortly before completion of this work. We thank R. L. Jack and P. G. Bolhuis for useful discussions. We are grateful to the Schiff Foundation (A.J.D.); Peterhouse, Cambridge (T.C.T.M.); the Swiss National Science Foundation (T.C.T.M.); the Ramon Jenkins Research Fellowship, Sidney Sussex College Cambridge (G.M.); National Natural Science Foundation of China Grants 21673278 and 31920103011 (to S.W. and S.P.); the Wellcome Trust (C.M.D. and T.P.J.K.); the Cambridge Centre for Misfolding Diseases (C.M.D. and T.P.J.K.); the Biotechnology and Biological Sciences Research Council (T.P.J.K.); the Swedish Research Council (S.L.); and the Frances and Augustus Newman Foundation (T.P.J.K.) for financial support. The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Seventh Framework Program (FP7/2007-2013) through the ERC grants PhysProt (Agreement 337969) and Molecular Mechanism of Amyloid β Aggregation (Agreement 340890).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
*The analytical solutions for the first two kinds of filament assembly are previously undescribed; the solution for the third kind is an incremental improvement over a model published recently by the authors (33).
†Note that in many of these systems, we might expect subpopulations of β-sheet oligomers to also be present, as it has frequently been observed that initially disordered oligomers mature over time into β-sheet–rich species (8, 31), but, if so, these clearly make a small contribution to the total oligomer population.
Note this metric is also related to the thermodynamic stability of oligomers compared with monomers.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1922267117/-/DCSupplemental.
References
- 1.Ahmed M., et al. , Structural conversion of neurotoxic amyloid-b(1-42) oligomers to fibrils. Nat. Struct. Mol. Biol. 17, 561–567 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lashuel H. A., Hartley D., Petre B. M., Walz T., Lansbury P. T., Neurodegenerative disease: Amyloid pores from pathogenic mutations. Nature 418, 291 (2002). [DOI] [PubMed] [Google Scholar]
- 3.Lashuel H. A., Overk C. R., Oueslati A., Masliah E., The many faces of a-synuclein: From structure and toxicity to therapeutic target. Nat. Rev. Neurosci. 14, 38–48 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ren Y., Sahara N., Characteristics of tau oligomers. Front. Neurol. 4, 102 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Narayan P., et al. , The extracellular chaperone clusterin sequesters oligomeric forms of the amyloid-b(1-40) peptide. Nat. Struct. Mol. Biol. 19, 79 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cremades N., et al. , Direct observation of the interconversion of normal and toxic forms of alpha-synuclein. Cell 149, 1048–1059 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shammas S. L., et al. , A mechanistic model of tau amyloid aggregation based on direct observation of oligomers. Nat. Commun. 6, 7025 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang J., et al. , Direct observation of oligomerization by single molecule fluorescence reveals a multistep aggregation mechanism for the yeast prion protein Ure2. J. Am. Chem. Soc. 140, 2493–2503 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee C. T., Terentjev E. M., Mechanisms and rates of nucleation of amyloid fibrils. J. Chem. Phys. 147, 105103 (2017). [DOI] [PubMed] [Google Scholar]
- 10.Dear A. J., Šarić A., Michaels T. C. T., Dobson C. M., Knowles T. P. J., Statistical mechanics of globular oligomer formation by protein molecules. J. Phys. Chem. B 122, 11721–11730 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Winner B., et al. , In vivo demonstration that alpha-synuclein oligomers are toxic. Proc. Natl. Acad. Sci. U.S.A. 108, 4194–4199 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guerrero-Muñoz M. J., et al. , Amyloid-b oligomers as a template for secondary amyloidosis in Alzheimer’s disease. Neurobiol. Dis. 71, 14–23 (2014). [DOI] [PubMed] [Google Scholar]
- 13.Conway K. A., et al. , Acceleration of oligomerization, not fibrillization, is a shared property of both alpha-synuclein mutations linked to early-onset Parkinson’s disease: Implications for pathogenesis and therapy. Proc. Natl. Acad. Sci. U.S.A. 97, 571–576 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cleary J. P., et al. , Natural oligomers of the amyloid-b protein specifically disrupt cognitive function. Nat. Neurosci. 8, 79–84 (2005). [DOI] [PubMed] [Google Scholar]
- 15.Chiti F., Dobson C. M., Protein misfolding, amyloid formation, and human disease: A summary of progress over the last decade. Annu. Rev. Biochem. 86, 27–68 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Bucciantini M., et al. , Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature 416, 507–511 (2002). [DOI] [PubMed] [Google Scholar]
- 17.Hellstrand E., Boland B., Walsh D. M., Linse S., Amyloid b-protein aggregation produces highly reproducible kinetic data and occurs by a two-phase process. ACS Chem. Neurosci. 1, 13–18 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Oosawa F., Kasai M., A theory of linear and helical aggregations of macromolecules. J. Mol. Biol. 4, 10–21 (1962). [DOI] [PubMed] [Google Scholar]
- 19.Oosawa F., Asakura S., Thermodynamics of the Polymerization of Protein (Academic Press, 1975). [Google Scholar]
- 20.Bishop M. F., Ferrone F. A., Kinetics of nucleation-controlled polymerization. a perturbation treatment for use with a secondary pathway. Biophys. J. 46, 631–644 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ferrone F. A., Hofrichter J., Eaton W. A., Kinetics of sickle hemoglobin polymerization. i. studies using temperature-jump and laser photolysis techniques. J. Mol. Biol. 183, 591–610 (1985). [DOI] [PubMed] [Google Scholar]
- 22.Ferrone F. A., Hofrichter J., Sunshine H. R., Eaton W. A., Kinetic studies on photolysis-induced gelation of sickle cell hemoglobin suggest a new mechanism. Biophys. J. 32, 361–380 (1980). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Michaels T. C. T., Knowles T. P. J., Mean-field master equation formalism for biofilament growth. Am. J. Phys. 82, 476–483 (2014). [Google Scholar]
- 24.Knowles T. P. J., et al. , An analytical solution to the kinetics of breakable filament assembly. Science 326, 1533–1537 (2009). [DOI] [PubMed] [Google Scholar]
- 25.Cohen S. I. A., et al. , Nucleated polymerization with secondary pathways. i. time evolution of the principal moments. J. Chem. Phys. 135, 065105 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cohen S. I. A., et al. , Proliferation of amyloid-b42 aggregates occurs through a secondary nucleation mechanism. Proc. Natl. Acad. Sci. U.S.A. 110, 9758–9763 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Burnham K. P., Anderson D. R., Model Selection and Multimodel Inference (Springer-Verlag, New York, NY, 2002). [Google Scholar]
- 28.Horrocks M. H., et al. , Fast flow microfluidics and single-molecule fluorescence for the rapid characterization of a-synuclein oligomers. Anal. Chem. 87, 8818–8826 (2015). [DOI] [PubMed] [Google Scholar]
- 29.Garcia G. A., Cohen S. I. A., Dobson C. M., Knowles T. P. J., Nucleation-conversion-polymerization reactions of biological macromolecules with prenucleation clusters. Phys. Rev. E 89, 032712 (2014). [DOI] [PubMed] [Google Scholar]
- 30.Tosatto L., et al. , Single-molecule FRET studies on alpha-synuclein oligomerization of Parkinson’s disease genetically related mutants. Sci. Rep. 5, 16696 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Iljina M., et al. , Kinetic model of the aggregation of alpha-synuclein provides insights into prion-like spreading. Proc. Natl. Acad. Sci. U.S.A. 113, E1206–E1215 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kjaergaard M., et al. , Oligomer diversity during the aggregation of the repeat region of tau. ACS Chem. Neurosci. 9, 3060–3071 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Michaels T. C. T., et al. , Dynamics of oligomer populations formed during the aggregation of Alzheimer’s Aβ42 peptide. Nat. Chem. 12, 445–451 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Meisl G., et al. , Scaling behaviour and rate-determining steps in filamentous self-assembly. Chem. Sci. 8, 7087–7097 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ferrone F. A., Hofrichter J., Eaton W. A., Kinetics of sickle hemoglobin polymerization. ii. a double nucleation mechanism. J. Mol. Biol. 183, 611–631 (1985). [DOI] [PubMed] [Google Scholar]
- 36.Šarić A., Michaels T. C. T., Zaccone A., Knowles T. P. J., Frenkel D., Kinetics of spontaneous filament nucleation via oligomers: Insights from theory and simulation. J. Chem. Phys. 145, 211926 (2016). [DOI] [PubMed] [Google Scholar]
- 37.Šarić A., et al. , Physical determinants of the self-replication of protein fibrils. Nat. Phys. 12, 874–880 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Meisl G., et al. , Differences in nucleation behavior underlie the contrasting aggregation kinetics of the Ab40 and Ab42 peptides. Proc. Natl. Acad. Sci. U.S.A. 111, 9384–9389 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Iljina M., et al. , Nanobodies raised against monomeric alpha-synuclein inhibit fibril formation and destabilize toxic oligomeric species. BMC Biol. 15, 57 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Glabe C. G., Structural classification of toxic amyloid oligomers. J. Biol. Chem. 283, 29639–29643 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Collins S. R., Douglass A., Vale R. D., Weissman J. S., Mechanism of prion propagation: Amyloid growth occurs by monomer addition. PLoS Biol. 2, e321 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Flagmeier P., et al. , Mutations associated with familial Parkinson’s disease alter the initiation and amplification steps of a-synuclein aggregation. Proc. Natl. Acad. Sci. U.S.A. 113, 10328–10333 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kundel F., et al. , Measurement of tau filament fragmentation provides insights into prion-like spreading. ACS Chem. Neurosci. 9, 1276–1282 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sang J. C., et al. , Direct observation of prion protein oligomer formation reveals an aggregation mechanism with multiple conformationally distinct species. Chem. Sci. 10, 4588–4597 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Buell A. K., et al. , Solution conditions determine the relative importance of nucleation and growth processes in a-synuclein aggregation. Proc. Natl. Acad. Sci. U.S.A. 111, 7671–7676 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wälti M. A., Orts J., Vögeli B., Campioni S., Riek R., Solution nmr studies of recombinant Ab(1–42): From the presence of a micellar entity to residual b-sheet structure in the soluble species. ChemBioChem 16, 659–669 (2015). [DOI] [PubMed] [Google Scholar]
- 47.Morel B., Carrasco M. P., Jurado S., Marco C., Conejero-Lara F., Dynamic micellar oligomers of amyloid beta peptides play a crucial role in their aggregation mechanisms. Phys. Chem. Chem. Phys. 20, 20597–20614 (2018). [DOI] [PubMed] [Google Scholar]
- 48.Hinshelwood C. N., On the chemical kinetics of autosynthetic systems. J. Chem. Soc. 136, 745–755 (1952). [Google Scholar]
- 49.Iljina M., et al. , Quantifying co-oligomer formation by a-synuclein. ACS Nano 12, 10855–10866 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Michaels T. C. T., Garcia G. A., Knowles T. P. J., Asymptotic solutions of the Oosawa model for the length distribution of biofilaments. J. Chem. Phys. 140, 194906 (2014). [DOI] [PubMed] [Google Scholar]
- 51.Michaels T. C. T., Lazell H. W., Arosio P., Knowles T. P. J., Dynamics of protein aggregation and oligomer formation governed by secondary nucleation. J. Chem. Phys. 143, 054901 (2015). [DOI] [PubMed] [Google Scholar]
- 52.Meisl G., et al. , Molecular mechanisms of protein aggregation from global fitting of kinetic models. Nat. Protoc. 11, 252–272 (2016). [DOI] [PubMed] [Google Scholar]
- 53.Wang Y. Q., et al. , Relationship between prion propensity and the rates of individual molecular steps of fibril assembly. J. Biol. Chem. 286, 12101–12107 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.