Abstract
The mechanical phenotype of a cell is an inherent biophysical marker of its state and function, with potential value in clinical diagnostics. Several microfluidic-based methods developed in recent years have enabled single-cell mechanophenotyping at throughputs comparable to flow cytometery. Here we present a highly standardized cross-laboratory study comparing three leading microfluidic-based approaches to measure cell mechanical phenotype: constriction-based deformability cytometry (cDC), shear flow deformability cytometry (sDC), and extensional flow deformability cytometry (xDC). We show that all three methods detect cell deformability changes induced by exposure to altered osmolarity. However, a dose-dependent deformability increase upon latrunculin B-induced actin disassembly was detected only with cDC and sDC, which suggests that when exposing cells to the higher strain rate imposed by xDC, other cell components dominate the response. The direct comparison presented here serves to unify deformability cytometry methods and provides context for the interpretation of deformability measurements performed using different platforms.
Keywords: cell mechanics, deformability cytometry, real-time deformability cytometry, suspended microchannel resonator, microfluidics, osmotic pressure, actin cytoskeleton
Introduction
Cell mechanical phenotype is a valuable indicator of changes in internal cell structure and is tightly associated with cell state and function1–3. Alterations in the mechanical properties of cells have been linked to many processes including cell cycle progression4, cancer malignancy5–8, leukocyte activation9–13, and stem cell differentiation11,14–16. Measurements of cell mechanics circumvent the need of extrinsic labels, such as fluorescent dyes, and therefore constitute an attractive, non-invasive biomarker for cell identification. Furthermore, as cell mechanics determines the magnitude of the mechanical response of cells to environmental forces, it can provide a biophysical perspective on cellular processes such as vascular circulation or migration in development and metastasis17,18.
Traditionally, methods such as atomic force microscopy19, micropipette aspiration20, optical stretching21, and parallel-plate rheology22 are used to quantify deformation of single cells under exposure to external stresses (compared in detail with a broader range of methods in a recent publication23). These methods evaluate time-resolved responses to force and enable extraction of physical properties such as elastic modulus or viscosity. They suffer, however, from technically-demanding and time-consuming procedures that limit measurement throughput and their extendibility beyond specialized laboratories. Microfluidic-based approaches developed in recent years constitute an attractive alternative3. They allow for robust, high-throughput assessment of the ability of cells to change shape under applied forces—their deformability—and enable thorough characterization of homogenous and heterogenous cell populations. Moreover, due to the ease of handling, these approaches have the potential to be implemented in biological laboratories and clinical settings.
The currently available microfluidic-based methods vary in type and magnitude of applied stress, the rate at which cells are deformed, and the way deformability is parametrized. One major class, constriction-based deformability cytometry (cDC), relies on driving cells through a constriction smaller than their diameter and measuring the time cells need to pass through the constriction7,13,24–26. The translocating cells are detected by means of optical imaging13,25,26, electrical resistance measurements24, or mechanical frequency changes of a suspended microchannel resonator (SMR)7. The deformability of cells is typically directly deduced from their passage time; however, in some variations of the method, additional image-based evaluation of cell deformation over time is performed and viscoelastic cell properties are extracted25,26. The remaining classes of deformability cytometry employ hydrodynamic flow to induce cell deformation in a contactless manner and infer cell deformability from image-based evaluation of cell shape. One class of such contactless methods, shear flow deformability cytometry (sDC), employs shear stress and pressure gradients in a long, narrow channel to deform cells into a bullet-like shape within a few milliseconds. A prominent example of this class constitutes real-time deformability cytometry (RT-DC)4 operating at strain rates on the order of 0.1 kHz. Another class of contactless methods, extensional flow deformability cytometry (xDC), uses an extensional flow usually associated with a cross slot microfluidic architecture. A well-established representative of this class is deformability cytometry (DC)11, typically operating at high strain rates on the order of 10 kHz. By increasing the viscosity of the measuring buffer and lowering flow rates, xDC can be adjusted to operate at lower strain rates (<2 kHz)27,28. Variabilities in the mode and timescales of operation, types of samples analyzed, and preparation conditions render it challenging to compare the published results obtained with the different deformability cytometry methods. Despite substantial work on identifying cellular structures that contribute to deformability changes with the individual methods4,7,11,16,29, a direct comparison of their performance is still missing.
To close this gap, we performed a highly-standardized cross-laboratory study comparing representatives of the three deformability cytometry classes: (i) an SMR-based cDC variant7, (ii) RT-DC4 as an example of sDC, and (iii) DC11 as an example of xDC. With these methods, we evaluated deformability of human promyelocytic leukemia (HL60) cells—from the same source and passage number—in two standardized assays subjecting the cells to osmotic changes and to latrunculin B-induced actin disassembly. Our results show that the deformability is altered by osmotic changes in all presented methods. In contrast, the deformability increase due to actin disassembly is detectable with cDC and sDC, but not with the xDC method implemented in this study. The direct comparison presented here provides context for interpretation of deformability measurements performed with the different high-throughput microfluidic-based techniques for measuring cell mechanics that operate at different strain rates and stress magnitudes.
Results
Microfluidic-based methods to assess cell deformability
In this work we employ three representatives of the major classes of microfluidic-based techniques for measuring cell deformability—cDC, sDC, and xDC. cDC refers here to an SMR-based variant utilizing a fluidic microchannel embedded in a silicon microcantilever7. Close to the cantilever apex, the microchannel features a constriction smaller than the cell size (6 μm wide, 15 μm high, and 50 μm long; Fig. 1a). Cells are driven through this constriction by a constant pressure of 1 kPa, and deform upon contact with the channel walls. The time taken by the cell to enter and pass through the constriction is assessed using changes in the resonance frequency of the microcantilever (Fig. 1a). In cDC, cell deformability, D, is defined as the inverse of cell passage time (Fig. 1a). The characteristic passage time of untreated HL60 cells is 23 ms (Supplementary Figure 1), entailing a throughput of a few cells per second and a strain rate of 0.04 kHz.
Figure 1|. Comparison of the microfluidic-based approaches for the determination of cell deformability used in this study.
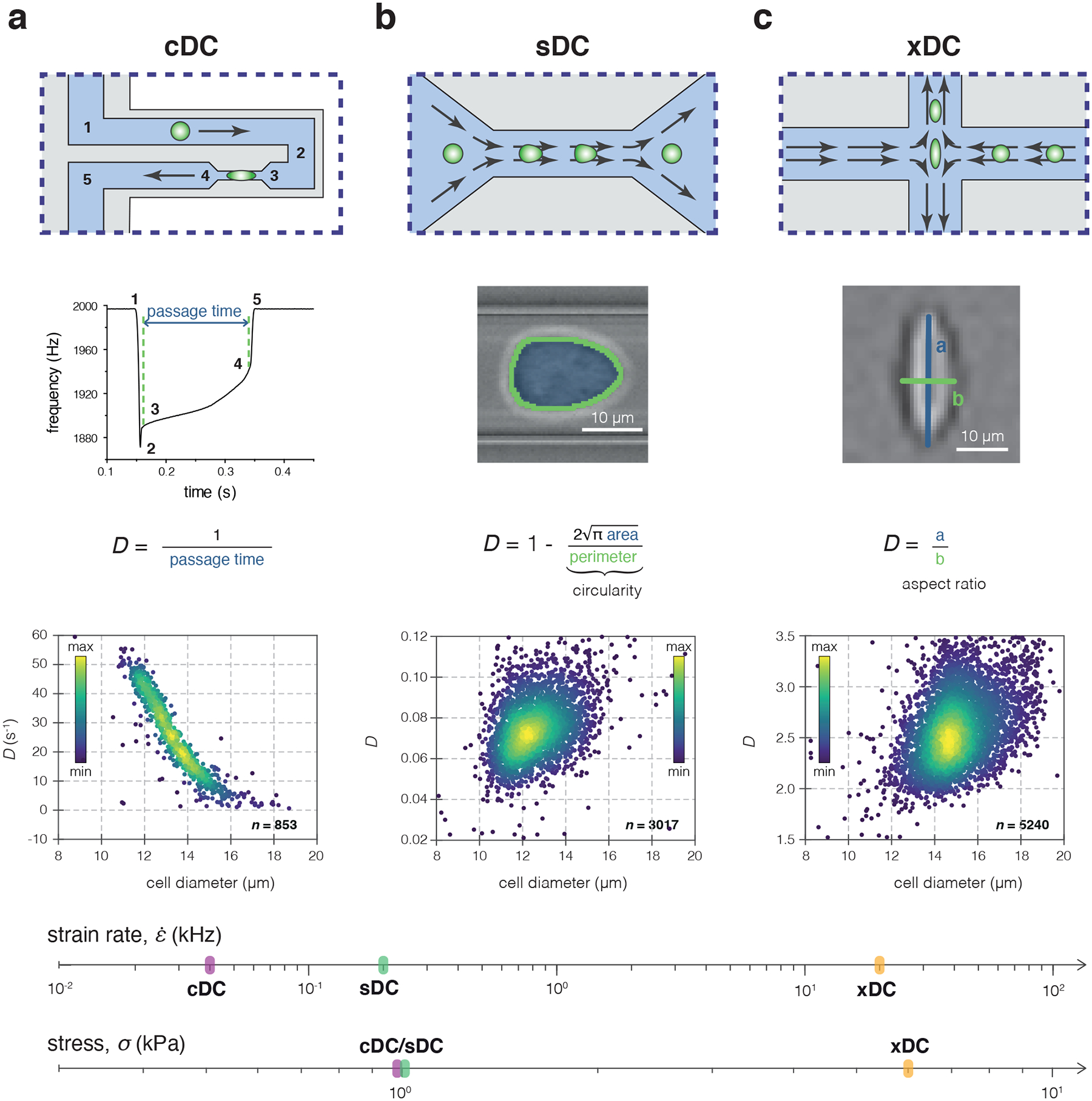
(a-c) Operation principle of cDC (a), sDC (b) and xDC (c). The upper row of each panel illustrates a schematic representation of the chip geometry used in the respective method. The middle row provides an overview of how the deformability, D, is defined for each method. The numbers 1–5 in the plot of frequency vs time correspond to the cell positions in the cDC microchannel indicated in the scheme above. In the lower row, typical scatter plots of D versus cell diameter from the respective measurements are presented. The color map corresponds to event density. The strain rate and stress applied to the cells in cDC, sDC and xDC are indicated on the corresponding axes at the bottom of the panel.
sDC and xDC (here referring to RT-DC4 and DC11, respectively) both rely on hydrodynamic flow to deform cells in a contactless manner, and on high-speed imaging to assess the ensuing cell deformation. Yet they operate using different channel geometries, and more importantly, different probing timescales and Reynolds numbers (see Table 1). The dimensionless Reynolds number (, where ρ is the fluid density, v the mean flow velocity, L the characteristic length of the flow system, and η the dynamic viscosity of the fluid) expresses the relative importance of inertial versus viscous forces and is equal to 0.4 for sDC and 150 for xDC. The very low Re in case of sDC (<< 1) indicates a dominance of viscous forces, characteristic for the type of laminar flow called Stokes flow. xDC, in turn, operates in an inertial flow regime, where inertial forces cannot be neglected and can lead to useful effects such as cell focusing30.
Table 1|.
Operation parameters of cDC, sDC, and xDC.
| cDC | sDC | xDC | |
|---|---|---|---|
| deformability measure | passage time−1 | 1−circularity | aspect ratio |
| detection | frequency shift | imaging | imaging |
| analysis | offline | real-time | offline |
| throughput (cells s−1) | 1 | 100 | 1,000 |
| timescale of cell deformation, τ(ms) | 10 | 1 | 0.01 |
| cell contact with channel walls | yes | no | no |
| channel width × height (μm) | 6 × 15 | 20 × 20 | 60 × 30 |
| mean flow velocity, v (m s−1) | 0.01 | 0.1 | 3.5 |
| viscosity of measuring buffer, η (mPa s) | 1 | 5.7 | 1 |
| Re number in the measuring channel | 0.1 | 0.4 | 150 |
| mean absolute strain, | 37% | 17% | 24% |
| strain rate, (kHz) | 0.04 | 0.2 | 20 |
| applied stress, σ (kPa) | ~ 1 | ~ 1 | ~6 |
In sDC, cells are driven into a funnel-like constriction in a microfluidic channel where they are deformed by shear forces and pressure gradients4,31 into a bullet-like shape (Fig. 1b). At the end of the ~300 μm long channel, the steady-state cell deformation, defined as 1−circularity (Fig. 1b), is evaluated, and constitutes cell deformability, D. Cells take a few milliseconds to travel through the channel and the strain is induced at a rate of 0.2 kHz. Typically, over 100 cells per second can be analyzed. For HL60 cells, chips with a square channel cross-section of 20 × 20 μm were used; which, together with hydrodynamic focusing implemented upstream of the deformation channel, assures that cells are not in contact with the channel walls. The stress acting on the cells during sDC measurements reaches values on the order of 1 kPa (see Supplementary Note 1).
In xDC, cells are stretched by an extensional flow in a cross-junction of a microfluidic chip (Fig 1c). The cells are delivered to the cross-junction at several meters per second, where they are fully decelerated and deformed via inertial forces within a few microseconds. This allows for analysis rates of over 1,000 cells per second. Cell size is determined from images recorded before the cell extension, and deformability, D, is defined as the maximal aspect ratio observed in the extensional flow region. The channels of the xDC chip have a rectangular cross-section of 60 × 30 μm. Before entry to the analysis region, cells are aligned via inertial focusing, and do not interact with the channel walls. Compared to sDC and cDC, xDC applies several-fold higher stress to the cells, and reaches a relatively high strain rate of 20 kHz (See Table 1 and Supplementary Note 1).
The raw data obtained with all three methods is typically displayed on a scatter plot of deformability versus cell diameter (Fig. 1). Hallmark parameters of the operation of cDC, sDC, and xDC are summarized in Table 1.
Osmotic shock-induced deformability changes are detectable consistently across methods
To compare the deformability measurements among cDC, sDC, and xDC, we first performed a series of osmotic shock experiments on HL60 cells. In hyperosmotic solutions water is driven out of cells (Fig. 2a), leading to a decrease in cell size and increased molecular crowding inside the cell, which has been linked to elevated cell stiffness32–35. On the contrary, in hypoosmotic conditions water enters the cells to compensate for the osmolyte concentration difference, leading to cell swelling and dilution of intracellular material (Fig. 2a), and a decrease in cell stiffness32,35.
Figure 2|. Effects of osmolarity changes on cell deformability.
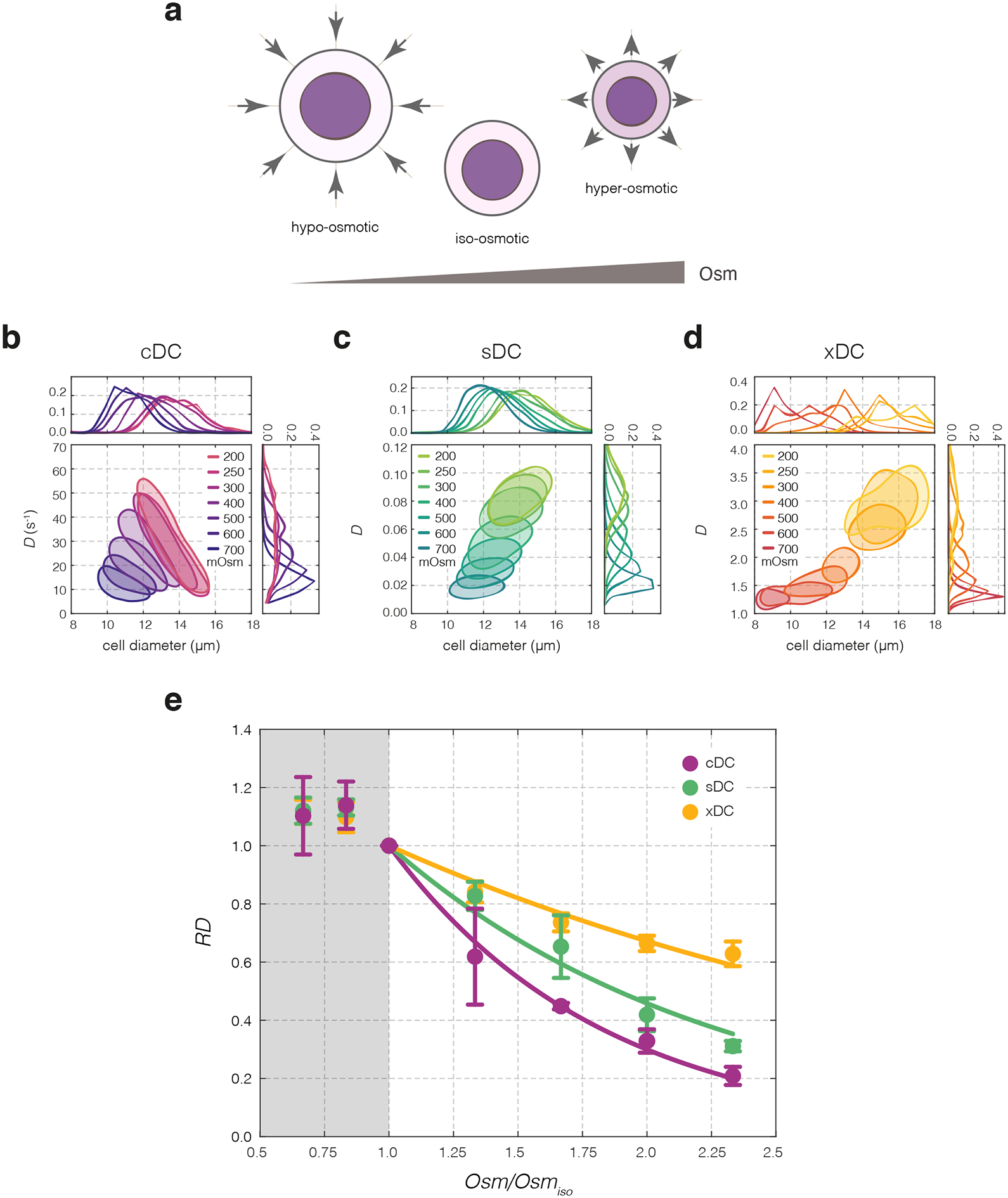
(a) Extracellular osmolarity when decreased beyond physiological (isoosmotic) conditions causes cell swelling and dilution of intracellular material, whereas an increase of extracellular osmolarity results in cell shrinkage and an increase in macromolecular crowding inside the cell. Arrows indicate the direction of water flow. (b–d) Deformability changes upon osmolarity treatment observed in exemplary cDC (b), sDC (c) and xDC (d) experiments. 50%-density contour plots of deformability, D, versus cell diameter for HL60 cells treated with increasing osmolarity is accompanied by deformability and cell diameter histograms. (e) Relative deformability, RD, as a function of normalized osmolarity, Osm/Osmiso, for cDC (purple), sDC (green) and xDC (yellow) measurements. Data points represent means of medians of multiple experimental replicates (n = 3, 4, and 4, for cDC, sDC, and xDC, respectively), and error bars represent standard deviation. Lines represent exponential fits to data. Hypoosmotic shock data excluded from the fitting procedure is shaded in gray.
To induce an osmotic shock response, the buffer’s osmolarity was altered with respect to the HL60 physiological osmolarity of 300 mOsm. Hyperosmotic solutions with osmolarities ranging from 400 to 700 mOsm were prepared by adding mannitol to the measurement buffer. Hypoosmotic solutions with osmolarities of 250 and 200 mOsm were prepared by diluting the measurement buffer with water. To minimize biological batch-to-batch variability in cell properties, we shared an HL60 cell subline (HL60/S4) between the three participating laboratories at the same passage number. Cells were exposed to altered osmolarity for 10 minutes before measuring. Consistently across the methods, we observed that the hyperosmotic conditions caused a decrease in cell size and deformability, while hypoosmotic conditions caused an increase of both parameters (Fig. 2b–d, Supplementary Figure 2 and 3). Since the observed deformability response to hypoosmotic shock shows non-monotonic evolution over time (Supplementary Figure 4), we excluded the hypoosmotic conditions from further analysis.
To facilitate the comparison of deformabilities measured with the individual methods, we introduced relative deformability, RD, calculated with respect to the control condition (see Online Methods and Supplementary Figure 3). The relationships between RD and the normalized extracellular osmolarity upon hyperosmotic shock for each method were fit with an exponential curve (Fig. 2e, Supplementary Table 1) with the following formula: , where λ is the decay constant that describes the sensitivity of RD to the change in the osmolarity, Osm, normalized to the isosmotic condition, Osmiso. The exponential fits provide the best description of the obtained results, as compared to linear and power law fits (Supplementary Figure 5).
Although all three methods follow the same exponential trend of decreasing RD with increasing osmolarity, the decay constants λ differ. This is confirmed by the results of pairwise F-tests, which show that there is a significant difference between the cDC and xDC curves (F1,35 = 70.6, p = 6.5 × 10−10), cDC and sDC curves (F1,35 = 29.8, p = 3.9 × 10−6), as well as between sDC and xDC curves (F1,38 = 89.6, p = 1.5 × 10−11). The sensitivity of the exponential decay, λ, is highest for cDC, reaching values that are 1.5 and 3 times higher than those obtained for sDC and xDC, respectively (Supplementary Table 1).
Sensitivity to actin disassembly is method-dependent
To further interrogate the differences in deformability measurements between cDC, sDC, and xDC, we compared their performance in detecting actin disassembly induced by latrunculin B (LatB). The actin cytoskeleton is recognised as a prominent contributor to cell mechanics at low strains, and its destabilisation with chemical agents is known to reduce cell stiffness26–29,36. In suspended cells, actin filaments are predominantly organised into an actin cortex—a thin, crosslinked network underlaying the plasma membrane37. LatB binds free actin monomers (G-actin) thereby inhibiting actin polymerization and destabilizing filamentous actin structures (F-actin), such as the actin cortex, in a dose-dependent manner38,39(Fig. 3a).
Figure 3|. Effects of LatB-induced actin disassembly on cell deformability.

(a) LatB causes dose-dependent disassembly of actin cytoskeleton by scavenging actin monomers. (b–d) Deformability changes of HL60 cells upon LatB treatment observed in exemplary cDC (b), sDC (c), and xDC (d) experiments. 50%-density contour plots of deformability, D, versus cell diameter for HL60 cells treated with increasing dose of LatB are accompanied by deformability and cell diameter histograms. (e) Relative deformability, RD, as a function of LatB dose for cDC (purple), sDC (green) and xDC (yellow) measurements (closed circles). Data points represent means of medians of multiple experiment replicates (n = 3, 5, and 4, for cDC, sDC, and xDC, respectively), and error bars represent standard deviation. Lines are four-parameter log-logistic fits, with LatB half maximal effective concentration, EC50, indicated with open circles.
We treated HL60 cells with a range of LatB concentrations (1−100 ng ml−1, corresponding to 2.53−253 nM), along with a DMSO vehicle control, and performed deformability measurements with cDC, sDC, and xDC (Fig. 3b–d). As revealed by analysis of variance (ANOVA), LatB treatement had a significant effect on the cell deformability as measured with cDC (F6,16 = 17.2, p = 3.6 × 10−6) and sDC (F6,28 = 34.3, p = 1.2 × 10−11). In contrast, the xDC measurements did not reveal significant deformability changes upon LatB treatment (F6,21 = 0.38, p = 0.89), though a subtle deformability decrease at the highest LatB concentration (100 ng ml−1) was observed (Fig. 3d–e, and Supplementary Figure 6). Interestingly, when an increased flow rate was used in sDC, cell deformability reached its maximum at 50 ng ml−1 LatB concentration and showed a decline at 100 ng ml−1 (Supplementary Figure 7a). Additionally, with increased flow rate the overall magnitude of the RD response showed a decrease (Supplementary Figure 7b). Increase of LatB concentration beyond 100 ng ml−1 caused decrease of deformability as observed with cDC and sDC (Supplementary Figure 8), consistent with the trend observed previously with xDC11. For all three methods, cell size remained fairly constant at low LatB concentrations. However, at LatB concentrations of 50 ng ml−1 (cDC) and 100 ng ml−1 (all three methods) the determined cell size decreased slightly (Supplementary Figure 9).
The change of RD in response to increasing LatB concentration exhibited a sigmoidal dose-response trend for cDC and sDC, while xDC results did not yield a significant fit (Fig. 3e, Supplementary Table 2). The half-maximal effective concentration, EC50, reached 11.9 ng ml−1 for cDC and 14.9 ng ml−1 for sDC. The upper RD response limit was also similar for these two methods, reaching 1.46 for cDC and 1.52 for sDC. Concurrently, there was no significant difference between the obtained cDC and sDC fits (F4,50 = 0.6, p = 0.69), whereas significant differences were found between separate cDC and xDC curves (F4,43 = 44.3, p = 1.0 × 10−14), as well as between sDC and xDC curves (F4,55 = 63.7, p = 5.3 × 10−20).
Discussion
Integrating mechanical characterization into the current view of cellular behaviour is paving the way towards a more comprehensive understanding of many physiological and pathological processes17,18 with potential clinical diagnostic value1,2,8,12,40. Establishment and validation of methods measuring the mechanical properties of cells is providing grounds for further developments in the field. In a recent publication23, elastic and viscous moduli of a standardized cell line were measured with several traditional techniques, revealing a spread of obtained values over several orders of magnitude. This variability was attributed to the magnitude of applied stress and strain rate, probe size, probing length scale, and whether the cells were attached or in suspension. Here we complemented this analysis by performing a cross-laboratory comparison of three widely-used microfluidic cell deformability measurement techniques, cDC, sDC, and xDC. While applying different strain rates and stresses (see Table 1), all three methods probe whole-cell deformation in a suspended cell state which reduces potential sources of variability.
All three techniques consistently measured an exponential decrease of deformability with increasing osmolarity, albeit with varying sensitivity (see Figure 2 and Supplementary Table 1). The change in cell volume induced by osmotic shock leads to a multifaceted change in the internal structure not only within the cytoplasm, but also in the cell nucleus41. Although the osmotic response can trigger changes in the relative F-actin content42 and actin cytoskeleton structure35, the overall changes in mechanical properties were shown to be actin-independent and attributed mostly to macromolecular crowding inside the cell33. We therefore conclude that the density of packing of the colloidal fraction inside the cell induces deformability changes detectable across all tested methods.
Deformability measured with cDC and sDC increased with increasing dose of the actin destabilizing drug LatB, while xDC measurements yielded no significant change in deformability upon treatment. This discrepancy can likely be attributed to the difference in applied strain rates. cDC and sDC induce strain at the rate of 0.04 and 0.2 kHz, respectively, and show an almost identical change in the measured deformabilities upon LatB treatment (see Figure 3 and Supplementary Table 2). xDC, on the other hand, applies strain at a rate of 20 kHz, and has been previously reported to not measure significant responses to actin cytoskeletal perturbations11, presumably due to fluidization of actin networks observed at high strains magnitudes and strain rates43,44. This is further supported by the fact that adapting xDC to operate at lower strain rates enables detection of deformability changes upon disruption of actin cytoskeleton in cells27,28 and by the decreased dynamic range of relative deformability response when using increased flow rates in sDC (Supplementary Figure 7). At high doses of LatB, corresponding to drug-induced substrate detachment observed for adherent cells11,38, the cells exhibit a reduction of deformability (Supplementary Figure 8 and previously published xDC measurements11), indicating a biphasic nature of the cell mechanical response to LatB-induced actin disassembly.
In addition to measuring cell deformability, each of the presented methods features a set of distinct functionalities that expand the dimensionality of performed measurements. The SMR-based cDC provides additional parameters describing cell passage through the constriction such as entry and transit velocities, and enables a highly sensitive readout of cell buoyant mass7,45. sDC stands out with its real-time data processing that renders the method compatible with active sorting downstream of deformability analysis46. Moreover, for sDC an integrated FACS-like readout of cell and cell compartment fluorescence is available47, as well as a theoretical framework allowing for the extraction of Young’s moduli from deformability data31,48. Recently developed dynamic RT-DC enables assignment of viscosity to measured cells by analysing the time evolution of cell deformation in the channel49. xDC surpasses cDC and sDC with its immense throughput. Finally, in all techniques bright-field cell images are collected and can be used for extraction of additional image-based features for further cell characterisation.
In the light of our results, the use of cDC or sDC is recommended when probing cellular changes involving the actin cytoskeleton, and all three methods are equally recommended when changes in cytoplasmic packing are at play. Since cDC is the only method which involves physical contact of cells with the channel walls, it is recommend for studies in which cell friction or retention in processes such as microcirculation is of interest. xDC, in turn, was previously shown to provide a good readout of changes in structures localised deeper in the cells, such as the nucleus11. For further reference, a comprehensive overview of studies performed using these deformability cytometry classes is presented in Supplementary Table 3.
Taken together, the comparison study presented here aids the understanding of the strengths and limitations of existing deformability cytometry methodologies, provides context for interpreting deformability measurements across various platforms, and fosters cell deformability as a powerful metric for mechanophenotyping at throughputs that mark a new era of measuring cell mechanics50.
Online Methods
Cell culture.
The HL60/S4 cell subline (RRID: CVCL_II77; received from Donald E. Olins and Ada L. Olins, Department of Biology, Bowdoin College, Brunswick, Maine, 04101, USA) was cultured in ATCC-modified RPMI 1640 medium (Gibco) with 1% penicillin/streptomycin (Gibco) and 10% heat-inactivated FBS (Gibco). Cells were grown at 37°C, with 5% CO2, at densities between 105 and 106 cells ml−1 with subculturing every second day. The cell line stocks were shared between the three participating laboratories at the same initial passage number and were used within 10 passages upon receipt.
Osmotic shock.
The measured osmolarity of the cell culture media and measurement buffers was 300 mOsm (Fiske 210 Micro-Sample Osmometer, Advanced Instruments, Nordwood, MA). Hyperosmotic media was prepared by adding 18.22, 36.43, 54.65, and 72.86 mg of D-Mannitol (MW: 182.172 g mol−1, Sigma Aldrich, St. Louis, MO) per 10 ml of the appropriate measurement buffer to obtain solutions of 400, 500, 600, and 700 mOsm, respectively. Hypoosmotic media was prepared by adding 1 part of DI H2O to 2 or 5 parts of the measurement buffer to obtain a solution of 200 or 250 mOsm, respectively. HL60 cells at a density between 0.5–1.0 × 106 ml−1 were centrifuged at 180 × g for 5 minutes and resuspended in osmolarity-adjusted measurement buffer. Cells were then incubated for 10 minutes at 37°C, 5% CO2 before measurement. The subsequent deformability measurements were conducted at room temperature (22–24°C).
LatB treatment.
Latrunculin B (MW 395.5 g mol−1, Sigma Aldrich, St. Louis, MO) stock solution was prepared by dissolving the powder in DMSO at a concentration of 1 mg ml−1 and the same stock solution was shared between the participating laboratories. The stock solution was further diluted in DMSO to 10,000× the desired concentration, to achieve equal DMSO concentration in all treatments (0.01 % v/v). Subsequently, LatB was diluted 10,000× in the appropriate measurement buffer to final LatB concentrations of 1, 5, 10, 25, 50 and 100 ng ml−1. HL60 cells at a density between 0.5 and 1.0 × 106 ml−1 were harvested by centrifugation at 180 × g for 5 minutes, resuspended in LatB-containing solution, and incubated for 30 minutes at 37°C, 5% CO2 prior to measurement. The subsequent deformability measurements were conducted at room temperature (22–24°C).
cDC measurements.
The suspended microchannel resonator (SMR) utilized in this manuscript consisted of a 6 μm wide, 50 μm long, and 15 μm deep constricted fluidic channel. Device dimensions and fabrication were similar to those described previously7. However, the device used in this study (fabricated by CEA-Leti, France) operated via piezoceramic actuation and had a piezoresistive readout system to monitor cantilever vibration frequency, similar to other types of SMR devices published previously51,52. Prior to each experiment, channel walls were passivated with 1 mg ml−1 polyethylene glycol (PLL(20)-g[3.5]-PEG(2), SuSoS, Switzerland). The applied pressure differential driving the fluid flow through the system remained constant at 1.0 kPa for each experiment. Single cell buoyant mass and passage time were determined from changes in the resonant frequency of the microcantilever. Individual cell diameters were determined by assuming a spherical shape for each cell, with its volume obtained by combining SMR buoyant mass measurements with Coulter counter volume measurements (Multisizer 4, Beckman Coulter, Brea, CA) as described previously7.
sDC measurements.
The production of the polydimethylsiloxane (PDMS) chip used for sDC measurements was performed according to previously described procedures4,53. The experimental procedure for sDC measurements is described in detail elsewhere15. In brief, cells were suspended in a viscosity-adjusted measurement buffer [phosphate saline buffer without Mg2+ and Ca2+ (PBS−) containing 0.5% (w/v) methylcellulose; adjusted in HAAKE Falling Ball Viscometer type C (Thermo Fisher Scientific, Waltham, MA) using ball number 3 to a viscosity of 15 mPa s, which corresponds to a viscosity of 5.7 mPa s at the measurement conditions54] and introduced to the device via a syringe pump. The overall flow rate during the experiments was equal to 0.04 μl s−1 (0.01 μl s−1 sample flow together with 0.03 μl s−1 focusing sheath flow) unless indicated otherwise. The imaging was performed at the end of a ~300 μm long channel with a 20 × 20 μm square cross-section with a high-speed camera at 2,000 frames s−1, and stroboscopic illumination with pulse duration <3 μs to avoid motion blurring. The cell area and deformation were determined from cell contours in real-time by an image processing algorithm developed in house4. Cell diameter was calculated during offline analysis from measured surface area and defined as for a circle with an equivalent surface area. To discard events with rough or incomplete contours, the results were filtered for an area ratio between 1.00 and 1.05. Area ratio is the ratio between the area enclosed by the convex hull of the cell contour and the raw area enclosed by the contour.
xDC measurements.
The xDC microfluidic device has been previously described11. Conventional soft lithography was used to fabricate the PDMS devices which were then bonded to glass slides. Cell suspensions were injected via a syringe pump at 750 μl min−1 into the microfluidic device with the channel dimensions of 60 × 30 μm. The region surrounding the cross-slot channel was imaged with a high-speed bright-field camera at approximately 500,000 frames s−1, with sub-microsecond exposure time. Videos were automatically analyzed by a MATLAB program that measures cell diameter before deformation, and cell aspect ratio while deforming the cells. Cell diameter is defined as the minimum cell diameter in the direction perpendicular to flow ±30° prior to the cell arrival at the cross-slot junction.
Relative deformability calculation.
Relative deformability, RD, expresses the deformability of the treated cells, Dt, normalized to the median deformability of cells in the control condition for a given experimental series, , according to the following formula: . Since the magnitude of deformability can be influenced by the cell size, RD calculations were based only on cells contained within the same 1-μm wide diameter bin most represented among all treatment and control samples for a given experimental set (see Supplementary Figure 3 and 6). This procedure facilitates the assessment of the effects of a treatment on deformability, independent of the effect on cell size. The influence of the bin selection on the observed trends is illustrated in Supplementary Figure 10 and 11.
Osmolarity data curve fitting.
The response of cells to an osmotic shock is a dynamic process and, after initial cell swelling or shrinking, cells are known to undergo a regulatory volume response55. Using sDC, we observed the response of cells between 2 and 30 minutes after exposure to osmotic shock. In the case of the hyperosmotic shock, the deformability and cell size decrease saturated in the first few minutes, whereas for the hypoosmotic shock, deformability and cell size values initially increased, but then began to slowly return to their original values (Supplementary Figure 4). Therefore, the values obtained for hypoosmotic shock at the fixed 10-minute measurement time were not included in the fitting procedure. The effect of normalized osmolarity, Osm/Osmiso, on relative deformability, RD, for hypertonic conditions was fit with: (i) exponential, (ii) power law, and (iii) linear functions, adjusted to pass through a fixed point (1,1) representing control measurement at the isotonic osmolarity, Osmiso. The fitting was performed using the nonlinear least-square nls function from the stats package in R (R Development Core Team). The goodness of different fits was assessed by evaluating their mean absolute residuals and Bayesian information criterion, BIC (BIC function in stats package in R). Exponential fit curves were compared in pairs via the F-test in R56. To account for multiple pairwise comparison across the three datasets, Bonferroni adjusted p values were calculated by multiplying p values by three57.
LatB dose–response curve fitting.
RD values calculated with respect to DMSO vehicle control for different LatB concentrations were used to fit a four-parameter log-logistic regression curve with the following formula58:
where [LatB] is the concentration of the drug, and b, c, d, e are the fit parameters, denoting: b – the steepness of the dose-response curve, c, d – the lower and upper limits of the response, and e – the effective does EC50 at which half-maximum response is obtained. The fitting was performed using drm function in drc package58 in R (R Development Core Team). Fit curves were compared in pairs via the F-test in R56. To account for multiple pairwise comparison across the three datasets, Bonferroni adjusted p values were calculated by multiplying p values by three57.
Data availability.
Source data for Figures 1–3 are provided alongside the manuscript. Dataset containing numerical values from all deformability measurements supporting findings of this study is available on figshare under the following identifier: doi:10.6084/m9.figshare.1170411959.
Code availability.
MATLAB and R codes used to perform statistical analysis and generate data representations shown in this manuscript are available on GitHub at https://github.com/dicarlo-lab/metadeformability.
Supplementary Material
Acknowledgements
The authors would like to thank P. Janmey for helpful discussions, J. H. Kang and D. Soteriou for useful comments on the manuscript, A. Mietke and C. Herold for sharing analysis codes, A. and D. Olins for the provision of the HL60/S4 cell line, the Microstructure Facility at the Center for Molecular and Cellular Bioengineering (CMCB) at Technische Universität Dresden (in part funded by the State of Saxony and the European Regional Development Fund) for help with the production of sDC chips. The authors acknowledge funding from the Alexander von Humboldt-Stiftung (Alexander von Humboldt Professorship to J.G.), the Ludwig Center for Molecular Oncology (S.R.M.), the Cancer Systems Biology Consortium U54 CA217377 from the NCI (S.R.M.), the German Federal Ministry of Research and Education (ZIK grant to O.O. under grant agreement 03Z22CN11), and a Presidential Early Career Award for Scientists and Engineers to D.D. (N00014-16-1-2997).
Footnotes
Competing Interests
M.U., H.E.M, J.S.B. and J.G. declare no competing interest. O.O. is a shareholder of Zellmechanik Dresden GmbH distributing real-time deformability cytometry; Zellmechanik Dresden GmbH owns a patent for Real-Time Deformability Cytometry (RT-DC): EU patent under the number EP 30 036 520 B1. S.R.M. is a founder of Travera and Affinity Biosensors. D.D. has financial interests in Cytovale Inc. which is commercializing deformability cytometry technology.
References
- 1.Di Carlo D A Mechanical Biomarker of Cell State in Medicine. J. Lab. Autom 17, 32–42 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Nematbakhsh Y & Lim CT Cell biomechanics and its applications in human disease diagnosis. Acta Mech. Sin 31, 268–273 (2015). [Google Scholar]
- 3.Darling EM & Di Carlo D High-Throughput Assessment of Cellular Mechanical Properties. Annu. Rev. Biomed. Eng 17, 35–62 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Otto O et al. Real-time deformability cytometry: on-the-fly cell mechanical phenotyping. Nat. Methods 12, 199–202 (2015). [DOI] [PubMed] [Google Scholar]
- 5.Guck J et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J 88, 3689–3698 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Swaminathan V et al. Mechanical Stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res. 71, 5075–5080 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Byun S et al. Characterizing deformability and surface friction of cancer cells. Proc. Natl. Acad. Sci. U. S. A 110, 7580–5 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tse HTK et al. Quantitative diagnosis of malignant pleural effusions by single-cell mechanophenotyping. Sci. Transl. Med 5, 212ra163 (2013). [DOI] [PubMed] [Google Scholar]
- 9.Bufi N et al. Human primary immune cells exhibit distinct mechanical properties that are modified by inflammation. Biophys. J 108, 2181–2190 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bashant KR et al. Real-time deformability cytometry reveals sequential contraction and expansion during neutrophil priming. J. Leukoc. Biol 1–11 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gossett DR et al. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci 109, 7630–7635 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Toepfner N et al. Detection of human disease conditions by single-cell morpho-rheological phenotyping of blood. Elife 7, e29213 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rosenbluth MJ, Lam WA & Fletcher DA Analyzing cell mechanics in hematologic diseases with microfluidic biophysical flow cytometry. Lab Chip 8, 1062–1070 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ekpenyong AE et al. Viscoelastic Properties of Differentiating Blood Cells Are Fate- and Function-Dependent. PLoS One 7, e45237 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Urbanska M et al. Single-cell mechanical phenotype is an intrinsic marker of reprogramming and differentiation along the mouse neural lineage. Development 4313–4321 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Lin J et al. High-throughput physical phenotyping of cell differentiation. Microsystems Nanoeng. 3, 17013 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mammoto T & Ingber DE Mechanical control of tissue and organ development. Development 137, 1407–20 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chan CJ, Heisenberg CP & Hiiragi T Coordination of Morphogenesis and Cell-Fate Specification in Development. Curr. Biol 27, R1024–R1035 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Radmacher M Studying the Mechanics of Cellular Processes by Atomic Force Microscopy. Methods Cell Biol. 83, 347–372 (2007). [DOI] [PubMed] [Google Scholar]
- 20.Hochmuth RM Micropipette aspiration of living cells. J. Biomech 33, 15–22 (2000). [DOI] [PubMed] [Google Scholar]
- 21.Guck J et al. The optical stretcher: a novel laser tool to micromanipulate cells. Biophys. J 81, 767–784 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thoumine O, Ott A, Cardoso O & Meister J-J Microplates: a new tool for manipulation and mechanical perturbation of individual cells. J. Biochem. Biophys. Methods 39, 47–62 (1999). [DOI] [PubMed] [Google Scholar]
- 23.Wu PH et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 1–8 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Adamo A et al. Microfluidics-based assessment of cell deformability. Anal. Chem 84, 6438–6443 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lange JR et al. Microconstriction Arrays for High-Throughput Quantitative Measurements of Cell Mechanical Properties. Biophys. J 109, 26–34 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nyberg KD et al. Quantitative Deformability Cytometry: Rapid, Calibrated Measurements of Cell Mechanical Properties. Biophys. J 113, 1574–1584 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Guillou L et al. Measuring Cell Viscoelastic Properties Using a Microfluidic Extensional Flow Device. Biophys. J 111, 2039–2050 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Armistead FJ, De Pablo JG, Gadêlha H, Peyman SA & Evans SD Cells Under Stress: An Inertial-Shear Microfluidic Determination Of Cell Behaviour. Biophys. J (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Golfier S et al. High-throughput cell mechanical phenotyping for label-free titration assays of cytoskeletal modifications. Cytoskeleton 74, 283–296 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Di Carlo D Inertial microfluidics. Lab Chip 9, 3038 (2009). [DOI] [PubMed] [Google Scholar]
- 31.Mietke A et al. Extracting Cell Stiffness from Real-Time Deformability Cytometry: Theory and Experiment. Biophys. J 109, 2023–2036 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Moeendarbary E et al. The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater 12, 253–261 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhou EH et al. Universal behavior of the osmotically compressed cell and its analogy to the colloidal glass transition. Proc. Natl. Acad. Sci 106, 10632–10637 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Guo M et al. Cell volume change through water efflux impacts cell stiffness and stem cell fate. Proc. Natl. Acad. Sci c, 201705179 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Guilak F, Erickson GR & Ting-Beall HP The effects of osmotic stress on the viscoelastic and physical properties of articular chondrocytes. Biophys. J 82, 720–727 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wakatsuki T, Schwab B, Thompson NC & Elson EL Effects of cytochalasin D and latrunculin B on mechanical properties of cells. J. Cell Sci 114, 1025–1036 (2001). [DOI] [PubMed] [Google Scholar]
- 37.Salbreux G, Charras G & Paluch E Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 22, 536–545 (2012). [DOI] [PubMed] [Google Scholar]
- 38.Spector I, Shorlet NR, Blasberger D & Kashman Y Latrunculins - novel marine macrolides that disrupt microfilament organization and affert cell growth: I. Comparison with cytochalasin D. Cell Motil. Cytoskeleton 13, 127–144 (1989). [DOI] [PubMed] [Google Scholar]
- 39.Morton WM, Ayscough KR & Mclaughlin PJ Latrunculin alters the actin-monomer subunit interface to prevent polymerization. Nat. Cell Biol 2, 376–378 (2000). [DOI] [PubMed] [Google Scholar]
- 40.Guck J & Chilvers ER Mechanics meets medicine. Sci. Transl. Med 5, 3–6 (2013). [DOI] [PubMed] [Google Scholar]
- 41.Finan JD & Guilak F The effects of osmotic stress on the structure and function of the cell nucleus. J. Cell. Biochem 109, 460–467 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hallows KR, Packman CH & Knauf PA Acute cell volume changes in anisotonic media affect F-actin content of HL-60 cells. Am. J. Physiol 261, C1154–61 (1991). [DOI] [PubMed] [Google Scholar]
- 43.Maruyama K, Kaibara M & Fukada E Rheology of F-actin I. Network of F-actin in solution. Biochim. Biophys. Acta - Protein Struct 371, 20–29 (1974). [DOI] [PubMed] [Google Scholar]
- 44.Janmey PA, Euteneuer U, Traub P & Schliwa M Viscoelastic properties of vimentin compared with other filamentous biopolymer networks. J. Cell Biol 113, 155–160 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Burg TP et al. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 446, 1066–1069 (2007). [DOI] [PubMed] [Google Scholar]
- 46.Nawaz AA et al. Using real-time fluorescence and deformability cytometry and deep learning to transfer molecular specificity to label-free sorting. 1–21 (2019). [Google Scholar]
- 47.Rosendahl P et al. Real-time fluorescence and deformability cytometry. Nat. Methods 15, 355 (2018). [DOI] [PubMed] [Google Scholar]
- 48.Mokbel M et al. Numerical Simulation of Real-Time Deformability Cytometry To Extract Cell Mechanical Properties. ACS Biomater. Sci. Eng (2017) doi: 10.1021/acsbiomaterials.6b00558. [DOI] [PubMed] [Google Scholar]
- 49.Fregin B et al. High-throughput single-cell rheology in complex samples by dynamic real-time deformability cytometry. Nat. Commun 10, 415 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Guck J Some thoughts on the future of cell mechanics. Biophysical Reviews vol. 11 667–670 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cermak N et al. High-throughput measurement of single-cell growth rates using serial microfluidic mass sensor arrays. Nat. Biotechnol 34, 1052–1059 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lee J et al. Suspended microchannel resonators with piezoresistive sensors. Lab Chip 11, 645–651 (2011). [DOI] [PubMed] [Google Scholar]
- 53.Herbig M et al. Real-Time Deformability Cytometry: Label-Free Functional Characterization of Cells. in 347–369 (Humana Press, New York, NY, 2018). doi: 10.1007/978-1-4939-7346-0_15. [DOI] [PubMed] [Google Scholar]
- 54.Herold C Mapping of Deformation to Apparent Young’s Modulus in Real-Time Deformability Cytometry. ArXiv http://arxiv.org/abs/1704.00572 (2017). [Google Scholar]
- 55.Hoffmann EK, Lambert IH & Pedersen SF Physiology of cell volume regulation in vertebrates. Physiol. Rev 89, 193–277 (2009). [DOI] [PubMed] [Google Scholar]
- 56.Motulsky H & Christopoulos A Comparing models using the extra sum-of-squares F test in Fitting models to biological data using linear and nonlinear regression: a practical guide to curve fitting. 138–142 (Oxford University Press, 2004). [Google Scholar]
- 57.Abdi H The Bonferonni and Šidák Corrections for Multiple Comparisons in Encyclopedia of Measurement and Statistics (ed. Salkind N) 103–107 (Sage, 2007). [Google Scholar]
- 58.Ritz C, Baty F, Streibig JC & Gerhard D Dose-response analysis using R. PLoS One 10, 1–13 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Urbanska M et al. MetaDeformability Dataset. figshare (2020) doi: 10.6084/m9.figshare.11704119. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source data for Figures 1–3 are provided alongside the manuscript. Dataset containing numerical values from all deformability measurements supporting findings of this study is available on figshare under the following identifier: doi:10.6084/m9.figshare.1170411959.


