Abstract
Computational fluid dynamics (CFD) modeling offers a powerful tool for the development of drug delivery devices using a first principles approach, but has been underutilized in the development of pharmaceutical inhalers. The objective of this study was to develop quantitative correlations for predicting the aerosolization behavior of a newly proposed dry powder inhaler (DPI). The dose aerosolization and containment (DAC) unit DPI utilizes inlet and outlet air orifices designed to maximize the dispersion of spray dried powders, typically with low air volumes (~ 10 ml) and relatively low airflow rates (~ 3 L/min). Five DAC-unit geometries with varying orifice outlet sizes, configurations, and protrusion distances were considered. Aerosolization experiments were performed using cascade impaction to determine mean device emitted dose (ED) and mass median aerodynamic diameter (MMAD). Concurrent CFD simulations were conducted to predict both flow field-based and particle-based dispersion parameters that captured different measures of turbulence. Strong quantitative correlations were established between multiple measures of turbulence and the experimentally observed aerosolization metrics of ED and MMAD. As expected, increasing turbulence produced increased ED with best case values reaching 85% of loaded dose. Surprisingly, decreasing turbulence produced an advantageous decrease in MMAD with values as low as approximately 1.6 μm, which is in contrast with previous studies. In conclusion, CFD provided valuable insights into the performance of the DAC-unit DPI as a new device including a two stage aerosolization process offering multiple avenues for future enhancements.
Keywords: Pharmaceutical aerosols, dry powder inhalers, quantitative analysis and design, spray dried powders, aerosolization with low air volumes, aerosol delivery to children
INTRODUCTION
Most dry powder inhalers (DPIs) contain the medication dose in either a capsule or blister (1–3). These common containment units enable accurate dose loading of the inhaler and protect the powder from environmental humidity and contamination, but are typically not optimized in terms of shape and piercing to maximize the powder aerosolization that occurs within them. In contrast, a new dose aerosolization and containment (DAC) unit is proposed that is engineered to protect the powder and maximize powder dispersion forming a high quality aerosol for efficient drug delivery to the lungs. This device was developed to enable aerosolization of spray dried powder formulation using a combination of a low actuation air volume (5–10 mL) delivered at a low flow rate (1–3 L/min) for pediatric applications and for use during various forms of non-invasive ventilation.
Using three-dimensional printing or injection molding the DAC unit is produced and contains single or multiple air inlet and outlet orifices that may protrude into the containment volume. Testing a similar device produced with hollow capillary inlets and exits, it was determined that aerosolization was improved when the inlet jet of air did not directly impinge upon the powder (4). Using a spray-dried powder formulation, these devices produced a typical mean (standard deviation, SD) mass median aerodynamic diameter (MMAD) of 1.8 (0.1) μm and mean (SD) emitted dose (ED) of 84.6 (6.3) % with small volumes (10 ml) of actuation air (5). The combination of low dispersion air volumes and flow rates results in short actuation times, which are expected to produce high turbulence, near sonic velocities, compressible flow, complex flow fields and sudden powder dispersion within the DAC devices (4, 5). Based on this high level of physical complexity, a computational fluid dynamics (CFD) model may be useful to better understand the performance of the DAC unit and to further optimize the system.
Computational fluid dynamics (CFD) simulates complex three-dimensional physics from a first principles approach using the conservation relations of mass and momentum (6, 7). As described in the study of Shur et al. (8), CFD simulations can capture features of DPIs that explain their performance during in vitro aerosolization testing. While useful, CFD and multi-physics models have not yet been developed that can capture both inhaler gas flow transport and breakup of an entire powder bed leading to microparticle formation (9–13). As an alternative, a potentially more efficient approach is to seek correlations between aerosolization metrics from in vitro experiments, such as measured MMAD and ED, and physically relevant dispersion parameters that can be captured with CFD (8, 14–18). For example, considering capsule-based devices, Shur et al. (8) report qualitative correlations between flow rate of air through the pierced capsule and aerosolization performance. Considering the particle phase, the impact velocity of particles on inhaler side walls was also qualitatively matched with performance (8).
From both in vitro experiments and CFD simulations, powder dispersion is typically directly correlated with turbulence exposure, which may be represented as a turbulent velocity, turbulent kinetic energy (k), turbulent intensity or turbulent shear stress. Using a test rig setup and a carrier-based powder formulation, Voss and Finlay (19) established a qualitative correlation between turbulent velocity and dispersion reported as fine particle fraction (FPF). Xu et al. (20, 21) proposed standardized entrainment tubes for the evaluation of aerosol formation and determined a direct quantitative relation between analytically calculated turbulent shear stress and FPF. Studies by Coates et al. (15–17, 22) were the first to compare CFD metrics with experimentally determined aerosolization performance. For a spray dried formulation and capsule-based DPI, Coates et al. demonstrated direct associations between a measure of turbulence (the integral scale strain rate) as well as inlet flow with FPF (15–17). Optimization of the Aerolizer device based on the analysis of Coates et al. and modified mouthpiece geometries produced a FPF of 63% with deposition in a mouth-throat replica of approximately 30% (23). Using spray dried powder formulations and a variety of dispersion designs including a 3D rod array, Longest et al. (14) could not identify a direct relationship between turbulent kinetic energy and deaggregation. However, a combination of turbulent kinetic energy and the turbulent length scale (l) revealed a strong correlation with deaggregation. Specifically, deaggregation was directly correlated high turbulent energy (signified by high k) occurring in small turbulent eddies (signified by small l).
While these previous in vitro and CFD analyses are useful for capsule-based DPIs, potentially different dispersion mechanisms are expected with the new DAC-unit design. If turbulence intensity or some other turbulent energy parameter were the most important, then designs where the inlet jet impacted the powder bed should produce better aerosolization. However, Farkas et al. (4) reported an opposite effect where improved dispersion was found in a device where the inlet jet and outlet orifice were aligned and the air jet did not impact the bed of powder. There is also a lack of quantitative CFD-based correlations for DPI performance using spray dried formulations, with the only exception being Longest et al. (14). Finally, only a few studies, have reported a relationship between aerodynamic factors and device emptying (15, 20, 21, 24), and no previous studies have established a quantitative relationship between turbulence and device emptying. A CFD model of the DAC unit in comparison with in vitro performance data would enable an understanding of the specific dispersion mechanisms occurring in this device and thereby enable optimization and accelerate development.
The objective of this study is to develop quantitative correlations that predict the performance of the new DAC units using concurrent CFD simulations and in vitro experiments. Using a highly dispersible spray dried formulation containing albuterol sulfate as the model drug (25, 26), aerosolization performance is assessed based on both ED and MMAD. CFD simulations of DAC units are used to evaluate dispersion factors based on both flow field and particle trajectory calculations. Comparisons between in vitro aerosol performance and CFD dispersion parameters are used to establish quantitative correlations capable of predicting performance. The predictive power of these correlations is then tested by operating the best performing device in a different orientation, which moves the location of the initial powder bed, and comparing CFD results with in vitro data.
MATERIALS AND METHODS
Materials
Albuterol Sulfate (AS) USP was purchased from Spectrum Chemicals (Gardena, CA) and Pearlitol® PF-Mannitol was donated from Roquette Pharma (Lestrem, France). Poloxamer 188 (Leutrol F68) was donated from BASF Corporation (Florham Park, NJ). L-leucine and all other reagents were purchased from Sigma Chemical Co. (St. Louis, MO). Quali-V, Hydroxypropyl methylcellulose (HPMC) capsules (size 0) were donated from Qualicaps (Whitsett, NC).
Device Designs and Operation
The main components of the dose aerosolization and containment unit are an inlet orifice, containment volume holding the spray dried powder, and outlet orifice (Figure 1). Airflow is injected into the inlet orifice with sufficient momentum to create a well-defined inlet air jet. This jet of inlet air is aligned with the inlet pathway and, due to momentum, continues in a straight line until it reaches a boundary or outlet. Secondary flows are induced by the inlet air jet and can occur in all other directions. The containment unit is loaded with a mass of spray dried powder which, due to gravity, forms an initial powder bed before the DPI is actuated. Based on the previous experimental study of Farkas et al. (4), the best dispersion of the powder occurs when the inlet air jet does not directly impinge on the powder bed. Instead, initial aerosolization of the powder should occur due to secondary flows. This initially aerosolized powder then enters the highly turbulent air jet and outflow orifice region where additional dispersion is expected to occur. In this manner, the rate of initial aerosolization can be controlled while maintaining regions of high turbulence to maximize dispersion. While this approach was shown to perform well, a number of design variables for optimal performance remain unresolved, such as inlet and outlet orifice diameters, inlet-to-outlet diameter ratio, and orifice protrusion distance into the containment volume.
Figure 1.
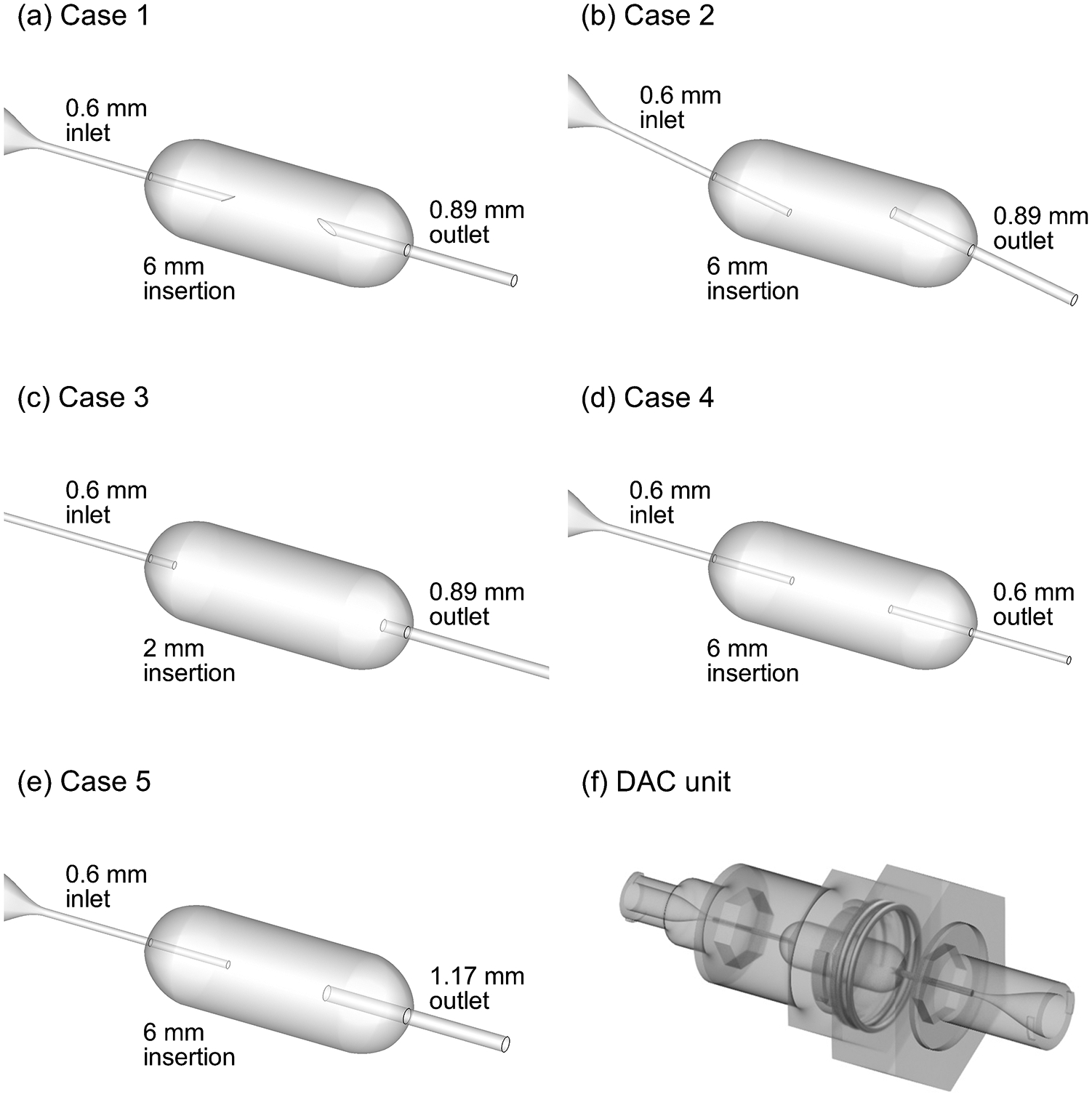
Inner surface geometries of the five dose aerosolization and containment (DAC) unit designs considered illustrating the inlet orifice (left-hand side), containment volume, and outlet orifice (right-hand side). Designs include (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5. (f) Rendering of the DAC unit device containing one of the five inner surface geometries.
In this study, multiple DAC-unit designs were considered, as shown in Figure 1. Based on best case performance in previous studies, the inlet orifice diameter was 0.6 mm in all five cases. The outlet orifice diameter ranged from 0.6 mm to 1.17 mm. A single design (Case 2) was considered in which the inlet air jet was directed toward the powder bed in order to ensure that the CFD-based correlations could capture performance with this arrangement. Inlet and outlet orifices protruded 6 mm into the containment volume in all cases except for Case 3, in which the inward protrusion distance was 2 mm. Sharpened capillaries were considered in Case 1; however, the presence of the sharpened capillary had little effect on dispersion metrics. Therefore, blunt orifices were considered in the remaining five cases to be consistent with the DAC-unit approach in which all components (inlet, containment volume and outlet) are manufactured as a single part.
Physical models of the DAC-unit DPIs were produced using 3D printing and rapid prototype assembly techniques. The DAC units were first drawn in Autodesk Inventor as separate inlet and outlet halves and saved as .STL files. Streamlined inlet and outlet sections were included in the physical models allowing for inlet and outlet diameters of 4.2 and 7.0 mm, respectively. The part files were then processed using Object Studio software and were built using a Stratasys Objet24 3D Printer (Stratasys Ltd., Eden Prairie, MN) using VeroWhitePlus material at a 32 μm resolution. Support material was cleaned away from the model material using a Stratasys waterjet cleaning station and the devices were allowed to fully dry before use. Custom cut stainless steel capillary tubes were inserted into the two halves of the DAC unit and glued into place using water-resistant epoxy. For ease of assembly and design parameter variation, the current study employed size 0 HPMC capsules to form an inner liner of the containment unit. The DAC unit was formed when the size 0 capsule was placed between the inlet and outlet halves, which were then sealed with a twisting motion. The hollow capillaries pierced the size 0 capsule forming the protruding inlet and outlet orifices. This flexible approach is intended for optimization of the flow pathway, and with future studies the DAC unit will be built from one material without the stainless steel capillaries and capsule.
To operate the DAC-unit DPI, the containment volume is initially filled with a mass of spray dried powder, which in this study was 10 mg. During operation, the long axis of the containment volume is typically oriented horizontally. As shown in Figure 2a, the resulting powder bed is formed by gravity and not in the path of the inlet air jet for all cases with the exception of Case 2. As an alternative orientation, Figure 2b illustrates a vertical positioning, which was only considered for the Case 3 geometry. Based on the 10 mg fill mass and inlet protrusion distance of 2 mm (Case 3), the vertical orientation also satisfied the condition of powder not in the direct path of the inlet air jet (Figure 2b). In this study, the DAC unit is actuated with 10 ml volumes of room air provided by a hand-actuated syringe. The syringe plunger is depressed quickly delivering the air in approximately 0.2 s (4), which results in a 3 L/min (LPM) flow rate through the system. In the experiments, five actuations of the syringe were performed for each trial, with a three-way valve used to fill the syringe with room air between each actuation.
Figure 2.
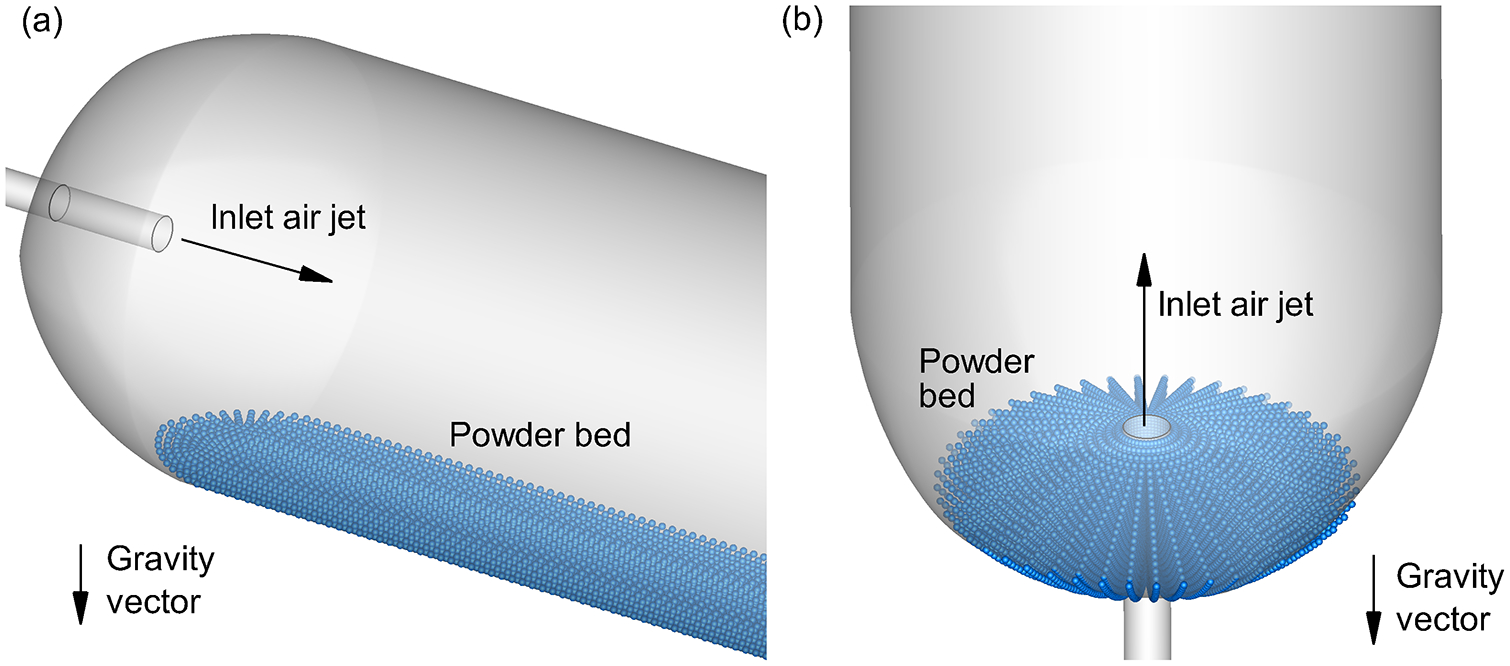
Representation of the powder bed for a 10 mg powder fill mass in the Case 3 design prior to actuation oriented in the (a) horizontal and (b) vertical directions.
Aerosol Characterization Experiments
Aerosol performance was assessed in each of the five cases in terms of aerodynamic particle size distribution and emitted dose. As a model formulation, a single batch of albuterol sulfate (AS) excipient enhanced growth (EEG) powder was produced using the optimized spray drying method described by Son et al. (25). A 10 mg dose of the EEG-AS formulation was weighed and manually filled into the size 0 capsules, which filled approximately 3% of the capsule volume, as shown in Figure 2. The capsule was placed within the two device halves, which were then closed and sealed with a 30° turn forming the DAC unit. The air-filled syringe was connected to the DAC-unit inlet. The outlet aerosol was fired directly into the preseparator of a Next Generation Impactor (NGI), which was turned on its side to avoid the need for an induction port. The DAC unit was positioned approximately 3 cm away from the NGI preseparator inlet using a custom adaptor. While approximately 3 LPM of airflow moved through the DAC unit in short bursts, a downstream vacuum pump was used to pull a total of 45 LPM of airflow through the NGI with makeup air entering in the gap formed by the custom adaptor between the device outlet and NGI inlet. The linear gap distance of the custom adaptor was approximately 1.1 cm providing an open area for flow of 283 mm2, which produces minimal turbulence and shear stress compared with conditions inside the DAC unit. The experiments were conducted under ambient conditions (T = 22 ± 3 °C and RH = 55 ± 5%) with the NGI at room temperature. The preseparator and individual stages of the NGI were coated with MOLYKOTE™ 316 silicone spray (Dow Corning, Midland, MI) to minimize particle bounce and re-entrainment. For each trial, the air syringe was refilled and actuated five times. All measurements were made with three replicates for each design configuration.
After aerosolization, drug masses retained in the DAC unit (containment volume, outlet orifice, and outlet flow pathway), and the drug collected on the preseparator, impaction plates and the filter of the NGI were recovered by washing with appropriate volumes of deionized water and quantified by high performance liquid chromatography (HPLC) analysis. The mass of AS retained in the device, determined by HPLC, was expressed as a percentage of the loaded AS dose. AS quantification was performed with a validated HPLC method using a Waters 2695 separations module with a 2475 fluorescence detector (Waters Co., Milford, MA). Chromatography was performed using a Restek Allure PFP 150 mm × 2.1 mm column (Bellefonte, PA). The mobile phase, consisting of methanol and ammonium formate buffer (20 mM, pH 3.4) in a ratio of 70:30, respectively, was eluted at a flow rate of 0.4 mL/min and the detector was set to an excitation wavelength of 276 nm and emission at 609 nm. The column temperature was maintained at 25 °C, and the volume of each sample injected was 100 μL. The limit of quantification was 0.5 μg/ml (25, 27). The DAC unit emitted dose (ED) was calculated by subtracting the mass of AS retained in the device from the loaded AS dose.
In order to determine the nominal dose of AS in the EEG-AS formulation, known masses of the formulation were dissolved in 50 ml of water and the mean AS content per mg of formulation was determined using HPLC analysis. For each aerosolization experiment, the measured formulation AS content and the mass of formulation loaded into the capsule was used to determine the loaded dose of AS.
The primary particle size of the powder formulation was tested using a Sympatec HELOS (Sympatec GmbH, Clausthal-Zellerfeld, Germany) laser diffraction system with a ASPIROS/RODOS aerosol dispersion accessory, which uses a pressure drop of 4 bar (400 kPa) to disperse a small amount of powder. Based on this preliminary analysis, the MMAD of the particles was calculated (using a theoretical particle density of 1.393 g/cm3) to be 1.18 μm. Fine particle fractions less than 5 μm (FPF<5 μm/ED) and less than 1 μm (FPF<1 μm/ED) were also calculated based on emitted dose to further determine aerosol characteristics. The FPF<5 μm/ED value for this powder batch was determined to be 100% while the FPF<1 μm/ED was 38.2%.
The cut-off diameters of each NGI stage at the operating flow rate of 45 LPM were calculated using the formula specified in USP 35 (Chapter 601, Apparatus 5) and were used to calculate MMAD and fine particle fractions of the delivered aerosol. MMAD was calculated by linear interpolation using a plot of cumulative percentage drug mass vs. cut-off diameter. T-tests were used with JMP-Pro® 12 (SAS Institute, Cary, NC) for statistical analysis. The p-value < 0.05 was considered as significant.
CFD Simulations
Based on a flow rate of 3 LPM (50 cm3/s) and inlet orifice diameter of 0.6 mm, the inlet velocity and Reynolds number are 176.8 m/s and 6,893, respectively. At this inlet velocity, the compressible effects of air should be considered and will result in variable air density and enhanced secondary velocities. The inlet airflow is also fully turbulent considering that the inlet Reynolds number of the jet is >4000. Based on previously established accuracy and computational efficiency (14, 28, 29), the two-equation low Reynolds number (LRN) k-ω turbulence model was selected including shear flow and compressible corrections (30). The standard ideal gas law was used to predict the variable density of air with isothermal wall conditions. Equations governing the conservation of mass and momentum as well as the LRN k-ω model can be found in previous publications (31, 32).
Multiple time scales exist in the DAC-unit flow field. At an upper level, the actuation period is 0.2 s. Moreover, flow oscillations with a period of approximately 0.001 s were also observed to occur. To address the inherent flow oscillations, a transient solution was performed with a time step of 0.0001 s. At this time step, simulating the entire 0.2 s actuation was computationally prohibitive. Instead, a consistent 100 time steps was applied to all CFD solutions. At the resulting 0.01 s time point, startup effects were observed to be negligible and the flow was in a state of cyclic oscillation. The quality of assessing the solution at one point in time will be assessed based on the predictive power of the correlations that are developed.
Particle trajectories were considered within the DAC-unit flow field. Sample particles were initialized within a powder bed as shown in Figure 2 for either horizontal or vertical actuation. These sample particles were only considered to be tracers recording a time history of turbulence exposure. As a result, a constant diameter of 1 μm was assessed. Moreover, inter-particle forces on the tracer particles were not considered. In this manner, a turbulent exposure history could be determined over the approximate trajectory course without the complexity of simulating the full scale breakup of the powder bed. The forces acting on each tracer particle were assumed to be drag and gravity, and the equations governing Lagrangian transport were provided in our previous publications (33, 34). To model random particle motion due to interactions with turbulent eddies, i.e., turbulent dispersion, a random walk method was employed (31, 35). A near-wall anisotropic correction to turbulent particle dispersion was also included (28, 36, 37). Particles were assumed to bounce with a restitution coefficient of unity upon wall contact. This boundary condition was selected because bouncing and re-entrainment are expected for primary particle aggregates through the system.
Construction of the computational grids and performance of the CFD simulations were based on previously established best practices (7, 28, 38). All grids were constructed with high quality hexahedral cells. As shown in our previous studies, hexahedral grids are more time intensive to construct, but provide higher quality solutions in shorter times with less cells (28, 39). For the five cases considered, grid independent results were achieved with meshes containing 976,000 – 1,028,000 cells based on negligible changes in the dispersion metrics. Consistent near-wall meshes and grid counts were also employed in all geometries.
The CFD package Fluent 14.5 was used to solve the flow field and particle trajectory equations in each of the cases. User-supplied Fortran and C programs were used for the calculation of initial flow and particle profiles, near-wall anisotropic turbulence approximations, near-wall particle interpolation, and dispersion metrics (34). All transport equations were discretized to be at least second order accurate in space. For the convective terms, a second order upwind scheme was used to interpolate values from cell centers to nodes. The diffusion terms were discretized using central differences. The particle trajectory solution was calculated using 4th-order Runge Kutta with an error control routine (40). Both wall impactions and discrete sampling of the turbulence field were conducted using approximately 12,000 or more representative monodisperse 1 μm particles with a density of 1.0 g/cm3. Simulating additional particles had a negligible effect on the particle-based dispersion metrics.
Dispersion Metrics
Dispersion metrics that were evaluated with CFD simulations were based on either flow field properties or history integrals of particles, as described in Table I. Based on previous studies (14–16, 19, 23), most dispersion metrics contained the turbulent kinetic energy, which is a measure of turbulent fluctuations and is defined (30)
| (1) |
where u′, v′ and w′ represent the fluctuating velocity components in three coordinate directions. In turbulence, the instantaneous velocity at a point (turbulent velocity) is composed of a fluctuating component, e.g., u′, and a time-averaged velocity component, e.g., . Viewed from a flow field perspective, the fluctuating velocities are caused by the turbulent eddies which occur due to instability and have a wide range of sizes. The presence of eddies can be represented as an enhanced viscosity, referred to as the turbulent viscosity (30), and is calculated as k / ω, where ω is the specific dissipation rate. The rate at which turbulent eddies are dissipated, or ω, is based on the energy in the eddy, represented as k, and the turbulent length scale, l, as (30)
| (2) |
where Cμ is a constant.
Table I.
Factors expected to influence dispersion of the aerosol.
| Factor name and symbol | Equation | Units | Interpretation |
|---|---|---|---|
| Flow Field Parameters | |||
| Volume-averaged turbulent kinetic energy of the flow field (kfield) |
Where Vol is the volume of the DAC unit and k is the turbulent kinetic energy at each location in the volume. |
m2/s2 | Turbulent kinetic energy arises from turbulent velocity fluctuations and is directly proportional to turbulent strength or intensity. It is expected that high k will break apart aggregates thereby reducing MMAD and will also help remove particles from the walls. |
| Volume-averaged specific dissipation rate of the flow field (ωfield) |
Where Vol is the volume of the DAC unit and ω is the specific dissipation rate at each location in the volume. |
1/s | The specific dissipation rate is defined as where l is the turbulent length scale and Cμ is a constant. High values of ω indicate elevated k together with small l. Longest et al. (14) interpreted this as high k in small eddies and proposed that this was ideal for maximizing small particle deaggregation using turbulence. |
| Non-dimensional turbulent kinetic energy of the flow field (k*field) |
Where Vinlet is the mean velocity of the inlet air jet. |
Non-dimensional | Vinlet has an inverse relation with expected particle residence time. Therefore, high Vinlet reduces the exposure time to the turbulent field and is expected to reduce deaggregation. A multiplier of 104 is used to increase values to O(10). |
| Non-dimensional specific dissipation rate of the flow field (ω*field) |
Where and provides a representative exposure time of particles to the flow field. |
Non-dimensional | Longer exposure time is expected to improve deaggregation. The resulting parameter is similar to the non-dimensional specific dissipation (NDSD) proposed by Longest et al. (14) and shown to correlate with deaggregation of airborne particles moving through a 3D array of rods. |
| Non-dimensional eddy viscosity (k*field / ω*field) | Non-dimensional | Represents turbulent or eddy viscosity, which significantly increases shear stress on the particles. The mean value represents eddy viscosity throughout the flow field. | |
| k*field x ω*field | Non-dimensional | Does not have a physical interpretation like the eddy viscosity. Instead, it represents a modified version of ωfield where k is increasingly important and represented as | |
| Wall shear stress (WSS) |
Where A is the surface area of the DAC unit, μtotal is the total viscosity at the wall including both laminar and turbulent components, u is the local velocity parallel to the wall and n is the local wall-normal coordinate. |
N/m2 | The WSS is an area-averaged value computed over the wall surface of the DAC unit. High WSS is expected to remove particles from the wall and therefore correlate with emitted dose. |
| Particle Trajectory Parameters | |||
| Average particle residence time (tpart) |
Where n particles are considered and the integral is performed for each particle from its starting point through the DAC outlet. |
s | Average particle residence time within the DAC unit geometry based on particle number. |
| Average particle turbulent kinetic energy (kpart) |
Where k is the local turbulent kinetic energy experienced by each particle along its trajectory. |
(m2/s2)*s or N*m or Joules |
Represents the history of k a particle experiences over its trajectory through the system. Both k and exposure time to k are expected to be directly proportional to deaggregation. Units represent work (J) performed by turbulence on the particle. |
| Non-dimensional particle turbulent kinetic energy (k*part) | Non-dimensional | Of the available time scales, use of tinlet provided the strongest correlation with the experimental data. | |
| Average particle specific dissipation rate (ωpart or ω*part) |
Where ω is the local specific dissipation rate experience by each particle along its trajectory. |
Non-dimensional | Represents the history of ω a particle experiences over its trajectory through the system. Both ω and exposure time to ω are expected to be directly proportional to deaggregation. |
| Non-dimensional ωpart / tpart |
Non-dimensional | Allows for consideration of ωpart without the influence of tpart. Inclusion of tpart may be confounding if deaggregation occurs quickly. | |
As shown in Table I, the flow field based quantities were computed as volume averages of the DAC-unit geometry starting in the containment volume and including the outlet flow passage. The particle-based properties were calculated for each trajectory and then combined with a particle count average. Trajectory integrals were halted if the particle residence time exceeded the 0.2 s physical actuation time of the device. In addition, based on high near-wall values of ω as previously reported (14), maximum trajectory integral values of ∫ ωdt were limited to 100,000.
Non-dimensionalization of the dispersion metrics is expected to be necessary so that the results can be translated to different inlet and geometry configurations. Based on convention, non-dimensional quantities are denoted with an asterisk. In this study, non-dimensionalization was based on velocity at the inlet orifice (Vinlet in m/s) and an inlet time scale (tinlet = Vol1/3/Vinlet), where Vol is the DAC-unit volume available for particle motion. This non-dimensionalization is slightly different from the previously proposed non-dimensional specific dissipation (NDSD) parameter, where a mean or exposure time was defined as Vol/Q, where Q is the volumetric airflow rate. Hence, the non-dimensionalized form of ω is denoted as ω*field and ω*part (Table I) instead of the NDSD. Further details of all non-dimensional parameters considered are provided in Table I.
RESULTS
Experimentally Determined Aerosolization Performance
Aerosolization characteristics based on in vitro experiments are presented in Table II for the five cases operated in the horizontal orientation and for Case 3 repeated in the vertical orientation. In all cases, the resulting MMAD is < 2 μm, which is expected to promote high efficiency lung delivery. In some cases, particle diameters closer to 1.5 μm are desirable, as achieved with Cases 1 and 4.
Table II.
In vitro measured aerosolization performance.
| Description | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 3 vertical a |
|---|---|---|---|---|---|---|
| MMAD (μm) | 1.56 (0.01) | 1.89 (0.10) | 1.77 (0.08) | 1.57 (0.04) | 1.64 (0.09) | 1.84 (0.05) |
| FPF < 5μm/ED (%) | 97.8 (0.1) | 95.4 (1.9) | 95.2 (0.4) | 95.5 (1.2) | 93.4 (1.3) | 93.8 (1.1) |
| FPF < 1μm/ED (%) | 23.9 (0.5) | 18.6 (0.5) | 20.2 (1.7) | 22.5 (0.8) | 23.0 (4.3) | 21.8 (1.0) |
| GSD | 1.80 | 1.85 | 1.87 | 1.80 | 1.86 | 1.98 |
| ED (%) | 63.1 (4.8) | 58.8 (7.7) | 84.6 (6.3) | 44.8 (4.8) | 57.3 (4.9) | 85.1 (1.8) |
Mean aerosol characteristics with standard deviations (SD) shown in parenthesis (n=3).
DAC unit was operated in the vertical position as shown in Figure 2b, with all other cases evaluated in the horizontal position.
Fine particle fractions based on the amount of drug mass in particles with aerodynamic diameters less than 5 μm (FPF<5 μm/ED) and less than 1 μm (FPF<1 μm/ED) as a fraction of ED are also presented in Table II. Fine particle fraction values for all devices are consistently very high compared with conventional products, indicating good dispersion of the spray dried formulations. However, values are lower than achieved with the Sympatec dispersion system. This reduced dispersion is expected considering that the DAC-unit DPI has an operating pressure that is approximately 10 times lower than the Sympatec large-scale test system. In general, the FPF values correlate with the MMAD results, with devices producing the highest FPFs also producing the lowest MMAD values. This correlation is expected for regularly dispersed monomodal particle size distributions, which were observed experimentally.
A wide spread of ED values was observed, with values ranging from 44.8 to 85.1 %. Unfortunately, the smallest aerosol size did not correlate with the highest ED. Changing the Case 3 orientation from horizontal to vertical did not significantly alter the MMAD (p = 0.31) or ED (p = 0.90). This is surprising considering that Case 3 in the vertical orientation must aerosolize powder that is initially behind the inlet jet.
Flow Field Characteristics
Velocity contours and 2D stream traces along two axial planes are illustrated in Figure 3. In all cases, complex vortical flow is observed with single or multiple recirculation zones occurring near the outlet. A clearly defined inlet jet region is observed in all cases with velocities in the range of 100 m/s. Significant secondary velocities are also observed in all cases in the region of the powder bed with velocity in the range of 5 m/s or higher. For Case 2, the inlet jet is observed to impact the containment unit wall in the region of the powder bed forming near-wall secondary velocities of approximately 20 m/s and higher. These observations can be used to define desirable levels of near-wall secondary velocity in future design optimizations.
Figure 3.
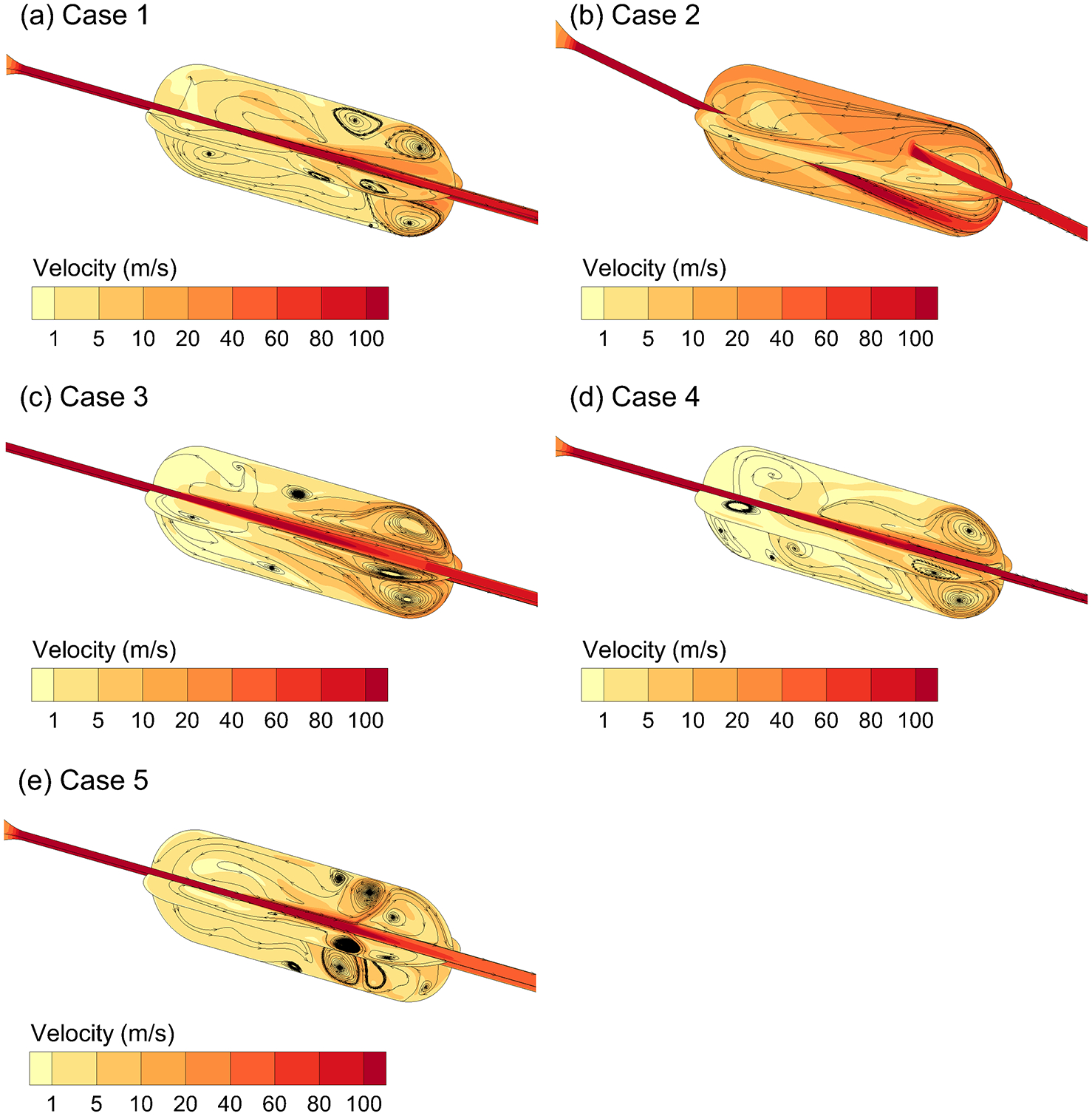
Contours of velocity magnitude on two axial planes and 2D stream traces on each plane. The central core of high speed flow (inlet jet) induces significant secondary motion and complex vortical flow fields. Designs include (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5.
Additional flow field characteristics are presented in online Supplemental Figures S1–S3. In Figure S1, turbulent kinetic energy (k) is observed to be highest in regions of significant flow recirculation with maximum values occurring for Case 2. Cases 1 and 4 are observed to have the lowest overall values of k. Values of ω are observed to be similar to k, but more uniform across the designs considered (Figure S2). Finally, WSS values are shown to be a good marker for near-wall secondary velocity magnitude, as expected (Figure S3 compared with Figure 1).
Flow Field Parameters
Considering potential flow field parameters, the following values were compared with experimentally determined MMAD and ED: k*field, ω*field, k*field × ω*field, k*field / ω*field, WSS. Parameters producing a correlation coefficient of R2 = 0.8 or greater with MMAD or ED are presented in Figures 4 and 5, respectively. Considering correlations with MMAD (Figure 4), a strong direct relationship was observed with the k-based parameters. However, it is surprising that increasing these parameters has the detrimental effect of also increasing the MMAD. This is the opposite effect reported in most previous studies that have assessed turbulent kinetic energy with dispersion. The strongest correlation was observed between MMAD and k*field × ω*field. As shown in Table I and Eq. (5), ω contains k in the numerator and this combination is proportional to k3/2 divided by the turbulent length scale (l). Therefore, to maximize dispersion, low k is desirable together with high l.
Figure 4.
Mass median aerodynamic diameter (MMAD) vs. flow field-based dispersion parameters that formed the strongest (R2 > 0.8) correlations: (a) k*field and (b) k*field × ω*field.
Figure 5.
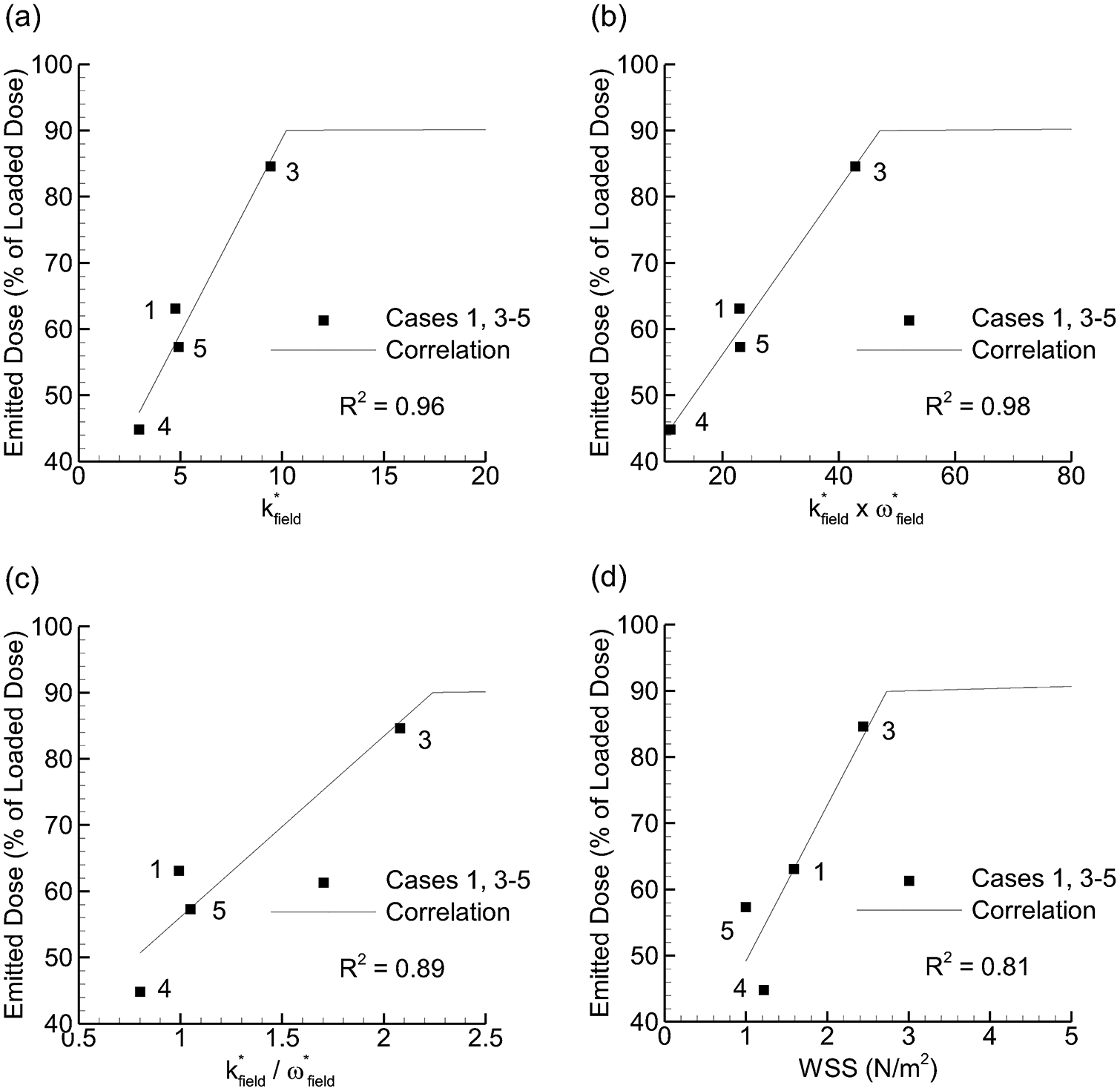
Emitted dose (ED) vs. flow field-based dispersion parameters that formed the strongest (R2 > 0.8) correlations: (a) k*field, (b) k*field × ω*field, (c) k*field / ω*field, (d) WSS.
Considering ED, multiple k-based factors and WSS were observed to form strong direct correlations (Figure 5). Due to a design flaw in Case 2, ED values were not included in correlation development. Furthermore, ED values predicted by the correlations were limited to 90% considering the experimental observation that a minimum of approximately 10% of the loaded dose adhered to the wall regardless of the operating conditions. The resulting direct association between k-based parameters and ED are expected considering that strong turbulent fluctuations will remove particles from the walls. From a design perspective, it is concerning that high k*field is beneficial for ED and detrimental for aerosol size. The product of k*field × ω*field again forms the strongest correlation with R2 = 0.98. However, the rank orders of values in ED and MMAD are different in Figures 4b and 5b, indicating that ED and MMAD are not fully coupled. Given that k*field × ω*field forms the strongest correlation for both MMAD and ED, it appears that improving both of these aerosolization characteristics may not be possible at the same time using knowledge from field parameters alone. Therefore, particle parameters are also considered to see if additional relationships exist that may be useful for optimization.
Particle Trajectory Characteristics
Approximately 20 selected particle trajectories are illustrated for Cases 1 and 2 in Figure 6, with the trajectories colored based on the time integration of k exposure. Case 2 trajectories have higher kparticle values and appear to have longer residence times, which, based on previous associations between turbulence and dispersion (15, 16, 19–21) would decrease particle size. In comparison, Case 1 trajectories have reduced kparticle values due to lower k-field exposure and shorter residence times.
Figure 6.
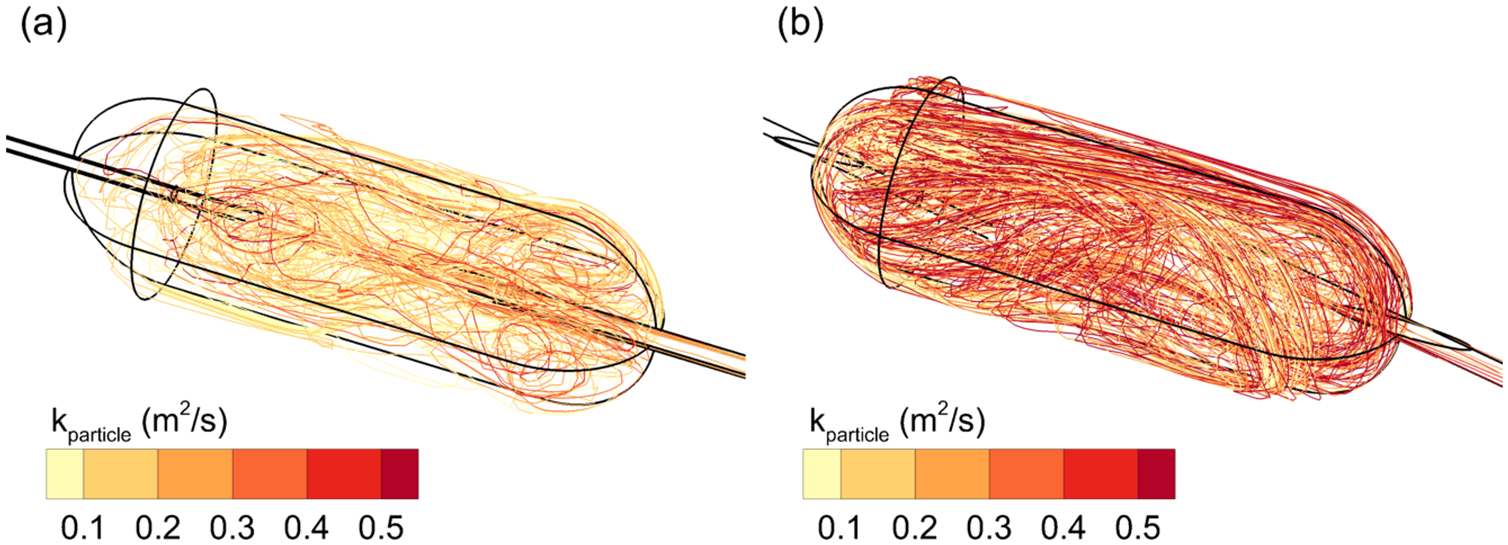
Particle trajectories contoured based on pathline integrations of k exposure for (a) Case 1 and (b) Case 2.
Particle Trajectory Parameters
Considering potential particle trajectory parameters, the following values were compared with experimentally determined MMAD and ED values: tpart, k*part, ω*part, ω*part / tpart, k*part × ω*part, k*part / ω*part, k*part / (ω*part / tpart), WSS. Parameters producing a correlation coefficient of R2 = 0.8 or greater with MMAD or ED are presented in Figures 7 and 8, respectively. As with field properties, parameters containing k showed the strongest correlations with MMAD and ED. Again, increasing k values increased particle size, which is counter to prior observations. Interestingly, with the particle parameters both ω and ω/t provided strong correlations with MMAD with the strongest correlation for the latter parameter. Considering ED (Figure 8), the only strong correlation observed was with k*part. Considering together, MMAD may be reduced by decreasing the ω*part / tpart parameter while maintaining an elevated value of k*part to support ED. While the steep slope of the curve may increase the R2 value, the correlation appears predictive of the data and captures the correct rank order.
Figure 7.
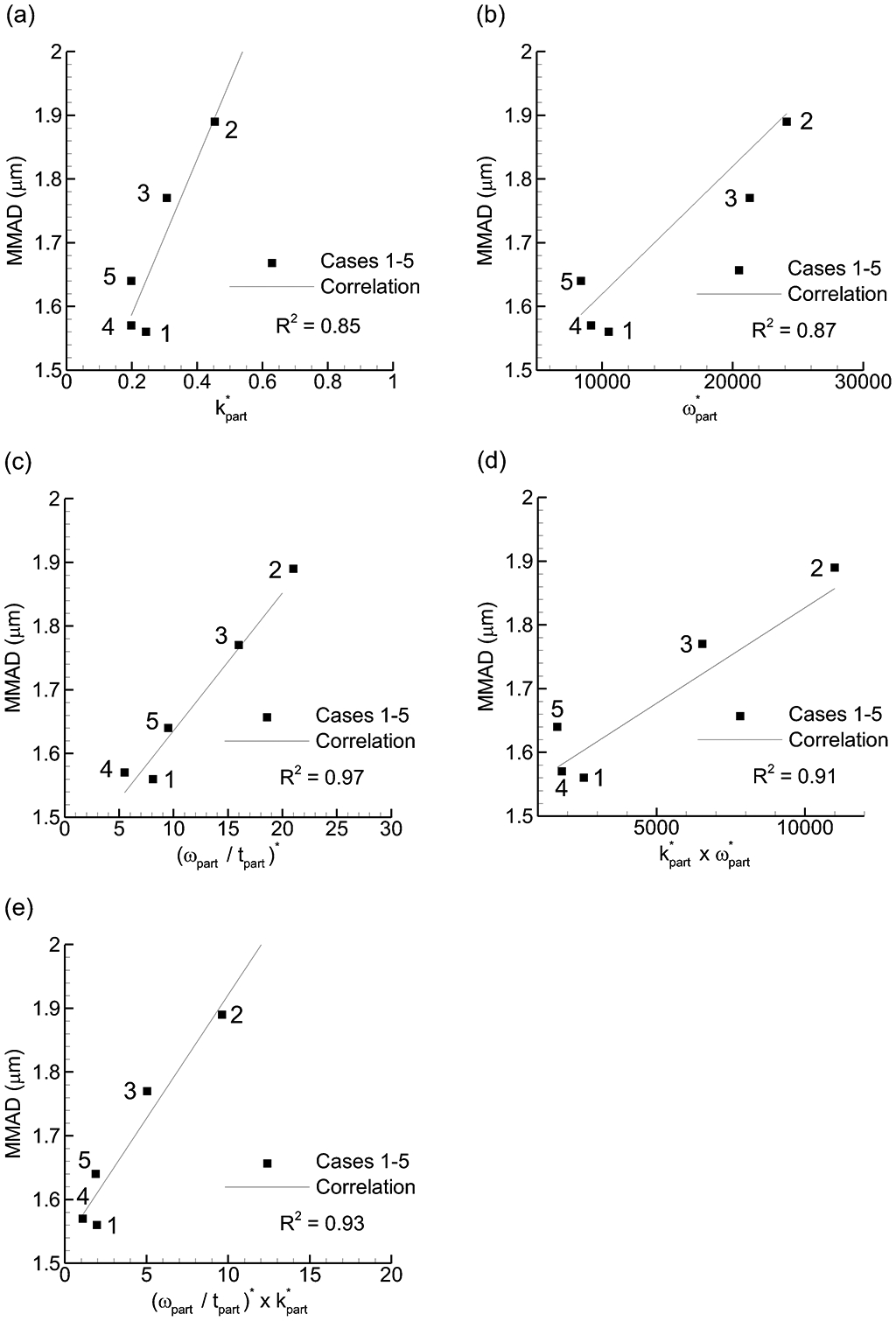
Mass median aerodynamic diameter (MMAD) vs. particle-based dispersion parameters that formed the strongest (R2 > 0.8) correlations: (a) k*part, (b) ω*part, (c) (ωpart / tpart)* (d) k*part × ω*part, (e) (ωpart / tpart)* × k*part.
Figure 8.
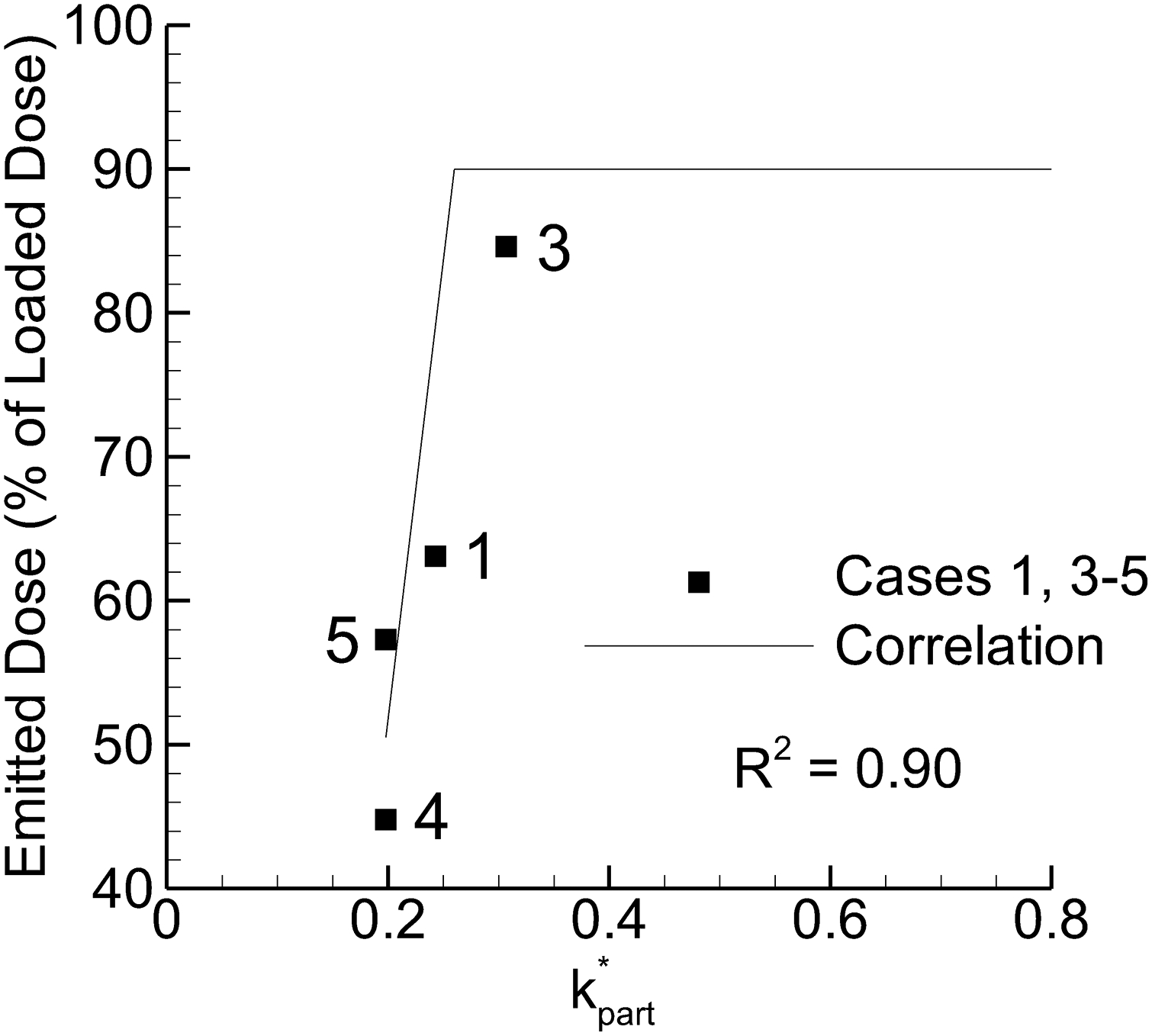
Emitted dose (ED) vs. particle-based dispersion parameter k*part, which was the only particle parameter to form a strong correlation (R2 > 0.8) with ED.
Predictions using the Correlations
To test the predictive ability of the correlations without creating a new device, Case 3 was operated vertically. As shown in Figure 2, this orientation moved the initial powder bed to a location behind the inlet orifice. Based on in vitro experiments (Table II), the resulting mean (SD) MMAD and ED values were 1.84 (0.05) μm and 85.1 (1.8) %, respectively. These values were not significantly different (MMAD p-value = 0.90 and ED p-value = 0.31) from Case 3 operated horizontally. CFD particle tracking simulations were run in the vertical orientation to produce updated particle-based dispersion parameters. Considering the flow field correlations established in Figures 4 and 5, all correlations performed well with the simplest k*field correlation predicting highly accurate values of MMAD = 1.82 μm and ED = 85.5%. WSS also provided a very good prediction of ED = 83.1%.
Considering the correlations for particles, the k*part correlations predicted MMAD = 1.70 μm and ED = 78.2%, where were both lower than expected, but still reasonably accurate. The best performing particle parameter was ω*part, which predicted MMAD = 1.79 μm and was within one SD of the experimental value. As a result, values that include ω*part should be considered in addition to k values in predictions of DAC-unit DPI performance.
DISCUSSION
A unique aspect of this study is the strong direct relationship between turbulent kinetic energy and aerosol size. For all cases tested, increasing the field-based or particle-based k parameters had the detrimental effect of also increasing the particle size of the aerosol. Almost all previous experimental and CFD studies have found the opposite effect in which increasing turbulence parameters decreased aerosol size, either in terms of reduced MMAD or increased fine particle fraction (FPF). For example, qualitative inverse relations between measures of turbulent kinetic energy and aerosol size were reported in the studies of Voss and Finlay (19) and Coates et al. (15, 16). Similarly, strong inverse quantitative relations between turbulent kinetic energy and aerosol size were reported in the studies of Louey et al. (24) and Xu et al. (20, 21). These previous studies, with the exception of Coates et al., used carrier-based, micronized or agglomerate powder formulations. The unique relationship identified in the current study may be due to the highly dispersible spray dried formulation, the DAC-unit device, or a combination of the two. The previous study of Longest et al. (14) considered spray dried formulations in a capsule-based device that included a 3D rod array and assessed deaggregation after initial powder breakup. While turbulent kinetic energy was not associated with aerosol size, a strong inverse relationship was established with a measure of ω, which contains k in the numerator. As a result, the study of Longest et al. (14) also suggests an inverse relationship between k and MMAD. Hence, it can be concluded that the direct relationship between k and MMAD discovered in this study is a unique feature of the DAC-unit DPI operated with a highly dispersible powder.
The direct relationship between turbulent kinetic energy and MMAD with the DAC-unit DPI may have important design implications. In most other inhalers, turbulence is maximized to provide an acceptable aerosol for inhalation. This high turbulence together with small diameter mouthpieces and relatively large particle aerosols leads to high mouth-throat depositional losses (36, 41–44). In contrast, turbulence can be reduced in the DAC-unit DPI producing smaller particles and potentially lowering mouth-throat deposition. It is also novel that this device produced a <2 μm aerosol with ED values over 80% using only 10 ml of air delivered at 3 LPM. In contrast, most popular commercial DPIs require 4 L of air for optimal operation, produce measured outlet aerosol sizes of around 5 to 7 μm (including the fraction in the NGI preseparator as was done in the current study), and lose approximately 60 to 80% of the aerosol in the mouth-throat region (36, 41–44).
Results of the current study together with previous studies have important implications for the improved understanding of DPIs, especially devices that do not include a vibrating capsule. Aerosol dispersion should be considered to occur in the separate steps of (i) initial or primary fluidization and (ii) secondary breakup of airborne particles. Based on the strong association between turbulent kinetic energy and ED, k-based parameters are likely instrumental in primary fluidization. Other forms of k, such as k × ω, are equally important in primary breakup. WSS is also linked to turbulent kinetic energy through eddy viscosity leading to increased initial fluidization and elevated ED. The previous study of Longest et al. (14) modeled aerosols after primary fluidization, so only evaluated mechanism (ii), secondary breakup of airborne particles. In this previous study (14), increasing the non-dimensional form of ω was the only factor shown to decrease aerosol size. Taken together, optimal performance of a device without a vibrating capsule should include low turbulent kinetic energy in the vicinity of the powder bed to reduce or slow the initial rate of primary breakup. It is not entirely clear why this slower initial fluidization is beneficial, but it may be due to some combination of:
Providing more time for turbulence to develop, as suggested for capsule devices by Coates et al. (16),
Increasing the exposure time to the turbulent field, or
Reduced chances of aggregate formation after aerosolization.
Thereafter, exposure to high turbulence, and in particular high ω, is most beneficial to achieve mechanism (ii), secondary breakup of airborne particles (14).
Based on this improved understanding of aerosol formation, the DAC-unit DPI is shown in this study to inherently slow primary dispersion and then increase secondary breakup. Specifically, by removing the powder from the pathway of the inlet air jet, initial exposure to elevated k is minimized. Once fluidized, the aerosol then quickly enters the area of high k, or more importantly high ω, which further reduces size through secondary breakup.
Using the quantitative correlations established in this study, improved designs of the DAC-unit DPI may be sought. Considering the field-based parameters, design improvement options may be limited considering that k*field × ω*field was strongly correlated with both MMAD and ED with R2 values > 0.95. As a result, based only on field parameters, it may not be possible to improve both ED and MMAD simultaneously. Instead, a minimum ED can be selected of say 80%. Above this ED, the device producing a minimum particle size is Case 3, with an MMAD of 1.8 μm (ED = 84.6%). Further decreases in MMAD will require decreased ED, based on the field correlations. Nevertheless, performance of Case 3 is very good and will most likely result in low ex-device loss considering a device flow rate of only 3 LPM.
Further design optimization may be possible using the particle-based parameters. This approach is reasonable considering that the particle parameters contain information about the initial breakup phase and subsequent turbulent exposure along likely particle trajectories. It initially appears advantageous that multiple parameters correlate with MMAD while only k*part correlates with ED. However, it is expected that most of the particle-based parameters are directly linked. That is, it may not be possible to significantly decrease ω*part to reduce particle size while maintain an elevated k*part for high ED. One exception to this linkage with turbulent kinetic energy may be (ωpart / tpart)*, which forms the strongest of the particle-based correlations with MMAD. It is suggested that performance can be enhanced by increasing particle residence time to decrease (ωpart / tpart)* and thereby reduce MMAD while maintaining ED. This may be accomplished by increasing the containment volume or moving the powder bed further from the inlet air jet. The resulting design would be asymmetrical about the primary axis with the air jet moving through the upper region. This strategy would be consistent with the previously reasoned approach (above) of (i) slowing initial fluidization and (ii) maintaining or increasing subsequent turbulent exposure to maximize secondary breakup.
The current study is not the first to suggest that improved performance may be achieved in DPIs by reducing turbulence. Voss and Finlay (19) considered a test rig setup in which increasing turbulence improved dispersion. However, in a commercial DPI also considered by Voss and Finlay (19), turbulent levels were lower than in the test rig but dispersion was improved. They concluded that perhaps turbulence in DPIs can be reduced by modifying the uptake region to improve dispersion and reduce mouth-throat deposition (19). Results of the current study illustrate this approach with the modified uptake region of the DAC unit.
It is envisioned that the base DAC unit can be integrated into DPI devices for multiple applications. Systems that would benefit from low air volumes and positive pressure (active) operation with a small particle aerosol include administration during non-invasive and invasive mechanical ventilation (45, 46), administration to infants (47) and administration of aerosols to test animals (48–50). Previous studies by Farkas et al. have illustrated active low-volume DPI delivery of pharmaceutical aerosol simultaneously with low flow nasal cannula (LFNC) therapy (51, 52). By using an approximate 10 ml burst of air at a flowrate of 3 LPM, aerosol administration did not interfere with LFNC ventilation support. Moreover, the small particle EEG aerosol was able to pass through the nasal cannula interface and nasal passages with low depositional loss. Specifically, considering aerosol delivery simultaneously with LFNC therapy, the steady flow cannula emitted dose was 75% of the capsule loaded dose and, with cyclic inhalation, up to 55% of the loaded dose reached a tracheal filter. In a similar study with a positive pressure DPI, Walenga et al. (53) previously demonstrated high efficiency lung delivery of an EEG aerosol through a mask interface during noninvasive positive pressure ventilation.
One limitation of the current study is the operation of Case 2 and its exclusion from evaluation of ED. Angling both the inlet and outlet capillaries was intended to maximize shear stress and minimize aerosol size. However, when the capsule was pierced by the angled capillaries and the device halves were twisted together, splits in the capsules occurred at the capillary insertion points. Powder was trapped between these splits and the device inner walls. Clearly, the large amount of powder lost in these splits could not be captured in the CFD simulations. However, powder that did exit was dispersed consistent with the developed correlations. Therefore, ED was excluded from the correlations for Case 2, but MMAD was included and compared well with the correlations.
Another limitation of the current study is the relatively small number of cases considered compared to the number of potential design changes. For example, inlet diameter, airflow rate, volume and powder fill mass will all affect performance; however, these variables were held constant in the current study. Instead of testing all potential cases, it is suggested that the CFD-based correlations with proper non-dimensionalization will be sufficiently robust to address a wide range of parameter variations. As a first test, operating the device in the vertical direction was adequately predicted using both field a particle-based parameters. Further studies will need to explore if the proposed correlations can capture other changes. For significantly different parameters beyond the range of those explored in this study, or for significant geometry changes, such as an asymmetrical design, new correlations may need to be developed.
It is important to note the differences between the simulated conditions and the physical DAC system. The CFD model assessed dispersion based on an initial actuation in which the powder bed was undisturbed. In contrast, the physical DPI was actuated five times. Based on observations, physical actuations after the first had a low ED and powder was coated on the containment unit walls. The DAC simulations used a simple reflection boundary condition for wall collisions, did not account for particle-to-particle collisions, and implemented a single tracer particle size. In the physical system, particle interaction forces and wall collisions are expected to be important and are strongly influenced by particle size and surface properties (8, 54, 55). Furthermore, the presence of powder on the flow field (two-way coupling) and potential for bulk powder motion are not included in the model.
Considering differences between the simulations and physical system, an apparent strength of the implemented CFD approach is its simplicity and predictive power. It is not expected that the dispersion parameters and perhaps the CFD assumptions made in this study will work as well for other aerosol formulations, such as with carrier-based, agglomerate and dry milled formulations (8, 18, 19). However, in those systems the development of different dispersion parameters and correlations may also hold promise as an efficient method to integrate CFD simulations into the inhaler design process compared with full simulation of powder breakup.
In conclusion, strong quantitative correlations were established between CFD-predicted dispersion parameters and experimentally determined aerosolization performance for the DAC-unit DPI. In contrast with most all previous studies, increasing turbulence was shown to produce an undesirable increase in aerosol size. It was concluded that this direct relationship between turbulence and aerosol size was a unique feature of the proposed DPI design coupled with a highly dispersible powder and could be used to further optimize future performance. Based on CFD results, it was determined that high turbulence resulted in the initial powder breakup phase occurring too quickly. To maximize future performance, low turbulence is desirable in the vicinity of the powder bed with subsequent high turbulence exposure, in the form of ω or ω/t, to increase secondary breakup of airborne aggregates. This approach is applied with the current DAC-unit DPI design and may be optimized with an asymmetric geometry. Performance with the current best case device was excellent with ED >80% and aerosol MMAD < 2 μm. Future studies will seek to maintain high ED and achieve aerosol particle sizes of 1.5 μm and below. Based on this new approach, the DAC-unit DPI is expected to significantly improve lung delivery of powder aerosols in challenging cases, such as with infants and children as well as in cases of respiratory insufficiency and respiratory disease.
Supplementary Material
Figure S1. Contours of turbulent kinetic energy (k) on two axial planes for designs (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5. Different patterns and magnitudes are observed with Case 2 experiencing the highest levels of overall k and Cases 1, 4 and 5 having lowest k in the region of the initial powder bed.
Figure S3. Contours of total wall shear stress (WSS) on surfaces of the DAC unit inner walls for designs (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5. Values differ among cases and are highly non-uniform for each case.
Figure S2. Contours of specific dissipation rate (ω) on two axial planes for designs (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5. Profiles appear similar among the designs with values increasing significantly at the wall, where differences among the geometries are expected to be greater.
Acknowledgements
Research reported in this publication was supported by the Eunice Kennedy Shriver National Institute of Child Health & Human Development of the National Institutes of Health under Award Number R01HD087339 and by the National Heart, Lung and Blood Institute of the National Institutes of Health under Award Number R01HL139673. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Dr. Michael Hindle is gratefully acknowledged for reviewing the manuscript and making helpful suggestions.
Footnotes
Author Disclosure Statement
Virginia Commonwealth University is currently pursuing patent protection of devices and methods described in this study, which if licensed and commercialized, may provide a future financial interest to the authors.
REFERENCES
- 1.De Boer A, Hagedoorn P, Hoppentocht M, Buttini F, Grasmeijer F, Frijlink H. Dry powder inhalation: past, present and future. Expert Opinion on Drug Delivery. 2017;14(4):499–512. [DOI] [PubMed] [Google Scholar]
- 2.Newman S. Respiratory Drug Delivery: Essential Theory and Practice. Richmond: RDD Online; 2009. [Google Scholar]
- 3.Islam N, Cleary MJ. Developing an efficient and reliable dry powder inhaler for pulmonary drug delivery - A review for multidisciplinary researchers. Medical Engineering and Physics. 2012;34:409–27. [DOI] [PubMed] [Google Scholar]
- 4.Farkas D, Hindle M, Longest PW. Development of an inline dry powder inhaler that requires low air volume. J Aerosol Med Pulm Drug Deliv. 2018;31(4):255–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Farkas D, Hindle M, Longest PW. Application of an inline dry powder inhaler to deliver high dose pharmaceutical aerosols during low flow nasal cannula therapy. International Journal of Pharmaceutics. 2018; 10.1016/j.ijpharm.2018.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ferziger JH, Peric M. Computational Methods for Fluid Dynamics. Berlin: Springer-Verlag; 1999. [Google Scholar]
- 7.Longest PW, Holbrook LT. In silico models of aerosol delivery to the respiratory tract - Development and applications. Advanced Drug Delivery Reviews. 2012;64:296–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shur J, Lee SL, Adams W, Lionberger R, Tibbatts J, Price R. Effect of device design on the in vitro performance and comparability for capsule-based dry powder inhalers. The AAPS Journal. 2012;14(4):667–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wong W, Fletcher DF, Traini D, Chan HK, Young PM. The use of computational approaches in inhaler development. Advanced Drug Delivery Reviews. 2012;64(4):312–22. [DOI] [PubMed] [Google Scholar]
- 10.Ariane M, Sommerfeld M, Alexiadis A. Wall collision and drug-carrier detachment in dry powder inhalers: Using DEM to devise a sub-scale model for CFD calculations. Powder Technol. 2018;334:65–75. [Google Scholar]
- 11.Cui Y, Sommerfeld M. Forces on micron-sized particles randomly distributed on the surface of larger particles and possibility of detachment. International Journal of Multiphase Flow. 2015;72:39–52. [Google Scholar]
- 12.Cui Y, Sommerfeld M. Application of lattice-Boltzmann method for analysing detachment of micron-sized particles from carrier particles in turbulent flows. Flow, Turbulence and Combustion. 2018;100(1):271–97. [Google Scholar]
- 13.Sommerfeld M, Schmalfuß S. Numerical analysis of carrier particle motion in a dry powder inhaler. Journal of Fluids Engineering. 2016;138(4):041308. [Google Scholar]
- 14.Longest PW, Son Y-J, Holbrook LT, Hindle M. Aerodynamic factors responsible for the deaggregation of carrier-free drug powders to form micrometer and submicrometer aerosols. Pharmaceutical Research. 2013;30:1608–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Coates MS, Chan H-K, Fletcher DF, Raper JA. Influence of air flow on the performance of a dry powder inhaler using computational and experimental analyses. Pharmaceutical Research. 2005;22(9):1445–53. [DOI] [PubMed] [Google Scholar]
- 16.Coates MS, Chan H-K, Fletcher DF, Raper JA. Effect of design on the performance of a dry powder inhaler using computational fluid dynamics. Part 2: Air inlet size. Journal of Pharmaceutical Sciences. 2006;95(6):1382–92. [DOI] [PubMed] [Google Scholar]
- 17.Coates MS, Fletcher DF, Chan H-K, Raper JA. Effect of design on the performance of a dry powder inhaler using computational fluid dynamics. Part 1: Grid structure and mouthpiece length. Journal of Pharmaceutical Sciences. 2004;93(11):2863–76. [DOI] [PubMed] [Google Scholar]
- 18.Wong W, Fletcher DF, Traini D, Chan HK, Crapper J, Young PM. Particle Aerosolisation and Break-Up in Dry Powder Inhalers: Evaluation and Modelling of Impaction Effects for Agglomerated Systems. Journal Of Pharmaceutical Sciences. 2011;100(7):2744–54. [DOI] [PubMed] [Google Scholar]
- 19.Voss AP, Finlay WH. Deagglomeration of dry powder pharmaceutical aerosols. International Journal of Pharmaceutics. 2002;248:39–40. [DOI] [PubMed] [Google Scholar]
- 20.Xu Z, Mansour HM, Mulder T, McLean R, Langridge J, Hickey AJ. Dry Powder Aerosols Generated by Standardized Entrainment Tubes From Drug Blends With Lactose Monohydrate: 1. Albuterol Sulfate and Disodium Cromoglycate. Journal Of Pharmaceutical Sciences. 2010;99(8):3398–414. [DOI] [PubMed] [Google Scholar]
- 21.Xu Z, Mansour HM, Mulder T, McLean R, Langridge J, Hickey AJ. Dry Powder Aerosols Generated by Standardized Entrainment Tubes From Drug Blends With Lactose Monohydrate: 2. Ipratropium Bromide Monohydrate and Fluticasone Propionate. Journal Of Pharmaceutical Sciences. 2010;99(8):3415–29. [DOI] [PubMed] [Google Scholar]
- 22.Coates MS, Fletcher DF, Chan H-K, Raper JA. The role of capusle on the performance of a dry powder inhaler using computational and experimental analyses. Pharmaceutical Research. 2005;22(6):923–32. [DOI] [PubMed] [Google Scholar]
- 23.Coates MS, Chan H-K, Fletcher DF, Chiou H. Influence of mouthpiece geometry on the aerosol delivery performance of a dry powder inhalation. Pharmaceutical Research. 2007;24(8):1450–6. [DOI] [PubMed] [Google Scholar]
- 24.Louey MD, VanOort M, Hickey AJ. Standarized entrainment tubes for the evaluation of phamaceutical dry powder dispersion. J Aerosol Sci. 2006;37:1520–33. [Google Scholar]
- 25.Son Y-J, Longest PW, Hindle M. Aerosolization characteristics of dry powder inhaler formulations for the excipient enhanced growth (EEG) application: Effect of spray drying process conditions on aerosol performance. International Journal of Pharmaceutics. 2013;443:137–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Son Y-J, Longest PW, Tian G, Hindle M. Evaluation and modification of commercial dry powder inhalers for the aerosolization of submicrometer excipient enhanced growth (EEG) formulation. European Journal of Pharmaceutical Sciences. 2013;49:390–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Behara SRB, Longest PW, Farkas DR, Hindle M. Development of high efficiency ventilation bag actuated dry powder inhalers. International Journal of Pharmaceutics. 2014;465:52–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bass K, Longest PW. Recommendations for simulating microparticle deposition at conditions similar to the upper airways with two-equation turbulence models. J Aerosol Sci. 2018; 10.1016/j.jaerosci.2018.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Longest PW, Vinchurkar S. Validating CFD predictions of respiratory aerosol deposition: effects of upstream transition and turbulence. J Biomech. 2007;40(2):305–16. [DOI] [PubMed] [Google Scholar]
- 30.Wilcox DC. Turbulence Modeling for CFD, 2nd Ed California: DCW Industries, Inc.; 1998. [Google Scholar]
- 31.Longest PW, Hindle M, Das Choudhuri S, Byron PR. Numerical simulations of capillary aerosol generation: CFD model development and comparisons with experimental data. Aerosol Science and Technology. 2007;41(10):952–73. [Google Scholar]
- 32.Longest PW, Vinchurkar S, Martonen TB. Transport and deposition of respiratory aerosols in models of childhood asthma. J Aerosol Sci. 2006;37:1234–57. [Google Scholar]
- 33.Longest PW, Hindle M, Das Choudhuri S, Xi J. Comparison of ambient and spray aerosol deposition in a standard induction port and more realistic mouth-throat geometry. J Aerosol Sci. 2008;39(7):572–91. [Google Scholar]
- 34.Longest PW, Xi J. Effectiveness of direct Lagrangian tracking models for simulating nanoparticle deposition in the upper airways. Aerosol Science and Technology. 2007;41(4):380–97. [Google Scholar]
- 35.Gosman AD, Ioannides E. Aspects of computer simulation of liquid-fueled combustors. Journal of Energy. 1981;7:482–90. [Google Scholar]
- 36.Longest PW, Tian G, Delvadia R, Hindle M. Development of a stochastic individual path (SIP) model for predicting the deposition of pharmaceutical aerosols: Effects of turbulence, polydisperse aerosol size, and evaluation of multiple lung lobes. Aerosol Science and Technology. 2012;46(12):1271–85. [Google Scholar]
- 37.Matida EA, Finlay WH, Grgic LB. Improved numerical simulation of aerosol deposition in an idealized mouth-throat. J Aerosol Sci. 2004;35:1–19. [Google Scholar]
- 38.Vinchurkar S, Longest PW. Evaluation of hexahedral, prismatic and hybrid mesh styles for simulating respiratory aerosol dynamics. Computers and Fluids. 2008;37(3):317–31. [Google Scholar]
- 39.Longest PW, Vinchurkar S. Effects of mesh style and grid convergence on particle deposition in bifurcating airway models with comparisons to experimental data. Medical Engineering and Physics. 2007;29(3):350–66. [DOI] [PubMed] [Google Scholar]
- 40.Longest PW, Kleinstreuer C, Buchanan JR. Efficient computation of micro-particle dynamics including wall effects. Computers & Fluids. 2004;33(4):577–601. [Google Scholar]
- 41.Delvadia R, Hindle M, Longest PW, Byron PR. In vitro tests for aerosol deposition II: IVIVCs for different dry powder inhalers in normal adults. J Aerosol Med Pulm Drug Deliv. 2013;26(3):138–44. [DOI] [PubMed] [Google Scholar]
- 42.Delvadia R, Longest PW, Byron PR. In vitro tests for aerosol deposition. I. Scaling a physical model of the upper airways to predict drug deposition variation in normal humans. Journal of Aerosol Medicine. 2012;25(1):32–40. [DOI] [PubMed] [Google Scholar]
- 43.Longest PW, Tian G, Walenga RL, Hindle M. Comparing MDI and DPI aerosol deposition using in vitro experiments and a new stochastic individual path (SIP) model of the conducting airways. Pharmaceutical Research. 2012;29:1670–88. [DOI] [PubMed] [Google Scholar]
- 44.Wei X, Hindle M, Kaviratna A, Huynh BK, Delvadia RR, Sandell D, et al. In Vitro Tests for Aerosol Deposition. VI: Realistic Testing with Different Mouth–Throat Models and In Vitro—In Vivo Correlations for a Dry Powder Inhaler, Metered Dose Inhaler, and Soft Mist Inhaler. J Aerosol Med Pulm Drug Deliv. 2018; 10.1089/jamp.2018.1454. [DOI] [PubMed] [Google Scholar]
- 45.Dhand R. Inhalation therapy in invasive and noninvasive mechanical ventilation. Current Opinion in Critical Care. 2007;13(1):27–38. [DOI] [PubMed] [Google Scholar]
- 46.Ari A, Fink JB. Inhalation therapy in patients receiving mechanical ventilation: an update. J Aerosol Med Pulm Drug Deliv. 2012;25(6):319–32. [DOI] [PubMed] [Google Scholar]
- 47.Laube BL, Sharpless G, Shermer C, Sullivan V, Powell K. Deposition of dry powder generated by solovent in Sophia Anatomical infant nose-throat (SAINT) model. Aerosol Science and Technology. 2012;46:514–20. [Google Scholar]
- 48.Hoppentocht M, Hoste C, Hagedoorn P, Frijlink HW, De Boer AH. In vitro evaluation of the DP-4M PennCentury insufflator. European Journal of Pharmaceutics and Biopharmaceutics. 2014;88(1):153–9. [DOI] [PubMed] [Google Scholar]
- 49.Duret C, Wauthoz N, Merlos R, Goole J, Maris C, Roland I, et al. In vitro and in vivo evaluation of a dry powder endotracheal insufflator device for use in dose-dependent preclinical studies in mice. European Journal of Pharmaceutics and Biopharmaceutics. 2012;81(3):627–34. [DOI] [PubMed] [Google Scholar]
- 50.Morello M, Krone CL, Dickerson S, Howerth E, Germishuizen WA, Wong Y-L, et al. Dry-powder pulmonary insufflation in the mouse for application to vaccine or drug studies. Tuberculosis. 2009;89(5):371–7. [DOI] [PubMed] [Google Scholar]
- 51.Farkas D, Hindle M, Longest PW. Application of an inline dry powder inhaler to deliver high dose pharmaceutical aerosols during low flow nasal cannula therapy. International Journal of Pharmaceutics. 2018;546(1–2):1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Farkas D, Hindle M, Longest PW. Efficient Nose-to-Lung Aerosol Delivery with an Inline DPI Requiring Low Actuation Air Volume. Pharmaceutical Research. 2018;35(10):194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Walenga RL, Longest PW, Kaviratna A, Hindle M. Aerosol drug delivery during noninvasive positive pressure ventilation: Effects of intersubject variability and excipient enhanced growth. J Aerosol Med Pulm Drug Deliv. 2017;30(3):190–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chan H-K. Dry powder aerosol drug delivery - Opportunities for colloid and surface scientists. Colloids and Surfaces A: Physicochem Eng Aspects. 2006;284–285:50–5. [Google Scholar]
- 55.Chan H-K. Dry powder aerosol delivery systems: Current and future research directions. Journal of Aerosol Medicine. 2006;19(1):21–7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Contours of turbulent kinetic energy (k) on two axial planes for designs (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5. Different patterns and magnitudes are observed with Case 2 experiencing the highest levels of overall k and Cases 1, 4 and 5 having lowest k in the region of the initial powder bed.
Figure S3. Contours of total wall shear stress (WSS) on surfaces of the DAC unit inner walls for designs (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5. Values differ among cases and are highly non-uniform for each case.
Figure S2. Contours of specific dissipation rate (ω) on two axial planes for designs (a) Case 1, (b) Case 2, (c) Case 3, (d) Case 4, and (e) Case 5. Profiles appear similar among the designs with values increasing significantly at the wall, where differences among the geometries are expected to be greater.


