The interplay of phenotypic variability and fitness in finite microbial populations

Abstract

In isogenic microbial populations, phenotypic variability is generated by a combination of stochastic mechanisms, such as gene expression, and deterministic factors, such as asymmetric segregation of cell volume. Here we address the question: how does phenotypic variability of a microbial population affect its fitness? While this question has previously been studied for exponentially growing populations, the situation when the population size is kept fixed has received much less attention, despite its relevance to many natural scenarios. We show that the outcome of competition between multiple microbial species can be determined from the distribution of phenotypes in the culture using a generalization of the well-known Euler–Lotka equation, which relates the steady-state distribution of phenotypes to the population growth rate. We derive a generalization of the Euler–Lotka equation for finite cultures, which relates the distribution of phenotypes among cells in the culture to the exponential growth rate. Our analysis reveals that in order to predict fitness from phenotypes, it is important to understand how distributions of phenotypes obtained from different subsets of the genealogical history of a population are related. To this end, we derive a mapping between the various ways of sampling phenotypes in a finite population and show how to obtain the equivalent distributions from an exponentially growing culture. Finally, we use this mapping to show that species with higher growth rates in exponential growth conditions will have a competitive advantage in the finite culture.

1. Introduction

A central problem in microbiology is understanding how measurable phenotypic traits such as a cell’s size, growth rate or expression of a gene affect population dynamics [1–4]. This problem is made difficult by the fact that there is rarely a well-defined mapping from genotype to phenotype; instead, a single genotype can give rise to a distribution of phenotypic traits throughout a population’s history. This distribution can be generated at the cellular level due to intrinsic factors, such as the stochasticity of biochemical reactions [5–10], or due to environmental fluctuations that affect the entire population [11–15]. It is now well established that a population’s long-term growth rate cannot be determined by the average values of single-cell traits, such as the growth rates or generation times of cells, but is instead determined by the variability and heritability of phenotypes measured throughout a population. The discrepancy is an example of non-ergodicity and results from epigenetic heritability of phenotypic traits that is present in all populations. It is therefore necessary to quantify the distribution of a phenotypic trait, and not just its average, in order to deduce how phenotypes affect fitness.

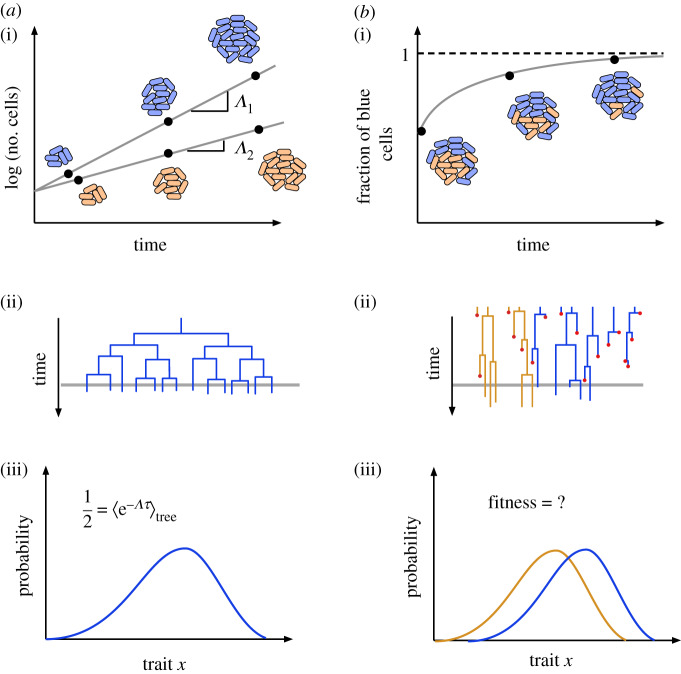
In the setting of exponential growth, a proxy for fitness is the population growth rate Λ, defined by the relation N ∼ e^Λt, where N is the number of cells at time t. The problem of how Λ is related to the distribution of generation times has a rich history in the field of mathematical population dynamics, starting with Euler in the seventeenth century. Euler derived an implicit relationship between Λ and the birth and death rates of individuals in a growing population [16]. Euler’s result was rediscovered by Lotka [16] and later adapted to microbial populations by Powell [17]. In its modern form, this result, known as the Euler–Lotka equation, states that for an exponentially growing population in which each individual has a generation time, τ, drawn independently from a distribution f(τ), Λ satisfies the implicit relationship

$$\frac{1}{2}={\int }_0^{\mathrm{\infty }}f(\tau ){\text{e}}^{-\mathit{\Lambda }\tau }\hspace{0.17em}\text{d}\tau .$$ 1.1

Note that when generation times are deterministic (f(τ) = δ(τ − τ₀)), this reduces to a relationship between the population’s doubling time and growth rate, Λ = ln(2)/τ₀. Equation (1.1) illustrates the importance of considering variation in phenotypic traits, not just the averages, as it can clearly be seen that the entire distribution of generation times shapes Λ. However, this formula has limited applicability to understanding fitness in microbial populations because generation times are typically not drawn independently, but rather they are correlated between mother and daughter cells. For example, negative correlations can arise due to cell-size regulation: if a cell grows abnormally large, its daughter cell will need to have a shorter generation time to account for the additional size inherited from its mother [18].

The relationship between the distribution of generation times and fitness in the presence of mother–daughter correlations is given by a more general equation, derived by Lebowitz [19]. This states that

$$\frac{1}{2}={\int }_0^{\mathrm{\infty }}{\text{e}}^{-\mathit{\Lambda }\tau }{\psi }_{\mathrm{tree}}(\tau )\hspace{0.17em}\text{d}\tau ,$$ 1.2

where ψ_tree(τ) is the distribution of generation times over the entire history of a growing population (figure 1a). Note that in generating this distribution, it is crucial to include the generation times of cells currently in the culture. The distribution ψ_tree(τ) is, in general, distinct from the distribution of generation times along an isolated lineage. If f(τ|τ′) is the distribution of generation times τ conditioned on the mother cell’s generation time, τ′ it was shown that ψ_tree(τ) satisfied the self-consistent equation [19]

$${\psi }_{\mathrm{tree}}(\tau )=2{\int }_0^{\mathrm{\infty }}f(\tau |{\tau }^{\prime }){\psi }_{\mathrm{tree}}({\tau }^{\prime }){\text{e}}^{-\mathit{\Lambda }{\tau }^{\prime }}\hspace{0.17em}\text{d}{\tau }^{\prime }.$$ 1.3

Figure 1.

(a)(i) In a population growing exponentially the population growth rate, Λ, which is a proxy for fitness, can be computed from temporal dynamics of the number of cells. (ii) A cartoon of genealogies obtained from an exponentially growing population. Each vertical line represents a cell and the length of the line its generation time. (iii) A histogram of some phenotypic trait that determines generation times obtained from the genealogical tree can be used to determine the fitness according to the Euler–Lotka equation. The precise procedure for sampling the phenotypes will be discussed in §3. (b)(i) In a finite population containing non-interacting genotypes, the principle of competitive exclusion says that one genotype will eventually dominate the culture. (ii) A cartoon of genealogies obtained from the two populations competing in the finite culture. (iii) How do the distributions of phenotypes obtained from the genealogies in the finite culture relate to fitness?

In both natural and experimental settings, populations cannot grow exponentially for very long. For example, in rich growth conditions Escherichia coli has a doubling time of about 20 min and the weight of an individual bacterium is of the order of 1 picogram; hence a single day of continuous exponential growth starting from one cell would yield a colony that weighs around 2^24×3 ≈ 4.7 × 10²¹ picograms, or around 5 tons. Another 24 h of doubling would yield a colony roughly four times the mass of the earth. In reality, populations of microbes are periodically diluted giving a population whose size is fixed, at least on average. For example, in a chemostat, cells are continuously flushed out as new medium is pumped into the culture. Analogous processes occur in natural environments, such as the digestive system of a host organism where waste is periodically disposed of. In both examples, exponential growth is an inaccurate model of the population dynamics. Instead, one could imagine a fixed population of N cells. One way to model such a population is with a Moran process, where N is kept fixed by selecting a cell to remove from the population at every division event. In the variant of the Moran process that we will adopt, the cell to remove is randomly selected from all of the N + 1 cells in the population after every division (which includes the N − 1 that did not divide and the two newborn daughter cells), thus reverting the population size back to N immediately after any cell divides. The assumption of this model, which we will study in the large N limit, is that the population is well mixed and hence the probability of any given cell being removed is independent of its age or genealogical history. If two species are present in such a population, the principle of competitive exclusion states that one of them will eventually dominate the population.

What does the distribution of phenotypes tell us about the fate of a species in a finite population? The standard theory [20] tells us that if two species with growth rates Λ₁ and Λ₂ compete in a Moran process, the species with a larger population growth rate will eventually dominate. However, equation (1.2) tells us that the exponential growth rates are determined by the entire history of cells in a growing population, yet in the Moran process, most of the cells are flushed out. This raises the question: How is the outcome of a competition experiment related to the distribution of generation times, or any other measurable trait affecting growth, among the cells in the culture? In this paper, we will address this question by analysing the dynamics of phenotypically heterogeneous populations. This will lead to a generalization of equation (1.2) for finite populations, equation (4.3), which relates the population growth rate to the distribution of generation times sampled over cells that remain in the culture. We find subtle distinctions between the phenotype distributions in the exponentially growing population and the finite population. However, it will be shown that the ultimate fate of species in the competition setting is independent of whether the population is growing or kept at a fixed size. In particular, one of our main results is that species with higher values of Λ_i in the exponentially growing culture will always dominate the finite culture, regardless of the initial conditions.

2. A general model of phenotypic variability

We start by introducing a general modelling framework allowing us to study intrinsic variability in an arbitrary phenotypic trait, which will be represented by the vector $\mathbf{x}=(x_1,\dots ,x_l)\in {\mathbb{R}}_{+}^l$. We assume each cell is born with a value of x drawn from a distribution f(x|x′) depending on the phenotype x′ of the mother cell. Importantly, x may not change over the cell cycle. For example, x could represent the initial concentration of a protein, or some macroscopic phenotype, such as the average growth rate over the cell cycle. However, it could not represent the age or volume of a cell, since these change over the course of the cell cycle. After a time τ(x), the cell divides and produces two new cells with phenotypes drawn from f(x|x′) and generation times depending on these phenotypes. This framework can capture any possible form of intrinsic (as opposed to environmental) generation time variability through the appropriate choices of the phenotype x and distribution f. Therefore, existing models can be derived as specific cases of this framework. These include models where division is asymmetric [21–24] and where the relationship between successive generation times is non-monotonic and nonlinear, such as the kicked cell-cycle model used to describe circadian rhythms [25].

2.1. Example: cell-size regulation model

As a concrete example, we will consider a model of cell-size regulation, which has been used extensively in the literature to understand how cells maintain homeostasis of their sizes [1]. This model will serve as a useful illustration of how our formalism can capture the effects of stochasticity in multiple phenotypic traits. The most important assumption of the cell-size regulation model is that cells grow exponentially at the single cell level and divide upon reaching a size depending on their size at birth, v_birth. We will assume that cells divide symmetrically so that v_birth is obtained by dividing the cell mother’s size at division by 2. Phenotypic variability is introduced by adding noise to both the single-cell growth rate as well as the volume at division. To this end, we take the growth rate λ and division volume v_div of a cell to obey

$$\begin{array}{rl}& \ln \lambda =\ln ⟨\lambda ⟩+{\eta }_{\lambda }\\ \text{and}& v_{\mathrm{div}}=2(1-\alpha )v_{\mathrm{birth}}+2\alpha v_0+{\eta }_v,\end{array}\}$$ 2.1

where η_λ and η_v are independent normally distributed random variables. The first equation captures the fact that growth rates are positive and approximately follow a Gaussian distribution for small noise, while the second equation tells us how cells decide when to divide based on their volume. Here, the cell-size regulation strategy is controlled by the parameter α. α = 1 corresponds to cells dividing at a critical size (known as a ‘sizer’), while α = 1/2 corresponds to cells adding a constant size v₀ (known as an ‘adder’). We refer to [1] for an in-depth discussion of the cell-size control model and its implications for population growth. Within this model, the generation time of a cell can be expressed as a deterministic function of the growth rate noise. In particular,

$$\begin{array}{rl}& \tau ({\eta }_{\lambda },{\eta }_v,v_{\mathrm{birth}})\\ & =\frac{1}{⟨\lambda ⟩{\mathrm{e}}^{{\eta }_{\lambda }}}\ln \left(\frac{2(1-\alpha )v_{\mathrm{birth}}+2\alpha v_0+{\eta }_v}{v_{\mathrm{birth}}}\right).\end{array}$$ 2.2

It follows that in the notation of our general modelling framework the phenotype that controls generation times is x = (η_λ, η_v, v_birth). The conditional distribution of phenotypes is given by

$$\begin{array}{rl}\hspace{0.17em}f(\mathbf{x}|{\mathbf{x}}^{\prime })& =\delta (v_{\mathrm{birth}}-\frac{v_{\mathrm{birth}}^{\prime }}{2}{\mathrm{e}}^{{\lambda }^{\prime }\tau ({\eta }_{\lambda }^{\prime },{\eta }_v^{\prime },v_{\mathrm{birth}}^{\prime })})\\ & \times \left(\frac{1}{\sqrt{2\pi {\sigma }_{\lambda }^2}}{\mathrm{e}}^{-{\eta }_{\lambda }^2/2{\sigma }_{\lambda }^2}\right)\left(\frac{1}{\sqrt{2\pi {\sigma }_v^2}}{\mathrm{e}}^{-{\eta }_v^2/2{\sigma }_v^2}\right),\end{array}$$ 2.3

where ${\sigma }_{\lambda }^2$ and ${\sigma }_v^2$ are the variances of η_λ and η_v, respectively. Note that in the special case where α = 1 and η_v = 0, the phenotype is given by x = ln(λ) and the generation time is simply τ = ln(2)/λ.

3. Relationship between phenotypic variability and fitness in a finite culture

We now consider a model where N, the number of cells in the population, is fixed. In order to achieve this, every division event must correspond to a cell being expelled from the culture. As discussed in the Introduction, this can be implemented by a Moran process [26]. Since the population is not growing, we can no longer obtain Λ from the exponential growth curves (as shown in figure 1a). Instead, one can measure growth in terms of the rate per cell at which cells are expelled from the population, or the dilution rate Λ_D.

Intuitively, if N is sufficiently large, the continuous expulsion of cells from the culture should have no influence on the relative frequencies of the phenotypes, and therefore the instantaneous rate at which cells are accumulated should be equal to ΛN. On the other hand, since the size of the culture remains fixed, this must be balanced by the rate at which cells are expelled, implying Λ ≈ Λ_D for sufficiently large N. It follows that Λ_D should satisfy the same relation as Λ. To make this intuition mathematically precise, we can derive a transport equation for the joint distribution of phenotypes (x) and ages (u) at a given time, denoted ψ(t, x, u), which is given by (see appendix A)

$$(\frac{\mathrm{\partial }}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }u})\psi (t,\mathbf{x},u)=-{\mathit{\Lambda }}_D\psi (t,\mathbf{x},u).$$ 3.1

This equation is the Von Foerster equation for an age-structured population [16], although the role of the ‘death rate’ is played by Λ_D, which is no longer an input to the model. Instead, Λ_D must be derived from a boundary condition to ensure the population remains finite. This boundary condition is

$$\psi (t,\mathbf{x},0)=2{\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}f(\mathbf{x}|{\mathbf{x}}^{\prime })\psi (t,{\mathbf{x}}^{\prime },\tau ({\mathbf{x}}^{\prime }))\hspace{0.17em}\text{d}{x}_1^{\prime }\cdots \hspace{0.17em}\text{d}{x}_l^{\prime }.$$ 3.2

The term f(x|x′)ψ(t, x′, τ(x′)) dx₁′ · · · dx_l′ in the integrand represents the probability of a cell with phenotype x′ dividing to produce a cell with phenotype x. The factor of 2 comes from the fact that each cell produces two daughters. Importantly, the probability that any specific cell is expelled is 1/N, which vanishes in the limit N → ∞; therefore, equation (3.2) does not need to account for the fact that one of the daughter cells could be expelled. Since each cell produces two offspring, integrating over all phenotypes and multiplying by a factor of 2 yields the distribution of phenotypes and ages evaluated at age u = 0. Note that this is proportional to the distribution of phenotypes among newborn cells, denoted ${\psi }_{\mathrm{birth}}^F(\mathbf{x})$.

We now look at equation (3.1) in steady state by setting the time derivative to zero,

$$\frac{\mathrm{\partial }}{\mathrm{\partial }u}\psi (\mathbf{x},u)=-{\mathit{\Lambda }}_D\psi (\mathbf{x},u).$$ 3.3

Solving equation (3.3) yields

$$\psi (\mathbf{x},u)=\psi (\mathbf{x},0){\mathrm{e}}^{-{\mathit{\Lambda }}_{D}u},u<\tau (\mathbf{x}).$$ 3.4

As shown in appendix A, ψ(x, 0) is proportional to the tree distribution, denoted ${\psi }_{\mathrm{tree}}^F(\mathbf{x})$. In order to obtain the tree distribution, we sample the phenotype of every cell throughout the entire history of the population, including those that are expelled from the culture, and make a histogram of their phenotypes. (In general, we will use the superscript F to indicate a distribution in the finite culture, but we omit this when there is no ambiguity.) After inserting (3.4) into (3.2), we find

$${\psi }_{\mathrm{tree}}^F(\mathbf{x})=2{\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}f(\mathbf{x}|{\mathbf{x}}^{\prime }){\psi }_{\mathrm{tree}}^F({\mathbf{x}}^{\prime }){\text{e}}^{-{\mathit{\Lambda }}_D\tau ({\mathbf{x}}^{\prime })}\hspace{0.17em}\text{d}{x}_1^{\prime }\cdots \text{d}{x}_l^{\prime }.$$ 3.5

When phenotypes are not correlated across generations, f(x|x′) = f(x), hence it follows from (3.5) that ${\psi }_{\mathrm{tree}}^F(\mathbf{x})=f(\mathbf{x})$. Otherwise, ${\psi }_{\mathrm{tree}}^F(\mathbf{x})$ will be distinct from the distribution of generation times obtained from a single, isolated lineage. We may integrate with respect to x and replace Λ_D with Λ in order to obtain

$$\frac{1}{2}={\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}{\psi }_{\mathrm{tree}}^F(\mathbf{x}){\mathrm{e}}^{-\mathit{\Lambda }\tau (\mathbf{x})}\text{d}{x}_1^{\prime }\cdots \text{d}{x}_l^{\prime }.$$ 3.6

This generalizes equation (1.3) in two ways: first, it extends equation (1.3) to the context of a finite culture, and second, it relates Λ to a distribution of a more general phenotype, not only the generation times. Using this formalism, it is possible to derive the self-consistent equation for ψ_tree(τ) in the exponentially growing culture (equation (1.3)) in terms of ${\psi }_{\mathrm{tree}}^F(\tau )$, the tree distribution of generation times in the finite culture. To see this, note that we can perform the derivation of equation (3.5) with x = τ, leading to

$$2{\int }_0^{\mathrm{\infty }}f(\tau |{\tau }^{\mathrm{\prime }}){\psi }_{\mathrm{tree}}^F({\tau }^{\mathrm{\prime }}){\mathrm{e}}^{-{\mathrm{\Lambda }}_D{\tau }^{\mathrm{\prime }}}\mathrm{d}{\tau }^{\mathrm{\prime }}.$$ 3.7

This equation is identical to equation (1.3), implying ${\psi }_{\mathrm{tree}}^F(\tau )$ obeys the same self-consistent equation as ψ_tree(τ). It follows that the tree distribution in the finite culture is identical to the tree distribution in the exponentially growing culture. Integrating both sides of equation (3.7) with respect to τ yields the Euler–Lotka equation in the finite culture:

$$\frac{1}{2}={\int }_0^{\mathrm{\infty }}{\psi }_{\mathrm{tree}}^F(\tau ){\text{e}}^{-{\mathrm{\Lambda }}_D\tau }\hspace{0.17em}\text{d}\tau .$$ 3.8

A similar procedure can used to obtain a simple equation for the population growth rate in terms of the distribution of any single-cell observable. For example, consider the cell-size regulation model with α = 1 and η_v = 0. In this case, the generation time is a deterministic function of the growth rate: τ = ln(2)/λ. It follows that the marginalization approach above can be used to obtain

$$\frac{1}{2}={\int }_0^{\mathrm{\infty }}{2}^{-\mathrm{\Lambda }/\lambda }f(\lambda )\hspace{0.17em}\text{d}\lambda .$$ 3.9

Here we have used that growth rates are uncorrelated to replace ${\psi }_{\mathrm{tree}}^F(\lambda )$ with f(λ). Within this model, f(λ) is simply a lognormal distribution with mean 〈λ〉 and variance ${\sigma }_{\lambda }^2$. This equation has previously been analysed in [27], where a saddle point approximation was carried out to obtain

$$\mathit{\Lambda }\approx ⟨\lambda ⟩[1-(1-\frac{\ln (2)}{2}){\text{CV}}_{\lambda }^2],$$ 3.10

where CV_λ represents the coefficient of variation (the standard deviation over the mean) of growth rates. This shows that within the context of this model, growth rate variation tends to decrease population growth [27].

4. Computing the population growth rate from cells in the culture

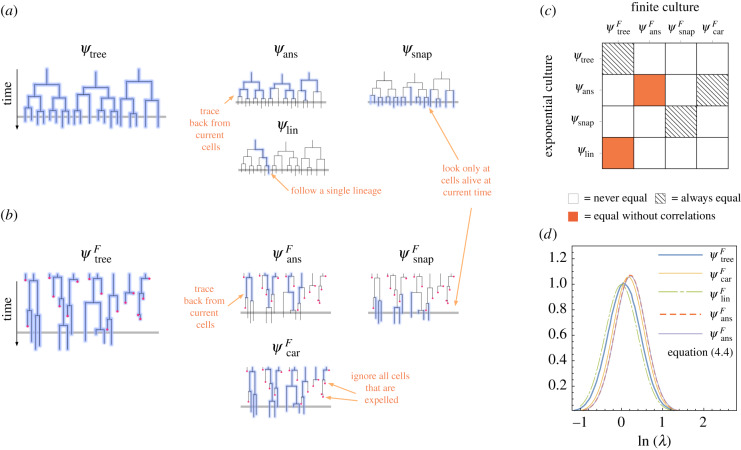
The tree distribution, which is required to compute the population growth rate using equation (1.2), is only one of a number of ways to quantify phenotypic variability in a lineage tree, and it is not always the most convenient to work with. For example, it is often the case that one does not have access to the cells that are expelled from the culture. An alternative distribution is given by the expression $2{\psi }_{\mathrm{tree}}^F(\mathbf{x}){\text{e}}^{-{\mathrm{\Lambda }}_D\tau (\mathbf{x})}$; this term is twice the integrand of equation (3.6), which implies it must be a probability distribution, as it is normalized. As was previously noted by Powell [17] in the context of a model with uncorrelated generation times, this expression can be interpreted as the distribution of x over all cells that divide before being expelled from the culture (figure 2). Following Powell’s terminology, we define the carrier distribution as

$${\psi }_{\mathrm{car}}^F(\mathbf{x})=2{\psi }_{\mathrm{tree}}^F(\mathbf{x}){\text{e}}^{-{\mathrm{\Lambda }}_D\tau (\mathbf{x})}.$$ 4.1

To derive Powell’s interpretation of the carrier distribution in the more general setting, first note that ${\text{e}}^{-{\mathrm{\Lambda }}_D\tau (\mathbf{x})}$ is the probability that a cell stays in the culture until it divides, given that is has phenotype x. Also, the probability that any cell throughout the history of the population divides in the culture must be 1/2 in order for the number of cells to remain fixed. The interpretation of ${\psi }_{\mathrm{car}}^F(\mathbf{x})$ then follows from an application of Bayes’ theorem where ${\psi }_{\mathrm{tree}}^F(\mathbf{x})$ and ${\psi }_{\mathrm{car}}^F(\mathbf{x})$ play the role of the prior and posterior, respectively.

Figure 2.

(a) The various ways of sampling phenotypes from a lineage tree obtained in an exponential culture. The grey horizontal line on the right panel indicates the current time of observation. The blue highlighted lines correspond to cells that are sampled to obtain the distribution indicated above the lineage tree. For example, to obtain ψ_ans we sample all the cells in the tree excluding those that are currently alive. (b) The same image for a finite culture. The red dots represent cells that are expelled from the culture before they divide. (c) The relationship between distributions in the finite and exponentially growing culture. (d) Plots of the various distributions of single-cell growth rates obtained from simulations of the cell-size regulation model with N = 10⁴, $C{V}_{\lambda }^2=0.25$, 〈λ〉 = 1, v_div = 2, α = 1 and ρ_λ = 0.2. The lineage distribution, which can be computed analytically for this model, is also shown. For the ancestral distribution, we have plotted both the histogram of lnλ over all ancestral cells (red dashed line) as well as the result of evaluating the right-hand side of equation (4.4), using the carrier and tree distributions (purple line).

In practice, the distribution ${\psi }_{\mathrm{car}}^F(\mathbf{x})$ may be easier to obtain than ${\psi }_{\mathrm{tree}}^F(\mathbf{x})$ because sampling ${\psi }_{\mathrm{tree}}^F(\mathbf{x})$ requires knowledge of generation times of cells that are expelled from the culture. In certain experimental settings, these cells may be difficult to track, and additionally, their growth may be not be statistically identical to those cells that remain in the culture due to the different conditions in and out of the device where cells are observed [28]. This motivates us to develop a method for estimating the population growth rate, Λ, from the available lineage data. To this end, we use the normalization of ${\psi }_{\mathrm{tree}}^F(\mathbf{x})$ to obtain

$$2={\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{\mathrm{\Lambda }\tau (\mathbf{x})}{\psi }_{\mathrm{car}}(\mathbf{x})\hspace{0.17em}\text{d}{x}_1\cdots \text{d}{x}_l.$$ 4.2

As we have done above in equation (3.7), we can marginalize over the phenotype x to recast this equation in terms of the corresponding generation time distribution:

$$2={\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{\mathrm{\Lambda }\tau }{\psi }_{\mathrm{car}}(\tau )\hspace{0.17em}\text{d}\tau .$$ 4.3

Equation (4.3) addresses the question of how Λ is related to the distribution generation times among cells in the culture.

4.1. The ancestral and division distributions

In the exponentially growing culture, the distribution 2ψ_tree(x)e^−Λτ(x) has a different interpretation; it is equal to the distribution over all the current cell’s ancestors, denoted ψ_ans(x) (this has been referred to as the branch distribution in [27]). This distribution is obtained by sampling all cells in the tree excluding those that are currently alive, as shown in figure 2a. The fact that $\psi {\hspace{0.17em}}_{\mathrm{car}}^F(\mathbf{x})={\psi }_{\mathrm{ans}}(\mathbf{x})$ suggests there may be an alternative interpretation of these distributions that is common to both types of cultures. In fact, in both the continuous culture and exponentially growing culture, the carrier (or branch) distribution can be interpreted as the distribution of phenotypes of cells that have just divided, or the division distribution ψ_div(x). We refer to appendix B for the derivation.

Now consider the the distribution over the ancestral cells in the finite culture, denoted ${\psi }_{\mathrm{ans}}^F(\mathbf{x})$. In order to obtain ${\psi }_{\mathrm{ans}}^F(\mathbf{x})$, we take the phenotypes of all cells currently alive in the culture and trace back through their ancestors, collecting their phenotypes. How might this distribution be related to ψ_ans(x) in the exponential culture (or equivalently, the carrier distribution in the finite culture, ${\psi }_{\mathrm{car}}^F(\mathbf{x})$)? Because all cells have a common ancestor we can compute ${\psi }_{\mathrm{ans}}^F(\mathbf{x})$ by taking only the ancestor cells of this common ancestor—as we trace back in time far enough the more recent cells make up a negligible fraction of the observed phenotypes. ψ_ans(x) is therefore the distribution of phenotypes obtained by looking backwards along a lineage beginning from an arbitrary cell in the culture. If phenotypes are not correlated across generations, then the phenotypes sampled along the lineage are independent and this is therefore equivalent to sampling cells in the population that have divided in the culture; as we saw before, this is ψ_car(x). However, if there are correlations across generations, we need to consider how the ancestor’s phenotypes along a lineage are biased by the descendants’ phenotypes. This is captured by the recursive formula for ψ_ans(x) (derived in appendix B):

$${\psi }_{\mathrm{ans}}^F(\mathbf{x})={\psi }_{\mathrm{car}}^F(\mathbf{x}){\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}f({\mathbf{x}}^{\prime }|\mathbf{x})\frac{{\psi }_{\mathrm{ans}}^F({\mathbf{x}}^{\prime })}{{\psi }_{\mathrm{tree}}^F({\mathbf{x}}^{\prime })}\text{d}{x}_1^{\prime }\cdots \text{d}{x}_l^{\prime }.$$ 4.4

From this equation, it is easy to see that ${\psi }_{\mathrm{ans}}^F(\mathbf{x})={\psi }_{\mathrm{car}}^F(\mathbf{x})$ precisely when f(x|x′) = f(x), as expected from the argument above.

Our results concerning the relationship between phenotype distributions in exponential and finite cultures are summarized in figure 2c. To explicitly demonstrate these relationships we performed simulations of the cell-size regulation model. Results of these simulations are shown in figure 2d. For realistic parameter values, we see that the differences between the distributions are quite small.

5. Competition between multiple species in a finite population

Having established that the Euler–Lotka equation can be generalized to the setting of the a finite culture in steady state, we now consider a model in which two cells compete in a finite culture. We will once again assume that the number of cells (N) is sufficiently large so that any stochastic fluctuations at the population level may be ignored. Before considering these competition dynamics directly, we suppose that the two species are grown separately in environments with unlimited space and nutrients. Under these conditions, the number N_i of cells in species i will then grow exponentially at some rate Λ_i. It is not difficult to see that the fraction of species 1, ϕ₁ = N₁/(N₁ + N₂), evolves according to the logistic growth equation

$$\frac{\text{d}}{\text{d}t}{\varphi }_1={\varphi }_1(1-{\varphi }_1)\mathrm{\Delta }\mathit{\Lambda },\mathrm{\Delta }\mathit{\Lambda }={\mathit{\Lambda }}_1-{\mathit{\Lambda }}_2.$$ 5.1

The quantity S = ΔΛ/Λ₂ is known as the selective advantage of species 1 over species 2 and its sign determines which species eventually takes over the culture.

We now imagine placing both species in a finite culture that can hold exactly N cells (figure 1b). As before, this is implemented by removing a randomly selected cell from the culture every time a cell division occurs. For the moment, we will assume that nutrients are not limiting growth and the environment is constant. Under these assumptions, we can heuristically obtain the dynamics of the frequency of species 1 in the finite setting, ϕ₁(t), from the exponentially growing population by uniformly sampling N cells from the exponentially growing population at each time; this would suggest that the outcome of a competition experiment is also determined by ΔΛ. However, we know that the steady-state phenotype distribution determines the population growth rates. Therefore, in order to justify the heuristic argument mathematically, it must be established that when two species are placed in a finite culture, their phenotype and age distributions converge to their steady states. If this condition is not met, then there is a possibility that the outcome of the competition depends on the initial phenotype distribution. From a biological perspective, it is important to understand what happens when the initial distribution is not in steady state, as it is rarely the case that ecological dynamics begin with each species in steady state. For example, two species from different environments may meet after being consumed by the same host organism. Unless the conditions within the host are identical to the conditions outside, the populations will not be in steady state at the onset of the competition.

In appendix C, we have derived the dynamics of ϕ₁(t) within the context of the two-species Moran process model, along with the generalization to the case of M species. There, we show that the joint density of phenotypes and ages among species i, denoted ψ_i(t, x, u), obeys

$$(\frac{\mathrm{\partial }}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }u}){\psi }_i(t,\mathbf{x},u)=-{\mathrm{\Lambda }}_i(t){\psi }_i(t,\mathbf{x},u).$$ 5.2

Here Λ_i(t) is the per capita division rate of cells of species i, which may depend on time if the system has not reached its steady state. In terms of ψ_i,

$${\mathrm{\Lambda }}_i(t)={\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}{\psi }_i(t,\mathbf{x},{\tau }_i(t,\mathbf{x}))\hspace{0.17em}\text{d}{x}_1\cdots \text{d}{x}_l.$$ 5.3

We have allowed for both the phenotype distribution and Λ_i(t) to be time-dependent, since the culture may not be in steady state. Equation (5.2) holds for u < τ_i(x) and is supplemented by the boundary conditions prescribing how the phenotypes are selected at birth,

$${\psi }_i(t,\mathbf{x},0)=2{\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}f(\mathbf{x}|{\mathbf{x}}^{\prime }){\psi }_i(t,{\mathbf{x}}^{\prime },{\tau }_i({\mathbf{x}}^{\prime }))\text{d}{x}_1^{\prime }\cdots \text{d}{x}_l^{\prime }.$$ 5.4

Importantly, equations (5.2) and (5.4) are completely decoupled from the phenotype distributions of other species and ϕ_i(t). In other words, the distributions of phenotypes evolve completely independently from the frequencies of species in the culture. Some of our main results follow from this observation. First, in a competition experiment, the phenotype distributions will converge to their steady states regardless of the initial conditions and relative fitnesses of each species. Second, the species with a higher value of Λ_i as determined by equation (1.2) will eventually dominate the culture, regardless of the initial state of the phenotype and age distributions. Finally, in the special case where the initial phenotype distributions are in their steady states satisfying equation (3.2) and there are two species, the frequency ϕ₁(t) will obey the logistic growth equation (5.1).

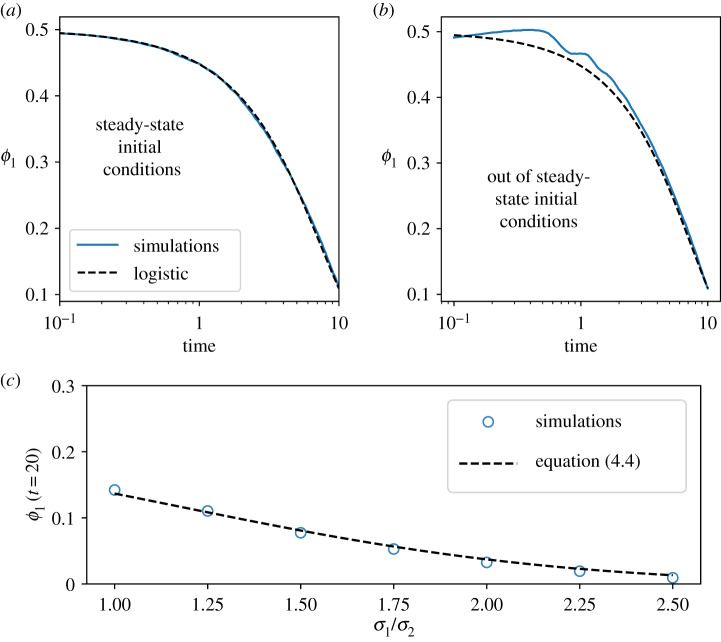
In figure 3, we show simulations for competition between two species modelled by the random growth rate model compared with the prediction of the logistic growth equation. When the competition begins with the phenotype distributions in their steady state, we see that the simulations agree exactly with the prediction. If the initial phenotype distributions are not in steady state, we find that the transient dynamics differ from the logistic growth equation; however, as predicted, they converge to the trajectory of the logistic equation within a few generations.

Figure 3.

(a,b) Simulations of two species, each modelled by the random growth rate model, competing in the Moran process compared with the prediction of the logistic growth equation (5.1). The blue lines represent the average over 1000 simulations. In (a), the phenotype distributions are initially taken to be in steady state, satisfying the self-consistent equation (1.3). In (b), the phenotype distributions are initially out of steady state. This is achieved by drawing the initial growth rates from Gaussian distributions with different means. In both cases, we have used σ_λ = 0.3 for both species 〈λ〉₁ = 1 and 〈λ〉₂ = 1.1 (hence species 2 has an advantage). We have used the sizer model for cell-size regulation and neglected any size additive noise. (c) ϕ₁(t) at t = 20 generations for two populations with the same average growth rate and different values of ${\sigma }_i^2$, the variance in growth rates. We have used 〈λ〉₁ = 1 and 〈λ〉₂ = 1.1, and we have fixed σ₂ = 0.2 and increased σ₁. For both species, growth rates are uncorrelated across generations. Each circle represents the average of 1000 simulations for the same parameter values.

6. Discussion

In this paper, we have studied the dynamics of competition between phenotypically heterogeneous populations in finite cultures. While a number of studies have explored the dynamics of phenotypically heterogeneous populations under exponential growth conditions and shown how to relate lineage statistics to the population growth rate (e.g. [1,27,29–33]), little work has been done concerning the dynamics of multiple species in finite populations. In exponentially growing populations, the population growth rate is related to the steady-state phenotype distribution. When studying competition dynamics, it is not clear that the transient dynamics of the phenotype and age distributions do not affect the fate of species. We have shown that even if the initial populations are not initially in steady state, the end result of a competition experiment can be predicted by the steady-state dynamics, which are the same for both exponential and finite cultures.

We have also clarified the relationship between the different distributions in both the exponentially growing and finite culture, as well as derived a simple mapping between the various distributions in the two types of cultures. Importantly, distributions obtained in equivalent ways do not always have the same meaning in different types of cultures. In particular, the ancestral distribution in a finite culture is not equivalent to the ancestral distribution of the exponentially growing culture due to a bias towards surviving cells, yet both are obtained by looking at the history of all cells in the culture. A corollary of our mapping between the lineage statistics in different cultures is a formula for the population growth rate (given by equation (4.3)) that requires knowledge only of the lineage data obtained in a sufficiently large finite culture. In addition to relating the lineage statistics to the population growth rate, we have shown that the population growth rate predicts the fitness of a species in a competition experiment.

By demonstrating that the outcomes of ecological competition are independent of the initial conditions, our results shed light on what is important in ecological dynamics of microbial populations. In particular, they suggest that, in the context of the Moran process, all memory of the transient phenotypic distributions is lost over the course of a few generations. This is important, as many natural populations do not live in constant environments, but are repeatedly transplanted to new environments where they are forced to compete (in a finite population) with new sets of species. For example, infectious bacteria may travel between many different hosts, each one containing distinct populations of microbes.

We emphasize that the simple Moran process in which species are non-interacting is a very simplified picture of ecological competition dynamics. However, by establishing the basic principles of competition in this context, we believe our results can help guide future studies seeking to understand higher order effects. An interesting extension of our work could involve investigating species interactions. When species interact, the principle of competitive exclusion breaks down, and it is possible that two species can coexist indefinitely [20]. How does variability within species affect coexistence? A second extension would be to understand how demographic fluctuations (fluctuations due to the finite size of the population) influence the dynamics. If one allows for demographic fluctuations in the model, it is possible that even the species with a larger population growth rate can go extinct. Therefore, the more relevant quantity to consider is the fixation probability, defined as the probability that one species will eventually completely dominate the culture. How are the fixation probabilities related to the population growth rates? Do the initial conditions significantly affect the fixation probabilities? To our knowledge, these questions have not been answered in the existing literature.

Appendix A. Derivation of Euler–Lotka equation

Here we give a more detailed derivation of equation (3.6). Let ψ(t, x, u) denote the joint distribution of species with phenotypes x and ages u in an instantaneous observation of a population with N ≫ 1 microbes. We are mostly interested in the steady-state distribution ψ(x, u). In this section, we omit the superscript F because we are only concerned with the finite culture. We proceed by considering the change in the number of cells with phenotypes in the hypercube $\prod _{i=1}^l[x_i^{\prime },x_i+\mathrm{d}{x}_i)$ and ages between u and u + du in an interval dt. This change is caused both by the aging of cells (not to be confused with the way this term is used in [22], where it corresponds to the deterioration of growth capacity) and the expulsion of cells from the culture. Since each cell is chosen to be expelled with equal probability whenever a cell divides, the probability that any given cell is expelled is simply the fraction of cells that divide per unit time multiplied by dt, or Λ_D dt. It follows that

$$\begin{array}{rl}& \underset{\mathrm{change}\hspace{0.17em}\mathrm{in}\hspace{0.17em}\mathrm{number}\hspace{0.17em}\mathrm{of}\hspace{0.17em}\mathrm{cells}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\mathrm{age}\hspace{0.17em}\mathit{u}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\mathrm{phenotype}\hspace{0.17em}\mathbf{x}}{\underbrace{N\psi (t+\mathrm{d}t,x,u)\hspace{0.17em}\text{d}{x}_1\cdots \text{d}{x}_l\hspace{0.17em}\text{d}t-N\psi (t,\mathbf{x},u)\hspace{0.17em}\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}\\ & \approx \underset{\mathrm{cells}\hspace{0.17em}\mathrm{gained}\hspace{0.17em}\mathrm{from}\hspace{0.17em}\mathrm{aging}}{\underbrace{N\psi (t,\mathbf{x},u-\text{d}t)\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}-\underset{\mathrm{cells}\hspace{0.17em}\mathrm{lost}\hspace{0.17em}\mathrm{from}\hspace{0.17em}\mathrm{aging}}{\underbrace{N\psi (t,\mathbf{x},u)\hspace{0.17em}\text{d}x\text{d}t}}\\ & -\underset{\mathrm{cells}\hspace{0.17em}\mathrm{expelled}\hspace{0.17em}\mathrm{from}\hspace{0.17em}\mathrm{the}\hspace{0.17em}\mathrm{culture}}{\underbrace{N\psi (t,\mathbf{x},u){\mathrm{\Lambda }}_D\hspace{0.17em}\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}.\end{array}$$ A 1

This equation is valid for cells that have not yet divided; hence, x and u are such that u < τ(x). Taking the limit dt → 0 and dividing by dt gives the Von Foerster equation (3.1). Consider the distribution of phenotypes among cells that are just born. This is given by ${\psi }_{\mathrm{birth}}(\mathbf{x})=\psi (\mathbf{x},0){\mathit{\Psi }}_0^{-1}$ where Ψ₀ is a normalization constant obtained by integrating ψ(x, 0); ${\mathit{\Psi }}_0={\int }_0^{\mathrm{\infty }}\psi (\mathbf{x},0)\text{d}{x}_1\cdots \text{d}{x}_l$. Empirically, ψ_birth(x) is obtained by taking an instantaneous observation of the population and sampling only the cells that have just been born. By solving equation (3.3) and inserting the solution into (3.2), it is straightforward to obtain

$${\psi }_{\mathrm{birth}}(\mathbf{x})=2{\int }_0^{\mathrm{\infty }}f(\mathbf{x}|{\mathbf{x}}^{\prime }){\psi }_{\mathrm{birth}}({\mathbf{x}}^{\prime }){\text{e}}^{-{\mathrm{\Lambda }}_D\tau ({\mathbf{x}}^{\prime })}\text{d}{x}_1\cdots \text{d}{x}_l.$$ A 2

Because this distribution is time invariant, sampling those cells that have just been born at any sequence of times t₁, t₂, … t_n yields the same distribution. Carrying out this sampling procedure at an infinite sequence of times samples every cell only once, and therefore ψ_birth(x) = ψ_tree(x). Integrating both sides of equation (A 2) results in equation (3.6).

Appendix B. Relationship between phenotype distributions

B.1. The age distribution

The distribution of ages in the culture g(u) is given by

$$g(u)={\int }_{x:\tau (x)>u}\psi (\mathbf{x},0){\text{e}}^{-u{\mathrm{\Lambda }}_D}\hspace{0.17em}\text{d}{x}_1\cdots \text{d}{x}_l.$$ B 1

Another way to derive this expression is by noting that it is the probability a cell is not flushed out by age u, times the probability that it has not yet divided by age u. In the specific context of the random generation time model (τ = x), we obtain the result found by Powell [17] without generation time correlations:

$$g(u)={\mathit{\Psi }}_0{\text{e}}^{-u{\mathrm{\Lambda }}_D}{\int }_u^{\mathrm{\infty }}{\psi }_{\mathrm{birth}}(\tau )\hspace{0.17em}\text{d}\tau .$$ B 2

To find Ψ₀, note that the number of cells that divide in a time dt is the number which have ages equal to their generation time, hence

$$\begin{array}{rl}N{\mathrm{\Lambda }}_D\hspace{0.17em}\text{d}t& =N\hspace{0.17em}\text{d}t{\int }_0^{\mathrm{\infty }}\psi (s,s)\hspace{0.17em}\text{d}s=N\hspace{0.17em}\text{d}t{\mathrm{\Psi }}_0{\int }_0^{\mathrm{\infty }}{\psi }_{\mathrm{birth}}(s){\text{e}}^{-s{\mathrm{\Lambda }}_D}\hspace{0.17em}\text{d}s\\ & =\frac{N{\mathrm{\Psi }}_0}{2}\hspace{0.17em}\text{d}t.\end{array}$$

It follows that Ψ₀ = 2Λ_D, which generalizes the conclusion Powell came to in the uncorrelated setting. Note that for ψ_birth(τ) = δ(τ − τ₀), we obtain an exponential age distribution.

B.2. The ancestral distribution

In the finite culture ψ_ans(x) is the distribution over all cells that have descendents in the current culture. Let $\hspace{0.17em}\tilde{f}({\mathbf{x}}^{\prime }|\mathbf{x})\hspace{0.17em}\text{d}{x}_1\cdots \text{d}{x}_l$ be the probability that a cell’s mother has phenotype in the hypercube $\prod _{i=1}^l[x_i^{\prime },x_i^{\prime }+\text{d}{x}_i)$ given that its phenotype is x. Bayes’ theorem tells us that

$$\widetilde{\hspace{0.17em}f}({\mathbf{x}}^{\prime }|\mathbf{x})=f(\mathbf{x}|{\mathbf{x}}^{\prime })\frac{{\psi }_{\mathrm{car}}({\mathbf{x}}^{\prime })}{{\psi }_{\mathrm{tree}}(\mathbf{x})}.$$ B 3

It follows that

$$\begin{array}{rl}{\psi }_{\mathrm{ans}}(\mathbf{x})& ={\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}\hspace{0.17em}\tilde{f}({\mathbf{x}}^{\prime }|\mathbf{x}){\psi }_{\mathrm{ans}}(\mathbf{x})\text{d}{x}_1\cdots \text{d}{x}_l\\ & ={\psi }_{\mathrm{car}}({\mathbf{x}}^{\prime }){\int }_0^{\mathrm{\infty }}f(\mathbf{x}|{\mathbf{x}}^{\prime })\frac{{\psi }_{\mathrm{ans}}(\mathbf{x})}{{\psi }_{\mathrm{tree}}(\mathbf{x})}\text{d}{x}_1\cdots \text{d}{x}_l.\end{array}$$ B 4

B.3. Division distribution

In both the continuous culture and exponentially growing culture, the carrier (or branch) distribution can be interpreted as the distribution of cells that have just divided, or the division distribution ψ_div(x). In terms of the joint density of phenotypes and ages throughout the population, ψ(x, u), the number of cells with phenotypic trait in $\prod _{i=1}^l[x_i,x_i+\mathrm{d}{x}_i)$ that have just divided is

$$\begin{array}{rl}N\psi (\mathbf{x},\tau (\mathbf{x}))\hspace{0.17em}\text{d}\mathbf{x}& =N\psi (\mathbf{x},0){\text{e}}^{-{\mathrm{\Lambda }}_D\tau (\mathbf{x})}\text{d}{x}_1\cdots \text{d}{x}_l\\ & =N2{\psi }_{\mathrm{tree}}(\mathbf{x}){\text{e}}^{-{\mathrm{\Lambda }}_D\tau (x)}\text{d}{x}_1\cdots \text{d}{x}_l.\end{array}$$ B 5

Dividing by N dx₁ · · · dx_l gives the distribution of phenotypes among recently divided cells, which is ${\psi }_{\mathrm{div}}(\mathbf{x})=2{\psi }_{\mathrm{tree}}(\mathbf{x}){\text{e}}^{-{\mathrm{\Lambda }}_D\tau (\mathbf{x})}$. As this argument works for both a finite and exponentially growing culture, the carrier distribution, branch distribution and division distributions are identical.

B.4. Summary of distributions in the finite culture

To summarize, we have discussed the following ways to sample cells in the finite culture:

• —Tree distribution (${\psi }_{\mathrm{tree}}^F(\mathbf{x})$): Sample all the cells throughout the history of the culture, including or excluding the current cells, but including those that are expelled before they divide.
• —Carrier distribution (${\psi }_{\mathrm{car}}^F(\mathbf{x})$): Sample all the cells throughout the culture, excluding those that are expelled before they divide.
• —Ancestral distribution (${\psi }_{\mathrm{ans}}^F(\mathbf{x})$): Sample all the cells in the history of the culture that have ancestors that are currently in the culture. Equivalently, select a random cell from the culture at any time and trace along a lineage backwards from this cell.
• —Current cells distribution (${\psi }_{\mathrm{snap}}^F(\mathbf{x})$): Sample all the cells that are currently in the culture.
• —Birth distribution (${\psi }_{\mathrm{birth}}^F(\mathbf{x})$): From all the cells that are in the culture at time t, sample only those that have just been born (meaning they have age ≈0), then repeat this for all t and average the results.
• —Division distribution (${\psi }_{\mathrm{div}}^F(\mathbf{x})$): From all the cells that are in the culture at time t, sample only those whose age is approximately equal to their generation time, then repeat this for all t and average the results.

Appendix C. Derivation of logistic growth equation

Here we provide a more systematic derivation of the logistic growth equation. Let n_i denote the number of cells of species i in a culture containing M species. Let ϕ_i = n_i/N be the fraction of cells of species i and ψ_i(t, x, u)dudx₁ · · · dx_l be the fraction of cells of species i with ages between u and du and phenotype x_k between x_k and x_k + dx_k. When a cell of species i reaches age τ_i(t, x) it divides, hence over an interval dt, the number of cells in species i that divide is the product of the total number of cells in species i, or ϕ_iN, and the fraction of the these cells that have reached age u = τ_i(t, x). It follows that the total number of cells dividing in an interval dt is

$$\sum _{i=1}^M\underset{\begin{array}{c}\mathrm{number}\hspace{0.17em}\\ \mathrm{of}\hspace{0.17em}\mathrm{cells}\hspace{0.17em}\\ \mathrm{in}\hspace{0.17em}\mathrm{species}\hspace{0.17em}\mathit{i}\end{array}}{\underbrace{{\varphi }_{i}N}}\underset{\mathrm{fraction}\hspace{0.17em}\mathrm{of}\hspace{0.17em}\mathrm{species}\hspace{0.17em}\mathit{i}\hspace{0.17em}\mathrm{cells}\hspace{0.17em}\mathrm{that}\hspace{0.17em}\mathrm{are}\hspace{0.17em}\mathrm{dividing}}{\underbrace{{\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}{\psi }_i(t,\mathbf{x},{\tau }_i(t,x))\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}.$$ C 1

The per capita dilution rate, Λ(t), is obtained by dividing this expression by N. That is,

$$\mathit{\Lambda }(t)=\sum _{i=1}^M{\varphi }_i{\mathit{\Lambda }}_i(t),$$ C 2

where Λ_i(t) is the contribution of each species to the total dilution rate:

$${\mathit{\Lambda }}_i(t)={\int }_0^{\mathrm{\infty }}\cdots {\int }_0^{\mathrm{\infty }}{\psi }_i(t,\mathbf{x},{\tau }_i(t,\mathbf{x}))\text{d}{x}_1\cdots \text{d}{x}_l.$$ C 3

At a given time, the number of bacteria of species i in the hypercube $\prod _{i=1}^l[x_i^{\prime },x_i^{\prime }+\mathrm{d}{x}_i)$ is

$${\varphi }_i(t)N{\psi }_i(t,\mathbf{x},u)\text{d}{x}_1\cdots \text{d}{x}_l\text{d}u.$$ C 4

Just as in the single species case, the change in the number of individuals of a given phenotype and age is caused by aging of cells and expulsion from the population. Therefore, over an interval dt, the change in the number of microbes of species i with age u < τ_i(x) is

$$\begin{array}{c}\underset{\mathrm{change}\hspace{0.17em}\hspace{0.17em}\mathrm{in}\hspace{0.17em}\hspace{0.17em}\mathrm{number}\hspace{0.17em}\hspace{0.17em}\mathrm{of}\hspace{0.17em}\hspace{0.17em}\mathrm{cells}\hspace{0.17em}\hspace{0.17em}\mathrm{with}\hspace{0.17em}\hspace{0.17em}\mathrm{age}\hspace{0.17em}\hspace{0.17em}\mathit{u}\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}\mathrm{phenotype}\hspace{0.17em}\hspace{0.17em}\mathbf{x}\hspace{0.17em}\hspace{0.17em}\mathrm{in}\hspace{0.17em}\hspace{0.17em}\mathrm{species}\hspace{0.17em}\hspace{0.17em}\mathit{i}}{\underbrace{{\varphi }_i(t+\mathrm{d}t)N{\psi }_i(t+\text{d}t,\mathbf{x},u)\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t-\varphi (t)N{\psi }_i(t,\mathbf{x},u)\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}\\ \approx \underset{\mathrm{cells}\hspace{0.17em}\hspace{0.17em}\mathrm{gained}\hspace{0.17em}\hspace{0.17em}\mathrm{from}\hspace{0.17em}\hspace{0.17em}\mathrm{aging}}{\underbrace{{\varphi }_i(t)N{\psi }_i(t,\mathbf{x},u-\text{d}t)\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}-\underset{\mathrm{cells}\hspace{0.17em}\hspace{0.17em}\mathrm{lost}\hspace{0.17em}\hspace{0.17em}\mathrm{from}\hspace{0.17em}\hspace{0.17em}\mathrm{aging}}{\underbrace{{\varphi }_i(t)N{\psi }_i(t,\mathbf{x},u)\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}\\ -\underset{\mathrm{cells}\hspace{0.17em}\mathrm{expelled}\hspace{0.17em}\mathrm{from}\hspace{0.17em}\mathrm{the}\hspace{0.17em}\mathrm{culture}}{\underbrace{{\varphi }_i(t)N\mathrm{\Lambda }(t)\text{d}{x}_1\cdots \text{d}{x}_l\text{d}t}}.\end{array}$$ C 5

For each i, this equation is almost the same as equation (A 1); however, we have the additional factors of ϕ_i which account for the fact that only a fraction of the cells are in species i. Taking the limit dt → 0 gives

$$(\frac{\mathrm{\partial }}{\mathrm{\partial }t}+\frac{\mathrm{\partial }}{\mathrm{\partial }u}){\psi }_i(t,\tau ,u)=-(\mathit{\Lambda }+\frac{1}{{\varphi }_i}\frac{\text{d}}{\text{d}t}{\varphi }_i(t)){\psi }_i(t,\tau ,u).$$ C 6

Compared to equation (3.3), we have picked up an additional term depending on ϕ_i, so that we need to consider the evolution of ϕ_i in order to completely specify the dynamics. The instantaneous growth of ϕ_i is the difference between the rate at which cells of species i are born (Λ_i(t)) and flushed out (Λ(t)). Hence,

$$\frac{\text{d}}{\text{d}t}{\varphi }_i=({\mathit{\Lambda }}_i(t)-\mathrm{\Lambda }(t)){\varphi }_i.$$ C 7

Note that with two species, equation (C 7) becomes the standard logistic growth equation:

$$\begin{array}{rl}\frac{\mathrm{d}}{\mathrm{d}t}{\varphi }_1& =({\mathit{\Lambda }}_1(t)-({\varphi }_1{\mathit{\Lambda }}_1(t)+(1-{\varphi }_1){\mathit{\Lambda }}_2(t))){\varphi }_1\\ & ={\varphi }_1(1-{\varphi }_1)({\mathit{\Lambda }}_1(t)-{\mathit{\Lambda }}_2(t)).\end{array}$$ C 8

By combining equation (C 7) with equation (C 6), we obtain equation (5.2). Along with an initial distribution ψ_i(0, x, u), equations (5.2) and (5.4) describe how the distribution of phenotypes and ages evolves in the mixed culture. Importantly, these equations are decoupled from ϕ_i(t) and each other. Moreover, they turn out to be identical to the transport equations for a homogeneous culture. This implies that the dynamics of the phenotype distribution are unchanged by the competition, and the fitnesses Λ_i are therefore determined by the population growth rates of the individual species in exponentially growing cultures.

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed to the paper.

Competing interests

We declare we have no competing interests.

Funding

We acknowledge funding support from National Science Foundation under award DMS-1902895 (E.L.), National Science Foundation grant DMR-1610737 (J.K.), MRSEC at Brandeis University DMR-1420382 (J.K.), the Simons Foundation (J.K.), MRSEC at Harvard University under grant DMR-1420570 (A.A.) and NSF CAREER 1752024 (A.A.).