Abstract
Nowadays, an infectious disease outbreak is considered one of the most destructive effects in the sustainable development process. The outbreak of new coronavirus (COVID-19) as an infectious disease showed that it has undesirable social, environmental, and economic impacts, and leads to serious challenges and threats. Additionally, investigating the prioritization parameters is of vital importance to reducing the negative impacts of this global crisis. Hence, the main aim of this study is to prioritize and analyze the role of certain environmental parameters. For this purpose, four cities in Italy were selected as a case study and some notable climate parameters—such as daily average temperature, relative humidity, wind speed—and an urban parameter, population density, were considered as input data set, with confirmed cases of COVID-19 being the output dataset. In this paper, two artificial intelligence techniques, including an artificial neural network (ANN) based on particle swarm optimization (PSO) algorithm and differential evolution (DE) algorithm, were used for prioritizing climate and urban parameters. The analysis is based on the feature selection process and then the obtained results from the proposed models compared to select the best one. Finally, the difference in cost function was about 0.0001 between the performances of the two models, hence, the two methods were not different in cost function, however, ANN-PSO was found to be better, because it reached to the desired precision level in lesser iterations than ANN-DE. In addition, the priority of two variables, urban parameter, and relative humidity, were the highest to predict the confirmed cases of COVID-19.
Keywords: sustainable development, COVID-19, artificial intelligence, PSO, DE, feature selection
1. Introduction
Sustainable development is an approach planned to improve human life and considers the development process while simultaneously analyzing related impacts [1,2,3]. Its critical role is becoming more and more important every day. After great efforts, in 2015, United Nations member states approved the 2030 Agenda for Sustainable Development, which includes 17 Sustainable Development Goals (SDGs) [4].
The main aspects of sustainable development are simultaneous consideration of environmental, social, and economic, and if the policies of governments consider these three factors separately, the effect on sustainable development can be negative [5,6]. There are many evaluation methods to analyze the previous efforts on sustainable development [7,8,9], and the selected techniques depend on the study goals [10,11,12,13,14].
Although sustainable development is not a new concept, these methods neglect important elements. Among them, epidemic diseases can have a temporary or permanent negative impact [15,16]. Moreover, urbanization also plays an important role in this regard, since one of its impacts is the increase of the population density, which can affect the epidemic rate of diseases directly [17,18,19,20]. COVID-19 is a recent pandemic disease [21]. There are several studies about coronavirus spread, the time the virus remains in the environment, the epidemic rate, and the mathematical models for the prediction of COVID-19 contagions [22,23,24,25,26].
Chen et al. developed a time-dependent mathematical model for the prediction of the total number of confirmed cases [27]. Pirouz et al. used artificial intelligence (AI) algorithm to study the correlation between environmental parameters and COVID-19. They found a significant correlation between urban and climate parameters and the number of confirmed cases of COVID-19 [28]. Hu et al. developed a predictive model for the transmission period of the COVID-19 using AI techniques. Their results showed a high-performance of AI in predicting the outbreak of coronavirus [29].
Kampf et al. investigated the time the coronaviruses survive on different surfaces. Their results show that COVID-19 can survive up to nine days, depending on the environment temperature and materials of the surface [30]. Grant and Giovannucci carried out a study about the impact of temperature on COVID-19 and showed that most patients had been exposed to temperatures between 3 and 17 degrees Celsius, and that the infection rates are lower in tropical regions [31]. In a previous study, Chan et al. had analyzed the effects of temperature and humidity on another type of coronavirus, SARS. According to this study, when the temperature increases, the survival time of the virus on the surfaces can decrease, and this leads to a lower epidemic rate [32].
The review of these previous studies and the size of the pandemic reveals that new coronavirus (COVID-19) as an infectious disease has undesirable social, environmental, and economic impacts and might lead to serious challenges and threats in many societies. Therefore, the paper will prioritize and analyze the role of certain environmental parameters, including daily average temperature, relative humidity, wind speed, and an urban parameter, population density, which have essential roles in reducing the negative impacts of this global crisis by using artificial intelligence techniques.
2. Methodology
Two analytical approaches have been used. At first, by using a multivariate linear regression (MLR) model, the correlations between the three climate parameters, including average temperature, humidity, and wind speed, and the confirmed cases of COVID-19 were investigated, and the required datasets for artificial intelligence prepared. Then, two artificial intelligence techniques based on ANN, including the PSO algorithm and DE algorithm, have been used for predicting the confirmed cases of COVID-19 and to prioritize and reduce the input parameters.
Analysis Conditions:
The analysis factors are the population density of each region, average daily temperature, relative humidity, wind speed, and the positive cases in the following days;
Since the incubation period of the virus is about 14 days, the sum of previous positive cases up to 14 days previously has been considered;
The analysis period is from 14 February 2020 to 24 March 2020.
In addition, it must be noticed that there are some delays between the exact dates when patients got infected by the COVID-19, and the dates when confirmed cases were registered in the media as follows:
The incubation period of COVID-19 varies from about 2 to 14 days [33];
The lab tests of COVID-19 were on patients with symptoms [34];
The symptoms of COVID-19 occur after 3 to 5 days [35];
The results of the laboratory tests took one day to be ready [36,37];
The daily announcement of new confirmed cases of COVID-19 usually refers to one day before [38].
Therefore, to find an appropriate correlation between weather data and confirmed cases, the climate factors have been shifted backward from one to nine days with respect to observations, and by the MLR method, the best correlation for each region has been selected. The results are presented in Appendix A, and have been used as a database in the artificial intelligence method.
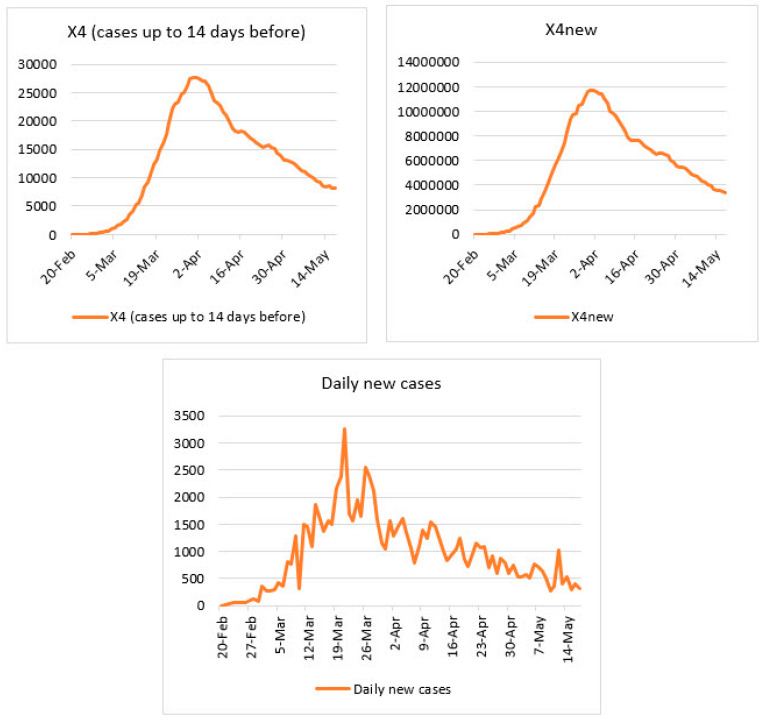
It is evident that using daily positive cases—and especially data from one day before—could not be correct, due to the incubation period of COVID-19 (2 to 14 days), the symptoms of COVID-19 (which occur after 3 to 5 days), and finally, the fact that the lab tests of COVID-19 were on patients with symptoms. Therefore, the new positive case in date X will depend on the accumulative positive cases up to 14 days ago (Date X-14). This variable cannot reach a plateau since it represents the accumulation of 14 days, not the period from start to end, as presented in Appendix B.
2.1. Artificial Intelligence Methods
2.1.1. Artificial Neural Network (ANN)
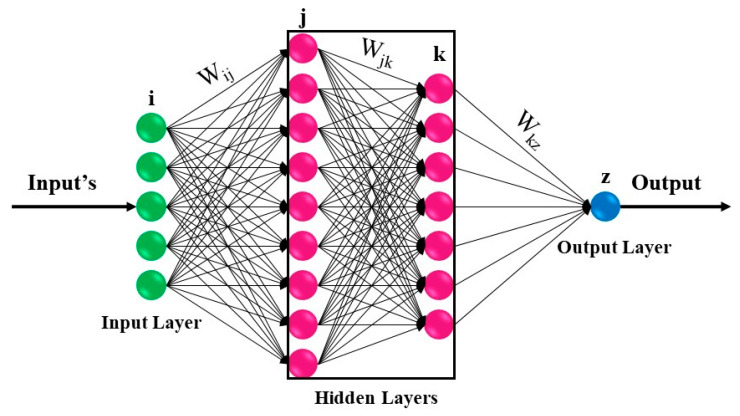
The human brain, as a complex natural system, is unique in its kind. Some of the processes in this natural system are so complex that their processing is also complex for many super systems [39,40,41,42,43,44]. Analytical processes are very complex, because of the high speed and power of information processing by brain cells. Researchers were enabled to design advanced methods for solving various problems of real world inspired by the function of the human brain. Hence, artificial intelligence (AI) is considered one of the most successful achievements of computer science, simulating the behavior of the human brain in data analysis [45,46,47,48,49,50,51]. One of the AI branches is the artificial neural network (ANN). This information processing system, by a simulating strategy like communication between brain neurons, has become a tool for analyzing complex and real systems. In recent years, ANN models have been developed to overcome the difficulties presented by health issues [52,53,54]. Many types of computational models have been introduced as general neural networks. The multilayer perceptron (MLP) model is one of the most efficient ones, and has been used in a variety of activities. The MLP is a supervised artificial neural network with at least three layers, including the input layer, hidden layer, and output layer. The basic form of an artificial neural network includes a set of connected units or nodes (artificial neurons), and connections (weights). The connections can transmit a signal from one neuron to another, as shown in Figure 1. Depending on a particular problem, the number of neurons and the hidden layer can be changed to find the best prediction model [55,56,57,58,59,60]. The performance indicators of the algorithm evaluate the difference between the predicted values and the last layer (output). The process of training and evaluating the results in this algorithm continues until a desirable convergence is reached, and then it stops.
Figure 1.
The basic form of multilayer perceptron artificial neural network (ANN) [61].
2.1.2. Particle Swarm Optimization (PSO) Algorithm
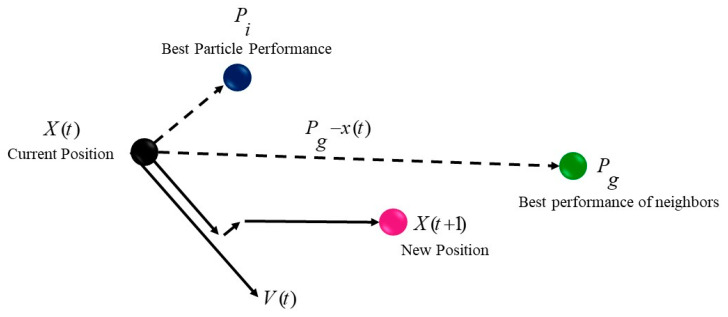
In recent years, the use of artificial intelligence by many researchers to solve complex and uncertain problems has become widespread [62,63,64,65,66,67,68,69,70,71], and there have been especially successful applications in the health problems [72,73,74,75,76]. One of these advanced techniques is the particle swarm optimization (PSO) algorithm, first introduced by Kennedy and Eberhart [77,78,79]. The algorithm was designed to simulate the swarm behavior of particles and to inspire the movement of birds and flocks. The PSO algorithm has been used successfully for modeling in engineering and academic applications. In this algorithm, each particle in the particle set is considered as a potential solution that the process of this algorithm begins with the generation of a random particle set. Then, the process continues by moving the set of particles to search for an optimal answer in the search space. In addition, if there is a D-dimensional set, including N particles, each i particle in this set is indicated with an Xi vector that includes vectors of position and velocity. In fact, the PSO algorithm differs from other algorithms in having a velocity vector. The new velocity vector and the new position vector of each particle are updated based upon Equations (1) and (2) in each moment. They depend on the particle’s best position (Pbest) and the global best position (Gbest) [80].
| (1) |
| (2) |
where and are the current position and velocity of the particle i, respectively, and and its new position and velocity. The parameter w is called the inertia weight, and varies between 0.4 and 0.9. The and are two random numbers within [0, 1]. The constants C1 and C2, called the individual learning factor and social learning factor, are positive and must satisfy Equation (3). Figure 2 shows the update of the velocity and position vectors of a particle in the set [81,82].
| (3) |
Figure 2.
The update of the velocity and position vectors [61].
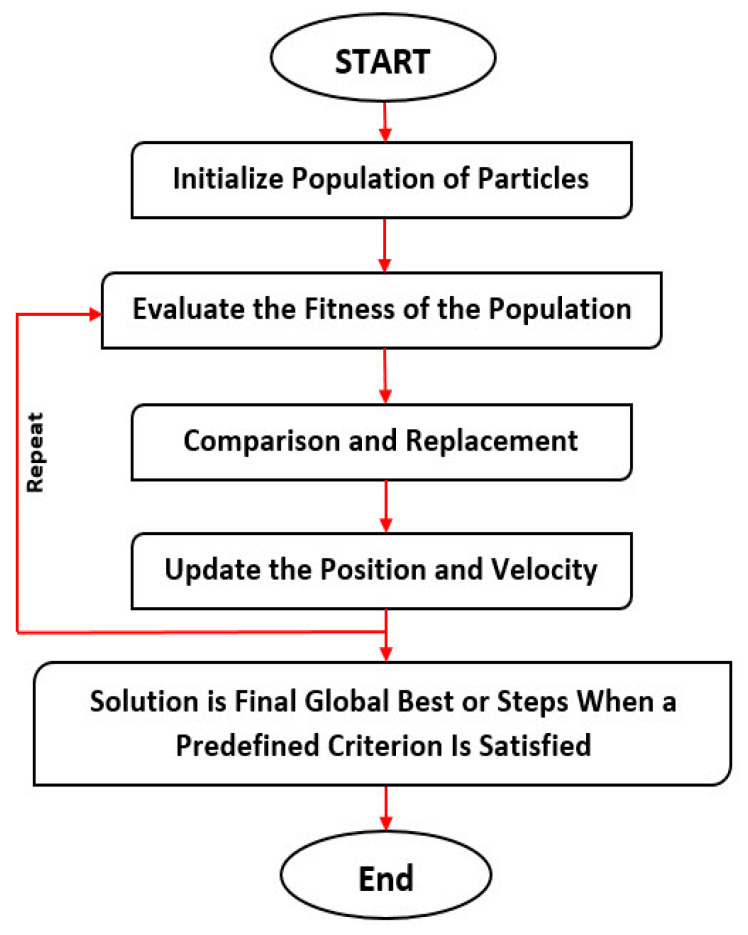
Eventually, all particles converge to the optimal point after a thorough search. Figure 3 presents the flowchart of the PSO algorithm.
Figure 3.
The particle swarm optimization (PSO) algorithm flowchart [83].
2.1.3. Differential Evolution (DE) Algorithm
The differential evolution (DE) is an evolutionary computation that is suitable for dealing with complex problems in the real world. The DE algorithm is a population-based algorithm that was proposed by Price and Storn for solving the continuous value problems [84,85,86,87]. Then, in the following years, the method developed and used for solving binary and discrete problems. The DE algorithm has been widely applied as an optimization algorithm to solve complex problems in various engineering sectors. The DE algorithm and some Meta heuristic algorithms like genetic algorithms have similar operators, including crossover, mutation, and selection. However, there are some differences among them, like the lack of local search in genetic algorithm, while the DE algorithm supports local search. In addition, the DE relies on mutation operation while the genetic algorithm relies on a crossover. Like other evolutionary algorithms, the DE starts by randomly generating the initial population. Then, after initialization, the search space is expanded by the mutation. The is the mutant solution vector of which is calculated based on Equation (4) [88].
| (4) |
where is the scaling factor varying in the range [0, 1] and determines the length of the mutation step. are solution vectors that are randomly selected, with the condition expressed by Equation (5) [89].
| (5) |
where “i” is the index of the current solution. The trial vector () is produced by mixing the mutated vector and the parent vector in a crossover operation based on Equation (6) [90].
| (6) |
where Randj is a randomly chosen real number in the interval between 0 and 1. The CR is a crossover constant. If the Randj is less than or equal to CR, the trial vector () is inherited from the mutant solution vector, otherwise, the CR is considered equal to . The flowchart of the DE algorithm is shown in Figure 4.
Figure 4.
The differential evolution (DE) algorithm flowchart [91].
2.2. Subsection
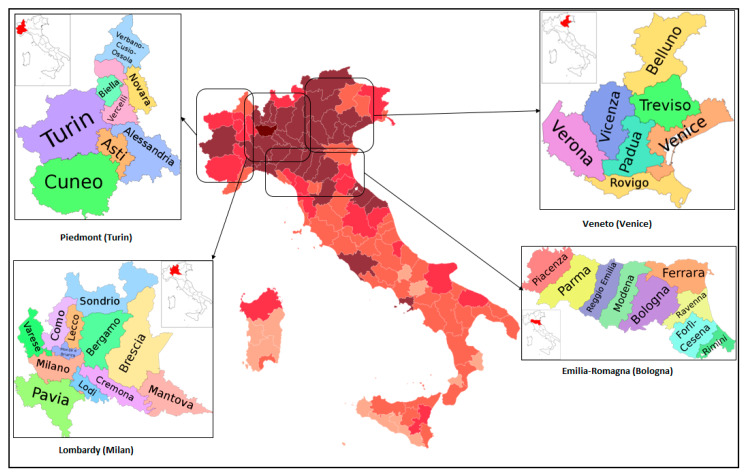
In this research, the case studies are the four regions in Italy with the largest numbers of confirmed cases of COVID-19, namely Lombardy (Milan), Piedmont (Turin), Veneto (Venice), and Emilia-Romagna (Bolonia), whose general data are presented in Table 1. The locations of the case studies are shown in Figure 5.
Table 1.
The selected case studies.
Figure 5.
Locations of the case study regions, Italy [94,95,96,97,98].
3. Model Development
3.1. PSO Modelling
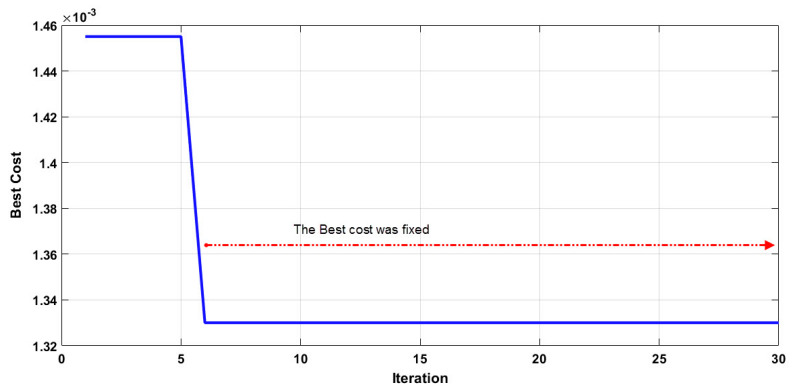
The main goal of PSO is to train the artificial neural network for determining the feature selection of confirmed cases of COVID-19, and the reduction of them under the highest relationship between several independent variables and the dependent variable. For this purpose, three notable climate parameters, namely daily average temperature, relative humidity, and wind speed, and one urban parameter (population density × positive cases up to 14 days before), were considered as input data set, and confirmed cases of COVID-19 were considered as the output dataset. It is worth mentioning that the 4 input parameters are evaluated and reduced to 2. Firstly, before modeling, the control parameters of an algorithm should be selected. There are no specific rules, and most of them are considered based on the experts’ opinions and previous studies [61,82]. Hence, a number of different modeling are done to determine an appropriate value for control factors, for instance, the size of a hidden layer of ANN was selected for 10, 20, and 30, the maximum iteration value was considered as 15, 20, 25, 30, 40, and 50 and the swarm sizes as 5, 10, 20, 30, and 40. Secondly, after the initial analysis and trial and error, the best developed model was constructed with a structure shown in Table 2. Finally, the developed model was implemented for determining the best answer with 2 parameters. The obtained result of the best cost in each iteration is shown in Figure 6 for 2 parameters, respectively. In fact, the best cost in each iteration shows the performance function of the algorithm depends on the values of error in each iteration of modelling. It should be noted that we consider the mean squared error (MSE) for evaluation of the performance, and 70% of data set were considered for training, and the rest were considered for validation (15%) and testing (15%) [99].
Table 2.
The control parameters of the developed model for ANN-PSO.
| Control Parameters | Values |
|---|---|
| Number of hidden layers | 10 |
| Swarm size | 15 |
| Individual learning factor (C1) | 1.49 |
| Social learning factor (C2) | 1.49 |
| Maximum number of iterations | 30 |
Figure 6.
The best cost per each iteration by PSO algorithm.
According to Figure 6, it is evident that after the sixth iteration with 0.00133, the best cost was reached, and the model achieves a worthy convergence, and it was fixed to the end of the iteration. In addition, the model reduced the number of parameters from 4 to 2 that, in fact, reveal that the urban parameter and relative humidity were the priority of the model.
3.2. DE Modelling
As mentioned earlier, the DE algorithm is used for training the artificial neural network to apply the feature selection with the four climate parameters, namely daily average temperature, relative humidity, and wind speed, and one urban parameter (population density × positive cases up to 14 days before) considered as the input data set, and the confirmed cases to COVID-19 considered as an output dataset. At first, the control parameters of DE algorithm are determined to find the optimum weights and biases of ANN model that can converge faster and accurately. For this purpose, similar to PSO model, the crossover probability coefficient was selected as 0.2, and other parameters were determined by trial and error method from previous studies and experts’ opinions [87,88]. In addition, the datasets for modeling were randomly divided into several subsets, including 70% for training and the rest for validation (15%) and testing (15%) [99]. Hence, population sizes of algorithm of 5, 10, 20, 30, and 40 were selected, and the maximum iteration was used with a range of values equal to 15, 20, 25, 30, 40, and 50. The values of 10, 20, and 30 were chosen for the size of the hidden layers of ANN. After the initial evaluation, the optimized model selected with the values of 5, 15, and 30 for the hidden layer, population size, and the maximum number of iterations, respectively. The process of optimization based on iterations is presented in Figure 7, which shows that the process reached the desired precision level of best cost with the value of 0.0014 from the 8th iteration, and it was fixed from the 8th to the 30th iteration.
Figure 7.
The best cost per each iteration by DE algorithm.
The developed model by DE algorithm determined the urban parameter and relative humidity as priorities of prediction in this research. More discussions regarding the comparison of algorithms’ performances and the priorities of the parameters in the forecast will be given in the following section.
4. Discussion
In this research, two machine learning techniques of artificial intelligence, namely ANN based on the PSO algorithm and DE algorithm, were used for prioritizing climate and an urban parameter based on the feature selection process. Both developed models based on PSO and DE algorithms selected the urban parameters and relative humidity in the feature selection process, and the reduction of number of parameters. In fact, at first, these models calculated and achieved the best relationships between the output and all inputs based on the values of best cost, then the models considered the features as a binary choice, and finally they could find out that the best values of best cost with these two features are very close to the values of the best cost of all features. The developed model by the PSO algorithm achieved a suitable convergence with good accuracy in the sixth iteration, while the developed model by DE algorithm reached an appropriate convergence in the eighth iteration. Consequently, it is clearly seen that, although there is no salient difference between the performances of the two models, the model developed by PSO algorithm has a better performance in this specific problem, based on the best cost value and the rate of convergence.
Our results are in good agreement with those of Chan et al. [32] about the important role of humidity in another type of coronavirus, SARS, and of Pirouz et al. [28], that identified relative humidity as the higher-impact weather parameter.
For further evaluation, the obtained results were validated by multivariate linear regression (MLR) technique and partial least squares regression (PLSR). For this, since for all four case studies, the correlations can be based on the two variables of humidity and urban parameter, the simplified final MLR and PLSR models are as follows:
Prediction of MLR y = 169.96 + 0.000284 X 1 + 0.59 X 2, R2 = 0.76
Prediction of PLSR y = 193.26 + 0.00028 X 1 + 0.257 X 2, R2 = 0.76
where X1 is the urban parameter, and X2 is the relative humidity. Therefore, the analysis shows that the prediction of confirmed cases of COVID-19 could be made by using two factors of relative humidity and urban parameter (population density X positive cases up to 14 days before).
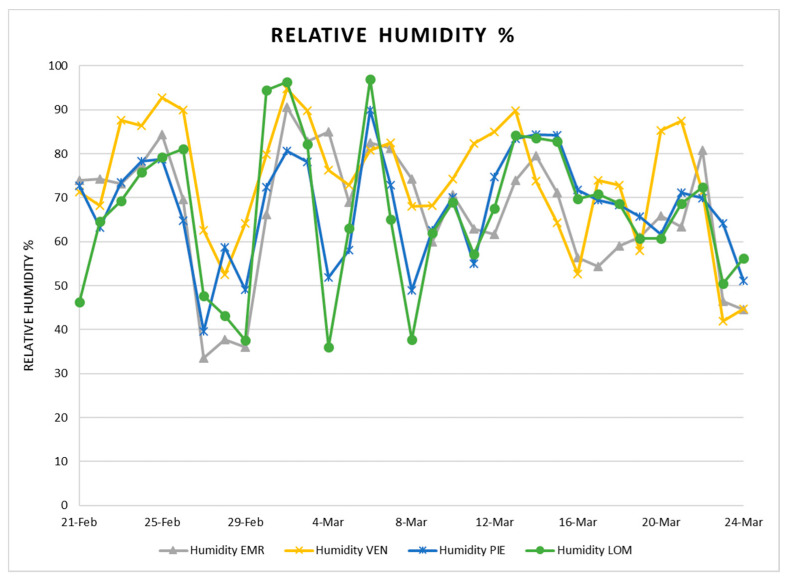
The trend of confirmed cases in four regions is shown in Figure 8, and the daily relative humidity in Figure 9. According to Figure 8, it is evident that the number of infections in all regions were equal at the beginning, but in Lombardy with the highest density increased more. Analysis of relative humidity exhibits that the fluctuations of humidity percentage was the highest in Lombardy, and then in Piedmont, as well as the number of confirmed cases that in both case studies show daily fluctuations.
Figure 8.
Daily confirmed cases of COVID-19 in four regions.
Figure 9.
Relative humidity in four regions.
In addition, the analysis determined that even in one climate type, as the climate type of all four regions is humid subtropical, there might be other essential variables such as population density that affect the final results. In addition, the differences in the fluctuation of relative humidity in one type of climate as an influential parameter in the number of confirmed cases of COVID-19 show that for other types of climates, the selection of different case studies is a necessity.
Finally, it is worth mentioning that the results of this research are derived explicitly for the studied regions in the north of Italy with a humid subtropical climate, and they should not be used directly in other countries. For possible future work referring to other countries, it is recommended to see the effectiveness of the other parameters, such as different climate conditions and urban parameters. In addition, the outdoor humidity could affect the indoor humidity, which might be another important parameter for future analysis. In addition, it might be worth studying whether the use of other machine learning methods may improve our results.
5. Conclusions
With regard to the immense importance of sustainable development to improve the conditions of today’s and future generations, evaluating its challenges and obstacles has considerable effects on government decisions. Hence, in this research, the pandemic novel coronavirus infection (COVID-19) as a new challenge of sustainable development was investigated, using two machine learning techniques. For this purpose, we evaluated several notable climate parameters and an urban parameter, in order to find a relationship between them and the confirmed cases of COVID-19. For this, two artificial intelligence techniques, including ANN based on the PSO algorithm and DE algorithm, were used to predict the confirmed cases of COVID-19 with highly acceptable degrees of accuracy and robustness, in order to prioritize and reduce input parameters. The obtained results indicated that both developed models by PSO and DE algorithms were able to select the urban parameter and relative humidity from other effective parameters. In addition, although the two developed models had the high capability in predictive process with best costs equal to 0.0013 and 0.0014 for the PSO and DE algorithms, respectively, the developed model by PSO algorithm was a more efficient approach, compared to the other predictive method. Finally, the results were tested by a MLR and PSLR, which described the correlation between the urban parameter and relative humidity and the confirmed cases of COVID-19, with R2 equal to 0.76 for both regression models. For future studies, it is recommended to focus on other algorithms, other parameters for proper feature selections, and other types of climate.
Appendix A
Table A1.
The dataset of Lombardy (Milan) according to results of multivariate linear regression (MLR), [100,101].
* Urban parameter is population density * positive cases up to 14 days before. , R2 = 0.79.
Table A2.
| X1, Average Temperature, °C | X2, Humidity, % | X3, Wind, km/h | X4, Positive Cases up to 14 Days before | X4 new (Urban Parameter) * |
Y, Confirmed Cases |
|---|---|---|---|---|---|
| [Shifted 6 Days (24-Feb to 18-Mar)] | [Shifted 9 Days (21-Feb to 15-Mar)] | [Shifted 9 Days (21-Feb to 15-Mar)] | [Shifted 2 Days (28-Feb to 22-Mar)] | [Shifted 2 Days (28-Feb to 22-Mar] | [1-Mar to 24-Mar] |
| 5.2 | 72.7 | 2.9 | 10 | 1720 | 38 |
| 10.2 | 63.2 | 3.2 | 10 | 1720 | 2 |
| 7.0 | 73.4 | 3.0 | 48 | 8256 | 5 |
| 2.9 | 78.3 | 4.3 | 50 | 8600 | 26 |
| 2.7 | 78.7 | 5.1 | 55 | 9460 | 26 |
| 3.5 | 64.7 | 14.3 | 81 | 13932 | 35 |
| 4.6 | 39.6 | 13.7 | 107 | 18404 | 64 |
| 3.1 | 58.7 | 6.3 | 142 | 24424 | 153 |
| 3.8 | 49 | 3.8 | 206 | 35432 | - |
| 4.1 | 72.4 | 4.3 | 359 | 61748 | 103 |
| 4.8 | 80.6 | 4.3 | 359 | 61748 | 48 |
| 2.6 | 78.1 | 7.5 | 462 | 79464 | 79 |
| 2.5 | 51.9 | 4.9 | 510 | 87720 | 260 |
| 4.9 | 58.1 | 6.3 | 588 | 101136 | 33 |
| 5.8 | 90.0 | 5.4 | 839 | 144308 | 238 |
| 4.1 | 72.8 | 3.7 | 872 | 149984 | 405 |
| 7.2 | 48.9 | 5.2 | 1072 | 184384 | 381 |
| 9.8 | 62.6 | 4.3 | 1475 | 253700 | 444 |
| 11.0 | 70.0 | 5.0 | 1851 | 318372 | 591 |
| 9.4 | 55.0 | 4.5 | 2269 | 390268 | 529 |
| 6.6 | 74.7 | 3.6 | 2834 | 487448 | 291 |
| 7.1 | 83.4 | 3.0 | 3328 | 572416 | 668 |
| 5.8 | 84.4 | 6.7 | 3555 | 611460 | 441 |
| 7.5 | 84.2 | 3.8 | 4070 | 700040 | 654 |
* Urban parameter is population density * positive cases up to 14 days before. , R2 = 0.79.
Table A3.
| X1, Average Temperature, °C | X2, Humidity, % | X3, Wind, km/h | X4, Positive Cases up to 14 Days before | X4 new (Urban Parameter) * |
Y, Confirmed Cases |
|---|---|---|---|---|---|
| [Shifted 5 Days (20-Feb to 19-Mar)] | [Shifted 8 Days (17-Feb to 16-Mar)] | [Shifted 6 Days (19-Feb to 18-Mar)] | [Shifted 4 Days (21-Feb to 20-Mar)] | [Shifted 4 Days (21-Feb to 20-Mar)] | [25-Feb to 24-Mar] |
| 7.5 | 92.2 | 5.6 | 2 | 544 | 11 |
| 7.2 | 89.9 | 6.3 | 18 | 4896 | 28 |
| 7.8 | 86.7 | 10.1 | 25 | 6800 | 40 |
| 7.4 | 74.3 | 7.9 | 32 | 8704 | 40 |
| 8.9 | 71.3 | 6.3 | 43 | 11696 | 40 |
| 9.3 | 68.2 | 7.9 | 71 | 19312 | 72 |
| 9.1 | 87.6 | 6 | 111 | 30192 | 10 |
| 8.2 | 86.4 | 10 | 151 | 41072 | 34 |
| 9.1 | 92.7 | 14.6 | 191 | 51952 | 53 |
| 7.3 | 90 | 10.7 | 263 | 71536 | 47 |
| 8.6 | 62.6 | 9 | 273 | 74256 | 81 |
| 7.1 | 52.5 | 9.7 | 307 | 83504 | 55 |
| 10 | 64.2 | 11.6 | 360 | 97920 | 127 |
| 9.1 | 79.8 | 14.8 | 407 | 110704 | 74 |
| 7.2 | 94.8 | 10.7 | 486 | 132192 | 112 |
| 7.5 | 89.8 | 5.6 | 525 | 142800 | 167 |
| 8.9 | 76.2 | 16.7 | 645 | 175440 | 361 |
| 9.4 | 72.8 | 5.3 | 712 | 193664 | 211 |
| 8.6 | 80.7 | 11.4 | 813 | 221136 | 342 |
| 9.1 | 82.5 | 7.9 | 952 | 258944 | 235 |
| 9.1 | 68 | 6.5 | 1273 | 346256 | 301 |
| 9.2 | 68.2 | 6.7 | 1444 | 392768 | 231 |
| 11.2 | 74.2 | 7.9 | 1746 | 474912 | 510 |
| 11.5 | 82.3 | 6.7 | 1909 | 519248 | 270 |
| 9 | 84.9 | 14.1 | 2200 | 598400 | 547 |
| 8.2 | 89.8 | 17.6 | 2397 | 651984 | 586 |
| 9 | 73.8 | 9.3 | 2854 | 776288 | 505 |
| 11.1 | 64.3 | 7.2 | 3077 | 836944 | 383 |
| 14.2 | 52.6 | 7.2 | 3543 | 963696 | 443 |
* Urban parameter is population density * positive cases up to 14 days before. , R2 = 0.82.
Table A4.
| X1, Average Temperature, °C | X2, Humidity, % | X3, Wind, km/h | X4, Positive Cases up to 14 Days before | X4 new (Urban Parameter) * |
Y, Confirmed Cases |
|---|---|---|---|---|---|
| [Shifted 8 days (17-Feb to 16-Mar)] | [Shifted 6 days (19-Feb to 18-Mar)] | [Shifted 8 days (17-Feb to 16-Mar)] | [Shifted 3 days (22-Feb to1-Mar)] | [Shifted 3 days (22-Feb to1-Mar)] | [25-Feb to 24-Mar] |
| 8.8 | 83.3 | 5.6 | 2 | 398 | 8 |
| 11.5 | 72.9 | 6.5 | 9 | 1791 | 21 |
| 10.2 | 74 | 6.3 | 18 | 3582 | 50 |
| 8.0 | 74.2 | 7.6 | 26 | 5174 | 48 |
| 9 | 73.2 | 4.3 | 47 | 9353 | 72 |
| 7.2 | 77.6 | 5.3 | 97 | 19303 | 68 |
| 8.8 | 84.3 | 7.4 | 145 | 28855 | 50 |
| 10 | 69.6 | 4.9 | 217 | 43183 | 85 |
| 9.8 | 33.6 | 5.8 | 285 | 56715 | 124 |
| 11.2 | 37.8 | 10.2 | 335 | 66665 | 154 |
| 8.6 | 36.1 | 20.8 | 420 | 83580 | 172 |
| 10.5 | 66.2 | 19.1 | 544 | 108256 | 140 |
| 8.6 | 90.5 | 7.2 | 698 | 138902 | 170 |
| 10 | 82.8 | 12 | 870 | 173130 | 206 |
| 6.2 | 84.9 | 7.9 | 1008 | 200592 | 147 |
| 10.3 | 69 | 14.1 | 1171 | 233029 | 206 |
| 7.5 | 82.5 | 9.7 | 1368 | 272232 | 208 |
| 7.5 | 81.3 | 8.1 | 1507 | 299893 | 316 |
| 8.5 | 74.3 | 13.9 | 1692 | 336708 | 381 |
| 8.7 | 59.9 | 10.6 | 1850 | 368150 | 449 |
| 8.8 | 70.6 | 6.7 | 2118 | 421482 | 429 |
| 8.6 | 62.9 | 7.6 | 2427 | 482973 | 409 |
| 8.1 | 61.7 | 7.4 | 2808 | 558792 | 594 |
| 9.1 | 74 | 6.3 | 3187 | 634213 | 689 |
| 11.5 | 79.6 | 8.1 | 3511 | 698689 | 754 |
| 13 | 71.1 | 5.1 | 3981 | 792219 | 737 |
| 13.2 | 56.4 | 9 | 4516 | 898684 | 850 |
| 9.2 | 54.4 | 8.3 | 5098 | 1014502 | 980 |
| 7.6 | 59 | 6.7 | 5695 | 1133305 | 719 |
* Urban parameter is population density * positive cases up to 14 days before. , R2 = 0.94.
Appendix B
The validity of using the sum of 14 days for confirmed cases for the updated data of Lombardy (Milan) until 17 April. The dataset and the graph as bellow:
Table A5.
The updated dataset of Lombardy (Milan).
| Date | Daily New Cases | X4 Positive Cases up to 14 Days before [Shifted 3 Days] |
X4new [Population Density *X4] |
Date | Daily New Cases | X4 Positive Cases up to 14 Days before [Shifted 3 Days] |
X4new [Population Density *X4] |
|---|---|---|---|---|---|---|---|
| 20-Feb | 0 | 0 | 0 | 04-Apr | 1598 | 27060 | 11419320 |
| 21-Feb | 15 | 0 | 0 | 05-Apr | 1337 | 26181 | 11048382 |
| 22-Feb | 40 | 0 | 0 | 06-Apr | 1079 | 25256 | 10658032 |
| 23-Feb | 57 | 0 | 0 | 07-Apr | 791 | 23603 | 9960466 |
| 24-Feb | 61 | 15 | 6330 | 08-Apr | 1089 | 23249 | 9811078 |
| 25-Feb | 67 | 55 | 23210 | 09-Apr | 1388 | 22773 | 9610206 |
| 26-Feb | 65 | 112 | 47264 | 10-Apr | 1246 | 21622 | 9124484 |
| 27-Feb | 98 | 173 | 73006 | 11-Apr | 1544 | 21068 | 8890696 |
| 28-Feb | 128 | 240 | 101280 | 12-Apr | 1460 | 19913 | 8403286 |
| 29-Feb | 84 | 305 | 128710 | 13-Apr | 1262 | 18750 | 7912500 |
| 01-Mar | 369 | 403 | 170066 | 14-Apr | 1012 | 18177 | 7670694 |
| 02-Mar | 270 | 531 | 224082 | 15-Apr | 827 | 18045 | 7614990 |
| 03-Mar | 266 | 615 | 259530 | 16-Apr | 941 | 18153 | 7660566 |
| 04-Mar | 300 | 984 | 415248 | 17-Apr | 1041 | 18118 | 7645796 |
| 05-Mar | 431 | 1254 | 529188 | 18-Apr | 1246 | 17380 | 7334360 |
| 06-Mar | 361 | 1520 | 641440 | 19-Apr | 855 | 17029 | 7186238 |
| 07-Mar | 808 | 1820 | 768040 | 20-Apr | 735 | 16615 | 7011530 |
| 08-Mar | 769 | 2251 | 949922 | 21-Apr | 960 | 16263 | 6862986 |
| 09-Mar | 1280 | 2597 | 1095934 | 22-Apr | 1161 | 15781 | 6659582 |
| 10-Mar | 322 | 3365 | 1420030 | 23-Apr | 1073 | 15437 | 6514414 |
| 11-Mar | 1489 | 4077 | 1720494 | 24-Apr | 1091 | 15606 | 6585732 |
| 12-Mar | 1445 | 5296 | 2234912 | 25-Apr | 713 | 15678 | 6616116 |
| 13-Mar | 1095 | 5551 | 2342522 | 26-Apr | 920 | 15363 | 6483186 |
| 14-Mar | 1865 | 6975 | 2943450 | 27-Apr | 590 | 15208 | 6417776 |
| 15-Mar | 1587 | 8322 | 3511884 | 28-Apr | 869 | 14377 | 6067094 |
| 16-Mar | 1377 | 9289 | 3919958 | 29-Apr | 786 | 13837 | 5839214 |
| 17-Mar | 1571 | 11070 | 4671540 | 30-Apr | 598 | 13165 | 5555630 |
| 18-Mar | 1493 | 12288 | 5185536 | 01-May | 737 | 13022 | 5495284 |
| 19-Mar | 2171 | 13395 | 5652690 | 02-May | 533 | 12981 | 5477982 |
| 20-Mar | 2380 | 14700 | 6203400 | 03-May | 526 | 12638 | 5333236 |
| 21-Mar | 3251 | 15893 | 6706846 | 04-May | 577 | 12334 | 5204948 |
| 22-Mar | 1691 | 17633 | 7441126 | 05-May | 500 | 11621 | 4904062 |
| 23-Mar | 1555 | 19652 | 8293144 | 06-May | 764 | 11292 | 4765224 |
| 24-Mar | 1942 | 22095 | 9324090 | 07-May | 720 | 11134 | 4698548 |
| 25-Mar | 1643 | 23017 | 9713174 | 08-May | 634 | 10674 | 4504428 |
| 26-Mar | 2543 | 23292 | 9829224 | 09-May | 502 | 10277 | 4336894 |
| 27-Mar | 2409 | 24912 | 10512864 | 10-May | 282 | 9924 | 4187928 |
| 28-Mar | 2117 | 25066 | 10577852 | 11-May | 364 | 9467 | 3995074 |
| 29-Mar | 1592 | 26164 | 11041208 | 12-May | 1033 | 9256 | 3906032 |
| 30-Mar | 1154 | 27478 | 11595716 | 13-May | 394 | 8618 | 3636796 |
| 31-Mar | 1047 | 27730 | 11702060 | 14-May | 522 | 8392 | 3541424 |
| 01-Apr | 1565 | 27735 | 11704170 | 15-May | 299 | 8556 | 3610632 |
| 02-Apr | 1292 | 27512 | 11610064 | 16-May | 399 | 8164 | 3445208 |
| 03-Apr | 1455 | 26988 | 11388936 | 17-May | 326 | 8088 | 3413136 |
Figure A1.
Confirmed cases of COVID-19 based on the variables of Table A5.
As, the graphs show, neither X4 nor X4new reached a plateau. Thus, the mentioned method for X4, using the shifted sum of 14 days previously that is in line with the COVID-19 incubation period, might be more exact than using daily confirmed cases.
Author Contributions
The author’s contributions in the paper are as follows: conceptualization, S.S.H. (Sina Shaffiee Haghshenas), B.P. (Behrouz Pirouz), B.P. (Behzad Pirouz); methodology, S.S.H. (Sina Shaffiee Haghshenas), S.S.H. (Sami Shaffiee Haghshenas); formal analysis, S.S.H. (Sina Shaffiee Haghshenas), B.P. (Behrouz Pirouz), B.P. (Behzad Pirouz); investigation, S.S.H. (Sina Shaffiee Haghshenas), B.P. (Behrouz Pirouz); writing—original draft preparation, S.S.H. (Sina Shaffiee Haghshenas), B.P. (Behrouz Pirouz); writing—review and editing, S.S.H. (Sina Shaffiee Haghshenas), B.P. (Behrouz Pirouz), Z.W.G.; supervision, P.P., K.-S.N., S.-E.C., Z.W.G., funding, Z.W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2020R1A2C1A01011131). This research was also supported by the Energy Cloud R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT (2019M3F2A1073164).
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Kates R.W., Parris T.M., Leiserowitz A.A. What is sustainable development? Goals, indicators, values, and practice. Environment. 2005;47:8–21. doi: 10.1080/00139157.2005.10524444. [DOI] [Google Scholar]
- 2.Blewitt J. Understanding Sustainable Development. Abingdon upon Thames; Routledge, UK: 2012. [Google Scholar]
- 3.Carbone M., Garofalo G., Nigro G., Piro P. A conceptual model for predicting hydraulic behaviour of a green roof. Procedia Eng. 2014;70:266–274. doi: 10.1016/j.proeng.2014.02.030. [DOI] [Google Scholar]
- 4.Sustainable Development Goals. [(accessed on 14 April 2020)]; Available online: https://sustainabledevelopment.un.org/?menu=1300.
- 5.Chen D., Schudeleit T., Posselt G., Thiede S. A state-of-the-art review and evaluation of tools for factory sustainability assessment. Procedia Cirp. 2013;9:85–90. doi: 10.1016/j.procir.2013.06.173. [DOI] [Google Scholar]
- 6.Jayal A.D., Badurdeen F., Dillon O.W., Jr., Jawahir I.S. Sustainable manufacturing: Modeling and optimization challenges at the product, process and system levels. Cirp J. Manuf. Sci. Technol. 2010;2:144–152. doi: 10.1016/j.cirpj.2010.03.006. [DOI] [Google Scholar]
- 7.Maiolo M., Carini M., Capano G., Piro P. Synthetic sustainability index (SSI) based on life cycle assessment approach of low impact development in the Mediterranean area. Cogent Eng. 2017;4:1410272. doi: 10.1080/23311916.2017.1410272. [DOI] [Google Scholar]
- 8.Piro P., Turco M., Palermo S.A., Principato F., Brunetti G. The Internet of Things for Smart Urban Ecosystems. Springer; Cham, Switzerland: 2019. A Comprehensive Approach to Stormwater Management Problems in the Next Generation Drainage Networks; pp. 275–304. [DOI] [Google Scholar]
- 9.Pirouz B., Arcuri N., Pirouz B., Palermo S.A., Turco M., Maiolo M. Development of an assessment method for evaluation of sustainable factories. Sustainability. 2020;12:1841. doi: 10.3390/su12051841. [DOI] [Google Scholar]
- 10.Piro P., Carbone M., Garofalo G., Sansalone J. CSO treatment strategy based on constituent index relationships in a highly urbanised catchment. Water Sci. Technol. 2007;56:85–91. doi: 10.2166/wst.2007.758. [DOI] [PubMed] [Google Scholar]
- 11.Palermo S.A., Talarico V.C., Pirouz B. Optimizing Rainwater Harvesting Systems for Non-potable Water Uses and Surface Runoff Mitigation. In: Sergeyev Y., Kvasov D., editors. Numerical Computations: Theory and Algorithms. NUMTA 2019. Volume 11973. Springer; Cham, Switzerland: 2020. pp. 570–582. Lecture Notes in Computer Science. [DOI] [Google Scholar]
- 12.Pirouz B., Maiolo M. The Role of Power Consumption and Type of Air Conditioner in Direct and Indirect Water Consumption. J. Sustain. Dev. Energy Water Environ. Syst. 2018;6:665–673. doi: 10.13044/j.sdewes.d6.0202. [DOI] [Google Scholar]
- 13.Maiolo M., Pirouz B., Bruno R., Palermo S.A., Arcuri N., Piro P. The Role of the Extensive Green Roofs on Decreasing Building Energy Consumption in the Mediterranean Climate. Sustainability. 2020;12:359. doi: 10.3390/su12010359. [DOI] [Google Scholar]
- 14.Pirouz B., Arcuri N., Maiolo M., Talarico V.C., Piro P. IOP Conference Series: Earth and Environmental Science. Volume 410. IOP Publishing; Thessaloniki, Greece: 2020. A new multi-objective dynamic model to close the gaps in sustainable development of industrial sector; p. 012074. [DOI] [Google Scholar]
- 15.Pirouz B., Golmohammadi A., Saeidpour Masouleh H., Violini G., Pirouz B. Relationship between average daily temperature and average cumulative daily rate of confirmed cases of COVID-19. medRixv. 2020 doi: 10.1101/2020.04.10.20059337. [DOI] [Google Scholar]
- 16.Pirouz B., Haghshenas S.S., Pirouz B., Haghshenas S.S., Piro P. Development of an Assessment Method for Investigating the Impact of Climate and Urban Parameters in Confirmed Cases of COVID-19: A New Challenge in Sustainable Development. Int. J. Environ. Res. Public Health. 2020 doi: 10.3390/ijerph17082801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Palermo S.A., Zischg J., Sitzenfrei R., Rauch W., Piro P. Parameter Sensitivity of a Microscale Hydrodynamic Model. In: Mannina G., editor. New Trends in Urban Drainage Modelling. UDM 2018. Springer; Cham, Switzerland: 2019. pp. 982–987. Green Energy and Technology. [DOI] [Google Scholar]
- 18.Giordano A., Spezzano G., Vinci A., Garofalo G., Piro P. A Cyber-Physical System for Distributed Real-Time Control of Urban Drainage Networks in Smart Cities. In: Fortino G., Di Fatta G., Li W., Ochoa S., Cuzzocrea A., Pathan M., editors. Internet and Distributed Computing Systems. IDCS 2014. Volume 8729. Springer; Cham, Switzerland: 2014. pp. 87–98. Lecture Notes in Computer Science. [DOI] [Google Scholar]
- 19.Piro P., Carbone M., Morimanno F., Palermo S.A. Simple flowmeter device for LID systems: From laboratory procedure to full-scale implementation. Flow Meas. Instrum. 2019;65:240–249. doi: 10.1016/j.flowmeasinst.2019.01.008. [DOI] [Google Scholar]
- 20.Carbone M., Turco M., Brunetti G., Piro P. A Cumulative Rainfall Function for Subhourly Design Storm in Mediterranean Urban Areas. Adv. Meteorol. 2015 doi: 10.1155/2015/528564. [DOI] [Google Scholar]
- 21.World Health Organization (WHO) Coronavirus Disease (COVID-2019) Situation Reports. [(accessed on 28 March 2020)]; Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/
- 22.Cascella M., Rajnik M., Cuomo A., Dulebohn S.C., Di Napoli R. Features, Evaluation and Treatment Coronavirus (COVID-19) StatPearls Publishing LLC; Tampa, FL, USA: 2020. [(accessed on 29 March 2020)]. Available online: https://www.ncbi.nlm.nih.gov/books/NBK554776/ [PubMed] [Google Scholar]
- 23.Shen M., Peng Z., Guo Y., Xiao Y., Zhang L. Lockdown may partially halt the spread of 2019 novel coronavirus in Hubei province, China. medRxiv. 2020 doi: 10.1101/2020.02.11.20022236. [DOI] [Google Scholar]
- 24.Phan L.T., Nguyen T.V., Luong Q.C., Nguyen T.V., Nguyen H.T., Le H.Q., Nguyen T.T., Cao T.M., Pham Q.D. Importation and human-to-human transmission of a novel coronavirus in Vietnam. N. Engl. J. Med. 2020;382:872–874. doi: 10.1056/NEJMc2001272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gilbert M., Pullano G., Pinotti F., Valdano E., Poletto C., Boëlle P.Y., D’Ortenzio E., Yazdanpanah Y., Eholie S.P., Gutierrez B., et al. Preparedness and vulnerability of African countries against importations of COVID-19: A modelling study. Lancet. 2020;395:871–877. doi: 10.1016/S0140-6736(20)30411-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yu H., Sun X., Solvang W.D., Zhao X. Reverse Logistics Network Design for Effective Management of Medical Waste in Epidemic Outbreaks: Insights from the Coronavirus Disease 2019 (COVID-19) Outbreak in Wuhan (China) Int. J. Environ. Res. Public Health. 2020;17:1770. doi: 10.3390/ijerph17051770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen Y.C., Lu P.E., Chang C.S. A Time-dependent SIR model for COVID-19. arXiv. 2020 doi: 10.1109/TNSE.2020.3024723.2003.00122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pirouz B., Shaffiee Haghshenas S., Shaffiee Haghshenas S., Piro P. Investigating a Serious Challenge in the Sustainable Development Process: Analysis of Confirmed cases of COVID-19 (New Type of Coronavirus) Through a Binary Classification Using Artificial Intelligence and Regression Analysis. Sustainability. 2020;12:2427. doi: 10.3390/su12062427. [DOI] [Google Scholar]
- 29.Hu Z., Ge Q., Jin L., Xiong M. Artificial intelligence forecasting of covid-19 in china. arXiv. 2020 doi: 10.3389/frai.2020.00041.2002.07112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kampf G., Todt D., Pfaender S., Steinmann E. Persistence of coronaviruses on inanimate surfaces and its inactivation with biocidal agents. J. Hosp. Infect. 2020;104:246–251. doi: 10.1016/j.jhin.2020.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Grant W.B., Giovannucci E. The possible roles of solar ultraviolet-B radiation and vitamin D in reducing case-fatality rates from the 1918–1919 influenza pandemic in the United States. Derm. Endocrinol. 2009;1:215–219. doi: 10.4161/derm.1.4.9063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chan K.H., Peiris J.S., Lam S.Y., Poon L.L., Yuen K.Y., Seto W.H. The effects of temperature and relative humidity on the viability of the SARS coronavirus. Adv. Virol. 2011 doi: 10.1155/2011/734690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Coronavirus Incubation Period. [(accessed on 27 March 2020)]; Available online: https://www.worldometers.info/coronavirus/coronavirus-incubation-period/#24.
- 34.Coronavirus Testing: How it Is Done, When you Should Get One and How Long Results Take. [(accessed on 27 March 2020)]; Available online: https://www.liverpoolecho.co.uk/news/uk-world-news/coronavirus-testing-how-done-you-17912266.
- 35.Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S.M., Lau E.H.Y., Xing X., et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N. Engl. J. Med. 2020 doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Coronavirus Testing: Information on COVID-19 Tests According to State Health Departments. [(accessed on 25 March 2020)]; Available online: https://www.nbcnews.com/health/health-news/coronavirus-testing-information-covid-19-tests-according-state-health-departments-n1158041.
- 37.In Italia ieri Record Mondiale di Decessi Rebus Lombardia. [(accessed on 26 March 2020)]; Available online: https://ilmanifesto.it/in-italia-ieri-record-mondiale-di-decessi-rebus-lombardia/
- 38.Coronavirus Cases. [(accessed on 26 March 2020)]; Available online: https://www.worldometers.info/coronavirus/
- 39.Mikaeil R., Haghshenas S.S., Hoseinie S.H. Rock penetrability classification using artificial bee colony (ABC) algorithm and self-organizing map. Geotech. Geol. Eng. 2018;36:1309–1318. doi: 10.1007/s10706-017-0394-6. [DOI] [Google Scholar]
- 40.Naderpour H., Mirrashid M. Moment capacity estimation of spirally reinforced concrete columns using ANFIS. Complex Intell. Syst. 2019:1–11. doi: 10.1007/s40747-019-00118-2. [DOI] [Google Scholar]
- 41.Naderpour H., Mirrashid M. Shear failure capacity prediction of concrete beam–column joints in terms of ANFIS and GMDH. Pract. Period. Struct. Des. Constr. 2019;24:04019006. doi: 10.1061/(ASCE)SC.1943-5576.0000417. [DOI] [Google Scholar]
- 42.Kayabekir A.E., Toklu Y.C., Bekdaş G., Nigdeli S.M., Yücel M., Geem Z.W. A Novel Hybrid Harmony Search Approach for the Analysis of Plane Stress Systems via Total Potential Optimization. Appl. Sci. 2020;10:2301. doi: 10.3390/app10072301. [DOI] [Google Scholar]
- 43.Na K.S., Cho S.E., Geem Z.W., Kim Y.K. Predicting future onset of depression among community dwelling adults in the Republic of Korea using a machine learning algorithm. Neurosci. Lett. 2020;721:134804. doi: 10.1016/j.neulet.2020.134804. [DOI] [PubMed] [Google Scholar]
- 44.Kandiri A., Golafshani E.M., Behnood A. Estimation of the compressive strength of concretes containing ground granulated blast furnace slag using hybridized multi-objective ANN and salp swarm algorithm. Constr. Build. Mater. 2020;248:118676. doi: 10.1016/j.conbuildmat.2020.118676. [DOI] [Google Scholar]
- 45.Geem Z.W. Transport energy demand modeling of South Korea using artificial neural network. Energy Policy. 2011;39:4644–4650. doi: 10.1016/j.enpol.2011.05.008. [DOI] [Google Scholar]
- 46.Rad M.Y., Haghshenas S.S., Kanafi P.R., Haghshenas S.S. Analysis of Protection of Body Slope in the Rockfill Reservoir Dams on the Basis of Fuzzy Logic; Proceedings of the 4th International Joint Conference on Computational Intelligence; Barcelona, Spain. 5–7 October 2012; pp. 367–373. [Google Scholar]
- 47.Rad M.Y., Haghshenas S.S., Haghshenas S.S. Mechanostratigraphy of cretaceous rocks by fuzzy logic in East Arak, Iran; Proceedings of the 4th International Workshop on Computer Science and Engineering-Summer; WCSE, Dubai. 22–23 August 2014. [Google Scholar]
- 48.Mikaeil R., Haghshenas S.S., Haghshenas S.S., Ataei M. Performance prediction of circular saw machine using imperialist competitive algorithm and fuzzy clustering technique. Neural Comput. Appl. 2018;29:283–292. doi: 10.1007/s00521-016-2557-4. [DOI] [Google Scholar]
- 49.Dormishi A., Ataei M., Mikaeil R., Khalokakaei R., Haghshenas S.S. Evaluation of gang saws’ performance in the carbonate rock cutting process using feasibility of intelligent approaches. Eng. Sci. Technol. Int. J. 2019;22:990–1000. doi: 10.1016/j.jestch.2019.01.007. [DOI] [Google Scholar]
- 50.Mikaeil R., Beigmohammadi M., Bakhtavar E., Haghshenas S.S. Assessment of risks of tunneling project in Iran using artificial bee colony algorithm. SN Appl. Sci. 2019;1:1711. doi: 10.1007/s42452-019-1749-9. [DOI] [Google Scholar]
- 51.Behnood A., Golafshani E.M. Machine learning study of the mechanical properties of concretes containing waste foundry sand. Constr. Build. Mater. 2020;243:118152. doi: 10.1016/j.conbuildmat.2020.118152. [DOI] [Google Scholar]
- 52.Cabaneros S.M.S., Calautit J.K., Hughes B.R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 2019;119:285–304. doi: 10.1016/j.envsoft.2019.06.014. [DOI] [Google Scholar]
- 53.Maleki H., Sorooshian A., Goudarzi G., Baboli Z., Birgani Y.T., Rahmati M. Air pollution prediction by using an artificial neural network model. Clean Technol. Environ. Policy. 2019;21:1341–1352. doi: 10.1007/s10098-019-01709-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Araujo L.N., Belotti J.T., Alves T.A., de Souza Tadano Y., Siqueira H. Ensemble method based on Artificial Neural Networks to estimate air pollution health risks. Environ. Model. Softw. 2020;123:104567. doi: 10.1016/j.envsoft.2019.104567. [DOI] [Google Scholar]
- 55.Mahdevari S., Shahriar K., Sharifzadeh M., Tannant D.D. Stability prediction of gate roadways in longwall mining using artificial neural networks. Neural Comput. Appl. 2017;28:3537–3555. doi: 10.1007/s00521-016-2263-2. [DOI] [Google Scholar]
- 56.Naderpour H., Poursaeidi O., Ahmadi M. Shear resistance prediction of concrete beams reinforced by FRP bars using artificial neural networks. Measurement. 2018;126:299–308. doi: 10.1016/j.measurement.2018.05.051. [DOI] [Google Scholar]
- 57.Mohammadi J., Ataei M., Kakaei R.K., Mikaeil R., Haghshenas S.S. Prediction of the production rate of chain saw machine using the multilayer perceptron (MLP) neural network. Civ. Eng. J. 2018;4:1575–1583. doi: 10.28991/cej-0309196. [DOI] [Google Scholar]
- 58.Mikaeil R., Haghshenas S.S., Ozcelik Y., Gharehgheshlagh H.H. Performance evaluation of adaptive neuro-fuzzy inference system and group method of data handling-type neural network for estimating wear rate of diamond wire saw. Geotech. Geol. Eng. 2018;36:3779–3791. doi: 10.1007/s10706-018-0571-2. [DOI] [Google Scholar]
- 59.Genc O., Kisi O., Ardiclioglu M. Modeling velocity distributions in small streams using different neuro-fuzzy and neural computing techniques. J. Water Clim. Chang. 2019 doi: 10.2166/wcc.2019.103. [DOI] [Google Scholar]
- 60.Faris H., Aljarah I., Mirjalili S. Improved monarch butterfly optimization for unconstrained global search and neural network training. Appl. Intell. 2018;48:445–464. doi: 10.1007/s10489-017-0967-3. [DOI] [Google Scholar]
- 61.Noori A.M., Mikaeil R., Mokhtarian M., Haghshenas S.S., Foroughi M. Feasibility of intelligent models for prediction of utilization factor of TBM. Geotech. Geol. Eng. 2020:1–19. doi: 10.1007/s10706-020-01213-9. [DOI] [Google Scholar]
- 62.Petrudi S.H.J., Pirouz M., Pirouz B. Application of fuzzy logic for performance evaluation of academic students; Proceedings of the 13th Iranian Conference on Fuzzy Systems (IFSC); Qazvin, Iran. 27–29 August 2013; pp. 1–5. [DOI] [Google Scholar]
- 63.Karahan H., Gurarslan G., Geem Z.W. Parameter estimation of the nonlinear Muskingum flood-routing model using a hybrid harmony search algorithm. J. Hydrol. Eng. 2013;18:352–360. doi: 10.1061/(ASCE)HE.1943-5584.0000608. [DOI] [Google Scholar]
- 64.Haghshenas S.S., Haghshenas S.S., Mikaeil R., Sirati Moghadam P., Haghshenas A.S. A new model for evaluating the geological risk based on geomechanical properties-case study: The second part of emamzade hashem tunnel. Electron. J. Geotech. Eng. 2017;22:309–320. [Google Scholar]
- 65.Salemi A., Mikaeil R., Haghshenas S.S. Integration of finite difference method and genetic algorithm to seismic analysis of circular shallow tunnels (Case study: Tabriz urban railway tunnels) KSCE J. Civ. Eng. 2018;22:1978–1990. doi: 10.1007/s12205-017-2039-y. [DOI] [Google Scholar]
- 66.Haghshenas S.S., Faradonbeh R.S., Mikaeil R., Haghshenas S.S., Taheri A., Saghatforoush A., Dormishi A. A new conventional criterion for the performance evaluation of gang saw machines. Measurement. 2019;146:159–170. doi: 10.1016/j.measurement.2019.06.031. [DOI] [Google Scholar]
- 67.Roohollah Shirani F., Haghshenas S.S., Taheri A., Mikaeil R. Application of self-organizing map and fuzzy c-mean techniques for rockburst clustering in deep underground projects. Neural Comput. Appl. 2019:1–15. doi: 10.1007/s00521-019-04353-z. [DOI] [Google Scholar]
- 68.Mikaeil R., Bakhshinezhad H., Haghshenas S.S., Ataei M. Stability analysis of tunnel support systems using numerical and intelligent simulations (case study: Kouhin Tunnel of Qazvin-Rasht Railway) Rud. Geološko Naft. Zb. 2019;34:1–10. doi: 10.17794/rgn.2019.2.1. [DOI] [Google Scholar]
- 69.Hosseini S.M., Ataei M., Khalokakaei R., Mikaeil R., Haghshenas S.S. Study of the effect of the cooling and lubricant fluid on the cutting performance of dimension stone through artificial intelligence models. Eng. Sci. Technol. Int. J. 2020;23:71–81. doi: 10.1016/j.jestch.2019.04.012. [DOI] [Google Scholar]
- 70.Tikhamarine Y., Souag-Gamane D., Ahmed A.N., Kisi O., El-Shafie A. Improving artificial intelligence models accuracy for monthly streamflow forecasting using grey Wolf optimization (GWO) algorithm. J. Hydrol. 2020;582:124435. doi: 10.1016/j.jhydrol.2019.124435. [DOI] [Google Scholar]
- 71.Pirouz B., Palermo S.A., Turco M., Piro P. New Mathematical Optimization Approaches for LID Systems. In: Sergeyev Y., Kvasov D., editors. Numerical Computations: Theory and Algorithms. NUMTA 2019. Volume 11973. Springer; Cham, Switzerland: 2020. pp. 583–595. Lecture Notes in Computer Science. [DOI] [Google Scholar]
- 72.Ho C.H., Chang P.T., Hung K.C., Lin K.P. Developing intuitionistic fuzzy seasonality regression with particle swarm optimization for air pollution forecasting. Ind. Manag. Data Syst. 2019;119:561–577. doi: 10.1108/IMDS-02-2018-0063. [DOI] [Google Scholar]
- 73.Lee C.Y., Lee Z.J., Huang J.Q., Ye F.L., Ning Z.Y., Yang C.F. Urban Air Quality Analysis and Forecast Based on Intelligent Algorithm with Parameter Optimization and Decision Rules. Appl. Sci. 2019;9:5445. doi: 10.3390/app9245445. [DOI] [Google Scholar]
- 74.Shamshirband S., Hadipoor M., Baghban A., Mosavi A., Bukor J., Várkonyi-Kóczy A.R. Developing an ANFIS-PSO model to predict mercury emissions in combustion flue gases. Mathematics. 2019;7:965. doi: 10.3390/math7100965. [DOI] [Google Scholar]
- 75.Wang J., Du P., Hao Y., Ma X., Niu T., Yang W. An innovative hybrid model based on outlier detection and correction algorithm and heuristic intelligent optimization algorithm for daily air quality index forecasting. J. Environ. Manag. 2020;255:109855. doi: 10.1016/j.jenvman.2019.109855. [DOI] [PubMed] [Google Scholar]
- 76.Zeinalnezhad M., Chofreh A.G., Goni F.A., Klemeš J. Air pollution prediction using semi-experimental regression model and Adaptive Neuro-Fuzzy Inference System. J. Clean. Prod. 2020:121218. doi: 10.1016/j.jclepro.2020.121218. [DOI] [Google Scholar]
- 77.Kennedy J., Eberhart R. Particle swarm optimization; Proceedings of the ICNN’95-International Conference on Neural Networks; Perth, WA, Australia. 27 November–1 December 1995; pp. 1942–1948. [DOI] [Google Scholar]
- 78.Shi Y. Particle swarm optimization: Developments, applications and resources; Proceedings of the 2001 Congress on Evolutionary Computation; Seoul, Korea. 27–30 May 2001; pp. 81–86. [DOI] [Google Scholar]
- 79.Poli R., Kennedy J., Blackwell T. Particle swarm optimization. Swarm Intell. 2007;1:33–57. doi: 10.1007/s11721-007-0002-0. [DOI] [Google Scholar]
- 80.Mikaeil R., Haghshenas S.S., Sedaghati Z. Geotechnical risk evaluation of tunneling projects using optimization techniques (case study: The second part of Emamzade Hashem tunnel) Nat. Hazards. 2019;97:1099–1113. doi: 10.1007/s11069-019-03688-z. [DOI] [Google Scholar]
- 81.Karaboga D., Akay B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2019;214:108–132. doi: 10.1016/j.amc.2009.03.090. [DOI] [Google Scholar]
- 82.Tharwat A., Elhoseny M., Hassanien A.E., Gabel T., Kumar A. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm. Clust. Comput. 2019;22:4745–4766. doi: 10.1007/s10586-018-2360-3. [DOI] [Google Scholar]
- 83.Aryafar A., Mikaeil R., Doulati Ardejani F., Shaffiee Haghshenas S., Jafarpour A. Application of non-linear regression and soft computing techniques for modeling process of pollutant adsorption from industrial wastewaters. J. Min. Environ. 2019;10:327–337. doi: 10.22044/jme.2018.6511.1469. [DOI] [Google Scholar]
- 84.Storn R., Price K. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces. International Computer Science Institute; Berkeley, CA, USA: 1995. Technical Report. [Google Scholar]
- 85.Storn R., Price K. Minimizing the real functions of the ICEC’96 contest by differential evolution, In Evolutionary Computation; Proceedings of the IEEE International Conference on Evolutionary Computation; Nagoya, Japan. 20–22 May 1996; pp. 842–844. [DOI] [Google Scholar]
- 86.Storn R., Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997;11:341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 87.Aryafar A., Mikaeil R., Haghshenas S.S., Haghshenas S.S. Application of meta-heuristic algorithms to optimal clustering of sawing machine vibration. Measurement. 2018;124:20–31. doi: 10.1016/j.measurement.2018.03.056. [DOI] [Google Scholar]
- 88.Dehghani H., Shafaghi M. Prediction of blast-induced flyrock using differential evolution algorithm. Eng. Comput. 2017;33:149–158. doi: 10.1007/s00366-016-0461-2. [DOI] [Google Scholar]
- 89.Yang J., Li W.T., Shi X.W., Xin L., Yu J.F. A hybrid ABC-DE algorithm and its application for time-modulated arrays pattern synthesis. IEEE Trans. Antennas Propag. 2013;61:5485–5495. doi: 10.1109/TAP.2013.2279093. [DOI] [Google Scholar]
- 90.Wang L., He J., Wu D., Zeng Y.R. A novel differential evolution algorithm for joint replenishment problem under interdependence and its application. Int. J. Prod. Econ. 2012;135:190–198. doi: 10.1016/j.ijpe.2011.06.015. [DOI] [Google Scholar]
- 91.Dormishi A.R., Ataei M., Khaloo Kakaie R., Mikaeil R., Shaffiee Haghshenas S. Performance evaluation of gang saw using hybrid ANFIS-DE and hybrid ANFIS-PSO algorithms. J. Min. Environ. 2019;10:543–557. doi: 10.22044/JME.2018.6750.1496. [DOI] [Google Scholar]
- 92.AdminStat Maps, Analysis and Statistics about the Resident Population. [(accessed on 27 March 2020)]; Available online: https://ugeo.urbistat.com/AdminStat/en/it/demografia/dati-sintesi/milano/15/3.
- 93.Regions of Italy. [(accessed on 27 March 2020)]; Available online: https://en.wikipedia.org/wiki/Regions_of_Italy.
- 94.2020 Coronavirus Pandemic in Italy. [(accessed on 25 March 2020)]; Available online: https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_Italy#cite_note-139.
- 95.Lombardy. [(accessed on 26 March 2020)]; Available online: https://commons.wikimedia.org/wiki/File:Map_of_region_of_Lombardy,_Italy,_with_provinces-it.svg.
- 96.Piedmont. [(accessed on 26 March 2020)]; Available online: https://commons.wikimedia.org/wiki/File:Map_of_region_of_Piedmont,_Italy,_with_provinces-en.svg.
- 97.Emilia-Romagna. [(accessed on 26 March 2020)]; Available online: https://en.wikipedia.org/wiki/Emilia-Romagna#/media/File:Map_of_region_of_Emilia-Romagna,_Italy,_with_provinces-it.svg.
- 98.Veneto. [(accessed on 26 March 2020)]; Available online: https://en.wikipedia.org/wiki/File:Map_of_region_of_Veneto,_Italy,_with_provinces-en.svg.
- 99.Nelson M.M., Illingworth W.T. A Practical Guide to Neural Nets. Addison- Wesley; Reading, MA, USA: 1991. OSTI Identifier: 5633084. [Google Scholar]
- 100.Meteorological Conditions in the World. [(accessed on 28 March 2020)]; Available online: https://www.ogimet.com/ranking.phtml.en.
- 101.Weather Forecast. [(accessed on 28 March 2020)]; Available online: https://yandex.com/weather/bologna/month/february.