Detection of anomalous high‐frequency events in human intracranial EEG

Abstract

Objective

High‐frequency oscillations (HFOs) are a promising biomarker for the epileptogenic zone. However, no physiological definition of an HFO has been established, so detection relies on the empirical definition of an HFO derived from visual observation. This can bias estimates of HFO features such as amplitude and duration, thereby hindering their utility as biomarkers. Therefore, we set out to develop an algorithm that detects high‐frequency events in the intracranial EEG that are morphologically distinct from background without requiring assumptions about event amplitude or shape.

Method

We propose the anomaly detection algorithm (ADA), which uses unsupervised machine learning to identify segments of data that are distinct from the background. We apply ADA and a standard HFO detector using a root mean square amplitude threshold to intracranial EEG from 11 patients undergoing evaluation for epilepsy surgery. The rate, amplitude, and duration of the detected events and the percent overlap between the two detectors are compared.

Result

In the seizure onset zone (SOZ), ADA detected a subset of conventional HFOs. In non‐SOZ channels, ADA detected at least twice as many events as the standard approach, including some conventional HFOs; however, ADA also identified many low and intermediate amplitude events missed by the standard amplitude‐based method. The rate of ADA events was similar across all channels; however, the amplitude of ADA events was significantly higher in SOZ channels (P < .0045), and the amplitude measurement was more stable over time than the HFO rate, as indicated by a lower coefficient of variation (P < .0125).

Significance

ADA does not require human supervision, parameter optimization, or prior assumptions about event shape, amplitude, or duration. Our results suggest that the algorithm's estimate of event amplitude may differentiate SOZ and non‐SOZ channels. Further studies will examine the utility of HFO amplitude as a biomarker for epilepsy surgical outcome.

Key Points.

• There is no physiological definition of an HFO, so detection relies on the empirical definition derived from visual observation. This can bias estimates of HFO features such as amplitude and duration, thereby hindering their utility as biomarkers

• We describe a new anomaly detection algorithm (ADA), which uses unsupervised machine learning to identify segments of data that are distinct from the background in the intracranial EEG

• The rate of ADA events was similar across all channels; however, the amplitude of ADA events was significantly higher in SOZ channels, and the threshold between SOZ and non‐SOZ channels was relatively consistent across patients

• ADA does not require human supervision, parameter optimization, or prior assumptions about event shape, amplitude, or duration

• Our results suggest that amplitude may differentiate SOZ and non‐SOZ channels

1. INTRODUCTION

Twenty to forty percent of epilepsy patients will not achieve seizure freedom using medication, leading them to consider surgery as a treatment option. ¹ Surgery often relies on localization of the seizure onset zone (SOZ) using intracranial electroencephalography (iEEG) to guide resection. Recent studies have shown that high‐frequency oscillations (HFOs) occur more frequently in the SOZ, ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ and the surgical removal of brain regions with high incidences of HFOs is correlated with a higher likelihood of seizure freedom after surgery. ² , ⁸ , ⁹ , ¹⁰ , ¹¹ These results suggest that HFOs may be a valuable marker for localization of epileptogenic tissue during surgical planning. Moreover, because HFOs occur in interictal periods, their use may enable clinicians to shorten the duration of invasive monitoring.

HFOs are empirically defined as spontaneous electrographic patterns consisting of at least four cycles of an 80‐500 Hz oscillation, with a high amplitude that is distinguishable from the background. ¹² , ¹³ , ¹⁴ Because these are transient events, detection of HFOs is a critical step in the localization procedure. The gold standard is visual identification, ⁷ , ¹⁴ , ¹⁵ but automated detectors are increasingly being implemented to save time and improve reliability and reproducibility. ¹⁶ , ¹⁷ Automatic detection algorithms generally follow a standard procedure: They identify a period of increased high‐frequency energy (measured with root‐mean‐square (RMS) amplitude, ¹⁵ , ¹⁸ , ¹⁹ amplitude of rectified filtered data, ²⁰ , ²¹ line length, ²² , ²³ Hilbert envelope, ³ , ²⁴ or as a peak in the time‐frequency decomposition ²⁵ ), then verify that the event exceeds a minimum duration or a minimum number of oscillations. Many algorithms include additional steps to merge consecutive events if they occur in close temporal proximity ³ , ¹⁸ , ²⁶ and reject false positives. ³ , ²⁷ , ²⁸ The time‐frequency representation of each event can also be used to separate HFOs from false oscillations due to artifacts, via visual or automated means. ²⁹

Despite the large number of automated algorithms that are currently available, two challenges of HFO detection have not yet been addressed. First, visual and automated detection rely on the empirical definition of an HFO derived from visual observation. ¹² There is currently no physiological definition that can guide the selection of detection parameters such as amplitude, duration, and number of cycles, as studies have shown significant overlap between pathological and physiological HFOs. ²³ , ²⁵ , ³⁰ , ³¹ , ³² However, the optimization of such parameters is critical to the accuracy of the detector. ¹⁵ , ²⁰ , ²¹ This is directly related to the second challenge: Existing detection methods require complex optimization procedures. These algorithms typically contain at least 3‐5 interrelated parameters, and the detection accuracy is highest when the parameters are optimized for individual subjects. ²¹ , ³³ As a result, these algorithms do not easily generalize to new datasets, and the effort needed for validation and optimization is a barrier to clinical implementation.

Here, we describe a new algorithm for detection of transient high‐frequency events in iEEG data that addresses these two challenges. Rather than identifying events with specific features, our anomaly detection algorithm (ADA) uses unsupervised machine learning to detect events that are morphologically distinct from background activity, regardless of amplitude or shape. This could include conventional HFOs, oscillations similar to HFOs but with lower amplitude, oscillations with irregular amplitude profiles, artifacts (if they are present in the data), and other unique patterns. While this method could be applied to any frequency band, we focus here on the ripple band (80‐250 Hz) as this allowed us to reduce the computation time by downsampling the data. The algorithm is fully automated and does not require parameter optimization or prior assumptions about the shape, amplitude, or duration of the events. We first present our algorithm, then demonstrate its use on human iEEG data, and compare the detection results to those of a standard HFO detection algorithm. We hypothesize that ADA will enable unsupervised estimation of HFO properties, which has the potential to lead to the development of more accurate biomarkers of the epileptogenic zone.

2. METHODS

2.1. Patients and recordings

Intracranial EEG recordings were collected from 36 adult patients between April 2015 and December 2017 at University of California, Irvine, Medical Center. All patients had medically refractory epilepsy and underwent electrode implantation to localize the SOZ for possible surgical resection. For inclusion, the recordings had to fulfill the following criteria: (a) diagnosis of temporal lobe epilepsy; (b) the SOZ was clearly localized to one or more iEEG channels by experienced neurophysiologists (JJL and IS) based on seizures recorded during the monitoring period; (c) electrode locations were confirmed using coregistered preimplantation and postimplantation structural T1‐weighted magnetic resonance imaging scans; (d) a minimum recording duration of six hours with no seizures, collected overnight while the patient was resting; and (e) a minimum sampling frequency of 2 kHz. In total, recordings from 11 patients (five females, 38.2 ± 16.9 years old) met these criteria. The recordings were 20 to 90 hours in duration with a 2 kHz (one subject) or 5 kHz (ten subjects) sampling rate and contained data from a total of 1186 depth electrodes (107.8 ± 31.7 electrodes per patient). Electrodes that could not be clearly localized to gray matter, electrodes with continuous electrographic artifact, and electrodes within the regions of immediate seizure spread outside of the SOZ were excluded from the analysis. Channels with bad signal quality or continuous electrographic artifact were visually identified and excluded. We analyzed the remaining 55 bipolar pairs of SOZ electrodes (average of 5.0 ± 3.0 channels per patient), and 119 bipolar pairs outside the SOZ (which we term nSOZ; average of 10.8 ± 6.2 channels per patient). We then selected multiple three‐minute segments of iEEG for each patient using the following rules. The segments were clipped from overnight iEEG records between 11 PM and 6 AM; concurrent scalp EEG was unavailable, so the data were not sleep staged. Each segment was at least one hour away from a seizure onset time, and we ensured that segments from the same patient were separated by at least 15 minutes. This resulted in the selection of approximately three segments per hour from each subject. In total, 118 segments were analyzed (mean of 10.7 ± 2.8 segments per patient or 32.1 ± 8.4 minutes per patient, with a range of 7 to 17 segments per patient).

2.2. Anomaly detection algorithm

The novel algorithm described here aims to separate anomalous high‐frequency events from the baseline background signal without human supervision or assumptions about the appearance of the events. The procedure consists of three parts: (a) preprocessing, (b) constructing a distance matrix, and (c) clustering and classification (Figure 1). All data analysis procedures were implemented in MATLAB 2018b (MathWorks) using custom‐written code, and the code for the anomaly detection algorithm will be provided as Material S1. The algorithm was developed using data from three subjects, and it was then applied with fixed parameters to all subjects.

FIGURE 1.

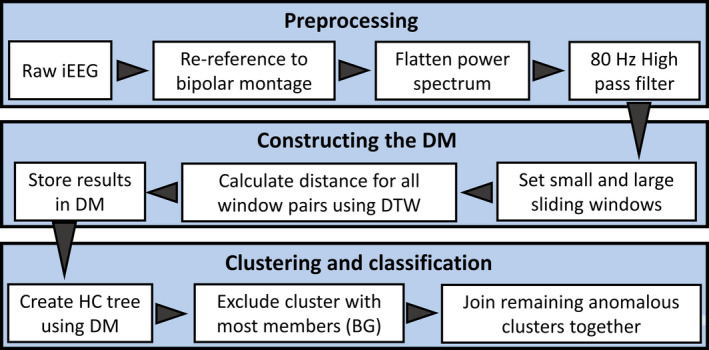
Data flow diagram for ADA. The algorithm consists of three main parts (large shaded boxes): preprocessing, constructing the DM, and clustering and classification. Each small white box represents a major processing step within each main part, and the arrowheads show the flow of the algorithm. Abbreviations are BG, background cluster; DM, distance matrix; DTW, dynamic time warping; HC, hierarchical cluster

2.2.1. Preprocessing

The iEEG was rereferenced to a bipolar montage via subtraction of adjacent electrodes, and the resulting signals were modified using the Simple Diff method. ³⁴ , ³⁵ This method flattened the power spectrum in the frequency domain by enhancing the energy of the high‐frequency activity and suppressing the low‐frequency components. This was done by taking the fast Fourier transform (FFT) of the data, then multiplying the FFT power spectrum by a constant scalar factor of 1−cos(2πf/fs), where f was the frequency and fs was the sampling rate. The final modified iEEG signal in the time domain was obtained by applying an inverse FFT to the modified flattened power spectrum. Each modified iEEG segment was then filtered using an 80 Hz high‐pass finite impulse response digital filter. The data were filtered in the forward and reverse directions to avoid phase distortion using the filtfilt function in MATLAB.

2.2.2. Constructing the distance matrix

To construct the distance matrix for one segment of data from one channel, we first selected two‐window sizes: a small window (1.5 ms) and a large sliding window (50 ms). The small window was used to downsample the iEEG, which was necessary to reduce processing time; within each small window, the representative amplitude of the iEEG was calculated as the average amplitude of all data points. This effectively downsampled the data to 666 Hz, which limited the algorithm to event detection in the ripple band (80‐250 Hz). The sliding window was used with 50% overlap for event detection. Each large window consisted of 33 small windows, which was long enough to contain a typical HFO event.

We then measured the distance between the iEEG time series in all pairs of large windows, using the MATLAB function dtw to calculate dynamic time warping (DTW). ³⁶ , ³⁷ DTW measures the similarity between two temporal sequences while being robust to phase differences. Then, the distance matrix (DM) was created by assembling these calculated distances into a nonnegative, square, two‐dimensional symmetric matrix with elements corresponding to the pairwise distances.

2.2.3. Clustering and classification

The upper triangular elements of each DM were converted into vector form for the linkage function used to create a hierarchical cluster tree. The unweighted average distance linkage method was applied to compute the distance between clusters. For clustering, a maximum of seven clusters was used, although comparable results were achieved with a maximum number of clusters ranging from seven to thirteen. The cluster containing the highest number of members (where each member was one 50‐ms window of iEEG data from the associated electrode) was designated as the background cluster, and the remaining six clusters were merged together and defined to be the anomaly group. Finally, for each iEEG electrode, any overlapping 50‐ms windows within the anomaly group were merged into single events. Note that this technique is unsupervised, and it therefore does not require a training set of visually marked HFOs and background segments. The algorithm identifies all data segments that are morphologically distinct from those in the background cluster, without specific requirements for amplitude, duration, or shape.

2.3. RMS detector

The RMS detector has become one of the most widely used automated detectors in publications related to HFOs. ² , ⁵ , ²⁷ , ³⁵ , ³⁸ It is based on the moving average RMS amplitude of the 100 to 500 Hz bandpass filtered signal (finite impulse response filter, roll‐off −33 dB/octave). The parameters for the RMS detector used in our study matched the original publication. ¹⁸ We calculated the RMS amplitude using a three‐ms sliding window, and the RMS threshold was defined as five standard deviations (SD) above the mean RMS value of the entire length of the signal. Segments of iEEG were considered to be HFO candidates when the RMS amplitude exceeded the threshold for at least six ms. Consecutive candidate events less than ten ms apart were joined together as a single event. Finally, the candidate events were accepted as HFOs if at least six rectified peaks exceeded a second threshold, defined as three SDs above the mean of the rectified filtered signal.

2.4. Characteristics of detected events

Hereafter, we will refer to events identified by the RMS detector as conventional HFOs (cHFO). Events identified via ADA, which do not have specific thresholds for amplitude or number of oscillations, will be referred to as anomalous high‐frequency activity (aHFA).

We compared the results of ADA and RMS detection by analyzing the shapes and characteristics of three groups of events: events detected only by ADA, only by RMS, and both by ADA and RMS, which we will refer to as ADA‐only, RMS‐only, and RMS + ADA, respectively. The shape of the events in each group was compared using the amplitude envelope from the Hilbert transform (median, 95th percentile, and maximum). We also measured four characteristics of the aHFA and cHFO: (a) rate, defined as the average number of events per minute per channel, (b) amplitude, defined as the average value of the upper amplitude envelope over the duration of the event, (c) duration, and (d) coefficient of variation (CV). We used the CV to measure the consistency of the event characteristics across all segments of data, defined as

$$\text{CV}=\sqrt{{\mathrm{e}}^{s_{\ln }^2}-1}$$

where s_ln is the sample standard deviation (SD) of the data after transformation with a natural log. The standard deviation was based on the mean amplitudes or rates for each segment of data in a single channel. All characteristics of aHFA and cHFO were compared between SOZ and nSOZ channels. We employed a Wilcoxon rank‐sum test to determine whether the event characteristics were significantly different, and the significance for all analyses was set at P < .05, except were adjusted to correct for multiple comparisons.

3. RESULTS

3.1. Incidence and morphology of aHFA and cHFO

Across all iEEG electrodes, a total of 598 SOZ and 1336 nSOZ three‐minute epochs from 11 patients were analyzed (Figure 2A‐B). Overall, 21 187 cHFOs (14 008 in SOZ and 7179 in nSOZ) were detected using the RMS detector, and 21 401 aHFAs (6208 in SOZ and 15 193 in nSOZ) were detected using ADA (Figure 2C‐D).

FIGURE 2.

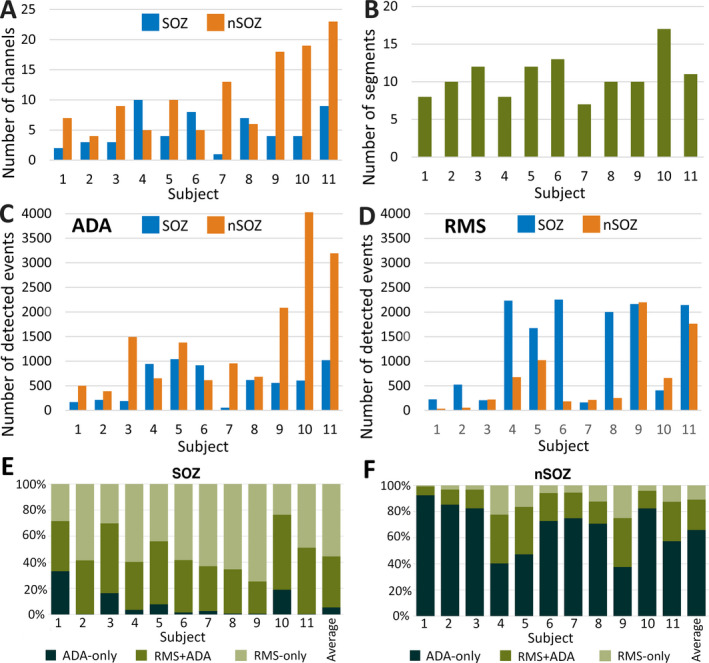
A, Total numbers of SOZ and nSOZ channels. B, Number of three‐minute segments of iEEG data analyzed for each individual patient. C, Total number of detected events by ADA from each individual patient divided into SOZ and nSOZ channels. D, Total number of detected events by RMS detector from each individual patient divided into SOZ and nSOZ channels. E, Percentages of the detected events in the ADA‐only, RMS + ADA, and RMS‐only groups for each subject for SOZ channels and F, nSOZ channels

The number of identified events in RMS + ADA, ADA‐only, and RMS‐only groups varied greatly between SOZ and nSOZ (Figure 2E‐F). In every subject, a subset of events was detected by both the ADA and RMS detectors. In the SOZ, most events were RMS‐only (55.5%), while 39.1% of events were RMS + ADA and 5.4% were ADA‐only. In five subjects, less than 5% of events in the SOZ were ADA‐only, indicating that the events detected by ADA were a subset of those identified by the RMS detector. In contrast, most events in the nSOZ channels were ADA‐only (65.9%), while 10.9% were RMS + ADA and 23.2% were RMS‐only.

To compare the morphology of events, we plotted the median, 95th percentile, and max amplitude envelopes for each group of events (Figure 3A). All groups of events exhibited amplitude profiles that reached a peak at the center of the event and tapered off at the edges, consistent with the traditional definition of an HFO. The amplitude of events in the RMS‐only group was higher than those in the ADA‐only group, suggesting that ADA may have considered a number of high‐amplitude events to be nonunique. The low‐amplitude events in ADA‐only (Figure 3B) were likely missed by the RMS detector due to the application of a strict amplitude threshold. This result is consistent with the data in Figure 2; because ADA detects low‐amplitude events, aHFA represents a larger percentage of events in nSOZ channels, where high‐amplitude events are infrequent.

FIGURE 3.

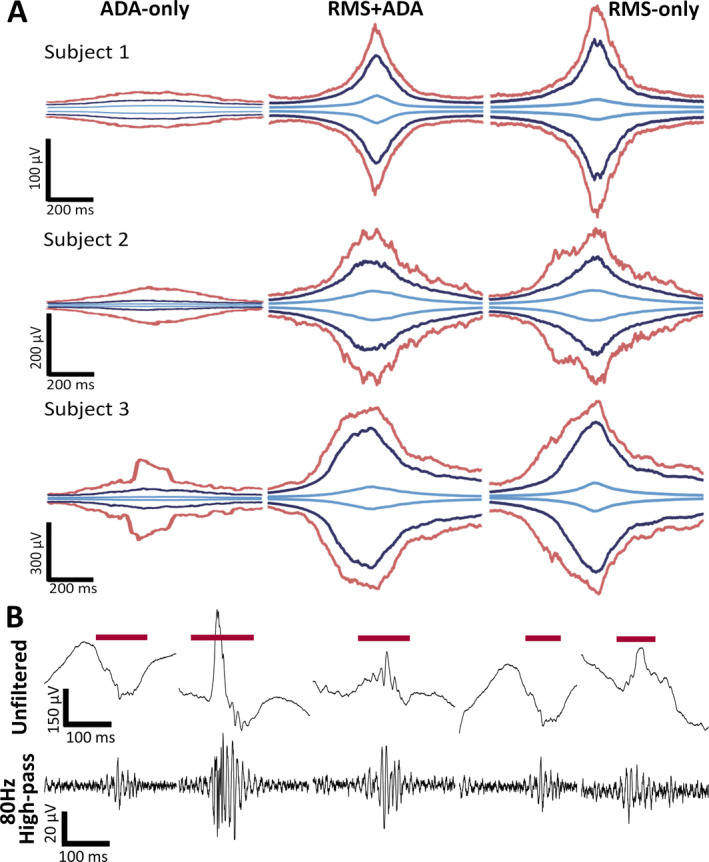
A, Amplitude envelopes of detected events separated into ADA‐only (left panel), RMS + ADA (center panel), and RMS‐only (right panel) from three representative subjects. The maximum, 95th percentile, and median amplitude envelope are represented by red, blue, and light blue lines, respectively. B, Examples of ADA‐only events

3.2. Characteristics of aHFA and cHFO

Because the rate has been almost exclusively used as an SOZ biomarker, we first measured the aHFA rate and cHFO rate in individual subjects, as well as the total rates when all events were pooled together (Figure 4A). Our results for rate using the RMS detector were consistent with previous studies: The rate of cHFO in the SOZ was 8.2 ± 4.2 min⁻¹, which was significantly higher than the rate in the nSOZ, 1.9 ± 2.7 min⁻¹. The individual results for all 11 patients also exhibited significant differences in cHFO rate between SOZ and nSOZ. The results for rate using ADA were less consistent. The average rate of aHFA was significantly different between the SOZ (3.5 ± 2.9 min⁻¹) and nSOZ (3.9 ± 2.1 min⁻¹), with the nSOZ having a higher rate. However, only six out of 11 patients had significantly different rates of aHFA in SOZ and nSOZ. In five out of these six patients, higher rate of aHFA was observed in nSOZ. Therefore, the rate of aHFA does not provide reliable separation between SOZ and nSOZ channels.

FIGURE 4.

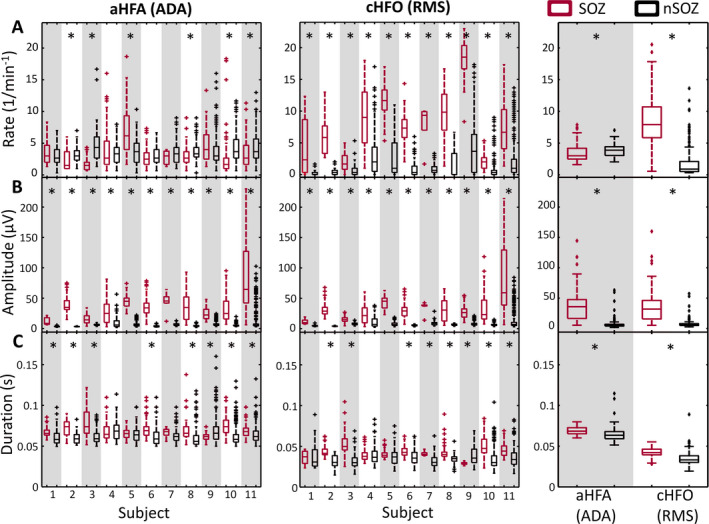
Characteristics of detected events separated into SOZ (red) and nSOZ channels (black). Boxplots show the (A) rate, (B) amplitude, and (C) duration of detected events for individual subjects (aHFA in left column and cHFO in middle column) and overall characteristics of detected events when all segments are pooled together (right column). *P‐value < .0045, Wilcoxon rank‐sum test with Bonferroni correction for 11 subjects

In contrast to rate, the event amplitude showed robust differences between SOZ and nSOZ channels using both ADA and the RMS detector (Figure 4B). The mean amplitudes of cHFO (37.0 ± 29.4 µV) and aHFA (39.7 ± 28.8 µV) in SOZ were significantly higher than in nSOZ (6.4 ± 8.1 and 7.2 ± 8.7 µV, respectively). These differences were statistically significant for all 11 individual subjects using both detection methods. Moreover, the amplitudes were consistent across subjects, such that a single, common threshold of approximately 15 µV could approximately separate SOZ and nSOZ across all subjects. This was not true for the rate, which would require a patient‐specific threshold to separate SOZ and nSOZ channels. The consistency of these results suggests that the amplitude of aHFA and cHFO may be robust biomarkers of the SOZ.

The average duration of detected events within SOZ channels was significantly longer than the duration in nSOZ channels for both detection schemes (Figure 4C). This difference was statistically significant for 8 subjects using ADA and 9 subjects using the RMS detector. However, for individual subjects, the duration of cHFOs provided smaller separation between SOZ and nSOZ channels than event amplitude or rate.

Despite differences in the filtering used for ADA and the RMS detector, we found that both aHFA and cHFO had median power spectra that peaked at ~90 Hz (Figure 5). The RMS events had higher power, as shown in Figure 3, but there did not appear to be a significant difference in the spectral content.

FIGURE 5.

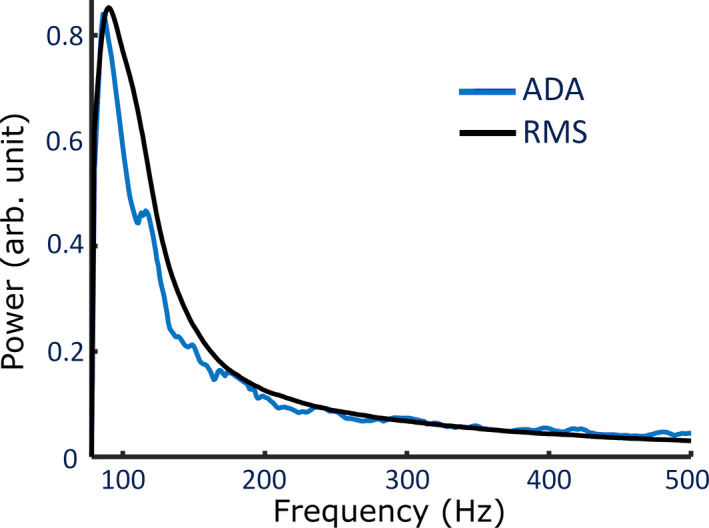
Normalized median power spectrum of detected events by ADA and RMS detector after applying an 80 Hz high‐pass filter to the broadband data. Each event was normalized to have a max amplitude of 1 prior to calculating the median value, and a correction was applied to account for the 1/f decrease in power with frequency

Finally, we calculated the CV to assess the consistency of the measurements across segments of data (Figure 6). The amplitude CV was significantly lower than the rate CV when calculated using the same detector and channels, suggesting that the estimates of amplitude are more stable over time for both detection schemes. The CV for amplitude in the SOZ was higher than in nSOZ, but it was still generally lower than the CV values for rate.

FIGURE 6.

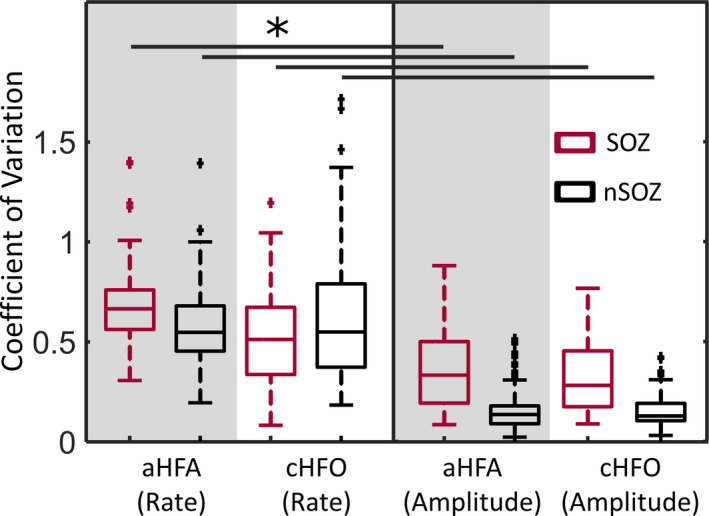
Boxplots of CV for the rate and amplitude of detected events, separated into SOZ (red) and nSOZ (black). *P‐value < .0125, Wilcoxon rank‐sum test

4. DISCUSSION

Here, we have presented a novel algorithm for detection of anomalous high‐frequency events and applied it to human iEEG. ADA is unsupervised and does not require complex optimization procedures or assumptions about the shape or amplitude of the events. While the aHFA rate was not consistently different between SOZ and nSOZ channels, the aHFA amplitude provided reliable and robust separation, suggesting this as a possible SOZ biomarker. We found significant overlap between aHFA and cHFOs, indicating that ADA is sensitive to traditionally defined HFOs. However, we also found that ADA identifies additional events that would not exceed the energy threshold of standard algorithms.

Robust identification of clinically relevant HFOs remains a challenge due to the lack of a physiological definition and the limitations of current detection methods. Because the mechanism underlying HFOs is not understood, detection is typically guided by the empirical definition which requires selection of an optimum energy threshold to separate events from the background. This is not trivial because the shape and amplitude of the HFO waveform can vary depending on the distance between the electrode and the neural generator, ³⁹ and the characteristics of the background activity vary over time. Therefore, a rigid template of shape and amplitude is likely insufficient for HFO detection. In addition, current automated algorithms require complex optimization procedures to maximize accuracy, ¹⁵ and it is common for them to suffer from a high number of false detections. ¹⁵ , ²⁰ Visual identification by expert reviewers has been widely used for detecting HFOs in both scalp and iEEG recordings, ⁴⁰ , ⁴¹ as humans can simultaneously adapt to changes in the background activity and reject artifacts. However, it is highly time‐consuming and has poor interrater agreement, ¹⁶ which reduces the generalizability of the results. ADA addresses these challenges, as it enables detection and estimation of event characteristics in an unsupervised manner. While ADA does not include postprocessing steps to reject false positives due to artifacts, these steps could be added after the detection procedure. There are many examples of such criteria, which can be applied to the raw data, filtered data, or the time‐frequency representation of the event. ³ , ²⁷ , ²⁸

Other machine learning techniques have been applied to the detection and analysis of HFOs. Support vector machines have been used to distinguish HFOs from false positives due to the filtering of sharp transients, ⁴² to distinguish between pathological and physiological HFOs, ²³ to classify individual channels based on HFO features, ⁴³ and to classify high‐frequency events as ictal or nonictal. Pearce et al ⁴⁴ also utilized logistic regression and k‐nearest neighbors clustering. Gaussian mixture models are another common technique for HFO detection and rejection of false positives, paired with k‐medoids clustering ⁴ , ⁴⁵ , ⁴⁶ or as part of a fuzzy‐c‐means quantization‐error‐modeling‐based expectation‐maximization Gaussian mixture model clustering algorithm. ⁵ There is one important difference between prior applications of machine learning and the algorithm reported here: All previous studies performed initial detection using an amplitude‐based detector. The most common methods were RMS amplitude, ⁵ , ⁴⁴ , ⁴⁶ line length, ²³ , ²⁶ and median operator threshold. ⁴ , ⁴⁵ This is fundamentally different from ADA, which separates events from the background using the shape of the filtered signal, rather than its amplitude.

In the present study, ADA was configured to detect anomalous events at frequencies greater than 80 Hz. A small window was used to downsample the data to reduce the calculation time; ⁴⁷ the approximate detection time for three minutes of data from a single channel of iEEG was ~4‐5 minutes using a desktop PC (CPU: i7‐4790k). With parallel computing or optimization of the algorithm, it may be possible for the size of this window to be reduced or to exclude this step. The 1.5‐ms small window effectively downsamples the signal to 666 Hz, which means that our algorithm is primarily detecting events in the ripple band (80‐250 Hz). However, the algorithm could be configured for other frequency bands as well, by changing the sizes of the small and large windows. The size of the small window determines the sampling rate, and the large sliding window was chosen to match the approximate duration of HFOs reported in prior studies. ¹⁸ , ²³ , ⁴⁸ Because the algorithm contains a step to join overlapping large windows in the anomaly group into single events, a range of large window sizes can be used without affecting the results. We used a maximum of seven clusters; however, this number can be altered, as long as it is higher than the expected number of anomalous patterns. We tested the algorithm with a range of seven to thirteen clusters, and there was no noticeable difference in the results because the background cluster was always several orders of magnitude larger than any other cluster. Therefore, we chose to use seven clusters, as it reduced the processing time.

We found that aHFA had a longer duration than cHFO, but this was likely due to differences between the two detection algorithms. The aHFA had a minimum duration of 50 ms, corresponding to the size of the large sliding window, while the cHFO duration was measured as the length of time that the RMS amplitude exceeded the energy threshold. This impacted the amplitude measurement, as well. The same event detected with ADA may have a lower amplitude than when it is detected with the RMS detector because the average amplitude will include some background activity at the edges of the window.

Conventionally, the cHFO rate has been used as an SOZ biomarker in studies of high‐frequency activity related to epilepsy. ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ However, every detected event increases the rate, whether the detections are true or false positives. This can drastically change the relative rates in SOZ and nSOZ channels (especially for ADA, which more frequently detects events in nSOZ) and can therefore alter the prediction of SOZ location. Moreover, we found that the CV of the rate was higher than for amplitude or duration, indicating a higher degree of variability across segments of iEEG.

In contrast to the rate, the aHFA and cHFO amplitudes were significantly higher in SOZ compared to nSOZ, with relatively consistent values across patients. The consistency of the values may be due, in part, to the homogenous patient population, as all subjects had mesial temporal lobe epilepsy. Other studies have also suggested that HFO amplitude is higher in SOZ than non‐SOZ electrodes. ⁹ , ³⁰ , ³¹ , ⁴⁹ , ⁵⁰ These differences were small, but statistically significant, with the exception of one study that found that the amplitude difference was not significant during nonictal periods. ⁴⁹ Furthermore, pathological HFOs recorded in the SOZ were shown to have significantly higher amplitudes than physiological HFOs induced by a visual or motor task (P < 1.0 × 10⁻¹⁰). ²³ Therefore, our algorithm may be valuable for detecting and separating pathological and physiological oscillations in the high gamma and ripple frequency bands.

Here, we found that the cHFO amplitude, aHFA amplitude, and the cHFO rate provided robust separation between SOZ and nSOZ in all 11 patients. However, the amplitude exhibited less variability over time and more consistency across patients. This suggests that amplitude may be another promising candidate for an SOZ biomarker. Further validation with a larger cohort of patients, more comprehensive inclusion of iEEG electrodes, and comparison to surgical outcome are needed to explore this hypothesis and will be the subject of future investigations.

CONFLICT OF INTEREST

None of the authors has any conflict of interest to disclose. We confirm that we have read the Journal's position on issues involved in ethical publication and affirm that this report is consistent with those guidelines.

Supporting information

Supplementary Material

Charupanit K, Sen‐Gupta I, Lin JJ, Lopour BA. Detection of anomalous high‐frequency events in human intracranial EEG. Epilepsia Open. 2020;5:263–273. 10.1002/epi4.12397