Mathematical Modeling to Address Challenges in Pancreatic Cancer

Abstract

Pancreatic ductal adenocarcinoma (PDAC) is regarded as one of the most lethal cancer types for its challenges associated with early diagnosis and resistance to standard chemotherapeutic agents, thereby leading to a poor five-year survival rate. The complexity of the disease calls for a multidisciplinary approach to better manage the disease and improve the status quo in PDAC diagnosis, prognosis, and treatment. To this end, the application of quantitative tools can help improve the understanding of disease mechanisms, develop biomarkers for early diagnosis, and design patient-specific treatment strategies to improve therapeutic outcomes. However, such approaches have only been minimally applied towards the investigation of PDAC, and we review the current status of mathematical modeling works in this field.

Introduction

Approximately 420,000 new cases of pancreatic cancer will have been diagnosed globally by 2020, of which ~410,000 patients are estimated to die [1]. Of these cases, 93% will be pancreatic ductal adenocarcinomas (PDAC) occurring in the exocrine part of the pancreas, and the remaining 7% will be pancreatic neuroendocrine tumors developing in the endocrine portion of the pancreas [2]. PDAC has very poor prognosis with a 5-year survival rate of ~5%, and <11-months of median survival. Thus, PDAC ranks as the third most lethal form of cancer after lung and colon [2]. The incidence of PDAC is expected to increase, with projections of more than two-fold rise in the number of new diagnoses and PDAC-related deaths within the next ten years [3]. In addition to demographic factors like age, gender, and ethnicity, other risk factors associated with PDAC include smoking, chronic diabetes mellitus, chronic pancreatitis, obesity or sedentary lifestyle, non-O blood group, and genetic susceptibility [4, 5]. Progression from healthy mucosa to invasive malignant PDAC occurs via a series of step-wise mutations that lead to the development of pre-cancerous precursor lesions namely, pancreatic intraepithelial neoplasm (PanIN), intraductal papillary mucinous neoplasm (IPMN), and mucinous cystic neoplasm (MCN), each bearing characteristic molecular, pathological, and clinical features [6]. The pathophysiological hallmarks of PDAC include nearly 100% KRAS mutation frequency [7]; strong desmoplastic reaction that leads to a dense extracellular matrix, hypovascularity, hypoxia, reprogrammed cell metabolism, evasion of immunity [8]; and a heightened tendency for local invasion and distant metastasis [9].

PDAC poses significant challenge in early diagnosis and is generally diagnosed in patients above 40 years of age, with the median age of diagnosis being 71 years, and the majority of cases presenting with a locally advanced or metastatic disease with nodal involvement [4, 5]. Sensitive and accurate serum biomarkers for early detection of PDAC are a work in progress. Carbohydrate antigen 19–9 (CA 19–9) and carcinoembryonic antigen (CEA) are the only two clinically used serum biomarkers for PDAC, but they suffer from low sensitivity and specificity [10]. Other biomarkers like circulating tumor cells or circulating tumor DNA suffer from similar issues of limited sensitivity or specificity [10]. MicroRNAs isolated from pancreatic tumor tissue, blood samples, pancreatic juice, stool, urine, and saliva are also being investigated for their diagnostic value [11]. Imaging techniques, such as computed tomography (CT scan), endoscopic ultrasound (EUS), and magnetic resonance imaging (MRI) are commonly used to confirm the diagnosis and to help assess whether the tumor is surgically resectable. Due to poor diagnosis and early metastasis of the disease, only few patients are eligible for curative-intent surgery, and thus systemic chemotherapy is the mainstay of treatment for patients diagnosed with PDAC, with the chemotherapeutics of choice being gemcitabine, 5-fluorouracil, capecitabine, and folfirinox [11–13]. With improvements in understanding of the in vivo behavior of nanomaterials [14–16], the development of novel nanoparticle-based therapies for cancer diagnosis and treatment has seen a surge in the past decade [17, 18]. This has also led to the development of nanomaterials for improved delivery of drugs in PDAC [19–21]. However, the clinical translation of such novel drug delivery platforms has been limited primarily due to preferential accumulation of nanomaterials in the mononuclear phagocytic system and heterogenous tumor penetration [22, 23]. Checkpoint inhibitor monoclonal antibodies in combination with other agents are also being investigated to overcome the immunosuppressive microenvironment of PDAC and recruit effector T cells for effective treatment [24].

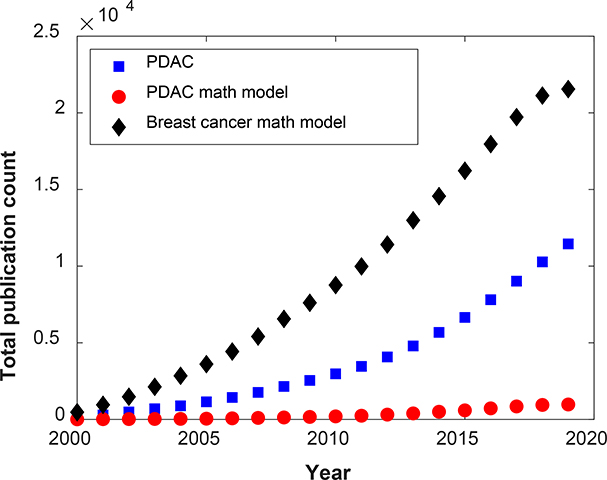
Over the last two decades considerable progress has been achieved in basic or translational research involving PDAC. However, the application of mathematical and computational tools to support explorations in PDAC biology, diagnosis, prognosis, and treatment has lagged behind, and this becomes even more evident when compared to the progress made in quantitative investigations of other cancer types (Figure 1) [25–41]. This gap highlights the need for the development and application of novel quantitative tools to improve the understanding of PDAC progression and support clinical care. Here, we review mathematical modeling efforts undertaken to understand PDAC progression, and explore their applications in PDAC diagnosis, prognosis, drug delivery, and precision medicine.

Figure 1.

Graph showing PubMed results of total publication count over the last two decades (1/1/2000–9/28/2019) for the keywords ‘pancreatic ductal adenocarcinoma’ (square shapes), ‘pancreatic ductal adenocarcinoma mathematical modeling’ (circle shapes), and ‘breast cancer mathematical modeling’ (diamond shapes).

Mathematical models of PDAC progression: Applications in treatment

The discrepancy between the highly successful in vitro efficacy of a therapeutic agent and its suboptimal performance in vivo can be attributed to tumor microenvironment variables that can radically influence drug delivery and cytotoxic potential of the drug, and simultaneously alter the aggressiveness of the targeted cells [42–44]. To this end, Lee et al. [45] combined in vitro cytotoxicity data with nutrient and oxygen concentration gradient dependent cell proliferation and death parameters to inform a nonlinear mathematical model of PDAC progression, which is an adaptation of a model developed by Cristini et al. [46–48]. The model assumes a quasi-steady state diffusion-reaction equation to describe the concentration of cell substrates (nutrients) throughout the tumor domain:

$${\nabla }^2\sigma -R=0$$ (1)

where σ is the concentration of substrate and R denotes the substrate addition rate, which incorporates i) the transport of material from the vasculature and ii) the loss of material due to the intrinsic consumption by tumor cells. The model also assumes that the cells move with velocity u due to intratumoral pressure gradients. The governing equation for the velocity follows the Darcy flow expression:

$$\mathit{u}=-\mu \nabla P$$ (2)

where μ denotes the cell mobility, and P is the intratumoral pressure.

Lastly, the equation that couples the concentration with the pressure is a characterization of the sinks and sources of cells in the domain. This is accomplished by means of the divergence operator applied to the velocity. Namely, ∇ ⋅ u = λ_p, where λ_p depends on the concentration of cells, their mitotic rate b and their apoptotic rate λ_A. Explicitly, λ_p = bσ − λ_A.

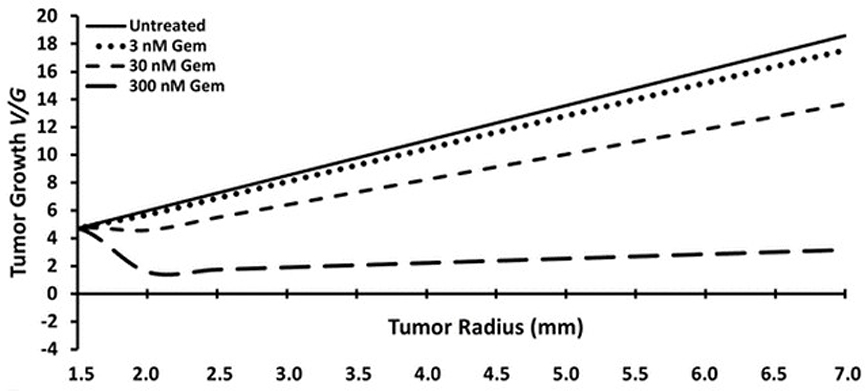
The model was informed by in vitro experiments on pancreatic cancer cell lines for cellular proliferation and apoptosis rates and used to simulate tumor growth and test the efficacy of gemcitabine. As shown in Figure 2, for the concentrations of the chemotherapeutic agent under consideration, the growth of the tumor always remained positive, which is consistent with in vivo observations on an orthotopic tumor model with the same cell line. This model provides a tool to simulate tumor growth under variable scenarios and thus predict therapeutic efficacy.

Figure 2.

Progression of tumor growth (V/G) and tumor radius as a function of the concentration of gemcitabine predicted by the model. Reproduced with permission from Lee et al. [45].

In the aforementioned model, the governing equations are deterministic and consider a localized tumor that grows in time but that does not invade proximal and distal tissues. However, in reality, several of the mechanisms that drive the evolution of cancer are stochastic in nature. Furthermore, one of the hallmarks of PDAC is metastasis. Hence, a model capable of incorporating these two aspects could be especially useful in predicting survival rates for patients. Moreover, with the appropriate parameters, it could be used to quantify the population of metastatic cells as a function of time, giving reasonable estimates for the progression of the disease. To this end, Haeno et al. [49] model cancer metastasis as a random process and assume an initial exponential growth using a rule-based modeling approach. To generate and later test their model, they use data from two clinical databases. The key players in the model are cancer cells classified into three categories, type 0, type 1, and type 2. Type 0 is characterized by non-metastatic cells residing in the primary tumor that possess a proliferation rate r and a death rate d. Type 1 cells are metastatic and originate from type 0 cells possibly through epigenetic mutations at a rate u per cell division. Similar to type 0 cells, type 1 cells continue to reside within the primary tumor and migrate to adjacent regions at a rate q to finally become type 2 cells. The proliferation and death rates for the cell type k for k = 1,2, is given by the constants a_k and b_k, respectively.

The system initiates with M₁ tumor cells, cell fitness is assessed, and the aforementioned transition rules are applied to 4 different scenarios: (i) no treatment, (ii) the patient has surgery and a fraction of the primary tumor is removed, (iii) chemoradiation or chemotherapy is administered diminishing the proliferation rate of all cell populations by a certain factor, and (iv) the patient undergoes both surgery and chemoradiation/chemotherapy. The parameters u (conversion into type 1) and q (migration) are determined through the available clinical data of tumor metastasis and computed, by means of probability generating functions [50]. The model was used to test the effect of variable treatment regimens on patient survival. Finally, we mention that a generalization to Haeno et al. [49] can be found in Yamamoto et al. [51], where the authors include the effects of metastasis suppressor genes and epithelial mesenchymal transition. Other avenues that also follow a stochastic approach based on the methods of Haeno et al. [49] involve the analysis of the effects of the genes KRAS, CDKN2A, TP53, and SMAD4 in determining the likelihood of the cancer becoming metastatic [52], and the investigation of optimal strategies in administering therapies consisting of the drugs Folfirinox, gemcitabine, and the combination of gemcitabine with nab-paclitaxel [53]. In all instances, the numerical results generated by the simulations correlated with the available clinical data.

Further, to elucidate the cause of drug resistance in PDAC, Yachida et al. [54] sequenced seven PDAC metastases and compared their clonal profile against primary and metastatic neoplasms, to test two hypotheses: i) cancer is detected too late, at a point where the damage is irreversible, and ii) cells become metastatic and migrate at a fairly early stage. To investigate this, they developed a mathematical model based on a Poisson process [55]. With this technique the authors concluded that on average 10 years elapse from the origin of the non-metastatic founder cell to the point where its lineage begins to exhibit the first traces of a metastatic mutation. Furthermore, they discovered that 5 additional years are necessary for the cells to fully develop their metastatic potential. From this point onwards the spread of the disease is extensive and the patients live on average 2 years. Thus, one can identify three relevant periods of time in the model. T1, the time between the origin of the founder cell and the first mutation, T2, the time after T1 acquires a completely functional metastatic potential, and T3, the remaining lifespan of the patient after T2.

We remark that a refinement of Yachida et al. [54] can be found in Makohon-Moore et al. [56], where the authors provide a more detailed description of the type of lesions under consideration. For instance, they make the distinction between PDAC, low-grade pancreatic intraepithelial neoplastic lesions (LG-PanIN) that possess a medium level of cytological abnormalities, and high-grade PanIN (HG-PanIN) with extensive cytological mutations that are hypothesized to enable the cancer to penetrate surrounding tissue. Furthermore, the proposed model considers three scenarios based on the number of somatic mutations that are shared between the various types of lesions. These mutations are in turn divided into two driver genes D1 and D2, whose simultaneous presence is necessary to result in an activated metastatic potential. The first scenario assumes no commonalities between the mutations and hence D1 is unique to PDAC and D2 is unique to PanIN. In the second case, an ancestral cell leads to the formation of PanIN and PDAC lineages by means of a founder cell, where both the founder cell and PanIN lack the metastatic potential. Hence, the founder cell possesses the first driver mutation D1 and PDAC the second D2, becoming fully metastatic. Finally, in the third scenario, the ancestral cell produces a metastatic founder cell having both driver mutations D1 and D2.

Pancreatic stellate cells (PSCs) are particularly relevant in processes that lead to pancreatic fibrosis, which is a hallmark of PDAC. Transcription factor STAT1 (signal transducer and activator of transcription 1) mediated interferon-γ (IFN-γ) signaling in PSCs is believed to reduce tumor progression by either inhibiting fibrogenesis, or by having a direct effect on the proliferation of tumor cells. To answer their question, Lange et al. [57] proposed a signaling pathway and developed a systems model comprising a system of ordinary differential equations (ODEs) that were solved numerically. Interestingly, their model incorporates delay terms, resulting in a system of delayed differential equations. Combining clinical data and their mathematical model, the authors concluded that the effectiveness of IFN-γ was independent of the presence of PSCs. Moreover, they observed that when PSCs are present the key mechanism is through fibrogenesis inhibition and that in their absence it is probably due to a combination of inhibitory effects on cells local to the microenvironment and the direct action on tumor cells. It is noteworthy to mention that in a follow-up study, Lange et al. [58] were able to generate numerical results consistent with observed experimental clinical data related to the selective tyrosine-kinase inhibitor drug erlotinib. Their findings provided supporting evidence to the proposed mechanisms of action and explain the effectiveness of erlotinib.

A detailed systems biology model of PDAC progression that incorporated cancer-stroma-immune interactions was developed by Louzoun et al. [59]. The model consisted of a system of 11 ODEs representing the following variables: pancreatic cancer cells (PCCs), PSCs, pro-inflammatory macrophages (M1), anti-inflammatory macrophages (M2 & MDSCs), cytotoxic T cells (CTL), and primary cytokines (TGFβ, IL6, MCSF, GMCSF, IL10 and IL12). In order to simplify the model, they used quasi-steady-state approximations for cytokine concentrations and ended up with four ODEs where the species of interest were: the density of PCCs, the density of PSCs, the density of CTL, and a new variable representing the ratio of M1/(M1+M2) macrophages. The model was validated with data from published literature and was used to investigate the relationship between drug efficacy and immune response. It was observed that immunotherapy is only effective when the killing rate of cancer cells by T cells (λ_c) and the parameters describing the effect of PCCs and PSCs (γ_c,γ_p, respectively) on polarization of the macrophages fall within a specific range, suggesting that the immune system has a certain window of opportunity to efficiently suppress cancer under treatment. When γ_c = 0 and γ_p =0, the steady state of tumor size C slowly decreases as λ_c increases, however if the values are non-zero, there is a faster decline in C. Further, it was seen that at λ_c=5e-8, C remains high regardless of the values of γ_c and γ_p, but if λ_c = 5e-7, C decreases significantly at low values of γ_c and γ_p.

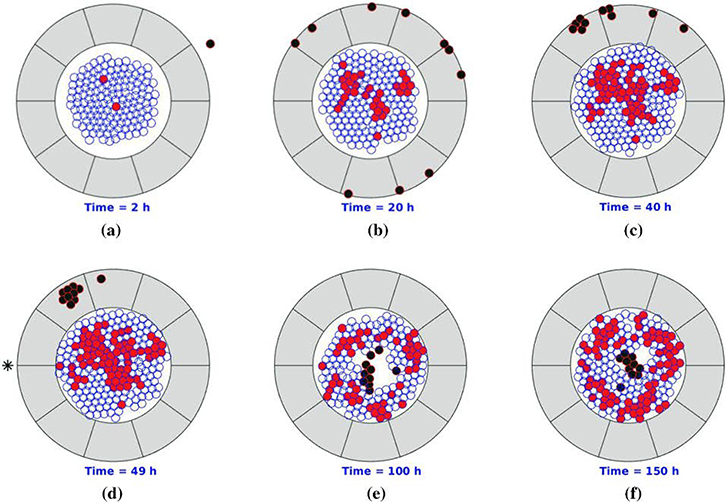
To describe pancreatic cancer progression under therapy, Chen et al. [60] used a cell-based mathematical modeling approach (Figure 3). The model is based on the following key simplifications: considers only three cell phenotypes (epithelial cells, cancer cells, and T-lymphocytes), considers two possible states for each cell (dead or viable), and assumes a uniform collagen density for the desmoplastic stroma. The migration of epithelial and cancer cells was modeled using the strain energy density, the total repulsive force, and random walks. T-lymphocytes migration modeling took into account chemotaxis, mechanical repulsion, random walk, and small range impingement. The probability of cell division, mutation, and death was simulated with stochastic processes. A two-dimensional orientation is created to simulate the changes in migration of the T-lymphocytes due to the orientation of the desmoplastic ECM. Treatment injection is modeled as a source point with a diffusive behavior afterwards. Monte Carlo simulations were used to investigate the propagation of uncertainties in the parameters and after each simulation is completed, the final fraction of cancer cells is calculated as an evaluation criterion for cancer development. The authors used the model to compare the effectiveness of PEGPH20 and gemcitabine therapy at different stages of diagnosis. It was observed that the final fraction of cancer cells is dependent on the fraction of cancer cells on which the treatments is initiated. This model can be used for testing treatment efficacy and could be used to design drug dosage regimen.

Figure 3.

Schematic of model domain showing epithelial cells, cancer cells, T-lymphocytes, and extracellular matrix in blue, red, black, and gray colors, respectively. Black asterisk represents the site of drug injection. Reproduced with permission from Chen et al. [60].

The kinetic model constructed by Roy et al. [61] consists of a system of 47 ODEs that intended to describe the metabolic network dynamics involved in glycolysis, glutaminolysis, tricarboxylic acid cycle (TCA), and the pentose phosphate pathway (PPP) in PDAC. It is based on a priori knowledge of the 46 metabolites involved in the different pathways and the 53 reactions and interactions between them. Each metabolite concentration change rate is represented by one ODE and the final ODE describes the time evolution of the number of cancer cells. Each metabolite’s initial concentration had the possibility to vary within a specific range; Latin Hypercube Sampling was applied to efficiently explore the entire spectrum of possibilities. In order to obtain the parameters for the model, only the reaction velocities and the growth parameters were fitted into the training data, and the rest of them used literature values. To validate the model, the authors used available experimental measurements for cell proliferation under conditions of nutrient deprivation. To test the robustness of the model they performed Monte Carlo analysis on the increase in number of cancer cells for varying metabolite initial conditions. The result of these simulations indicate that cell proliferation is sensitive to the initial metabolite concentrations. This model predicts a nonlinear influence of glucose and glutamine availability on cell proliferation and a stronger dependency of the number of pancreatic cells with glutamine availability, as compared to glucose. By predicting the dynamic reaction fluxes under varying conditions, the model is also able to provide insight into the metabolic phenotype of the pancreatic cancer cells. Additionally, the model has the capability of predicting system-level response to various metabolic perturbations and novel strategies to reduce cell proliferation. Using this model, the authors were able to show the importance of targeting the PPP, TCA cycle, and mitochondrial-cytoplasmic shuttle reactions for regulating tumor metabolism.

Using a priori knowledge of signaling pathways in pancreatic cancer, Gong et al. [62] developed a Boolean network model to study the interplay between tumor growth, cell cycle arrest, and apoptosis. The major signaling pathways included were: the Hedgehog, WNT, KRAS, RB-E2F, NFκB, p53, TGFβ, and apoptosis pathways. The input signals for the model represent different growth factors; the output signals are apoptosis, proliferation, and cell arrest. Each node in the model represents a protein or lipid in the signaling pathway, and it has two states: ON (1) or OFF (0). The time evolution of each node state is described by a Boolean transfer function that depends on the neighbor’s node state. The total Boolean network consisted of 61 nodes, which included 7 input nodes and 3 output nodes. Symbolic Model Checking was used to verify that the model satisfies temporal logic properties related to cell fate, cell cycle, and oscillations. In order to use it, the model’s intended behaviors were expressed as Computation Tree Logic formulas. Some results that the model provides are: (i) inhibition of apoptosis and cell cycle arrest are not unavoidable and permanent, (ii) apoptosis can be activated even when p53 is not, (iii) an initial overexpression of TGFβ or PIP3 always leads to oscillations in the expression level of NFκB’s. The model results present new interesting properties for future testing.

Mathematical models for PDAC diagnosis and prognosis

Imaging-based diagnosis and prognosis

The metastatic potential of PDAC has been found to be controlled by the stroma around the tumor, hence certain characteristics of the stroma may serve as measurable biomarkers to assess PDAC aggresiveness. To investigate this, Koay et al. used quantitative computed tomography (CT) imaging on preoperative tumors to measure the “delta” value at the tumor-normal tissue interface [63]. The “delta” value is defined as the difference between the mean Hounsfield unit value of the tumor contour and the normal tissue contour at the interface. The “delta” measurement was used for a binary classification of patients into high-delta and low-delta that correlated with more aggressive and less aggressive disease, respectively. High-delta patients also demonstrated poorer response to therapy than low-delta patients. To investigate the biophysical mechanisms leading to the morphological differences in PDAC tumors, they developed a mathematical model of macroscopic tumor progression that accounts for cell proliferation and cell migration. The model is based on a multicomponent mixture modeling framework that accounts for the tumor and healthy tissue comprising of a mixture of viable and dead cells with volume fractions ϕ_V and ϕ_D, respectively. The mass balance equation describing the temporal evolution of ϕ_V or ϕ_D is:

$$\frac{\partial {\varphi }_i}{\partial t}+\nabla \bullet ({\mathrm{u}}_i{\varphi }_i)=-\nabla \bullet {\mathrm{J}}_i+{\mathrm{S}}_i,i=\mathrm{V},\mathrm{D}$$ (3)

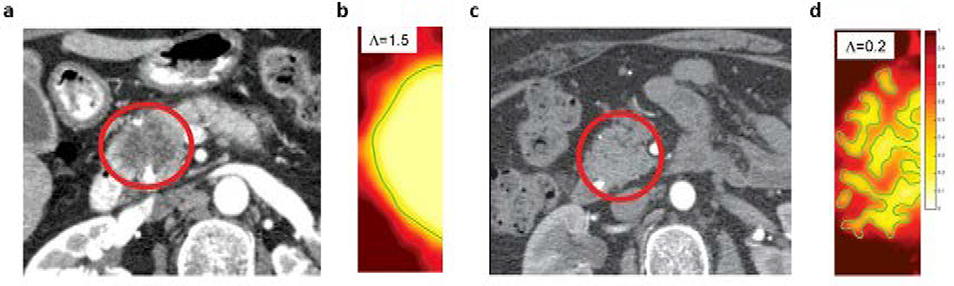
where, u_i is the velocity, J_i is a flux, and S_i is a source term accounting for cell proliferation and death. The model is used to numerically simulate tumors with cell proliferation rate (Λ_P) lower than cell migration rate (Λ_M), and tumors with the opposite behavior. The stability parameter Λ = Λ_P/Λ_M characterizes the stability of the tumor-host tissue interface, and as shown in Figure 4, low Λ values show tumor intermingling with stroma, which is representative of low-mode instability that manifests as finger-like projections, and high Λ produces simulations of tumors with distinct tumor-stroma interface. The simulation results were analogous to macroscopic features observed in patient CT scans (Figure 4a,c). Thus, using the mathematical model they explain the observed phenomena of high- and low-delta tumors, and provide a tool based on standard CT scans that can be used pre-treatment to predict disease prognosis and thus tailor patient-specific treatments.

Figure 4.

a,c) Tumor images from CT scans (circled in red) showing high-delta (a) and low-delta (c) tumors, and b,d) corresponding simulations of the mathematical model showing distinct tumor-healthy tissue interface patterns that explain the CT scan observations. Values of the stability parameter Λ used for simulations are shown in the inset. Reproduced with permission from Koay et al. [63].

To improve the diagnosis of PDAC and be able to accurately differentiate between cancerous and non-cancerous pancreatic lesions, Bali et al. [64] used quantitative parameters obtained from mathematical modeling of dynamic contrast enhanced magnetic resonance imaging (DCE MRI) data to correlate with fibrosis content and microvascular density (MVD) in the lesions. They used one-compartment and two-compartment pharmacokinetic models to fit to the contrast enhancement kinetics data obtained from DCE MRI, in order to estimate mechanistic parameters that characterize the transport properties of the contrast agent in the lesions. Contrast enhancement kinetics is modeled using the following equations:

One compartment model:

$$C_{\mathrm{T}}(t)=K^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}}{\int }_0^t{C}_{\mathrm{a}\mathrm{r}\mathrm{t}}(t^{\mathrm{\prime }})e^{-\frac{K^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}}(t-t^{\mathrm{\prime }})}{f}}d{t}^{\mathrm{\prime }}$$ (4)

where, C_T and C_art represent the concentration of contrast agent in tissue interstitium and abdominal aorta, respectively; K^trans is the mass transfer rate constant representing the transvascular transfer of contrast agent; and f is the volume fraction of tissue available to the contrast agent (includes, plasma and extravascular extracellular space).

Two compartment model:

$$C_{\mathrm{T}}(t)=K^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}}{\int }_0^t{C}_{\mathrm{a}\mathrm{r}\mathrm{t}}(t^{\mathrm{\prime }})e^{-\frac{K^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}}(t-t^{\mathrm{\prime }})}{v_i}}d{t}^{\mathrm{\prime }}+v_{\mathrm{p}}{C}_{\mathrm{a}\mathrm{r}\mathrm{t}}\left(t\right)$$ (5)

where, v_p and v_i represent the tissue volume fraction occupied by plasma and extravascular extracellular space, respectively. The two-compartment model is permeability-limited, while the one compartment model is perfusion-limited. As a result, the K^trans parameter in the one compartment model is a measure of tissue perfusion, rather than of tissue permeability, and fits the DCE MRI data for hypovascular lesions that have low tissue perfusion better than the two-compartment model. Overall, the K^trans values were lower for malignant tumors than for benign lesions and healthy tissue. Also, the two-compartment model revealed smaller values of v_p for hypovascular tumors and also for benign lesions and healthy pancreatic tissues. However, in hypervascular tumors the two-compartment model provided better fits and larger values for the v_p parameter. Further, the estimates of model parameters showed significant correlation with histopathological measures of fibrosis and MVD. K^trans estimates from the two models were negatively correlated with fibrosis content in the lesion, whereas f and v_i showed a positive correlation with fibrosis content and MVD. This study thus demonstrates the application of DCE MRI and pharmacokinetic modeling as a prognostic and diagnostic tool for pancreatic lesions.

A similar approach was employed by Liu et al. where they used two-compartment and three-compartment pharmacokinetic models to estimate transport parameters from DCE MRI data of PDAC patients to test the correlation with tumor fibrosis and vascularization [65]. The analysis revealed significant correlations between the pharmacokinetic model parameters and tumor characteristics like fibrosis and vascular density, further supporting the application of integrated DCE MRI imaging with mathematical modeling for predictive applications in the clinic.

Blood biomarker-based diagnosis

In order to improve early diagnosis of PDAC, a mathematical model was developed by Root et al. to investigate the feasibility of application of blood-based biomarkers in PDAC detection [66]. The model consists of a mass balance-based ODE that defines the blood concentration kinetics of the biomarker by taking into account biomarker secretion into blood from normal and cancerous cells, and its elimination (clearance) from the blood (Equation 6).

$$\frac{dB}{dt}=f{s}_{\mathrm{c}}{V}_{\mathrm{c}}(t)+f{s}_{\mathrm{n}}{V}_{\mathrm{n}}-kB\left(t\right)$$ (6)

where, B represents blood biomarker concentration; f represents the fraction of biomarker entering the blood from tumor or healthy tissue interstitium; s_c and s_n are the rates of shedding or secretion of biomarker from the cancerous and normal cells, respectively; k is the rate of excretion of the biomarker from blood; V_c and V_n represent the volume of tumor and healthy tissue, respectively. V_n is assumed to be constant and V_c grows exponentially over time as defined by the tumor growth equation: V_c(t) = V₀e^gt. V₀ is the volume of primary tumor at diagnosis, and g is the tumor growth rate constant.

Model simulations reveal that PDAC detection through a blood-based biomarker is feasible and can help with detection almost a year and a half before the lower limit for detection through imaging is reached, provided the biomarker production rate is moderately high.

Mathematical models of drug delivery in PDAC

The traditionally accepted predictor of therapeutic efficacy, i.e. plasma drug concentration kinetics may not reflect the drug concentration kinetics in the vicinity of cancerous cells due to the barriers to drug diffusion imposed by the dense extracellular matrix of PDAC. Thus, the tumor microenvironment of PDAC plays a crucial role in the transport of drug molecules from the tumor microvasculature to the cancerous cells. Further, due to patient- or tumor-specific variability, a greater difference in the tumor site drug concentration may exist across patients, thereby leading to differential therapy response to gold-standard treatment regimens in the patient population. To investigate the role of mass transport properties of the PDAC microenvironment in inducing therapeutic resistance to gemcitabine, Koay et al. conducted a clinical trial on patients with resectable primary PDAC tumors that were administered intraoperative gemcitabine infusion during curative-intent surgery [67]. Using integrated CT imaging and mathematical modeling, they estimated transport parameters of the tissue and assessed their correlation with incorporation of gemcitabine in the cellular DNA. Also, they investigated the correlation of transport properties with response to neoadjuvant therapy (Figure 5). The mathematical model consists of an ODE that models the density kinetics of the contrast agent in the tissue of interest:

$$\frac{dY}{dt}=R(Y_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{V}}{e}^{-R_{\mathrm{c}}t}-Y)$$ (7)

where, Y is the density of contrast in the tissue at time t, $Y_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{V}}$ is the imposed density of contrast in the vasculature, R is the transvascular mass transfer rate constant, and R_c is the rate of excretion of the contrast agent from blood. Following fitting of the model to CT data from individual patient scans, the estimated transport parameter (normalized area under the curve (AUC)) correlated inversely with gemcitabine incorporation into tumor DNA and with response to therapy, indicating that better transport improves drug delivery and thus treatment outcome. The study provides a clinical tool that can be used to assess the transport properties of PDAC and other solid tumors and design treatment regimens accordingly. A follow up study on the same patients was then conducted to understand intratumoral heterogeneity in gemcitabine transport, which revealed significant differences in drug transport within a tumor and across the patient population as determined by the drug transport model parameter estimates [68].

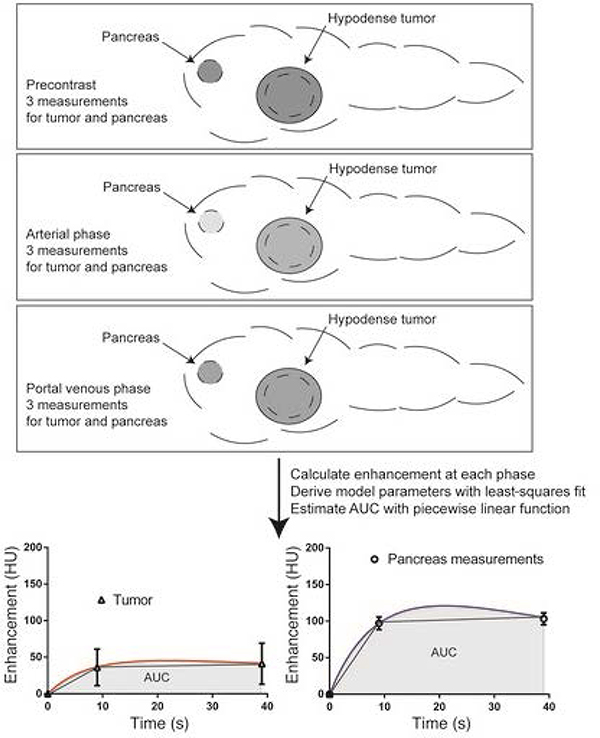
Figure 5.

A schematic showing the protocol for measurement of transport properties through CT imaging. Abdominal CT scans at the precontrast, arterial phase, and portal venous phase are obtained to acquire the contrast enhancement kinetics in the tumor and healthy pancreatic regions. The mathematical model is then fit to the imaging data to obtain an estimate for the area under the curve for both tumor and healthy regions. Reproduced with permission from Koay et al. [67].

Conclusions

The challenges associated with early diagnosis and drug resistance in PDAC make it one of the most lethal cancer types. For improved pathophysiological understanding of the disease, development of novel biomarkers for early diagnosis, investigation of the effects of inter-individual and intra-tumoral-heterogeneity, a multidisciplinary approach involving basic research, imaging, and mathematical modeling holds the key to bring a significant change in the state of affairs. In this review, we highlight such interdisciplinary studies that have performed to model PDAC disease progression for testing therapy efficacy, develop biomarkers for early diagnosis, and investigate drug delivery challenges due to pathological conditions in the tumor It is essential to invest more efforts in the direction of personalized treatment through the application of quantitative tools to overcome the status quo in the clinical management of PDAC.