Cardiac substructure segmentation with deep learning for improved cardiac sparing

Abstract

Purpose

Radiation dose to cardiac substructures is related to radiation-induced heart disease. However, substructures are not considered in radiation therapy planning (RTP) due to poor visualization on CT. Therefore, we developed a novel deep learning (DL) pipeline leveraging MRI’s soft tissue contrast coupled with CT for state-of-the-art cardiac substructure segmentation requiring a single, non-contrast CT input.

Materials/methods

Thirty-two left-sided whole-breast cancer patients underwent cardiac T2 MRI and CT-simulation. A rigid cardiac-confined MR/CT registration enabled ground truth delineations of 12 substructures (chambers, great vessels (GVs), coronary arteries (CAs), etc.). Paired MRI/CT data (25 patients) were placed into separate image channels to train a three-dimensional (3D) neural network using the entire 3D image. Deep supervision and a Dice-weighted multi-class loss function were applied. Results were assessed pre/post augmentation and post-processing (3D conditional random field (CRF)). Results for 11 test CTs (seven unique patients) were compared to ground truth and a multi-atlas method (MA) via Dice similarity coefficient (DSC), mean distance to agreement (MDA), and Wilcoxon signed-ranks tests. Three physicians evaluated clinical acceptance via consensus scoring (5-point scale).

Results

The model stabilized in ~19 h (200 epochs, training error <0.001). Augmentation and CRF increased DSC 5.0 ± 7.9% and 1.2 ± 2.5%, across substructures, respectively. DL provided accurate segmentations for chambers (DSC = 0.88 ± 0.03), GVs (DSC = 0.85 ± 0.03), and pulmonary veins (DSC = 0.77 ± 0.04). Combined DSC for CAs was 0.50 ± 0.14. MDA across substructures was <2.0 mm (GV MDA = 1.24 ± 0.31 mm). No substructures had statistical volume differences (P > 0.05) to ground truth. In four cases, DL yielded left main CA contours, whereas MA segmentation failed, and provided improved consensus scores in 44/60 comparisons to MA. DL provided clinically acceptable segmentations for all graded patients for 3/4 chambers. DL contour generation took ~14 s per patient.

Conclusions

These promising results suggest DL poses major efficiency and accuracy gains for cardiac substructure segmentation offering high potential for rapid implementation into RTP for improved cardiac sparing.

1. INTRODUCTION

Increased risks of radiation-induced heart disease (RIHD) including acute (pericarditis) and late (congestive heart failure, coronary artery disease (CAD), and myocardial infarction) cardiotoxicities have been linked to dose from thoracic radiation therapy (RT) for lymphoma, lung, breast, and esophageal cancers.^1–4 RIHD presents earlier than previously expected, beginning only a few years after RT and with elevated risk persisting for ~20 yr.⁴ Importantly, dose escalation evaluation for locally advanced non-small cell lung cancer in RTOG 0617⁵ revealed that the volumes of the heart receiving ≥5 and ≥30 Gy were independent predictors of survival.⁵ Furthermore, heart dose/volume metrics are significantly associated with quality of life.⁶

At present, dosimetric evaluation is currently limited to simplified heart volume/dose relationships, such as those recommended by QUANTEC, where the heart is considered a single organ. It is currently recommended that <10% of the heart receive >25 Gy with the clinical endpoint of long-term cardiac mortality.⁷ Despite having whole-heart dose limits, evidence suggests that dose to sensitive cardiac substructures may lead to cardiac toxicities^4,8,9 including cardiomyopathy, CAD, as well as pericardial, and conduction system diseases.¹⁰ Specifically, an increased rate of cardiac events and ischemic diseases have been associated with increased radiation dose to the left ventricle,⁸ left atrium,⁹ and left anterior descending artery (LADA).¹¹ Patel et al. found that a maximum dose >10 Gy to the LADA was a significant threshold for increased odds of developing coronary artery calcification (CAC). When compared to mean heart dose, maximum dose to the LADA had a stronger association with CAC onset.¹² However, following these dosimetric thresholds is currently limited by the poor visualization and ability to delineate these sensitive cardiac substructures on non-contrast CT simulation (CT-SIM) scans.

Several studies have assessed atlas-based segmentation of cardiac substructures in rt^13–15 to avoid the time consuming (6–10 h/patient) and tedious task of manual delineation.¹⁶ However, most atlases fail in segmenting the coronary arteries, with Dice similarity coefficients (DSCs) between ground truth and auto-segmentation of the LADA ranging from 0.09 to 0.27.^13–15,17 Incorporating multiple imaging modalities (i.e., contrast enhanced CT and magnetic resonance imaging (MRI)) has improved visualization and yielded successful chamber and great vessel segmentation, yet coronary artery segmentation remains an unmet need.^13,14

Recently, deep neural networks (DNNs), such as U-Net,¹⁸ have shown great promise for generating accurate and rapid delineations for RT.¹⁹ Here, a DNN learns a mapping function between an image and a corresponding feature map (i.e., segmented ground truth). Payer et al. implemented a U-Net for substructure segmentation and obtained a DSC of 94% in the aorta as compared to ground truth.²⁰ Various DNNs have been applied to medical image segmentation,¹⁹ specifically for cardiac substructure segmentation. These include deep convolutional neural networks (CNNs) with adaptive fusion²¹ or multi-stage²⁰ strategies, as well as generative adversarial networks (GANs)²². Adaptation of these segmentation strategies has greatly improved cardiac chamber²⁰ and pulmonary artery²¹ segmentations on contrast-enhanced CTs (DSCs > 85%). Additionally, deep residual learning techniques are currently being used to generate cardiac substructure segmentation models that are robust against the presence or absence of image contrast.²³ However, most of these models have not been applied to conventional CT-SIM images and have yet to implement segmentations of the pulmonary veins (PVs) and coronary arteries.

The current work builds upon recent DNN results to develop an efficient and accurate cardiac substructure deep learning (DL) segmentation pipeline that can be implemented into routine practice on standard, non-contrast CT-SIMs, thus requiring no additional image acquisitions. Here, training is performed via labeled MRI/CT pairs inputted into a three-dimensional (3D) U-Net coupled to predict cardiac substructure segmentations using a single non-contrast CT-SIM input. We further improve agreement to ground truth delineations by introducing a 3D dense conditional random field (CRF) as a post-processing step, which has been recently merged with DNNs for state-of-the-art results in medical image segmentation.²⁴ Overall, the overarching goal is to enable widespread implementation of DL to improve cardiac sparing in RT planning (RTP) accomplished via cardiac sparing trials and improved risk assessment evaluation.

2. METHODS

2.A. Imaging and ground truth contour delineation

Thirty-two left-sided whole-breast cancer patients, with 36 unique datasets, were consented to an Institutional Review Board approved study and underwent cardiac MRI scans (two-dimensional T2 single-shot turbo spin echo sequence, TR = 927.9 ms, TE = 81 ms, voxel size = 0.7 × 0.7 × 8.0 mm³) at end-expiration (EE) on a 3T Philips Ingenia (Philips Medical Systems, Cleveland, OH). Imaging was completed in a single breath hold (acquisition time = 22.1 ± 4.4 s). Non-contrast CT-SIM images were acquired on a Brilliance Big Bore CT simulator (Philips Medical Systems, Cleveland, OH) (voxel size = 1.1 × 1.1 × 3. mm³−1.4 × 1.4 × 3.0 mm³, 120–140 kVp, and 275–434 mAs) with patients immobilized in the supine position on a Posiboard (Civco, The Netherlands). Twenty-four patients were imaged under free breathing conditions, while the other eight underwent four-dimensional CT (4DCT).

To develop a mutual coordinate system between datasets, an automatic global rigid registration between the T2 MR (moving image) and CT-SIM (target image) images was performed in MIM (version 6.9.1, MIM Software Inc., Cleveland, OH). An automated local rigid registration was then applied via a manually drawn cardiac-confined bounding box. For both rigid registrations, normalized mutual information was used as the similarity metric as it has been shown to perform well with multi-modality image registration tasks.²⁵ For patients who underwent 4DCT, the 50% phase was used as it most closely matched the EE MRI.

The evaluation and approval of the co-registration of the T2 MRI to the non-contrast CT were performed through visual verification by a radiation oncologist. To generate the contours, a consensus atlas was followed²⁶ as implemented in our previous work.¹³ In brief, 12 cardiac substructures (left/right ventricles (LV, RV) and atria (LA, RA), superior/inferior venae cavae (SVC, IVC), pulmonary artery/veins (PA, PV), ascending aorta (AA), right coronary artery (RCA), left main coronary artery (LMCA), and LADA) were manually delineated by a radiation oncologist and verified by a radiologist with a cardiac subspecialty. Due to the enhanced soft tissue contrast that MRI provides, preference was given to anatomical information from the MRI.

2.B. Data preparation

All work was performed using an NVIDIA Quadro M4000 graphical processing unit (NVIDIA, Santa Clara, CA). To improve generalizability, zero-mean normalization²⁷ (i.e., subtracting the mean intensity from the image and dividing by the standard deviation of the image) was performed to maintain intensity consistency across MRI/CT datasets and patients. To generate ground truth images, substructure masks were combined into a single image volume (ground truth (GT) image in Fig. 1) with intensity values for the 12 substructures indexed every 20 grayscale values from 35 to 255 with no overlap among substructures. MR and CT images were all resampled to a 650 × 650 mm in-plane resolution using bilinear interpolation. Bilinear interpolation was also used to interpolate MR images in the z-direction to match the 3 mm CT slice thickness (final voxel size of 1.27 × 1.27 × 3 mm³). Registered MR and CT image volumes were cropped to 64 slices (in-plane dimension of 128 × 128 pixels), centered on the centroid of the whole heart, and padded with 32 blank slices both superiorly and inferiorly for a final size of 128 × 128 × 128 pixels.

Fig. 1.

3D U-Net architecture with CT and MR inputs in different image channels, along with the ground truth (GT) labels. Prediction maps are outputted for each substructure. [Color figure can be viewed at wileyonlinelibrary.com]

2.C. Neural network architecture and training

The proposed 3D U-Net shown in Fig. 1 was based on an existing architecture designed for brain tumor auto-segmentation²⁸ with several customizations as follows: (a) including deep supervision, (b) training using the entire 3D image volume simultaneously with multi-channel data inputs (i.e., MRI, CT, and cardiac substructure ground truth masks), (c) optimizing hyperparameters of a Dice-weighted multi-class loss function,²⁸ (d) utilizing deconvolution in the upsampling process, and (e) optimizing the number of feature maps used in the first layer.

This 3D U-Net is composed of a contraction pathway (Fig. 1, left) to aggregate high level information using context modules and an expansion pathway (Fig. 1, right) to combine feature and spatial information for localization.²⁸ Context modules (Fig. 1, left) were composed of a dropout layer with 30% probability between two 3 × 3 × 3 convolutional layers. Deep supervision was implemented by adding segmentation layers at each step of the localization pathway (Fig. 1, right). Deep supervision allows for the injection of gradient signals deep into the network,²⁹ as it speeds up convergence and enhances training efficiency when there is a small amount of available labeled training data.^28,30 An elementwise summation with upsample was then applied across all added segmentation layers to generate the final segmentation. As coarse segmentation results may yield unrealistic results, skip connections were applied (i.e., concatenation) by fusing earlier layers in the network where the downsampling factor is smaller to recover the original spatial resolution.³¹ To rebuild high-resolution feature maps, deconvolution was used in the localization pathway in order to learn the upsampling.³²

To prevent model overfitting (i.e., ensuring the model remains generalizable to the hold-out dataset after being tuned to a training set), data augmentation¹⁸ including flipping, rotating (0–30°, 1° increments), scaling (±25%, 1% increments), and translating (10 pixels in the left-right, anterior-posterior, and superior-inferior directions) was applied. Originally proposed as a novel objective function based on DSC,³³ a Dice-weighted multi-class loss function was used^28,34 to manage the different image features among substructures, as shown in Eq. 1:

$${\mathcal{L}}_{DSC}=-\frac{2}{\left|B\right|}\sum _{b\in B}\frac{{\sum }_a{x}_{a,b}{y}_{a,b}}{{\sum }_a{x}_{a,b}+{\sum }_a{y}_{a,b}}$$ (1)

As label encoding is not sufficient for model training, y represents the ground truth segmentation map converted from categorical to binary variables (i.e., one-hot encoding). For training voxel a in class b, x_a,b and y_a,b represent the prediction and ground truth, respectively. As a larger DSC represents better overlap between ground truth and the prediction, the loss function is negative due to it being minimized during the training. Each value of correspondence between both the training and validation datasets to ground truth is represented by an average across all 12 substructures.

An adaptive momentum estimation (Adam) optimizer³⁵ was used along with randomly initialized weights. Patience (i.e., number of epochs to wait without validation loss improvement before reducing the learning) was also implemented during training. An epoch is defined as one forward pass and one backward pass (i.e., backpropagation process) of all the training samples.³⁶ Optimized hyperparameters included an initial learning rate of 5 × 10⁻⁴, 50% learning rate reduction, a batch size of 1, patience of 10 epochs, and 16 base filters in the first layer of the localization pathway.

Patient data were split into 25 patients for training data and 7 (11 unique datasets) patients for a hold-out dataset for network testing. No hold-out datasets used for testing were implemented in the network training. Training data were split via random assignment into 80% training and 20% validation data. Paired MRI and CT data were placed into separate image channels along with indexed ground truth labels for 25 patients to train the 3D U-Net using the entire 3D MR and CT images and all substructures simultaneously. Training was considered to be sufficiently converged when the training error between two adjacent epochs (i.e., one forward and backward pass of all the training samples) was <0.001.³⁶

All work was performed using Windows 10 operating system in Python version 3.6. The 64-bit Microsoft Windows system is equipped with a quad-core Intel® Xeon® CPU-E5–1630 v4 at 3.70 GHz and 16 GB of memory. The employed graphics processing unit was an NVIDIA Quadro M4000 with 8 GB of RAM and 1664 CUDA cores where Keras 2.0 was implemented with a Tensorflow backend.

2.D. Contour post-processing and optimization

Coarse output maps from the DL network containing holes and spurious predictions from neural networks are common.³⁷ Thus, contour post-processing was performed on the 3D U-Net output using a fully connected CRF³⁸ that imposes regularization constraints through minimizing an energy function.³⁹ A 3D-CRF model was developed based on an initial 2D implementation³⁹ and optimized to refine segmentations by smoothing, filling holes, and removing false positives, such as small remote regions.

3D-CRF was implemented on a GPU for improved computation and inference time. Inference here is with regard to the number of iterations applied to minimize the Kullback-Leibler (KL) divergence.³⁹ Both bilateral⁴⁰ (i.e., appearance kernel) and Gaussian³⁹ (i.e., smoothness kernel) pairwise energies were used to account for the grayscale intensity similarity as well as the spatial proximity of pixels. The applied kernel involves the sum of a smoothness and appearance kernel which are shown in the following equations³⁹:

$$\text{smoothness}\text{kernel}=k_s=\exp \left(-\frac{\left|P_{\alpha }-{P_{\beta }}^2\right|}{2{\theta }_x^2}\right).$$

$$\begin{gathered} \text{appearance}\text{kernel}=k_a \\ =\exp \left(-\frac{\left|P_{\alpha }-{P_{\beta }}^2\right|}{2{\theta }_x^2}-\frac{\left|Q_{\alpha }-{Q_{\beta }}^2\right|}{2{\theta }_y^2}\right). \end{gathered}$$

$$\text{applied}\text{kernel}=w_1*k_s+w_2*k_a$$

where P and Q represent intensity and position vectors at pixel (α, β). The smoothness kernel works to remove small remote regions⁴¹ and is controlled by scaling factor θ_x. Parameter θ_y is an additional scaling factor in the appearance kernel, which controls the degree of similarity in predicted pixels. The appearance and smoothness kernel are equally weighted with weights w₁ = w₂ = 1.

CRF hyperparameters θ_x and θ_y were optimized automatically⁴² for each substructure by stepping through different parameter values and then comparing the prediction result back to ground truth through DSC. Based on the range of utilized values found in the current literature,^39,43,44 full integer values (1–80) were stepped through for θ_x and in steps of 0.05 from 0–1 for θ_y, yielding 100 individual tests. Ten inference steps per substructure prediction were used.^39,42 Finally, predictions both with and without CRF post-processing were assessed by comparing agreement with ground truth and calculating the Hausdorff distance (HD, maximum nearest neighbor Euclidean distance⁴⁵).

Network testing on the hold-out dataset was conducted using the remaining 11 test patient CTs containing the heart and thorax from seven unique patients. Binary mask segmentations were converted to contours in Digital Imaging and Communications in Medicine (DICOM) format and imported into MIM.

2.E. Evaluations and statistical assessment

Quantitative evaluations between DL and ground truth segmentations were performed via DSC,⁴⁶ mean distance to agreement (MDA, average of the shortest distance between all voxels of the predicted and ground truth segmentations⁴⁷), and centroid displacement in three cardinal axes. DL segmentations were also compared to our previously published multi-atlas (MA) results, which implemented simultaneous truth and performance level estimation (STAPLE) with ten atlas matches¹³ using a shared cohort of 11 test subjects. Lastly, qualitative consensus scoring of DL segmentations was conducted to evaluate clinical utility. Before the qualitative grading was performed, three physicians (two radiation oncologists and a radiologist with a cardiac subspecialty) reviewed DL segmentations from a patient who was excluded from the grading. The physicians were instructed on the image grading system and a grading consensus scale was established for each substructure and then applied for five unique patients. Qualitative consensus scoring was completed on five of the test subjects as evaluated in our previously published atlas study.¹³ Scoring was completed using a 5-point scale^13,48 as follows: (a) not clinically acceptable, (b) clinically acceptable with major changes, (c) clinically acceptable with moderate changes, (d) clinically acceptable with minor changes, (e) clinically acceptable. Contours were converted to a 0.25 mm high resolution display for final evaluation in MIM.

For volume size similarity assessment, two-tailed Wilcoxon signed-ranks tests were performed between ground truth and auto-segmented DL segmentations, with P < 0.05 considered significantly different. Statistical assessments using two-tailed Wilcoxon signed-ranks tests were also used to compare DL segmentations to our previous MA method via DSC, MDA, and qualitative consensus scores.

3. RESULTS

3.A. Segmentation and post-processing time

The initial manual ground truth delineations of the 12 cardiac substructures required ~3 h per patient. The DL network stabilized in ~19.4 h after training the network for 200 epochs, including ~2 h after implementing data augmentation. Figure 2 shows the results for the training and validation datasets over the 200 epochs. The final training and validation DSC values were 83.1% and 81.5%, respectively (difference <2%), which represents an average over all 12 substructures.

Fig. 2.

3D U-Net training and validation results over 200 epochs. Values for mean Dice similarity coefficient (DSC) represent an average over all 12 substructures. [Color figure can be viewed at wileyonlinelibrary.com]

Augmentation led to an overall DSC increase of 5.0 ± 7.9% across all substructures, with greatest improvements in the coronary arteries (LMCA = 18.6 ± 15.5%, RCA = 8.7 ± 9.1%, LADA = 7.8 ± 7.1%). Substructure contour generation (12 substructures) for a new patient using a single non-contrast CT-SIM dataset input took 5.0 ± 0.6 s. CRF post-processing time from a single test patient using ten inference steps for 12 substructures was 9.3 ± 0.3 s, for a total DL generation time of 14.3 s (range: 13.5–15.6 s).

3.B. CRF post-processing

CRF hyperparameter optimization revealed that differing values of (θ_x,θ_y) provided maximal DSC when three different sets of optimized parameters were employed for (a) coronary arteries and PV (2.0, 0.40), (b) superior/inferior venae cavae (2.0, 0.50), and (c) chambers and great vessels (8.0, 0.55). CRF applications lead to an average improvement in DSC, MDA, and HD over all substructures of 1.2 ± 2.5%, 0.11 ± 0.31 mm, and 5.58 ± 14.25 mm, respectively. The LMCA had the greatest improvement in DSC (6.2 ± 6.6%, range: 1–22%) after CRF application, whereas the RV and RA saw the least improvement (0.3 ± 0.2%, range: 0.0–1.0%). The LV showed the greatest improvement in MDA (0.3 ± 0.5 mm, range: 0.0–1.2 mm) and HD (34.4 ± 23.0 mm, range: 0.1–64.7 mm) after 3D-CRF application. Lastly, after applying CRF, the mean improvement in MDA ranged from 0.04 to 0.21 mm over the 12 substructures.

3.C. Geometric performance of segmentation

DL segmentation results are presented in Table I.

Table I.

Improvement in automatic segmentation performance in Dice similarity coefficient (DSC) after augmentation and in Hausdorff distance (HD) after implementation of conditional random fields (CRF) post-processing.

	Segmentation Improvement
Substructures	Augmentation DSC	CRF HD (mm)	Final DSC	Final MDA (mm)
Chambers (LA, LV, RA, RV)	0.03 ± 0.03	10.23 ± 19.34	0.88 ± 0.03	1.53 ± 0.26
Great Vessels (SVC, PA, AA)	0.03 ± 0.05	3.59 ± 10.79	0.85 ± 0.03	1.24 ± 0.31
Inferior Vena CavaSS	0.00 ± 0.05	6.61 ± 15.23	0.78 ± 0.04	1.45 ± 0.45
Pulmonary Veins	0.05 ± 0.04	2.82 ± 4.41	0.77 ± 0.04	1.04 ± 0.21
Coronary Arteries
Left Anterior Descending Artery	0.08 ± 0.07	0.16 ± 0.27	0.53 ± 0.08	1.90 ± 0.90
Right Coronary Artery	0.09 ± 0.09	5.01 ± 15.86	0.50 ± 0.09	1.97 ± 0.46
Left Main Coronary Artery	0.19 ± 0.16	0.65 ± 0.96	0.50 ± 0.18	1.27 ± 0.68

The table also shows the final agreement to ground truth via DSC and mean distance to agreement (MDA). Additional abbreviations defined in the text.

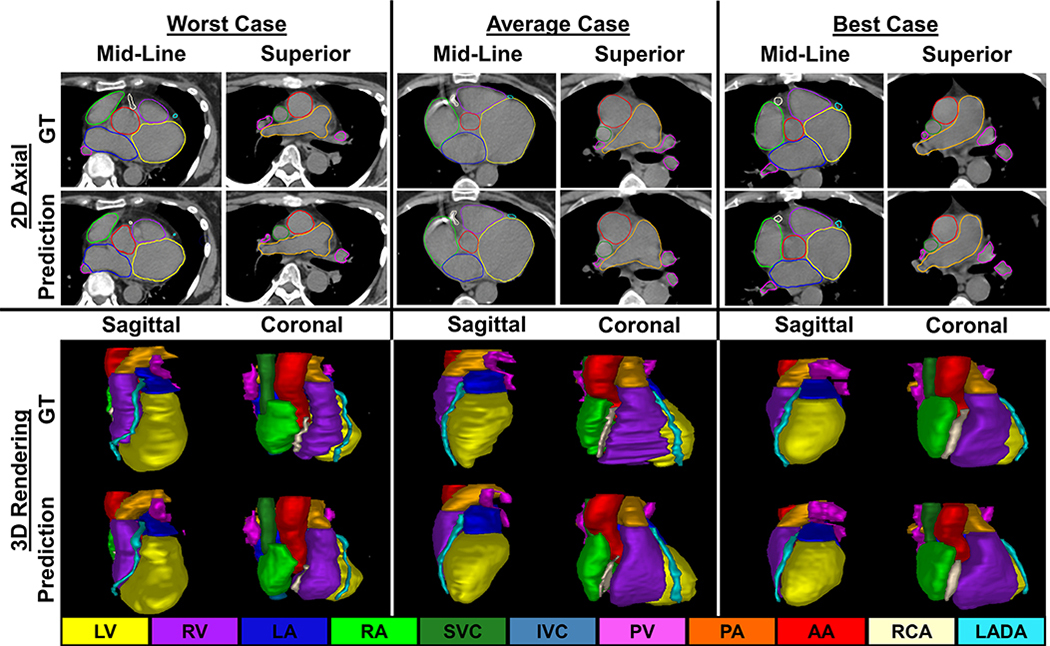
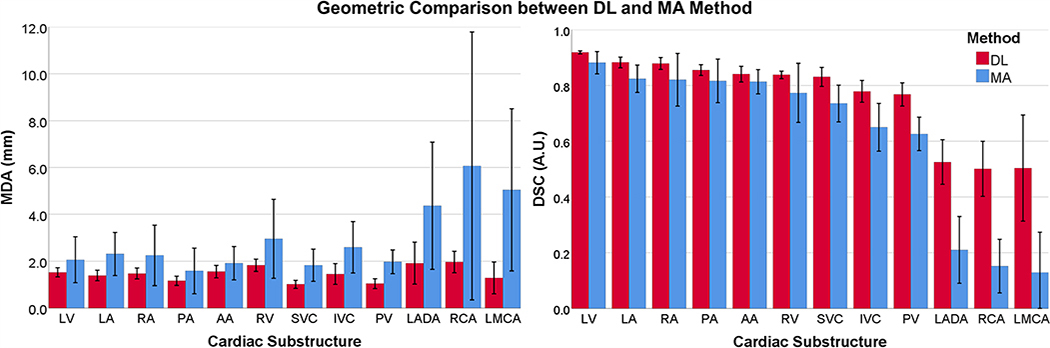
Figure 3 presents comparisons between ground truth and DL segmentations across substructures (LMCA not shown). The best case patient (Fig. 3, right) had chamber DSCs > 0.90 and MDAs < 2 mm for all substructures with favorable results for the RCA (DSC = 0.72, MDA = 1.67 mm). MDA (Fig. 5, left) across all 12 substructures was <2.0 mm (MDA = 1.46 ± 0.50 mm).

Fig. 3.

Comparisons between contours generated via deep learning and ground truth (GT) in 2D axial slices (top) and 3D renderings (bottom) for the worst (left), average (center), and best (right) cases. [Color figure can be viewed at wileyonlinelibrary.com]

Fig. 5.

Agreement between manually drawn ground truth and auto-segmentation methods (Blue: Previous multi-atlas method (MA), Red: Novel DL method) over 11 test cases. Left: Mean MDA, Right: Mean DSC. DSC, Dice similarity coefficient; MDA, mean distance to agreement. [Color figure can be viewed at wileyonlinelibrary.com]

Wilcoxon signed-ranks tests revealed no significant differences in cardiac substructure volumes between DL and ground truth (P > 0.05). Figure 4 summarizes the centroid shifts in all cardinal axes. On average, the smallest displacements (<2 mm) occurred in the anterior-posterior direction for 11 substructures. The largest displacements occurred in the superior-inferior direction.

Fig. 4.

Substructure centroid displacements in the left-right (left), anterior-posterior (center), and superior–inferior (right) directions. Legend: interquartile range = box, median = line, minimum and maximum = whiskers, circles and stars = 1.5 and 3 times the interquartile range, respectively. [Color figure can be viewed at wileyonlinelibrary.com]

3.D. DL vs. MA segmentation

Figure 5 summarizes MDA and DSC results over 11 test cases and compares DL with our previously developed MA method for the same cohort.¹³ MDA and DSC for all cardiac substructures improved with DL.

Specifically, DSC agreement to ground truth increased 3–7% for chambers, 9–11% for the superior/inferior venae cavae and PV, and reached 23–35% for the coronary arteries. On average, MDA improved by ~1.4 mm with DL, with greatest agreement in the SVC (MDA = 0.99 ± 0.15) and worst agreement in the RCA (MDA = 1.97 ± 0.46). For four test CTs, our DL method yielded LMCA contours, whereas our previous atlas-based model failed to produce any segmentation. Overall, DL provided a significant improvement (P < 0.05) over the previous MA method for every substructure in terms of MDA and DSC.

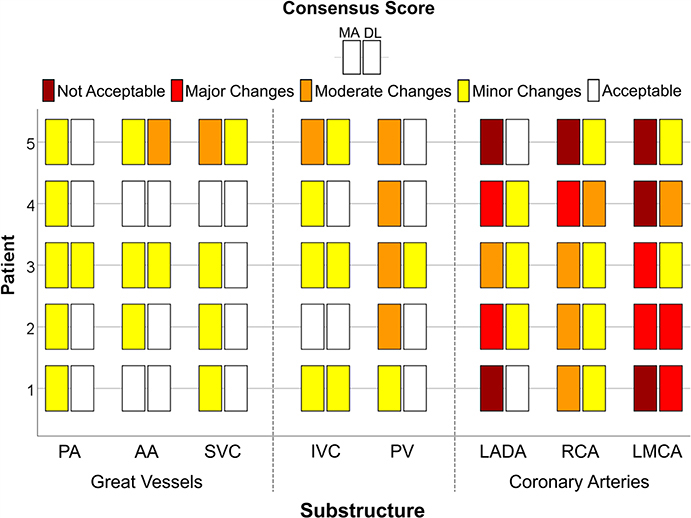
3.E. Qualitative analysis

Physician consensus scores are summarized in Fig. 6. All patients had clinically acceptable contours (score of 5) for the LV, RA, and RV (results not shown), while the SVC, PA, and PV had clinically acceptable contours for 4/5 patients with DL. For the cardiac chambers, 6/20 comparisons between DL and MA methods were equivalent, while all others improved by at least one grade with DL. The LMCA and RCA had the lowest average scores of 3.0 ± 1.0 and 3.8 ± 0.4, respectively, with all other substructures scoring an average of ≥4.4. DL provided significant improvements (P < 0.05) over the MA method for the LADA, RCA, PV, PA, SVC, LA, RA, and RV. Improvements in 44/60 (5 patients, 12 substructures) qualitative scores were observed with DL. For only one instance, DL scored worse than MA (AA: grade 4 to 3). For two LADA segmentations, MA yielded a grade of 1 (clinically unusable) and improved to a 5 (clinically acceptable) with DL (Fig. 6, right).

Fig. 6.

Qualitative consensus scoring (not clinically acceptable, clinically acceptable with major, moderate, and minor changes, and clinically acceptable) of five patients for the multi-atlas (MA) and deep learning (DL) auto-segmentations (chambers not shown). For each substructure, the MA and DL methods are shown on the left and right, respectively. [Color figure can be viewed at wileyonlinelibrary.com]

4. DISCUSSION

This work presented a novel DL pipeline to segment sensitive cardiac substructures using a 3D U-Net with the principal goal of applying to non-contrast CT-SIM for RT planning. Data augmentation and CRF post-processing improved DL contour agreement with ground truth. Overall, our method provided accurate segmentations of the chambers, great vessels, and PVs, and led to promising results in coronary artery segmentation on non-contrast CT-SIM datasets.

While cardiac substructure segmentation has been explored previously, to our knowledge, none have included paired MR/CT multi-channel data inputs to yield robust segmentations on non-contrast CT inputs. Several atlas segmentation methods have been recently published^13–15 and report cardiac chamber DSCs > 0.75. However, these methods have had limited success segmenting coronary arteries as atlas methods rely on image registration quality and are unable to consider large amounts of patient data due to computational demands.⁴⁹ Our work parallels recent applications of DNNs where CT coronary angiography (CTCA) scans specifically optimized for cardiac imaging were utilized. Here, DSC in the RA (87.8%)²⁰ and PA (85.1%)²¹ were within 1% of our DL method, while we were within 5% of their chamber segmentation results. Our work adds to the current literature by including additional substructures and allowing for predictions to be made on non-contrast CT-SIM scans.

Data augmentation improved DL segmentation accuracy by ~5% across all substructures. Although no comparison values exist in the literature for cardiac substructure segmentation, this value is consistent with studies performed on liver lesion segmentation.^50,51 One extreme outlier (>3 times the interquartile range) observed for the RV in the left-right axis occurred for the worst-case patient (Fig. 4, left), where the heart was rotated clockwise and shifted posteriorly/left. While this patient’s anatomy was an anomaly, this result may be addressed in the future by further augmenting the data (i.e., rotation >30°). Furthermore, both the LADA and RCA had larger centroid shifts in the superior–inferior plane (Fig. 4, right). This can be further visualized in Fig. 3 (left), where the inferior extent of the LADA and RCA were underrepresented with some narrowing of these substructures observed in the midline axial slice. To address this, recent atlas-based methods have standardized the size of the LADA to 4 mm throughout its entire length.¹⁷ Nevertheless, our DL pipeline performed well for coronary artery contours on non-contrast CTs (DSC ~ 0.50, MDA < 2.0 mm), particularly as compared to recent atlas results where coronary artery (LADA, RCA, and LMCA) DSCs ranged from 0.09 to 0.27^13–15 and had MDAs > 4 mm.¹⁴ Coronary artery segmentations may be improved through the use of high resolution (0.78 × 0.78 × 1.6 mm³) CTCA²¹ that use contrast and yield DSCs ~ 60%.⁵² Additionally, implementing a Dice loss function weighted on the inverse of the class size may improve the results for smaller substructures such as the coronary arteries. Originally proposed by Crum et al.,⁵³ the generalized Dice loss (GDL) function has been shown to improve hyperparameter robustness for unbalanced tasks (i.e., when each class is not represented equally in the dataset), and improve overall segmentation accuracy for small structures.⁵⁴

While rare cases involved the removal of spurious remote predictions that resided within the ground truth delineation, 3D-CRF led to an overall improvement in segmentation agreement. The coronary arteries experienced the greatest improvement from CRF post-processing, with the LCMA improving ~6% in DSC. Additionally, there were improvements in MDA up to 1.21 mm and 1.96 mm for the LV and LA, respectively. Aside from removing spurious outlying points, CRFs also improved the smoothed appearance of the segmentations as needed for clinical application.⁵⁵ CRF tuning required different parameters for cardiac substructures based on size and shape, much like the work completed by Rajchl et al.⁵⁶ The improvement in segmentation agreement observed, along with the use of a 3D-CRF to remove spurious isolated regions, parallels other emerging uses of 3D-CRF post-processing in medical imaging.^57,58 Although this study implemented CRFs as a post-processing step, some current studies have integrated CRFs into the utilized neural network and have seen improved segmentation performance^42,43,59 and can be explored in future work for possible coronary artery segmentation improvement.

The overall time to generate DL segmentations on preprocessed CT-SIM data was rapid: 14 s for all 12 substructures. This value can be compared to Mortazi et al. who segmented seven cardiac substructures in ~50 s on high resolution CTCA and 17 s on MRI.²¹ Moreover, our previous MA method required ~10 min to generate substructure contours per patient without post-processing.¹³

Although the in-plane resolution was 0.7 × 0.7 mm², our study may have been limited by the 8 mm slice thickness of the MRI. Despite our data augmentation techniques, increasing the training sample size may further improve segmentation results. However, similar training and testing cohort sizes with augmentation have been used previously.⁶⁰ While paired cardiac MRI/CT data are commonly limited for cancer patients, the training cohort may be expanded in the future by applying our DL model to generate additional ground truth segmentations. Data quantity may also be increased through utilizing unlabeled images for unsupervised learning via generative models such as a cycle⁶¹ or a stacked⁶² GAN, which implement multiple GANs for data synthesis. Recently, Zhang et al.²² proposed a novel cardiac chamber segmentation method using a GAN integrating cycle and shape consistency. They obtained DSCs comparable to atlas segmentations (DSC ~ 0.75) on CT and MRI by using ~14% real data and augmenting their dataset by incorporating synthetic MRI and CT data into training. Our model may be enhanced similarly by incorporating synthetic images in the network training, while also providing additional substructures, such as pulmonary veins and coronary arteries. Nevertheless, even with the current limited training dataset, our results outperform other currently available approaches. As shown in Fig. 2, training and validation results increased to a point of stability with a difference of <2% after convergence. Moreover, to further limit potential overfitting in this more limited cohort, data augmentation (i.e., flipping, scaling, rotating, and translating) and model regularization (dropout = 0.3) were implemented. Even though the presented dataset was limited in size, overfitting was not an issue in this work.

As both the CT and MR images were acquired in breath hold conditions, respiratory motion is assumed to be negligible during this study. However, due to extended scan times, one limitation of this study is that numerous cardiac cycles are captured during imaging. Thus, the substructures are represented by their average intensity over the course of the scan and cardiac motion is not taken into consideration. Currently, cardiac motion is not managed clinically due to limitations in available treatment technologies. Nevertheless, the magnitude of cardiac motion is on the order of 3–8 mm⁶³ suggesting internal motion may be incorporated into future margin design as has been previously proposed.^64,65

As MR-guided RT and MR-only planning become more prevalent, future work will include training an MR-only model. It has been recently recommended that the LADA be included as an avoidance structure in RTP;¹² thus, a natural clinical endpoint of this work includes dosimetric analysis and implementing cardiac avoidance strategies via accurate and efficient cardiac substructure segmentation made possible by DL.

5. CONCLUSIONS

These promising results suggest that our novel DL application offers major efficiency and accuracy gains for cardiac substructure segmentation over previously published MA results, using only non-contrast CT inputs. Future work involves further refinement of coronary artery segmentation using conditional random fields as a recurrent neural network and through expanding the patient cohort. Coupled with robust margin design, improved cardiac sparing in treatment planning can be realized.