Highlights
-
•
COVID-19 remains a major pandemic currently facing all the countries of the world, Nigeria inclusive.
-
•
We build some statistical model to the available data.
-
•
We choose the best model to make some forecast.
Keywords: COVID-19, Curve Estimation Statistical Models, Quartic Linear Regression Model, Estimators, Forecast Values
Abstract
COVID-19 remains a major pandemic currently threatening all the countries of the world. In Nigeria, there were 1, 932 COVID-19 confirmed cases, 319 discharged cases and 58 deaths as of 30th April 2020. This paper, therefore, subjected the daily cumulative reported COVID-19 cases of these three variables to nine (9) curve estimation statistical models in simple, quadratic, cubic, and quartic forms. It further identified the best of the thirty-six (36) models and used the same for prediction and forecasting purposes. The data collected by the Nigeria Centre for Disease Control for sixty-four (64) days, two (2) months and three (3), were daily monitored and eventually analyzed. We identified the best models to be Quartic Linear Regression Model with an autocorrelated error of order 1 (AR(1)); and found the Ordinary Least Squares, Cochrane Orcutt, Hildreth–Lu, and Prais-Winsten and Least Absolute Deviation (LAD) estimators useful to estimate the models’ parameters. Consequently, we recommended the daily cumulative forecast values of the LAD estimator for May and June 2020 with a 99% confidence level. The forecast values are alarming, and so, the Nigerian Government needs to hastily review her activities and interventions towards COVID-19 to provide some tactical and robust structures and measures to avert these challenges.
1. Introduction
Coronavirus Diseases (COVID-19), a respiratory disease characterized by fever, dry cough, and fatigue, and occasional gastrointestinal symptoms, had its initial outbreak in Wuhan city, Hubei, China in late December 2019 [2,9,11,13,21]. Within a month, the disease has escalated in China and further spread to other countries including Thailand, Japan, Republic of Korea, Vietnam, Germany, United States, and Singapore [15,28,31]. On the 30th January 2020, the WHO publicly declared COVID-19 as a disease of international concern [32] and later on 11th March 2020 reported it as a pandemic based on its alarming levels of spread and severity over the world [6].
According to the World Health Organization (WHO) COVID-19 situation report of 29th April 2020, there were 3,018,052 confirmed cases and 207,973 deaths globally. The disease has spread to at least fifteen (15) countries in the Western Pacific Region with 146,720 confirmed cases and 6,037 deaths; fifty-three (53) nations in the European Region with 1,406,899 confirmed cases and 129,311 deaths; ten (10) countries in the South-East Asia Region with 51,351 confirmed cases and 2,001 deaths; twenty-one (21) countries in Eastern Mediterranean Region with 176,928 confirmed cases and 7,304 deaths; thirty-five (35) counties in Region of the Americas with 1,213,088 confirmed cases and 62,404 deaths; and forty-five (45) countries in African Region with 23,254 confirmed cases and 903 deaths of which Nigeria had 1,337 confirmed cases and 40 deaths [29]. Actually, this was the Nigerian situation report of 27th April 2020 [22,30].
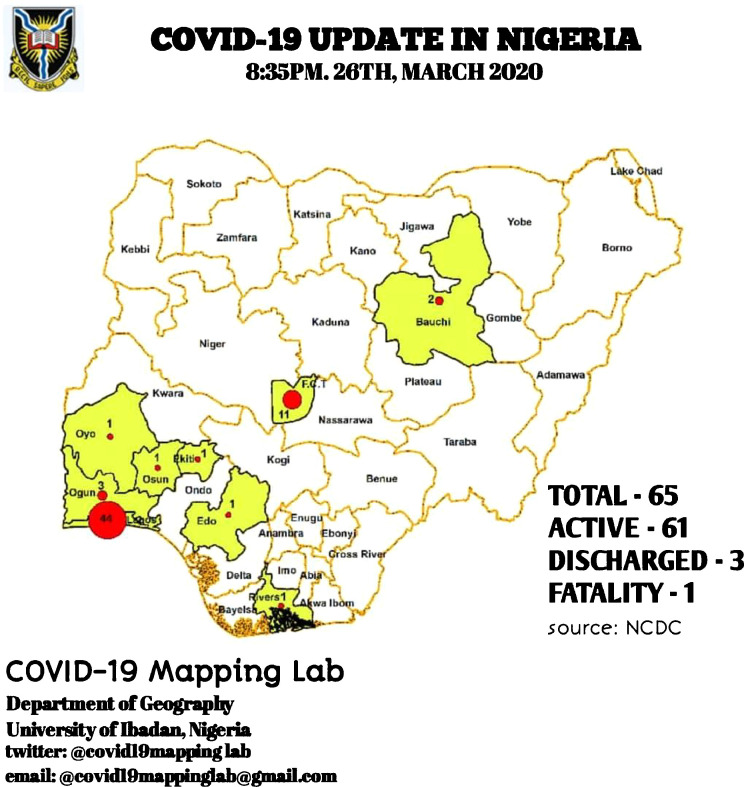
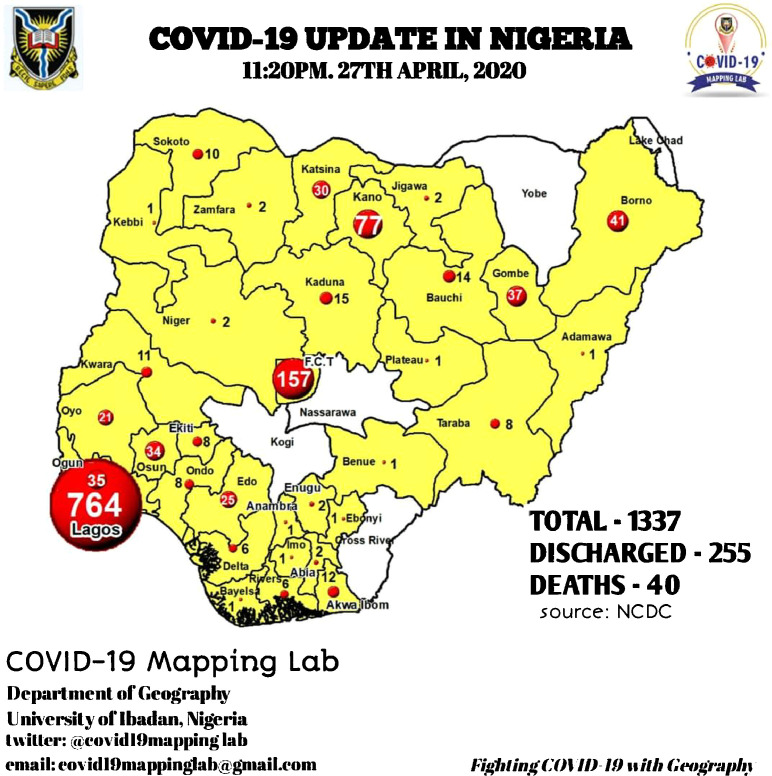
The first COVID-19 confirmed case in Nigeria was reported on 27th February 2020, when an Italian citizen in Lagos tested positive for the virus [22,23]. The second case was recorded on the 9th March 2020 in Ewekoro, Ogun State, a Nigerian citizen who had contact with the Italian citizen [30]. Within the first month, the confirmed cases were around 70 but drastically increased to number almost 1,350 cases before the end of the second month. The discharged cases increased from 3 to about 250 in the first two months. The number of recorded deaths increased from 1 to 40. Fig. 1, Fig. 2 presented the situation over the states of the country between the first and second months of occurrence.
Fig. 1.
Nigerian COVID-19 cases after one month of occurrences.
Fig. 2.
Nigerian COVID -19 cases after two months of occurrences.
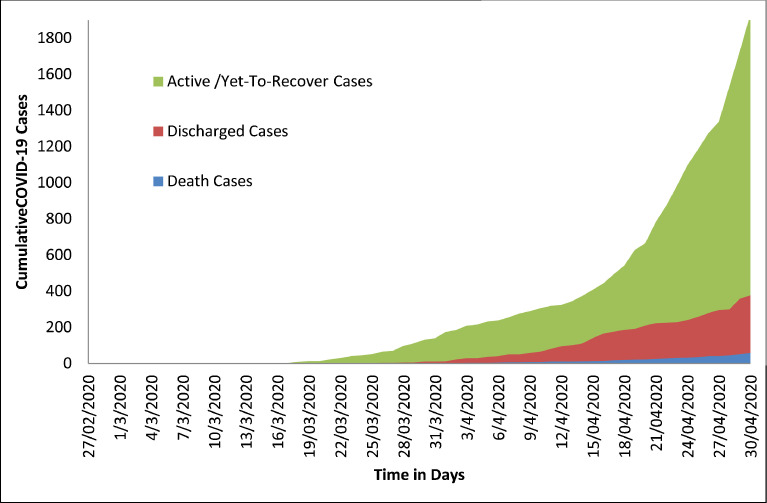
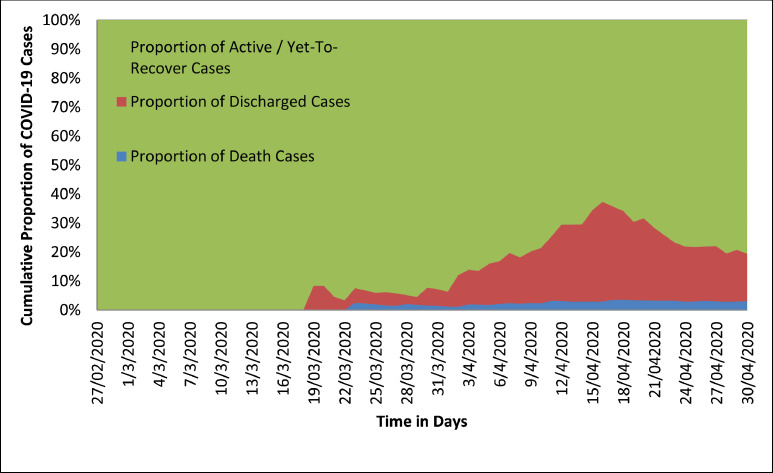
From Figs. 1 and 2, it is not only evident that CIVID-19 cases had increased, but had also spread significantly from eight (8) states to thirty-three (33) (including FCT, Abuja). There were only four states that had no confirmed cases; namely Yobe, Nasarawa, Kogi and Cross River States. At present, only Nasarawa and Yobe States have no record of COVID-19 while Lagos State, Kano State and FCT remained topmost in Nigeria. Fig. 3 presented the cumulative COVID-19 confirmed cases, discharged cases, death cases and yet-to-recover (active) cases. In contrast, Fig. 4 showed the proportion of death cases, the discharged cases and yet-to-recover cases over the cumulative COVID-19 confirmed cases for the periods of the data collection.
Fig. 3.
Nigerian COVID 19 Reported Cases in the First Sixty Four Days.
Fig. 4.
Proportions of Nigerian Cumulative COVID 19 Cases in First Sixty Four Days.
The seriousness of this pandemic becomes evident from Figs. 3 and 4. We observed that there was no day within the periods of the data collection that percentage of active / yet-to recover cases is less than 62. Meanwhile, the World Health Organization has listed Nigeria to be among thirteen (13) other African countries with high-risk for the spread of the virus [14].
Apart from the first measure of the Federal Government of Nigeria (FGN) to strengthen surveillance at Enugu, Lagos, Rivers, Kano and FCT International Airports on the 28th January 2020. The FGN on 31st January 2020, set up a group known as Coronavirus Preparedness Group to militate against its should incase it spread to Nigeria [30]. Other measures taken by FGN and various State Governments include the establishment of Presidential Task Force, suspension of all activities and religious gatherings, indefinite closure of public and private schools/institutions, extension of the travel ban to some countries, suspension of the operation of Nigerian Railway Corporation, closing of borders, shops, markets, motor parks, offices, restriction of intra-states and inter-states movements and travelling of the country. However, few states have recently relaxed the lockdown due to difficulties encountered by their citizens [30].
At the beginning of this pandemic, the unavailability of data has made forecasting and predictions a complicated task. A search for numerical models to forecast the epidemic evolution is underway [1,15]. Recent works provided forecasting models for confirmed COVID-19 cases for Germany, Italy, Japan, Canada, Russia, UK, Turkey and France [9,33]. Consequently, this paper attempts to model the daily cumulative reported COVID-19 confirmed cases, discharged cases and death cases using nine (9) statistical models to identify and utilize the best one for prediction.
2. Methodology
NCDC has been monitoring and reporting the cumulative and the new number of confirmed cases, number of discharged cases and recorded death since the first occurrence of COVID-19 in Nigeria. These data were collected daily on NCDC site [22] over a period over sixty-four days (2 months and three days) beginning from 27th February 2020 (first day of occurrence) until 30th April2020. The first discharged case occurred on the 19th March 2020 while the first death case occurred on 23rd March 2020. With the cumulative nature of the data, the number of cases at a time t depends on previous time t-1. We proposed the following curve estimation models with an autoregressive model of order 1 (AR(1)) in their simple, quadratic, cubic and quartic forms to study the pattern of the data so as to use the best one to forecast for the next two months, May and June 2020.
These Statistical Linear Regression Models are:
-
1Classical Linear Regression Model: In the Simple Linear form, the model is defined as:
(1)
The Quadratic Linear Regression Model is defined as:
| (2) |
The Cubic Linear Regression Model: The model is defined as:
| (3) |
The Quartic Linear Regression Model: The model is defined as:
| (4) |
-
2Logarithm Linear Regression Model: In the Simple form, the model is defined as:
(5)
The Logarithm Quadratic Linear Regression Model is defined as:
| (6) |
The Logarithm Cubic Linear Regression Model is defined as:
| (7) |
The Logarithm Quartic Linear Regression Model is defined as:
| (8) |
-
3Inverse Linear Regression Model: The Simple form of the model is defined as:
(9)
Similarly, the Quadratic, Cubic and Quartic forms are respectively defined as:
| (10) |
| (11) |
| (12) |
-
4Power Linear Regression Model: The Simple form of the model is defined as:
(13)
Similarly, the Quadratic, Cubic and Quartic forms are respectively defined as:
| (14) |
| (15) |
| (16) |
-
5Compound Linear Regression Model: In the Simple form, the model is defined as:
(17)
In the same way, the Quadratic, Cubic and Quartic forms are respectively defined as:
| (18) |
| (19) |
| (20) |
-
6S– Curve Linear Regression Model: The simple form of the model is defined as:
(21)
In the same way, the Quadratic, Cubic and Quartic forms are respectively defined as:
| (22) |
| (23) |
| (24) |
-
7Growth Linear Regression Model: The Simple form of the model is defined as:
(25)
Similarly, the Quadratic, Cubic, and Quartic forms are respectively defined as:
| (26) |
| (27) |
| (28) |
-
8Exponential Linear Regression Model: The simple form of the model is defined as:
(29)
In the same way, the forms of Quadratic, Cubic and Quartic are respectively defined as:
| (30) |
| (31) |
| (32) |
-
9Logistic Linear Regression Model: The Simple form of the model is defined as:
(33)
Similarly, the forms of Quadratic, Cubic and Quartic are respectively defined as:
| (34) |
| (35) |
| (36) |
where u is the upper boundary value, which must be a positive number greater than the largest value of y, the dependent variable.
It should be noted that model (5) to (36) are intrinsically linear regression model in that they are all linear in parameters; and that in all the models, the error terms
Also, the three variables: Cumulative COVID-19 Confirmed Cases (CCCOC), Cumulative COVID-19 Discharged Cases (CCDIC), and Cumulative COVID-19 Death Cases (CCDEC) were each considered as dependent variable in this study. The independent variable is time, t, and it takes values 1,2,…,64 for CCCOC; 1, 2,…,43 for CCDIC; and 1,2,…,39 for CCDEC. The model regression parameters are; β 0,β 1,β 2,β 3,β 4, and the auto-correlated parameter, ρ. The Ordinary Least Square (OLS) Estimator is the most common estimator to estimate the parameters of the Classical Linear Regression Model. The estimator is best linear unbiased estimator (BLUE) provided none of the assumptions of the model is violated [5,18,20]. In model (1) to (36), the assumption of independent error terms is not satisfied, leading to the problem of autocorrelated error terms. Using the OLS estimator in this kind of situation produces unbiased but inefficient estimates [3,4]. Researchers had developed estimators to handle linear regression Model with AR(1). These include the Cochrane Orcutt (CORC) estimator developed by Cochrane and Orcutt [7], Prais-Winsten (PW) developed by Prais and Winsten [25], and Hildreth-LU (HILU) estimator developed by Hildreth and Lu [12]. Reports show that the efficiency of these estimators depends on the structure of the explanatory variables [3,16]. Durbin [8] developed the Durbin Watson test statistic to test for the presence of AR(1) in a regression model after OLS estimation. Also in modeling (1) to (36), it is expected that the error terms are normally distributed. This may not always be true and as a result, hypothesis testing is affected. Saphiro-Wilk (SW) test developed by Shapiro and Wilk [26] and recently recommended by Kuranga et al. [17] is often being used to test for the assumption of normality of error terms; and the Least Absolute Deviation (LAD) estimator, a robust estimation method originated by KF Gauss and PS Laplace as mentioned by Taylor [27], is often recommended for handling parameter estimation of models with non-normal error terms or outliers [19,24]. These test statistics and estimators were also found useful in this study. Consequently in this study, we adopted these five (5) estimators and utilized proportion of variation explained by each estimator through their Adjusted coefficient of determination (Adj. R2) as a major criterion for a model to be used prediction and forecast purpose. For each of the four (4) forms in a particular model, a form was preferred if it has the highest Adj. R2 among the four (4) forms; and most preferred if it has the highest Adj. R2 among the preferred forms and hence called the best model. An estimator was considered best, among the estimators considered, if it gives highest Adj. R2 when applied to the best model. The best one and the competing ones were employed to produce forecast values. We adopted the [10], to achieve all these in this study.
3. Results and discussion
Results obtained from the analysis carried out on COVID-19 confirmed cases, discharged cases and death cases are presented as follows:
3.1. COVID-19 Confirmed Cases
We presented the form of the model that gave the highest value of adjusted coefficient of determination in Table 1 with some other relevant results.
Table 1.
Preferred form of the Nine Curve Estimation models with OLS estimator: COVID-19 Confirmed Cases.
| Models | Form | Adj. R2 | DW-test |
SW-test |
||
|---|---|---|---|---|---|---|
| Value | P-value | Value | P-value | |||
| Linear | Quartic | 0.9949 | 0.3204 | 4.783e-013*** | 0.9695 | 0.1137 |
| Logarithm | Simple+ | 0.3448 | 0.0312 | 1.798e-018*** | 0.7721 | 1.37e-008*** |
| Inverse | Quartic | 0.4137 | 0.112 | 1.798e-018*** | 0.8302 | 4.32e-007*** |
| Power | Simple+ | 0.7876 | 0.0848 | 1.798e-018*** | 0.9156 | 0.0003*** |
| Compound | Quartic | 0.9891 | 0.3768 | 5.459e-013*** | 0.9087 | 0.0002*** |
| S-Curve | Quartic | 0.9318 | 0.526 | 1.798e-010*** | 0.9271 | 0.001*** |
| Growth | Quartic | 0.9891 | 0.3768 | 5.459e-013*** | 0.9087 | 0.0002*** |
| Exponential | Quartic | 0.9891 | 0.3768 | 5.459e-013*** | 0.9087 | 0.0002*** |
| Logistic (u=2000) | Quartic | 0.9901 | 0.5327 | 1.798e-010*** | 0.9097 | 0.0002*** |
NOTE: (i) Bold implies most preferred of the nine models.
(ii) + implies exact multicollinearity made other forms of the variable to be omitted.
(iii) The maximum COVID-19 confirmed cases for the period of study was1932.
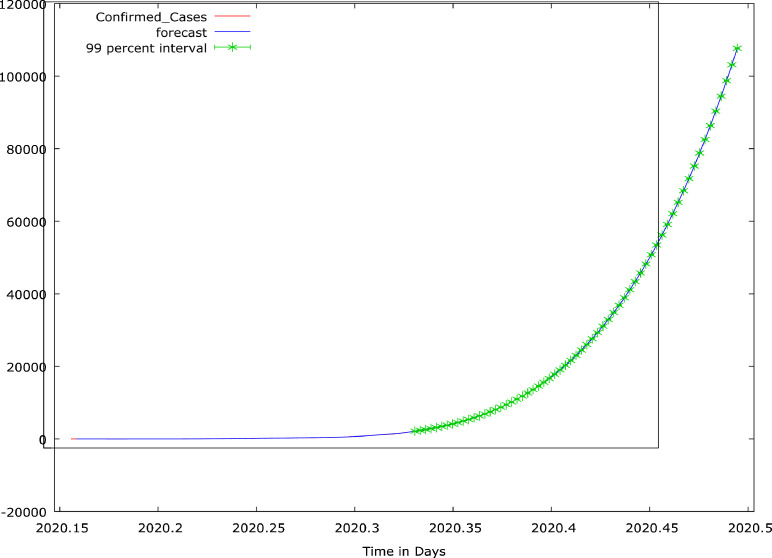
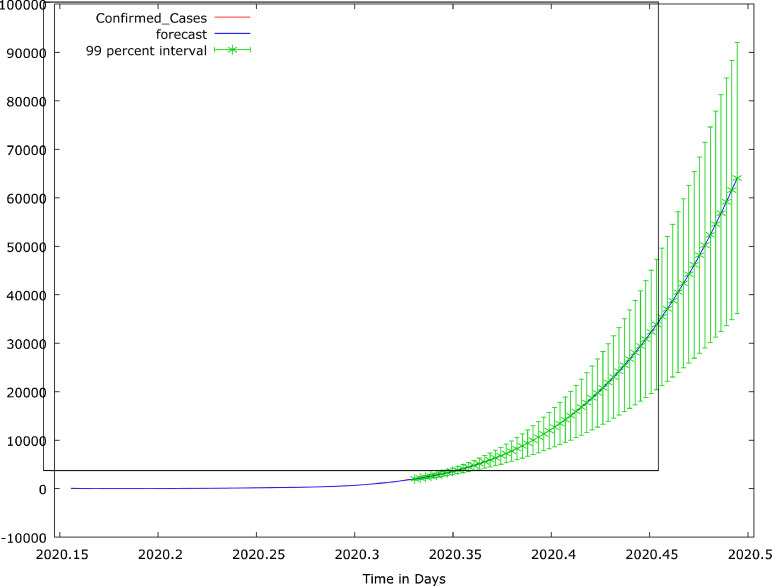
From Table 1, we preferred the quartic form for all the models except under Logarithm and Inverse model. At these exceptions, the simple form is most preferred. However, they were removed by the software due to exact multicollinearity that exists among the independent variables. Also, the Durbin-Watson statistic shows that the models possess autocorrelation problems; and that the residuals are non-normal except in linear model. Thus, the quartic form linear regression model is identified as the most preferred model and hence classified as the best model. The parameter estimation of the most preferred model using OLS estimator is available in Table 2 . Result reveals that the data set has an autocorrelation problem (P-value of DW Statistic <0.01); and this was addressed using CORC, HILU, and PW estimators. All these estimators indicated that time factors have a significant contribution to the COVID-19 confirmed cases reported. However, their residuals were not normally distributed (P-value of Shapiro-Wilk <0.001); and this eventually brought in the idea of using the LAD estimator as an alternative estimator. Of all these estimators, the HILU estimator is best. We used HILU and LAD estimator for forecasting. The forecast values for May and June 2020 for the two (2) estimators are provided in Appendix A and pictorially presented in Fig. 5, Fig. 6. From the appendix and Figs. 5 and 6, it is expected that the increase in the next two (2) months shall be alarming; increase from 1,932 cases to 107,678 cases by the HILU estimator and from 1,932 cases to 64,070 cases by the LAD estimator. Therefore, there are needs for a tactical and robust approach for COVID-19 confirmed case number not to get out of control.
Table 2.
Results of the most preferred model with the estimators: COVID-19 Confirmed Cases.
| Estimator | Estimation Methods |
|||||
|---|---|---|---|---|---|---|
| OLS | CORC | HILU | PW | LAD | ||
| Estimate | 82.7245 | 973.484 | 2202.75 | 26.5725 | 86.4171 | |
| Std. Error | 22.9895 | 282.385 | 657.795 | 44.5336 | 53.7316 | |
| T-value | 3.598 | 3.447 | 3.349 | 0.5967 | 1.608 | |
| P-value | 0.0007*** | 0.0011*** | 0.0014*** | 0.553 | 0.1131 | |
| Estimate | -29.3698 | -137.069 | -236.525 | -21.3927 | -26.1172 | |
| Std. Error | 4.8198 | 34.8878 | 65.3742 | 8.8188 | 11.6074 | |
| T-value | -6.094 | -3.929 | -3.618 | -2.426 | -2.250 | |
| P-value | 9.04e-08*** | 0.0002*** | 0.0006*** | 0.0184** | 0.0282** | |
| Estimate | 2.4042 | 7.09748 | 10.2454 | 2.1892 | 2.0848 | |
| Std. Error | 0.29825 | 1.53021 | 2.4873 | 0.5831 | 0.7606 | |
| T-value | 8.061 | 4.638 | 4.119 | 3.754 | 2.741 | |
| P-value | 4.3e-011*** | 2.1e-05*** | 0.0001*** | 0.0004*** | 0.0081*** | |
| Estimate | -0.0673 | -0.1533 | -0.1984 | -0.0676 | -0.0587 | |
| Std. Error | 0.0069 | 0.028 | 0.0414 | 0.0137 | 0.0185 | |
| T-value | -9.791 | -5.483 | -4.791 | -4.926 | -3.166 | |
| P-value | 5.6e-014*** | 9.5e-07*** | 1.2e-05*** | 7.1e-06*** | 0.0024 | |
| Estimate | 0.0007 | 0.001243 | 0.0015 | 0.0007 | 0.0006 | |
| Std. Error | 5.2438e-05 | 0.0002 | 0.0003 | 0.0001 | 0.0001 | |
| T-value | 13.00 | 6.885 | 5.920 | 6.861 | 4.103 | |
| P-value | 5.7e-019*** | 4.6e-09*** | 1.8e-07*** | 4.7e-09*** | 0.0001*** | |
| 0.889991 | 0.896892 | |||||
| Adj. R2 | 0.995909 | 0.994873 | 0.998779 | 0.998562 | 0.994562 | |
| DW | Stat-value | 0.3204 | 1.7542 | 1.8352 | 1.5832 | 0.3035 |
| P-value | 4.8e-013*** | |||||
| SW | Stat-value | 0.9695 | 0.8667 | 0.8484 | 0.9010 | |
| P-value | 0.113699 | 6.3e-006*** | 1.7e-006*** | 8.7e-005*** | ||
Note: (i)** and *** imply significance at alpha = 0.05 and 0.01 respectively.
Fig. 5.
COVID-19 Confirmed Cases for First Sixty Four Days and its forecast values for May and June, 2020: HILU Estimator.
Source:Appendix A
Fig. 6.
COVID-19 Confirmed Cases for First Sixty Four Days and its forecast values for May and June, 2020: LAD Estimator.
Source:Appendix A
3.2. COVID-19 Discharged Cases
By the adjusted coefficient of determinations (Adj.R2) presented in Table 3 , we generally preferred the Quartic form of the models except in Logarithm and Power model. At these instances, the simple form is most preferred. The most preferred model is the Linear Regression Model even though those of Compound, Growth and Exponential compete favourably. Furthermore, we observed that all the models have an auto-regressive error of order one (P-value of DW<0.01) and that the residuals of the models, except Linear and Inverse, are not normally distributed (SW P-value<0.1).
Table 3.
Results of Preferred Model with OLS estimator in each of the Nine Curve Estimation models: COVID-19 Discharged Cases.
| Models | Form | Adj.R2 | DW-test |
SW-test |
||
|---|---|---|---|---|---|---|
| Value | P-value | Value | P-value | |||
| Linear | Quartic | 0.9925 | 0.6965 | 4.69e-009 *** | 0.9724 | 0.3819 |
| Logarithm | Simple+ | 0.5613 | 0.0656 | 7.029e-01*** | 0.8965 | 0.001*** |
| Inverse | Quartic | 0.7682 | 0.3143 | 1.798e-010*** | 0.9733 | 0.4078 |
| Power | Simple+ | 0.8857 | 0.2762 | 3.954e-012*** | 0.8803 | 0.0003*** |
| Compound | Quartic | 0.9918 | 1.448 | 0.005*** | 0.9503 | 0.0613* |
| S-Curve | Quartic | 0.9826 | 1.172 | 0.0007*** | 0.9128 | 0.0031*** |
| Growth | Quartic | 0.9918 | 1.4478 | 0.005*** | 0.0613 | 0.0613* |
| Exponential | Quartic | 0.9918 | 1.4478 | 0.005*** | 0.0613 | 0.0613* |
| Logistic(u=350) | Quartic | 0.9916 | 1.3065 | 0.0010*** | 0.9694 | 0.3003 |
NOTE: (i) Bold implies most preferred of the nine models.
(ii) + implies exalt multicollinearity made other forms of the variable to be omitted.
(iii) The maximum COVID-19 discharged cases for the period of study was 319.
The results of the parameter estimation of the most preferred model using OLS estimator and the other three (3) estimators are available in Table 4 . From the OLS results, the two observed problems are in the residual. These are autocorrelation problem (P-value of DW Statistic < 0.05) and problem of non-normality (P-value of SW Statistic < 0.1).
Table 4.
Results of the most preferred model with the estimators: COVID-19 Discharged Cases.
| Estimator | Estimation Methods |
|||||
|---|---|---|---|---|---|---|
| OLS | CORC | HILU | PW | LAD | ||
| Estimate | 8.8236 | 87.4791 | 91.4391 | 7.13149 | 0.4897 | |
| Std. Error | 9.3703 | 69.7831 | 72.8257 | 13.8694 | 5.2657 | |
| T-value | 0.9417 | 1.254 | 1.256 | 0.5142 | 0.093 | |
| P-value | 0.3523 | 0.2179 | 0.2171 | 0.6101 | 0.9264 | |
| Estimate | -3.0062 | -19.9917 | -20.6673 | -3.6692 | 0.6712 | |
| Std. Error | 2.8784 | 14.5542 | 15.0457 | 4.403 | 2.1814 | |
| T-value | -1.044 | -1.374 | -1.374 | -0.8333 | 0.3077 | |
| P-value | 0.3029 | 0.1778 | 0.1778 | 0.4099 | 0.76 | |
| Estimate | 0.1972 | 1.4509 | 1.4928 | 0.344 | -0.1777 | |
| Std. Error | 0.2618 | 1.0268 | 1.0551 | 0.4165 | 0.2679 | |
| T-value | 0.7532 | 1.413 | 1.415 | 0.8259 | -0.6633 | |
| P-value | 0.456 | 0.166 | 0.1655 | 0.414 | 0.5111 | |
| Estimate | 0.0037 | -0.0339 | -0.035 | -0.0036 | 0.0169 | |
| Std. Error | 0.0089 | 0.0294 | 0.0301 | 0.0143 | 0.0117 | |
| T-value | 0.4131 | -1.154 | -1.164 | -0.2496 | 1.443 | |
| P-value | 0.6819 | 0.2558 | 0.2517 | 0.8042 | 0.1572 | |
| Estimate | -6.89e-05 | 0.0003 | 0.0003 | 3.28e-05 | -0.0002 | |
| Std. Error | 0.0001 | 0.0003 | 0.0003 | 0.0002 | 0.0002 | |
| T-value | -0.687 | 1.101 | 1.114 | 0.2032 | -1.39 | |
| P-value | 0.4963 | 0.2779 | 0.2726 | 0.8401 | 0.1726 | |
| 0.7133 | 0.719 | 0.6968 | ||||
| Adj. R2 | 0.992512 | 0.993402 | 0.993402 | 0.993328 | 0.9932 | |
| DW | Stat-value | 0.6965 | 2.0548 | 2.0669 | 1.9497 | 2.06048 |
| P-value | 4.7e-009*** | |||||
| SW | Stat-value | 0.9724 | 0.8717 | 0.8676 | 0.8622 | 0.8434 |
| P-value | 0.3819 | 0.0002*** | 0.0002*** | 0.0001*** | 3.6e-005*** | |
Note: (i) *** implies significance at alpha = 0.01.
Addressing these problems respectively with CORC, HILU and PW estimators; and the LAD estimator, the best estimators, are identified to be CORC and HILU estimators in that they have the highest Adj.R2.
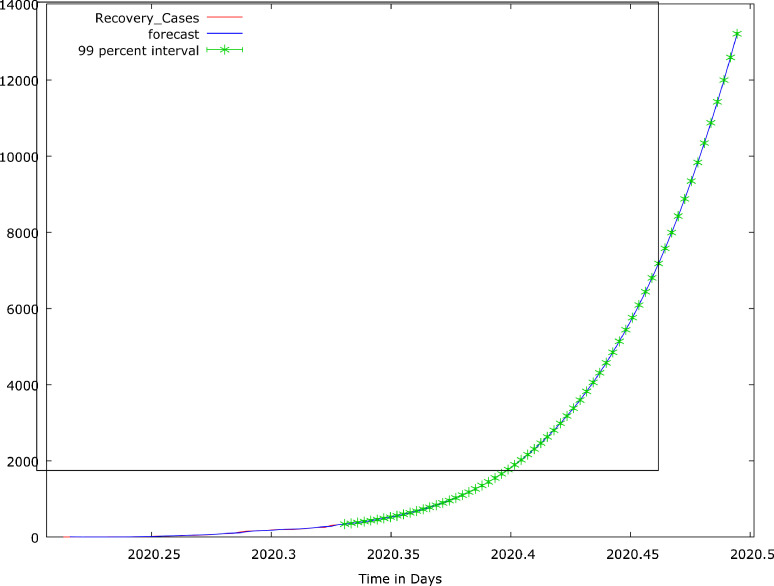
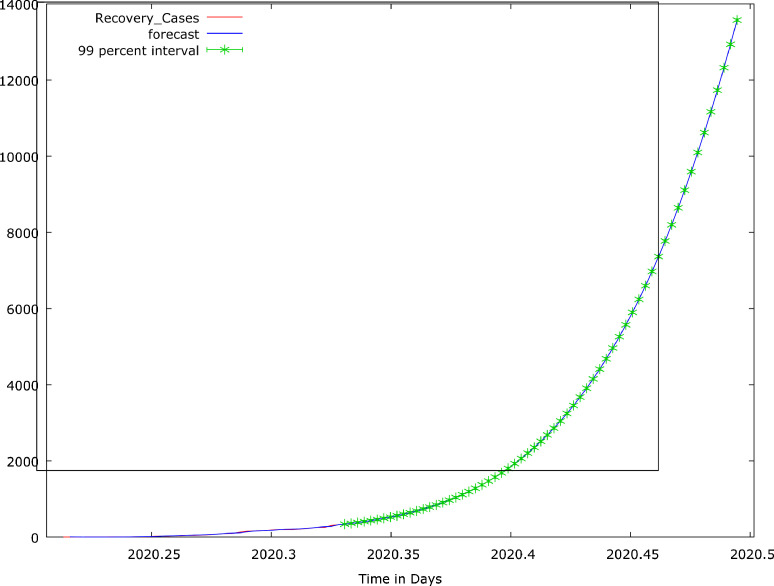
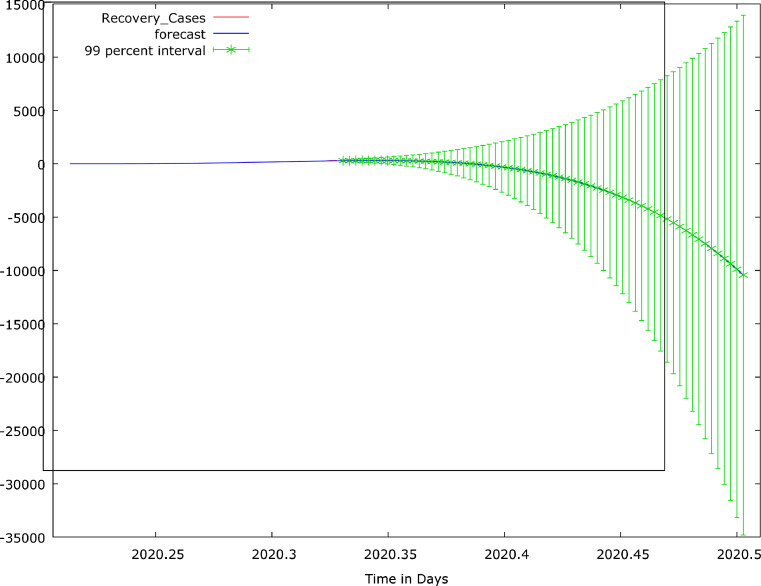
Meanwhile, the effect of time as the independent variable is not significant in all the estimators (P-value >0.1). It might be due to the inevitable multicollinearity problem. Furthermore, the non-normality of the residuals of the autocorrelation problem handling estimators necessitated the use of LAD as an alternative estimator. Thus, we adopted the CORC, HILU and the LAD estimators for forecasting and their forecast values, in Appendix B, are pictorially presented in logarithm form in Fig. 7, Fig. 8, Fig. 9. If existing measures and structures are maintained and improved upon, the recovery cases will increase from 319 to about 13,000 cases. However, the LAD estimator reveals a situation whereby, instead of having recovery cases increasing, it may be static since the cumulative cases can't decrease.
Fig. 7.
COVID-19 Discharged Cases for First Sixty Four Days and its forecast values for May and June, 2020: CORC Estimator.
Source:Appendix B
Fig. 8.
COVID-19 Discharged/ Recovery Cases for First Sixty Four Days and its forecast values for May and June, 2020: HILU Estimator.
Fig. 9.
COVID-19 Discharged Cases for First Sixty Four Days and its forecast values for May and June, 2020: LAD Estimator.
3.3. COVID-19 Death Cases
We employed the OLS estimator to analyse the nine statistical models in Table 5. From the table, the preferred form of the model is generally Quartic except in Logarithm and Power where exact multicollinearity prevented others forms to be used in the analysis. All these preferred models have autocorrelation problem (P-value of DW Statistic < 0.01); only the residuals of Logarithm, Inverse, Power and Logistic do not follow normal distribution (P-value of SW Statistic < 0.1). Thus, the most preferred model is the Linear Regression Model with Quartic form having explained 99.53% of the variation in COVID-19 death cases.
Table 5.
Results of Preferred Model with OLS estimator in each of the Nine Curve Estimation models: COVID-19 Death Cases.
| Models | Form | Adj. R2 | DW-test |
SW- test |
||
|---|---|---|---|---|---|---|
| Value | P-value | Value | P-value | |||
| Linear | Quartic | 0.9953 | 1.3563 | 0.0021*** | 0.9581 | 0.153984 |
| Logarithm | Simple+ | 0.4988 | 0.0703 | 3.63e-011*** | 0.8552 | 0.0001*** |
| Inverse | Quartic | 0.6856 | 0.2494 | 1.798e-015*** | 0.9449 | 0.0553* |
| Power | Simple+ | 0.842 | 0.2441 | 1.798e-015*** | 0.945971 | 0.0602* |
| Compound | Quartic | 0.9896 | 1.6627 | 0.0345106** | 0.97267 | 0.4513 |
| S-Curve | Quartic | 0.9518 | 0.6449 | 7.704e-008*** | 0.9751 | 0.5301 |
| Growth | Quartic | 0.9896 | 1.6627 | 0.0345106** | 0.97267 | 0.4513 |
| Exponential | Quartic | 0.9896 | 1.6627 | 0.0345106** | 0.97267 | 0.4513 |
| Logistic(u=60) | Quartic | 0.9824 | 1.2658 | 0.00074*** | 0.941344 | 0.0422** |
NOTE: (i) Bold implies most preferred of the nine models.
(ii) + implies exact multicollinearity made other forms of the variable to be omitted.
(iii) The cumulative death cases recorded within the period was 58.
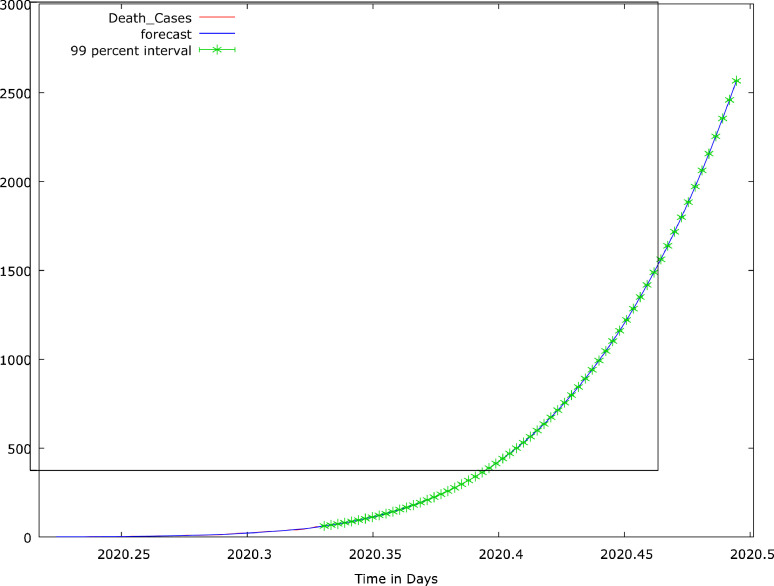
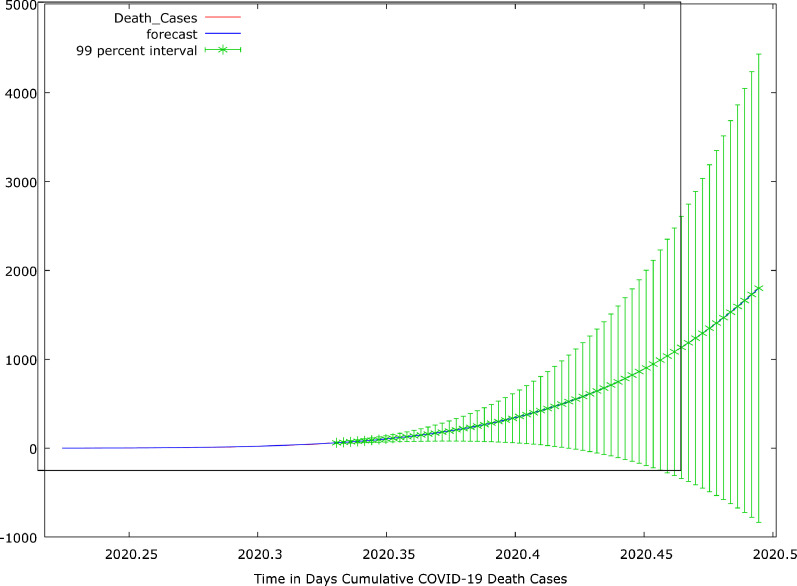
The parameter estimation of the most preferred model using OLS estimator is available in Table 6. From the results, there is the presence of autocorrelation. Addressing the autocorrelation problem with CORC, HILU and PW only produced estimates slightly better than the OLS. Moreover, the quartic time variable only has a significant impact (P-value<0.1) on cumulative of COVID-19 death cases using the OLS and PW estimators. Consequently, it became necessary to adopt the LAD estimator, a robust estimation method for comparison. Eventually, we employed the PW and LAD estimators for forecasting because of their performance. The results are provided in Appendix C and shown in Fig. 10, Fig. 11. The forecast results for the next two months revealed that death cases would increase from 58 to 1800 and 2567, respectively, with the use of LAD and PW estimator. Moreover, forecast values from LAD estimator indicate a situation whereby cumulative COVID-19 death cases may be static since it can't decrease. This increase in death cases is alarming and therefore, effective planning and action are required to be able to avert this incidence.
Table 6.
Results of the most preferred model with the estimators: COVID-19 Death Cases.
| Estimator | Estimation Methods |
|||||
|---|---|---|---|---|---|---|
| OLS | CORC | HILU | PW | LAD | ||
| Estimate | 1.1464 | 1.9173 | 1.9189 | 1.3449 | 1.0711 | |
| Std. Error | 1.0108 | 2.447 | 2.4494 | 1.2579 | 0.8036 | |
| T-value | 1.134 | 0.7835 | 0.7834 | 1.069 | 1.333 | |
| P-value | 0.2647 | 0.4389 | 0.439 | 0.2925 | 0.1915 | |
| Estimate | -0.117 | -0.3897 | -0.3902 | -0.2352 | -0.0958 | |
| Std. Error | 0.3407 | 0.7087 | 0.7093 | 0.43189 | 0.3297 | |
| T-value | -0.3434 | -0.5499 | -0.5502 | -0.5446 | -0.2907 | |
| P-value | 0.7334 | 0.5861 | 0.5859 | 0.5896 | 0.7731 | |
| Estimate | 0.0308 | 0.0591 | 0.0592 | 0.0462 | 0.0252 | |
| Std. Error | 0.034 | 0.0639 | 0.0639 | 0.0437 | 0.0384 | |
| T-value | 0.9052 | 0.9258 | 0.926 | 1.058 | 0.6576 | |
| P-value | 0.3717 | 0.3613 | 0.3612 | 0.2973 | 0.5152 | |
| Estimate | -0.0009 | -0.002 | -0.002 | -0.0015 | -0.0005 | |
| Std. Error | 0.0013 | 0.0022 | 0.0022 | 0.0016 | 0.0016 | |
| T-value | -0.6694 | -0.8767 | -0.8770 | -0.9354 | -0.2741 | |
| P-value | 0.5078 | 0.3870 | 0.3868 | 0.3562 | 0.7857 | |
| Estimate | 2.7e-05 | 4.13e-05 | 4.13e-05 | 3.66e-05 | 2.007e-05 | |
| Std. Error | 1.56e-05 | 2.63e-05 | 2.63e-05 | 2.03e-05 | 2.323e-05 | |
| T-value | 1.717 | 1.569 | 1.569 | 1.801 | 0.8643 | |
| P-value | 0.095* | 0.1262 | 0.1262 | 0.0805* | 0.3935 | |
| 0.347 | 0.347 | 0.3389 | ||||
| Adj. R2 | 0.995342 | 0.995638 | 0.9956 | 0.995737 | 0.995047 | |
| DW | Stat-value | 1.3563 | 1.7146 | 1.7151 | 1.7056 | 1.23802 |
| P-value | 0.0021*** | |||||
| SW | Stat-value | 0.9581 | 0.9576 | 0.9576 | 0.9571 | 0.918514 |
| P-value | 0.15398 | 0.1585 | 0.1581 | 0.1428 | 0.0078*** | |
Note: (i)*and *** imply significance at alpha = 0.1 and 0.01respectively.
Fig. 10.
Death COVID-19 Cases for First Sixty Four Days and its forecast values for May and June, 2020: PW Estimator.
Source:Appendix C
Fig. 11.
Death COVID-19 Cases for First Sixty Four Days and its forecast values for May and June, 2020: LAD Estimator.
Source:Appendix C
3.4. Models Assessment with Observed/True values (TV)
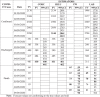
The COVID-19 data for the first five days in May 2020 were further collected and compared with the forecast value (FV). These values are presented as follows in Table 7. From the table, we observed that the observed original values are in agreement with the forecast values except on few cases especially on the fifth day. Notwithstanding, the actual values and forecast values of LAD estimator are most frequently in agreement; and so, we recommend the estimator.
Table 7.
Comparison of forecast values with the true values.
 |
4. Conclusion
This study provided the statistical curve model for the daily cumulative reported COVID-19 confirmed cases, discharged cases and death cases in Nigeria using data collected by the Nigeria Centre for Disease Control (NCDC) for the first sixty-four days of the incidence using five estimation methods. It further identified the best model for each of the variables and used the same to forecast for May and June 2020. Comparing the actual values with the forecast ones in the first five days of May 2020, we recommended the forecast values of the LAD estimator because of its precision. The forecast values are alarming and therefore require serious planning and intervention by the Government to avoid the pandemic becoming a huge health problem for the country.
CRediT authorship contribution statement
Kayode Ayinde: Conceptualization, Methodology, Formal analysis, Software, Writing - original draft. Adewale F. Lukman: Conceptualization, Methodology, Resources, Writing - original draft. Rauf I. Rauf: Conceptualization, Methodology, Resources, Supervision. Olusegun O. Alabi: Conceptualization, Methodology, Supervision. Charles E. Okon: Conceptualization, Methodology, Writing - original draft. Opeyemi E. Ayinde: Conceptualization, Methodology, Resources.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A. Forecast vales of COVID-19 confirmed cases for May and June, 2020
| HILU | LAD | |||||
|---|---|---|---|---|---|---|
| 99% C.I. | 99% C.I. | |||||
| DATE | F.V | L.V | U.V | F.V | L.V | U.V |
| 1/5/2020 | 2134.49 | 2090.91 | 2178.07 | 1997.93 | 1776.17 | 2219.7 |
| 2/5/2020 | 2355.38 | 2297.04 | 2413.71 | 2177.03 | 1912.4 | 2441.67 |
| 3/5/2020 | 2595.81 | 2528.02 | 2663.59 | 2369.03 | 2055.6 | 2682.45 |
| 4/5/2020 | 2856.95 | 2782.53 | 2931.37 | 2574.54 | 2206.24 | 2942.84 |
| 5/5/2020 | 3140.03 | 3060.75 | 3219.31 | 2794.21 | 2364.7 | 3223.72 |
| 6/5/2020 | 3446.29 | 3363.36 | 3529.22 | 3028.69 | 2531.36 | 3526.02 |
| 7/5/2020 | 3777.02 | 3691.3 | 3862.73 | 3278.65 | 2706.58 | 3850.72 |
| 8/5/2020 | 4133.53 | 4045.68 | 4221.38 | 3544.77 | 2890.7 | 4198.84 |
| 9/5/2020 | 4517.19 | 4427.68 | 4606.7 | 3827.75 | 3084.07 | 4571.43 |
| 10/5/2020 | 4929.38 | 4838.58 | 5020.18 | 4128.3 | 3287.02 | 4969.58 |
| 11/5/2020 | 5371.54 | 5279.72 | 5463.35 | 4447.15 | 3499.89 | 5394.41 |
| 12/5/2020 | 5845.12 | 5752.51 | 5937.73 | 4785.03 | 3723.02 | 5847.05 |
| 13/5/2020 | 6351.63 | 6258.4 | 6444.86 | 5142.71 | 3956.74 | 6328.69 |
| 14/5/2020 | 6892.6 | 6798.88 | 6986.32 | 5520.96 | 4201.4 | 6840.51 |
| 15/5/2020 | 7469.61 | 7375.5 | 7563.71 | 5920.55 | 4457.35 | 7383.75 |
| 16/5/2020 | 8084.25 | 7989.84 | 8178.66 | 6342.29 | 4724.93 | 7959.65 |
| 17/5/2020 | 8738.17 | 8643.52 | 8832.83 | 6787 | 5004.49 | 8569.5 |
| 18/5/2020 | 9433.05 | 9338.21 | 9527.9 | 7255.5 | 5296.4 | 9214.59 |
| 19/5/2020 | 10170.6 | 10075.6 | 10265.6 | 7748.63 | 5601.01 | 9896.25 |
| 20/5/2020 | 10952.6 | 10857.5 | 11047.7 | 8267.26 | 5918.7 | 10615.8 |
| 21/5/2020 | 11780.7 | 11685.5 | 11876 | 8812.26 | 6249.82 | 11374.7 |
| 22/5/2020 | 12656.9 | 12561.7 | 12752.2 | 9384.52 | 6594.76 | 12174.3 |
| 23/5/2020 | 13583 | 13487.7 | 13678.4 | 9984.93 | 6953.9 | 13016 |
| 24/5/2020 | 14560.9 | 14465.5 | 14656.3 | 10614.4 | 7327.62 | 13901.2 |
| 25/5/2020 | 15592.4 | 15497 | 15687.8 | 11273.9 | 7716.32 | 14831.5 |
| 26/5/2020 | 16679.6 | 16584.2 | 16775.1 | 11964.4 | 8120.38 | 15808.4 |
| 27/5/2020 | 17824.5 | 17729 | 17920 | 12686.8 | 8540.2 | 16833.3 |
| 28/5/2020 | 19029.1 | 18933.6 | 19124.6 | 13442 | 8976.2 | 17907.8 |
| 29/5/2020 | 20295.4 | 20199.9 | 20390.9 | 14231.2 | 9428.77 | 19033.6 |
| 30/5/2020 | 21625.6 | 21530.1 | 21721.1 | 15055.2 | 9898.34 | 20212.1 |
| 31/5/2020 | 23021.8 | 22926.2 | 23117.3 | 15915.1 | 10385.3 | 21445 |
| 1/6/2020 | 24486.2 | 24390.6 | 24581.7 | 16812 | 10890.1 | 22733.9 |
| 2/6/2020 | 26020.9 | 25925.4 | 26116.5 | 17746.9 | 11413.2 | 24080.6 |
| 3/6/2020 | 27628.4 | 27532.8 | 27723.9 | 18720.8 | 11955 | 25486.7 |
| 4/6/2020 | 29310.7 | 29215.2 | 29406.3 | 19734.9 | 12516 | 26953.9 |
| 5/6/2020 | 31070.3 | 30974.8 | 31165.9 | 20790.2 | 13096.5 | 28483.9 |
| 6/6/2020 | 32909.5 | 32814 | 33005.1 | 21887.8 | 13697 | 30078.7 |
| 7/6/2020 | 34830.7 | 34735.2 | 34926.3 | 23028.9 | 14318.1 | 31739.8 |
| 8/6/2020 | 36836.4 | 36740.8 | 36931.9 | 24214.6 | 14960 | 33469.2 |
| 9/6/2020 | 38928.8 | 38833.3 | 39024.4 | 25446.1 | 15623.5 | 35268.7 |
| 10/6/2020 | 41110.7 | 41015.2 | 41206.3 | 26724.4 | 16308.7 | 37140.1 |
| 11/6/2020 | 43384.5 | 43288.9 | 43480.1 | 28050.9 | 17016.4 | 39085.3 |
| 12/6/2020 | 45752.8 | 45657.2 | 45848.3 | 29426.6 | 17746.9 | 41106.3 |
| 13/6/2020 | 48218.1 | 48122.5 | 48313.7 | 30852.8 | 18500.7 | 43205 |
| 14/6/2020 | 50783.2 | 50687.6 | 50878.7 | 32330.8 | 19278.3 | 45383.3 |
| 15/6/2020 | 53450.6 | 53546.2 | 53355.1 | 33861.7 | 20080.2 | 47643.3 |
| 16/6/2020 | 56223.2 | 56127.6 | 56318.8 | 35446.9 | 20906.9 | 49986.9 |
| 17/6/2020 | 59103.6 | 59008 | 59199.2 | 37087.6 | 21758.9 | 52416.2 |
| 18/6/2020 | 62094.7 | 61999.1 | 62190.2 | 38785 | 22636.8 | 54933.2 |
| 19/6/2020 | 65199.2 | 65103.6 | 65294.7 | 40540.5 | 23541 | 57540 |
| 20/6/2020 | 68420 | 68324.4 | 68515.6 | 42355.4 | 24472 | 60238.8 |
| 21/6/2020 | 71760 | 71664.4 | 71855.6 | 44231 | 25430.4 | 63031.6 |
| 22/6/2020 | 75222.1 | 75126.6 | 75317.7 | 46168.7 | 26416.8 | 65920.6 |
| 23/6/2020 | 78809.4 | 78713.8, | 78904.9 | 48169.8 | 27431.5 | 68908 |
| 24/6/2020 | 82524.7 | 82429.1 | 82620.2 | 50235.6 | 28475.3 | 71996 |
| 25/6/2020 | 86371.1 | 86275.5 | 86466.6 | 52367.7 | 29548.6 | 75186.8 |
| 26/6/2020 | 90351.6 | 90256.1 | 90447.2 | 54567.3 | 30652 | 78482.7 |
| 27/6/2020 | 94469.5 | 94373.9 | 94565.1 | 56836 | 31786 | 81886 |
| 28/6/2020 | 98727.8 | 98632.2 | 98823.3 | 59175 | 32951.2 | 85398.9 |
| 29/6/2020 | 103130 | 103034 | 103225 | 61585.9 | 34148.1 | 89023.8 |
| 30/6/2020 | 107678 | 107583 | 107774 | 64070.2 | 35377.4 | 92763 |
Appendix B. Forecast vales of COVID-19 confirmed cases for May and June, 2020
| CORC | HILU | LAD | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 99% C.I. | 99% C.I. | 99% C.I. | |||||||
| DATE | F.V | L.V | U.V | F.V | L.V | U.V | F.V | L.V | U.V |
| 1/5/2020 | 337.634 | 315.966 | 359.302 | 337.826 | 316.158 | 359.494 | 291.609 | 198.702 | 384.516 |
| 2/5/2020 | 358.013 | 331.397 | 384.628 | 358.406 | 331.718 | 385.094 | 298.421 | 184.439 | 412.404 |
| 3/5/2020 | 380.186 | 351.378 | 408.994 | 380.802 | 351.858 | 409.747 | 304.034 | 165.471 | 442.596 |
| 4/5/2020 | 404.237 | 374.375 | 434.098 | 405.109 | 375.065 | 435.154 | 308.304 | 141.456 | 475.152 |
| 5/5/2020 | 430.275 | 399.892 | 460.659 | 431.445 | 400.847 | 462.043 | 311.085 | 112.018 | 510.152 |
| 6/5/2020 | 458.431 | 427.786 | 489.077 | 459.948 | 429.068 | 490.828 | 312.225 | 76.7531 | 547.696 |
| 7/5/2020 | 488.853 | 458.075 | 519.631 | 490.772 | 459.748 | 521.797 | 311.566 | 35.2337 | 587.897 |
| 8/5/2020 | 521.703 | 490.858 | 552.548 | 524.088 | 492.989 | 555.188 | 308.945 | -12.9903 | 630.879 |
| 9/5/2020 | 557.155 | 526.276 | 588.035 | 560.076 | 528.938 | 591.214 | 304.193 | -68.3885 | 676.775 |
| 10/5/2020 | 595.396 | 564.499 | 626.293 | 598.928 | 567.77 | 630.086 | 297.138 | -131.449 | 725.726 |
| 11/5/2020 | 636.621 | 605.715 | 667.526 | 640.848 | 609.68 | 672.016 | 287.6 | -202.677 | 777.878 |
| 12/5/2020 | 681.035 | 650.125 | 711.946 | 686.048 | 654.874 | 717.221 | 275.395 | -282.594 | 833.385 |
| 13/5/2020 | 728.855 | 697.942 | 759.767 | 734.748 | 703.572 | 765.925 | 260.333 | -371.74 | 892.407 |
| 14/5/2020 | 780.301 | 749.387 | 811.215 | 787.181 | 756.003 | 818.358 | 242.219 | -470.669 | 955.107 |
| 15/5/2020 | 835.606 | 804.692 | 866.521 | 843.583 | 812.405 | 874.762 | 220.853 | -579.951 | 1021.66 |
| 16/5/2020 | 895.01 | 864.095 | 925.924 | 904.204 | 873.025 | 935.382 | 196.029 | -700.172 | 1092.23 |
| 17/5/2020 | 958.76 | 927.845 | 989.674 | 969.297 | 938.118 | 1000.48 | 167.535 | -831.934 | 1167 |
| 18/5/2020 | 1027.11 | 996.196 | 1058.03 | 1039.13 | 1007.95 | 1070.31 | 135.157 | -975.853 | 1246.17 |
| 19/5/2020 | 1100.33 | 1069.41 | 1131.24 | 1113.97 | 1082.79 | 1145.15 | 98.6706 | -1132.56 | 1329.9 |
| 20/5/2020 | 1178.68 | 1147.77 | 1209.59 | 1194.1 | 1162.92 | 1225.28 | 57.8505 | -1302.71 | 1418.41 |
| 21/5/2020 | 1262.45 | 1231.53 | 1293.36 | 1279.8 | 1248.62 | 1310.98 | 12.4636 | -1486.96 | 1511.89 |
| 22/5/2020 | 1351.92 | 1321 | 1382.83 | 1371.38 | 1340.2 | 1402.56 | -37.7276 | -1685.99 | 1610.53 |
| 23/5/2020 | 1447.39 | 1416.47 | 1478.3 | 1469.14 | 1437.96 | 1500.32 | -92.9663 | -1900.49 | 1714.55 |
| 24/5/2020 | 1549.15 | 1518.24 | 1580.07 | 1573.39 | 1542.21 | 1604.56 | -153.501 | -2131.17 | 1824.17 |
| 25/5/2020 | 1657.53 | 1626.62 | 1688.45 | 1684.44 | 1653.26 | 1715.62 | -219.585 | -2378.75 | 1939.58 |
| 26/5/2020 | 1772.84 | 1741.92 | 1803.75 | 1802.64 | 1771.46 | 1833.81 | -291.478 | -2643.98 | 2061.02 |
| 27/5/2020 | 1895.39 | 1864.48 | 1926.31 | 1928.3 | 1897.12 | 1959.48 | -369.445 | -2927.61 | 2188.72 |
| 28/5/2020 | 2025.54 | 1994.62 | 2056.45 | 2061.79 | 2030.61 | 2092.97 | -453.755 | -3230.4 | 2322.89 |
| 29/5/2020 | 2163.61 | 2132.7 | 2194.53 | 2203.45 | 2172.27 | 2234.62 | -544.682 | -3553.14 | 2463.77 |
| 30/5/2020 | 2309.96 | 2279.05 | 2340.88 | 2353.63 | 2322.45 | 2384.81 | -642.509 | -3896.63 | 2611.61 |
| 31/5/2020 | 2464.94 | 2434.03 | 2495.86 | 2512.72 | 2481.54 | 2543.9 | -747.52 | -4261.68 | 2766.64 |
| 1/6/2020 | 2628.92 | 2598.01 | 2659.84 | 2681.08 | 2649.9 | 2712.25 | -860.007 | -4649.13 | 2929.12 |
| 2/6/2020 | 2802.27 | 2771.36 | 2833.19 | 2859.09 | 2827.91 | 2890.27 | -980.265 | -5059.82 | 3099.29 |
| 3/6/2020 | 2985.37 | 2954.46 | 3016.29 | 3047.16 | 3015.98 | 3078.34 | -1108.6 | -5494.6 | 3277.4 |
| 4/6/2020 | 3178.61 | 3147.69 | 3209.52 | 3245.68 | 3214.5 | 3276.86 | -1245.31 | -5954.35 | 3463.73 |
| 5/6/2020 | 3382.38 | 3351.46 | 3413.29 | 3455.05 | 3423.87 | 3486.23 | -1390.72 | -6439.97 | 3658.53 |
| 6/6/2020 | 3597.08 | 3566.16 | 3627.99 | 3675.7 | 3644.52 | 3706.88 | -1545.14 | -6952.36 | 3862.07 |
| 7/6/2020 | 3823.13 | 3792.21 | 3854.04 | 3908.05 | 3876.87 | 3939.23 | -1708.89 | -7492.43 | 4074.64 |
| 8/6/2020 | 4060.94 | 4030.02 | 4091.85 | 4152.53 | 4121.35 | 4183.7 | -1882.31 | -8061.12 | 4296.49 |
| 9/6/2020 | 4310.94 | 4280.02 | 4341.85 | 4409.57 | 4378.39 | 4440.75 | -2065.73 | -8659.38 | 4527.93 |
| 10/6/2020 | 4573.57 | 4542.65 | 4604.48 | 4679.64 | 4648.46 | 4710.81 | -2259.48 | -9288.18 | 4769.22 |
| 11/6/2020 | 4849.26 | 4818.34 | 4880.17 | 4963.17 | 4931.99 | 4994.35 | -2463.91 | -9948.5 | 5020.68 |
| 12/6/2020 | 5138.46 | 5107.55 | 5169.38 | 5260.64 | 5229.47 | 5291.82 | -2679.38 | -10641.3 | 5282.58 |
| 13/6/2020 | 5441.64 | 5410.72 | 5472.55 | 5572.53 | 5541.35 | 5603.71 | -2906.23 | -11367.7 | 5555.23 |
| 14/6/2020 | 5759.25 | 5728.34 | 5790.17 | 5899.3 | 5868.12 | 5930.47 | -3144.82 | -12128.6 | 5838.94 |
| 15/6/2020 | 6091.78 | 6060.86 | 6122.69 | 6241.44 | 6210.26 | 6272.62 | -3395.53 | -12925.1 | 6134.02 |
| 16/6/2020 | 6439.69 | 6408.77 | 6470.6 | 6599.46 | 6568.28 | 6630.64 | -3658.73 | -13758.2 | 6440.76 |
| 17/6/2020 | 6803.48 | 6772.56 | 6834.39 | 6973.85 | 6942.67 | 7005.03 | -3934.78 | -14629.1 | 6759.51 |
| 18/6/2020 | 7183.64 | 7152.72 | 7214.55 | 7365.13 | 7333.95 | 7396.31 | -4224.08 | -15538.7 | 7090.57 |
| 19/6/2020 | 7580.67 | 7549.76 | 7611.59 | 7773.81 | 7742.63 | 7804.99 | -4527 | -16488.3 | 7434.27 |
| 20/6/2020 | 7995.1 | 7964.18 | 8026.01 | 8200.43 | 8169.25 | 8231.61 | -4843.95 | -17478.8 | 7790.94 |
| 21/6/2020 | 8427.43 | 8396.51 | 8458.34 | 8645.51 | 8614.34 | 8676.69 | -5175.32 | -18511.6 | 8160.92 |
| 22/6/2020 | 8878.19 | 8847.27 | 8909.1 | 9109.61 | 9078.43 | 9140.79 | -5521.52 | -19587.6 | 8544.55 |
| 23/6/2020 | 9347.92 | 9317 | 9378.83 | 9593.28 | 9562.1 | 9624.46 | -5882.95 | -20708.1 | 8942.17 |
| 24/6/2020 | 9837.15 | 9806.24 | 9868.07 | 10097.1 | 10065.9 | 10128.2 | -6260.02 | -21874.2 | 9354.13 |
| 25/6/2020 | 10346.4 | 10315.5 | 10377.4 | 10621.5 | 10590.4 | 10652.7 | -6653.16 | -23087.1 | 9780.77 |
| 26/6/2020 | 10876.4 | 10845.4 | 10907.3 | 11167.3 | 11136.1 | 11198.5 | -7062.79 | -24348 | 10222.5 |
| 27/6/2020 | 11427.4 | 11396.5 | 11458.4 | 11734.9 | 11703.7 | 11766.1 | -7489.34 | -25658.3 | 10679.6 |
| 28/6/2020 | 12000.3 | 11969.4 | 12031.2 | 12324.9 | 12293.7 | 12356.1 | -7933.25 | -27019 | 11152.5 |
| 29/6/2020 | 12595.5 | 12564.6 | 12626.4 | 12938 | 12906.8 | 12969.2 | -8394.95 | -28431.4 | 11641.5 |
| 30/6/2020 | 13213.6 | 13182.7 | 13244.5 | 13574.7 | 13543.5 | 13605.9 | -8874.9 | -29896.8 | 12147 |
Appendix C. Forecast vales of COVID-19 death cases for May and June, 2020
| PW | LAD | |||||
|---|---|---|---|---|---|---|
| 99% C.I. | 99% C.I. | |||||
| DATE | F.V | L.V | U.V | F.V | L.V | U.V |
| 1/5/2020 | 62.1187 | 59.316 | 64.9214 | 60.1645 | 50.4 | 69.9291 |
| 2/5/2020 | 67.4243 | 64.4651 | 70.3836 | 65.2303 | 53.0899 | 77.3706 |
| 3/5/2020 | 73.4412 | 70.4645 | 76.4179 | 70.6406 | 55.714 | 85.5673 |
| 4/5/2020 | 80.0263 | 77.0476 | 83.005 | 76.4128 | 58.2577 | 94.568 |
| 5/5/2020 | 87.1501 | 84.1712 | 90.1291 | 82.5647 | 60.7041 | 104.425 |
| 6/5/2020 | 94.8222 | 91.8433 | 97.8011 | 89.1144 | 63.0345 | 115.194 |
| 7/5/2020 | 103.066 | 100.087 | 106.045 | 96.0807 | 65.228 | 126.933 |
| 8/5/2020 | 111.909 | 108.93 | 114.888 | 103.483 | 67.2626 | 139.703 |
| 9/5/2020 | 121.384 | 118.405 | 124.363 | 111.341 | 69.1148 | 153.566 |
| 10/5/2020 | 131.521 | 128.542 | 134.5 | 119.674 | 70.7597 | 168.588 |
| 11/5/2020 | 142.355 | 139.376 | 145.334 | 128.504 | 72.1715 | 184.836 |
| 12/5/2020 | 153.92 | 150.941 | 156.899 | 137.851 | 73.3229 | 202.379 |
| 13/5/2020 | 166.25 | 163.271 | 169.229 | 147.737 | 74.1857 | 221.289 |
| 14/5/2020 | 179.383 | 176.404 | 182.362 | 158.185 | 74.7306 | 241.639 |
| 15/5/2020 | 193.354 | 190.375 | 196.333 | 169.216 | 74.9271 | 263.506 |
| 16/5/2020 | 208.202 | 205.223 | 211.181 | 180.855 | 74.7436 | 286.966 |
| 17/5/2020 | 223.965 | 220.986 | 226.944 | 193.123 | 74.1476 | 312.099 |
| 18/5/2020 | 240.683 | 237.704 | 243.662 | 206.047 | 73.1054 | 338.988 |
| 19/5/2020 | 258.396 | 255.417 | 261.375 | 219.649 | 71.5823 | 367.715 |
| 20/5/2020 | 277.145 | 274.166 | 280.124 | 233.955 | 69.5425 | 398.367 |
| 21/5/2020 | 296.974 | 293.995 | 299.953 | 248.99 | 66.9493 | 431.031 |
| 22/5/2020 | 317.924 | 314.945 | 320.903 | 264.781 | 63.7646 | 465.798 |
| 23/5/2020 | 340.04 | 337.061 | 343.019 | 281.354 | 59.9497 | 502.758 |
| 24/5/2020 | 363.366 | 360.387 | 366.345 | 298.735 | 55.4646 | 542.006 |
| 25/5/2020 | 387.949 | 384.97 | 390.928 | 316.953 | 50.2682 | 583.638 |
| 26/5/2020 | 413.834 | 410.855 | 416.813 | 336.035 | 44.3185 | 627.751 |
| 27/5/2020 | 441.07 | 438.091 | 444.049 | 356.009 | 37.5725 | 674.445 |
| 28/5/2020 | 469.705 | 466.726 | 472.683 | 376.904 | 29.986 | 723.822 |
| 29/5/2020 | 499.787 | 496.808 | 502.766 | 398.75 | 21.5138 | 775.985 |
| 30/5/2020 | 531.367 | 528.388 | 534.346 | 421.576 | 12.1098 | 831.042 |
| 31/5/2020 | 564.496 | 561.517 | 567.475 | 445.413 | 1.7266 | 889.099 |
| 1/6/2020 | 599.225 | 596.246 | 602.204 | 470.291 | -9.684 | 950.266 |
| 2/6/2020 | 635.608 | 632.63 | 638.587 | 496.242 | -22.1713 | 1014.66 |
| 3/6/2020 | 673.699 | 670.72 | 676.678 | 523.297 | -35.7858 | 1082.38 |
| 4/6/2020 | 713.55 | 710.571 | 716.529 | 551.489 | -50.5788 | 1153.56 |
| 5/6/2020 | 755.219 | 752.24 | 758.198 | 580.851 | -66.6028 | 1228.3 |
| 6/6/2020 | 798.76 | 795.781 | 801.739 | 611.415 | -83.9112 | 1306.74 |
| 7/6/2020 | 844.232 | 841.253 | 847.211 | 643.215 | -102.559 | 1388.99 |
| 8/6/2020 | 891.692 | 888.713 | 894.671 | 676.285 | -122.601 | 1475.17 |
| 9/6/2020 | 941.199 | 938.22 | 944.178 | 710.66 | -144.094 | 1565.41 |
| 10/6/2020 | 992.813 | 989.834 | 995.792 | 746.376 | -167.096 | 1659.85 |
| 11/6/2020 | 1046.59 | 1043.62 | 1049.57 | 783.467 | -191.665 | 1758.6 |
| 12/6/2020 | 1102.61 | 1099.63 | 1105.58 | 821.969 | -217.862 | 1861.8 |
| 13/6/2020 | 1160.91 | 1157.93 | 1163.89 | 861.92 | -245.747 | 1969.59 |
| 14/6/2020 | 1221.56 | 1218.58 | 1224.54 | 903.357 | -275.381 | 2082.09 |
| 15/6/2020 | 1284.64 | 1281.66 | 1287.62 | 946.316 | -306.828 | 2199.46 |
| 16/6/2020 | 1350.2 | 1347.22 | 1353.18 | 990.836 | -340.152 | 2321.82 |
| 17/6/2020 | 1418.31 | 1415.33 | 1421.28 | 1036.96 | -375.417 | 2449.33 |
| 18/6/2020 | 1489.03 | 1486.05 | 1492.01 | 1084.71 | -412.689 | 2582.11 |
| 19/6/2020 | 1562.44 | 1559.46 | 1565.42 | 1134.15 | -452.036 | 2720.33 |
| 20/6/2020 | 1638.6 | 1635.62 | 1641.58 | 1185.3 | -493.526 | 2864.13 |
| 21/6/2020 | 1717.58 | 1714.61 | 1720.56 | 1238.21 | -537.226 | 3013.65 |
| 22/6/2020 | 1799.46 | 1796.48 | 1802.44 | 1292.92 | -583.209 | 3169.05 |
| 23/6/2020 | 1884.3 | 1881.32 | 1887.28 | 1349.47 | -631.544 | 3330.49 |
| 24/6/2020 | 1972.18 | 1969.2 | 1975.15 | 1407.9 | -682.304 | 3498.11 |
| 25/6/2020 | 2063.16 | 2060.18 | 2066.14 | 1468.26 | -735.562 | 3672.08 |
| 26/6/2020 | 2157.32 | 2154.35 | 2160.3 | 1530.58 | -791.393 | 3852.56 |
| 27/6/2020 | 2254.75 | 2251.77 | 2257.73 | 1594.92 | -849.871 | 4039.71 |
| 28/6/2020 | 2355.5 | 2352.52 | 2358.48 | 1661.31 | -911.074 | 4233.69 |
| 29/6/2020 | 2459.67 | 2456.69 | 2462.64 | 1729.79 | -975.078 | 4434.66 |
| 30/6/2020 | 2567.32 | 2564.34 | 2570.29 | 1800.42 | -1041.96 | 4642.81 |
References
- 1.Ademir, X. (2020). A C++ code for predicting COVID-19 cases by least-squares_tting of the Logistic model. Preprint. DOI: 10.13140/RG.2.2.28264.01283.
- 2.Adhikari S.P., ShaMeng S., Wu Y., Mao Y., Ye R., Wang Q., Sun C., Sylvia S., Rozelle S., Raat H., Zhou H. Epidemiology, causes, clinical manifestation and diagnosis, prevention and control of coronavirus disease (COVID-19) during the early outbreak period: a scoping review. Infectious Diseases of Poverty. 2020;9(1):29. doi: 10.1186/s40249-020-00646-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ayinde K. Performances of Some Estimators of Linear Model when Stochastic Regressors are correlated with Autocorrelated Error Terms. European Journal of Scientific Research. 2008;20(3):558–571. [Google Scholar]
- 4.Ayinde K., Olaomi J.O. A Study of Robustness of Some Estimators of Linear Model with Autocorrelated Error Terms When Stochastic Regressors Are Normally Distributed. Journal of Modern Applied Statistical Methods. 2008;7(1):246–252. [Google Scholar]
- 5.Ayinde K., Lukman A.F., Samuel O.O., Omokova M.A. Some New Adjusted Ridge Estimators of Linear Regression Model. International Journal of Civil Engineering and Technology. 2018;9(11):2838–2852. [Google Scholar]
- 6.Bedford J., Enria D., Giesecke J., Heymann D.L., Ihekweazu C., Kobinger G. COVID-19: towards controlling of a pandemic. Lancet North Am Ed. 2020;395(10229):1015–1018. doi: 10.1016/S0140-6736(20)30673-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cochrane D., Orcutt G.H. Application of least square to relationship containing autocorrelated error terms. J Am Statist Assoc. 1949;44:32–61. [Google Scholar]
- 8.Durbin J. Estimation of Parameters in time – series regression models. Journal of the Royal Statistical Society, B. 1960;22:139–153. [Google Scholar]
- 9.Giordano G., Blanchini F., Bruno R., Colaner P., Filippo A.D., Matteo A.D., Colaneri M. Nat Med. 2020:1–32. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gretl Statistical Software (version 1.7.1): http://gretl.en.softtonic.com.
- 11.Guo Y., Cao Q., Hong Zhong-Si, Yan Y. The origin, transmission and clinical therapies on coronavirus disease 2019 (COVID-19) outbreak – an update on the status. Military Medical Research. 2019;7(1) doi: 10.1186/s40779-020-00240-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hildreth C., Lu J.Y. Agricultural Experiment Statistical Bulletin 276. Michigan State University; East Lansing, MI: 1960. Demand relationships with autocorrelated disturbances. [Google Scholar]
- 13.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395:497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ifijeh, M. (31 January2020). “FG Sets up Coronavirus Preparedness Group”. This Day Newspaper. Retrieved 10 March 2020.
- 15.Khan M.A., Atangana A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alexandria Engineering Journal. 2020 in press. [Google Scholar]
- 16.Kramer W. Finite sample efficiency of ordinary least squares in the linear regression model with autocorrelated errors. J Am Statist Assoc. 1980;81:150–154. [Google Scholar]
- 17.Kuranga J.O., Ayinde K., Solomon G.S. Empirical Investigation of Type 1 Error Rate of Some Normality Test Statistics. International Journal of Psychosocial Rehabilitation. 2020;24(4):591–599. doi: 10.37200/IJPR/V24I4/PR201037. [DOI] [Google Scholar]
- 18.Lukman A.F., Ayinde K., Binuomote S., Clement O.A. Modified Ridge-Type Estimator to Combat Multicollinearity: Application to Chemical Data. J Chemom. 2019;2019:e3125. doi: 10.1002/cem.3125. [DOI] [Google Scholar]
- 19.Lukman A.F., Ayinde K., Alabi O., Bamidele R., Aladeitan B.B., Adagunodo T.A. Developing a New Estimator in Linear Regression Model. J Phys: Conf Ser. 2019;1299 doi: 10.1088/1742-6596/1299/1/012128. [DOI] [Google Scholar]
- 20.Lukman A.F., Ayinde K., Aladeitan B.B., Rasak B. An Unbiased Estimator with Prior Information. Arab Journal of Basic and Applied Sciences. 2020;27(1):45–55. [Google Scholar]
- 21.Nadeem S. Coronavirus COVID-19: Available Free Literature Provided by Various Companies. Journals and Organizations around the World. J Ong Chem Res. 2020;5(1):7–13. doi: 10.5281/zenodo.3722904. 2020Document ID: 2020JOCR37. [DOI] [Google Scholar]
- 22.NCDC (2020): http://covid19.ncdc.gov.ng. Accessed April, 28 2020.
- 23.MacLean, O.A., Orton, R., Singer, J. B., Robertson, D. L. (2020). Response to “On the origin and continuing evolution of SARS-CoV-2”. http://virological.org/t/response-to-on-the-origin–and-continuing-evolution-of-sars-cov-2/418.
- 24.Portnoy S., Koenker R. The Gaussian Hare and the Laplacian Tortoise: computability of squared-error vs. absolute-error estimators with discussion. Statistical Science. 1997;12:279–300. [Google Scholar]
- 25.Prais, G.J. and Winsten, C.B. (1954). Trend Estimates and Serial Correlation. Cowles Commission Discussion Paper, Stat. No. 383, University of Chicago, Chicago.
- 26.Shapiro S.S., Wilk M.B. An analysis of variance test for normalty. Biometrika. 1965;52(3):591–611. [Google Scholar]
- 27.Taylor L.D. Estimation by minimizing the sum of absolute errors. In: Zerembka P., editor. Frontiers of Econometrics. Academic Press; New York: 1974. [Google Scholar]
- 28.WHO (2020). World Health Organization Novel Coronavirus (2019-nCoV): Available athttps://www.who.int/emergencies/diseases/novel-coronavirus-2019. Accessed February 7, 2020.
- 29.WHO (2020): Coronavirus disease 2019 (COVID-19) situation report–100. Available athttps://www.who.int/20200425-sitrep-96-19.pdf. Accessed April 27, 2020.
- 30.Wiki (2020): http://en.wikipedia.org/wiki/2020_coronavirus_pandemics_in_Nigeria. Accessed April, 19 2020.
- 31.Wu Y., Chen C., Chan Y. The outbreak of COVID-19: An overview. J Chin Med Assoc. 2020;83(3):217–220. doi: 10.1097/JCMA.0000000000000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Xiang Y., Li W., Zhang Q., Jin Y., Rao W., Zeng L. Timely research papers about COVID-19 in China. Lancet North Am Ed. 2020 doi: 10.1016/S0140-6736(20)30375-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yonar H., Yonar A., Tekindal M.A., Tekindal M. Modeling and Forecasting for the number of cases of the COVID-19 pandemic with the curve estimation models, the Box-Jenkins and exponential smoothing methods. EJMO. 2020;4(2):160–165. [Google Scholar]