Forecasting US recessions: The role of economic uncertainty

Abstract

This letter highlights the role of macroeconomic and financial uncertainty in predicting US recessions. In-sample forecasts using probit models indicate that the two variables are the best predictors of recessions at short horizons. Macroeconomic uncertainty has the highest predictive power up to 7 months ahead and becomes the second best predictor – after the yield curve slope – at longer horizons. Using data up to end-2018, out-of-sample forecasts show that uncertainty has significantly contributed to lower the probability of a recession in 2019, which indeed did not occur.

Highlights

• •Macroeconomic and financial uncertainty indexes contribute to predict US recessions.
• •Using probit recession models, the two indexes are best predictors in the short run.
• •Macro uncertainty is the second best, after the yield curve slope, in the long run.
• •Out-of-sample forecasts show that the two indexes improve model performance.

1. Introduction

It is widely recognized that the yield curve slope has been a good predictor of US economic fluctuations since the 1950’s (Estrella and Hardouvelis, 1991, Estrella and Mishkin, 1998 among others). More recently, Jurado et al. (2015) have emphasized the role of both macroeconomic and financial uncertainty as key drivers of the business cycle: higher uncertainty dampens investment and hiring hence harming growth. We thus investigate whether indicators of economic uncertainty can improve the prediction performance of the typical recession model that uses the yield slope alone in a probit framework.

The most general version of our empirical model includes, among the regressors, the yield curve slope, the macroeconomic and financial uncertainty indexes of Jurado et al. (2015) and other variables that have proven useful to forecast the business cycle, e.g., the policy uncertainty index as shown by Karnizova and Li (2014).

We find that higher levels of both macro and financial uncertainty raise the probability of a recession at different horizons. Evaluating in-sample predictive ability, we show that macroeconomic uncertainty is the best predictor of recessions occurring up to 7-months ahead, while it becomes the second best – after the yield curve slope – for longer horizons. Financial uncertainty is the second best predictor in the short run.

We then use our best model specifications, which always include macroeconomic uncertainty and the yield curve slope, to make out-of-sample forecasts based on observations ending in December 2018. Our augmented models imply a tiny probability of a recession at the end of 2019 (about 5%), much smaller than the roughly 30% probability predicted by a model based on the slope alone. Economic uncertainty is what makes the difference: accounting for the relatively low level of uncertainty in 2018 has significantly reduced the estimated probability of a subsequent recession. Notice that, indeed, there was no recession in 2019.

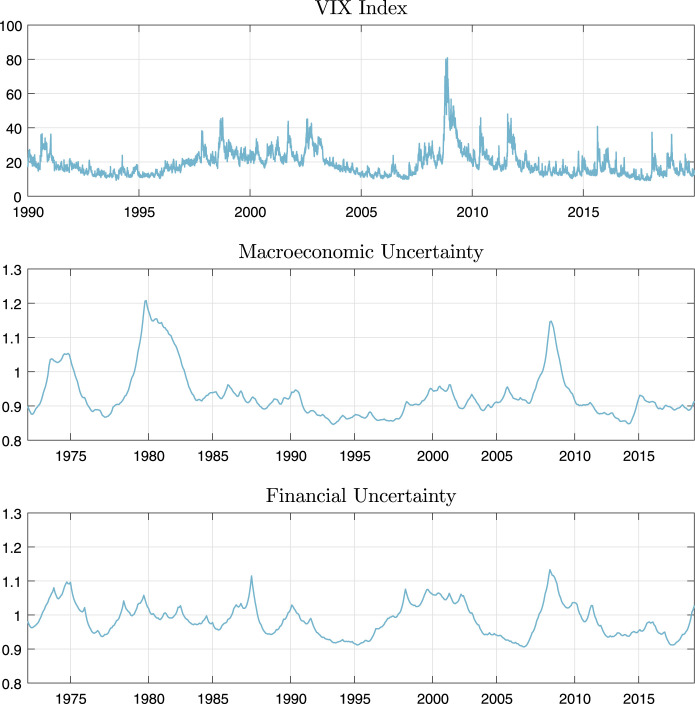
On the opposite side, the first quarter of 2020 saw a marked increase in economic uncertainty due to the Covid-19 outbreak. For example, Ercolani and Natoli (2020) show that the high level of the VIX index – which reached its historical peak in March – signals that the current recession could last beyond 2020.

2. Model and data

In order to estimate the probability of recession in the US, we rely on the standard probit framework:

$$Pro{b}_t(Re{c}_{t+h}=1)=F(\alpha +\beta x_t)$$ (2.1)

where the dependent variable is a dummy equal to one (zero) if the economy is (is not) in an NBER recession (Rec) at time $t+h$, being $h$ the forecast horizon; $x$ represents the set of regressors; $F(.)$ denotes the standard normal cumulative distribution function; $\alpha$ is a constant.

The variable traditionally used to forecast recessions is the yield curve slope, proxied by the 10-year vs. 3-month yield spread. In addition, we consider the macroeconomic and financial uncertainty indexes developed by Jurado et al. (2015) as proxies for US domestic economic uncertainty; to the best of our knowledge, we are the first to use them within such a setting.1

We include other variables whose importance in predicting recessions has been documented in the literature: the US Economic Policy Uncertainty index (EPU); the monthly (log) return on the S&P500 index; the corporate bond spread (yield differential between Moody’s AAA corporate bonds and 10-year Treasuries), proxying credit risk in the corporate sector; the 3-month T-bill rate minus expected inflation, i.e., the short-term real interest rate.2

3. Results

The model is estimated by maximum likelihood using monthly data from January 1972 to December 2018, where predictive horizons $h$ range from 1 to 18 months ahead. While the most updated uncertainty series by Jurado et al. (2015) are available up to end-2019, we rely on the end-2018 vintage. Indeed, these series are not real time, but instead obtained as smoothed estimates using all observations; this fact only allows for an out-of-sample forecast that starts from the end of our sample. Therefore, using information up to December 2018, we compute the probability of a recession happening in 2019 and compare our forecasts with the observed dynamics of the US business cycle.

3.1. Marginal effects

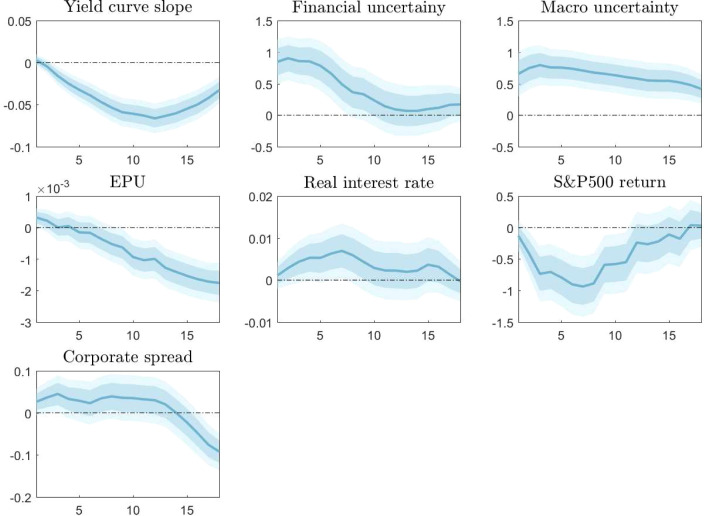
Fig. 3.1 shows the average marginal effects of a specification including all the above-listed variables for all horizons $h$, with 68% and 90% confidence bands. Our results confirm the predictive power of the slope of the yield curve, whose coefficient is negative and significant at all leads: a flatter yield curve increases the probability of a recession.

Fig. 3.1.

Average marginal effects, 1- to 18-month horizons. 68% and 90% confidence bands.

The sign of both macroeconomic and financial uncertainty are also expected. A higher uncertainty, both on the financial and macroeconomic side, increases the probability of a recession at any horizon; differently from financial uncertainty, which is significant only for short-run predictions, macroeconomic uncertainty is statistically significant at any horizon.

As for the EPU, the shape of the associated marginal effects is virtually identical to that found in Karnizova and Li (2014), suggesting that an increase in EPU signals a higher recession probability in the short run, whilst a lower probability in the longer run.

Concerning the other regressors, our results are in line with those found in the literature. For example, when significant, the coefficients associated to the S&P500 return is negative and that of the real interest rate is positive. The effect of the corporate spread is less straightforward: at shorter horizons it is positive, which fits with the intuition that higher spreads embody expectations and/or are the cause of worsening economic conditions; at longer horizons it is instead negative, in line with the idea of a financial cycle expansion sowing the seeds of a subsequent correction and, therefore, economic downturn (see, e.g. Borio et al., 2018).

3.2. Model selection and fit

In this section, we first test whether “augmented models”, which include the uncertainty indexes and other variables on top of the yield curve slope, are better in anticipating recessions than the simplest specification – “slope model” – which features a constant and the slope. Further, we quantify the contribution of each regressor to the in-sample forecasting performance.

As for the first task, we consider three horizons (6, 12, and 18 months) and, for each of them, we select the most parsimonious specification by including only the regressors whose marginal effects are significant (e.g., slope, EPU, and macro uncertainty at 12-month horizon): these are the augmented models. Table 1 shows that the latter always perform better than slope models in terms of Pseudo $R^2$, BIC (Bayesian Information Criterion) and AUROC (Area Under ROC curve), where higher values are associated with higher predictive power.3 Notice that macro uncertainty is present in all the augmented specifications, which highlights its empirical relevance in anticipating recessions; at the 6-month horizon, financial uncertainty is also present.

Table 1.

Goodness-of-fit measures.

Augmented models
Horizon (months)	6	12	18
Regressors	slope	slope	slope
	real rate	EPU	EPU
	S&P500	MacroUnc	MacroUnc
	FinUnc		corp spread
	MacroUnc
Pseudo $R^2$	0.36	0.30	0.32
BIC	−148.03	−157.70	−154.53
AUROC	0.94	0.91	0.90
Slope models
Horizon (months)	6	12	18
Regressors	slope	slope	slope
Pseudo $R^2$	0.16	0.27	0.22
BIC	−188.26	−159.92	−171.37
AUROC	0.80	0.88	0.86

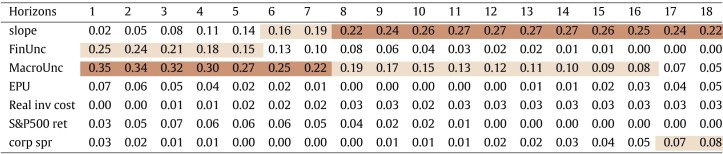
Concerning the second point, Table 2 shows Pseudo $R^2$ for models containing only one regressor at a time, on top of the constant, for horizons up to 18 months. The results are overall consistent with those of Table 1. Macroeconomic uncertainty is the best predictor up to the 7-month horizon, while it becomes the second best, after the slope, from 8 months onwards. Financial uncertainty is the second best predictor up to the 5-month horizon.

Table 2.

Pseudo $R^2$ of single-variable models. First (second) best highlighted in dark (light) brown.

3.3. An out-of-sample forecasting exercise

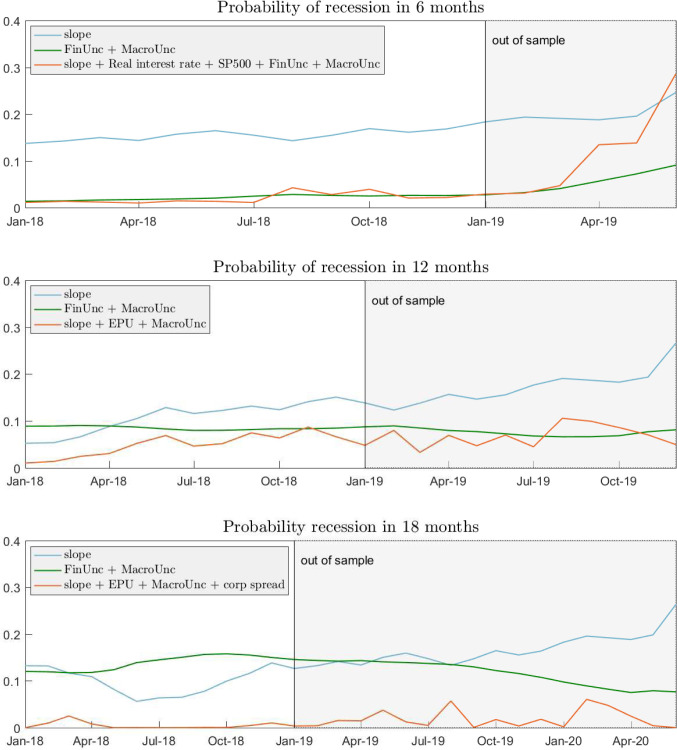
Out-of-sample forecasts are produced using the slope model and the augmented specifications of Table 1, as well as a model including only macroeconomic and financial uncertainty (“uncertainty model”). Fig. 3.2 shows predictions at 6, 12 and 18 months. The out-of-sample period, starting in January 2019, is denoted by gray shaded areas; the slope, augmented and uncertainty model(s) are represented by blue, orange and green lines. As common practice, probabilities are shifted $h$ months ahead to be located exactly when recession is predicted.

Fig. 3.2.

Recession probabilities at different horizons. Slope model (blue lines), augmented model (red lines) and uncertainty model (green lines). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Two results stand out. First, except at the very end of the 6-month forecast, the augmented models imply a much lower recession probability than what the slope model does. For example, at 12-month horizon – which ended in December 2019 without recessions – the slope model predicts recession with probability close to 30%, while the augmented model with probability around 5%.4

Second, macroeconomic and financial uncertainty significantly contribute to reduce recession probabilities, especially in the out-of-sample period where green lines are substantially below blue lines (at any horizon). Arguably, this can be accounted for by the relatively low levels of macro and financial uncertainty prevailing during the last part of the sample. As Fig. 3.3 shows both variables, as well as the popular VIX index, have remained around their historically low levels during the last years. According to the literature, low uncertainty sustains economic growth, therefore shrinking recession probabilities in our model.

Fig. 3.3.

Uncertainty measures over time .

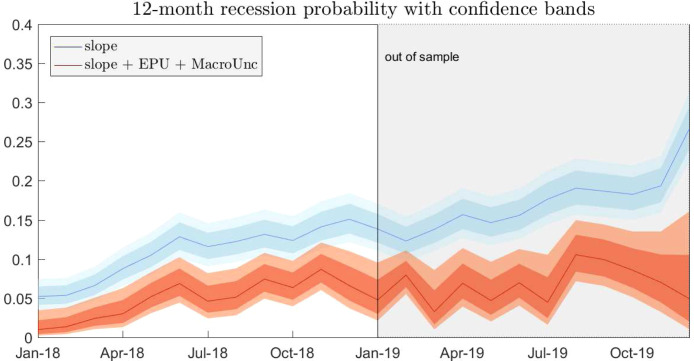
Finally, Fig. 3.4 shows that, for the 12-month horizon, recession probabilities associated to the augmented model are statistically different from the ones of the slope model. We indeed report 68% and 90% bands as shaded areas around estimated probabilities.

Fig. 3.4.

Out-of-sample forecasts. 68% and 90% confidence bands.

3.4. Conclusions

We have shown that both macroeconomic and financial uncertainty can play an important role, together with the yield curve slope, in predicting economic downturns in the United States. Using data up to December 2018, uncertainty indicators have contributed to significantly reduce the estimated probability of a recession during 2019, which ended with no recession.

Declaration of Competing Interest

No author associated with this paper has disclosed any potential or pertinent conflicts which may be perceived to have impending conflict with this work. For full disclosure statements refer to https://doi.org/10.1016/j.econlet.2020.109302.