Simulation-based methods for model building and refinement in cryo-electron microscopy

Abstract

Advances in cryo-electron microscopy (cryo-EM) have revolutionized the structural investigation of large macromolecular assemblies. In this review, we first provide a broad overview of modeling methods used for flexible fitting of molecular models into cryo-EM density maps. We give special attention to approaches rooted in molecular simulations – atomistic molecular dynamics and Monte Carlo. Concise descriptions of the methods are given along with discussion of their advantages, limitations and most popular alternatives. We also describe recent extensions of the widely used molecular dynamics flexible fitting (MDFF) method and discuss how different model building techniques could be incorporated into new hybrid modeling schemes and simulation workflows. Finally, we provide two illustrative examples of model building and refinement strategies employing MDFF, cascade MDFF and RosettaCM. These examples come from recent cryo-EM studies that elucidated transcription preinitiation complexes and shed light on the functional roles of these assemblies in gene expression and gene regulation.

Graphical Abstract

Introduction

Macromolecular assemblies and their diverse functions underlie all of biology. Critical cellular activities - genome duplication and maintenance, gene expression and gene regulation, protein synthesis, chromosome segregation, cell differentiation and development among many others - depend primarily on intricately assembled macromolecular machines rather than individual macromolecules. At present, structural biology is undergoing a revolutionary transition, shifting its focus from structural determination of isolated proteins and small complexes toward the study of enormous biological assemblies and subcellular components. For decades the most successful structural techniques had been X-ray crystallography and nuclear magnetic resonance (NMR). Both techniques are limited by the size of macromolecular complexes that can be studied. In addition, a prerequisite for a successful crystallographic determination is that the complex of interest must be crystallized. For large complexes and macromolecular machines this requirement can be prohibitive, given their considerable flexibility and inherent conformational variability. Yet another complication in crystallography, is the possibility of artificially induced structures due to crystal packing effects. In contrast, NMR may solve true solution-phase structures as well as yield information on flexible complexes and protein dynamics. However, NMR is limited to complexes with small molecular weights, typically below 40–50 kDa.¹

In recent years, cryo-electron microscopy (cryo-EM) has emerged as the most promising technique for the elucidation of large biological structures². Advances in detector technology and image-processing³ have eliminated long-standing limits on cryo-EM resolution and enabled high-resolution EM structures not only for complexes with high symmetry and stability^4–6 but also routinely for a wide range of large, asymmetric or conformationally diverse biological complexes^7–9. Prominent examples of this ‘resolution revolution’ in cryo-EM are listed as follows. In 2013, the structure of the mammalian TRP channel (TRPV1) was determined at 3.4 Å resolution^10–11 and marked the first cryo-EM experiment to break the side-chain resolution barrier without the need for crystallization. In 2014, notable successes of cryo-EM included the solved 3 – 5 Å resolution structures of β-galactosidase¹², membrane proteins^13–15 and ribosomal machineries¹⁶. In 2015, Campbell and colleagues achieved a 2.8-Å resolution cryo-EM reconstruction of the Thermoplasma acidophilum 20S proteasome¹⁷. Also in 2015, the Subramaniam group refined β-galactosidase to an unprecedented 2.2-Å resolution¹⁸. More recently, structures of the human and yeast transcription machineries were determined at near-atomic resolution^19–23.

Apart from tremendously improved resolution, cryo-EM has certain fundamental advantages over traditional X-ray crystallography. First, cryo-EM does not require crystallization and, therefore, smaller amounts of the protein/macromolecular complex may prove adequate for structure determination. Samples are prepared by cryogenic freezing in ‘vitreous ice’ - a frozen, hydrated state on an EM grid. This allows cryo-EM to visualize biological complexes closer to in vivo conditions²⁴, thus avoiding potential artifacts from crystallization. Finally, cryo-EM is superior to crystallography in its ability to uncover the conformational variability of complex biological systems. Single-particle image classification in EM typically leads to multiple classes of conformations simultaneously preset in the sample, thus capturing biological complexes in multiple functional states^25–28. Further advances of cryo-EM analysis along this direction, hold the promise of visualizing the native dynamics of complex molecular machinery or obtaining direct experimental insight into the free energy landscapes that govern conformational changes upon protein association, ligand binding or ATP-hydrolysis. Finally, parallel advances in cryo-electron tomography (cryo-ET) and cryo-ET focused-ion-beam milling are likely to push the resolution of this imaging technique to levels where it becomes compatible with single-particle cryo-EM^29–30. Bridging the resolution gap between cryo-ET and cryo-EM could open a new window into cell biology, allowing the creation of structural models of subcellular components at unprecedented near-atomic structural detail.

As a technique, Cryo-EM relies on extensive data processing to produce a 3-D atomistic model from the original single-particle data. The last stage in this data processing involves the creation of atomistic models that best conform to the experimental cryo-EM density. Model generation is where cryo-EM analysis converges with the field of molecular modeling as most of the techniques for model fitting have their origins in the molecular modeling field. Molecular modeling has a long history of addressing the structures, flexibility and microscopic dynamics of molecular complexes while also uncovering the rugged free energy landscapes that underly conformational change in biological systems. Furthermore, hybrid and integrative modeling is an emergent area that brings together experimental data from diverse biophysical techniques to shed light on biological complexes not amenable to routine structural methods^31–32. From the above, it is clear that molecular modeling has many points of intersection with the field cryo-EM and the synergy between the two areas of inquiry goes well beyond the issue of model fitting into cryo-EM maps.

This review aims to provide a broad overview of modeling methods used for flexible fitting into cryo-EM envelopes. We then give special focus on approaches rooted in molecular simulations – atomistic MD and Monte Carlo. We describe recent extensions of the widely used molecular dynamics flexible fitting (MDFF) method^33–34. Finally, we present two non-trivial applications of the method to transcription preinitiation complexes while emphasizing the important aspects of model validation.

Overview of methods for rigid and flexible fitting

The simplest way to generate models from a 3D cryo-EM reconstruction is by rigid body fitting of components of the biological complex, e.g. known high-resolution structures of protein subunits or domains. Homology modeling can be applied when suitable structures with high sequence conservation to the target protein are available in the Protein Data Bank. When neither structures nor structural homologs are available, the EM map can still be used to identify and position secondary structure elements via computational tools like SSHunter³⁵, ab initio protein modeling using EM-fold³⁶ and de novo protein structure prediction using RosettaCM^37–38. Automated rigid-body docking performs an exhaustive search over a 6-dimensional space (encompassing all translational and rotational degrees of freedom) to maximize the cross-correlation between the cryo-EM map and a density map simulated from the atomic model^39–40. Fast Fourier Transform (FFT) can reduce the complexity of this 6-D search by transforming the translational degrees of freedom to Fourier space, leaving only the rotational degrees of freedom to be evaluated in real space⁴¹. Over the years, improvements were added to rigid-body docking, including local cross-correlation score (LLC)⁴², core-weighted (CW)⁴³ cross-correlation score, vector quantization and geometric hashing⁴⁴. These were introduced in order to either customize the docking process or improve computational efficiency. By now rigid body docking is considered routine and has been made readily available in packages like Situs⁴¹ or in visualization software such as UCSF Chimera⁴⁵. We briefly mention rigid body docking in this review only because it constitutes a necessary initial step before more sophisticated flexible fitting protocols could be applied.

Flexible fitting allows conformational variation to occur in the model during the fitting procedure, thus greatly increasing the correlation between the cryo-EM map and the modeled structure. A variety of flexible fitting methods have been proposed, including real-space refinement upon segmented rigid-body docking⁴⁶, normal-mode calculation based on optimization of the correlation between structure and map⁴⁷, coarse-grained model fitting based on vector quantization⁴⁸. Other methodologies have implemented external forces that are applied in conjunction with molecular dynamics (MD) simulations to drive the atoms along the gradient of the EM map³³ or the cross-correlation coefficient of the structure and the EM map^49–50.

High-resolution cryo-EM maps pose particular challenges to traditional map-guided structure determination techniques as the interpretation of such maps requires extremely precise model building and validation protocols⁵¹. Specifically, high-resolution maps contain an extraordinary amount of structural detail resulting in many sharp features that could potentially confound gradient search fitting methods by trapping the conformation into local minima. Additionally, high resolution EM maps reveal conformations of protein sidechains in the core of the complex, which are more flexible than the backbone. As a result, new structure determination techniques must now be able to precisely model protein dihedral angles up to the C_β atoms while also respecting the boundaries of the EM map⁵². In order to produce atomic models with correct backbone and sidechain geometries, as well as minimum potential energy, a variety of methods have been proposed. Automated model-building protocols, which rely heavily on geometric optimization, include Buccaneer⁵³, ARP/wARP⁵⁴ and Moulder⁵⁵. Similar to PHENIX^{46, 56} and COOT⁵⁷, these tools were designed for X-ray crystallography but have also proven useful in cryo-EM. More recently, Monte Carlo simulation-based segment building and refinement protocols with heuristic force fields were introduced in the Rosetta package⁵¹. Building on the capabilities of flexible fitting approaches, Flex-EM⁵⁸ combines a Monte Carlo search with conjugate gradient minimization and simulated annealing MD, while DireX⁵⁹ employs a deformed elastic network to flexibly fit models into high-resolution EM maps.

Molecular dynamics flexible fitting

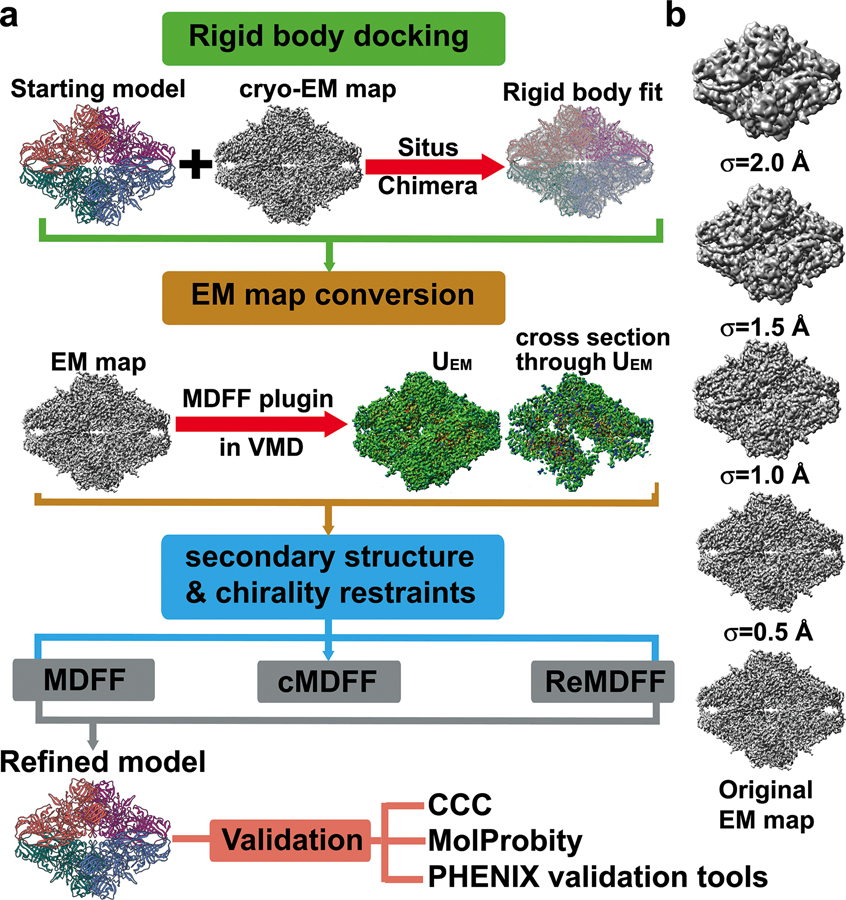
In 2008, Trabuco et al. proposed the use of molecular dynamics (MD) simulations to flexibly fit atomic structures into EM maps³³. Since its inception, the molecular dynamics flexible fitting method (MDFF) has gained increasing popularity due to its automated setup, which has been integrated into the visualization package VMD⁶⁰, as well as its success in generating pseudoatomic models from varying quality EM maps (Figure 1). MDFF brings together the most desirable features of several existing methods. First, MDFF takes into account all information contained within the cryo-EM map and thus avoids the use of reduced representations or global similarity measures to drive the fitting. Since the external force is applied locally, it is possible to fit some of the components of the macromolecule even when the structure of the remaining components is not known. Importantly, the degree of success is expected to be independent of system size, which proves advantageous over optimization and Monte-Carlo methods that rely on global-optimization criteria³³.

Figure 1. Simulation-based methods for flexible fitting into cryo-EM maps.

a) Flowchart representing the popular MDFF, cascade MDFF and resolution exchange MDFF methods; b) A series of Gaussian-blurred EM maps and the original unfiltered cryo-EM map used for cascade MDFF and resolution exchange MDFF. The maps illustrate the change in smoothness and level of detail of the resulting U_EM potentials used for the intermediate stages of the fitting protocol.

In MDFF, an external potential is derived from the 3D cryo-EM map and incorporated into the MD simulation by adding two terms to the MD potential energy function,

$$U_{MDFF}= U_{MD}+ U_{EM}+ U_{SS}$$ (1)

U_MD is the MD potential energy function (or force field) that describes the interactions between all atoms in the system. During MD simulations, the forces experienced by the atoms are obtained from U_MD and used to iteratively solve the Newtonian equations of motion. When coupled with flexible fitting, U_MD maintains the stereochemical quality of the structure, ensuring that it does not stray into non-physical states. U_EM is the potential derived from the experimental EM map and U_SS preserves the secondary structure of the protein or nucleic acid. The EM potential term takes the form,

$$U_{EM}\left(\mathit{R}\right)={\sum }_j{w}_j{V}_{EM}\left({\mathit{r}}_j\right)$$ (2)

where R is the set of Cartesian coordinates of all atoms in the system and V_EM is defined as,

$$V_{EM}\left(\mathit{R}\right)=\{\begin{array}{c}\xi \left[1- \frac{\Phi \left(r\right) - {\Phi }_{thr}}{{\Phi }_{max} - {\Phi }_{thr}}\right]if \Phi \left(\mathit{r}\right)\ge {\Phi }_{thr}\\ \xi \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} if \Phi \left(\mathit{r}\right)< {\Phi }_{thr}\end{array}$$ (3)

Here, Φ(r) is the EM density at position r, Φ_max is the maximum value of all voxels in the EM map, Φ_thr is the threshold value used to discard data not corresponding to the biomolecule, ξ, is an arbitrary scaling factor, w_j is a weight that can be varied according to the atomic mass of the atom type and r_j is the position of atom j. Typically, the threshold value, Φ_thr, is selected based on minimum value between density peaks in the EM density histogram. The higher peaks correspond to the solvent’s contribution to the EM density and can be ignored during fitting. Given the equation for the EM potential (U_EM), the force applied to each atom inside the EM map is,

$${\mathit{f}}_i^{EM}= -\frac{\partial }{\partial {\mathit{r}}_i}{U}_{EM}\left(\mathit{R}\right)= -w_i\frac{\partial }{\partial {\mathit{r}}_i}V\left({\mathit{r}}_i\right)$$ (4)

Thus, the external forces drive the system along the negative gradient of EM density, effectively steering atoms away from low-density regions and into higher-density regions. The external forces, ${\mathit{f}}_i^{EM}$, can be tuned via the scaling factor ξ, which is applied uniformly. Additionally, one can adjust w_i on a per-atom basis. Due to the large external forces the structure experiences during MDFF, it becomes necessary to maintain the integrity of the secondary structure elements through harmonic restraints,

$$U_{SS}={\sum }_{\mu }{k}_{\mu }{\left(X_{\mu }-X_{\mu }^0\right)}^2$$ (5)

In equation 5, the restraints X_μ represent the protein dihedral angles φ and ψ, RNA/DNA dihedral angles α, β, γ, δ, ε, ζ, χ and interatomic distances d₁ and d₂, which describe the hydrogen-bonding between base pairs. Equilibrium values, $X_{\mu }^0$, are generally taken from the initial atomic structure, although these can be set to a different value.

Generally, the fitting procedure is carried out in a multistep fashion, varying parameters at every step, such that the atomic structure gradually converges into the EM map. Prior to running MDFF, the atomic structure is docked into the EM map through rigid-body fitting. Following this, multiple MDFF steps are executed with decreasing values for the scaling factor, ξ (typically 0.3 – 0.1 kcal/mol). At the end of every step, convergence is evaluated through a goodness measure, either by the stabilization of root-mean-square deviation (RMSD) or the cross-correlation between the trajectory and the EM map. For cross-correlation, the Pearson’s correlation coefficient (cross-correlation coefficient) is computed between the original EM map and a simulated map, generated from the MDFF trajectory,

$${\rho }_{SE}= \frac{\langle (S-\langle S\rangle )(E-\langle E\rangle )\rangle }{{\sigma }_S{\sigma }_E}$$ (6)

In the above equation, $\langle S\rangle$ and $\langle E\rangle$ denote the average voxel values of the simulated and experimental maps, while ${\sigma }_S$ and ${\sigma }_E$ corresponds to their standard deviation. Typically, cross-correlation coefficients should be computed considering only voxels inside the molecular envelope of the simulated map (local correlation)⁶¹. The global correlation, which is commonly reported in the EM literature, is sensitive to the box size arbitrarily selected in the electron microscopy experiment. Larger boxes result in artificially higher correlation values, leading to overestimation of the quality of fit.

Cascade MDFF

The weakness of the original MDFF implementation lies in the method’s reliance on the MD engine to sample the conformational space confined to the EM map potential (V_EM). The equilibrium structure obtained from MD simulations represents a global minimum in V_EM. This is not an issue for normal MDFF and low-resolution maps (6 – 15 Å), where the global minimum is broad and can accommodate an ensemble of conformations defined by the overall shape of the macromolecule^{33, 50}. However, at higher resolution (< 4 Å), the landscape of V_EM becomes very rugged and features multiple proximal local minima corresponding to recurring spatial patterns within a macromolecule (i.e. helices, β-sheets). The energetic barriers separating such potential minima are typically twice as high as those in low-resolution maps, which allows the fitted structure to become “trapped” within undesired local minima instead of reaching the global minimum of V_EM. Consequently, relying on normal MDFF alone will likely yield structurally poor or functionally irrelevant models with high-resolution EM maps.

In cascade MDFF (cMDFF), the initial structure is sequentially fitted to a series of density maps filtered to lower resolution from the original EM map (Figure 1). The protocol starts at the lowest resolution level and proceeds in order of increasing resolution ending with the original EM map (Figure 1b). Fitting at lower resolution allows model fitting to be guided first by the largest scale features of the EM density. This is followed by smaller-scale refinements performed with the higher-resolution densities. This enables an efficient conformational search that avoids entrapment into local minima and allows accurate modeling of both the global and local features of the EM density. The assumption in cMDFF is that the original map can be expressed as a sum of Gaussians,

$$V_{EM}={\sum }_n{c}_{n}G\left(\mathit{r};{{\mathit{r}}^{\prime }}_n,s_n\right)$$ (7)

Here, c_n, is a weight, G(r; r’_n, s_n) is a Gaussian function centered at r’_n with half-width s_n and evaluated at r. New maps are obtained by applying a Gaussian blur of width ${\sigma }_i\ge 0$ Å to the original EM map, where i is the i^th map in a series of potential maps of length L. Given equation 7, the result of a Gaussian blur on $V_{EM}$ with half-width ${\sigma }_i$ is,

$$V_{{\sigma }_i}\left(\mathit{r}\right)= {\sum }_n{c}_{n}G\left(\mathit{r};{{\mathit{r}}^{\prime }}_n,\sqrt{s_n^2+ {\sigma }_i^2}\right)$$ (8)

Equation 8 reveals that the half-width ${\sigma }_i$ allows one to tune the characteristic width of the EM map through the half-widths of its component Gaussians $\sqrt{s_n^2+ {\sigma }_i^2}$. Thus, initial fitting starts with a large ${\sigma }_1$, corresponding to a smoother potential that allows more structure mobility. Decreasing values of ${\sigma }_i$ correspond to narrower potentials with steeper gradients, permitting the structure to the gradually settle into the original EM map, which is characterized by ${\sigma }_L\ge 0$ Å. In practice, optimal values for ${\sigma }_1$ and the change in ${\sigma }_i$ from one map to another are case-dependent. Generally, initial structures far from the ideal conformation benefit from a large ${\sigma }_i$ (> 5 Å) so as to better explore the conformational space. On the other hand, if the original map has a high resolution, small changes in ${\sigma }_i$ (< 1 Å) would allow a gradual convergence required to avoid being trapped in local potential minima.

Resolution exchange MDFF

Resolution exchange MDFF combines the advantages of cascade MDFF with the efficient sampling of the replica exchange MD method (REMD)⁶² (Figure 1). Briefly, REMD is an enhanced sampling method that explores conformational space separated by energetic barriers too high to be sampled by conventional MD. Multiple simulations (replicas) are executed in parallel at increasing temperatures (T₁ < T₂ < T₃…), where the lowest temperature (T₁) is the temperature of interest. At regular time intervals, the instantaneous conformations of neighboring replicas are compared in terms of their energy. Exchange of configuration between neighboring replicas are then permitted according to the Metropolis criterion. Under the REMD paradigm, the highest temperature replicas overcome the energetic barriers between conformational intermediates. Applying the Metropolis criterion guarantees that the lowest temperature replica is Boltzmann-distributed and ergodic. An important generalization of REMD is Hamiltonian REMD (H-REMD)⁶³, in which the force field or Hamiltonian of the system (in addition to the temperature) could be used as a replica-coordinate. Analogously, resolution exchange MDFF (ReMDFF) builds upon the H-REMD ideas by defining neighboring replicas in terms of their EM map half-widths, ${\sigma }_i$, instead of temperature. By increasing the characteristic width of the original EM map (${\sigma }_1< {\sigma }_2< {\sigma }_3\dots$), ReMDFF can be thought of as a fully automated variant of cMDFF. Specifically, for ReMDFF the Metropolis acceptance probability is,

$$p\left(x_i, {\sigma }_i, x_j, {\sigma }_j\right)=\min \left(1,exp\left(\frac{-E\left(x_i,{\sigma }_j\right)-E\left(x_j,{\sigma }_i\right)+E\left(x_i,{\sigma }_i\right)+E\left(x_j,{\sigma }_j\right)}{k_{B}T}\right)\right)$$ (9)

Here, $k_B$ is the Boltzmann constant, $E\left(x,\sigma \right)$ is the total energy of configuration x within a fitting potential map of blur width σ. Based on equation 9, exchanges occur between a poorly-fitted model at a high resolution with a well-fitted model at low resolution leading to stepwise improvements in the overall fit. The well-fitted model is further refined against the high-resolution map until exchanges between the chosen resolution ceases and convergence is reached. In terms of efficiency and automation, ReMDFF has advantages over normal MDFF and cMDFF as it can take advantage of massively-parallel computer architectures and the powerful and adaptive interface of NAMD⁶⁴.

Pipelines and hybrid modeling schemes

While the MDFF protocols have been highly successful at the refinement of models from low- to high-resolution cryo-EM data, they typically use as starting points high quality homology models, which may not always be available. In cases where the resolution is sufficiently high (2 – 5 Å), de novo modeling may be employed to construct a primary sequence directly into the density without a structural template⁶⁵. However, as resolution decreases, sequence registration and overall topology become more ambiguous and additional structural information is required to build a de novo model. Most de novo techniques employ a hierarchical approach and build up the structure beginning with predefined secondary structure elements within the density^{35, 66}. Following this, a Cα trace is constructed, either through pathwalking⁶⁷ or other pattern recognition strategies^68–69. A fully atomistic model, including unresolved loop segments and side-chains, can then be derived and optimized from the Cα trace using density-guided model building as implemented for instance in the Rosetta package⁵¹. Briefly, Rosetta iteratively assembles the protein backbone into the EM density using small fragments from a PDB-generated fragment library. Fragments are selected based on local sequence homology and Monte Carlo sampling is employed with an empirical force field to assemble and optimize each fragment. Throughout the Monte Carlo trajectory trial moves replace poorly fitted regions of the model with backbone fragments from the PDB that have been pre-minimized to fit the density. During the minimization step, proper peptide bond geometry at the fragment endpoints is maintained through coordinate constraints while backbone and sidechain geometry is maintained through Ramachandran and rotameric constraints. Due to the variable resolution observed in most EM maps, the Rosetta package alternates between refinement of atomic B factors and model rebuilding to maximize real-space correlation between model and map. Collectively, this approach enables the progression from a poor-quality starting model to a highly accurate atomic model and has a substantially better radius of convergence than MDFF⁵¹. However, as resolution decreases ( > 5 Å) the limited structural information from the EM map constrains Rosetta’s ability to correctly position fragments from large protein segments⁵¹. To alleviate this constraint, DiMaio and co-workers introduced RosettaES⁷⁰. Building on the previous fragment-assembly approach, RosettaES utilizes fragment ensembles that are pruned in a “beam search” fashion. This approach was shown to accurately and automatically model missing segments up to 100 residues from cryo-EM maps in the absence of a template structure.

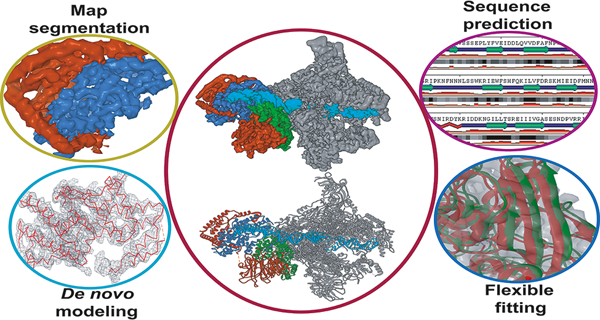
Generally, the construction of accurate atomic models from high-resolution cryo-EM data will require the combination of several methodologies in a pipeline or hybrid modeling scheme. For example, Rosetta has been combined with MDFF in an iterative protocol⁷¹ to refine starting models generated from EM-Fold³⁶. Guided by the cryo-EM map, the iterative MDFF-Rosetta method cycles between rounds of MDFF, to refine secondary structure, and Rosetta, to refine sidechains and loops regions. In a similar fashion, homology modeling has been combined with iterative MDFF-Rosetta to build conformers of the 26S proteasome at less than 5 Å resolution⁷². Another recent study combined a wide range of modeling tools and MD simulations to derive atomic models for the AMPA receptor-TARP in closed, active and desensitized states⁷³. Arguably, the most automated and sophisticated pipeline to date is CryoFold⁷⁴, which was recently proposed by Singharoy and co-workers. CryoFold is an atomistic-physical algorithm that combines three different refinement methodologies (discussed below) to derive structures from EM data in a fully automated fashion (Figure 2). In CryoFold, search models are constructed de novo using Modeling Employing Limited Data (MELD)^75–76 simulations guided by backbone traces generated from MAINchain Model tracing from Spanning Tree (MAINMAST)⁶⁹. These models are then refined in the EM density with ReMDFF to produce an accurate atomic model.

Figure 2.

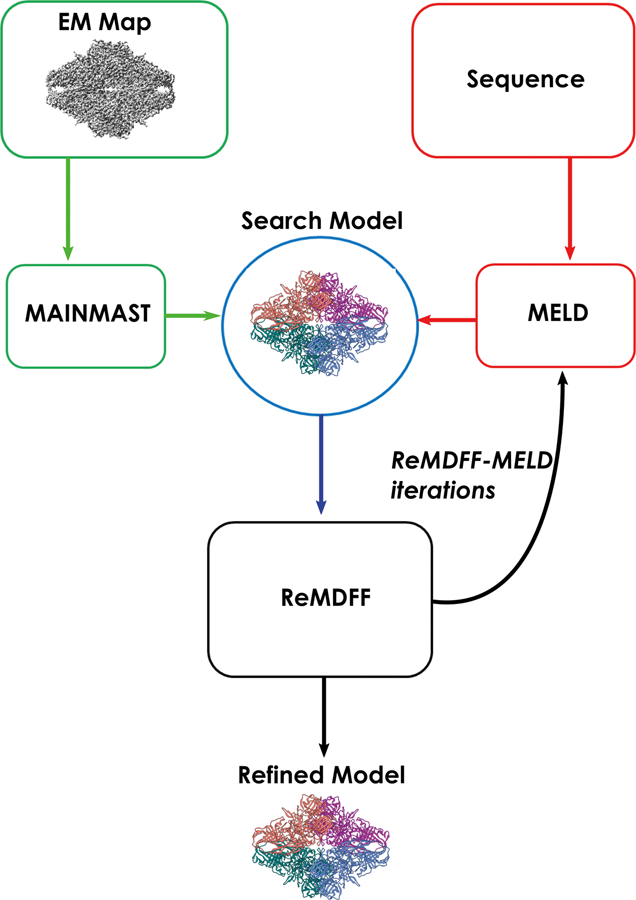
Schematic representation of the Cryo-fold fitting protocol.

MELD incorporates empirical data into MD simulations through a Bayesian inference approach. The first step in the CryoFold pipeline constructs the Bayesian likelihood from secondary structure prediction (PSIPRED) of the target sequence. A 70% confidence is employed, which has been shown to be an optimal condition for MELD to recover from uncertainties in secondary structure prediction⁷⁷. Additionally, MELD extracts information for the Bayesian prior from the MD force field. Following this, Cartesian restraints are derived for any region that was determined with high accuracy. These restraints are imposed on the Cα atoms during MELD simulations which allows already resolved residues to fluctuate around their initial position. Distance restraints are then derived through the application of MAINMAST, a de novo modeling program that directly builds main-chain structures from EM maps. Briefly, MAINMAST recognizes and identifies local dense points (LDPs) in the EM map through the mean shifting algorithm. Once identified, LDPs are connected through a minimum spanning tree (MST). The MST is then iteratively refined with the tabu search algorithm which attempts to explore a large search space through a list of moves that were once considered and then forbidden. In the last step, the target sequence is aligned with the longest path of the refined MST. Combined with the Cartesian restraints, MAINMAST-derived distance restraints guide the sampling of the search model via flat-bottom harmonic potentials.

In the next step of CryoFold a Hamiltonian and temperature replica exchange (H,T-REMD) protocol is employed to accelerate the sampling of the low-energy conformations in MELD. The Hamiltonian term is altered by modifying the force constant of the harmonic restraints derived from secondary structure prediction and MAINMAST. Under this paradigm, higher temperature simulations have vanishing force constants so that sampling is improved. In contrast, force constants are enforced at their maximum for lower temperature simulations. From the ensemble of structures generated by H,T-REMD, the model with the best cross-correlation to the EM map is selected for subsequent refinement with ReMDFF. Although ReMDFF parameters may vary depending on the system, the authors report that 5 to 11 blurred maps with an increasing half-width of $\sigma$ = 0.5 Å seems sufficient to improve cross-correlation and structural statistics. From ReMDFF, the model with the highest EMRinger⁵² score is selected as the starting point for the next round of MELD-ReMDFF. This process continues iteratively until the change in cross-correlation between consecutive rounds is less than 0.1. During iterative refinement distance restraints from the ReMDFF model are updated and the pairs of residues present in those interactions are enforced at different accuracy levels.

CryoFold appears to be a promising technique for deriving macromolecular complexes from cryo-EM data. Nonetheless, success of the modeling strategy is largely dependent on the initial Cα trace generated by MAINMAST. Even with MELD accelerated MD it is not clear if the simulation could recover from a poorly determined mainchain trace. This highlights the fact that even the availability of sophisticated semi-automated modeling tools and pipelines may require intervention from an experienced molecular modeler. Success of the protocols and the quality of the final models for complicated cases critically depend on the quality of the experimental map, the variability of local resolution, potential difficulties in tracing the protein backbone through ambiguously resolved regions of the EM density. In all instances, careful evaluation and validation of the final models is required.

Model validation

In principle, data from single-particle cryo-EM is representative of a diverse ensemble of configurations present in solution^{26, 78}. Yet, a single model representing the best fit to the EM density is usually reported. As a consequence, EM reconstructions even at high resolution feature poorly resolved regions from either conformational ensemble averaging or motion smearing. Thus, assessing the model quality and reliability has to encompass three distinct aspects: 1) quality of the EM map itself as represented by the local resolution; 2) the extent of correspondence between the atomic model and the EM density (map-to-model fit); and 3) molecular geometry, including the stereochemical properties of the derived structure.

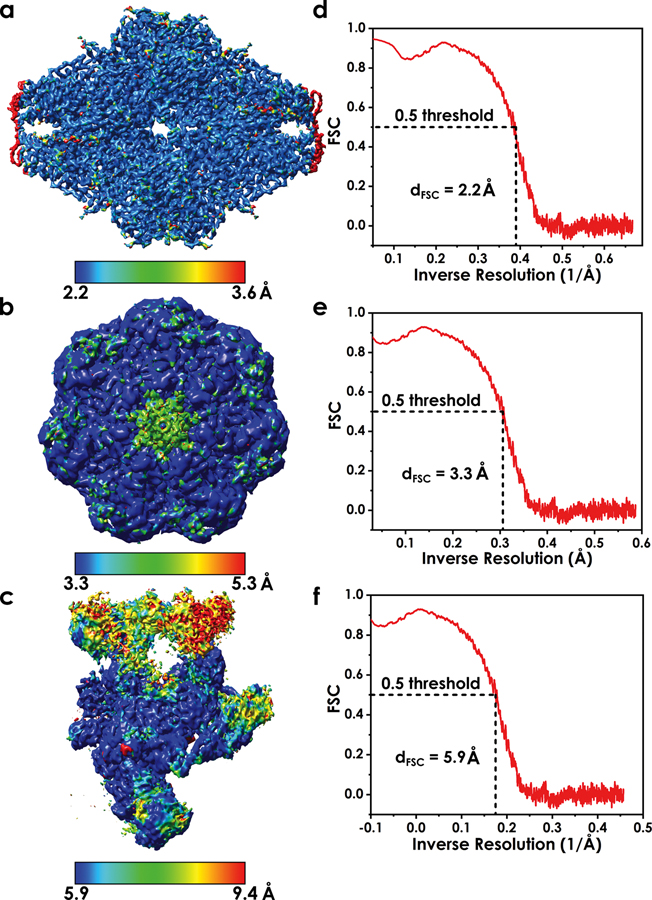
Global measures for map resolution, such as the Fourier shell correlation (FSC) procedure, cannot assess local variations in resolution (Figure 3a–c) which may be caused by sample heterogeneity or image-processing errors⁷⁹. Additionally, FSC estimation of overall resolution (Figure 3d–f) relies on an arbitrary threshold (0.143 or 0.5)^80–81 which has been subjected to various interpretations on its meaning⁸². Consequently, relying on a global assessment of map resolution can lead to over-fitting of the model to the EM data. To avoid over-fitting, tools like ResMap⁸³ or Bsoft⁸⁴ can identify regions of spatially variable resolution, thus, revealing local regions of reduced information that may affect model accuracy^85–86. From a global perspective, over-fitting can be minimized by reducing the number of refined parameters, either through the use of secondary structure constraints, selective inclusion of certain atoms or by providing supplemental structural information via a physics-based force field⁸⁷.

Figure 3. Variable local resolution as a major challenge for model building in cryo-EM.

a-c) Local resolution color mapped onto three example EM maps. The maps were chosen to showcase narrow, intermediate and wide range of local resolution; d-f) FSC curves are presented for each of the maps to illustrate how overall map resolution is determined. Notably, overall resolution of a cryo-EM map is a global property and may not be indicative of quality for specific region of the EM density.

Although several metrics exist to measure the goodness-of-fit between the model and the experimental density^88–89, the most commonly used metric is Pearson’s correlation coefficient (CC)^{61, 90}. Calculated in real-space, the model-map CC can take both global (GCC) and local (LCC) forms. Additionally, reciprocal space metrics, such as integrated Fourier shell coefficients (iFSC) and estimated phase error⁵¹, can be employed to judge goodness-of-fit. Finally, EMRinger⁵² can assess both the stereochemical quality and the map-to-model fit for high resolution EM maps, wherein protein side chains have been resolved. Additionally, several cross-validation metrics have been proposed to identify over-fitting to high-resolution EM maps^{51, 91–93}. These metrics split the original EM data into multiple independent sets that are subsequently used for model construction, refinement and accuracy assessment.

MolProbity⁹⁴ is a common structural biology tool for evaluating the integrity of biomolecular models. The package was originally developed for X-ray crystallography but has become the de-facto standard for analyzing of protein geometry in cryo-EM structures as well. By comparing a number of geometric properties of the model to statistics derived from the Protein Data Bank, MolProbity reveals geometric defects (bond, angle or torsion deviations), atomic clashes, Ramachandran and sidechain rotameric outliers post refinement. Recently, a comprehensive set of cryo-EM validation tools was integrated into the PHENIX software package⁴⁶.

Application examples

Here we provide two illustrative examples of model building and refinement strategies that include MDFF or cascade MDFF. These examples come from recent studies that have focused on solving the structures of transcription preinitiation complexes (PICs) from cryo-EM: 1) modeling RNA Polymerase I PIC in multiple functional states; and 2) integrative structural determination of RNA Polymerase II PIC, including the flexible transcription factor IIH (TFIIH) subcomplex. Transcription initiation complexes are large and amazingly dynamic macromolecular machines whose function and regulation underlie all of gene expression. Their size, complexity and dynamic nature present non-trivial challenges for molecular modeling. PICs encompass numerous subunits in complex arrangements (>20 protein chains, singe-stranded and double-stranded DNA and a DNA/RNA hybrid). The presence of flexible and unstructured regions interspersed into the assemblies complicates tracing of the protein backbone through the EM densities. Moreover, a degree of mobility for certain parts of the structure results in significant variation in the local EM resolution. For these reasons, the PIC systems present a more realistic modeling challenge as compared to structures typically used for benchmarking and assessment of EM modeling methods (e.g. TRVP or β-galactosidase), which are characterized by more uniform local resolution and high secondary structure content.

1. Modeling RNA polymerase I PIC

Eukaryotic RNA synthesis is catalyzed by three classes of RNA Polymerases (Pol I, II and III). RNA Polymerase I (Pol I) transcribes large ribosomal precursor RNA (pre-rRNA) and accounts for a major fraction of cellular RNA synthesis. Pol I function is highly regulated, and misregulation has been linked to many diseases including various types of cancer. The following regulatory factors - Rrn3, the Core Factor (CF), the TATA-box Binding Protein (TBP), and the Upstream Activation Factor (UAF) - are key for Pol I PIC assembly and function. Rrn3 ensures that Pol I adopts a monomeric initiation-competent form. CF recruits Pol I/Rrn3 to the ribosomal DNA promoter and plays a role in transcription bubble opening. While not strictly required, UAF and TBP play a stimulatory role in Pol I transcription. Despite extensive experimental studies, many aspects of Pol I PIC assembly and function remained enigmatic: (i) how Pol I PIC opens promoter DNA without any requirement for force generation through ATPase activity; (ii) what is the role of the Core Factor in promoter opening; (iii) how protein dynamics promotes the ordered transitions of the Pol I-CF assembly from a closed complex (CC), through initial transcribing complex (ITC) and eventually an elongation complex (EC)? Answering these questions requires detailed structural knowledge of the Pol I PIC.

Here we describe a recent study, which combined single-particle cryo-EM and computational modeling to determine structures of Pol I PIC in three distinct functional states visualized at 3.8 – 4.3 Å resolution⁹⁵. The computational strategy employed homology modelling and de novo model building combined with molecular dynamics flexible fitting to the cryo-EM data. The analysis unveiled the modular architecture of the Pol I PIC, providing unique insights into the mechanism of transcription initiation. The overall modeling protocol involved five stages: 1) collecting all available experimental data, including sequences for all protein chains, existing structures and homologs; 2) using the GeneSilico metaserver to predict secondary structures for all protein chains and register the sequences; 3) building a homology model for Pol I or de novo models for the protein chains comprising CF; 4) applying MDFF fitting to the initial model of core Pol I; and 5) structure refinement after combining Pol I, CF and DNA.

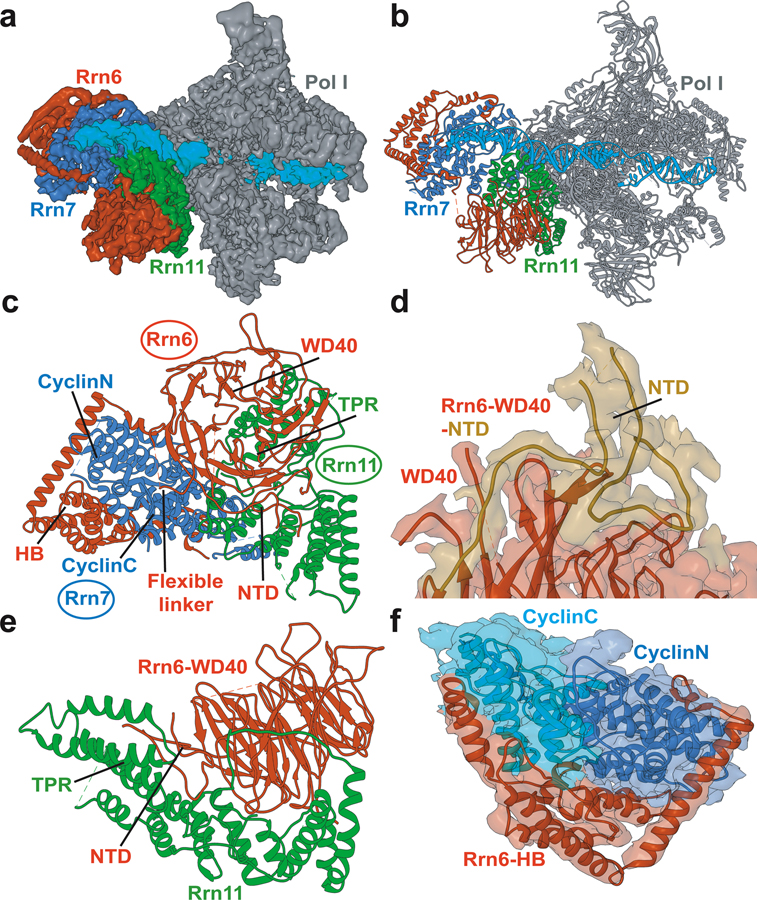
Three protein chains come together to form Core Factor - Rrn6, Rrn7 and Rrn11 (Figure 4). Rrn6 contains a predicted WD40 β-propeller and a helical domain. Rrn7 is predicted to share sequence homology with TFIIB containing an N-terminal zinc ribbon domain, two cyclin domains, and a C-terminal domain. Rrn11 contains a predicted tetratricopeptide repeat (TPR) domain. Due to lack of suitable templates for homology modeling the chains of CF were primarily built de novo. De novo model building requires map segmentation. The CF structure consists of intertwined subunits with hard to distinguish protein-protein interfaces, which made map segmentation difficult. Without proper segmentation, automatic de novo model building tools such as RosettaCM de novo model building or Phenix.map_to_model cannot be successfully employed. In this case, known homologues of Rrn6-WD40, the two cyclin folds from TFIIB, along with other structural elements were used to segment the CF density into three regions, corresponding to the three distinct protein chains of CF. Individual secondary structure fragments were then constructed and inserted into the segmented EM density. The main-chain trace was extended to connect the secondary structure fragments using the density-guided loop building functionality in PHENIX. Residues along the main-chain trace were then converted to the correct amino acid sequence and adjusted with COOT. The protocol also highlighted the advantages of using Rosetta for model building. Specifically, the Rrn6 WD40 β-propeller was constructed using the X-ray structure of the N-terminal domain of the human proto-oncogene Nup214 as a template. Density-guided homology modeling with RosettaCM was then employed. The agreement to the experimental EM density was assessed by Rosetta’s scoring function to select the best fitting models. The RosettaCM procedure was repeated iteratively until satisfactory agreement was achieved between the best model for the WD40 β-propeller and the corresponding EM density.

Figure 4. Structure of Pol I preinitiation complex from cryo-EM and integrative modeling.

a) Cryo-EM reconstruction of Pol I initial transcribing complex; b) Atomistic model of Pol I initial transcribing complex; c) Atomistic model of Core Factor. The Core Factor subunits are depicted in red (Rrn6), blue (Rrn7) and green (Rrn11). Modeled structural elements include NTD, N-terminal domain; HB, helical bundle; CyclinC/N, C/N-terminal Cyclin Fold domain and TPR, tetratricopeptide repeats; d) Interface between Rrn6 HB and Rrn6 WD40 domains; e) Interface between Rrn6 WD40 and Rrn11 TPR domains; f) The two cyclin domains of Rrn7 are embedded in the Rrn6 HB protein chain.

To model the core of the RNA Polymerase I (Figure 4), crystal structures of yeast Pol I and A49 tandem winged helix domain of Pol I were rigid body fit into the corresponding EM density for the three PIC functional states. The DNA-RNA hybrid structure of the yeast Pol I elongation complex was fit into the densities and modified to include the DNA bubble region. MDFF flexible fitting was then applied to adjust the initial conformation and ensure model conformance with the cryo-EM maps. In the last stage of the protocol, each atomic structure was visualized with UCSF Chimera in its corresponding density map and inspected with COOT.

The final models revealed numerous surprising new features of CF binding to Pol I and promoter DNA. Comparison of the three Pol I PIC functional states to the known structures of the Pol II PIC suggested that a ratcheting motion of CF with respect to upstream DNA facilitates promoter melting in an ATP-independent manner. Importantly, the study advanced a new Pol I initiation mechanism, in which the intrinsic mobility of DNA-bound CF drives promoter opening without any need for ATP hydrolysis. Collectively, the findings suggest distinct initiation mechanisms between Pol I and II PICs and provide novel insight into the mechanism of Pol I initiation.

2. Modeling RNA Polymerase II PIC and the general transcription factor IIH

Here we summarize an integrative structure determination and analysis of the RNA polymerase II (Pol II) transcription pre-initiation complex, including the flexible TFIIH general transcription factor⁹⁶ (Figure 5). This study addressed a grand challenge for structural biology by providing the first essentially complete structural model of the human Pol II PIC/TFIIH complex (holo-PIC) (Figure 6). It also afforded a comprehensive structural and dynamic characterization of the holo-PIC assembly appropriate for mechanistic understanding of its key biology. Pol II PIC encompasses Pol II in complex with general transcription factors (GTFs), which recognize and bind to promoter DNA^97–98. TFIIH is the most complex of all GTFs, comprised of ten protein subunits. Recent cryo-EM studies had achieved near atomic visualization of core Pol II PICs¹⁹ (excluding the mobile TFIIH) in multiple states and enabled side-by-side comparison of the conformations leading to a competent elongation complex. Two subsequent EM structures showed the TFIIH both with²⁰ and without core-PIC¹⁹. Yet, the models from these breakthrough studies were incomplete (>20% of residues unassigned in sequence or not modelled), preventing further detailed molecular modeling. To address this challenge, the new integrative study synthesized all available cryo-EM data (from multiple EM maps) to produce the most complete atomistic model of the human PIC to date⁹⁶. The approach employed a combination of homology modeling, de novo structure building, flexible fitting with both conventional MDFF and cascade MDFF and real space refinement with the PHENIX package^{46, 56}. Moreover, the quality of the hybrid PIC model revealed new atomic insights into the macromolecular assembly and proved to be an excellent starting point for subsequent MD simulations.

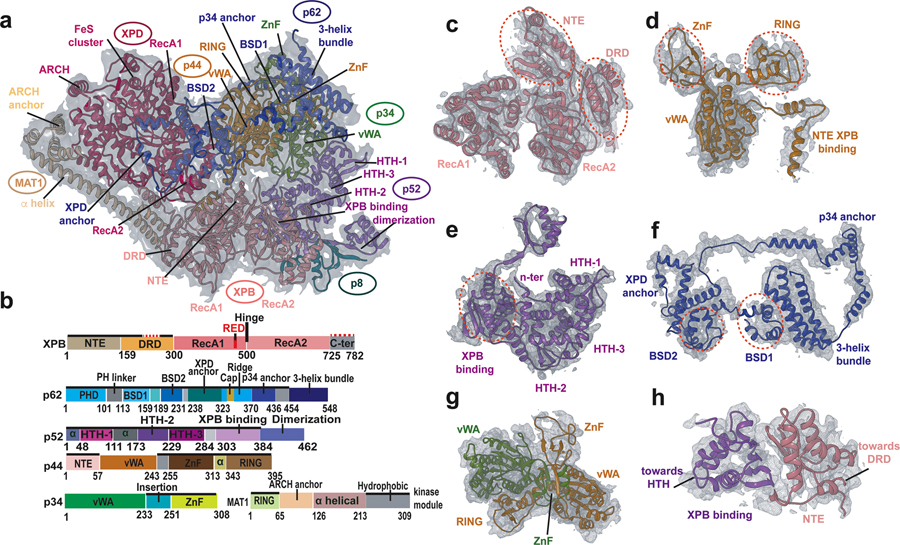
Figure 5. Structure of transcription factor IIH from cryo-EM and integrative modeling.

a) Overall fit of the apo-TFIIH structure to the apo-TFIIH density; b) Domain organization of the TFIIH subunits highlighting newly modeled regions (solid black lines); The structural motifs were labeled for each TFIIH subunit; c–f) Selected TFIIH subunits fitted into the EM density. Domains in each subunit are indicated with red dashed circles. c) XPB; d) p44; e) p52; f) p62; g) p34 and p44; h) XPB and p52.

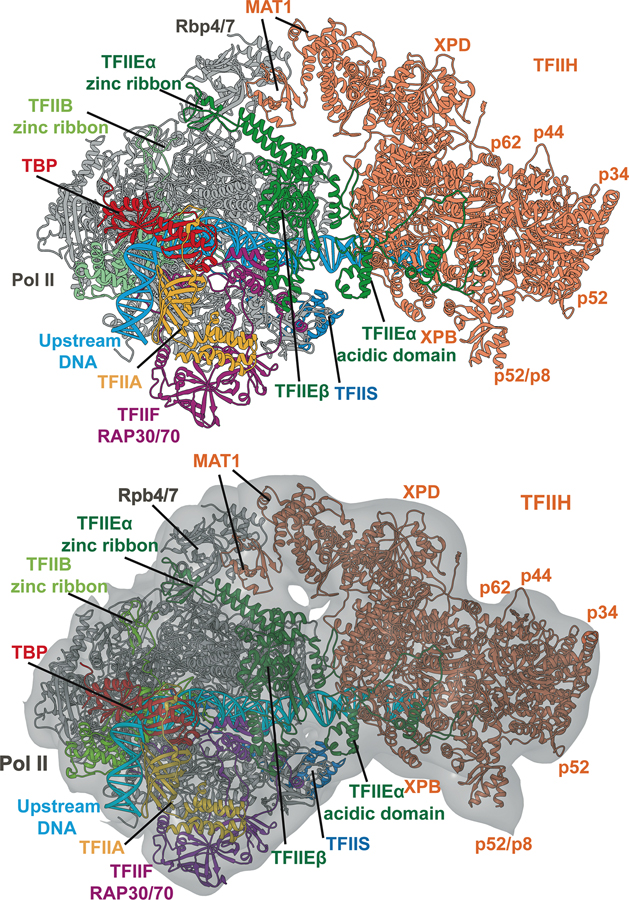
Figure 6. Structure of human Pol II preinitiation complex from cryo-EM and integrative modeling.

Positions of the general transcription factor subunits are indicated by color coding. The model is based on integration and comparative analysis of cryo-EM densities for human apo-TFIIH, human closed-state holo-PIC density and yeast core-PIC–TFIIH–DNA. Atomic model for the entire complex is shown with (a) and (b) without the EM envelope.

Initial model building was based on comparative analysis of cryo-EM densities for apo-TFIIH (EMDB accession code: EMD-3802)²² and yeast core-PIC/TFIIH/DNA (EMDB accession code: EMD-3846)²⁰. The protocol began with assessment of all available experimental data (available structures of domains or fragments, structures of suitable homologs, sequence data from NCBI, crosslinking data on TFIIH⁹⁹). Secondary structure prediction was performed for all TFIIH protein chains using the GeneSilico metaserver¹⁰⁰. The two EM density maps were inspected and visualized in Chimera and subsequently segmented into submaps guided by the available TFIIH subunit structures and the secondary structure prediction. The density corresponding to the very extended p62 TFIIH subunit was most conveniently visualized by eliminating the densities corresponding to the six neighboring TFIIH subunits.

A number of TFIIH structural elements had no close homologues in the PDB and, therefore, had to be built de novo. These included the XPB damage recognition domain (DRD), the XPB N-terminal extension domain (NTE), the p52 XPB binding domain, the p34 insertion, the p44 N-terminus and α-helix insertion, the MAT1 ARCH anchor and practically the entire p62 subunit. Using results obtained from consensus secondary structure prediction¹⁰⁰, the sequence register was established in the EM density. Individual fragments were built using COOT⁵⁷ to generate backbone-only models by tracing the protein chains through the EM densities. Polypeptide segments were then connected by extending the main-chain trace and side-chain orientations were built and manually corrected based on the EM density. Other missing regions in the apo-TFIIH structure were modeled either through rigid-body docking of a previously determined structure or by homology modeling followed by rigid-body docking. Once a suitably complete initial apo-TFIIH model was established MDFF was used to flexibly adjust the conformation of the newly constructed XPB, XPD, p52, p62, p34, p44, p8 and MAT1 subunits into the human apo-TFIIH density.

The next step was guiding the atoms from the initial TFIIH model into the holo-PIC EM density. This required the use of cascade MDFF³⁴. First, the initial model was fitted to the density of yeast PIC-TFIIH using a series of Gaussian-blurred maps. Regions of the model where the human and yeast densities showed substantive differences were excluded from fitting by setting the corresponding atomic weights w_j in MDFF to zero. Starting with a half-width of $\sigma$ = 3 Å, Gaussian-smoothed maps were generated using Chimera⁴⁵, with the half-width of each subsequent map decreasing by 1 Å. Including the original EM density, four maps were used for cMDFF. At each resolution, 4-ns MDFF simulations were performed until convergence.

To complete the holo-PIC assembly it was necessary to model the TFIIH – core-PIC interface. To this end, the C-terminal region of TFIIEα (α7/β5/α8/α9) was built by positioning the α7 helix between the TFIIEα winged-helix (WH) domain and the p62 BSD2 domain. The β5/α8/α9 elements were docked into the human holo-PIC EM density. Positioning of the TFIIEα segments was validated from available cross-linking data⁹⁹. TFIIH and core-PIC were separately flexibly fitted into the closed-state human holo-PIC density (EMDB accession code: EMD-3307)¹⁹ during 4-ns normal MDFF runs with a scaling factor ξ of 0.2 and then combined to assemble the full PIC/TFIIH/DNA complex. The final Pol II PIC-TFIIH model underwent 10 cycles of real space refinement in PHENIX, which as a rule always improves MolProbity statistics by removing atomic clashes and correcting Ramachandran and rotamer outliers. Final models were adjusted with COOT to correct accidental sidechain misplacements that may not have been fixed during the automated stages of refinement. Validation was performed using the integrated cryo-EM validation tools in the PHENIX package⁴⁶.

The newly built models allowed extensive MD simulations to unveil the functional dynamics of Pol II holo- and core-PICs. To our knowledge, these were the first atomistic simulations of the human transcription initiation machinery. Modeling the above systems (comprised of >1,000,000 atoms) took advantage of the capabilities of Summit, the world’s fastest supercomputer. Importantly, the analysis unveiled the hierarchical organization of the PIC machinery into dynamic communities and explained how its interwoven structural elements function together to remodel the DNA substrate and facilitate promoter opening. Strikingly, mapping patient-derived TFIIH mutations onto the newly discovered interfaces and dynamic communities revealed that mutations cluster at critical junctures in the TFIIH dynamic network. Thus, the study was able to annotate and explain the role of 36 mutations linked to inherited genetic diseases. These findings provided foundational understanding for the etiology of three distinct genetically validated disorders associated with cancer, aging, and developmental defects – xeroderma pigmentosum (XP, cancer), trichothiodystrophy (TTD, aging) and XP/Cockayne syndrome (XP/CS, development) – by unveiling their three distinguishing molecular mechanisms. Notably, the approach serves as a roadmap for future biochemical and mutational experiments to understand the interplay between TFIIH mechanisms and disease phenotypes.

Concluding remarks and outlook

Cryo-EM has emerged as a powerful tool for understanding large nucleoprotein complexes and molecular machines. To structurally define such inherently dynamic biological assemblies, cryo-EM data needs to be combined with computational methods for model building and refinement. Numerous techniques have been developed over the years to flexibly fit atomic models into density maps with variable local resolution. Despite recent dramatic improvements in cryo-EM map quality, the need for sophisticated model-building strategies is not likely to disappear. As cryo-EM advances to solve the structures of ever larger biological complexes, the issue of variable local resolution is likely to persist. Non-specific crosslinking, introducing inactivating mutations, applying inhibitors or non-hydrolysable ATP analogs are all techniques widely used in cryo-EM to drive the structural ensemble toward a single dominant conformation. Nonetheless, most EM maps do not achieve uniform local resolution. The situation reflects the expected conformational and dynamic variability of large biological complexes. The path forward in addressing the complexity of such assemblies is to apply integrative modeling methods. Known high-resolution structures of constituents in these complexes are combined not only with the cryo-EM maps but also with biochemical, mutational and crosslinking data to constrain the modeling and yield structures of the larger assemblies through integrative/hybrid computational protocols.

Looking forward, the molecular modeling field is poised to take advantage of the exciting advances in cryo-EM that have boosted resolution to near-atomic level. Importantly, single particle cryo-EM data could be combined with molecular simulations to characterize more fully the conformational ensembles of macromolecular assemblies rather than solving a single structure. A great advantage of cryo-EM compared to crystallography is the ability to capture biological assemblies in their natural state with all dynamic motions and multiple conformers represented in the ensemble. Through unbiased classification methods, cryo-EM could access some of the dominant states, which are often functionally relevant. Sophisticated path sampling and optimization techniques could be employed in conjunction with cryo-EM to connect the experimentally observable multiple functional states, define complete biological mechanisms and identify important intermediates in pathways for conformational transitions. An example could be a DNA helicase at various stages of its ATP-binding and hydrolysis cycle. Path optimization could be used to bridge the observed cryo-EM states and elucidate the mechanism by which the helicase translocates on DNA or separates the two DNA strands. Such close interplay of computation and cryo-EM experiments is needed for in-depth mechanistic and functional analyses in structural biology.