Fluence-matching technique using photoacoustic radiofrequency spectra for improving estimates of oxygen saturation

Abstract

Photoacoustic (PA) signals encode information about the optical absorption and spatial distribution of absorbing chromophores as well as the light distribution in the medium. The wavelength dependence of the latter affects the accuracy in chromophore quantification, including estimations of oxygen saturation (sO₂) with depth. We propose the use of the ratio of the PA radiofrequency (RF) spectral slopes (SS) at different optical wavelengths to generate frequency filters which can be used to match the fluence profiles across separate images generated with different optical wavelengths.

Proof-of-principle experiments were carried on a plastic tube with blood of a known oxygenation inserted into a porcine tissue. The algorithm was tested in-vivo in the hind leg of six CD1 mice, each under three different breathing conditions (100 % O₂, room air and 100 % CO₂). Imaging was done using the VevoLAZR system at the wavelengths 720 and 870 nm. The SS was calculated from the linear fit of the ratio of the photoacoustic RF power spectra at the two wavelengths. An ultrasound frequency filter was designed and applied to each segmented PA signal in the frequency domain and inversely transformed into the time domain to correct for the differences in the fluence profiles at both wavelengths. Linear spectral unmixing was used to estimate sO₂ before and after applying the ultrasound frequency filter.

The estimated blood sO₂ in the plastic tube for the porcine tissue experiment improved by 10.3% after applying the frequency filter when compared to the sO₂ measured by a blood gas analyzer. For the in-vivo mouse experiments, the applied sO₂ correction was 2.67, 1.33 and -3.33% for every mm of muscle tissue for mice breathing 100% O₂, room air and 100% CO₂, respectively. The approach presented here provides a new approach for fluence matching that can potentially improve the accuracy of sO₂ estimates by removing the fluence depth dependence at different optical wavelengths.

1. Introduction

Photoacoustic (PA) imaging has been one of the fastest growing modalities, as it can simultaneously deliver structural and functional information about blood vessels [1,2]. The high optical absorption and weak ultrasound scattering of soft tissues allow for real time imaging with high contrast at depths and resolutions that cannot be matched by optical techniques.

Among the numerous applications of PA imaging [3], one of the main applications of PA imaging is mapping the spatial distribution of the chromophores inside biological structures [2], [[4], [5], [6]]. Hemoglobin, a major optical absorbing molecule in tissue, encodes functional information through changes in its biochemical structure. Detecting endogenous chromophores like hemoglobin allows one to generate tissue oxygenation maps, a routinely monitored physiological parameter used in diagnosis and monitoring the efficacy of various treatments [4,6].

The resulting PA images primarily depend on the absorbing molecules present in the sample and the tissue optical illumination pattern. The absorption spectra of different forms of hemoglobin vary greatly for different optical wavelengths. By illuminating the sample with multiple optical wavelengths, estimations of the relative chromophore concentration can be achieved [7]. However, chromophore quantification is hindered by the dependence of the tissue light distribution on the different optical wavelengths [8].

Several tissue optical properties govern the light distribution in tissues, including the absorption coefficient $\left({\mu }_a\right)$, the scattering coefficient $\left({\mu }_s\right)$ and the anisotropy parameter $\left(g\right)$. These optical properties are a function of the optical wavelength [9]. The wavelength dependence of optical properties and how these properties change the light distribution in tissue introduces a challenge in accurately extracting the relative chromophore concentration.

Approaches for fluence compensation in PA imaging include correcting the light distributions using light diffusion models [[10], [11], [12]] or Monte Carlo simulations [13], both of which require prior knowledge of the tissue optical properties. Inverse iterative approaches have been used to estimate the optical properties [[14], [15], [16], [17], [18], [19], [20], [21], [22]], however they are computationally intensive. Recent work on the use of fluence eigenspectra to account for wavelength-dependent light attenuation has been introduced [23], [24], this approach increases the number of optical wavelengths required for imaging. Other methods include reference dyes of known optical properties [25], the use of multiple light sources to estimate the fluence profile [18,[26], [27], [28]] or a priori knowledge of tissue optical properties and their spatial distribution [29], all of which are difficult to implement for real-time imaging.

Regardless of the fluence correction method used, a suitable unmixing technique is required to estimate chromophore concentrations. Multiple methods have been proposed in PA imaging for unmixing samples with unknown chromophores and chromophores with known absorption profiles that differ from the background (e.g. nanoparticles) [[30], [31], [32], [33]]. The most common method to quantify endogenous chromophores (e.g. hemoglobin) is linear spectral unmixing. Linear spectral unmixing assumes that the PA signals generated are due to a linear combination of the product of each optical absorber and its concentration [34]. Knowledge of the extinction coefficients of the chromophores present in the sample is necessary. Linear spectral unmixing has been used to quantify the relative concentration of oxy- and deoxyhemoglobin which can be used to assess oxygen saturation (sO₂) [8].

In PA oxygenation measurements, spectral coloring can result in errors in the accuracy of the estimated values [8]. For example, for highly oxygenated tissue, the measured sO₂ maps decrease with depth relative to the actual oxygenation of the tissue. The optical absorption of oxygenated hemoglobin as a function of optical wavelength increases in the near-infrared (NIR) regime. The increase in the optical absorption with wavelength results in a decrease in light fluence. After applying linear spectral unmixing this results in underestimation of tissue oxygenation with depth. For highly deoxygenated tissues, the optical absorption of hemoglobin decreases as a function of wavelength in the NIR regime. After applying linear spectral unmixing, this results in overestimation of tissue oxygenation with depth. Improving the estimation of sO₂ maps using PA imaging would be advantageous in biomedical imaging applications.

In ultrasound imaging, the ratio of the power spectra of the backscattered ultrasound signal to a reference signal has been used to estimate the ultrasound attenuation of a phantom [35,36]. The advantage of using a reference signal is to remove system dependent parameters. The advantage of using a reference signal is to remove system dependent parameters. Similarly, the ratio of the power spectra of the generated PA signals at two wavelengths can be used to eliminate system dependent parameters and estimate the optical properties [[37], [38], [39], [40]]. This is because the changes in the optical diffusion is reflected in the frequency domain of the PA signals. Other simulations of the generated PA signals have demonstrated dependence of the PA ultrasound frequency spectra on the optical absorption coefficient [[41], [42], [43]]. The ratio of the of the generated PA signals at multiple wavelengths has been used as a self-calibrating method to estimate the optical attenuation parameters and to correct for oxygenation estimates in tissues [[37], [38], [39], [40]]. However, those proposed methods have been limited to PA microscopy and were used to image superficial vasculatures.

The purpose of this paper is to present a new method which uses the ratio of the PA power spectra at two different optical wavelengths to match the fluence deep in the tissue. To match the fluence at the imaged wavelengths, the difference in the optical fluence is extracted from the ratio of the power spectra calculated of the radiofrequency (RF) signals. This has the potential to improve sO₂ estimates deep in the tissue without the need to prior knowledge of the optical properties of the imaged tissue.

2. Description of fluence matching approach

Previous work has shown that the acoustic spectra ratio of PA signals at two different optical wavelengths can be used to extract information about the absolute optical absorption of dye and oxygen saturation of hemoglobin in tissues [[37], [38], [39]]. These seminal studies demonstrate that the frequency of PA signals encodes information related to the optical fluence of the surrounding tissues. The main assumption incorporated into these approaches is that the reduced scattering coefficient is much smaller than the absorption coefficient. This limits the application of the models to optical wavelengths (500–600 nm) of high absorption that can only be used in PA microscopy imaging.

For those reasons, the proposed fluence matching approach in this paper uses information directly extracted from the acoustic spectra ratio of the PA signal. However, our fluence matching model does not require the assumption mentioned above. A well-controlled test phantom is introduced to further investigate the correlation between the acoustic spectra ratio to the effects of optical fluence at two optical wavelengths. The phantom is imaged at higher optical wavelengths (680–910 nm) that can be used to examine deeper tissues in PA imaging. The concept of the acoustic spectral ratio in PA imaging is introduced below.

The received ultrasound signal carries information about the initial pressure rise, the system used ($H$), and the ultrasound attenuation ($\alpha$) the medium pulse propagates through. For the convenience of the reader, a brief review of the representation of ultrasound power spectra can be found in [37,38,[41], [42], [43], [44]]. The detected ultrasound signal has spectral power $S$ and can be described as:

$$S(\omega ,\lambda )=p(\omega ,\lambda )H(\omega )\alpha (\omega )$$ (1)

where $\omega$ is the ultrasound angular frequency $p$ is the received pressure rise detected by the transducer. By imaging the sample using two different optical wavelengths, the impact of the system dependent parameters ($H$) can be eliminated as previously done in ultrasound imaging [35,36,41,44] and later adapted in PA imaging by taking the ratio of the power spectra at two different optical wavelengths [37,38]. This ratio can be represented as:

$$\frac{S(\omega ,{\lambda }_1)}{S(\omega ,{\lambda }_2)}=\frac{p(\omega ,{\lambda }_1)H(\omega )\alpha (\omega )}{p(\omega ,{\lambda }_2)H(\omega )\alpha (\omega )}=\frac{p(\omega ,{\lambda }_1)}{p(\omega ,{\lambda }_2)}=\frac{\left(\varphi \left(\omega ,{\lambda }_1\right){\mu }_a(\omega ,{\lambda }_1\right)}{\left(\varphi \left(\omega ,{\lambda }_2\right){\mu }_a(\omega ,{\lambda }_2\right)}$$ (2)

After the mathematical cancellation of these parameters, the ratio of the power spectra can be thought of to represent the ratio of the received PA pressure ($p$), which conveys information related to the absorption coefficient (${\mu }_a$) and light fluence ($\varphi$) [45].

Knowing that changes in the frequency content of the ratio of the power spectra does carry information about the changes in the optical fluence at the imaged wavelengths, a test phantom is introduced to further investigate this relationship.

Measuring this change in the optical fluence can then be used to match the fluence profile of the images at the imaged wavelengths. A schematic diagram of fluence matching method is shown in Fig. 1. We propose to use this method to improve spectral unmixing for the accurate assessment of oxygen saturation.

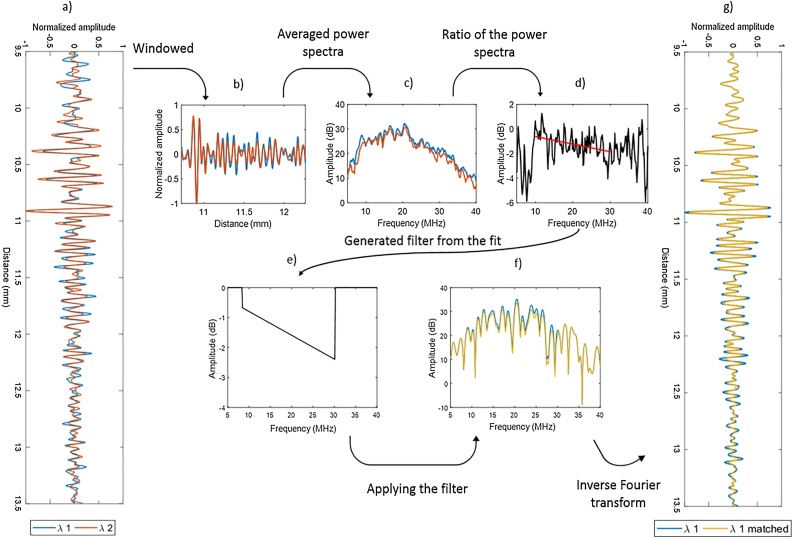
Fig. 1.

Representation of fluence matching method. (a) The normalized RF signals acquired at the two wavelengths (blue, red). (b) The windowed RF signals from (a). (c) Averaged power spectral of the neighboring 20 RF in (b). (d) The ratio of the power spectra shown in (c). (e) The generated frequency filter from the cumulative spectral slope (SS) of the ratio of the power spectra in (d). (f) Applying the generated frequency filter in (e) to the power spectra of the RF signal shown in (b). Blue is before applying the frequency filter and yellow is after applying the frequency filter. (g) The generated RF signal after applying the frequency filter in yellow. Original signal shown in blue.

3. Materials and methods

This section summarizes the sample preparation methods, the system used for PA imaging and the procedures applied for fluence matching and spectral unmixing in ex-vivo tissues and mice in-vivo.

3.1. Test phantom to examine the generated frequency filter

A test phantom was used to validate approach. The phantom was prepared by heating degassed water to 80 °C. 10% by volume of gelatin porcine skin (Sigma Aldrich, St. Louis, Missouri, United States) was added, mixed and left to cool down. At 37 °C, 5% of intralipid (Sigma Aldrich, St. Louis, Missouri, United States) and 5% of blood (Canadian blood services, Alberta, Canada) by volume were added, and the phantom was left in the fridge. The blood sample was mixed in a test tube prior to use to increase its oxygenation state.

Next day the phantom was immersed into a water bath at 37 °C and placed on top of a microscope slide coated with 20 nm of gold. This setup is similar to the insertion loss method used to measure ultrasound attenuation of a phantom [46]. The test phantom was imaged using the VevoLAZR system (FujiFilm-VisualSonics Inc., Toronto, CA) coupled with the LZ250 transducer. The gain was adjusted to prevent the saturation of the signal from the gold. The gold-plated microscope slide was imaged in the absence and presence of the test phantom at 720 nm and 870 nm with 20 frames for each wavelength. ROI were applied to select the signal acquired from the gold-plated microscope slide. By comparing the signal amplitude of the images acquired of the microscope slide alone and with the test phantom above the slide, the difference in the power spectra due to the presence of the test phantom was measured. The ratio of the power spectra at the two imaged wavelengths were calculated. The linear best fit was computed (the spectral slope (SS)) at the -6 dB of the transducer bandwidth. The SS value was measured and used to generate the frequency filter as discussed in Section 3.4 and shown in Fig. 1. The alteration in the signal amplitude after applying the frequency filter was measured and was used to compensate for the fluence induced changes in the signals.

3.2. In-vivo sample preparation

Porcine tissue was acquired from a local grocery store. A plastic tube of 350 μm in diameter was inserted into the porcine tissue at approximately 5 mm below the tissue surface. Three different blood samples were prepared in EDTA coated vacutainers (Fisher Scientific, Hampton, USA). The blood was acquired from female CD1 mice using cardiac puncture (animal protocol: ACC 788). The first sample was prepared by gently mixing the vial to increase the oxygenation of the blood. The second sample was prepared by adding 1 mg of Sodium Nitrite (Sigma-Aldrich Inc., Canada) to 1 mL of blood to decrease its oxygenation. The final sample was prepared by mixing 0.5 mL of first sample with 0.5 mL of the second sample. All three samples were injected into the respective plastic tube separately and imaged using the VevoLAZR system. The oxygenation of the blood in each vial was measured prior to imaging using a blood gas analyzer (Radiometer Medical, London, CA).

Female CD1 mice (Charles River, Toronto, CA) aged 7–8 weeks and weighing 25−30 g were used. The hair on the mouse hind leg was removed using hair removal products (Nair) prior to imaging. All the experimental protocols in this study were approved from the Animal Care Committee at St. Michael's Hospital and the Research Ethic Board at Ryerson University (protocol #788).

3.3. Photoacoustic imaging

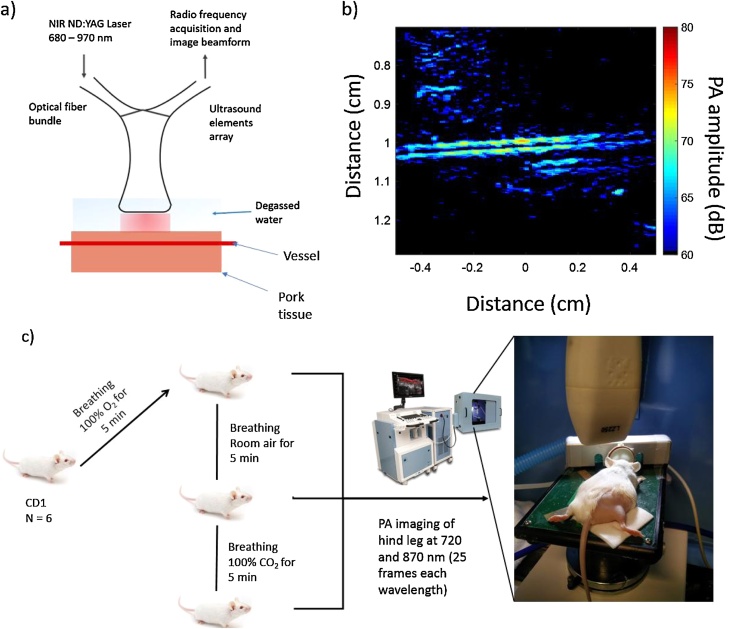
The two samples (the porcine tissue with the plastic tube and the mice) were imaged using the commercial VevoLAZR PA system as shown in Fig. 2a, c. Ultrasound liquid gel was used as a coupling media. A heating platform was used to monitor the temperature to be within 37 ± 0.5 °C. The same platform was also equipped with electrocardiography leads for monitoring the respiratory and heart rate of the mice during imaging. A 100 mW heating lamp was used to maintain a physiological temperature for the mice during anesthesia. The LZ-250 linear array PA transducer with a center frequency of 21 MHz was used for imaging. All mice were anaesthetized with a flow of isofluorane (1.5 %) in air at 0.5−1 L/min. The breathing air was altered for each mouse starting with 100 % O₂ before switching to room air and terminating with 100 % CO₂ inducing asphyxiation. A period of 5 min was allowed for each breathing condition to ensure stabilization prior to imaging (Fig. 2c). All samples were imaged at 720 and 870 nm, and 25 frames at the same location (frame rate 5/sec) were acquired for each image at the two wavelengths. The pre-beamformed RF signals were extracted from the system and beamformed using a delay-and-sum algorithm.

Fig. 2.

(a) Schematic representation of the PA system used for vessel imaging. (b) Representative PA image acquired at 720 nm using a 21 MHz transducer. (c) Schematic representation of the experimental setup used for imaging the CD1 mice. The mice were exposed to three different oxygenation states of 100 % O₂, room air and 100 % CO₂. The hind legs were shaved and imaged using the VevoLAZR system with liquid gel as a coupling media (not shown in the image).

3.4. Procedures for fluence matching

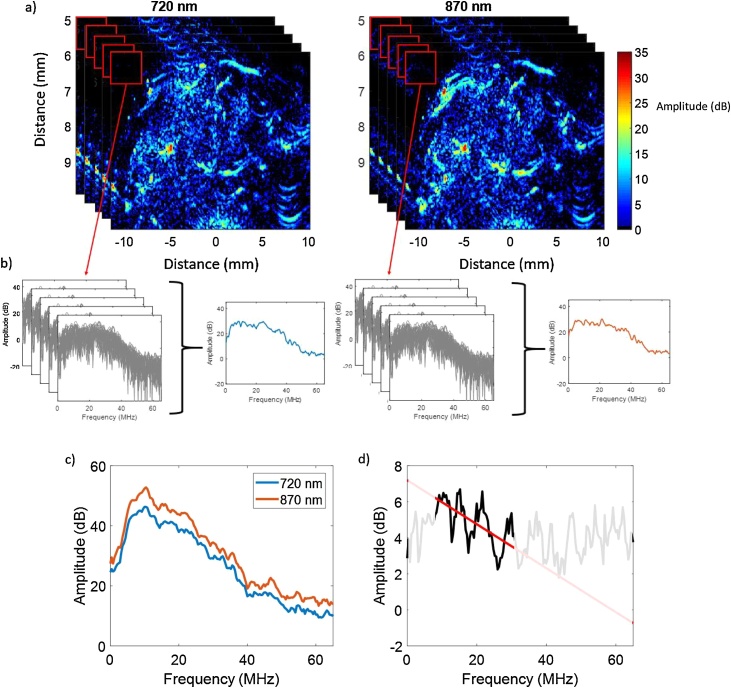
To match the fluence profile of a PA image acquired at 720 nm to a PA imaged acquired at 870 nm, a moving rectangular window of size 0.77 × 1.80 mm (10 times the ultrasound wavelength) with 66 % axial overlap was applied to the time domain PA signals at each wavelengths (Fig. 3). The windowed beamformed RF signals were transformed to the frequency domain using the Fast Fourier Transform. Averaging 20 neighboring power spectra (or 1.80 mm) was applied for 25 frames at each wavelength. The ratio of the average power spectra acquired at 870 nm and 720 nm were calculated, and a line best fit was used to estimate the SS within the bandwidth of the transducer (8.5–31.5 MHz) in the logarithmic scale (Fig. 3). The cumulative SS was computed by integrating the measured SS as a function of depth.

Fig. 3.

Procedures used in the fluence matching method for the images acquired from a mouse hind leg at two wavelengths used to calculate the normalized averaged power spectra. (a) Thresholded PA images acquired at the 720 and 870 nm with 25 frames collected for each wavelength (in the image only 5 frames are showing for illustrative purposes). A moving rectangular window sized 0.77 × 1.80 mm was applied. (b) the normalized power spectra of the selected window in (a) are shown in gray for the images at the two wavelengths (which represent background noise). The averaged power spectra for 720 and 870 nm wavelengths are shown in blue and red, respectively. (c) Representative of the normalized averaged power spectra calculated. (d) the ratio of the power spectral shown in (c) with the line best fit within the bandwidth of the transducer (solid black line).

The cumulative SS was used to design the frequency filters. The filters were composed of an antilog value to the cumulative SS at the bandwidth of the transducer. Outside the bandwidth of the transducer a value of one was assigned to the filters. The filters carry information about the ratio of the optical fluence profiles of the images at the two wavelengths (${\varphi }_2/{\varphi }_1$). The filter was applied to the PA image acquired at 720 nm. An inverse Fast Fourier Transform was applied to transform the signals back to its time domain.

This method was applied on the PA images acquired at 720 nm to match the fluence profile of PA imaged acquired at 850 nm (a summary of fluence matching method is shown in Fig. 1). Linear spectral unmixing was performed before and after applying the proposed fluence matching method to quantify the sO₂ values.

3.5. Spectral unmixing

To quantify the sO₂ values from the PA images, linear spectral unmixing was applied after thresholding the PA image using Otsu’s threshold [47]. For wavelength (λ₁) the generated PA signal can be represented as:

$${p_{{\lambda }_1}=\Gamma {\varphi }_{{\lambda }_1}[C}_{Hb{O}_2}{\epsilon }_{Hb{O}_2{\lambda }_1}+C_{Hb}{\epsilon }_{Hb{\lambda }_1}]$$ (3)

where, $\Gamma$ is Grüneisen parameter, $\varphi$ is the light fluence, ${\text{C}}_{\text{H}\text{b}{\text{O}}_2},{\text{C}}_{\text{H}\text{b}}$ are the concentration of the oxy-, deoxyhemoglobin in the sample, respectively and ${\text{ε}}_{\text{H}\text{b}{\text{O}}_2{\text{λ}}_1},{\text{ε}}_{\text{H}\text{b}{\text{λ}}_1}$ are the extinction coefficients of oxy-, deoxyhemoglobin from previously published measurements [48]. In the case of multiple wavelengths, the equation above can be re-written in matrix notation:

$$\Gamma \left[\begin{array}{cc}{{\varphi }_{{\lambda }_1}\epsilon }_{Hb{O}_2{\lambda }_1}& {{\varphi }_{{\lambda }_1}\epsilon }_{Hb{\lambda }_1}\\ {{\varphi }_{{\lambda }_2}\epsilon }_{Hb{O}_2{\lambda }_2}& {{\varphi }_{{\lambda }_2}\epsilon }_{Hb{\lambda }_2}\end{array}\right]\left[\begin{array}{c}{C}_{Hb{O}_2}\\ C_{Hb}\end{array}\right]\propto \left[\begin{array}{c}\begin{array}{c}{p}_{{\lambda }_1}\\ p_{{\lambda }_2}\end{array}\end{array}\right]$$ (4)

The equation takes the form $Ax=b$, where $A$ is the product of the Grüneisen parameter with the fluence and extinction coefficients, $x$ is the concentration of the chromophores in the sample (the unknown parameters) and $b$ is a measured PA pressure matrix. By implementing fluence matching, Eq. (4) can be re-written as:

$${\varphi }_{{\lambda }_2}\Gamma \left[\begin{array}{cc}{\epsilon }_{Hb{O}_2{\lambda }_1}& {\epsilon }_{Hb{\lambda }_1}\\ {\epsilon }_{Hb{O}_2{\lambda }_2}& {\epsilon }_{Hb{\lambda }_2}\end{array}\right]\left[\begin{array}{c}{C}_{Hb{O}_2}\\ C_{Hb}\end{array}\right]\propto \left[\begin{array}{c}\begin{array}{c}{p}_{{\lambda }_1}\\ p_{{\lambda }_2}\end{array}\end{array}\right]$$ (5)

The solution was limited to positive values to avoid negative concentrations and the sum of all the chromophores at a selected location was set to 1. These two restrictions can be represented by $0<{{\text{C}}_{\text{H}\text{b}{\text{o}}_2},\text{C}}_{\text{H}\text{b}}<1$ and ${{\text{C}}_{\text{H}\text{b}{\text{o}}_2}+\text{C}}_{\text{H}\text{b}}=1$, respectively [4]. Finally, the mean square error of the measured and calculated pressure is minimized to solve for the chromophores concentrations.

To assess the proposed fluence matching method, multiple ROIs were selected for each PA image. The ROIs were selected using the PA images acquired at 870 nm wavelength. Five to fifteen vessels were segmented for each image. The change in the average oxygenation before and after applying the fluence matching method was computed and plotted as a function of depth from the skin surface. This was done for each oxygenation state.

4. Results and discussion

This section displays the results of fluence matching approach on the ex-vivo porcine tissue and in-vivo muscle tissue of mice and the discussion associated with it.

4.1. Test Phantom to validate fluence matching approach

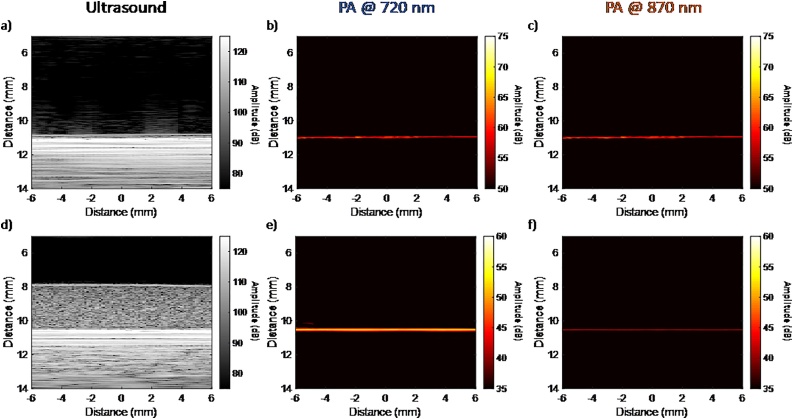
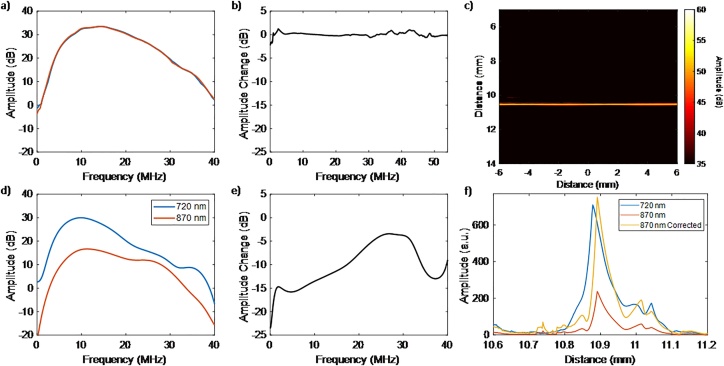
The ultrasound and PA images acquired of the test phantoms are shown Fig. 4 for illumination wavelengths of 720 and 870 nm. The first setup has a gold-plated microscope slide alone and the second setup has the same gold-plated slide with a tissue mimicking phantom placed on top of it. Ultrasound images are shown of the two set-ups in Fig. 4 (a, d). The gold-plated has almost identical signals when imaged at the two wavelengths Fig. 4 (b, c). When the test phantom was introduced between the transducer and the gold-plated slide, the signals were modified (Fig. 4 e, f). This is due to change in optical fluence of light as it propagates through the phantom. The power spectra computed from the PA RF signals of the two setups shown in Fig. 4 are shown in Fig. 5 (a, d). The ratio of the power spectra at the two imaged wavelengths for the two setups are shown in Fig. 5 (b, e). When the test phantom is present, the ratio of the power spectra shows dependence on the ultrasound frequency (Fig. 5e). This is not the case in the absence of the phantom (Fig. 5b). This demonstrates the impact of the optical fluence on the acoustic spectral ratio.

Fig. 4.

(a-c) Imaging of the gold-plated microscope slide alone and (d-e) the test phantom placed on top of the gold-plated microscope slide using the VevoLAZR system. The ultrasound (a, d), PA image at 720 nm (b, e) and PA image 870 nm (c, f) of two different geometrical setups. Note the difference in the color bars for the PA images in the top and bottom rows.

Fig. 5.

(a, d) Representative power spectra of the PA signals acquired from gold-plated microscope slide from the two set-ups shown in Fig. 4. (b, e) The ratio of the two power spectra in (a, d) respectively. (c) The corrected PA image at 870 nm after applying the fluence matching approach. (f) Axial profiles of the PA signal amplitudes at 720 nm, 870 nm and the corrected PA signal at 870 nm for the central element (x = 0 mm).

Fluence loss due to the present of the test phantom was calculated by comparing the measured signals from the gold at the two different optical wavelengths in the presence and absence of the test phantom. The change in the optical fluence at the two imaged wavelengths in the presence of the test phantom was measured to be 11.2 ± 0.6 dB. The fluence matching method proposed was applied. The change in the PA image of the gold plate at 870 nm after applying the frequency filter is shown in Fig. 5c. An axial profile of the PA signal amplitude at 720 nm and 870 nm, and the corrected amplitude PA signal amplitude at 870 nm after fluence matching is shown in Fig. 5f. After applying the proposed fluence matching approach the PA signal amplitude at 870 nm better matches the PA signal amplitude at 720 nm.

Here we are exploring the use of a simple, easy-to-use linear filter that can correct for the effects of optical fluence. Using a highly scattering phantom (Fig. 4) positioned over a strongly absorbing gold film, we demonstrate how the optical fluence changes at two wavelengths of illumination (720 nm and 870 nm) alters the PA power spectra. As shown in Fig. 5, the optical fluence broadens the frequency spectrum at the lower optical absorption (in this case 870 nm). This change was used here to detect the fluence difference between the two imaged wavelengths and compensated for accordingly as shown in Fig. 5 f.

4.2. Ex-vivo porcine tissue

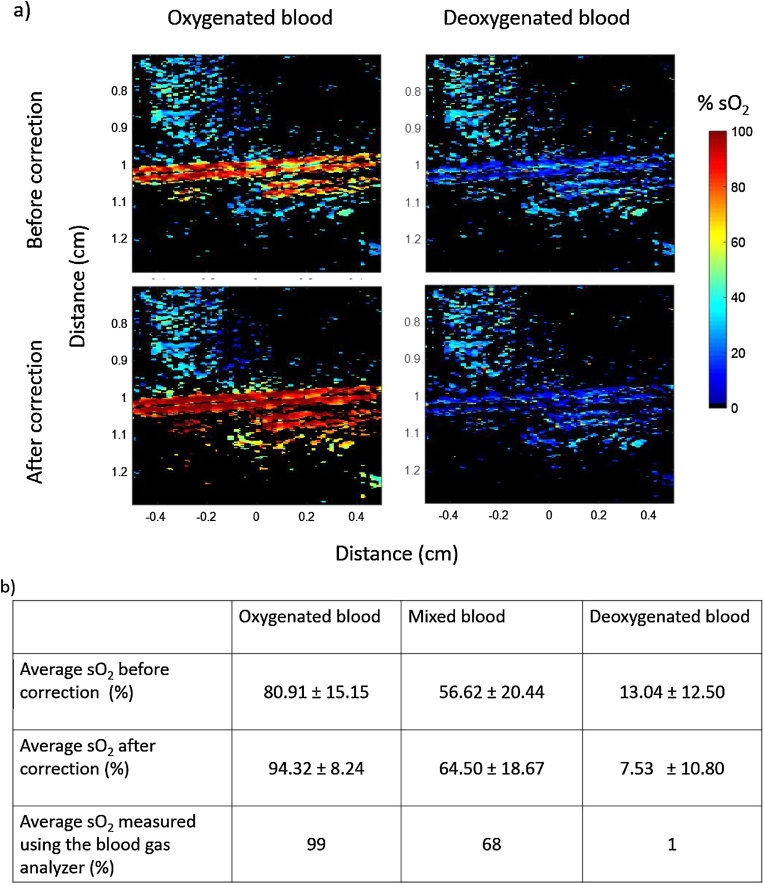
The sO₂ maps of the samples measured before and after applying the fluence matching method for oxygenated and deoxygenated blood samples are shown in Fig. 6 a. The estimated sO₂ of the blood before applying the fluence matching method is lower than the oxygenation as measured using the blood gas analyzer for oxygenated blood and higher for the deoxygenated blood. This result was expected because of spectral coloring of tissue with depth [8]. After applying the fluence matching method, the estimated sO₂ values were closer to the oxygenation values measured with the blood gas analyzer. These changes are summarized in Fig. 6b. The percent difference between the blood gas analyzer measurements and the sO₂ estimate before applying fluence matching were 18.3%, 16.7% and 12.2% for the oxygenated, mixed and deoxygenated blood samples, respectively. The differences after applying the fluence matching method were 4.7%, 5.1% and 6.6%, respectively. This demonstrates the capability of the fluence matching method to improve the estimated sO₂ with depth.

Fig. 6.

(a) PA sO₂ maps for oxygenated and deoxygenated blood samples in a plastic tube inserted into porcine tissue before and after applying fluence matching method. (b) Average sO₂ values measured for blood samples in a plastic tube inserted into porcine tissue before and after applying fluence matching method. The same blood samples were measured using the blood gas analyzer.

4.3. In-vivo muscle tissue

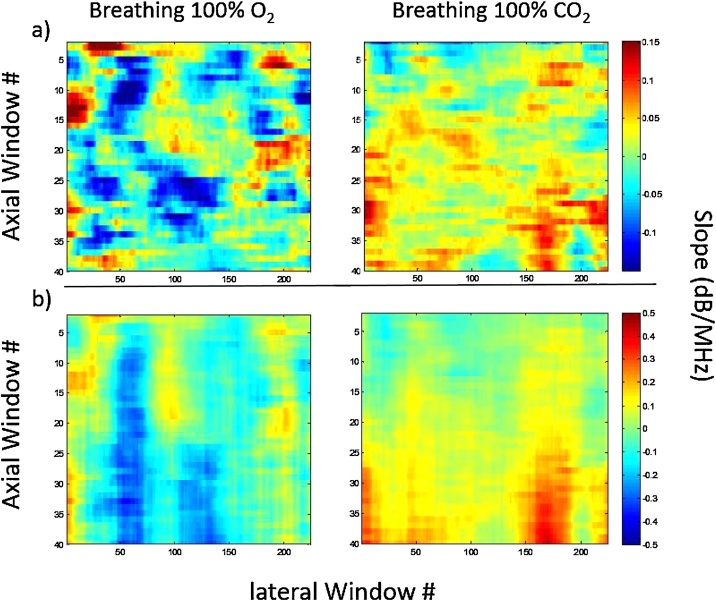
The fluence matching method was tested on six different CD1 mice. Each mouse was imaged under three different breathing conditions of 100% O₂, room air and 100% CO₂. The ratio of the SS was calculated as demonstrated in Fig. 3. The measured SS and the cumulative SS maps are presented in Fig. 7 for a representative mouse breathing 100% O₂ (left panels) and 100% CO₂ (right panels). Negative SS values were more common when the mouse was breathing 100% O₂ while positive SS values were more common when the mice were breathing 100% CO₂. The correction factor applied for mice breathing 100% O₂ is reversed compared to the correction factor applied for mice breathing 100% CO₂. This is also reflected in the cumulative SS shown in Fig. 7b. The greater values for the cumulative SS measured, the greater the necessary correction for the PA signal amplitude.

Fig. 7.

(a) Spectral slope maps calculated using the proposed method for fluence matching, (b) the cumulative spectral slope maps with depth calculated from (a). Each calculated slope is used to create a frequency filter at that depth.

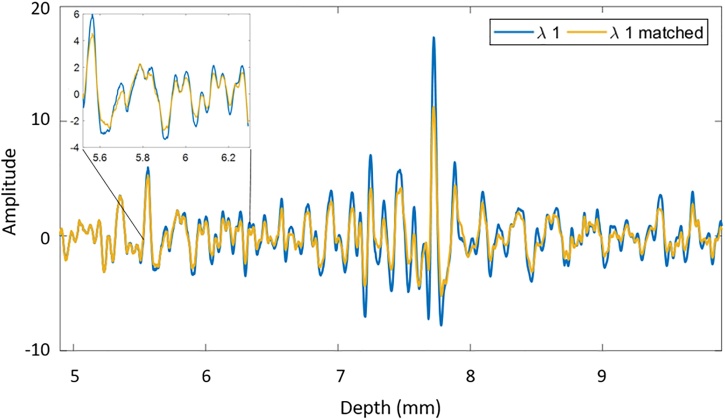
The calculated cumulative SS shown in Fig. 7 was used to construct the frequency filter applied to the power spectra (within the limits of the transducer bandwidth). The effect of applying the frequency filter on the RF data is illustrated in Fig. 8. The time domain RF signals of a mouse breathing 100% O₂ before and after the matching is shown through the use of inverse Fourier Transform (Fig. 8). As expected the amplitude of the PA signal decreased with depth before the matching. After applying the frequency filter, the rate of the decrease of the PA signal as a function of depth increases. The filters were applied to the PA RF data acquired at 720 nm. The goal of the filter was to match the fluence profile of 720 nm to that at 870 nm. The signals at 870 nm were not modified.

Fig. 8.

Representative RF signals (acquired at 720 nm) for a mouse breathing 100 % O₂ before and after fluence matching. Applying the frequency filter decreases the amplitude of the PA signal with depth.

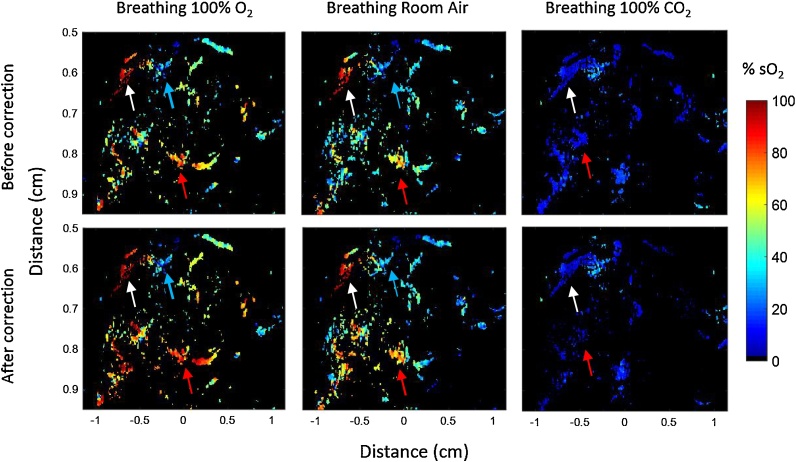
The resulting sO₂ maps after applying linear spectral unmixing on the thresholded PA images are presented in Fig. 9. For superficial vessels (white arrows), the estimated sO₂ before and after applying fluence matching method is comparable for the three breathing states. For deeper vessels (red arrows), the differences in the estimated sO₂ between the two methods become more pronounced. For mice breathing 100% O₂, the estimated sO₂ becomes higher after correction, while for mice breathing 100% CO₂, the estimated sO₂ becomes lower after correction. This was expected as the effect of spectral coloring is inverted for normoxic and hypoxic mice. Specifically, the optical absorption coefficient for oxygenated blood is higher at 870 nm than at 720 nm while for deoxygenated blood the opposite trend holds. For mice breathing room air, the trend is closer to that of mice breathing 100% O₂, albeit the correction is smaller.

Fig. 9.

sO₂ maps acquired using 720 and 870 nm wavelengths before and after applying fluence matching method for mice breathing 100% O₂, room air and 100% CO₂.

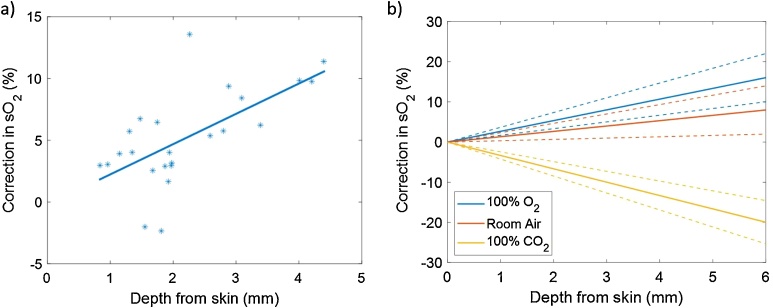
To examine the oxygenation of vessels in all the imaged mice, ROIs were applied to select multiple vessels at different depths in the PA images. The average sO₂ values were computed for each ROI. The change in the estimated sO₂ before and after applying the matching filter is plotted as a function of depth from the skin. Representative data of a mouse breathing 100% O₂ are shown in Fig. 10a, where each star represents one selected vessel ROI. The line best fit is also plotted to demonstrate the trend (Fig. 10b).

Fig. 10.

(a) The relative changes in the estimated sO₂ as a function of depth before and after applying the fluence matching method for multiple ROIs of a mouse breathing 100 % O₂. The line represents the line best fit for the data. (b) The average of the line best fit for all the 6 mice for mice breathing 100 % O₂, room air and 100 % CO₂. The dashed lines represent the standard deviation of the slope for each fit.

The average of the fitted slopes (Figure a) of the six mice and the standard deviations are plotted in Figure b for all three mice breathing states. The results show an increase in the SO₂ measurements with depth for the mice breathing 100% O₂ and room air of 2.67 and 1.33 % per mm and a decrease in the SO₂ with depth for mice breathing 100% CO₂ of 3.33% per mm. The correction needed for the mice breathing 100% O₂ was higher than that for mice breathing room air. This was expected as room air contains an average of 21% O₂ which will result in less oxygenated blood. For less oxygenated blood, the ratio of the absorption coefficients at 870 to 720 nm decreases [8,14]. For mice breathing 100% CO₂, the trend was reversed due to the ratio of the absorption coefficient at 870 to 720 nm being opposite for deoxygenated blood. In addition, the amplitude of the correction for mice breathing 100% CO₂ was the highest. The reason behind it is that in mice breathing 100% O₂ and room air, fewer oxygenated blood vessels are present due to the consumption of tissue to oxygen (Fig. 9 blue arrows). However, for mice breathing 100% CO₂, all vessels are expected to be deoxygenated.

4.4. Assumptions of fluence matching method

This work demonstrates how calculating the ratio of the PA ultrasound power spectra at two different optical wavelengths can be used to compensate for fluence loss. One of the assumptions used in the fluence matching approach is the linearity of the fit to the ratio of the power spectra within the bandwidth of the transducer. Previous work has shown that the ratio of the power spectra at two different optical wavelengths can take a sigmoidal shape for specific geometrical set-ups [37,38]. The ultrasound transducer used in these experiments has smaller bandwidth. Within the bandwidth of our transducer (10−30 MHz) and for ultrasound resolution PA imaging, the ratio of the power spectra can be approximated as a linear function of frequency (R² = 0.95 Fig. 5e).

The second assumption used in the proposed fluence matching approach, is that the spatial distribution of the chromophores at the two imaged wavelengths is invariant and can be eliminated when the ratio of the power spectra is computed. This can be further explained through representing the absorption coefficient by two parameters one is optical wavelength dependent ($A\left({\lambda }_1\right)$) and one is ultrasound frequency dependant ($B(\omega )$) such that ${\mu }_a\left(\omega ,{\lambda }_1\right)=A\left({\lambda }_1\right)B(\omega )$. Since the main absorbers in blood are dominated by hemoglobin at the imaged wavelengths, the spatial distribution of the absorbing structures is the same for both wavelengths. The spatial distribution of the chromophores can be converted into a time dependence for the generated PA signals through the speed of sound which will be reflected in the frequency domain (and calculated using power spectra). This allow re-writing Eq. 2 such that:

$$\frac{S(\omega ,{\lambda }_1)}{S(\omega ,{\lambda }_2)}=\frac{\left(\varphi \left(\omega ,{\lambda }_1\right)A\left({\lambda }_1\right)B(\omega \right)}{\left(\varphi \left(\omega ,{\lambda }_2\right)A\left({\lambda }_2\right)B(\omega \right)}=\frac{\left(\varphi \left(\omega ,{\lambda }_1\right)A({\lambda }_1\right)}{\left(\varphi \left(\omega ,{\lambda }_2\right)A({\lambda }_2\right)}$$ (6)

since the power spectra are represented in the log domain, the above equation can be modified to:

$${log}_{10}\left[\frac{S(\omega ,{\lambda }_1)}{S(\omega ,{\lambda }_2)}\right]={\log }_{10}\left[\frac{\varphi \left(\omega ,{\lambda }_1\right)}{\varphi \left(\omega ,{\lambda }_2\right)}\right]+{\log }_{10}\left[\frac{\left(A({\lambda }_1\right)}{\left(A({\lambda }_2\right)}\right]$$ (7)

by applying a linear fit of slope (m) and y-intercept (b) to the logarithmic form of Eq. 7, the changes in the frequency content (SS) of the ratio of PA power spectra at two different optical wavelengths (of the same absorbing chromophore spatial distribution) can be attributed to changes in the optical fluence at these two optical wavelengths. This difference in optical fluence (due to the different fluence distribution maps that are related to the tissue bulk optical properties at these two wavelengths) create changes in the spatial distribution of the energy deposition maps that in turn create changes in the ultrasound PA signals.

The proposed fluence matching method takes advantage of the similarity in the absorbing chromophores at the two optical wavelengths to generate a frequency filter using power spectra normalization. The approach provides a new simple and rapid method which can aid in relative chromophore quantification. However, some of the limitations of the method include signal averaging, as the method uses RF frequency analysis. A high signal-to-noise ratio (SNR) is required for accurate quantification of the frequency filter. Low SNR can increase the error in the estimated frequency filter. In addition, motion can result in a significant alteration in the estimated frequency filter as the location of the absorbing chromophores changes from one wavelength to another. Motion can create a change in the frequency filters. Further experiments to test the fluence matching method can include imaging organs with greater motion (e.g. liver and kidney) and applying respiratory motion gating to reduce the effects of this motion. Also, direct comparison of the method to other fluence compensation approaches can help to improve in chromophore quantification.

5. Conclusions

Extracting information from the photoacoustic RF SS to be used for fluence matching to improve chromophore quantification and better oxygenation estimates. The SS has been shown to carry information that can be used to correct the light distribution at different wavelengths which results in spectral coloring. In multi-wavelength PA imaging, the absorber's size remains unchanged; this allows the relating the SS and light distribution as long as the absorbing structures are the same for each optical wavelength and are optically thin. The results demonstrate that accounting for light distribution through the frequency content of PA signals can improve the accuracy of the reported sO₂ values.

Funding source

The Terry Fox Foundation//Natural Sciences and Engineering Research Council of Canada

The Canada Research Chairs Program

The funding sources did not have any involvement in the study.

Declaration of Competing Interest

The authors declare no conflicts of interest.

Biographies

Muhannad N. Fadhel completed his B.Sc. Hons in Biology with biophysics minor at Ryerson university in 2011. In 2014, he earned my M.Sc. in Biomedical physics from Ryerson University with a title of "Ultra-high frequency acoustic impedance imaging of cancer cells". The research focused on understanding the source of the scattered ultrasound signals from biological structures to improve the current techniques in analyzing and quantifying ultrasound images. He is currently a PhD student in the department of physics at Ryerson university under the supervision of Dr. Michael Kolios. Muhannad’s doctoral research focuses on the use of quantitative analysis and multispectral imaging to improving the capability of photoacoustics imaging to detect physical and biochemical changes red blood cells undergo in response to cancer therapy.

Eno Hysi is a PhD candidate in the Department of Physics at Ryerson University and a Vanier Scholar. Eno received his BSc degree in 2010 from Ryerson University (Toronto) in Medical Physics where he was first introduced to photoacoustic imaging. He continued his research at Ryerson’s Department of Physics where, in 2012, he graduated from his MSc in Biomedical Physics with a Gold Medal. His research has resulted in a number of publications and he has co-authored a book chapter. Throughout his studies, Eno has been the recipient of numerous academic awards and scholarships including the Ontario Graduate Scholarship, NSERC’s Alexander Graham Bell Canada Graduate Scholarship and most recently the Vanier Canada Graduate Scholarship. His research interests include ultrasound and photoacoustic tissue characterization for biomedical applications such as cancer treatment monitoring and blood hemodynamics.

Hisham Assi finished his Ph.D. in Electrical Engineering and Biomedical Engineering from the University of Toronto, under the supervision of Prof. Richard Cobbold, in the field of biomedical ultrasound. He is currently a postdoctoral fellow in the Physics Department and the Institute for Biomedical Engineering, Science and Technology (iBEST) at Ryerson University and St. Michael’s Hospital in Toronto. His current research focuses on quantitative imaging, especially photoacoustic and ultrasound imaging, and on monitoring and control of cancer hyperthermia treatments.

Michael C. Kolios is a Professor in the Department of Physics at Ryerson University and associate Dean of Research and Graduate Studies in the Faculty of Science. His work focuses on the use of ultrasound and optics in the biomedical sciences. He has published 140 peer-reviewed journal publications, 5 book chapters, and 190 papers in conference proceedings. He has received numerous teaching and research awards, including the American Institute of Ultrasound in Medicine Joseph H. Holmes Basic Science Pioneer Award, the Canada Research Chair in Biomedical Applications of Ultrasound and the Ontario Premier’s Research Excellence Award. He is on the editorial board of the journals Ultrasound Imaging and Photoacoustics and is member of many national and international committees, including the IEEE International Ultrasonics Symposium Technical Program Committee. He regularly reviews for various funding agencies and was a charter member of the National Institutes of Health (NIH) Biomedical Imaging Technology A study section and is a member of the College of Reviewers for the Canadian Institutes of Health Research (CIHR).