Abstract
Due to the outbreak and spread of COVID-19, SARS-CoV-2 has been proven to survive in aerosols for hours. Virus-containing aerosols may intrude into an uncontaminated area from a confined source space under certain ventilated conditions. The penetration factor, which is the most direct parameter for evaluating the invasion process, can effectively reflect the penetration fraction of aerosols and the shielding efficiency of buildings. Based on the observed concentrations of aerosols combined with a widely used concentration model, four numerical calculations of the penetration factor are proposed in this study. A theoretical time-correction Pest was applied to a size-dependent Pavg by proposing a correction coefficient r, and the error analysis of the real-time P(t) and the derived Pd were also performed. The results indicated that Pavg supplied the most stable values for laboratory penetration simulations. However, the time-correction is of little significance under current experimental conditions. P(t) and Pd are suitable for rough evaluation under certain conditions due to the inevitability of particles detaching and re-entering after capture. The proposed optimal penetration factor and the error analysis of each method in this study can provide insight into the penetration mechanism, and also provide a rapid and accurate assessment method for preventing and controlling the spread of the epidemic.
Keywords: Penetration factor, Invasion process, Virus-containing aerosols, Confined space, Optimal value, Correction coefficient
Graphical abstract
Highlights
-
•
An optimal penetration factor was proposed.
-
•
Penetration mechanism was further explored.
-
•
The inevitability of particles detaching and re-entering after capture was proved.
-
•
Time correction under current experimental conditions is of little significance.
1. Introduction
The global outbreak of coronavirus disease (COVID-19) has seriously endangered the health and safety of all human beings. Scientists have conducted extensive research on the Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), referring to transmission dynamics (Morawska and Cao, 2020; Bourouiba, 2020; Cao et al., 2020), removal technology (Zhao et al., 2020), and climate factor (Sobral et al., 2020). Correia et al. (2020) pointed out that improper use of the ventilation system could aggravate the spread of the virus (Correia et al., 2020). van Doremalen et al. (2020) experimentally generated SARS-CoV-2-containing aerosols with a diameter of <5 μm, and illustrated that SARS-CoV-2 can survive and be infectious in aerosols for hours, in some cases even days on surfaces (van Doremalen et al., 2020). Moreover, it is well known that coronavirus is more likely to exist in confined and poorly ventilated spaces. In this case, aerosols can carry or combine with viruses into an uncontaminated area under certain ventilated conditions. However, the most effective evaluation method for aerosols penetrating from the polluted area or the source area to the unpolluted space is still not clear.
In recent decades, the fate of aerosols penetrating from outdoor has received widespread attention from scientists due to the direct relationship with human health (Zhuo et al., 2019; Cao et al., 2019; Xu et al., 2018; Azuma et al., 2018; Morawska et al., 2017). Related penetration research is usually carried out in two ways: field measurement and laboratory simulation. Field experiments are always conducted in real buildings such as school classrooms, dormitories, and offices (Chao et al., 2003; Chatoutsidou et al., 2015; Cong et al., 2018; Hu et al., 2018; Hussein, 2017; Lai et al., 2015; Liu et al., 2018; Zhao et al., 2019; Wang et al., 2019; Chen and Zhao, 2017), while a test chamber or a building brick is usually used as the object to simulate the indoor or outdoor environment in laboratory simulations (Chen and Zhao, 2017; Lai and Nazaroff, 2000; Li et al., 2017; Liu and Nazaroff, 2001; Lv et al., 2018; Wang et al., 2020). The difference between laboratory simulation and field testing is a greater control of the conditions in a laboratory setting. Additionally, the change in concentration of aerosols is one of the basic characteristics in the penetration process. Based on the law of mass balance, Thatcher et al. (2003) had represented the indoor concentration over time “t” as (Thatcher et al., 2003),
| (1) |
where, C in and C out are the indoor and outdoor particle concentrations (cm−3), a is air exchange rate (AER) (h−1) associated with ventilation system, k is the rate of particles deposition loss onto interior surfaces (h−1), while P is the penetration factor. G, S, F, K and H represent the particle generation from the indoor source, particles for dissociation/vaporization, the formation of new particles due to chemical reactions, the particles for coagulation and for hygroscopic growth (cm−3 h−1), respectively.
For the source, concentrations, size of particles and the experimental conditions used in most simulations, it is assumed that the effects of dissociation/vaporization (S), new chemical formation (F), coagulation (K) and hygroscopic growth (H) are avoided in the analysis. If the study only focuses on the single penetration process, the indoor source (G) also has no significance. In this case, Eq. (1) is simplified to the expression with parameter a, k and P, as
| (2) |
Similarly, assuming that the particle flow passing from the outdoor compartment is the only path under ideal conditions, the outdoor particle concentration in a confined space could be affected by the air exchange rate “a” of the indoor compartment and the deposition rate “k” of outdoor particles. Therefore, the outdoor particle concentration over time can be expressed as,
| (3) |
It is assumed that a certain number of particles tend to penetrate from the outdoor compartment at time “t” under the action of a ventilator, but only a portion enters the indoor compartment while the rest is trapped by the sash gap. In this case, “P 0” represents the total proportion of the particles participating in the penetration at a certain AER “a”. If those trapped particles do not detach and re-enter the outdoor compartment, P 0 can be estimated as 1.
A review of the literature shows that the portion of “P” entering the indoor compartment can be defined as follows: the parameter P, associated with infiltration airflow, denotes the fraction of outdoor particles passing through building cracks, leakage paths and window openings (Thornburg et al., 2001; Nazaroff, 2004; Rim et al., 2013). In Eq. (2), “a” and “k” are the only influencing factors, and the equilibrium solution (dC in/dt = 0) is derived as,
| (4) |
In the experiments of penetration simulations in recent decades, Eq. (4) is widely used for quantification of the particle penetration through building cracks. Thornburg et al. (2001) reported penetration factor using this equation, and C in and C out were described as the time average of the indoor and outdoor concentrations (Thornburg et al., 2001); Rim et al. (2013) mentioned in the derivation that the equation was for the particle size category (Rim et al., 2013); while other literatures defaulted the P value to the size-resolved one (Chatoutsidou et al., 2015; Long et al., 2001; Rim et al., 2010). However, there is little reference to the optimal method for determining the P value.
Recently, we performed penetration simulations for emergency evacuation (Wang et al., 2020). A fully enclosed chamber used aerosols with a size range of 69–500 nm to simulate the penetration process from outdoor to indoor. This range can represent some fine particles and ultra-fine particles (FPs/UFPs) in accidents or extreme weather related to air pollution. As the particles gradually pass through the window under a set AER, the indoor concentration may increase, maintain or decrease, while the outdoor concentration continues to decline. In the previous experiment, the initial outdoor concentration of each test changed over time, that is, a stable and continuous particle source could not be provided. This is also the limiting factor for laboratory simulations. Therefore, two questions require further discussions: (1) “is the parameter P of Eq. (4) without a time attribute suitable for the case where the concentration changes in a confined source space?” and (2) “what is the optimal P value?”
Based on the aforementioned properties of SARS-CoV-2 regarding its ability to survive in aerosols for hours, FPs/UFPs may carry or combine with SARS-CoV-2 and then penetrate into uncontaminated areas together. To evaluate the invasion process of aerosols from a confined source space to an uncontaminated area, based on our previous work and the widely used concentration model Eqs. (2), (3), (4), we will thus be (1) proposing four numerical calculations of penetration factor, the size-dependent P avg, the time-corrected P est, the real-time P(t), and the direct-derived P d; (2) comparing and evaluating the observed indoor concentrations and the estimated ones; and (3) selecting the optimal P value for penetration process. The proposed optimal P value and the error analysis could help provide insight into the penetration mechanism, and can also provide a rapid and accurate assessment method for preventing and controlling the spread of the epidemic.
2. Methodology
2.1. Experimental basis
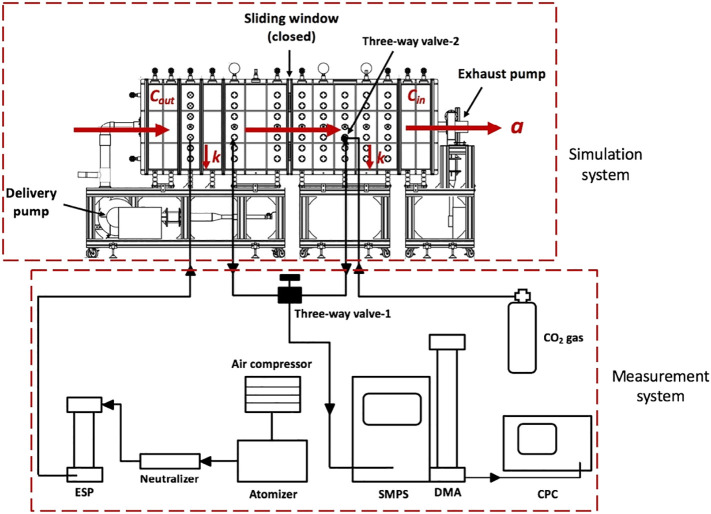
Based on our previous work on penetration simulation for emergency evacuation, Fig. 1 gives the schematic of the whole experimental system, including a simulation system and a measurement system. A fully enclosed chamber as the main body of the simulation system was conducted in the laboratory (laboratory environment has insignificant influence on the test chamber). The chamber contains two parts, an outdoor compartment (left) and an indoor compartment (right), with each inner size of 1.01 m × 0.80 m × 0.80 m. The two parts are divided by a household sliding window, which is kept closed during the measurement. In the measurement system, polydisperse sodium chloride particles with a mass concentration of 10% are sprayed into the outdoor compartment by a 6-jet atomizer (TSI model 3706). The full size range of the particles, ranging from 69 nm to 500 nm with a peak range of 100–300 nm according to size distribution characteristics, imitate virus-containing aerosols in this range. They passed through a silicone desiccant, a neutralizer (Am241, 3 MBq), and an electrostatic precipitator (ESP, prepared in laboratory). Running the test for 36 min displays a concentration change of the two compartments in time distribution by a scanning mobility particles sizer (SMPS, TSI model 3938) and an electrostatic classifier (TSI model 3082) with a long differential mobility analyzer (DMA, TSI model 3081A); meanwhile, the series of real-time concentrations corresponding to indoor (each even-minute, that is, 2, 4, 6…32, 34, 36 min) and outdoor (each odd-minute, that is, 1, 3, 5…31, 33, 35 min) are recorded by an ultrafine condensation particle counter (CPC, TSI model 3776). Additionally, particle concentration accuracy is ±10% and sizing accuracy is 1% at 100 nm for 10:1 sheath/aerosol flow ratio (sheath flow and aerosol flow are 3.0 L/min ± 2.0% and 0.3 L/min ± 1.5% as of reading, respectively). Fig. 2 shows the photos of the experiment.
Fig. 1.
Experimental system for penetration simulation.
Fig. 2.
Experimental photos. (a) The test chamber in simulation system (delivery pump and exhaust pump are not mentioned) and (b) CPC and SMPS with DMA in measurement system.
In this study, the outdoor compartment simulates a closed source space filled with virus-containing aerosols, where a certain amount of particles (around 1.0 × 104 cm−3) are introduced at the initial moment; while the indoor compartment with an initial concentration close to zero simulates an uncontaminated room. Due to the particle flow gradually passing through the crack and entering the indoor compartment while the ventilation system is in operation, the series of the indoor and the outdoor concentrations recorded at every time “t” reported in our previous research exhibits a tendency for continuous attenuation (Wang et al., 2020). The AER of the ventilation system was controlled from 0.31 h−1 to 3.70 h−1, where 0.31 h−1, 1.20 h−1 and 3.70 h−1 were selected for discussion according to their penetration properties. These experimental concentrations are named as “observed concentration(s)” in this study as a basis for judging proposing calculation methods.
2.2. Numerical calculation of penetration factor
Assuming C in (t) and C out (t) as the real-time indoor and outdoor concentrations for instantaneous calculation, respectively, and P(t) as the real-time value of penetration factor at time t, or P avg representing the average penetration factor for a short-term evaluation, Eq. (4) can be expressed as,
| (5) |
and
| (6) |
where, C in,avg and C out,avg are the time-averaged concentrations for each particle size. P(t) is “time-dependent/size-averaged” penetration factor of the indoor compartment, that is, the penetration factor corresponds to the total concentration per minute at the average diameter. P avg is “size-dependent/time-averaged” penetration factor of the indoor compartment, representing the penetration factor corresponding to the average concentration of 36 min at each particle size. However, P avg is a size-dependent parameter without a time property. Therefore, the theoretical value P est is introduced for time correction in this study.
In case of C in ≠ 0, C in (0) and C out (0) represent for the initial conditions. Therefore, by integrating Eqs. (2), (3), the real-time concentrations at t time can be obtained as follows,
| (7) |
| (8) |
Considering the continuous change in concentration from 0 to T time, then
| (9) |
| (10) |
| (11) |
| (12) |
Combined Eqs. (6), (10), (12),
| (13) |
| (14) |
Here, we defined the item “” involving in the parameters “a” “k” and “t” as “correction coefficient r”, then
| (15) |
so,
| (16) |
In case of C in = 0,
| (17) |
To search for an approximation close to the expected value, a simple equation is visually derived from the ratio of Eqs. (7), (8) (assumed P 0 = 1) to directly estimate the penetration factor,
| (18) |
Here, P d represents a time series of approximate values over 36 min.
In case of C in (0)=0, Eq. (18) changes to
| (19) |
P d can be also used to estimate the penetration factor at a certain time t. Compared to P(t) in Eq. (5), P d calculated by Eq. (19) ignores the effect of k but adds the time attribute.
2.3. Application of concentration model
If taking the indoor compartment as the research object, and also fully considering the situation where C out gradually decreases in the laboratory simulation experiment, Eq. (3) is derived to be
| (20) |
where, Δt represents time interval, and the indoor concentration at “t + Δt” time is estimated as,
| (21) |
In this study, the deposition rate k was approximated using the model of Okuyama according to our published work, the value of which is <0.25 h−1 with a particle size of <500 nm (Wang et al., 2020; Okuyama et al., 1986). The penetration factor P, denoted as P(t), P avg, P est and P d, respectively, is substituted into Eq. (21), and the optimal P value is discussed and determined by comparing with the observed indoor concentration over time.
3. Results
3.1. Correction coefficient r
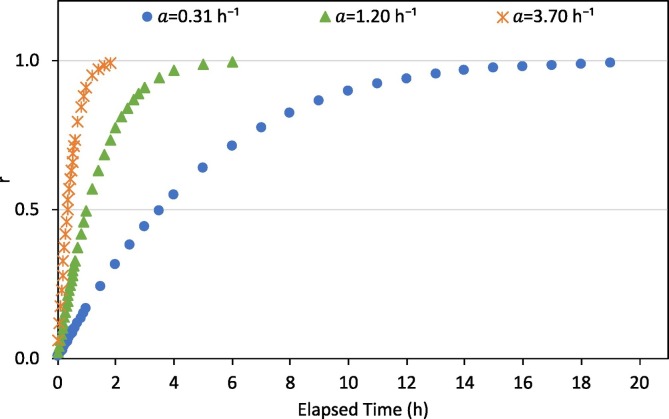
In the experiment, four size segments, 69–100 nm, 100–200 nm, 200–300 nm and 300–500 nm, were divided according to their similar P avg in each segment. Fig. 3 gives the relationship between correction coefficient r and the elapsed time (taking 69–100 nm as an example). These curves are extended indefinitely, and they all finally equal to 1. The larger the AER, the shorter the time.
Fig. 3.
The relationship between correction coefficient r and elapsed time (taking 69–100 nm as an example).
3.2. Values of P(t), Pavg, Pest and Pd in the four size segments
P(t), P avg, P est and P d are determined by Eqs. (5), (6), (16), (18), respectively. As displayed in Table 1 , each time average value of P(t), P avg and P d shows a growth trend with the increase of AER, which is consistent with the literature that a high AER corresponds to a high P value when C out is higher than C in (Wang et al., 2020), but for P est. In addition, the average values of P avg in the four size segments are gradually approaching that of P est as AER is increasing. Moreover, P(t) at an AER of 3.70 h−1, P d at AERs of >1.20 h−1 and all the P est values are >1. Comparing with other P values in the four size segments, P d has a large error while the largest error occurs at P(t) at 3.70 h−1.
Table 1.
Time average and standard deviation of P(t), Pavg, Pest and Pd in four size segments respectively.
| AER (h−1) | Size segment (nm) | P(t) | ±SD | Pavg | ±SD | Pest | ±SD | Pd | ±SD |
|---|---|---|---|---|---|---|---|---|---|
| 0.31 | 69–100 | 0.19 | 0.05 | 0.20 | 0.01 | 4.85 | 0.14 | 0.59 | 0.21 |
| 100–200 | 0.18 | 0.05 | 0.18 | 0.01 | 5.53 | 0.21 | 0.50 | 0.25 | |
| 200–300 | 0.20 | 0.06 | 0.18 | 0.01 | 4.98 | 0.17 | 0.70 | 0.27 | |
| 300–500 | 0.20 | 0.07 | 0.20 | 0.03 | 4.61 | 0.46 | 1.02 | 0.56 | |
| Total average | 0.19 | – | 0.19 | – | 4.99 | – | 0.70 | – | |
| 1.20 | 69–100 | 0.56 | 0.30 | 0.45 | 0.01 | 3.16 | 0.05 | 1.12 | 0.32 |
| 100–200 | 0.56 | 0.30 | 0.45 | 0.02 | 3.04 | 0.12 | 1.10 | 0.34 | |
| 200–300 | 0.54 | 0.32 | 0.43 | 0.01 | 2.75 | 0.06 | 1.05 | 0.37 | |
| 300–500 | 0.57 | 0.33 | 0.46 | 0.05 | 2.87 | 0.29 | 1.12 | 0.37 | |
| Total average | 0.56 | – | 0.45 | – | 2.95 | – | 1.10 | – | |
| 3.70 | 69–100 | 1.37 | 0.85 | 0.75 | 0.04 | 1.72 | 0.08 | 0.99 | 0.30 |
| 100–200 | 1.46 | 0.86 | 0.75 | 0.03 | 1.94 | 0.07 | 1.07 | 0.32 | |
| 200–300 | 1.52 | 0.83 | 0.77 | 0.03 | 1.91 | 0.07 | 1.13 | 0.34 | |
| 300–500 | 1.67 | 1.08 | 0.77 | 0.05 | 1.82 | 0.11 | 1.26 | 0.41 | |
| Total average | 1.50 | – | 0.76 | – | 1.85 | – | 1.11 | – |
3.3. Observed and estimated indoor concentration
In Fig. 4 , the dotted curves present the observed indoor concentration and the estimated concentrations from P(t), P avg, P est and P d at 0.31 h−1, 1.20 h−1 and 3.70 h−1, respectively. The curve using the P est value clearly deviates from the observed concentration. It means the time-corrected P est has a large error, while the real-time P(t), the size-dependent P avg and the direct-derived P d are much closer to the expected value. Additionally, the change trend of the curves, growth, maintenance and decline, is summarized in Table 2 , referring to C out > C in, C out = C in and C out < C in, respectively, which are consistent with the previous reported results (Wang et al., 2020).
Fig. 4.
Comparison of observed indoor concentration and the estimated concentrations from different P values. (a) a = 0.31 h−1 for 100–200 nm, (b) a = 0.31 h−1 for 200–300 nm, (c) a = 1.20 h−1 for 100–200 nm, (d) a = 1.20 h−1 for 200–300 nm, (e) a = 3.70 h−1 for 100–200 nm and (f) a = 3.70 h−1 for 200–300 nm.
Table 2.
Change trend of indoor concentration at different AERs.
| AER (h−1) | Growth | Maintenance | Decline |
|---|---|---|---|
| 0.31 | + | − | − |
| 1.20 | + | + | − |
| 3.70 | + | + | + |
Note: “+” represents yes; “-” represents no.
4. Discussion
4.1. Correction coefficient r value and its time limit
In the case of C in ≠ 0, Eq. (16) gives the theory relationship between P est and P avg. Numerically, the two values gradually approach each other as AER increases (see Table 1). In Eq. (16) there are two terms, “” and “”. In the laboratory simulation, the initial concentration can be seen as a constant, and the value of “a” ranges from 0.31 h−1 to 3.70 h−1 with k being negligible compared to the increased AER. Therefore, “” tends to 1 with the increases of AER and the term “” has little effect on the value P est. In the term “”, r plays an important role. As shown in Table 3 , the correction coefficient r for different size segment at different AER values will have similar maximum and minimum. Generally, correction coefficient r values are all <1, ranging from 0.006 to 0.737. Therefore, the estimated-P est is around 1.37–167 times larger than the size-dependent P avg.
Table 3.
The maximum and minimum of correction coefficient r.
| AER (h−1) |
0.31 |
1.20 |
3.70 |
|||
|---|---|---|---|---|---|---|
| Size range (nm) | Max | Min | Max | Min | Max | Min |
| 69–100 | 0.103 | 0.006 | 0.328 | 0.021 | 0.734 | 0.061 |
| 100–200 | 0.100 | 0.006 | 0.325 | 0.020 | 0.733 | 0.061 |
| 200–300 | 0.102 | 0.006 | 0.327 | 0.021 | 0.734 | 0.061 |
| 300–500 | 0.110 | 0.006 | 0.334 | 0.021 | 0.737 | 0.062 |
Fig. 3 presents the r value with the size range of 69–100 nm, indicating the larger the AER, the shorter the required time for the “r” value to reach 0.99. Table 4 displays the other size segments. Generally, the averaged required time at each AER is 18.7 h (0.31 h−1), 5.7 h (1.20 h−1), and 2.4 h (3.70 h−1), respectively. After the required time, r will not play a role between P est and P avg. Eq. (16) changes to,
| (23) |
Table 4.
The time required for r to reach 0.99 (Unit: h).
| Size segment (nm) | AER (h−1) |
||
|---|---|---|---|
| 0.31 | 1.20 | 3.70 | |
| 69–100 | 19.0 | 6.0 | 1.8 |
| 100–200 | 19.6 | 5.6 | 2.6 |
| 200–300 | 18.6 | 5.6 | 2.6 |
| 300–500 | 17.6 | 5.6 | 2.6 |
| Average | 18.7 | 5.7 | 2.4 |
The relationship between P est and P avg is completely related to the term “”, and as the AER value increases, it depends only on the fixed initial concentration. And in the case of C in = 0, Eq. (23) changes to
| (24) |
Therefore, the time correction under the effect of the correction coefficient r is of little significance due to the simulated ideal experimental conditions in the laboratory, including the good airtightness of the experimental chamber, the mild testing environment, and the controllable particle concentration and ventilation power. In this case, the controllable concentration ratio of the indoor and the outdoor results in the averaged concentrations being similar to the real-time ones. In contrast, it can be speculated that P est could become necessary for the system if the outdoor concentration is much higher than the indoor one, or if there is a large AER (i.e. a »3.70 h−1), but further demonstration it still needed.
4.2. The estimated indoor concentration at an estimated P value
Fig. 4 gives the comparison between the estimated values at different P and the observed indoor concentration. The concentration model in Eq. (21) is time dependent. The interval time Δt and the indoor and outdoor concentrations at time t, C in (t) and C out (t), jointly determine the tendency of the concentration change. Visually, the estimated concentrations at P(t), P avg, and P d are in good agreement with the observed ones compared to the concentration at P est: (1) P(t) is a series of time-dependent values determined by Eq. (5). In the P(t) series, the values corresponding to each time t well reflect the real-time penetration situation, thus obtaining a curve close to the observed concentration; (2) P avg in Eq. (6) is an average value from the time-averaged indoor and outdoor concentrations (C in, avg and C out, avg), representing the penetration ratio of each particle size in an average time of 36 min. Numerically, it is a series that changes with particle size and does not vary by time. However, the curves in Fig. 4 are fitting well with the actual observed concentrations, illustrating that the average value can reflect the penetration situation in a short-term evaluation of at least 36 min. Additionally, outdoor concentration in the laboratory simulation is controlled, the experimental chamber has good air tightness and the AER value is preset. Therefore, there are no drastic changes in concentrations from complex conditions such as turbulence or air leakage. In this case, the error between the average concentration and the real-time concentration is similar so that the fitting results are approximate; (3) P est is the theoretical time-corrected value of P avg because P avg is lacking time-varying characteristics. However, Fig. 4 displays that the estimated concentration has a large error at P est. As described in the previous Section 4.1, the error of P est originates from the correction coefficient r. Eq. (15) shows that “r” is a strongly time-dependent parameter, and the minimum action time is 1.8 h at 69–100 nm with the experimental setting of the maximum AER (3.70 h−1). Therefore, the error of P est exists in the whole experimental process due to the current laboratory simulation only being 36 min long. In addition, the P avg value is similar to the expected value, and the time attribute is not significant in this experiment due to the small change in concentrations. In this case, further correction on P avg may bring more errors; (4) P d in Eq. (18) is derived visually from the ratio of C in (t) and C out (t), ignoring deposition rate k and introducing real-time t. The ignored k value indicates that the deposition portion is negligible compared to the increased AER in the present laboratory penetration simulation. The result agrees with those in previous studies of the literature (Chao et al., 2003; Liu and Nazaroff, 2001; Thornburg et al., 2001; Long et al., 2001; Rim et al., 2010; Okuyama et al., 1986; Vette et al., 2001; Wallace et al., 2004). Rim et al. (2010) found for smaller UFP (d p < 30 nm) the loss due to deposition is substantially higher than that due to AER, and deposition rate k usually decreases to <0.1 h−1 at a particle size of >100 nm (Rim et al., 2010). Additionally, both P(t) and P avg originate from Eq. (4) and this equation has set “C in (0) = 0” as a prerequisite while P est in Eq. (16) and P d in Eq. (18) include the condition of “C in (0) ≠ 0”. It can be considered that P est in Eq. (16) and P d in Eq. (18) are the corrections of the default item of the initial indoor concentration.
4.3. Error analysis and selection of the optimal penetration factor
Table 5 gives the relative errors between the estimated results at different penetration values and the observed indoor concentrations. Generally, the minimal relative errors from P(t), P avg and P d occur at the AER as 0.31 h−1 are approximate. Taking the segment of 100–200 nm as an example, the error ranges (%) are (−15.1 to 18.5) for P(t), (−14.8 to 19.0) for P avg and (−14.3 to 21.4) for P d, respectively. As the AER increases, the errors from P(t) and P d increase, for example, (−65.3 to 38.7) for P(t) and (−69.6 to 29.3) for P d at the AER as 3.70 h−1, and the large errors are mainly concentrated in the early period around 0.233 h.
Table 5.
Relative errors between estimated results at different penetration values and observed concentrations.
| Size segment (nm) |
100–200 |
200–300 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| t |
AER |
P(t) |
Pavg |
Pest |
Pd |
P(t) |
Pavg |
Pest |
Pd |
| h | h−1 | % | % | % | % | % | % | % | % |
| 0.033 | 0.31 | – | – | – | – | – | – | – | – |
| 0.067 | 2.2 | 2.8 | 55.7 | 1.0 | −1.8 | −0.9 | 56.5 | −3.1 | |
| 0.100 | −5.7 | −5.2 | 42.8 | −5.4 | −17.4 | −16.7 | 30.0 | −16.6 | |
| 0.133 | 18.5 | 19.0 | 74.2 | 21.4 | 1.5 | 2.0 | 49.2 | 7.4 | |
| 0.167 | −10.1 | −9.5 | 38.4 | −11.6 | 8.1 | 8.5 | 55.4 | 13.9 | |
| 0.200 | −15.1 | −14.8 | 24.8 | −14.3 | −0.2 | 0.2 | 44.7 | 3.4 | |
| 0.233 | −9.3 | −9.2 | 26.1 | −6.5 | −24.2 | −23.9 | 10.4 | −22.2 | |
| 0.267 | 6.6 | 6.7 | 44.8 | 10.2 | −4.9 | −4.9 | 27.4 | −0.4 | |
| 0.300 | −7.5 | −7.3 | 28.4 | −5.5 | −9.0 | −9.1 | 19.4 | −4.8 | |
| 0.333 | −3.3 | −3.3 | 30.4 | −0.9 | 11.5 | 11.2 | 42.7 | 16.5 | |
| 0.367 | −2.4 | −2.4 | 30.1 | 0.0 | −2.5 | −2.7 | 27.1 | 0.9 | |
| 0.400 | −9.1 | −9.2 | 19.9 | −7.0 | −7.9 | −8.1 | 18.9 | −4.9 | |
| 0.433 | 4.3 | 4.1 | 33.7 | 7.0 | −11.1 | −11.4 | 11.9 | −8.1 | |
| 0.467 | −5.3 | −5.5 | 22.0 | −3.2 | 15.1 | 14.6 | 41.0 | 19.0 | |
| 0.500 | −10.2 | −10.4 | 13.5 | −8.1 | −4.4 | −4.6 | 21.5 | −2.0 | |
| 0.533 | 11.1 | 10.7 | 37.2 | 13.9 | −9.9 | −10.2 | 12.1 | −7.6 | |
| 0.567 | −7.5 | −7.8 | 17.1 | −5.8 | −11.5 | −11.9 | 7.4 | −9.1 | |
| 0.600 | 4.4 | 4.1 | 29.2 | 6.5 | 15.4 | 14.8 | 38.0 | 18.4 | |
| 0.633 | – | – | – | – | – | – | – | – | |
| 0.033 | 1.20 | – | – | – | – | – | – | – | – |
| 0.067 | −36.2 | −22.9 | 67.2 | −38.7 | −33.9 | −18.1 | 80.9 | −36.6 | |
| 0.100 | −35.6 | −27.5 | 32.3 | −26.7 | −49.8 | −42.2 | 9.8 | −43.9 | |
| 0.133 | −22.9 | −17.9 | 26.8 | −10.5 | −4.3 | 1.0 | 50.8 | 12.7 | |
| 0.167 | −18.7 | −15.9 | 18.0 | −7.4 | −14.8 | −10.8 | 29.7 | −3.8 | |
| 0.200 | −6.3 | −4.3 | 26.6 | 4.8 | −21.6 | −19.1 | 11.7 | −13.3 | |
| 0.233 | −3.8 | −2.3 | 26.2 | 5.5 | −0.7 | 0.4 | 28.8 | 8.6 | |
| 0.267 | −0.6 | 0.4 | 26.6 | 7.4 | 0.8 | 1.5 | 27.7 | 8.6 | |
| 0.300 | −14.5 | −13.8 | 7.5 | −8.7 | −15.7 | −15.4 | 5.4 | −10.4 | |
| 0.333 | −3.8 | −3.9 | 15.5 | 1.9 | −4.9 | −5.4 | 13.1 | 0.4 | |
| 0.367 | −1.8 | −2.2 | 15.6 | 3.3 | −3.8 | −4.7 | 11.8 | 0.8 | |
| 0.400 | −6.3 | −6.9 | 8.7 | −2.1 | −11.8 | −13.0 | 0.2 | −8.2 | |
| 0.433 | 1.7 | 0.8 | 15.9 | 5.8 | 20.9 | 18.7 | 33.6 | 25.1 | |
| 0.467 | −1.4 | −2.6 | 11.3 | 1.8 | −9.3 | −10.6 | 2.1 | −6.7 | |
| 0.500 | 2.1 | 0.6 | 13.7 | 5.0 | 5.9 | 3.8 | 16.2 | 8.5 | |
| 0.533 | −2.0 | −3.3 | 9.1 | 0.6 | −5.8 | −7.7 | 3.2 | −3.9 | |
| 0.567 | −1.8 | −3.5 | 7.8 | 0.2 | −6.4 | −8.6 | 0.9 | −4.9 | |
| 0.600 | 2.1 | 4.0 | 15.1 | 7.9 | 1.3 | −1.2 | 8.0 | 2.7 | |
| 0.633 | – | – | – | – | – | – | – | – | |
| 0.033 | 3.70 | – | – | – | – | – | – | – | – |
| 0.067 | −65.3 | −27.8 | −69.6 | −69.6 | −65.4 | −30.0 | 28.6 | −69.7 | |
| 0.100 | −26.1 | −7.5 | −35.4 | −9.4 | −32.4 | −15.2 | 22.7 | −18.0 | |
| 0.133 | −12.6 | −4.1 | −23.6 | 0.4 | −18.7 | −10.8 | 15.9 | −7.0 | |
| 0.167 | 3.6 | 6.1 | −9.3 | 13.5 | 0.9 | 2.7 | 24.0 | 10.4 | |
| 0.200 | 7.9 | 7.7 | −5.5 | 13.9 | −0.1 | −1.2 | 15.4 | 5.5 | |
| 0.233 | −4.6 | −6.4 | −16.3 | −2.0 | 0.2 | −2.9 | 11.0 | 3.0 | |
| 0.267 | 6.0 | 0.8 | −7.1 | 7.0 | 13.7 | 7.9 | 20.2 | 14.7 | |
| 0.300 | 14.1 | 7.5 | −0.1 | 13.4 | 5.4 | −0.9 | 9.3 | 4.7 | |
| 0.333 | 10.2 | 3.8 | −3.5 | 8.1 | 4.8 | −2.3 | 6.5 | 2.8 | |
| 0.367 | 11.4 | 4.4 | −2.1 | 8.2 | 24.8 | 16.0 | 25.9 | 21.1 | |
| 0.400 | 13.2 | 5.0 | −1.1 | 8.9 | 9.2 | 2.0 | 11.4 | 5.0 | |
| 0.433 | 17.9 | 9.1 | 3.2 | 12.7 | −2.5 | −9.5 | −1.8 | −6.9 | |
| 0.467 | 19.0 | 9.7 | 4.2 | 13.0 | 25.5 | 14.9 | 22.5 | 19.1 | |
| 0.500 | 24.0 | 14.0 | 8.3 | 17.0 | 15.8 | 7.0 | 15.2 | 9.3 | |
| 0.533 | 15.6 | 6.9 | 1.2 | 8.6 | 11.9 | 3.3 | 11.3 | 5.1 | |
| 0.567 | 1.2 | −6.6 | −11.5 | −5.4 | 5.9 | −2.8 | 3.9 | −0.9 | |
| 0.600 | 38.7 | 25.9 | 21.3 | 29.3 | 36.1 | 23.8 | 30.7 | 26.9 | |
| 0.633 | – | – | – | – | – | – | – | – | |
In terms of P values, Table 1 shows the average and standard deviation of P(t), P avg, P est and P d in four size segments, respectively. A large standard deviation indicates that the variation of P value in the size segment fluctuates greatly over 36 min, with the largest errors appearing on P(t) at the AER of 3.70 h−1. P(t) in Eq. (5) contains two terms, “” and “”. For the first term “”, it has reported that deposition rate k usually <0.1 h−1 as d p > 100 nm and k < 0.25 h−1 as d p < 100 nm (Rim et al., 2010; Okuyama et al., 1986), so the term is around 1 to 2 (AER ranges from 0.30 h−1 to 3.70 h−1). As we can see in Table 1, the values of P(t) is >1 at a large AER of 3.70 h−1 with the term “” making the main contribution to the value of P(t). Based on the experimental basis (Wang et al., 2020), the curve of indoor concentration shows three trends during 36 min at the three different settings of AERs (Table 2). Before the decline, the curve of growth and maintenance last 0.233 h (first 14 min) at the AER of 3.70 h−1, that is, P(t) can only be ensured ranging from 0 to 1 before the occurrence of “C out < C in”. Additionally, the real-time value is >1, indicating that the indoor concentration is already higher than outdoor and P(t) is no longer applicable for evaluation. Different with P(t), the AER “a” and the time attribute “t”, contained in the term “”, gives the main contribution to the P d value. As shown in Table 1, P d indicates a higher value than other three P values at a small AER of <1.20 h−1, but the relative errors between the estimated results at P d and the observed concentrations are similar to P(t) and P avg in Table 5; while in the later period (last 22 min) and at a large AER of >1.20 h−1, “a” and “t” corrected the deviation caused by the “” term to some extent, but P d values are >1. Due to the term “” being included by P(t) and P d, the observed indoor concentration at the beginning of the experiment is much lower than the outdoor one, so that both P(t) and P d values are lower. However, the low penetration values cannot reflect the actual situation of a large number of particles penetrating caused by a large AER and a large concentration difference at the initial time (“” tends to zero). The concentrations estimated from P(t) and P d therefore have more significant errors than the actual observed concentration in the early period prior to 0.233 h, especially when the AER is more than or equal to 1.20 h−1 (Table 5). Similarly, P d in Eq. (18) including the term of “” has insignificant correction because the initial indoor concentration tends to zero in this study. Additionally, as described in Eq. (8), we assumed “P 0=1” under the ideal condition, indicating that those trapped particles do not detach and re-enter the outdoor compartment. However, the errors indicate that the assumed P 0 exists and the value of P 0 is <1, implying that detaching and re-entering are inevitable in the actual situation. Therefore, in a 36-min penetration evaluation, both P(t) and P d are applicable to conditions where the AER is <1.20 h−1, but they cannot be equal due to the different derivations. In addition, P(t) can be also used for the late stage at the AER as 1.20 h−1, and unlike “” in P d, “” in P(t) has a certain correction effect on the P value under the condition of AER <1.20 h−1.
It is worth noting that the estimated result at P avg has small errors among all the P values at each size segment and at each AER in Table 5. Like P(t) in Eq. (5), the “” term eliminates the effect from AER to some extent, and C in, avg and C out, avg in Eq. (6) eliminates the fluctuation of concentration changes at two adjacent times (i.e. 0.033 h and 0.067 h). Therefore, the estimation at P avg is more stable than other values.
In contrast, the increase of the AER value tends to decrease the error from P est, i.e. from (13.5 to 74.2) at 0.31 h−1 to (−69.6 to 21.3) at 3.70 h−1. Correction coefficient r brings a large error to P est, resulting in a change trend that is negatively correlated with AER growth. Similarly, a large AER reduces the action time of the r value. In addition, the overall P est value far exceeding 1 indicates its inapplicability in the 36-min evaluation. Similar to P d in Eq. (18), P est in Eq. (16) includes the condition of “C in (0)≠0” and is insignificant for the correction of P avg due to a low ratio of “” in this study, and may even cause large errors. Additionally, for systems with large indoor and outdoor concentration changes or an existing large AER (i.e. a > 3.70 h−1), whether or not the error caused by P est would decrease still needs further demonstration.
5. Conclusion
This work proposes four numerical calculations of penetration factor to select the optimal value. In addition, a widely used concentration model is employed to evaluate the penetration process of aerosols from a confined source space to an uncontaminated area within 36 min, and the following conclusions can be applied to the invasion evaluation of virus-containing aerosols.
During the 36-min penetration process in this study, the proposed correction coefficient r has its own time limit if time-correction is necessary under some non-ideal condition. Moreover, the time limit gets shorter as the AER increases. According to the present experimental design, it ranges averagely from 2.4 h (3.70 h−1) to 18.7 h (0.31 h−1).
Additionally, size-dependent P avg is time-corrected to be P est by the correction coefficient r. However, the time correction is of little significance due to the simulated ideal experimental conditions in the laboratory within the current experimental 36 min. P est was assumed to be necessary for the system if the confined source space has a much higher initial concentration than the indoor one or there is a large AER (i.e. a »3.70 h−1), but it still needs further demonstration.
The error analysis of the real-time P(t) and the direct-derived P d proves that the assumed P 0 exists and the value of P 0 is <1 in the actual situation, indicating that detaching and re-entering are inevitable. Both of them are only suitable for rough evaluation in the case of AER <1.20 h−1 and P(t) is also applicable to the later stage when the AER is equal to 1.20 h−1. Additionally, the size-dependent P avg is the optimal value among the four under current experimental conditions, due to minimal effect from the AER value and fluctuations in concentration.
CRediT authorship contribution statement
Wenlu Wang:Conceptualization, Methodology, Investigation, Writing - review & editing.Minoru Yoneda:Supervision, Formal analysis.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was financially supported by the Nuclear Regulation Authority (NRA) Japan and Japan Atomic Energy Agency (JAEA).
References
- Azuma K., Ikeda K., Kagi N., Yanagi U., Osawa H. Physicochemical risk factors for building-related symptoms in air-conditioned office buildings: ambient particles and combined exposure to indoor air pollutants. Sci. Total Environ. 2018;616–617:1649–1655. doi: 10.1016/j.scitotenv.2017.10.147. [DOI] [PubMed] [Google Scholar]
- Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions: potential implications for reducing transmission of COVID-19. JAMA. 2020;323(18):1837–1838. doi: 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
- Cao Z., Wang M., Chen Q., Zhu C., Jie J., Li X., Dong X., Miao Z., Shen M., Bu Q. Spatial, seasonal and particle size dependent variations of PAH contamination in indoor dust and the corresponding human health risk. Sci. Total Environ. 2019;653:423–430. doi: 10.1016/j.scitotenv.2018.10.413. [DOI] [PubMed] [Google Scholar]
- Cao Q., Chen Y.C., Chen C.L., Chiu C.H. SARS-CoV-2 infection in children: transmission dynamics and clinical characteristics. J. Formos. Med. Assoc. 2020;119(3):670–673. doi: 10.1016/j.jfma.2020.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao C.Y.H., Wan M.P., Cheng E.C.K. Penetration coefficient and deposition rate as a function of particle size in non-smoking naturally ventilated residences. Atmos. Environ. 2003;37(30):4233–4241. [Google Scholar]
- Chatoutsidou S.E., Maskova L., Ondrackova L., Ondracek J., Lazaridis M., Smolik J. Modeling of the aerosol infiltration characteristics in a cultural heritage building: the Baroque Library Hall in Prague. Build. Environ. 2015;89:253–263. [Google Scholar]
- Chen C., Zhao B. A modified Brownian force for ultrafine particle penetration through building crack modeling. Atmos. Environ. 2017;170:143–148. [Google Scholar]
- Cong X.C., Zhao J.J., Jing Z., Wang Q.G., Ni P.F. Indoor particle dynamics in a school office: determination of particle concentrations, deposition rates and penetration factors under naturally ventilated conditions. Environ. Geochem. Hlth. 2018;40:2511–2524. doi: 10.1007/s10653-018-0116-x. [DOI] [PubMed] [Google Scholar]
- Correia G., Rodrigues L., Gameiro da Silva M., Gonçalves T. Airborne route and bad use of ventilation systems as non-negligible factors in SARS-CoV-2 transmission. Med. Hypotheses. 2020;141 doi: 10.1016/j.mehy.2020.109781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Doremalen N., Bushmaker T., Morris D.H. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N. Engl. J. Med. 2020;382(16):1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y.J., Bao L.J., Huang C.L., Li S.M., Liu P., Zeng E.Y. Exposure to air particulate matter with a case study in Guangzhou: is indoor environment a safe haven in China? Atmos. Environ. 2018;191:351–359. [Google Scholar]
- Hussein T. Indoor-to-outdoor relationship of aerosol particles inside a naturally ventilated apartment - a comparison between single-parameter analysis and indoor aerosol model simulation. Sci. Total Environ. 2017;596:321–330. doi: 10.1016/j.scitotenv.2017.04.045. [DOI] [PubMed] [Google Scholar]
- Lai A.C.K., Nazaroff W.W. Modeling indoor particle deposition from turbulent flow onto smooth surfaces. J. Aerosol Sci. 2000;31(4):463–476. [Google Scholar]
- Lai D., Karava P., Chen Q. Study of outdoor ozone penetration into buildings through ventilation and infiltration. Build. Environ. 2015;93:112–118. [Google Scholar]
- Li A., Ren T., Yang C., Lv W., Zhang F. Study on particle penetration through straight, L, Z and wedge-shaped cracks in buildings. Build. Environ. 2017;114:333–343. [Google Scholar]
- Liu D.L., Nazaroff W.W. Modeling pollutant penetration across building envelopes. Atmos. Environ. 2001;35(26):4451–4462. [Google Scholar]
- Liu C., Yang J., Ji S., Lu Y., Wu P., Chen C. Influence of natural ventilation rate on indoor PM2.5 deposition. Build. Environ. 2018;144:357–364. [Google Scholar]
- Long C.M., Suh H.H., Catalano P.J., Koutrakis P. Using time- and size-resolved particulate data to quantify indoor penetration and deposition behavior. Environ. Sci. Technol. 2001;35(10):2089–2099. doi: 10.1021/es001477d. [DOI] [PubMed] [Google Scholar]
- Lv Y., Wang H.F., Wei S., Wu T., Liu T., Chen B. The experimental study on indoor and outdoor penetration coefficient of atmospheric fine particles. Build. Environ. 2018;132:70–82. [Google Scholar]
- Morawska L., Ayoko G.A., Bae G.N., Buonanno G., Chao C.Y.H., Clifford S., Fu S.C., Hanninen O., He C., Isaxon C., Mazaheri M., Salthammer T., Waring M.S., Wierzbicka A. Airborne particles in indoor environment of homes, schools, offices and aged care facilities: the main routes of exposure. Environ. Int. 2017;108:75–83. doi: 10.1016/j.envint.2017.07.025. [DOI] [PubMed] [Google Scholar]
- Morawska L., Cao J. Airborne transmission of SARS-CoV-2: the world should face the reality. Environ. Int. 2020;139 doi: 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nazaroff W.W. Indoor particle dynamics. Indoor Air. 2004;14:175–183. doi: 10.1111/j.1600-0668.2004.00286.x. [DOI] [PubMed] [Google Scholar]
- Okuyama K., Kousaka Y., Yamamoto S., Hosokawa T. Particle loss of aerosols with particle diameters between 6 and 2000 nm in stirred tank. J. Colloid Interface Sci. 1986;110:214–223. [Google Scholar]
- Rim D., Wallace L., Persily A. Infiltration of outdoor ultrafine particles into a test house. Environ. Sci. Technol. 2010;44:5908–5913. doi: 10.1021/es101202a. [DOI] [PubMed] [Google Scholar]
- Rim D., Wallace L.A., Persily A.K. Indoor ultrafine particles of outdoor origin: importance of window opening area and fan operation condition. Environ Sci Technol. 2013;47(4):1922–1929. doi: 10.1021/es303613e. [DOI] [PubMed] [Google Scholar]
- Sobral M.F.F., Duarte G.B., da Penha Sobral A.I.G., Marinho M.L.M., de Souza Melo A. Association between climate variables and global transmission of SARS-CoV-2. Sci. Total Environ. 2020;729 doi: 10.1016/j.scitotenv.2020.138997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thatcher T.L., Lunden M.M., Revzan K.L., Sextro R.G., Brown N.J. A concentration rebound method for measuring particle penetration and deposition in the indoor environment. Aerosol Sci. Technol. 2003;37(11):847–864. [Google Scholar]
- Thornburg J., Ensor D.S., Rodes C.E., Lawless P.A., Sparks L.E., Mosley R.B. Penetration of particles into buildings and associated physical factors. Part I: model development and computer simulations. Aerosol Sci. Technol. 2001;34(3):284–296. [Google Scholar]
- Vette A.F., Rea A.W., Lawless P.A., Rodes C.E., Evans G., Highsmith V.R., Sheldon L. Characterization of indoor-outdoor aerosol concentration relationships during the Fresno PM exposure studies. Aerosol Sci. Technol. 2001;34(1):118–126. [Google Scholar]
- Wallace L.A., Emmerich S.J., Howard-Reed C. Effect of central fans and in-duct filters on deposition rates of ultrafine and fine particles in an occupied townhouse. Atmos. Environ. 2004;38(3):405–413. [Google Scholar]
- Wang X., Gao Z., Yang J., Yang X. In situ investigation on linkage between particle penetration and air exchange through building envelope. Int. J. Vent. 2019;18(4):233–245. [Google Scholar]
- Wang W., Kato N., Kimoto S., Matsui Y., Yoneda M. Simulation and evaluation of sheltering efficiency of houses equipped with ventilation systems. Build. Environ. 2020;168 [Google Scholar]
- Xu H., Guinot B., Cao J., Li Y., Niu X., Ho K.F., Shen Z., Liu S., Zhang T., Lei Y., Zhang Q., Sun J., Gao J. Source, health risk and composition impact of outdoor very fine particles (VFPs) to school indoor environment in Xi’an, Northwestern China. Sci. Total Environ. 2018;612:238–246. doi: 10.1016/j.scitotenv.2017.08.101. [DOI] [PubMed] [Google Scholar]
- Zhao H., Gall E.T., Stephens B. Measuring the building envelope penetration factor for ambient nitrogen oxides. Environ. Sci. Technol. 2019;53(16):9695–9704. doi: 10.1021/acs.est.9b02920. [DOI] [PubMed] [Google Scholar]
- Zhao B., Liu Y., Chen C. Air purifiers: a supplementary measure to remove airborne SARS-CoV-2. Build. Environ. 2020;177 doi: 10.1016/j.buildenv.2020.106918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuo M., Ma S., Li G., Yu Y., An T. Chlorinated paraffins in the indoor and outdoor atmospheric particles from the Pearl River Delta: characteristics, sources, and human exposure risks. Sci. Total Environ. 2019;650(Pt 1):1041–1049. doi: 10.1016/j.scitotenv.2018.09.107. [DOI] [PubMed] [Google Scholar]