mDixon-Based Synthetic CT Generation for PET Attenuation Correction on Abdomen and Pelvis Jointly Using Transfer Fuzzy Clustering and Active Learning-Based Classification

Abstract

We propose a new method for generating synthetic CT images from modified Dixon (mDixon) MR data. The synthetic CT is used for attenuation correction (AC) when reconstructing PET data on abdomen and pelvis. While MR does not intrinsically contain any information about photon attenuation, AC is needed in PET/MR systems in order to be quantitatively accurate and to meet qualification standards required for use in many multi-center trials. Existing MR-based synthetic CT generation methods either use advanced MR sequences that have long acquisition time and limited clinical availability or use matching of the MR images from a newly scanned subject to images in a library of MR-CT pairs which has difficulty in accounting for the diversity of human anatomy especially in patients that have pathologies. To address these deficiencies, we present a five-phase interlinked method that uses mDixon MR acquisition and advanced machine learning methods for synthetic CT generation. Both transfer fuzzy clustering and active learning-based classification (TFC-ALC) are used. The significance of our efforts is fourfold: 1) TFC-ALC is capable of better synthetic CT generation than methods currently in use on the challenging abdomen using only common Dixon-based scanning. 2) TFC partitions MR voxels initially into the four groups regarding fat, bone, air, and soft tissue via transfer learning; ALC can learn insightful classifiers, using as few but informative labeled examples as possible to precisely distinguish bone, air, and soft tissue. Combining them, the TFC-ALC method successfully overcomes the inherent imperfection and potential uncertainty regarding the co-registration between CT and MR images. 3) Compared with existing methods, TFC-ALC features not only preferable synthetic CT generation but also improved parameter robustness, which facilitates its clinical practicability. Applying the proposed approach on mDixon-MR data from ten subjects, the average score of the mean absolute prediction deviation (MAPD) was 89.78±8.76 which is significantly better than the 133.17±9.67 obtained using the all-water (AW) method (p=4.11E-9) and the 104.97±10.03 obtained using the four-cluster-partitioning (FCP, i.e., external-air, internal-air, fat, and soft tissue) method (p=0.002). 4) Experiments in the PET SUV errors of these approaches show that TFC-ALC achieves the highest SUV accuracy and can generally reduce the SUV errors to 5% or less. These experimental results distinctively demonstrate the effectiveness of our proposed TFC-ALC method for the synthetic CT generation on abdomen and pelvis using only the commonly-available Dixon pulse sequence.

I. Introduction

PET/MR is a hybrid imaging modality which has several advantages over conventional PET/CT [1], [2], particularly in the areas of the abdomen and pelvis. In addition, the lack of ionizing radiation given the lack of CT may be beneficial for long-term surveillance of pediatric patients. The MR aspect of PET/MR also provides information on soft tissue composition via contrast enhancement as well as defined tissues margins for surgical or radiation therapy planning [61].

However, despite these advantages, PET/MR cannot be realized in clinical trials. PET/MR often exhibits SUVs that differ by as much as 20% from the values of PET/CT. This exceeds the 10% specification for SUV accuracy of the National Cancer Institute/American College of Radiology Imaging Network (NCI/ACRIN) [3] and the Society of Nuclear Medicine Clinical Trials Network [4] and thus disqualify PET/MR for use in multicenter clinical trials. The difference in SUVs is primarily due to inaccuracy in attenuation correction (AC). A PET/CT scanner uses CT to measure photon absorption and to make its determination of attenuation correction. Lacking a CT, this information is not available with PET/MR as MR data is based on the resonance signal from hydrogen atoms in water and not on photon attenuation.

Currently, there are several proposed methods for obtaining MR-AC, including the template, atlas, and model-based segmentation. These methods used previously collected MR and CT dataset pairs to generate a “best-fit” attenuation map [58]. However, given the great diversity of human anatomy and morphological changes over time even within a patient, these approaches have difficulty capturing a patient-specific anatomy and pathological lesions progression [5], [6]. Moreover, proximity of bone and air [7], [8] and intra-subject variability in lung density [9] remains an unsolved challenge for AC with these approaches. Other methods include using patient-specific MR data or brain anatomy with constrained structure. With all these techniques, reported errors in SUVs still exceed 20% in both lesions and normal organs. The most egregious errors are seen in or adjacent to bone [3], [10]–[19]. In the fact, bone and air lie at the extremes with regard to photon attenuation yet both have very low MR signals and are hard to differentiate using MR. Some advanced sequences such as ultra-short echo time (UTE) or zero echo time (ZTE) have been also used, but they are often technically challenging and not available on many scanners [10], [11], [14], [20]–[26], [60].

State-of-the-art methods are to use advanced imaging processing approaches based on machine learning and pattern recognition techniques [28], [32], [59], [61]–[65]. These methods attempt to synthesize a CT by classifying image voxels according to their composition of the four key materials: bone, air, fat, and soft tissue [27]–[32]. Although these methods have been shown to be able to generate accurate brain and pelvis synthetic CT [30], [57], [59]–[61], it would be difficult to use them for other body sections, e.g. abdomen, as the training data would contain lots of incorrect, mismatched information due to the complicated and deformable anatomy that leads to imperfect CT and MR co-registration [46], [54].

So, for accurate synthetic CT generation on abdomen and pelvis, we propose a five-interlinked-phase method that jointly leverages transfer fuzzy clustering and active learning-based classification (TFC-ALC for short). Our contributions lie in four aspects:

1. TFC-ALC is based solely on common Dixon-based sequences, by organically incorporating two key techniques - knowledge-leveraged transfer fuzzy c-means (KL-TFCM) and active learning-based support vector machine (AL-SVM). As such, TFC-ALC method is suitable for synthetic CT generation for the challenging abdominal body section.

2. Due to transfer fuzzy clustering, KL-TFCM can reliably partition voxels in MR images into the four initial groups for the key materials. Since only fat is well-defined by KL-TFCM, AL-SVM strives to figure out insightful classifiers, using as few informative labeled examples as possible, to further accurately refine the bone, air, and soft tissue. As such, jointly leveraging KL-TFCM and AL-SVM, TFC-ALC is capable of overcoming the inherent imperfection and potential uncertainty existing in the training phases and of generating better synthetic CTs than those obtained using methods currently in use, for the body sections of abdomen and pelvis.

3. Compared with existing methods, TFC-ALC features better parameter robustness, which facilitates its clinical practicability.

4. Results of PET SUV errors indicate that TF-ALC obtains the general 5% or better accuracy, which ultimately verifies the effectiveness of our work for PET AC on abdomen and pelvis.

The remainder of this manuscript is organized as follows. Related work, e.g., KL-TFCM, SVM, and active learning, are reviewed briefly in Section II. The proposed TFC-ALC method, including from Phase I to Phase V, is introduced specifically in Section III. The complexity analysis of TFC-ALC is given in Section IV. The experimental studies are presented in Sections V–VII. Conclusions are given in Section VIII.

II. Related Work

A. Knowledge-Leveraged Transfer Fuzzy c-Means (KL-TFCM)

Fuzzy c-means (FCM) is a classic representative of fuzzy clustering [33]–[36], [63], which aims to optimally group the data instances in one data set into C disjoint clusters so that not only the overall intra-cluster deviation is minimum but also the overall inter-cluster separation is maximum. FCM has been extensively applied in image compression [37], image segmentation [35], [38], target tracking [39], and gene expression analysis [40]. However, FCM is sometimes inefficient and even invalid when facing situations where target data are quite distorted by interference information, e.g., noise and outliers [35]. To address such challenges, and inspired by transfer learning [34]–[36], [41], we proposed the KL-TFCM approach [35]. KL-TFCM is associated with two data domains: the target domain in which target data need to be partitioned into C clusters and the source domain from which some knowledge, e.g., cluster prototypes, can be used as the reference in the target domain.

Notations involved in KL-TFCM are listed in Table I. Based on the entities defined, the framework of KL-TFCM can be reformulated as

$$\min \left(\begin{array}{l}{J}_{\text{KL}-\text{TFCM}}\left({\mathit{U}}_{\text{T}},{\mathit{V}}_{\text{T}}\right)\\ =\sum _{i=1}^{N_{\text{T}}}\sum _{j=1}^{C_{\text{T}}}{\mu }_{ij,\text{T}}^m{\Vert {\mathit{x}}_{i,\text{T}}-{\mathit{v}}_{j,\text{T}}\Vert }^2\\ +\lambda \sum _{j=1}^{C_{\text{T}}}{\Vert {\mathit{v}}_{j,\text{T}}-{\tilde{\mathit{v}}}_{j,\text{S}}\Vert }^2\end{array}\right)$$ (1)

s.t. i ∈ [1, N_T], j ∈ [1,C^T], μ_ij,_T ∈ [0, 1], $\sum _{j=1}^{C_{\text{T}}}{\mu }_{ij,\text{T}}=1$ where, x_i,_T (i = 1, …, N_T) ∈ X_T, ${\tilde{\mathit{v}}}_{j,\text{S}}\in {\tilde{\mathit{V}}}_{\text{S}}$, v_j,_T ∈ V_T, and λ ≥ 0 is a regularization coefficient.

TABLE I.

Notations Used in KL-TFCM

Symbol	Meaning
NT, CT	NT and CT denote the example number and cluster number in the target domain, respectively
$X_{\text{T}}=\left\{{\mathit{x}}_{1,\text{T}},\dots {\mathit{x}}_{N_{\text{T}},\text{T}}\right\}\in R^{N_{\text{T}}\times d}$	The data set in the target domain with NT data instances and d dimensions
${\mathit{U}}_{\text{T}}={\left[{\mu }_{ij,\text{T}}\right]}_{C_{\text{T}}\times N_{\text{T}}}$	The generated CT×NT membership matrix in the target domain with μij,T indicating the membership degree of xj (j = 1,…, NT) belonging to cluster i (i = 1,…,CT)
${\mathit{V}}_{\text{T}}={\left[{\mathit{v}}_{1,\text{T}},\cdots ,{\mathit{v}}_{C_{\text{T}},\text{T}}\right]}^{\text{T}}$	The cluster prototype matrix in the target domain with ${\mathit{v}}_{j,\text{T}}={\left[v_{j1,\text{T}},\cdots ,v_{jD,\text{T}}\right]}^{\text{T}}\left(j=1,\dots ,C_{\text{T}}\right)$ signifying the jth cluster prototype (centroid)
${\mathit{V}}_{\text{S}}={\left[{\mathit{v}}_{1,\text{S}},,{\mathit{v}}_{C_{\text{T}},\text{S}}\right]}^{\text{T}}$	The employed cluster representatives from the source domain for the eventual knowledge utilization in the target domain with ${\mathit{v}}_{j,\text{S}}={\left[v_{j1,\text{S}},,v_{jD,\text{S}}\right]}^{\text{T}}\left(j=1,\dots ,C_{\text{T}}\right)$ denoting the jth cluster representative in the source domain

Eq. (1) is composed of two terms. The first attempts to partition the target data into C_T groups with optimal intercluster purity, while the second is devoted to suitably and flexibly exploit the referenced knowledge, i.e., the cluster representatives, ${\tilde{\mathit{V}}}_{\text{S}}={\left[\begin{array}{ll}{\tilde{\mathit{v}}}_{1,\text{S}},\cdots ,\hfill & {\tilde{\mathit{v}}}_{C_{\text{T}},\text{S}}\hfill \end{array}\right]}^{\text{T}}$, from the source domain. The parameter λ determines the referenced degree across the two domains. Large values of λ indicate that the target domain should learn much from the source domain, i.e. V_T should be close to ${\tilde{\mathit{V}}}_{\text{S}}$; conversely, small values of λ mean that the overall similarity between V_T and ${\tilde{\mathit{V}}}_{\text{S}}$ is not strongly enforced. As for the acquirement of ${\tilde{\mathit{V}}}_{\text{S}}$, it is a systematic procedure; one can refer to [35] for the details. Here we would like to clarify that ${\tilde{\mathit{V}}}_{\text{S}}$ can be the historical cluster prototypes (also called cluster centroids), ${\mathit{V}}_{\text{S}}={\left[{\mathit{v}}_{1,\text{S}},\cdots ,{\mathit{v}}_{C_{\text{S}},\text{S}}\right]}^{\text{T}}$, of the source domain if and only if the cluster numbers of the target and source domains are the same.

Using the Lagrange optimization, the updating equations regarding cluster prototype v _j,T and membership μ_ij,T in (1) can be deduced as

$${\mathit{v}}_{j,\text{T}}=\frac{\sum _{i=1}^{N_{\text{T}}}{\mu }_{ij,\text{T}}^m{\mathit{x}}_{i,\text{T}}+\lambda {\tilde{\mathit{v}}}_{j,\text{S}}}{\sum _{i=1}^{N_{\text{T}}}{\mu }_{ij,\mathrm{T}}^m+\lambda }$$ (2)

$${\mu }_{ij,\text{T}}=\frac{1}{\sum _{l=1}^{C_{\text{T}}}{\left(\frac{{\Vert {\mathit{x}}_{i,\text{T}}-{\mathit{v}}_{j,\text{T}}\Vert }^2}{{\Vert {\mathit{x}}_{i,\text{T}}-{\mathit{v}}_{l,\text{T}}\Vert }^2}\right)}^{\frac{1}{m-1}}}$$ (3)

B. Support Vector Machine (SVM)

SVM is a well-accepted classification technique of machine learning. Instead of minimizing the empirical risk, SVM is devoted to the overall risk minimization by minimizing the upper bound of the generalization error. Via a certain Mercer kernel [42], [43], SVM can map the original data into one high-dimensional feature space in order to seek the optimal separating hyperplane in terms of maximizing the margin between two classes.

Let X = {x_i ⊂ R^d, i = 1, …, l} denote the training set, l be the training example number, and y_i ∈ {+1, −1} (i = 1, …, l) signify the labels of the corresponding data instances in X. Suppose that f (.) represents the decision function, and H_K denotes the reproducing kernel Hilbert space (RKHS) associated with one Mercer kernel K. The framework of SVM can then be formulated as

$$\underset{f\in H_k}{\min }\left(\frac{1}{l}\sum _{i=1}^l{\left(1-y_{i}f\left(x_i\right)\right)}_{+}+\gamma \Vert f{\Vert }_K^2\right)$$ (4)

where ( )₊ is the hinge loss function, (1 − yf (x))₊ = max(0, 1 − yf (x)), an γ > 0 is the regularization parameter.

According to the Representer Theorem [42], [43], the solution of (4) is given by

$$f^{*}(x)=\sum _{i=1}^l{\alpha }_i^{*}K\left(\mathit{x},{\mathit{x}}_i\right)$$ (5)

Following the SVM expositions and adding an unregularized bias term b to (5), we can rewrite (4) as

$$\begin{gathered} \underset{\mathit{\alpha }\in {\text{R}}^l,{\xi }_i\in \text{R}}{\min }\left(\frac{1}{l}\sum _{i=1}^l{\xi }_i+\gamma {\mathit{\alpha }}^{\text{T}}\mathit{K}\alpha \right), \\ \text{s.t.}{y}_i(\sum _{j=1}^l{\alpha }_{j}K\left({\mathit{x}}_i,{\mathit{x}}_j\right)+b)\ge 1-{\xi }_i,i=1,\dots ,l, \\ {\xi }_i\ge 0,i=1,\dots ,l, \end{gathered}$$ (6)

where K is l × l the Gram matrix with K_ij = K(x_i, x _j) and K(.,.) being the enlisted kernel function.

Based on the Karush-Kuhn-Tucker (KKT) conditions, the dual form of (6) is derived as

$$\begin{gathered} \underset{\mathit{\beta }\in {\text{R}}^l}{\max }\left(\frac{1}{l}\sum _{i=1}^l{\beta }_i-\frac{1}{2}{\mathit{\beta }}^{\text{T}}\mathit{Q}\mathit{\beta }\right), \\ \text{s.t.}\sum _{i=1}^l{\beta }_i{y}_i=0, \\ 0\le {\beta }_i\le \frac{1}{l},i=1,\dots ,l, \end{gathered}$$ (7)

where β = [β₁, …, β_l]^T ∈ R^l are the Lagrange multipliers, Q = Y (K/2γ) Y, Y = diag(y₁, …, y_l), and diag(·) signifies the generating function of the diagonal matrix.

Via the optimum β* of (7), the eventual solution of (6) can be obtained, i.e. α* = Yβ*/2γ.

C. Active Learning

In machine learning, the accuracy and generalizability of classifiers depend greatly on the quality and quantity of labeled examples in the training set. However, obtaining informative examples for training is usually computationally expensive or labor-intensive. Instead, we often have a limited quantity of labeled data, due to the limitation of time and cost. Active learning is a special modality of classification learning that iteratively trains the classifier by purposively acquiring a few examples that are informative and hence require to be labeled for training.

Active learning can be modeled as A = (C, L, S, Q, U), in which C is the learned classifier, L denotes the subset of labeled examples, Q is a function qualified to inquire the examples full of information and beneficial to train the classifier, U is the unlabeled data set, and S is the supervisor capable of labelling examples. The entire procedure of active learning includes two phases:

1). Initialization phase

In this phase, a small number of examples are randomly selected from the unlabeled data set U to initialize the classifier C after being labeled by the supervisor S.

2). Iteration phase

During this phase, according to the inquiry standard Q, the supervisor S selects some examples from the unlabeled data set U, then labels them and adds them to the training data set L. After that, the newly-obtained training data set L is used to retrain the classifier C until a certain criterion of termination is satisfied.

Active learning is an iterative procedure. The classifier is continuously retrained with the feedback of newly-labeled examples throughout the iteration, and the classification performance of the learned classifier can be gradually improved.

III. The Proposed TFC-ALC Method

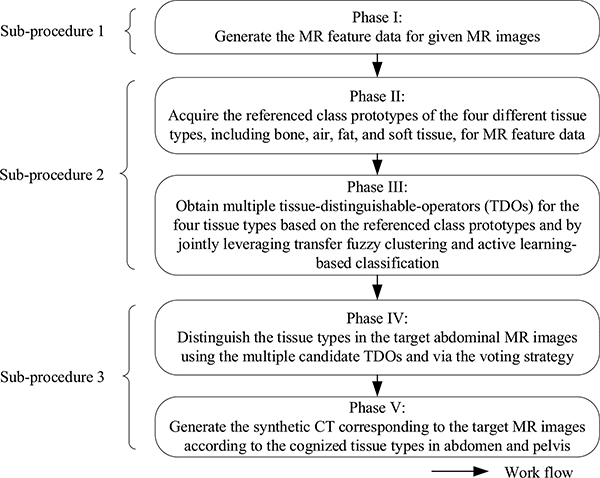
The proposed TFC-ALC method consists of five phases and these phases can be further divided into three sub-procedures, as shown in Fig. 1. In Sub-procedure 1, by means of the strategies of the weighted convolutional sum as well as grid partition, Phase I generates the seven-dimensional MR feature data from mDixon MR images for each subject. In Sub-procedure 2, Phase II obtains the referenced class prototypes regarding the tissue types of the four key materials for transfer learning; Phase III, using two key machine learning techniques, KL-TFCM and AL-SVM, generates multiple candidate tissue-distinguishable-operators (TDOs). In Sub-procedure 3, Phase IV recognizes the tissue types of voxels in target MR images using the multiple candidate TDOs and the voting strategy; Phase V synthesizes target CT images according to component tissue types of voxels. Next, we detail each phase as follows.

Fig. 1.

Overall workflow of the proposed TFC-ALC method

1). Phase I: Generate MR feature data for given MR images

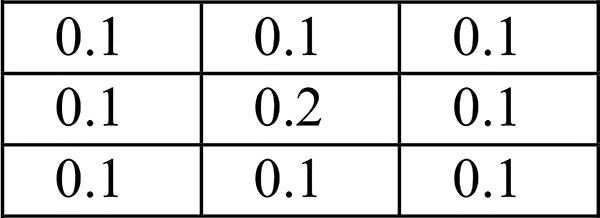
Feature extraction determines, to a great extent, the realistic performance of processing. In this regard, inspired by convolutional neural network (CNN)-based deep learning [44], the weighted convolutional sum is used to extract local texture features in our research. For each subject, with the mDixon MR scan (voxel size: 0.98×0.98×5 mm³), four different types of 3D MR images of the body sections of abdomen and pelvis, including water, fat, in-phase (IP), and opposed-phase (OP) [45], are the inputs to our TFC-ALC method. We extract texture features from each of the 3D MR images in terms of the 512×512 pixel slices of Z-axis. Specifically, let IV denote the intensity value image corresponding to one Z-axial slice, having pixels, iv (i,j), 1≤ i ≤512, 1≤ j ≤512. The matching texture value image, TV, can be calculated by discrete convolution with the weighting matrix W_3×3 indicated in Fig. 2:

$$\mathit{TV}=\mathit{IV}\otimes {\mathit{W}}_{3\times 3}$$ (8)

In the weighting matrix W_3×3, for a pixel in one Z-axial slice, the other eight surrounding pixels are equally treated and their weights are identically 0.1 and the weight of the pixel itself is 0.2.

Fig. 2.

Weighting matrix W_3×3

In addition, the position of pixel (i, j) in the slice is also used and the strategy of grid partition is adopted. Because the voxel spacing of the 3D MR images is 0.98×0.98×5 mm³, we partition each Z-axial slice into grids with the grid size being 5×5 pixels corresponding to 4.9×4.9 mm². In this way, from the 3D perspective, the grids are approximately isotropic, i.e., approximately 5 mm. Then the position information of pixel (i, j) can be expressed as the indices of the grid belonged to, e.g., (m, n, z), 1≤ m ≤103, and 1≤ n ≤103.

As such, we are able to obtain the seven-dimensional feature vector for pixel (i, j): [tv_water(i, j), tv_fat(i, j), tv_IP(i, j), tv_OP(i, j), m, n, z]^T. All of the pixel features in all slices constitute the MR feature data set.

2). Phase II: Acquire the referenced class prototypes of bone, air, fat, and soft tissue

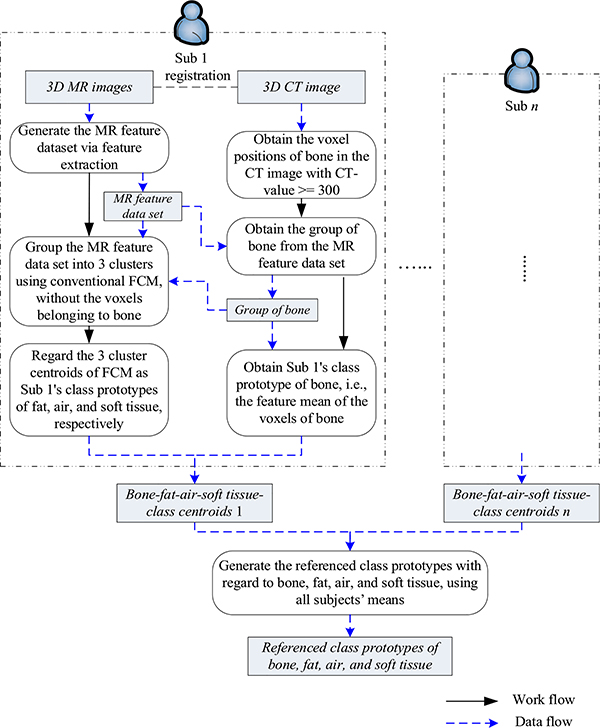
To perform transfer fuzzy clustering, the class prototypes of the four tissue types in abdomen and pelvis, i.e., bone, air, fat, and soft tissue, termed as the referenced class prototypes, play important roles in our TFC-ALC method. Therefore, they need to be effectively estimated in this phase. For this purpose, several pairs of MR and CT images of the body sections of abdomen and pelvis are required, and each pair was deformably registered beforehand [46], [54], recognizing this is imperfect as there is no wellestablished, robust method.

The work and data flows of Phase II are shown in Fig. 3. Suppose that there are n pairs of registered MR and CT images of abdomen and pelvis, denoted as Subject 1 (Sub 1) to Subject n (Sub n). Taking one subject as an example, we explain our design as follows. Because air and bone are difficult to differentiate using only Dixon-based MR images, we start from the subject’s CT image. We first get the positions of bone from the CT image using the threshold segmentation at the value of 300 Hounsfield Unit (HU). Then, mapping these positions from the CT image into the registered MR images, we acquire the group of bone voxels from the matching MR feature data set, and the feature mean of this group is enlisted as this subject’s class prototype of bone. After removing the examples affiliated to bone from the subject’s original MR feature data, we then group the leftover MR feature data into three clusters using the conventional FCM algorithm and regard the obtained cluster centroids as the subject’s class prototypes with respect to fat, air, and soft tissue. In this phase, given empirical knowledge is dependent. Specifically, the knowledge, e.g., clinical experience as well as given values from existing references [47], are used to confirm the appropriate tissue types of the cluster centroids. Afterwards, we obtain the subject’s four-class prototypes corresponding to the key materials. This process is applied to all subjects and the means of all subjects’ obtained four class prototypes are the referenced class prototypes.

Fig. 3.

Illustration of work and data flows in Phase II

3). Phase III: Obtain multiple candidate tissue-distinguishable-operators (TDOs) for the four tissue types

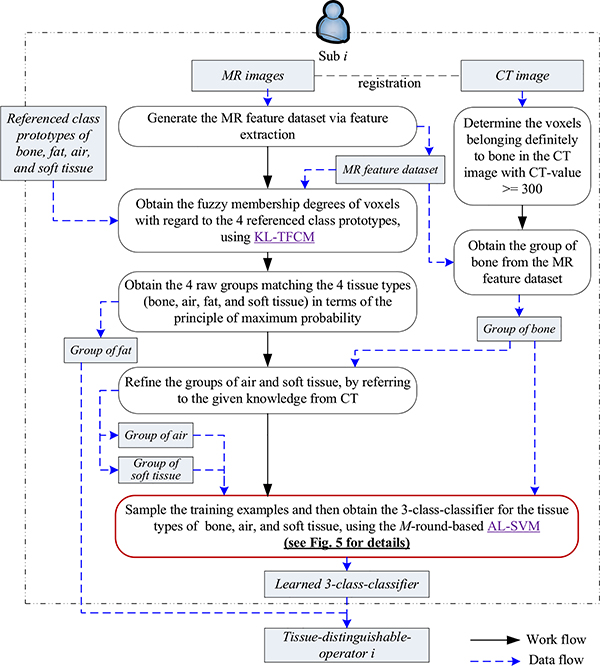
Phase III aims to obtain several candidate TDOs, and the overall work and data flows are illustrated in Fig. 4.

Fig. 4.

Illustration of work and data flows in Phase III

We also take one subject as an example to explain how we obtain the anticipated candidate TDOs from this subject. We first generate the MR feature data set via the feature extraction sketched in Phase I. Then, two embedded machine learning techniques, i.e., KL-TFCM and AL-SVM, play vital roles in our TFC-ALC method. We utilize KL-TFCM to partition the target subject’s MR feature data into four clusters with referring to the class prototypes obtained in Phase II. Here the n previous subjects’ MR feature data are treated as the source domain and the current target subject’s MR feature data as the target domain. The class prototypes obtained in the source domain are used as the beneficial knowledge to assist the KL-TFCM clustering in the target domain. In this way, we can obtain the four initial partitions of the key materials, based on the principle of maximum probability.

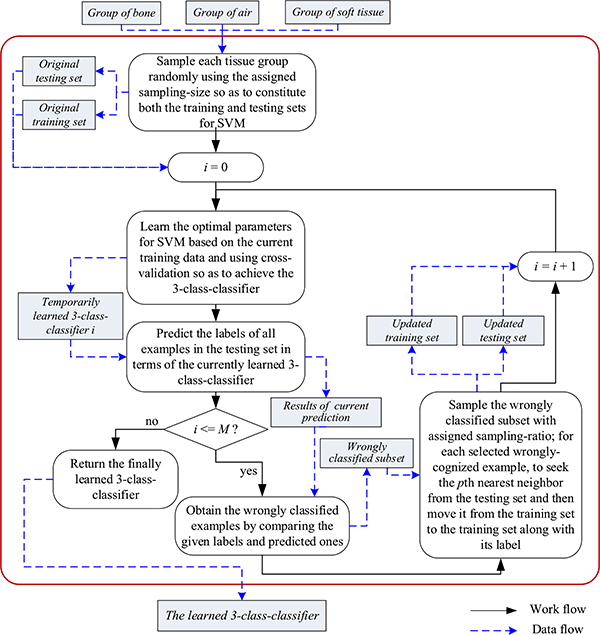
Due to the fact that mDixon sequences are good at embodying the fat tissue, the obtained group of fat is generally satisfactory versus the others. To reliably distinguish the other three tissue types, i.e., bone, air, and soft tissue, the strategy of classification is further enlisted in our method. With the help of the subject’s CT image, we acquire the group of bone and the purified group of air with removing voxels that belong to bone but could be wrongly partitioned to air by KL-TFCM, and then all leftover voxels are designated as the group of soft tissue. Thus, numerous labeled examples for classification learning are available. However, because of the high computing cost (O(N³)) as well as considerable memory space complexity (O(N²)) [48], we cannot straightforwardly use the whole labeled data for SVM training. In such case, active learning-based SVM (i.e., AL-SVM) is ideal. With a limited number of informative, labeled examples, AL-SVM is capable of learning insightful classifiers.

Fig. 5 sketches our design of M-round-based AL-SVM. Specifically, with a fixed sampling-size ss_III, we randomly sample each of the groups of bone, air, and soft tissue to constitute the original training set, and the leftover examples constitute the original testing set. Via the strategy of cross-validation [49], SVM is able to determine the optimal parameter settings on the current training data, e.g., the regularization coefficient l and the Gaussian kernel width σ commonly used in (9), and then to output a preliminary three-class classifier. We subsequently obtain current prediction results on the current testing set in terms of the learned classifier. By comparing the given labels with the predicted ones, we achieve currently, wrongly classified subset particularly significant for our TFC-ALC method for active learning. To determine which examples should be newly labeled for coming rounds of active learning, we randomly sample the currently, wrongly classified subset according to the given sampling-ratio sr_III. Afterwards, for each selected, misclassified example, we seek the p^th nearest neighbor from the testing set in which all already chosen examples for active learning have been excluded, and move the neighbor, along with its label, from the testing set to the training set. As such, we successfully update the training set, adding a few elaborately selected, informative examples. What makes us employ the p^th nearest neighbor instead of the wrongly classified example itself is due to the consideration of reinforcing the generalizability of the learned classifier as well as reducing the potential bias existing in the registration between abdominal MR and CT images.

Fig. 5.

Sketch of M-round-based AL-SVM

Thus far, we described one round of AL-SVM. Additional rounds of active learning improve classification performance but at the cost of increased computation and runtime. The number of rounds M may be determined to balance the performance and cost.

The three-class classifier of bone, air, and soft tissue achieved after the whole procedure of multiple rounds of AL-SVM together with the partition of fat achieved by KL-TFCM are collectively called the subject’s tissue-distinguishable-operators (TDOs).

As such, using all of the given subjects’ MR and CT image data (e.g., m subjects), we are able to obtain m candidate TDOs.

4). Phase IV: Distinguish tissue types in target MR images using the multiple candidate TDOs

In terms of the m candidate TDOs obtained in Phase III, in theory, the tissue types of voxels in new subject’s MR images can be decided using the voting strategy. Nonetheless, in our method, Phase IV belongs to the prediction stage using all learned TDOs, which certainly requires rapid performance for clinical use. As the orders of magnitude of subjects’ feature data are usually as high as millions in this study, the computational time is infeasible to directly apply these candidate TDOs on the whole new MR feature data. In response to such challenge, the “sampling + K nearest neighbors (KNN)” mechanism is enlisted to speed up our method.

Specifically, first, by referring to the class prototypes of bone, fat, air, and soft tissue and applying KL-TFCM, we identify the group of fat voxels on the target MR feature data set. Second, we randomly sample the remaining, non-fat voxels according to the given sampling-capacity sc_IV to obtain a subset denoted as SB_IV. Third, for each voxel in SB_IV, we gain m predicted outcomes in terms of the m candidate TDOs, and then decide the tissue type of this voxel based on the majority principle. Finally, with the obtained tissue types of SB_IV as the reference, all of the other unknown voxels are cognized using the KNN algorithm.

In this way, the target MR images is eventually segmented into the four groups: fat, bone, air, and soft tissue.

5). Phase V: Generate synthetic CT image corresponding to target MR images using the identified tissue types for the voxels

Given voxel labels, with assigning appropriate CT values to corresponding tissue types, we can reconstruct a synthetic CT image for the target MR images. In our research, the CT values of bone, air, fat, and soft tissue are set to 380, −700, −98, and 32, respectively [47].

In addition, as described in Phase I, the strategy of grid segmentation is used to acquire the position information of voxels in our TFC-ALC method. Despite the fact that this prevents TFC-ALC from over-fragmented segmentation on target MR images, there still is a certain extent of uncertainty with regard to voxel coordinates, because now all voxels affiliated to the same grid have the same position values. In response to such issue, we smooth the originally-synthesized CT image using a Gaussian filter with the full-width-at-half-maximum being 2.5 mm.

IV. Computation Complexity in TFC-ALC

The three sub-procedures in TFC-ALC can be grouped to two parts: the off-line and the on-line. Both Phases II and III belong to the off-line part wherein the multiple candidate TDOs are learned, whereas Phases I, IV, and V are on-line in which we generate MR feature data as well as synthetize CT images.

The computation complexity is different in each sub-procedure corresponding to phases in TFC-ALC. This is detailed in Table II. Specifically, the time complexity of Sub-procedure 1 is roughly O(N×4×9)=O(N) in which N denotes the total number of voxels in the MR images, digit 9 is the number of elements in the weighting matrix, and digit 4 indicates the four different types of 3D MR images, i.e., water, fat, IP, and OP. The time cost of grid partition can be ignored against the feature convolution calculation. In Sub-procedure 2, to obtain the referenced class prototypes for transfer fuzzy clustering in Phase II, the time complexity is O(max_iter×(N × C + C)) =O(N) on each subject’s MR feature data, in which max_iter denotes the maximal number of iterations and C is the cluster number. In Phase III, to roughly partition one subject’s MR feature data into the four clusters with referring to the given class prototypes, the time complexity of KL-TFCM is O(max_iter×(N×C+C+C×C)) =O(N). Further, to learn each of the multiple insightful classifiers, the time complexity of M-round-based AL-SVM is $\text{O}\left(s{s}_{\text{III}}^3+{\sum }_{i=1}^M{\left(s{s}_{III}+\left({\sum }_{j=1}^i{R}_j\right)\times s{r}_{\text{III}}\right)}^3\right)$ where R_j signifies the data number of the wrongly classified subset in the j^th round of active learning. In Sub-procedure 3, the time complexity of Phase IV is O(sc_IV × n + K × (N-sc_IV)) = O(N) in which n denotes the multiple learned TDOs, K is the neighbor parameter in KNN, and N signifies the total voxel number in target MR images.

TABLE II.

Computation Complexity in TFC-ALC

Sub-procedures	Including phases	On-line/Off-line for new subjects	Computation complexity
1	I	On-line	O(N)
2	II and III	Off-line	$\text{O}(N)+\text{O}(\begin{array}{l}s{s}_{\text{III}}^3+\\ {\sum }_{i=1}^M{\left(s{s}_{\text{III}}+\left({\sum }_{j=1}^i{R}_j\right)\times s{r}_{\text{III}}\right)}^3\end{array}$
3	IV and V	On-line	O(N)

In brief, the off-line time complexity is polynomially-related with the numbers of MR voxels and of the training examples during active learning-based classification, whereas the on-line complexity is generally linear with the total voxel number in the MR images. Due to the fact that the off-line part can be completed in advance, it does not impact the practicability of our proposed method for clinical translation.

V. Experimental Setup

In this section, we assess the effectiveness of the proposed TFC-ALC method for generating synthetic CTs for PET attenuation correction on abdomen and pelvis, using only commonly-available Dixon MR sequences [50]. For this purpose, ten subjects were recruited using a protocol approved by the University Hospitals Cleveland Medical Center Institutional Review Board. An MR mDixon scan (voxel size: 0.98 × 0.98 × 5.00 mm³) and a low-dose, 120-kV CT scan (voxel size: 1.17 × 1.17 × 5.00 mm³) were separately acquired using the MR of a Philips Ingenuity TF PET/MR [51], [52] and the CT of either a GEMINI TF PET/CT or a Gemini TF Big Bore PET/CT [53]. The raw mDixon data were reconstructed to generate the water, fat, IP, and OP images. A deformable registration was performed to warp the CT image to the MR images using OpenREGGUI, an open-source image registration package [54]. As such, we obtained ten sets of MR images (including water, fat, IP, and OP images) as well as matching CT images on the body sections of abdomen and pelvis, designated as Sub 1 - Sub 10 in our studies.

We evaluate our proposed method in competition against two existing methods. One is the four-cluster-partitioning method (FCP) [7] in which the MR feature data are straightforwardly partitioned into four disjoint clusters, i.e., external-air, internal-air, fat, and soft tissue, using the FCM algorithm, due to the insensitivity of bone in Dixon-based MR sequences. The other is the all-water method (AW) [56], i.e., all voxels within the body are regarded as water, which is a commonly-used uniform approximation for diagnostic imaging and radiation therapy treatment applications.

As is evident, TFC-ALC is a systematic method composed of five phases, in which several system parameters are involved, as additionally shown in Table III. System parameters usually facilitate the flexibility of algorithms. However, too many indeterminate parameters conversely weaken the practicability. In this content, by means of the grid search [36], [65], most system parameters were eventually assigned fixed values, listed in Table III, based on our extensive empirical studies. Exceptions were the regularization l and Gaussian kernel width σ in SVM that were adaptively determined using the 5-fold cross-validation on target data sets as usual. Also, the trial ranges of these parameters are given in Table III. As such, our TFC-ALC method can be implemented automatically, without any manual intervention.

TABLE III.

Primary Parameters Used in TFC-ALC

Parameters	Suggested settings	Trial Ranges
Regularization parameter λ in KL-TFCM in (1)	λ = 500	λ ∈ {10,50,100,200,500,800,1000,2000,5000,10000}
Regularization parameter l and Gaussian kernel width σ used in SVM in (7)	Determined by 5-fold cross-validation	l ∈ {2^-6,2^-3,2^-1,2^1,2^2,2^3,2^4,2^5,2^6} σ ∈ {2^-6τ,2^-3τ,2^-1τ,2^1τ,2^2τ,2^3τ,2^4τ,2^5τ,2^6τ}, where τ denotes the average distance among all data instances.
Parameter ssIII to constitute initial training set; Parameter srIII to sample wrongly classified subsets; Parameter p to pick up the pth nearest neighbor to update training sets during active learning in Phase III	ssIII = 4000; srIII = 40%; p = 3	ssIII ∈ {1000,2000,3000,4000,5000,6000} srIII ∈ {15%,20%,25%,30%,35%,40%} p ∈ {1,2,3,4,5,6,7}
Parameter scIV to obtain SBIV and parameter K for KNN in Phase IV	scIV = 2E4; K = 7	scIV ∈ {1E4,2E4,3E4,4E4,5E4,6E4} K ∈ {1,3,5,7,9,11}

For performance comparisons, three metrics were used throughout our experiments: mean absolute prediction deviation (MAPD), root mean square error (RMSE), and R [28], [29]. Measured CT, after deformable registration, served as the reference. The outcomes of TFC-ALC were achieved using the leave-one-out strategy with respect to subjects. Specifically, TFC-ALC obtained ten candidate TDOs in terms of the ten subjects’ feature data, following Phases I to III. However, in Phase II, for each of the subjects, the referenced class prototypes, i.e., the knowledge used for transfer clustering, were acquired using the data from all of the other nine subjects and excluding the current one being processed. Then, in Phase IV, likewise, for each of the subjects, TFC-ALC recognized the tissue types of image voxels by means of the other nine candidate TDOs learned excluding the current subject and based on the majority principle.

Our experimental studies were carried out on a computer with an Intel i5–4590 3.3 GHz CPU, 12 GB of RAM, Microsoft Windows 10 (64 bit), and MATLAB 2016a.

VI. Results

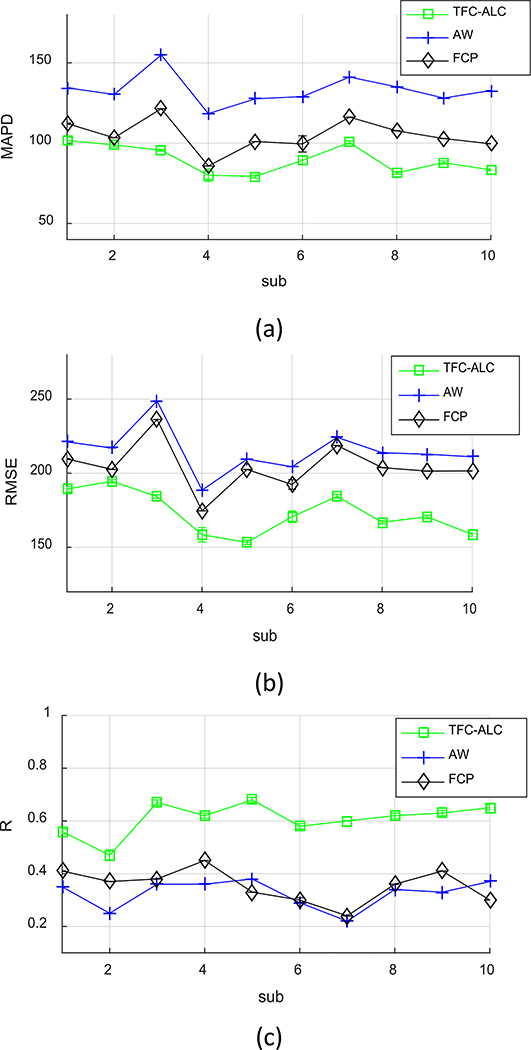
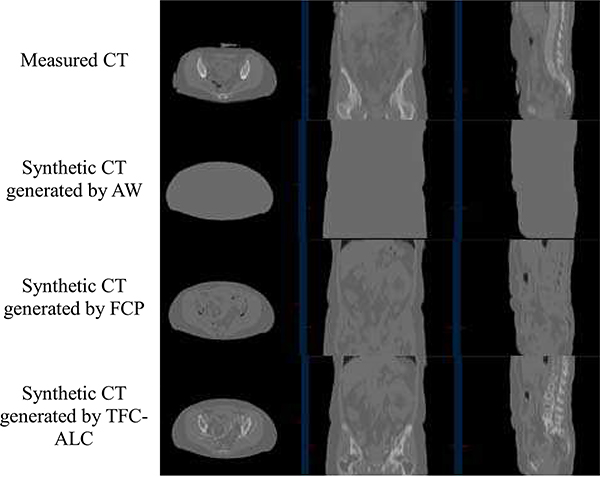
We separately ran TFC-ALC, FCP, and AW methods on data from the ten subjects. We first evaluated their generating performance of synthetic CTs using MAPD, RMSE, and R metrics. Means and standard deviations of validity metrics are reported in Table IV after 20 times of running each method for individual subject. In Phase III, the initialization of both KL-TCVM and AL-SVM are random which provides different TDOs and different results each time. Meanwhile, p-values, calculated using a paired two-tailed t-test and α = 0.05, are listed to support the significance of the improvement of our method. Fig. 6, which shows the performance curves of the three involved methods against each subject with respect to the MAPD, RMSE, and R metrics, provides a visualization of the performance advantage of our method. Fig. 7, for example, shows the synthetic CT images from Sub 2 for all three methods.

TABLE IV.

Performance Comparison of Generating Synthetic CTs Among the Proposed TFC-ALC and Two Other Methods

Sub		MAPD			RMSE			R
		TFC-ALC	AW	FCP	TFC-ALC	AW	FCP	TFC-ALC	AW	FCP
1	mean	101.70	134.44	112.20	189.29	221.13	209.60	0.56	0.35	0.41
	std	1.95	0	0.33	1.98	0	0.16	0.01	0	3.33E-4
2	mean	98.88	130.32	103.34	194.58	217.02	202.59	0.47	0.25	0.37
	std	1.33	0	2.60E-4	1.14	0	2.43E-4	0.02	0	1.22E-06
3	mean	95.56	154.90	121.43	184.24	248.72	236.22	0.67	0.36	0.38
	std	0.62	0	1.29E-4	1.20	0	1.08E-4	0.01	0	8.81E-07
4	mean	80.02	118.39	85.81	158.48	188.57	174.58	0.62	0.36	0.45
	std	3.91	0	9.34E-06	4.83	0	0	0.01	0	0
5	mean	79.34	127.61	101.01	153.42	209.49	202.50	0.68	0.38	0.33
	std	1.01	0	1.79E-05	1.48	0	3.74E-05	0.01	0	2.76E-07
6	mean	89.28	128.98	99.53	170.66	204.35	192.38	0.58	0.29	0.30
	std	2.76	0	5.05	3.88	0	3.24	0.01	0	8.59E-3
7	mean	100.40	141.16	116.22	184.37	224.20	218.70	0.60	0.22	0.24
	std	1.03	0	0	1.24	0	0	0	0	1.83E-08
8	mean	81.45	135.03	107.67	166.97	213.82	203.76	0.62	0.34	0.36
	std	0.80	0	6.61E-05	1.11	0	2.64E-05	0.01	0	0
9	mean	87.89	128.09	102.86	170.54	212.82	201.43	0.63	0.33	0.41
	std	1.07	0	1.32E-05	1.26	0	2.16E-05	0.01	0	1.13E-07
10	mean	83.32	132.73	99.60	158.71	211.09	201.54	0.65	0.37	0.30
	std	0.57	0	5.47E-3	1.20	0	0.01	0.01	0	1.25E-4
Average	mean	89.78	133.17	104.97	173.13	215.12	204.33	0.61	0.33	0.36
	std	8.76	9.67	10.03	14.27	15.37	15.99	0.06	0.05	0.06
p-value		—	4.11E-9	0.002	—	5.76E-6	2.20E-4	—	2.14E-9	3.75E-8

Fig. 6.

Performance curves shows that, for all subjects, the proposed TFCALC method has lower mean absolute prediction deviation (MAPD), lower root mean square error (RMSE), and higher correlation (R) than the fourcluster-partitioning (FCP) and all-water (AW) methods.

Fig. 7.

Synthetic CTs generated by three employed methods on a representative subject (Sub 2)

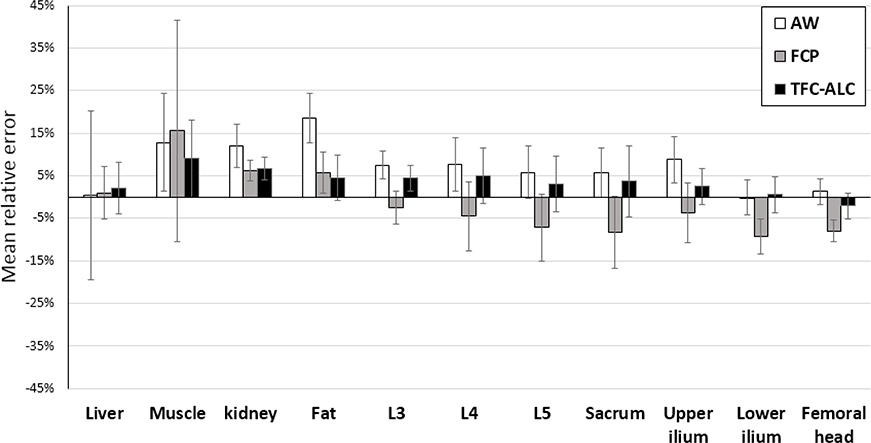
We continued to compare the performance of PET attanuation correction regarding these three methods, based on their generated synthetic CT images and by means of the metric of SUV error. As shown in Fig. 8, the comparisons of SUV errors of these three methods with regard to multiple tissue types existing in the body sections of abdomen and pelvis are given. An example image volume, using the data from the same patient as was used in Fig. 7, is shown in Fig 9. Our data are from Na¹⁸F- PET scans and emphasize SUVs in and near bone areas wherein currently existing methods are particularly inaccurate. In this regard, in terms of the Dice coefficient [57], the consensus of bone between our synthetized CTs and measured CTs used before PET attenuation correction is additionally listed in Table V.

Fig. 8.

Means and standard deviations of SUV errors of three methods are depicted as the column heights and error bars, respectively, for different tissue types in abdomen and pelvis. They are calculated from the 20 runs of each method for each of the 10 subjects (see Section VI.) The reference standard is taken from the images reconstructed using the measured CT after deformable registration (Section V).

Fig. 9.

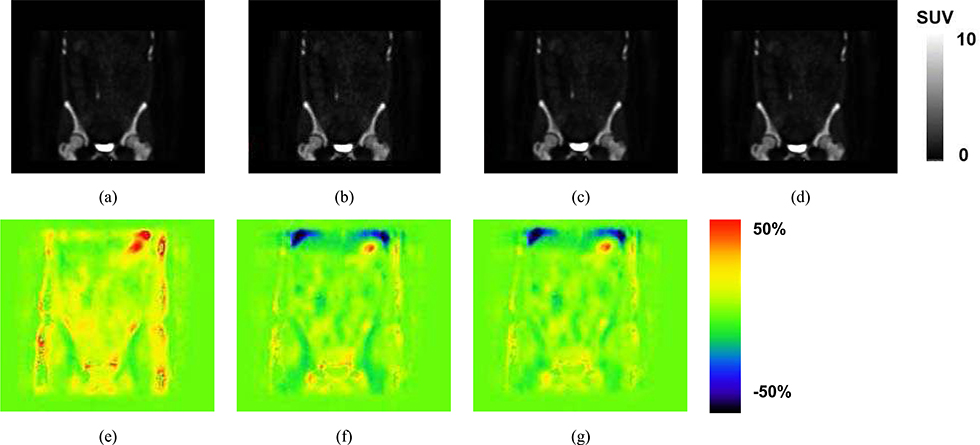
Example NaF-PET SUV images reconstructed using attenuation correction based on (a) CT, (b) All Water, AW, (c) Four Cluster Prototype, FCP, (d) our proposed method TFC-ALC. The subject and location correspond to those of Fig. 7. The SUV scale has been set to 10 as a balance between allowing the low concentration features to be visualized without excessive saturation in bone and bladder. Differences between the images are difficult to visualize so we present corresponding difference images. %SUV error maps are computed as the SUV result using (e) All Water, AW, (f) Four Cluster Prototype, FCP, or (g) our proposed method TFC-ALC, each minus the SUV image determined using the CT-based AC which serves as the reference. A threshold of 0.1 was applied to avoid exacerbation of errors in tissues having low uptake. The color bar spans plus or minus 50% error. Negative errors, tending toward blue, correspond to where the method has an SUV that is lower than the reference whereas positive errors, tending toward red, correspond to where the method has an SUV that is higher than the reference. The blue area towards the top of the image is at the interface of the lung and liver.

TABLE V.

Dice Coefficient of Bone Between the Synthetic CTs Generated by TFC-ALC and Measured CTs Used Before PET AC

Subjects	Dice bone Mean ± Std
1	0.6877 ± 0.0013
2	0.6592 ± 0.0005
3	0.6480 ± 0.0007
4	0.6375 ± 0.0011
5	0.6462 ± 0.0008
6	0.6332 ± 0.0005
7	0.6121 ± 0.0008
8	0.6737 ± 0.0002
9	0.6218 ± 0.0006
10	0.6802 ± 0.0011
Average	0.6499 ± 0.0242

We also recorded the running time of TFC-ALC in terms of the separate sub-procedures on the ten subjects whose mean MR voxel number is N = 6,864,159. On the average, we spent approximately 79 seconds in Sub-procedure 1 and 225 seconds in Sub-procedure 3. That is, our method spent approximately 5 minutes in generating synthetic CTs for new subjects. By the way, in our experiments, the off-line Sub-procedure 2 generally required 22451 seconds (370 minutes) to learn the TDOs for each subject with a commonly available PC. Only three rounds of active learning were conducted in our experiments, as the data capacity of the latest training set was as high as tens of thousands in our studies after three rounds of AL-SVM, e.g., around 60,000 on Sub 1, which is actually near the limitation of our condition. In comparison to our proposed method, FCP running time was approximately 89.5 s per subject and the AW method had negligible computation time.

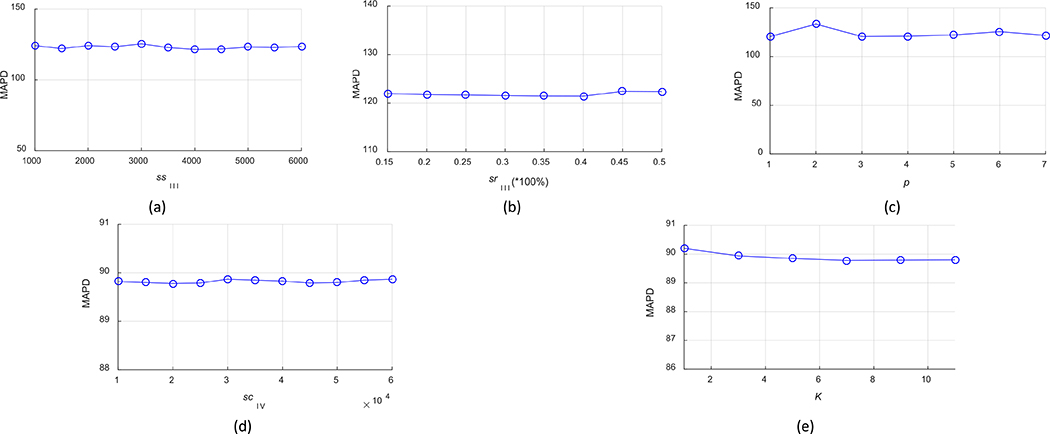
Lastly, we evaluated the robustness of TFC-ALC with respect to several system parameters, including parameters ss_III to constitute initial training set, sr_III to sample misclassified subsets, p to find the p^th nearest neighbor for updating the training set during active learning, sc_IV to obtain SB_IV, and K for KNN in Phase IV. For all subjects, with first assigning the suggested or optimal settings to all parameters, as shown in Table III, we then took turns fixing all of the others but gradually varied one parameter near its optimum. Meanwhile, we recorded the performance measure in terms of the enlisted validity metrics. For the sake of conciseness, here we only report our experimental results in terms of the MAPD metric, as shown in Fig. 10. These results are reported according to the means of TFC-ALC after ten times of running on each subject’ data.

Fig. 10.

Parameter robustness of TFC-ALC method. (a) MAPD VS ss_III. (b) MAPD VS sr_III. (c) MAPD VS p. (d) MAPD VS sc_IV. (e) MAPD VS K.

VII. Discussion

Our work addresses a challenging topic in current medical imaging trials; few investigators have reported an effective means to distinguish the bone, air, fat, and soft tissue in abdomen and pelvis without using UTE or ZTE pulse sequences [57], [66]. These sequences particularly help to differentiate air and bone and may be preferable to use when available. However, they might not be available at all clinical sites and the ability of algorithms to predict bone and air in abdomen and pelvis without them merits investigation. With Dixon MR sequences alone, it is difficult to differentiate the tissues of air and bone as both have low MR signal. Unavoidable factors, e.g., separate scans, human respiration, organ motion, different contrasts, etc., make CT and MR images of the body section of abdomen, even from the same subject, difficult to robustly and precisely coregister, meaning that even the training data are imperfect. This implies that accurate standards that traditional supervised or unsupervised machine learning methods need for measuring the effectiveness of processing are rare. Our results, as shown in Table IV and Fig. 6, demonstrate that our proposed TFC-ALC method outperforms the other two methods in all metrics and that the improvement is statistically significant. All of these demonstrate that our design to acquire desirable TDOs, from Phase I to Phase III, is able to overcome, to a great extent, the inherent inaccuracy and other potential uncertainty between given MR and CT abdomen and pelvis images, which facilitates the synthetic CT generation of TFC-ALC (see Fig. 7).

KL-TFCM as well as AL-SVM are two key embedded techniques in our proposed TFC-ALC method. With the guidance of the referenced class prototypes of tissues, KL-TFCM is capable of reliably initializing voxels in MR images into the four key materials: bone, air, fat, and soft tissue. AL-SVM is devoted to learning insightful SVM-based classifiers to further reliably refine the bone, air, and soft tissue classes, using as few but informative labeled examples as possible. Benefiting from jointly leveraging both KL-TFCM and AL-SVM, our proposed method is effective as well as practicable in synthetic CT generation for abdomen and pelvis. Unlike the other methods considered, TFC-ALC is a systematic method including the dedicated means for feature extraction itself, i.e., Phase I. Hence, differing from both AW and FCP that worked merely upon the MR intensity features of all subjects, TFC-ALC handled the seven dimensional feature data extracted from target MR images.

The given, measured CTs are not perfect standard in our study, because in our experiments, the subjects were moved between CT and MR scanners. It is difficult to attain the strictly same posture and position of a subject in separate CT and MR scans. Therefore, given measured CT images can only be regarded as good references rather than ground truth.

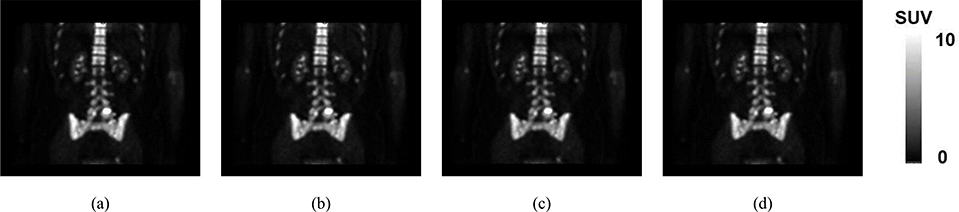
The results in Figs. 8 and 9 show that the proposed TFC-ALC method achieves the overall highest SUV accuracy and can reduce the SUV errors to below 5% for most of the tissue types, except for the muscle, kidney, and at the interface of the lung and liver. Further, the difference image, Fig. 9, shows good performance in comparison to a similarly-formatted difference image shown in [67], noting that they were working with FDG data whereas we were working with NaF which may be a more challenging correction. The largest error, at the interface of the lung and liver, indicated as the blue area on top of the Fig. 9G, is attributed to the imperfect registration as our proposed TFC-ALC method to not classify the lung tissue type. The muscle and kidney errors are attributed to the soft-tissue miss-registration between CT and MR and thus an artifact of the validation process. Fig. 11 shows a view through the kidneys from the same patient as in Figs 7 and 9. Although the deformable registration was employed to reduce this error, the miss-registration was still inevitable and is the limitation of this evaluation approach given the data used for this work. Specifically, in the kidney, the attenuation correction maps were within 5% agreement so they are a small factor in the SUV inaccuracy. Instead we attribute the inaccuracy mainly to a combination of imperfect registration and the high spatial heterogeneity of the activity concentration distribution of NaF; a slight misregistration can cause inflated relative SUV errors. In the muscle, while the attenuation correction maps were also within 5% agreement, the comparatively large relative errors are attributed to a combination of imperfect registration and generally low concentration of NaF. Therefore, a small absolute error in SUV is magnified to a high relative error and standard deviation when divided by SUV to calculate relative error.

Fig. 11.

Example NaF-PET SUV images reconstructed using attenuation correction based on (a) CT, (b) All Water, AW, (c) Four Cluster Prototype, FCP, (d) our proposed method TFC-ALC showing the kidney location. The subject corresponds to that of Fig 7 and 9.

The general 5% or less SUV accuracy of our method is quite good and well-within the National Cancer Institute/American College of Radiology Imaging Network (NCI/ACRIN) 10% specification for SUV accuracy [3], [4]. In addition, our TFC-ALC method only requires the Dixon-based sequence, which means that our approach is applicable at most clinical sites, and would not require extra scanning time for institutions that already do Dixon, as Dixon is commonly used with PET/MR for localization.

As revealed in Fig. 10, the performance curves of TFC-ALC are relatively stable when each system parameter is within the proper range, which indicates that TFC-ALC generally features good robustness against parameter settings.

One limitation of the generalizability of this study is the lack of patients having implants. The focus of this work is methods development. Also, we used pre-existing data available from an IRB-approved protocol of patients having breast cancer and receiving clinical PET/CT scans who were invited to have research PET/MR scanning. None of these patients had implants. Regardless, we believe that we made significant progress over previously described methods in that we achieved SUV errors of generally 5% or less for abdomen and pelvis using only Dixon data. Evaluating the method in data from patients having implants would be an excellent topic for a future work. Both acquisition and analysis methods could be considered. We would seek acquisition methods that could image hip and other implant materials without excessive artifact and differentiate them from human tissues.

Finally, our experiments were conducted on 10 patients with breast cancer but the synthetic CT generation method itself can be applied to other patient populations. Future studies in specific sub-populations such as post-surgical patients, pediatric populations, obese or cachectic patients can be investigated for validation and parameters tuning. Likewise, with appropriate training, our method can be applied to data collected using further refinement of the pulse sequences or to data collected using other types of MR scanners when such data are informative and training is done.

VIII. Conclusion

For Dixon-based synthetic CT generation for PET attenuation correction on abdomen and pelvis, particularly for the challenging abdomen in medical imaging, we propose the dedicated five-phase-based TFC-ALC method as effective and practical. TFC-ALC has incorporated multiple techniques and strategies, such as weighted convolutional sum and grid partition based feature extraction, transfer fuzzy clustering, active learning based classification, and multiple candidate TDOs based voting decision. Consequently, TFC-ALC proves preferable generation quality of synthetic CT, good system-parameter insensitivity, and satisfied accuracy of SUV errors, which greatly facilitates its applicability for generating synthetic CT scans that would be used for attenuation correction of PET data and for radiation treatment planning.