Depixelation and enhancement of fiber bundle images by bundle rotation

Abstract

Fiber bundles have become widely adopted for use in endoscopy, live-organism imaging, and other imaging applications. An inherent consequence of imaging with these bundles is the introduction of a honeycomb-like artifact that arises from the inter-fiber spacing, which obscures features of objects in the image. This artifact subsequently limits applicability and can make interpretation of the image-based data difficult. This work presents a method to reduce this artifact by on-axis rotation of the fiber bundle. Fiber bundle images were first low-pass and median filtered to improve image quality. Consecutive filtered images with rotated samples were then co-registered and averaged to generate a final, reconstructed image. The results demonstrate removal of the artifacts, in addition to increased signal contrast and signal-to-noise ratio. This approach combines digital filtering and spatial resampling to reconstruct higher-quality images, enhancing the utility of images acquired using fiber bundles.

1. INTRODUCTION

Fiber bundles have been widely adopted in the optics community as a conduit for light delivery, and if the spatial arrangement of the fibers within the bundle is consistent at both distal and proximal ends, fiber bundles can be used for imaging. In contrast to single-core optical fibers, fiber bundles consisting of thousands of individual fibers provide the benefit of having a large field of view due to larger bundle diameters (500 μm–1.5 mm), in addition to allowing for selective illumination of subsets of fibers within the bundle. Individual fibers in these bundles range from a few micrometers to tens of micrometers in diameter, which makes them ideal for illuminating selective regions on a given sample. These fibers are single-mode fibers surrounded by a cladding material, which also acts as the material used to separate individual fibers. These are also individually surrounded by a clad jacket and then fused to form coherent bundles. This technology has been used for endoscopy [1–3], optical coherence tomography [4,5], fluorescence imaging [6–13], nonlinear optical imaging [14,15], and increasingly for neural imaging in optogenetics research [9,12,16,17]. The inherent disadvantage of these fiber bundles is the superimposed pixilation artifact due to the inter-fiber material that is not optically transparent or light conducting. This artifact obscures underlying object features, making it difficult to interpret imaging results. Different methods have been proposed to reduce this artifact [18,19], ranging from spatial interpolation techniques [1,20], mosaicking [2,3], and reduction of the artifact in the spatial Fourier domain [4,21–23]. Implementation of computational techniques has also been demonstrated, such as speckle-based correlations [6], high-resolution estimates from low-resolution, smoothened images [24], generation of a transmission matrix [25], and compressive sensing reconstruction [5,26]. More recently, deep learning has also been suggested as a technique for reducing these artifacts [27]. The study and results presented here offer a combined sampling and computational approach for reduction of the superimposed artifact. Rather than repositioning the sample or translating the fiber to mosaic images, as previously demonstrated [2,3], we performed on-axis rotation of the fiber bundle over the sample and reconstructed the final image from rotationally sampled image data. In the context of lateral mosaicking, previous work has demonstrated that this spatial resampling provides robust image reconstruction compared to spatial interpolation alone [28]. As it can be difficult to limit lateral movement while imaging with fiber bundles due to the high degrees of freedom possible during movement, additional methods beyond co-registration of lateral translation are necessary to correct for imperfect registrations due to bundle rotation. We thus present an extension of this mosaicking approach for fiber bundle reconstruction that integrates corrections to translations and rotations into the co-registration algorithm, with a heavy emphasis on bundle rotations.

In principle, by rotating the fiber bundle over the fixed field of view, the fluorescence or reflected light from the object is acquired from different locations. By affine co-registration of each of these images post-acquisition, and by averaging or acquiring larger pixel intensities at subsequent registrations for each of these images, the final image of the object can be reconstructed, even with the superimposed fiber patterns introduced while imaging. Experimental verification for this reconstruction technique demonstrates a higher signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) for the acquired images, and improved resolution.

2. METHODS

A. Theory

The fiber-pattern artifact itself can be modeled as a super imposed binary pattern over the imaging sample. More specifically, this binary pattern can be defined as

$$A(r,\theta ,t)=\mathrm{circ}\left(\frac{r}{a},\theta ,t\right)*\delta \left(r+k{f}_r,\theta +k{f}_{\theta },t\right),$$ (1)

where r denotes radial position, θ angular rotation, and t is time. The term circ(r, θ, t) is defined as the circular function, δ(r, θ, t) is the Dirac delta function, a is a coefficient to define the radial width, k is an integer multiple for the number of fibers present in each dimension (given as 51), and f_r and f_θ are the spatial frequency, or inter-fiber spacing, on the image. In this work, the asterisk (*) will denote the convolution operation. Given this definition, we can model the superimposed artifact on the image as

$$I(r,\theta ,t)=e^{\frac{-(r^2)}{2{\sigma }^2}}*S(r,\theta ,t)A(r,\theta ,t),$$ (2)

where I(r, θ, t) is the image acquisition, and S(r, θ, t) is the signal expected from the object without the superimposed pattern. Here, σ denotes the width of the Gaussian function, which is modeled as the point-spread function (PSF) of the fibers, convolved with the fiber geometry. The imaging process also introduces artifacts inherent in imaging, as well as autofluorescence generated by the fiber glass material within the bundle. This also can be modelled according to

$$I(r,\theta ,t)=e^{\frac{-(r^2)}{2{\sigma }^2}}*S(r,\theta ,t)A(r,\theta ,t)+ϵ(r,\theta ,t)+\gamma (r,\theta ,t),$$ (3)

where (r, θ, t) denotes the background noise, and γ(r, θ, t) denotes variations in noise over time. Variations in inter-fiber spacing and diameter inherent in fiber production will also conveniently be integrated into this term. For simplicity, hereon these variables will be combined into ∈. This artifact can be removed by background subtraction:

$$I(r,\theta ,t)-ϵ(r,\theta ,t)=S(r,\theta ,t)A(r,\theta ,t);$$ (4)

however, background subtraction alone does not replace the image signal that was lost in the inter-fiber regions. For simplicity, this background-subtracted image could be combined as one variable and defined as

$$I_e(r,\theta ,t)=I(r,\theta ,t)-ϵ(r,\theta ,t);$$ (5)

hence,

$$I_e(r,\theta ,t)=e^{\frac{-(r^2)}{2{\sigma }^2}}*S(r,\theta ,t)A(r,\theta ,t).$$ (6)

Practically, dividing I_e by A is effectively dividing the signal by the low values (effectively zero) from in between the fibers, increasing the true image signal and making the artifact more pronounced. This result becomes more pronounced when a binary mask is used in lieu of the signal intensities imposed by imaging on the detector with the fiber bundle. This makes background subtraction and division an unsuitable solution. By taking the Fourier transform, this becomes a deconvolution problem:

$$I_e\left(k_r,k_{\theta },t\right)=e^{\frac{-(r^2)}{2{\sigma }^2}}S\left(k_r,k_{\theta },t\right)*A\left(k_x,k_y,t\right).$$ (7)

Unfortunately, deconvolution in the frequency domain yields very poor results, as the exact superimposed pattern will be required and binarized to remove this artifact. In practice, this becomes very difficult, cumbersome, and computationally intensive. To correct for this, an algorithm was designed to reconstruct the images through a series of low-pass and median filtering. This removes any image distortion introduced through consecutive resampling, as well as corrects for the reduced intensity from blurring, throughout all the acquired images. Through a sequence of rotations and translations, consecutively acquired images are co-registered and summed (for simulations), averaged, or acquired from the maximum intensity for each pixel between images (real fiber bundle data) to collect image signals from regions that would have otherwise been obscured in a static (non-rotated) single image due to the artifact. Maximum projection was a necessary step to facilitate co-registration in this work, and was thus adopted for the experimental cases. Additionally, the effect of summing or using the projection approach for co-registered images instead of solely averaging is also investigated, should averaging remove some significant image features. Translated images can be defined as

$$I_{\text{trans}}(r,\theta ,t)=I_e(r+\text{Δ}r,\theta +\text{Δ}\theta ,t).$$ (8)

If we define N number of translated and/or rotated images, the final reconstructed image can be defined by

$$I_{\text{recon}}=\sum _{n=1}^N\frac{I_{\text{trans},n}(r+\text{Δ}r,\theta +\text{Δ}\theta ,t)+I_e(r,\theta ,t)}{N},$$ (9)

assuming adequate co-registration of I_trans(r, θ, t) by Δr and Δθ, where these correspond to translations from previous images. In the case of summing co-registered images, this becomes

$$I_{\text{recon}}=\sum _{n=1}^N{I}_{\text{trans},n}(r+\text{Δ}r,\theta +\text{Δ}\theta ,t)+I_e(r,\theta ,t).$$ (10)

Assuming the maximum projection case, this becomes

$$I_{\text{recon}}=\sum _{n=1}^N\max \left\{I_{\text{trans},n}(r+\text{Δ}r,\theta +\text{Δ}\theta ,t)+I_e(r,\theta ,t)\right\}.$$ (11)

B. Experimental Setup

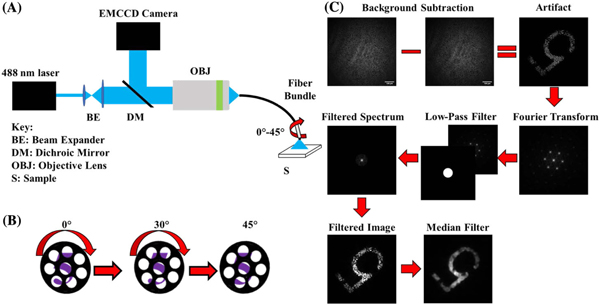
The imaging setup consisted of a 488 nm wavelength optically pumped semiconductor laser (Sapphire 488 LP, Coherent), directed into a 1 m long, coherent fiber bundle (1534702, Schott) with a 530 μm diameter (430 μm working area) via a 0.5 NA objective lens with 20× magnification (UPLFLN 20×, Olympus) [Fig. 1(A)]. The light from this laser was used to illuminate the object, and any resulting reflectance or fluorescence was detected by an EMCCD camera (iXon Ultra EMCCD, Andor). The fiber bundle had an outer diameter of 0.53 mm, with 4500 individual fibers arranged in a hexagonal packing arrangement, with each individual fiber within the bundle being 7.5 μm in diameter. The space between the fibers, regions with semi-opaque cladding-like material, appears as black spaces and obscures regions of the object from detection. Although the cladding-like material is not completely opaque to light, this does not significantly impede imaging quality, as the fluorescence intensity on neighboring pixels on average is similar. The coherently arranged fibers within the bundle allow for imaging of the object by guiding light to and from the object, but also contribute a background noise signal due to autofluorescence from the fiber[29].

Fig. 1.

Fiber bundle imaging setup and processing algorithm flow chart. (A) Setup for imaging of resolution target and brain slices. Output from the laser is passed through a beam expander and then passed by a dichroic mirror to a 20× objective, which focuses the light onto the proximal face of the fiber bundle. The back-scattered light or fluorescence from the object is collected by the objective and directed to the CCD camera via a dichroic mirror. (B) The bundle itself is manually rotated over the object incrementally during image acquisition to sample previously obscured features for image reconstruction. (C) The conditioning process is highlighted at each step. The image of the sample is first background-subtracted to correct for background fluorescence, and then passed through a series of filters.

A filter wheel with a 525 ± 25 nm filter was placed in front of the EMCCD camera to isolate the fluorescence when imaging fluorescence samples, attenuate excitation light, and to reduce background autofluorescence inherent from the glass fibers within the bundle. Additionally, the settings on the EMCCD camera were adjusted such that the framerate was 15 Hz, with a 512 × 512 pixel image size. The distal end-face of the fiber bundle was positioned at the surface of the object. The proximal end-face of the fiber bundle was placed at the focus of the objective to focus the light to the EMCCD camera for imaging.

C. Image Conditioning and Reconstruction

Following acquisition of the images from the fiber bundle, images were run through an algorithm designed to reduce the pixilation artifact introduced by the individual fiber packing arrangement in the bundle, as shown in Fig. 1(C). Initially, a reference image of the fiber bundle without a sample was used to calculate the average background intensity throughout the fiber bundle. The bundle was then positioned on the sample, and following image acquisition, the fiber bundle background was subtracted from each individual image to reveal the underlying object features. The algorithm proceeds by taking the 2D FFT of each successive image in the series. Each image is then low-pass filtered with a circular, 45-pixel-radius binary mask in the Fourier domain to remove higher-order, periodic peaks. This mask constitutes 8.78% of the total image size (512 × 512 pixels). This significantly reduces the high-frequency content introduced from the artifact. Subsequently, the inverse Fourier transform is taken, and the artifact is further reduced by running each image through a median filter with a window size of 16 × 16 pixels. This window size was chosen, as it resulted in superior image quality without further blurring object features, as higher-order windows would do. Improvement in image quality was quantified using SNR and CNR. This results in a smoothened representation of the object for each image. These filtering steps were necessary to enhance object features in the image to facilitate co-registration, as the honeycomb artifact is too prominent to allow for adequate co-registration even in the presence of signal from the individual fibers. Next, each individual image in the acquisition was co-registered by a phase-based affine registration [30] to the initial (reference) image using the “imregcorr” function in MATLAB. For each co-registration, a 2D correlation coefficient was determined between the registered image and the reference to determine the strength of the co-registration, quantified as

$$R=\frac{\sum _i\sum _j(X_{ij}-{\mu }_X)(Y_{ij}-{\mu }_Y)}{\sqrt{(\sum _i\sum _j{(X_{ij}-{\mu }_X)}^2)(\sum _i\sum _j{(Y_{ij}-{\mu }_Y)}^2)}},$$ (12)

where X and Y are each individual image, μ_x and μ_y are the means for images X and Y, respectively, and i and j represent individual indices along each dimension on the image. Co-registrations where this coefficient was below 0.7 were ignored and not included in the final reconstruction. This cutoff was determined based on poor reconstruction efficiency below this threshold, and minimal image improvement at thresholds above this. This was also quantified using SNR and CNR at various correlation coefficients. The final reconstructed image was then generated by taking the average of all successful co-registrations. This process was also performed by acquiring the maximum pixel intensity between images, rather than averaging. In this case, the images were co-registered using an intensity-based co-registration that iteratively registers images using a Mattes mutual information metric [31]. Successful co-registration is determined upon convergence to a global maximum between two images, using a One Plus One Evolutionary optimizer [32]. This increases computation time, but more adequately co-registers images and, consequently, leads to increased image quality. This was necessary for this approach because even slight mis-registrations from a simple phase-based registration mechanism after summing leads to significant spill over between regions of high signal intensity and dark pixels, often resulting in poor reconstruction quality. This was not as much of an issue during the averaging process, and hence, was not a necessary step. Figure 1(C) provides a visual overview of the conditioning process prior to image registration. All image processing and reconstruction were performed on an Alienware Area-51 R2 PC with an Intel Core i7–5820K CPU operating at 3.3 GHz, with 16GBRAManda64-bitprocessor.

D. Rotation and Sampling

Prior to imaging, the distal end of the fiber bundle was positioned above the object, and background fluorescence generated from the fiber bundle was detected for 30 s. Post-acquisition, images in a series were averaged and the fluorescence background was subtracted from the averaged images of the object. This process for removal (subtraction) of autofluorescence is shown in Fig. 1(C), where the bundle was positioned over a “5” on a USAF resolution target, representing an object. For the image reconstruction experiments, the fiber bundle was positioned over the object of interest. The distal end of the fiber bundle, which was mounted in a calibrated rotational mount, was then rotated from 0° up to 45° [Fig. 1(B)], then back down to 0°, while collecting CCD images at 15 Hz. This was repeated five times, taking approximately 25 s for all five cycles. Each cycle thus took approximately 5 s, for a total of 75 frames per cycle. Each step, on average, yielded a 5° rotation between frames (data not shown). Upon sampling, the images were background-subtracted using the background-fluorescence image detected prior to imaging. The image sequence was then processed using the algorithm to generate the reconstructed image. The SNR and CNR are defined and calculated for these data as follows:

$$\text{SNR}=20{\log }_{10}\left(\frac{{\mu }_{\text{sig}}}{{\sigma }_{\text{background}}}\right),$$ (13)

$$\text{CNR}=20{\log }_{10}\left(\frac{{\mu }_{\text{sig}}-{\mu }_{\text{background}}}{{\sigma }_{\text{background}}}\right),$$ (14)

where μ_sig is the mean signal from the region of interest (ROI), μ_background is the mean background signal, and σ_background is the standard deviation of the signal from the background.

E. Simulations

To verify this technique prior to experimental conditions, simulations were performed in MATLAB to determine the effectiveness of the algorithm for removing the artifact. Stock MATLAB images were loaded and superimposed with a binary mask that replicated the pattern introduced by imaging with fiber bundles. The artifact was superimposed by multiplication of the mask (51 × 51 pixels, total of 2601 modeled fibers) with the stock image [Figs. 2(A)–2(C)]. Once this artifact was introduced, the fiber pattern was run through a slightly modified version of the algorithm that “samples” this original image multiple times by on-axis rotations and translations, translating/rotating back to its original position, and then reconstructing by summing the registered images, and lowpass filtering to remove the radial disk-like pattern shown in Fig. 2(D). This involves translation and rotation of the original image, followed by superimposing the binary fiber bundle pattern on each modified image. The samples were rotated a full 360^◦ in one-degree increments, generating a total of 360 sampled images of the object. In the simulations involving translation, the images were randomly translated along ±x and ±y by up to 10 pixels, in addition to being rotated. The simulated images were then run through the algorithm, as described in Section 2.C. The two-dimensional Pearson’s correlation coefficient was calculated between the reconstructed and original image to determine the strength of the image reconstruction.

Fig. 2.

Simulated fiber bundle artifact and removal. (A) Simulated image of a sample with biological features. (B) Binarized mask representing the fiber array within the fiber bundle. (C) Resulting effect of the artifact shown as the product of the images in (A) and (B). (D)–(F) Representative results of algorithm efficacy by rotation of the superimposed fiber pattern. There is a concentric artifact after summing of subsequent images after rotation (D), which is easily removed after low-pass filtering (E) to yield the final, reconstructed image. When translation and rotation are both integrated, the reconstructed image (F) still yields strong reconstruction efficiency. Correlation coefficients (R=#) shown in red text are between the reconstructed image and the original image, showing the degree to which the algorithm is successful in retaining information from the original image.

F. Brain Tissue Imaging

Brain slices in these studies were acquired from transgenic mice with green fluorescence protein (GFP)-labeled neurons under an IACUC approved protocol at the University of Illinois at Urbana-Champaign. GFP-labeled mice were anesthetized with ketamine/xylazine, followed by transcardial perfusion of chilled cutting solution (234 mM sucrose, 11 mM glucose, 26 mM NaHCO₃, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 10 mM MgCl₂, 0.5 mM CaCl₂). Coronal slices (500 μm thick) were sectioned and then incubated in artificial cerebral spinal fluid (aCSF, 26 mM NaHCO₃, 2.5 mM KCl, 10 mM glucose, 126 mM NaCl, 1.25 mM NaH₂PO₄, 2 mM MgCl₂, and 2 mM CaCl₂) at 33^oC, and incubated at 25°C in aCSF thereafter. Slices were continuously perfused with 95% oxygen, 5% CO₂. For imaging, slices were kept in aCSF in a Petri dish, and the distal end of the fiber bundle was positioned at the cut surface of the slice for imaging.

3. RESULTS

A. Simulations

Representative simulation results using the algorithm are shown in Fig. 2, along with their respective correlation coefficients. The images show the effect of this algorithm for images that were rotated and reconstructed [Fig. 2(D)], rotated, reconstructed, then low-pass filtered [Fig. 2(E)], and after images that were rotated, translated, and low-pass filtered [Fig. 2(F)]. Figure 2(F) demonstrates the amount of blur introduced from this co-registration. Many of the features from this simulation are blurred, but the structure of the sample can be adequately visualized. Additionally, there is a Gaussian-like decay in the intensity radially outward from the center of the image, post-reconstruction. As a result of this unanticipated artifact, the outer regions of the reconstructed images are not easily discernable, making interpretations along these sections difficult. This problem partially arises as a consequence of the “imrotate” function used in MATLAB, which cuts off some of the outer regions of the image upon rotation due to the rectangular geometry of the images. Imperfections in the co-registration also can result in this blurring effect, causing distortions to the image intensity, and hence the registration efficiency. Because of this, the artifact is less of a problem experimentally, but the Gaussian-like decay in intensity nonetheless affects interpretation along the perimeter of the image. The correlation coefficients between the original and reconstructed images were lower than expected, especially given the strong visual correspondence between them. This partially can be attributed to the Gaussian edge effect introduced in the reconstruction, fine features that are lost in registration, and notable differences in intensity distribution from the center to the outer edge of these images. It can also be due to imperfections in co-registration, since numerically altering each registered image by averaging over time could cause distortions from the original to the final, re-constructed image.

B. Resolution Target

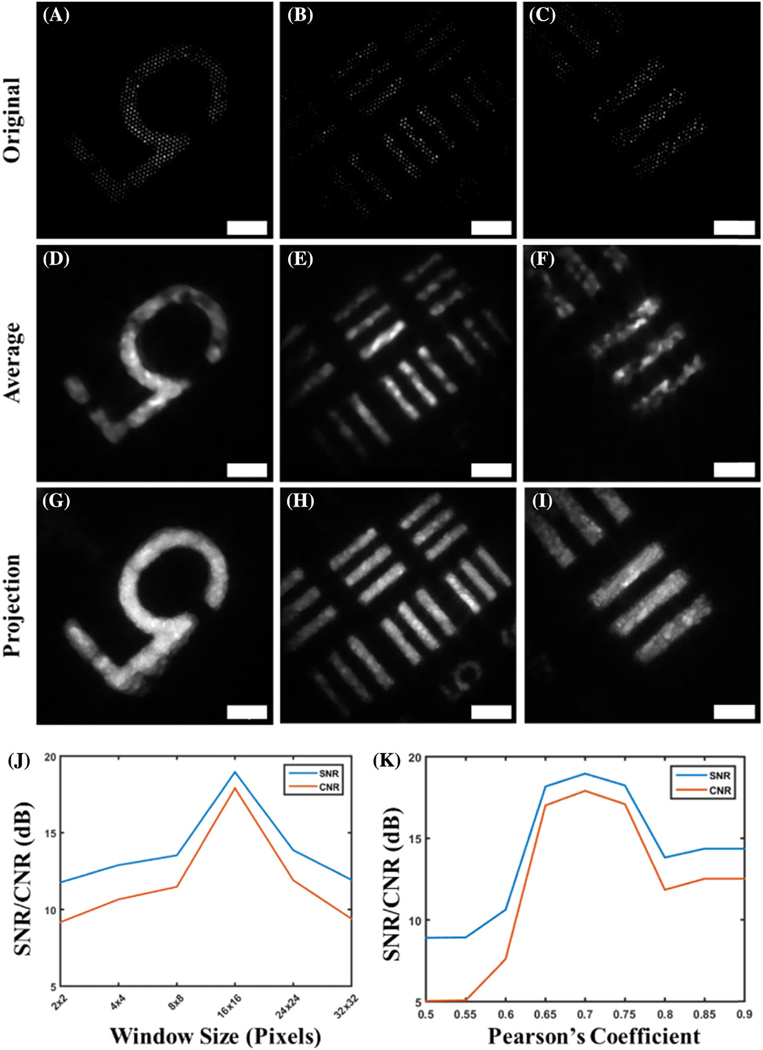
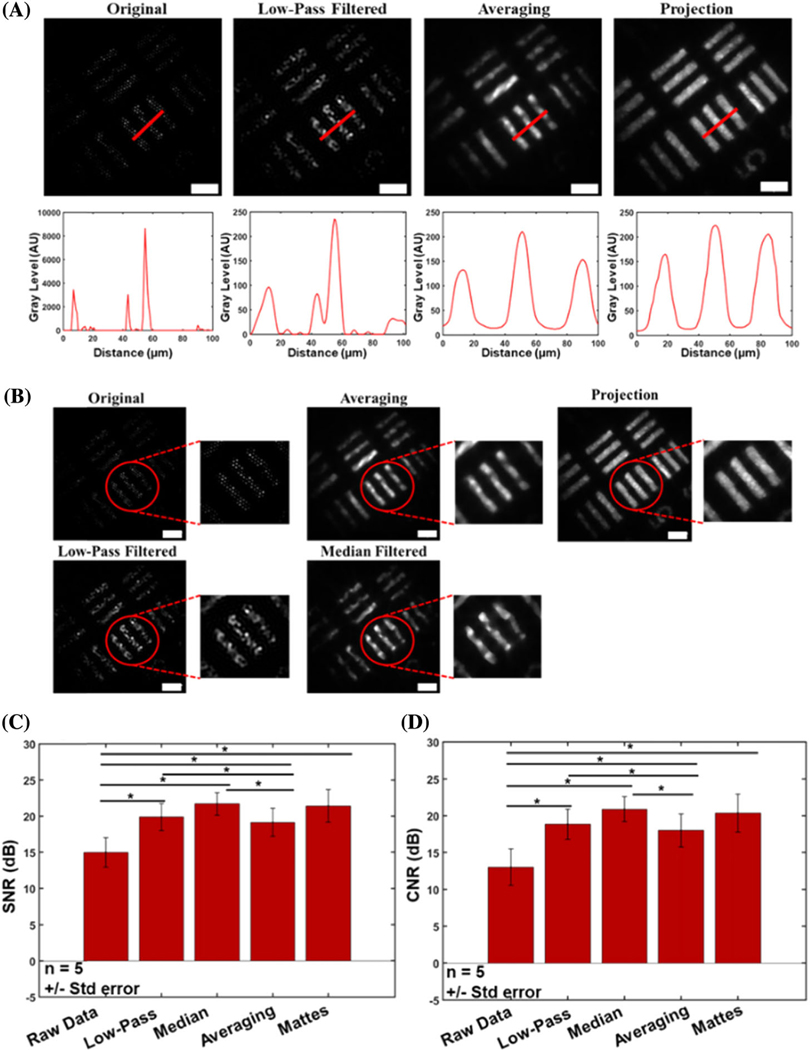
Results with the resolution target demonstrate not only clarity of the object, but also a significant retention of object features [Fig. (3)]. In addition to the reconstruction of the underlying object features, edges are also very well preserved, especially in comparison to images reconstructed using only low-pass and median filtering [Figs. 4(A) and 4(B)]. Low-pass filtering alone results in significant intensity fluctuations along the surface of the object. Median filtering removes these artifacts, but edges are not very sharp, and gaps along the object surface arise from the gaps imposed by the fiber bundle artifact. The reconstructed image shows more prominent edges, with many of the aforementioned gaps removed as a result of the spatial resampling after bundle rotation. The increased number of homogeneous features further allows for the display and accurate distinction of neighboring object features[Figs.3(D)–3(I)], which is especially visible in the Mattes mutual co-registered images [Figs. 3(D)–3(I)]. A reference resolution target image was used for optimization of image quality by quantifying the SNR and CNR of there constructed image using various median filter sizes and Pearson’s coefficients [Figs. 3(J)–3(K)]. It is clear that optimal image quality was obtained when a window size of 16 × 16 was used, along with a Pearson’s coefficient of 0.7, leading to the use of this combination of these conditioning metrics for all subsequent analyses. The line profile of a bar on the USAF target[Fig.4(A)]shows the results before any processing, after low-pass filtering, and after reconstruction with the presented algorithms. In addition to increasing the contrast of the underlying object features, the line profiles reveal inhomogeneities in intensity along the object surface, and single objects can be identified. Furthermore, image quality enhancement is further demonstrated using SNR and CNR comparisons for each object [Figs. 4(C) and 4(D)]. We observe a universal increase in both SNR and CNR with each reconstruction technique, with the fiber bundle rotation resulting in an even greater increase overall. More specifically, these SNR values were 6.26, 10.91, 13.02, 9.98, and 13.29 dB for the raw, low-pass filtered, median filtered, average reconstruction, and Mattes mutual reconstruction techniques, respectively. The CNR resulted in values of 5.26, 9.91, 12.01, 8.98, and 12.14 dB for the raw, lowpass filtered, median-filtered, average reconstructed, and Mattes mutual reconstruction, respectively. There is a statistically significant difference between the averaging reconstruction method proposed here and all other datasets, with the exception of the Mattesmutual method.

Fig. 3.

Comparison of the original and reconstructed images of features on a USAF resolution target. Three different locations are shown, one in each column. Results demonstrate the degree to which the algorithm is able to reveal object features that are otherwise obscured because of the superimposed fiber-pattern artifact, which is apparent in (A)–(C). More specifically, some regions do not appear in the original images, but can be seen after reconstruction [compare (B) and (E)]. Furthermore, regions with “dead” fibers, or fibers that do not transmit light, such as those seen in the number “5,” are effectively interpolated and show intensity after reconstruction [compare (A) and (D)]. These voids are more prominently filled when reconstruction involves taking the maximum value at each pixel between multiple images, as shown in (G)–(I). The image conditioning process for experimental data is optimized by selection of the optimal median window size (J) and inter-frame Pearson’s coefficient (K) that yields optimal image quality, as quantified using SNR and CNR. Scale bars represent 50 μm.

Fig. 4.

Improved resolution following reconstruction. (A) Profiles of USAF resolution target showing increased ability for resolving discrete neighboring bars. Original unfiltered data and low-pass filtered data provide false perceptions of two separate objects, based on their line profiles. The proposed reconstruction method, however, demonstrates a clear distinction between the discrete objects (bars). (B) Edge preservation and image quality are both enhanced after applying the algorithm. The reconstructed image shows much more refined edges, morphology, and uniform intensity distribution than after median filtering without image registration. (C) CNR and (D) SNR values of various techniques for removal of the superimposed fiber pattern, tested on a USAF resolution target. Significance stars between red bars represent P < 0.05. Values are given as mean ± S.E. (n= 5). Scale bars represent 50 μm.

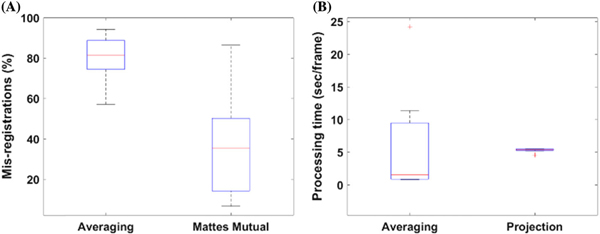
Because of the large variance in SNR with the Mattes mutual method, it was significantly different from only the raw data. The same is true for the CNR. This is attributed to the large variability in SNR and CNR calculated in these experiments. Although there is no statistically significant difference between the SNR/CNR for the Mattes mutual information metric, it is clear from looking at the images that this method demonstrates a superior ability to resolve object features and preserve edges that is not present in the other metrics. The Mattes mutual metric is also superior to the averaging reconstruction method, in that it resulted in considerably less mis-registrations, as shown in Fig. 5(A). Consequently, this resulted in more details of the object being retrieved, thus improving reconstruction efficiency andSNR/CNR.

Fig. 5.

Algorithm performance. (A) Mis-registration distribution and (B) computational processing time distribution of the two algorithms proposed in this work. The Mattes mutual approach (projection) results in considerably fewer mis-registrations than the averaging method, and is much more consistent in its processing time.

C. Computational Time

One of the primary factors for each of the reconstruction approaches proposed in this work is the computation time. The descriptive statistics for computation time are illustrated in Fig. 5. The reconstruction algorithm utilizing the averaging method takes on average 6.08 s per frame, with a large distribution of processing times. In contrast, the Mattes mutual algorithm takes on average 5.28 s per frame, with a much more consistent frequency. Additionally, the Mattes mutual projection method results in considerably fewer mis-registrations [Fig. 5(B)], with a 36% mis-registration rate, compared to the average algorithm, which results in an 80% mis-registration rate. In this work, mis-registrations include co-registrations that result in a 2D Pearson’s correlation below 0.7 between successive images. This discrepancy accounts for the dramatic difference in image quality seen between the two methods, and why so many object features are unveiled using this metric and method. Overall, the results presented demonstrate that with effective co-registrations, the image quality is greatly increased by bundle rotation and the implementation of the algorithms proposed. The primary weakness is the computation times, however. With the average for the Mattes mutual method, processing 500 images would take 3000 s (roughly 50 min), making real-time processing impractical. This speed can be improved through the use of a lower-level programming language, GPU processing, use of a more powerful processor, or through the use of a more rapid and effective co-registration algorithm. By improving automated registration algorithms between successive frames, image quality would also improve, demanding the need for more sophisticated image registration techniques than those used in this work.

D. Biological Object

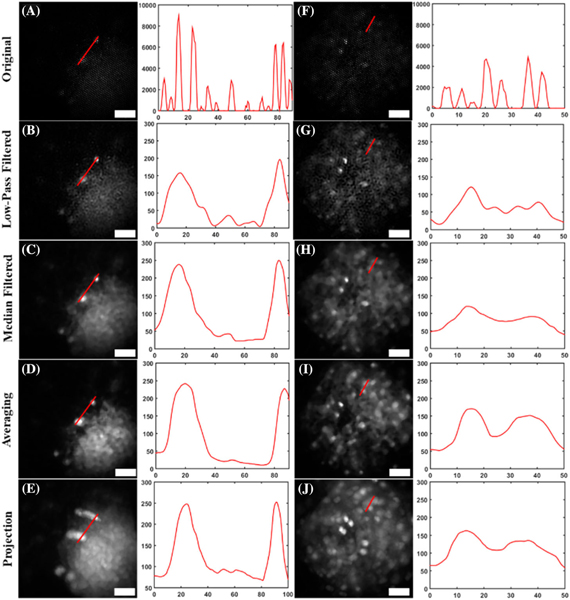
Once the reconstruction algorithm was verified with a USAF resolution target, it was further verified by imaging GFP-labeled brain slices from a transgenic mouse line. Background autofluorescence from the tissue was prominent, but individual cell bodies could be discerned with the reconstruction technique (Fig. 6). This is most noticeable in the second slice [Figs. 6(F)–6(J)], where individual cell bodies that are otherwise low in intensity[Fig. 6(F)]become more prominent[Fig. 6(I)].

Fig. 6.

Reconstructed images of brain slices from transgenic mice expressing GFP, and corresponding line plots for each image. Two separate brain slices [(A)–(E) and (F)–(J)] are shown after (B), (G) low-pass filtering; (C), (H) median filtering; (D), (I) averaging with the proposed reconstruction technique; and (E), (J) using the maximum projection method in the proposed technique. Notice how in the sparser neural samples, imperfections in image registration lead to poorer image reconstruction (E), (J), compared to the less sparse resolution targets. The vertical axes of the profile plots have gray-scale value units, and the horizontal axes represent distance, in micrometers. Scale bars in images represent 50 μm.

Although median filtering after low-pass filtering provides good quality of resolved features, our technique reveals even more features. Low-pass filtering alone [Figs. 6(B) and 6(G)] does not facilitate visualization much, as many cell bodies are still hidden from view. However, after reconstruction [Figs.6(D) and 6(I)], all cellbodies are more resolved, even those previously not visualized. Many of the neuron bodies otherwise obscured by background fluorescence from the tissue were adequately resolved. This can be largely attributed to the registration process. Only regions with strong signal intensity will be adequately co-registered, as will the relative locations between successive images. Co-registration promotes localization of all cell bodies between images, but does not do so with background noise. Thus, the signal becomes much more pronounced over the noise. Overall increased contrast of individual neurons enhances the visualization of individual cell bodies compared to the superimposed fiber pattern, or even after low-pass and median filtering. This was problematic only with the maximum projection method [Figs. 6(E) and 6(J)]. This is likely due to imperfections in co-registration that, rather than averaging and removing inadequate co-registrations, result in a spill-over effect where these imperfections add up, resulting in poor image reconstruction. This is still present even when higher scorrelation coefficients are used as a cutoff, therefore presenting an inherent problem with sparse samples. Despite this, the proposed averaging method does adequately resolve individual cell bodies, and acts as an efficient method for reconstruction. These results demonstrate that the described technique and algorithm are robust for different samples, and can be used to obtain images with enhanced contrast.

4. DISCUSSION

This paper demonstrates the use of fiber bundle rotation and translation for image reconstruction and depixelation of fiber bundle images. An algorithm was developed to reconstruct images acquired through a fiber bundle system, which not only guides light to and collects light from fluorescent and/or reflective samples, but also allows for rotation and translation of the fiber bundle for rapid and more comprehensive spatial sampling. The resulting algorithm corrects for the superimposed honeycomb artifact introduced from fiber bundle imaging. We have shown significant increases in the SNR and CNR of the images using this technique, in addition to retention of the resolution after reconstruction, resulting in an overall improvement in image quality.

The correlation coefficients between simulations and their original images—around 0.30–0.35, are low primarily because of the loss of finer features following the reconstruction. Intensity fluctuations of the reconstructed images gradually decrease from the center of the image and radially outward. This happens to the point that features along the outer edge of the image are nearly indiscernible, which also contributes to this decreased coefficient. It should be noted that this intensity distribution is less pronounced in the images reconstructed through the actual fiber bundle system, although it is still present. This is due largely to the Gaussian intensity distribution of the incident light, and consequently, the back-scattered and fluorescent light. As more light is incident on the sample near the center, and less along the outer perimeter, this artifact manifests itself in a similar Gaussian intensity profile in these images.

This technique has been shown to be not only more effective than solely filtering in the frequency domain for fiber bundle pixilation artifact removal, but also more straightforward to implement with optical systems. The technique, however, does have some inherent limitations, with the primary one being computation time. On average, the algorithm takes about 10min to process the data and generate are constructed image—contingent on the number of images in an imaging sequence, sampling rate of the camera, etc. This poses limitations for real-time imaging of cellular structures, especially in the case of in vivo imaging. Finer samples also pose difficulties for this algorithm—in particular for the Mattes mutual reconstruction approach, as any imperfections in co-registration, which are more likely to happen for samples with similar underlying features, will impose their own artifacts upon reconstruction. As the results demonstrate, the choice of image registration metric and technique is pivotal to enhancing image quality using this approach. Mis-registrations in this work, defined as inter-frame correlations below 0.7, were considerably higher when averaging than when using the Mattes mutual registration approach, which resulted in poorer reconstruction. Hence, optimization of image registration algorithms may be necessary to ensure sufficient image quality for imaging. Although henhancedSNRmay facilitate this, the obscured honeycomb pattern will inherently lead to decreased SNR, so sophisticated image conditioning and enhancement are pivotal. The usability of this algorithm is also limited by memory capacity, which comes primarily from memory storage. The program is written so that the entire image sequence is loaded into the MATLAB workspace and processed thereafter. If the images immediately after acquisition at different orientations are temporarily stored prior to reconstruction, this time can be reduced. Additionally, rewriting the algorithm with lower-level programming languages such as C₊₊ or Python, or parallelizing computation with GPUs, would also increase the processing speed of this technique.

This study assumes that the focus remains planar throughout the duration of imaging. Should there be significant changes in the focus, image quality could be disrupted, and improvements following image reconstruction may not be possible. Adaptive focusing to maintain axial positions while imaging, if adequately implemented, could facilitate this. The technique also inherently requires rotation of the fiber bundle to complete the reconstruction. However, fiber bundles are often handheld in biological imaging, or positioned within a cannula, where on-axis rotation is possible. Use of distal focusing optics would reduce the need for direct contact with tissue, reducing the possibility of tissue damage, which would also impair image quality. The fiber bundle may also be coupled to a motor that rotates the bundle in a precisely defined manner. Reference landmarks or guide stars during imaging could also facilitate co-registration if implemented into fiber bundles. Coupling endoscopic imaging with a gyroscope or similar technology to have known rotation angles that are integrated into the reconstruction software would reduce the need for co-registration, promoting real-time processing with fewer computation demands. These imaging scenarios would promote the use of the reconstruction technique for real-time in vivo imaging, endoscopy, and other similar applications.

5. CONCLUSION

In this work, we present an imaging technique and algorithm for reconstruction of fiber bundle images to reduce the inherent pixilation artifact that obscures object features during imaging. A simulated framework was developed to reconstruct images that would be hindered by this artifact, and the use of this algorithm was demonstrated for reconstructing images of a USAF resolution target, showing an increased SNR and CNR relative to simple Fourier-filtering techniques. Finally, this algorithm and method were used on biological images of fresh mouse brain slice tissue expressing GFP. This framework provides an alternative way for image reconstruction and removal of fiber bundle artifacts. With future integration and computational acceleration, this technique and algorithm can be widely adopted for a variety of imaging applications.