Computational simulations of the helical buckling behavior of blood vessels

Abstract

Tortuous vessels are often observed in vivo and could hinder or even disrupt blood flow to distal organs. Beside genetic and biological factors, the in vivo mechanical loading seems to play a role in the formation of tortuous vessels but the mechanism for formation of helical vessel shape remains unclear. Accordingly, the aim of this study was to investigate the biomechanical loads that trigger the occurrence of helical buckling in blood vessels using finite element analysis (FEA). Porcine carotid arteries were modeled as thick-walled cylindrical tubes using generalized Fung and Holzapfel-Gasser-Ogden (HGO) constitutive models. Physiological loadings, including axial tension, lumen pressure, and axial torque were applied. Simulations of various geometric dimensions, different constitutive models at various axial stretch ratios, lumen pressures, and twist angles were performed to identify the mechanical factors that determine the helical stability. Our results demonstrated that axial torsion can cause wringing (twist buckling) that leads to kinking or helical coiling and even looping and winding. The specific buckling patterns depend on the combination of lumen pressure, axial torque, axial tension and the dimensions of the vessels. This study elucidates the mechanism of how blood vessels buckle under various mechanical loads and how complex mechanical loads yield helical buckling.

1. Introduction

Mechanical stability of blood vessels is essential for their normal physiological functioning. However, large amount of clinical observations have shown that tortuous blood vessels (curving, coiling, kinking, and looping) often occur in human body as anomalies or pathological conditions [1–3]. It has been shown that vascular tortuosity is associated with atherosclerosis, aging, hypertension, and other vascular disorders [3–5], and it may lead to ischemic attacks to distal organs and other pathological changes [1]. Therefore, it is of clinical interest to better understand the mechanisms of artery tortuosity.

While various modes/patterns of tortuous vessels are seen in various vessels, arteries, veins, as well as other tubular organs, it is unclear what the determining factors leading to different patterns are. Besides genetic and biological factors, physical factors may play important roles in the tortuous vessels [6]. It is well known that excessive external pressure can cause vessel lumen to collapse [7–11]. Our recent studies have shown that bending buckling under hypertensive pressure can lead to curving of the vessels, and axial twist can lead to torsion and kinking of blood vessels [12–16]. However, the mechanical loading conditions that may lead to other form of buckling remain unclear.

Beside these curving and kinking patterns, arteries also demonstrate helical and looping patterns in vivo. Helical vessels have been observed in carotid, umbilical, and other arteries [17–20]. Helical shape could increase the wall stress and hinder blood flow, which may lead to ischemia to distal organs. It has also been reported that carotid artery tortuosity (kinking and helical coiling) are associated with carotid artery dissection, which is a noteworthy cause of ischemic stroke at all ages [21]. Thus, it is important to understand the mechanical loads that may lead to helical buckling.

There is a lack of understanding in helical buckling of blood vessels under mechanical loads. Previous computational model simulations of the twist buckling of arteries and veins were mostly done with thin wall isotropic linear elastic or hyperelastic materials [22–24] except our previous simulation of vein twist buckling that used an anisotropic hyperelastic materials [14]. The effects of material nonlinearity and anisotropy on artery twist buckling remain unknown. It is unclear whether the helical shape can yield from mechanical loading and what kind of mechanical loading leads to helical buckling.

Therefore, the objective of this study was to assess the helical buckling of blood vessels under mechanical loads and evaluate the effects of dimensional size, material models, axial tension, lumen pressure, and angle of twist on the buckling mode using FEA. It will clarify how the interplay of lumen pressure, axial tension, axial torsion, dimensions, and material models/properties determine the mode of vessel buckling. Our study intends to shed some light on the nature of helical blood vessels.

2. Materials and Methods

Computational models of porcine carotid arteries were developed based on our experimental database to determine the loading conditions to generate helical buckling and to examine the effects of axial tension, lumen pressure, twist angle, constitutive models, and geometric features on buckling patterns.

2.1. Model geometries

Thick-walled cylindrical tube models were employed for the analysis. The primary models are assumed to have the dimensions given in Table 1 as obtained from our previous experimental data of porcine carotid arteries [13]. These dimensions (specifically, length and wall thickness) were varied in additional analyses to examine their influence on the helical buckling. The residual stress was ignored in these models as our previous studies showed that the residual stress has insignificant effect on artery buckling [12, 25].

Table 1.

Summary of the initial dimensions of five normal porcine carotid arteries (from Ref. [13]) used in the simulations.

Artery	Initial length (mm)	Inner diameter (mm)	Thickness (mm)	Opening angle (°)
1	43.06	3.24	2.00	109.09
2	38.49	3.11	1.41	68.43
3	57.49	3.04	1.08	50.64
4	39.04	4.54	1.69	109.77
5	66.00	3.63	1.13	92.41
Mean ± SD	48.82 ± 12.31	3.51 ± 0.62	1.46 ± 0.39	86.07 ± 25.97

2.2. Constitutive models for the arterial wall

The arterial wall material was assumed to be homogenous, incompressible with nonlinear orthotropic materials using generalized Fung strain energy function. The Holzapfel-Gasser-Ogden (HGO) strain energy function was also used for comparison.

2.2.1. Generalized exponential Fung model

The general strain energy of exponential Fung is given by [13, 26]

$$w=\frac{1}{2}C\left(\text{exp}\left(\text{Q}\right)-1\right)$$ (1a)

Where C is a material constant and Q is given by

$$Q=b_1{E_{\theta }}^2+b_2{E_z}^2+b_3{E_r}^2+2b_4{E}_{\theta }{E}_z+2b_5{E}_z{E}_r+2b_6{E}_r{E}_{\theta }+2b_7{E_{\theta z}}^2$$ (1b)

Here b₁ to b₇ are dimensionless material constants and E_ij, with i, j = r, $\theta$, z, are the components of Green-Lagrange strain tensor [13]. Subscripts r, θ, z indicate the radial, circumferential and axial directions in a cylindrical coordinate system, respectively. This formulation includes a shear constant b₇ regarding the axial-circumferential shear deformation.

2.2.2. Holzapfel-Gasser-Ogden (HGO) model

Holzapfel-Gasser-Ogden (HGO) model with two families of diagonally oriented collagen fibers was also employed to describe the anisotropic hyperelastic behavior of arterial wall. The strain energy density function is given by [27, 28]

$$w=C_{10}\left(I_1-3\right)+\frac{k_1}{2k_2}\sum _{i=4,6}\left(e^{k_2{\left[\kappa I_1+\left(1-3\kappa \right)I_i-1\right]}^2}-1\right)$$ (2)

Where $C_{10}>0$ and $k_1>0$ are stress-like material constants and $k_2>0$ is nondimensional. The parameter $\kappa$ is the dispersion parameter which indicates the degree of anisotropy and distribution of the collagen fibers within the two families of fibers [28]. $I_1=tr\left({\text{F}}^T\text{F}\right)={\lambda }_r^2+{\lambda }_{\theta }^2+{\lambda }_{\text{z}}^2$ is the first invariant of the right Cauchy-Green tensor, $I_4$ and $I_6$ are the square of the stretches corresponding to the two fiber families, $I_{4,6}={\lambda }_z^2{\text{cos}}^2\left(\alpha \right)+{\lambda }_{\theta }^2{\text{sin}}^2\left(\alpha \right)$ with α being the mean fiber angle with respect to the longitudinal vessel axis and λ_z, λ_θ, and λ_r being the stretch ratios in the axial, circumferential and radial directions, respectively.

2.3. Finite element analysis of helical buckling

Idealized cylindrical shaped artery models were created in SolidWorks®. The models were meshed using 8-node linear hybrid hexahedral element with constant pressure (C3D8H) for finite element analysis using the ABAQUS® package. Hexahedral elements were deployed due to the higher accuracy and a better convergence rate than any others [29]. To investigate the grid independency, four grids with increasing number of elements (by 50%) were modeled. FEA results were deemed grid-independent when a further increase in mesh density would not change the both critical twist buckling torque and critical twist angle (by more than 4%). The critical twist buckling torque and critical twist angle are the maximum value of torque and twist angle before a sharp drop due to the helical buckling [13, 14]. The final grid is consisted of 23,616 hexahedral elements.

One end of the artery was fixed from lateral movement and rotation while allowing radial expansion. The other end was stretched and twisted axially using a kinematic coupling constraint to gradually increase the rotation angle. A small initial curvature (1 degree along the central axis) was introduced as a geometric imperfection to facilitate buckling. Our previous studies on bent buckling showed that this imperfection led to the base sinusoidal buckling mode and had little effect on the critical buckling pressure [30] and our pilot studies on twist buckling showed no effect on twist buckling mode and critical twist buckling torque. To better describe the complexed deformed shape and prevent unphysical surface penetration, self-contact was defined as the normal (hard contact) and tangential (frictionless) contact of the arterial wall. A static pressure was applied to the lumen of stretched arteries, while the outer surface was traction-free. The axial torsion was implemented using a quasi-static implicit scheme. The arterial wall density was assumed to be 1020 kgm⁻³. The full Newton method with extra convergence properties was utilized to solve the nonlinear equilibrium equations in ABAQUS /Standard.

3. Results

3.1. Material constants of porcine carotid arteries

The convex material parameters of Fung model (Table 2) obtained for a set of five porcine carotid arteries from our previous study [13] were employed. The material constants were determined for axial stretch ratios of 1.3 and 1.5, lumen pressures between 20 and 100 mmHg, and rotation angle of 0–270°. These material constants showed a good match with the experimental data of arteries (pre-buckling) under axial tension, inflation, and torsion (see Ref. [13] for further details). The convex material constants for the HGO model (Table 3) were obtained by refitting the same experimental data to the HGO strain energy function using the same process as described previously [31]. The obtained constants described the mechanical behavior matched the experimental data well with R² greater than 0.9 for all arteries (Fig. 1). These 5 arteries with the material constants (both Fung and HGO) obtained were used in the following buckling simulations.

Table 2.

Convex material constants of five normal porcine carotid arteries for a generalized Fung strain energy function including shear constant (b₇) (from Ref. [13]). The material constants were determined for axial stretch ratios of 1.3 and 1.5, lumen pressures between 20 and 100 mmHg, and rotation angle of 0–270°.

Artery	b1	b2	b3	b4	b5	b6	b7	C (KPa)
1	3.766	0.267	5.000	0.001	0.001	0.95	0.841	9.955
2	1.502	0.810	5.000	0.760	1.750	1.744	0.258	152.236
3	5.000	0.436	4.950	0.576	0.001	2.758	0.865	28.029
4	4.085	0.071	5.000	0.437	0.001	2.634	0.55	19.276
5	0.910	0.323	1.506	0.130	0.131	0.648	0.167	83.362

Table 3.

Material constants of the five normal porcine carotid arteries obtained by refitting the same experimental data (from Ref. [13]) with the Holzapfel-Gasser-Ogden (HGO) model with two-fiber families.

Artery	C10 (KPa)	k1 (KPa)	k2	α	κ
1	2.50	1.40	1.30	76.6	0.105
2	2.09	1.12	1.43	71.7	0.113
3	1.71	1.22	0.21	66.3	0.106
4	7.31	4.12	0.53	76.3	0.008
5	4.17	1.11	0.96	78.3	0.124

Fig. 1.

Comparison of torque versus rotation angle curves generated by the Fung model, HGO model and experimental data for five porcine carotid arteries under an axial stretch ratio of 1.3 and a lumen pressure of 20 mmHg. The curves are truncated at the critical buckling torque, the point with a sharp drop in the value of axial torque.

3.2. Helical buckling behavior of arteries

For all the arteries in general, different combinations of mechanical loadings yielded different buckling phenotypes such as curving, wringing, kinking, helical coiling, looping and winding (Fig. 2, see helical buckling behavior in the supplementary video). Without axial torsion, blood vessels deflected laterally (in-plane buckling or curving) when lumen pressure reaches a critical buckling pressure and its deflection increased with increasing lumen pressure. The critical buckling pressure is the lumen pressure when an artery starts to deflect laterally (without torsion) which depends on the axial stretch ratio and vessel dimensions [6, 32]. With the application of axial torsion, the buckling mode becomes complex. A curved vessel (either due to initial natural curvature or bent buckling under high lumen pressure) can easily turn into a helical shape with the application of a small axial torsion (Fig. 2A). For a straight blood vessel at low stretch ratios (≤1.3), it wrings and becomes helical when axial torsion exceeds a critical twist angle which depends on the geometric features and axial stretch ratios (Fig. 2B). The helical shape gradually transforms to looping and intertwined (winding) with further increase of axial twist. For a straight blood vessel at higher stretch ratios (≥1.5), it becomes wringing and then gradually kinked (local or prolonged depending on vessel length) when axial torsion exceeds a critical twist angle which depends on the geometric features and stretch ratios (Fig. 2C).

Fig. 2.

Buckling behavior of arteries and definition of the various buckling patterns (curving, wringing, kinking, helical coiling, looping, and winding). Each artery was first axially stretched, pressurized and then axially twisted.

(A) artery 1 (HGO model): (a) curving (bent buckling), (b) post-bent buckling (in-plane) at higher lumen pressure (75 mmHg), (c) helical buckling (out-of-plane) at a critical rotation angle (36 degrees), (d) looping and (e) winding occurred under increasing rotation angle (shown at smaller scale).

(B) Artery 5 (HGO model): (a) wringing (at a rotation angle of 18 degrees), (b-c) helical buckling (at a critical rotation angle of 42 degrees and higher), (d) looping and (e) winding under increasing rotation angle (shown at smaller scale).

(C) Artery 2 (Fung model): (a) wringing (twist buckling), (b-c) kinking under increasing rotation angle.

3.3. Comparison of generalized Fung and HGO constitutive models

For all arteries, helical buckling was well captured by both generalized Fung and HGO constitutive models in the same fashion when the lumen pressure was equal or greater than the critical buckling pressure (Fig. 2). However, at a lumen pressure less than the critical buckling pressure and low stretch ratio (≤1.3), arteries under increased axial torsion become helical when using generalized Fung model (See Fig. 3 a & b) but form kinks when using HGO model (not shown). The Fung model results agree with our previous experimental observations that helical buckling of porcine carotid arteries occurred at low pressures and low stretch ratios (see discussion). Therefore, the generalized Fung model was used in simulations of arteries under low pressures and low stretch ratios to better capture the helical buckling mode.

Fig. 3.

The impact of vessel length (L/3, 2L/3, L) and axial tension: (a) 1.1, (b) 1.3, (c) 1.5, (d) 1.7 on helical buckling behavior of an artery at a constant lumen pressure (20 mmHg) and critical axial torque (Artery 2, Fung model).

3.4. Effect of vessel length and axial tension on artery helical buckling

For arteries with given diameter and wall thickness, changing the length adversely affects the critical twist buckling torque but did not change the buckling pattern; meanwhile, increasing axial stretch ratio increases the critical twist buckling torque and changes the buckling pattern (from helical coiling to kinking, and increased wavelength) (Fig. 3).

Further simulations demonstrated that the transition from helical coiling to kinking occurs at a certain axial stretch ratio. At this transition stretch ratio, both the critical twist angle and critical twist torque are at their maximum (Fig.4), though the transition was not observed in our previous experiment. It is also seen that helical coiling also can occur in short vessels (one-third of the vessel length) (Fig. 3a) though they require a higher critical twist buckling torque (Fig. 4b).

Fig. 4.

Comparison of (a) critical twist angle (normalized to stretched vessel length) and (b) critical torque plotted as functions of axial stretch (Artery 2, Fung model) at three different vessel lengths under a lumen pressure of 20 mmHg. Diamond symbols are the experimental measurements of artery 2 (mean ± SD of repeated measurements) [13].

3.5. Effect of wall thickness to lumen radius ratio on artery buckling pattern

FEA simulations demonstrated that the wall thickness to lumen radius ratio (t/r) had a prominent role in determining the buckling pattern. Decreasing the wall thickness in the primary models, while keeping the lumen radius constant, could lead to a gradual change in artery buckling mode from a helical to a kink (Fig. 5). However, when decreasing or increasing both the lumen radius and wall thickness while keeping their ratio constant did not affect the buckling pattern. These results suggest that the (t/r) ratio is a determining factor for the buckling pattern. Higher t/r ratio (thicker wall) leads to helical coiling while lower t/r ratio (thinner wall) leads to kinking. In general, arteries and veins are thick-walled and thin-walled vessels, respectively. Therefore, arteries are more prone to the helical coiling mode while veins are prone to kinking. This is in good agreement with clinical observations [14, 33]. In addition, increasing t/r increases the critical twist buckling torque and critical buckling twist angle. At stretch ratio of 1.3, the critical twist buckling torques for t/r=0.31 and 1.25 are 0.24 and 6.98 N-mm, respectively (Fig. 5).

Fig. 5.

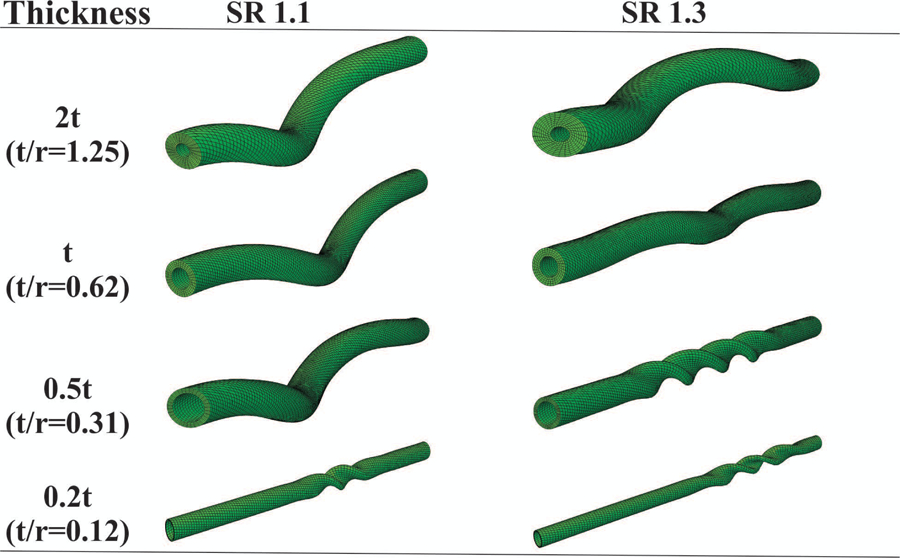
The effect of wall thickness to lumen radius ratio on helical buckling behavior at a constant lumen pressure of 20 mmHg (Artery 2, Fung model). SR = axial stretch ratio.

3.6. Role of shear constant (b₇) in generalized Fung model

To investigate the effect of shear constant b₇ in generalized Fung model (Eq. 1), its value was increased without altering other material constants. Our results showed that increasing the value of shear constant b₇ caused an increment in the critical twist buckling torque and transition of kink buckling into helical buckling pattern (Fig. 6a). However, it had a negligible effect on the critical bent buckling pressure (Fig. 6b). It is important to include the shear constant b₇ when modeling blood vessels under torsion.

Fig. 6.

The effect of shear constant (b₇) in the Fung model on the critical buckling loads in five porcine carotid arteries (see Table 1): (a) twist buckling torque at a stretch ratio of 1.1 and a lumen pressure of 20 mmHg (artery 4 was not included since its FEA failed to converge at the specified loading conditions with the material parameters given in Table 2), (b) bent buckling pressure at a stretch ratio of 1.1. The parameter b₇ was increased while keeping other material constants unchanged.

3.7. Influence of mechanical loadings on buckling phenotypes

Simulations demonstrated that axial torsion in combination with lumen pressure and axial stretch ratio can lead to different buckling patterns including wringing, kinking, helical coiling, and winding (Fig. 7). All 5 arteries demonstrated similar buckling patterns but the magnitude of the critical buckling loads were different due to their different material properties and dimensions. It is evident that lumen pressure plays a significant role in determining the buckling patterns. At low pressure (below critical pressure), arteries may buckle into a kink or helical depending on dimension and axial stretch ratio, but at high pressure (above critical pressure), arteries always buckle into helical shape and can be looping or winding at high torsion. At low pressure, increasing the axial tension could change an artery from the helical coiling into kinking. The trend of artery buckling was the same for all arteries (both Fung and HGO models) except at a lumen pressure less than the critical buckling pressure and low stretch ratio. In addition, the magnitude of critical buckling loads for five arteries were different due to their different material properties and different dimensions.

Fig. 7.

Summary of wringing, kinking, helical coiling, looping, and winding patterns as results of various lumen pressures, axial torques, and axial tensions based on simulation results of the 5 arteries. All 5 arteries demonstrated similar artery buckling patterns (see text for details) but the magnitude of the critical buckling loads were different due to their different material properties and dimensions (SRtr = transition stretch ratio).

Interestingly, for a curved artery (either due to initial curvature or bent buckling), application of axial torsion could lead to helical coiling, looping and winding depending on the amplitude of the torsion (Fig. 8). At the very beginning when a small torsion is applied, curved vessels become helical (point a) and the level of twist increases with increasing torque (point a to point b). Then, a loop starts to form with a sharp drop in torque (point c), and further increase in torsion results in the intertwining of the vessel (winding, point d and beyond). The higher the rotation angle, the higher the torque and maximum wall stress (increased by 3 times), though fluctuations are seen in the process. It is noticed that axial torsion is the dominating load in determining the buckling pattern of blood vessels while others such as lumen pressure and axial tension do have their influences.

Fig. 8.

Variations of axial torque and the vessel configurations with rotation angle in an artery (artery 1, HGO model) at a lumen pressure of 75 mmHg and an axial stretch ratio of 1.3. The artery buckled initially under lumen pressure (40 mmHg). (a-f) deformations with increasing twist angle at a constant lumen pressure. The maximum principal stress is color-coded.

4. Discussion

In this study, helical stability of blood vessels was analyzed to determine the biomechanical factors that induce helical buckling. The results demonstrated that mechanical loads such as axial torsion can lead to helical buckling and the torsion in combination with lumen pressure and axial tension control buckling pattern such as wringing and kinking. Excessive torsion can lead to helical coiling, looping and winding. Arteries under axial torsion and low pressure may buckle into kink or helical shape depending on dimension and axial stretch ratio, but always buckle into helical shape under axial torsion and high blood pressure. In addition, at low axial tensions, blood vessels are more susceptible to helical buckling. Axial stretching increases arterial stability and can change helices to multiple kinks.

Beside axial torsion, our results demonstrated that the arterial wall material model, axial stretch/tension, lumen pressure and vessel dimensions (wall thickness and length) also play important roles in determining the buckling patterns. The shear constant b₇ in generalized Fung model directly links to the shear stiffness of the vessel as the shear stress is given by [13, 26]

$${\sigma }_{\theta z}=\left[\frac{\pi r\lambda }{{\theta }_{o}R}\left(2b_7{E}_{\theta z}\right)+r\gamma \lambda \left(b_2{E}_z+b_4{E}_{\theta }+b_5{E}_r\right)\right]C{e}^Q$$ (3)

Therefore, increasing the b₇ will increase the shear stiffness and thus make it harder for local shear deformation – that prevents the formation of a focal kink, and thus make it takes helical configurations at buckling. The HGO model was not able to describe the helical buckling at low pressure range may due to the fact that it describes the isotropic mechanical behavior at small pressures [27]. To test the speculation that isotropic models are more prone to helical buckling pattern, we performed a parametric study by assuming b₁=b₂=b₃, b₄=b₅=b₆, and b₇=0.5(b₁–b₄) in generalized Fung model (Eq. 1) [34] and our results indeed showed that some of the vessels buckled into kink rather than helical at low pressures. It supports our speculation that isotropic vessels are more prone to kink pattern while anisotropic vessels are prone to helical buckling pattern.

It has been shown that collagen fibers make arterial wall to be anisotropic [35] and veins or small arteries might be less anisotropic in nature due to the lower percentage of collagen in comparison with large arteries (i.e. carotid and aorta) [26]. High susceptibility of kinking in veins or small arteries might be due to both less anisotropy and smaller wall thickness. However, the effect of wall thickness is more dominant than wall anisotropy since our simulation results showed that helical coiling changed into kinking by decreasing the wall thickness in all five arteries while only some of the arteries buckled into a kink rather than helical coiling when making the vessel wall isotropic at normal thickness. In addition, aging and hypertension could lead to vascular dysfunction and remodeling which can alter the structural and mechanical properties of the arterial wall through arterial growth (radial enlargement or wall thickening) and remodeling (reorientation of collagen fibers) [36, 37] and thus change their buckling pattern. Further studies are needed to examine the growth and remodeling of arteries after the occurrence of buckling to increase our understanding of permanent tortuosity [38].

Previously, we have observed different buckling patterns such as wringing, kinking, helical coiling, and looping patterns (Fig. 9) in porcine carotid arteries under various mechanical loads [6, 13]. Compared to previous experimental observations [12, 13], our FEA results capture the buckling features of bending and twist buckling. The torque versus rotation angle curves obtained in our previous study [13] were well predicted by our computational model with an error of less than 5% in terms of the critical torque (Fig. 10). These observations confirmed our model predictions of helical buckling. In addition, Clinical observations have shown that carotid arteries and umbilical arteries sometimes become helical [17–20]. The axial torsion due to head rotation and baby rotation, respectively, could be possible causes. Furthermore, aging and vascular diseases reduce the longitudinal tension in arteries [39] which can make blood vessels are more susceptible to helical buckling. The severe tortuous shape like looping and helical coiling have also been observed in clinical patients [1–3]. There is also a possibility of barrel-shape buckling in arteries though it rarely happens [40]. Interestingly, there are some reports suggesting that aneurysms can be formed as a result of buckling [41, 42].

Fig. 9.

Photographs of porcine carotid arteries demonstrating (a) wringing, (b) kinking (at high stretch ratios ≥1.5), (c-d) helical coiling and looping (at low stretch ratios ≤1.3) pattern under combined mechanical loads. All arteries were under a lumen pressure less than the critical (bent) buckling pressure.

Fig. 10.

Comparison of torque versus rotation angle curves from experimental measurements [13] and computational simulations. (a) Artery 5 (HGO model): (1) wringing and (2) kinking, under an axial stretch ratio of 1.5 and a lumen pressure of 40 mmHg. (b) Artery 5 (HGO model): (1) helical buckling, (2) looping, and (3) winding, under an axial stretch ratio of 1.3 and a lumen pressure of 40 mmHg.

The difference between FEA and experimental results (see Fig. 10) might be due to two factors: first, the model assumed perfect cylindrical shape while the actual arteries in the experiment are imperfect in dimensions (diameter and wall thickness). Secondly, the material parameters were estimated with curve fitting of experimental data that may cause error as well.

There were a few limitations in the present study. First, an idealized porcine carotid artery geometry with uniform wall thickness was used for simplicity. Although using artery-specific realistic geometries would enhance the accuracy of our findings, employing idealized geometries is a well-accepted method to perform a parametric study in computational biomechanics [43, 44] and the nearly cylindrical shape of the porcine carotid arteries used made it reasonable to use the cylindrical assumption. Second, we have neglected the surrounding tissue since its effect has been studied in our previous works [12, 45], which have showed that the surrounding tissues, in general, increased the critical buckling loads and made arteries more likely to buckle into higher mode. Third, although the material constants were determined for axial stretch ratios of 1.3 and 1.5, we extrapolated the model for a wider range of axial stretch ratios between 1.1 and 1.7. While it may be not reliable to use extrapolation, our simulation results showed good agreement with our previous experimental results [12, 13] and simulation results of cylindrical vessel buckling in the literature [22–24, 46, 47]. These agreement gives us confidence in using the model for the slightly extended stretch ratio range. However, further experimental studies are needed to verify the material model at higher axial stretch ratios. Finally, the presence of blood flow may increase the arterial instability due to the generated shear forces [48–50]; consequently, fluid-structure interaction (FSI) analysis of helical vessels need to be investigated in future works.

5. Conclusion

Helical buckling in arteries occurs under axial torsion in combination with other mechanical loads. A new finding from the present study is that the critical values of axial tension, axial torque, and lumen pressure will control the mode of buckling under complex mechanical loads. Our results illustrated the influences of vessel dimensions, material models/properties, and mechanical loading conditions on formation of tortuous vessels (curving, helical coiling, kinking, and looping). Although this work is focused on helical buckling of arteries, this model can be applied to any tubular organs and vascular implants (graft/stent). Considering the torsional and bending stability of blood vessels and vascular grafts are important for future vascular implants design and vascular disease treatments.