Abstract
A flexible framework has been created for modeling multi-dimensional hydrological and water quality processes within stormwater green infrastructure (GI) practices. The framework conceptualizes GI practices using blocks (spatial features) and connectors (interfaces) representing functional components of a GI. The blocks represent spatial features with the ability to store water (e.g., pond, soil, benthic sediments, manhole, or a generic storage zone) and water quality constituents including chemical constituents and particles. The hydraulic module can solve a combination of Richards equation, kinematic/diffusive wave, Darcy, and other user-provided flow models. The particle transport module is based on performing mass-balance on particles in different phases, e.g., mobile and deposited in soil with constitutive theories controlling their transport, settling, deposition, and release. The reactive transport modules allow constituents to be in dissolved, sorbed, bound to particles, and undergo user-defined transformations. Four applications of the modeling framework are presented that demonstrate its flexibility for simulating urban GI performance.
Keywords: Low impact development, Rain garden, Porous pavement, Stormwater management, Green infrastructure, Modeling fate and transport
1. Introduction
Urban stormwater GI systems, also referred to as low impact development (LID) practices, are designed to reduce the volume, peak flow, and the contaminant loading associated with stormwater runoff. A GI design relies on processes such as infiltration, evapotranspiration, sedimentation, filtration, deposition, and plant uptake for mitigating stormwater runoff impacts. A variety of GI types are used for stormwater management, including dry and wet ponds, infiltration basins or trenches, constructed wetlands, bioretention systems, rain gardens, rain barrels, green roofs, bio-swales, and porous pavement; for a review (Ahiablame et al., 2012). Innovative or non-conventional approaches including combining multiple types of GI practices or using non-standard GI designs have also been proposed and proven to be effective in some cases (Dickson et al., 2011, Liu et al., 2015, Page et al., 2012).
To evaluate the long-term performance of GI design and explore potential improvements, it is important to model the processes affecting GI hydraulics and the fate and transport of contaminants fluxing through these facilities. This is particularly important because field studies have shown that the performance of stormwater GI practices can be highly dependent on their design configuration and the properties of the fill medium (Liu et al., 2014) as well as the intensity and duration of rain events (Qin et al., 2013). Furthermore, the recommended design standards for GIs are often different among jurisdictions in the United States and around the world (He and Davis, 2010).
Process-based mathematical modeling provides a cost-effective way to examine the effects of various design guidelines on the performance of GI practices tailored to specific sites and geographies. Modeling is also beneficial in characterizing the relative importance of various treatment processes within GIs and to optimize their performance at meeting hydraulic and water quality goals.
Most available models for GI performance analysis are either developed for catchment-scale applications or for specific LID practices with a pre-defined structure and limited scope. For a complete review, see Elliott and Trowsdale (2007). At the catchment scale, although there exist useful tools for large-scale assessment of the effectiveness of LID practices and for planning purposes, these tools often lack the details needed to consider site-specific design aspects or detailed processes occurring within one or more LID practices. For example, a LID feature was added in the Storm Water Management Model (SWMM) version 5.0 (Rossman, 2004, Rossman, 2015); where different types of LID practices can be modeled as a combination of several compartments including surface, soil, storage and underdrain in which the downward infiltration is considered using the Green-Ampt equation (Green and Ampt, 1911) and first order decay of water quality constituents can also be modeled. The hydraulic retention time and the first order decay coefficient is used to calculate the effluent concentration based on the influent concentration to an LID. However, SWMM does not allow for more detailed considerations of how important internal reactive transport processes interact with GI structural design to influence contaminant removal or transformation to groundwater (Niazi et al., 2017). Similarly, the Soil and Water Assessment Tool (SWAT) 2009 (Neitsch et al., 2011); treats LID systems as storage blocks or reservoirs with given outflow, infiltration and evapotranspiration functions. Some other stormwater models that have the capability to consider GI practices include Source Loading and Management Model (WinSLAMM) (Pitt and Voorhees, 2004), and Model for Urban Stormwater Improvement Conceptualization (MUSIC) (Wong et al., 2002). Some simpler stormwater models (e.g., L-THIA-LID) (Lim et al., 1999) treat LID systems by considering alternate effective lumped parameters governing run-off generation and infiltration on modeled sub-catchments (e.g., L-THIA-LID https://engineering.purdue.edu/mapserve/LTHIA7/lthianew/lidIntro.htm). Ackerman and Stein (2008) implemented best management practices (BMPs) into the HSPF hydrological model (Bicknell et al., 2001) by treating them as reservoirs with the capability to retain water through orifices and spillways or as water flowing through channels with bank overflow; the model then determines the load reduction of contaminants proportional to the volume reduction and first-order degradation. However, these models do not have the capability to consider detailed processes that can affect the performance of GI practices such as exfiltration, short-circuting, evapotranspiration, plant uptake, reactive-transport/biogeochemical transformation of constituents, or suspended/colloidal particle-associated transport within the GI systems.
As an alternative to catchment-scale models, LID-specific models have also been developed for specific types of GI with pre-defined structures including models representing bioretention systems (Brown et al., 2013, Dussaillant et al., 2004, Dussaillant et al., 2005, He and Davis, 2010, Palhegyi, 2009) and Permeable Pavements (Lee et al., 2014) among others. Dussaillant et al. (2004) developed a model based on Richards equation called RECHARGE to evaluate the hydraulic performance of bioretention systems. Dussaillant et al. (2005) developed another model based on the Green-Ampt equation and compared it to the RECHARGE model. Brown et al. (2013) used DRAINMOD (Skaggs, 1990) to model the performance of bioretention systems. DRAINMOD is designed for the prediction of surface and subsurface drainage processes in agricultural land using the Green-Ampt equation for infiltration. WinDetPond (Pitt and Voorhees, 2003) is a process-based modeling tool designed mainly to evaluate the performance of detention-type GI systems with the main focus being pond hydraulic effects and particle capture through gravity settling. In this model, the hydraulic routing is done through weir outflow relationships and the stage-storage relationship can be explicitly entered by the user allowing modeling of irregularly shaped ponds with arbitrary topography. Regarding water quality, WinDetPond can evaluate the capture efficiency of ponds based on the particle size distribution of the incoming suspended solids, with water quality simulated by considering partitioning of contaminants onto particles. Although these models are intended to be applied to individual GI systems as separate entities, and in order to consider more detailed processes affecting performance, their application is restricted to a limited purpose and scope.
General purpose models such as those designed for modeling flow and transport in unsaturated soil or surface water hydraulics and water quality have also been used to study certain aspects of GI performance (Hilten et al., 2008, Massoudieh and Ginn, 2008, Meng et al., 2014). However, these general models, which are typically developed based on a single medium, cannot model the performance of real-world GI practices that are controlled by interactions among many processes in multiple media types. A convenient stand-alone model representation of GI performance is needed: One that models flow and transport in surface ponds, variably saturated soil, aggregate or underdrain layers, overland flow, and pipes, along with having the flexibility of coupling these multiple components.
In this paper, the development of a flexible process-based modeling framework, GI Flexible Model (GIFMod), is described. GIFMod can evaluate the hydrological and water quality performance of a wide range of GI practices with user-defined structure and levels of complexity. GIFMod was developed to allow user flexibility in modeling the following three critical aspects of GI performance: 1) hydraulics, 2) particle/colloid transport, and 3) dissolved and particle-bound reactive transport of contaminants. The flexibility of the hydraulic component allows for flow considerations in different media often seen in stormwater GI practices including ponds, overland flow, saturated and unsaturated porous media, storage layers or structures, pressurized or free-surface flow in pipes as well as evaporation and transpiration. GIFMod also allows users to introduce new media with user-defined head-storage (H-S) and head-flow (H-Q) relationships. The particle/colloid transport module within the GIFMod framework allows the introduction of multiple particle types, each with different transport properties. Particles are considered to be present in different phases including mobile, reversibly deposited, irreversibly deposited or bound to the air-water interface (AWI) while undergoing exchange between these phases. A user can specify the number and nature of the phases that each particle class can be present in as well as the exchange mechanisms/rates between the phases. Particle transport is especially important in predicting the water quality effects of GI practices because particle retention is one of the most important mechanisms for removal of contaminants with high affinity to solid materials. The contaminant reactive transport module allows consideration of multiple reactive components based on user-provided networks and stoichiometric coefficients. Contaminants can undergo sorption-desorption with the soil matrix as well as mobile and immobile particles. Build-up, wash-off, and atmospheric exchange of contaminants can also be considered. This paper summarizes the governing equations for modeling hydraulic, particle transport, and transport/transformation of water quality constituents using the GIFMod framework. The numerical approaches for approximating the equations are also presented as well as methods used to calculate model uncertainty. An overview of the Graphical Unser Interface (GUI) associated with the framework will also be presented. Finally, four demonstration applications of the GIFMod framework—a bioretention system, a permeable pavement system, an infiltration basin and a wet pond—are presented. The source code of the model, the distribution package and a user’s manual with a more detailed description of underlying governing equations including several additional examples can be found on the program website (Massoudieh et al., 2016).
2. Model framework and components
2.1. Hydraulics
A GI system is modeled with GIFMod using a number of “blocks” that are connected using “interfaces” (See Fig. 1 as a general example). Each block represents one spatial feature such as an unsaturated/saturated soil element, pond, manhole, stream segment, among many others. The size of the blocks can be chosen by the user according to the desired resolution of the model. Expressions determining how the flow is computed between the blocks can be specified for each interface.
Fig. 1.
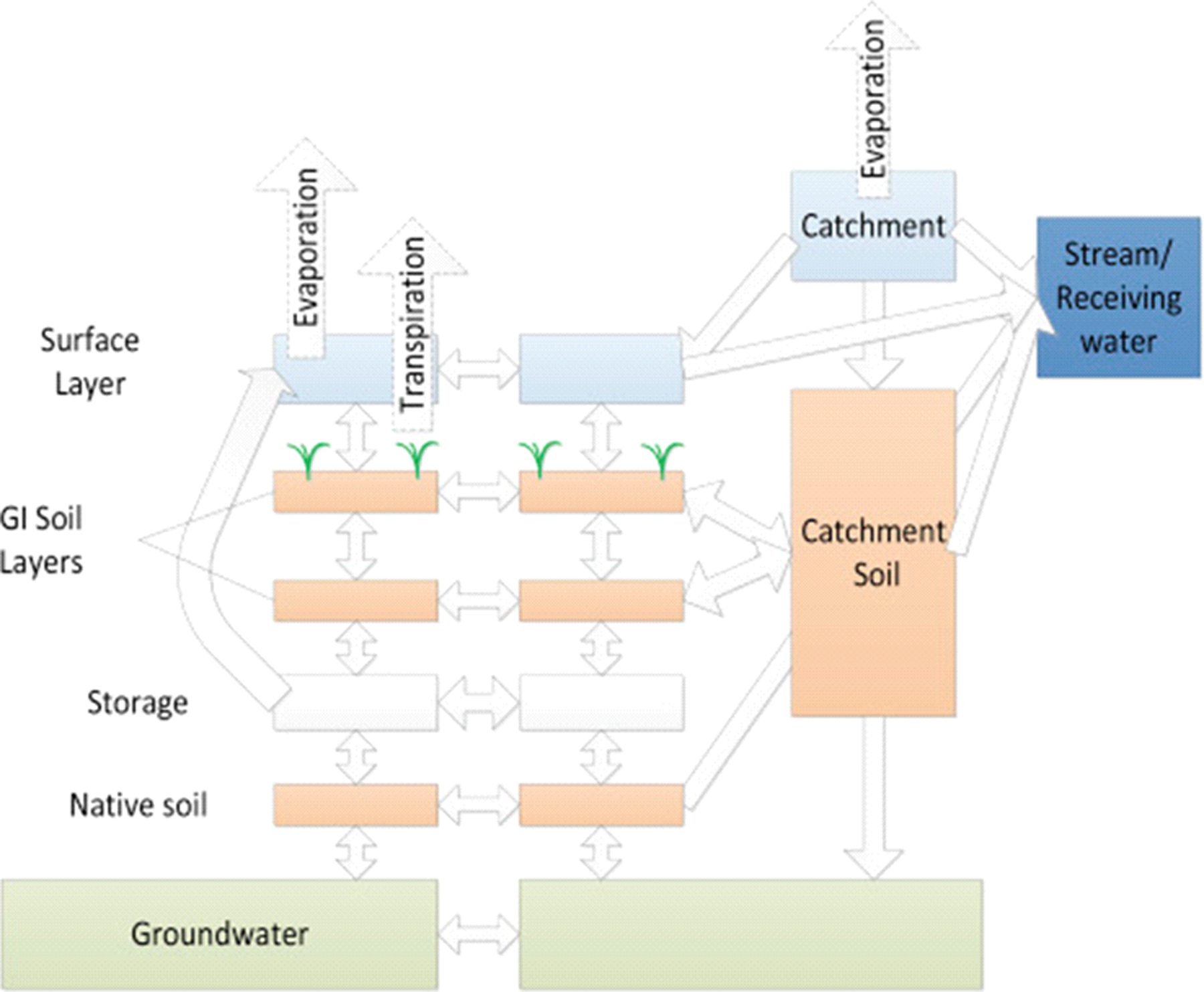
An example depiction of how blocks and connectors can be used to represent a GI system consisting of different components. The boxes represent block and arrows represent connectors. Each block and connector can be assigned governing equations controlling their hydraulic and transport properties.
This expression can be specified by the user or selected from a pre-defined catalog of relationships provided in the software package that includes Richards equation for unsaturated medium, Darcy’s law equations for saturated medium, Hazen-Williams equations for pipes, or Manning/diffusive wave equation for ponds, streams and overland flow. The water balance equation for each block can be written as:
| (1) |
where Si [L3] is the water storage (volume) in block i, Qw,ij [L3/T] is the liquid water flow from block i to block j (Qw,ij=−Qw,ij), nj is the number of neighboring blocks exchanging water with block i, Qev,ij [L3/T] is the water vapor flux from block i to block j, which simplistically is determined using a diffusive term proportional to the void area occupied by the air phase and can be specified to be a function of temperature. QSi,j is source or sink of water flow within the block i due to direct precipitation, external inflow or evapotranspiration [L3/T], and ns is the number of sources/sinks within block i.
A relationship between Q and S is needed to solve the system of ordinary differential equations consisting of Eq. (1) applied to all of the blocks. This is typically done by linking both Q and S to the hydraulic head in the block.
| (2a) |
| (2b) |
| (2c) |
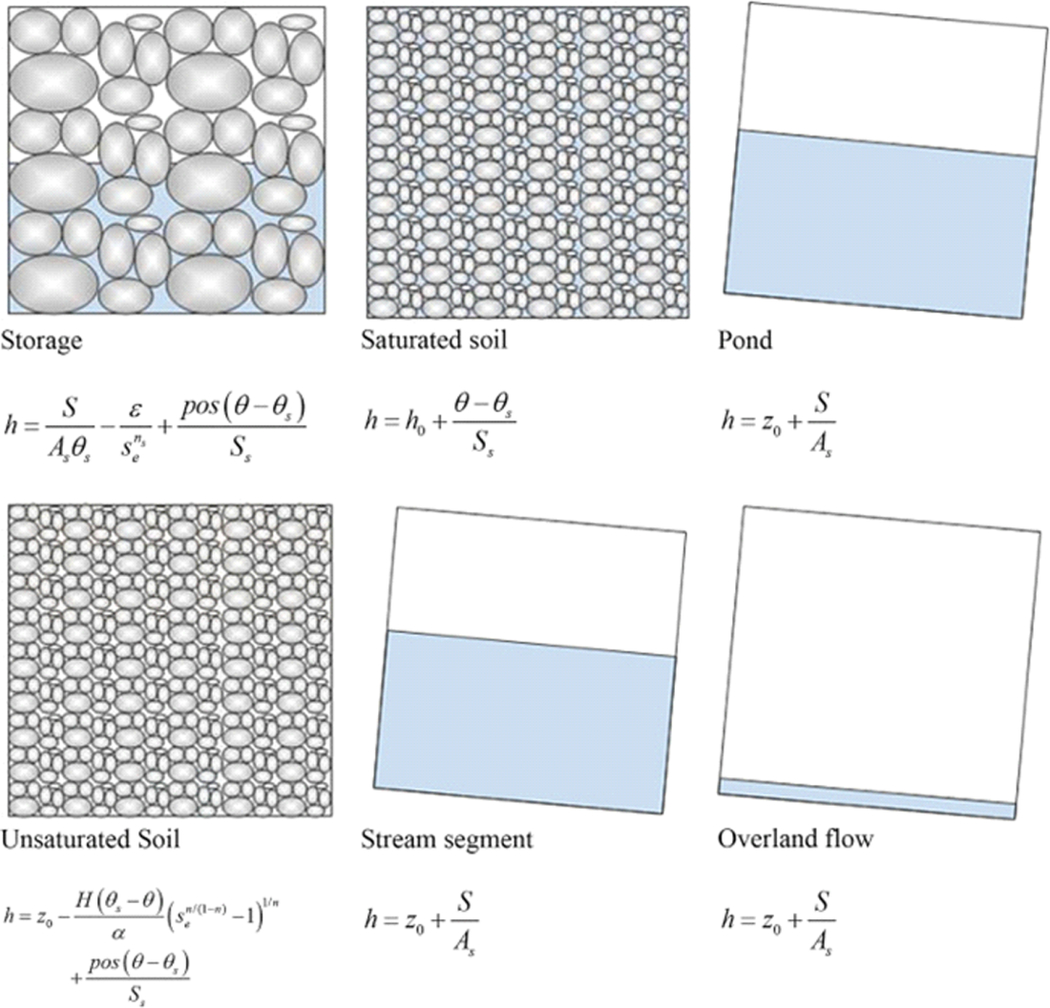
where Θ represents all other physical parameters controlling the H-S and Q-H relationships such as geometrical dimensions, roughness, hydraulic characteristics of the soil, etc. Six generic GI media types including unsaturated and saturated soil, pond, stream, overland flow, and storage are provided with the framework. Other custom media types can be defined by the user by providing the H-S relationship for the blocks and Q-H relationships for the interfaces. It should be noted that the unsaturated soil media type can be chosen to perform under a saturated condition, but when a block is known to be saturated throughout the modeling time series, choosing a saturated block type reduces the computational burden. The H-S relationship and Q-H models for the aforementioned six pre-defined block types are listed in Table 1, Table 2, respectively. In addition to the default (Q-H) relationships shown in Table 2, the user can select from three other default interface types including rating curve, free surface, and pressurized flow in a pipe (via Hazen-Williams equation), and normal flow.
Table 1.
Six default media types implemented in the model and the H-S equations. In the equations h [L] is the hydraulic head, S [L3] is the storage, As[L2] is the surface/bottom area, ε and ns are matrix suction parameters for storage blocks under near dry condition (Brooks and Corey, 1964), se = (θ – θr/(θs − θr) is the effective saturation, n is the Van Genuchten soil retention parameter, Ss[1/L] is specific storage, z0 is the bottom elevation, h0 is the top elevation of the block, H() is the Heaviside function and pos(x) = H(x)x.
|
Table 2.
Default Q-H relationships based on the blocks connected
| Bottom\top | Unsaturated Soil | Pond | Storage | Overlandflow | Saturated Soil | Stream Segment |
|---|---|---|---|---|---|---|
| Unsaturated Soil | VGM* | VGM | VGM | VGM | VGM | VGM |
| Pond | NA** | DWM*** | Darcy | DWM | Darcy | DWM |
| Storage | VGM | Darcy | Darcy | NA | Darcy | Darcy |
| Overland flow | NA | NA | NA | DWM | NA | NA |
| Saturated Soil | VGM | Darcy | Darcy | NA | Darcy | Darcy |
| Stream Segment | NA | DWM | NA | DWM | NA | DWM |
VGM: Van Genuchten-Maulem,
NA: No default Q-H equation is available,
DWM: Diffusive Wave/Manning
One point worth noting is that the use of Richards equation for modeling soil percolation may be excessive for some applications where simpler approaches like Green-Ampt or the SCS curve number method is typically used by practitioners. The Richards equation requires a larger number of parameters and is computationally burdensome. However, due to the block-connector representation of GI systems in GIFMOD, and the continuous nature of simulations, it is not fully compatible with those approaches. So, in the future simplified approaches to represent infiltration/percolation consistent with the block-connector representation as an alternative option will be explored.
For modeling transport (in particular diffusion and dispersion mechanisms), it is important to indicate the relationship between cross-sectional areas of the interfaces and storages in the connected blocks for the blocks with free surface (such as stream, pond, and overland flow as for these blocks the interface area can also be dynamically variable).
| (2d) |
Similar to most other models, the storage variation in interfaces (such as pipes) are not accounted for in the calculations assuming the flow in and out of such interfaces is always equal. This simplification is justified since the storage variation in pipes in GI systems is typically insignificant at the spatial scales it will most often be employed to represent (i.e., less than an entire sewer-shed).
Evapotranspiration can also be modeled using generic evaporation and transpiration models provided in the framework such as the aerodynamic model for evaporation (Chow et al., 2013), Priestly-Taylor model (Priestley and Taylor, 1972) and Penman method (Penman, 1948), and several commonly used root water uptake models including the single crop FAO-56 model (Allen et al., 2005) and the model proposed by Li et al. (2001). In the latter, the functional dependence of the vegetation water stress factors are defined by the user in terms of the field capacity, wilting point moisture and matrix suction. Alternative expressions for calculation of evaporation and transpiration rates can also be introduced by the user. For the sake of brevity, the detailed governing equations of the evaporation model is not provided here but can be found in the GIFMod User’s manual that can be downloaded from the program website (Massoudieh et al., 2016). In addition to the examples provided in this paper several other worked examples can be found at http://gifmod.com/worked-examples/.
2.2. Particle transport
Within the GIFMod framework, the particle transport module allows simulation of multiple classes of particles. Each particle class can be attributed different transport characteristics including settling, resuspension, reversible and irreversible attachment to the solid matrix, entrapment into the air-water interface (AWI) and other user-defined processes. Each particle class can be exchanged between different phases as specified by the user. For example, a particle class can be specified to transfer between mobile aqueous phase and reversibly (or irreversibly) attached phase and the AWI. The general form of the transport equation for particles can be written based on the mass balance of the particles as the following unified equation that encompasses the fate and transport of particles in mobile and immobile phases:
| (3) |
Eq. (3) is a general equation that describes the mass balance of colloid class p in phase l in block i which lumps together the sets of equations representing the mass balance of mobile and immobile colloids (Massoudieh and Ginn, 2007, Massoudieh and Ginn, 2008). In Eq. (3) Γi,l is referred to as the capacity of phase l in block i. For example, in the case of a two-phase colloid transport model with an aqueous phase and a reversibly or irreversibly captured colloidal phase soil, Γi,0=Si or Γi,0=Si+KawSaw where equilibrium entrainment of particles into AWI with an interface area of Saw and equilibrium air-water partition coefficient of Kaw. Also, Γi,1=ρbV when the captured colloidal phase is expressed as colloidal mass per mass of soil matrix or Γi,1=fiV when the attached particles are expressed as mass of particles per surface area of the soil matrix. ρb[M/L3] is the bulk density and fi[L2/L3] is the specific surface area. αl is an indicator representing the mobility of the particle phase l(0 when phase l is immobile and 1 when it is mobile). Gp,l,i is the concentration of particles of class p in phase l and block i,nj represent the number of connectors attached to block i, pos(x)=xH(x) where H is the Heaviside function, vs,p,ij is the settling velocity of particle class p projected on the direction of interface ij,Aij is the area of the interface ij, nlp is the number of phases that particles of class p can be present in, Kl,l′ is particle mass transfer rate from phase l to l′ which can be a function of concentration in the destination phase (due to blocking), flow velocity, or other factors and Dp,ij is the dispersion coefficient of particles in class p in interface ij which can be a function of flow velocity and other factors. The user interface allows one to input Kl,l′ and Dp,ij either as constant numbers or as functions of other physical state variables such as velocity.
There are three pre-defined models for particle transport within the GIFMod framework. These include a single phase model with only mobile colloids, a dual phase model with mobile and reversibly or irreversibly attached phases, and a three-phase model including mobile, reversibly attached and irreversibly attached phases. In the three-phase model, the user must indicate the fraction of particles undergoing irreversible deposition. The interaction of colloids with AWI can be activated by indicating a partitioning coefficient with respect to the AWI. Sedimentation can be activated by indicating a settling velocity for particle types. The user interface of the GIFMod framework provides the list of model parameters for which values are needed to be supplied by the user depending on the type of model selected for the particle transport.
2.3. Coupled particle-bound and/or dissolved reactive transport
A coupled particle-bound and dissolved reactive transport module can solve the transport phenomena as a series of multiple reactive species both in the aqueous phase or as sorbed to mobile particles. The adsorption and desorption both to the immobile soil matrix and immobile particles can be accounted for by the model. Most models used for GI modeling in the past ignore the fact that some contaminants can move not only in dissolved phase but as bound to mobile particles. Colloid/Particle-facilitated transport can play an important role particularly in the transport of constituents with high affinity to solid material. This is particularly important in the modeling of GI systems when sedimentation results in removal of contaminants due to the settling of the particle-bound contaminants. Processes such as atmospheric exchange and pollutant build-up on soil or other surfaces can also be considered via user-defined expressions indicating their flux into each block. The mass balance equation for a contaminant in any of these phases can be represented by the following unified equation:
| 4 |
where Γi,p,l [dimension depends on the phase] is the capacity of particle class p in phase l in block i(p = 0 is reserved for the aqueous phase and p = −1 indicates the constituent fraction sorbed to the solid matrix), Cp,l,i,k is the concentration of chemical constituent k adsorbed to phase l of particle class p in block i, αp,l is the mobility indicator for phase l of particle type p(i.e., αp,l = 1 for mobile phases and αp,l = 0 for immobile phases), Ds,i,j,k is the dispersion/diffusion coefficient of chemical constituent k, G′p,l,i is the concentration of particulate class p in phase l for p ≠ 0 and equal to 1 for p = 0 (aqueous phase), vc,p,ij,k is the settling velocity of chemical constituent k projected in the direction of ij connector which is used when settlable constituents such as algae, biomass, or particulate organic matter are considered, κp,p′ is the direct mass exchange rate between particle type p and p′, ϕk,p is the partition coefficient of constituent k with respect to particle size class p which is equal to 1 for aqueous phase (p = 0), Rr is the rate of reaction/process number r and ψr,k is the stoichiometric constant of constituent k in process number r, which is negative when constituent k is used as a result of the process. ξp,l,i,k is the source of constituent k as bound to particle class p in the aqueous phase or adsorbed to the soil matrix (p = 0), which is determined using a user defined expression. Typically, the elements of the matrix κp,p′ are zero except for the case when either p or p′ is zero (i.e. one of the phases is the aqueous phase) as the constituent mass transfer typically occurs through the aqueous phase. βp,l,j is a switch that determines whether a water sink (such as evaporation or transpiration) also results in uptake of a particular constituent. The code allows expressing both Rr and ψr,k as a function of other constituent concentrations and some given process parameters through external input files. The reaction rate expressions and stoichiometric constants can be entered as a Petersen matrix (Russell, 2006) into the user interface of the GIFMod framework (see section 4.2.3 of the GIFMod user’s manual for an example showing how to enter a Petersen matrix). Bio-kinetic reaction parameters can be specified to depend on temperature through the simplified Arrhenius equation (i.e. kT = kT0θT−T0) by providing the temperature correction factor, θ for each parameter. The temperature is provided by the user as a time-series representing the temperature variation over the period of simulation. It should be noted that although expressing the transport governing equations for particles and other constituents as a single unified equation may make its comprehension difficult, this form is consistent with how the code is implemented. It is also worth noting that Eq. (4) represents the most general set of processes that can be included into the model. It does not mean that all these terms are active in every GI model. The reason for using a unified form that expresses the mass balance for mobile and immobile phases into a single equation is to enhance the flexibility of the model.
2.4. Numerical solution
Although several different adaptive solvers have been proposed and successfully used in water resources models (Clark and Kavetski, 2010, Kavetski et al., 2001, Kavetski et al., 2002), the use of such algorithms in GI modeling have been limited. Given that GI systems undergo a variety of conditions in terms of being wet or dry, an adaptive time-step that can use larger time-steps during less dynamically changing conditions and vice-versa can substantially lower the computational time. In GIFMod, a semi-implicit scheme based on a damped Newton-Raphson (NR) method with an adaptive time-step and a numerical evaluation of the Jacobian matrix is used to solve the hydraulic, particle transport, and water quality equations. The adaptive time-step automatically increases the solver time step-size under numerical conditions where the system of ordinary differential equations (ODEs) are less stiff (e.g., under dry conditions) and reduces the time step-size during the times when the stiffness of the ODE system is high (e.g., wet conditions). This adaptation process lowers the number of computations that occur during dry periods and in between rain events where the hydraulic movement of water is minimal; therefore, the adaptive time-step implementation is a computationally efficient approach. By moving all the terms to the right hand side in Eqs. (1), (3), (4), they all can be written in the general form:
| (5) |
Applying Euler’s approximation and Crank-Nicholson time weighting with non-equal weighting, the discretized form of Eq. (5) can be written as:
| (6) |
where X is the vector of all state variables, the superscript indicates the time at which X will be evaluated and ω is the time weighting factor. F is the residual vector and the goal at each time-step is to find the Xt+Δt that results in F = 0. Solving Eq. (6) using NR method requires evaluating the Jacobian matrix J = ∂F (Xt+Δt)/∂Xt numerically, which can be computationally intensive. Therefore, an approach was adopted to reuse a Jacobian matrix as long as it is possible until its use is not economical in terms of the NR method convergence. For this purpose, the NR equation is modified as:
| (7) |
where JJ is the Jacobian matrix calculated at a previous time-step that is being reused and ΔtJ is the time-step size at the time the Jacobian matrix has been calculated and Δtt is the current time step. λ is a damping coefficient which is initially set to 1 and is decreased by a factor of 0.5 if the error norm increases in an iteration. Subscripts i and I + 1 indicate the NR iteration counter. The iterations continue until the norm of the residual is below a given threshold . To save computational time, the inverse of the Jacobian matrix, (JJ)−1 is stored in the memory. The adaptive time step algorithm works based on limiting the number of NR iterations to achieve convergence. At each time step, the time step size is either increased, decreased or remains unchanged based on the number of iterations required in the previous time step:
| (8) |
where NI is the number of iterations to reach convergence at the previous time step, NImin and NImax are numerical iteration thresholds and γ is the time-step expansion factor which can be adjusted by the user. If the NR does not converge with a given time-step size, the algorithm keeps reducing the time-step until the convergence is achieved. The optimal values of the solver control parameters NImin,NImax and γ are problem-dependent, a default set of these values are provided and used by the program, but when desired the user can specify another set.
When modeling GI systems, some of the blocks often become completely dry or stay dry for a long period (e.g., a dry pond, stream, storage or catchment components). This results in a stiff system of equations and requires very small time-step sizes. To avoid this problem, a new method is implemented that is based on changing the state variables from storage to the outflow from a block when the block is entering a zero storage condition. When the calculated storage in a block is calculated as a negative number, the calculation is redone by setting and modifying the discretized form of Eq. (1) as:
| (9) |
where υi is the flow correction factor, which reduces the outflows in order to satisfy the dryness condition at time t+Δt. For a dry block, υi is treated as a state variable to be solved among other storages using the NR approach. The dryness condition will be maintained until the υi is calculated to be larger than 1, which indicates the initiation of a wet stage for the block, and at this time the mass balance equation for the block is switched to the normal (wet) form.
2.5. Inverse modeling and uncertainty analysis
The GIFMod framework is equipped with a built-in deterministic and stochastic inverse modeling capability. The deterministic inverse modeling is performed by using a hybrid genetic algorithm (Massoudieh et al., 2008) to find the parameters maximizing the likelihood of the observed data. The stochastic parameter estimation algorithm is based on Bayesian Inference and Markov-Chain Monte Carlo (MCMC) (Gamerman and Lopes, 2006). The framework allows for any of the parameters in the model to be treated as unknowns that can then be estimated by providing their prior distributions. The user can choose among normal, log-normal and uniform prior distributions.
The observed data can be specified to represent any of the state variables in the model including hydraulic (i.e., flow rates, head, cross-sectional areas), particle and/or constituent concentrations in each block. As is typically done in Bayesian inference, the error is defined as a quantity encompassing measurement error, model structural error, and all other errors resulting from the uncertainties associated with the external forcing (input data) such as weather data, inflow rates and concentrations. For the sake of brevity, the details of parameter estimation algorithms available in GIFMod are not provided here. For detailed description and examples, the user can refer to Chapter 5 of the GIFMod user’s manual (Massoudieh et al., 2016).
2.6. Graphical user interface
The GIFMod framework is written using C++ programming language. Two alternative versions of the program are available: A console version that receives the input files as text files and a user-friendly graphical user interface (GUI) version that allows building, running and post-processing using “drag and drop” features. A screen-shot of the graphical user interface is presented in Fig. 2. The installation package for GIFMod can be downloaded from http://www.gifmod.com/download/. A detailed user’s manual, input files for the demonstration cases presented in this paper in addition to a number of simple examples have also been made available as part of the installation package.
Fig. 2.
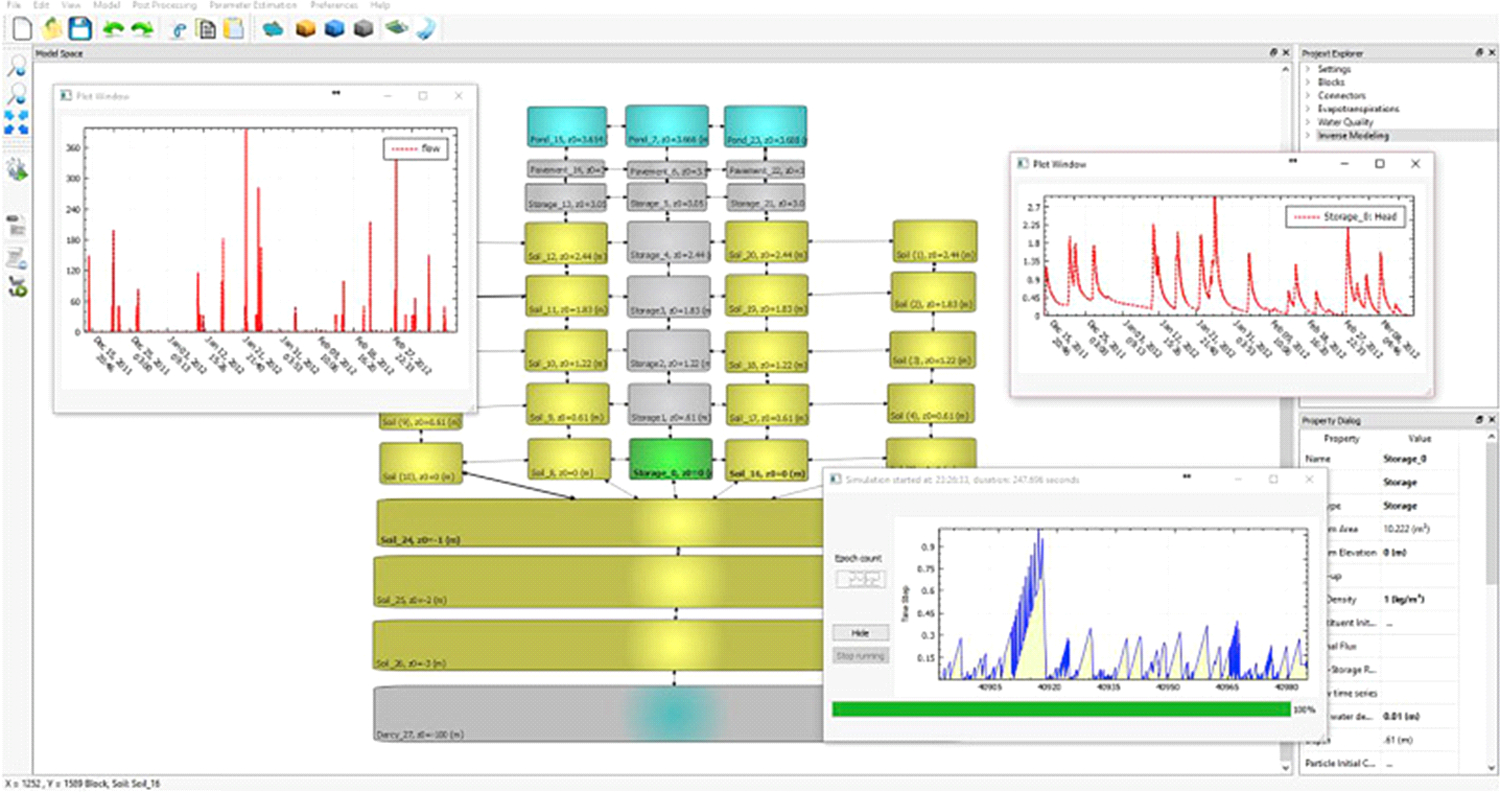
A snapshot of the GUI version of the GIFMod with the model representation for the permeable pavement example.
3. Demonstrating GIFMod applications
Four use cases are provided subsequently that demonstrate how the GIFMod framework can be used to model the performance of different types of GI systems. The intention of these demonstrations is to showcase the potential of the modeling framework rather than to provide rigorous analysis of the processes represented in each. Therefore, for the sake of the brevity, the level of detail provided for the complex GI treatment mechanisms at play in each case is kept to a minimum. More detailed applications of the model to specific GI systems, along with detailed results from deterministic and stochastic inverse modeling approaches will be the topics of future publications.
3.1. Application example 1: a bioretention system comprised of two rain gardens
3.1.1. Site description
The first demonstration applies the GIFMod framework to explain the performance of a bioretention GI system located in Cincinnati, OH. The system consists of two rain gardens built in series to mitigate stormwater volume and pollutant loading to a combined sewer network. The two rain gardens are connected by an underdrain pipe which carries runoff from the aggregate storage zone of the upper cell to the surface of the lower cell. The system was originally designed for a catchment of 94,500 ft2 (Dumouchelle and Darner, 2014). The catchment area is composed of an upland wooded area, a parking lot, and a grassed sloped area below the parking lot, as shown in Fig. 3. The runoff produced from the wooded area and the parking lot is collected at a catch basin within the parking lot and is diverted to the upper rain garden through an underground 12” polyvinyl chloride (PVC) pipe (solid arrow in Fig. 3a). This pipe carries the main inflow to the upper rain garden. In our model conceptualization, the contribution of direct runoff from the sloped grassed area to the upper rain garden is considered minor for storms with average intensity as confirmed by field observations.
Fig. 3.
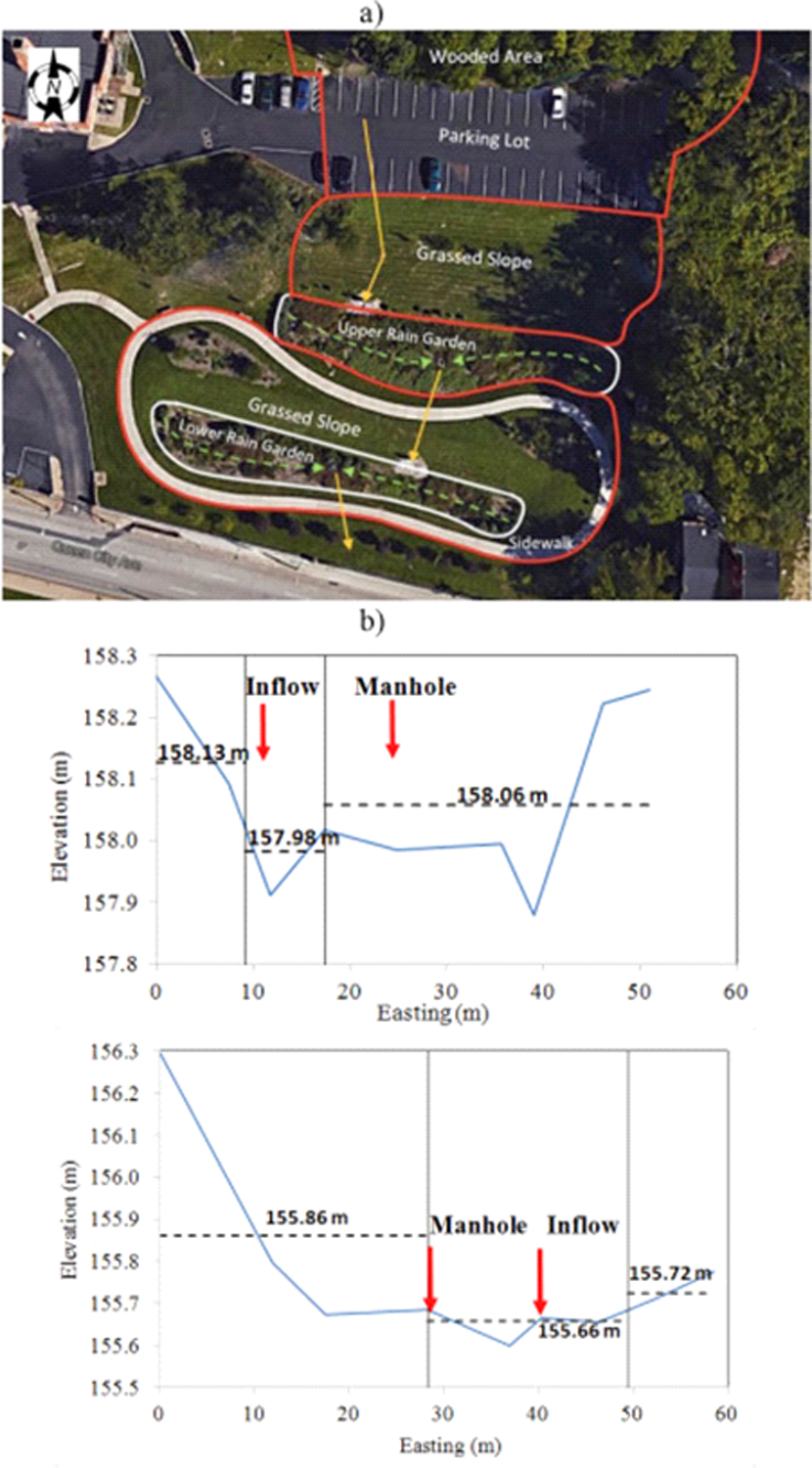
a) Aerial image of St. Francis Apartment rain gardens and b) longitudinal surface elevation profiles of the upper (left) and the lower (right) rain gardens. The dash lines represent the average surface elevation of the rain garden.
The inflow to the upper rain garden infiltrates through at least 24 inches (0.61 m) of engineered soil (a mixture of sand, soil, and compost) laying above 15 inches (0.38 m) of gravel aggregate, from where it percolates to the native soil underneath. The excess water at the aggregate layer is collected by a porous 6″ PVC pipe situated at the top of this layer (dashed-line arrows in Fig. 3a) and is diverted to a manhole. The excess water from the ponding at the rain garden surface is also collected by the same manhole. The manhole diverts excess water to the lower rain garden using a 12″ PVC pipe (solid arrow in Fig. 3a). The contribution of the direct runoff to the lower rain garden from the sloped grassed area and the sidewalk between upper and lower rain gardens is considered negligible. The lower rain garden was designed with specifications similar to the upper rain garden, as shown in Table 3. The excess water from the lower rain garden is finally discharged to the city’s combined sewer system.
Table 3.
Design specifications of the St. Francis rain gardens (Cincinnati, OH). Source (Dumouchelle and Darner, 2014): and design maps.
| Media | Parameter | Value | ||||
|---|---|---|---|---|---|---|
| Pond | Area | Upper: 3816 ft2 (354.52 m2) + Lower: 3241 ft2 (301.10 m2) | ||||
| Input PVC Culvert | Diameter | 12 inches (0.30 m) | ||||
| Substrate Soil Layer | Texture | Engineered Soil | ||||
| Minimum Depth | 24 inches (0.61 m) | |||||
| Saturated Hydraulic conductivity (Ks) | 3 m/day | |||||
| Van Genuchten parameter α | 3.0 m−1 | |||||
| Van Genuchten parameter n | 2.94 | |||||
| Residual moisture content ϑr | 0.1 | |||||
| Saturated moisture content ϑs | 0.35 | |||||
| Native soil | Saturated Hydraulic conductivity (Ks) | 0.0045 m/day | ||||
| Van Genuchten parameter α | 0.8 m−1 | |||||
| Van Genuchten parameter n | 1.09 | |||||
| Residual moisture content ϑr | 0.068 | |||||
| Saturated moisture content ϑs | 0.38 | |||||
| Underdrain Aggregate Layer | Depth | 15 inches (0.38 m) | ||||
| Underdrain PVC Pipe |
Diameter | 6 inches (0.15 m) | ||||
| Slope | 0.50% | |||||
| Parameter | ||||||
| Geom. Parameters: | Upper Rain Garden | Lower Rain Garden | ||||
| Western | Middle | Eastern | Western | Middle | Eastern | |
| Surface Elevation (m) | 158.13 | 157.98 | 158.06 | 155.86 | 155.66 | 155.72 |
| Soil Depth (m) | 0.76 | 0.61 | 0.69 | 0.81 | 0.61 | 0.67 |
| Surface Area (m2) | 61.67 | 85.71 | 207.14 | 182.14 | 98.00 | 20.97 |
| Easting Length (m) | 9.17 | 8.24 | 33.57 | 28.29 | 21.18 | 9.06 |
The horizontal cross-sectional topography of the rain gardens is displayed in Fig. 3b as obtained from a surveying field-trip in March 2015. The cross-sectional profile of the lower rain garden represents the width-averaged surface elevation. The stormwater flows in and out of each of the bioretention cells has been monitored continuously using a pressure transducer V-Notch weir set-up for 3 yrs. The evapotranspiration was estimated at the site based on standardized reference evapotranspiration equation (Walter et al., 2000) which was input directly (as an external time-series) into the model. The required climatic data for this evapotranspiration equation are air temperature, humidity, solar radiation, and wind speed. These data were continuously collected on site using a Campbell Scientific ET107 station (ET 107 Instruction Manual) (Campbell Scientific, 2014). The precipitation at the site was also measured using a tipping bucket rain gage. Details of the monitoring program can be found in Dumouchelle and Darner (2014).
3.1.2. Bioretention model setup
Each rain garden was divided into three vertical compartments each containing a surface water component, a soil column represented by multiple layers (blocks), a storage layer (block), and a single soil layer (block) at the bottom representing the native soil. The horizontal segmentation was added to the model to account for the irregular surface topography of the rain gardens (Fig. 3b) and the possibility of short-circuiting. That is, the middle section of each rain garden receives the inflow and has the lowest surface elevation. Hence, more ponding of water and infiltration is expected to occur here. Unless there is a high volume of storm runoff, the two end surface water blocks remain unsaturated.
Based on the horizontal segmentation, the average surface elevations and areas of the three compartments were modeled as presented in Table 3. Based on this simplified surface topography, the inflow initially enters the middle column of the upper rain garden. The flows from each surface water component to the adjacent ones are computed with Manning’s equation based on the diffusive wave approximation, meaning that the difference between the hydraulic heads is used to compute the flow rate (Table 2). The water flow in the lower cell is similar to the upper one with the exception that the effluent from the upper cell is the main inflow into the lower cell.
Fig. 4 shows the GIFMod model representation of the system. To better represent the moisture distribution in the unsaturated soil layer, each soil column was vertically discretized into five layers. The five layers were chosen since they adequately captured the dynamics of the moisture variation measured in time (Dumouchelle and Darner, 2014).
Fig. 4.
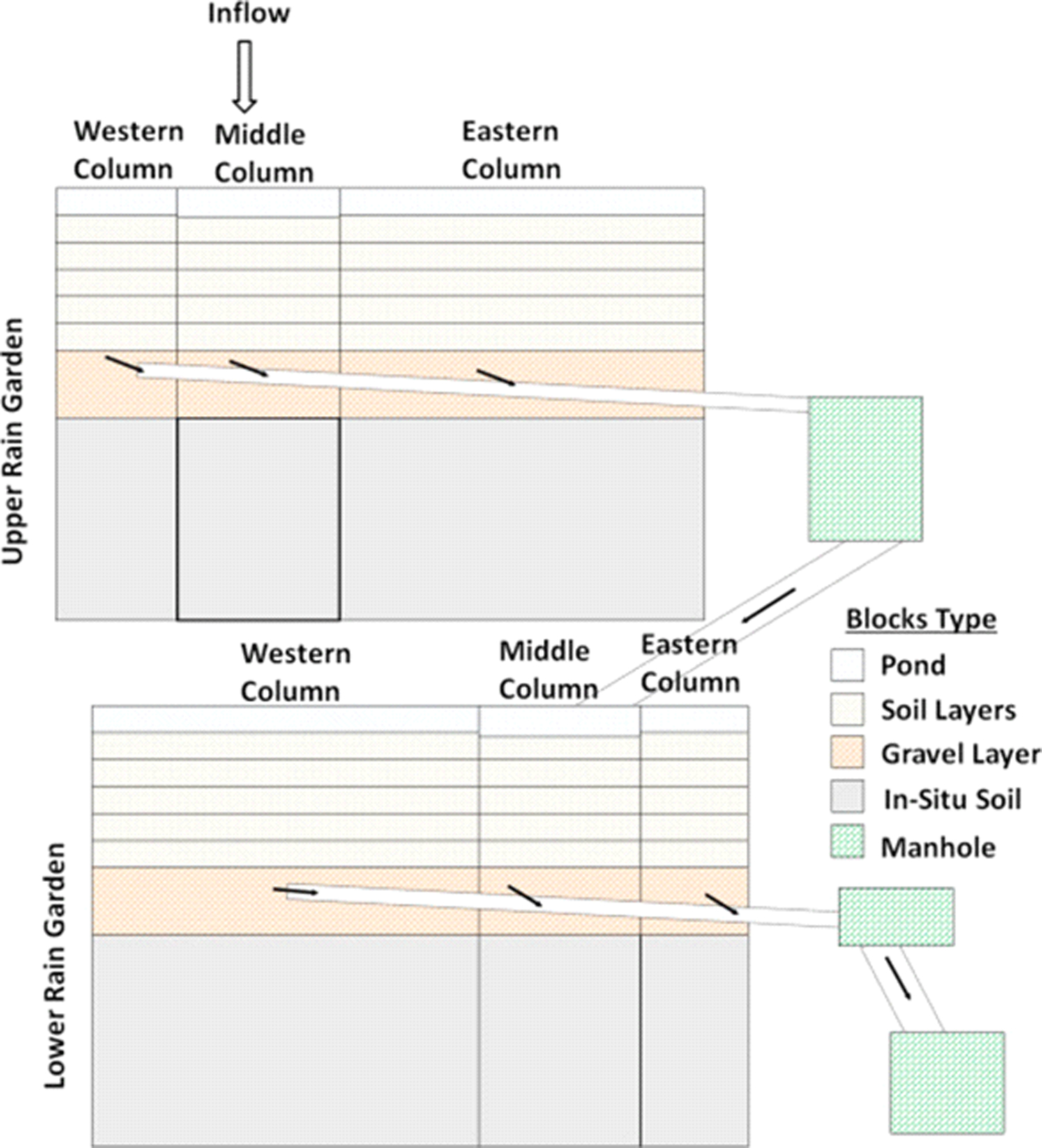
Block-Connector representation of the bioretention system.
The proper definition of the connectors and their governing equations are critical because they control the water transport in the system. The surface Manning’s roughness coefficient used to compute flow rates between the surface pond blocks was set to 0.2 s m−1/3 where the friction head is calculated based on the slope of the water surface. The value of the Manning’s roughness coefficient was consistent with calibrated values for a vegetated surface according to Krebs et al. (2014). However, the travel time from surface pond to surface pond is substantially shorter than the time-scale of other processes, including infiltration; this value has little effect on the final hydrological outcomes. The flow relationships for the connectors between soil layer blocks were based on the Mualem-van Genuchten relationship (Mualem, 1976, Van Genuchten, 1980) with the parameter values listed in Table 4. The flow between the gravel layer blocks were based on the Darcy equation with K = 50 m/d, which results in a quick horizontal equilibrium among the three aggregate blocks. The hydraulic conductivity of the native soil was obtained as K = 0.0045 m/d through manual calibration. The flow rate in pipe connectors was obtained using the Hazen-Williams equation (Chaudhry, 2013) with PVC roughness coefficient of 150.
Table 4.
Model parameters used in the porous pavement model.
| Hydraulic conductivity (Ks) of the pavement | 80 m/d |
| Hydraulic conductivity (Ks) of aggregates in storage zone | 80 m/d |
| Soil horizontal saturated hydraulic conductivity | 0.9 m/d |
| Soil vertical saturated hydraulic conductivity | 0.012 m/d |
| Soil van Genuchten parameters α | 3 m−1 |
| Soil van Genuchten parameters λ | 0.5 |
| Soil van Genuchten parameters n | 1.28 |
| Soil Saturated moisture content θs | 0.4 |
| Soil Residual moisture content θr | 0.1 |
3.1.3. Model results
The model was run for the period March 27 and June 30, 2014. The comparison of the outflows from the upper and lower rain gardens with the observations are displayed in Fig. 5. The modeled stormwater outflows follow the observed trend.
Fig. 5.
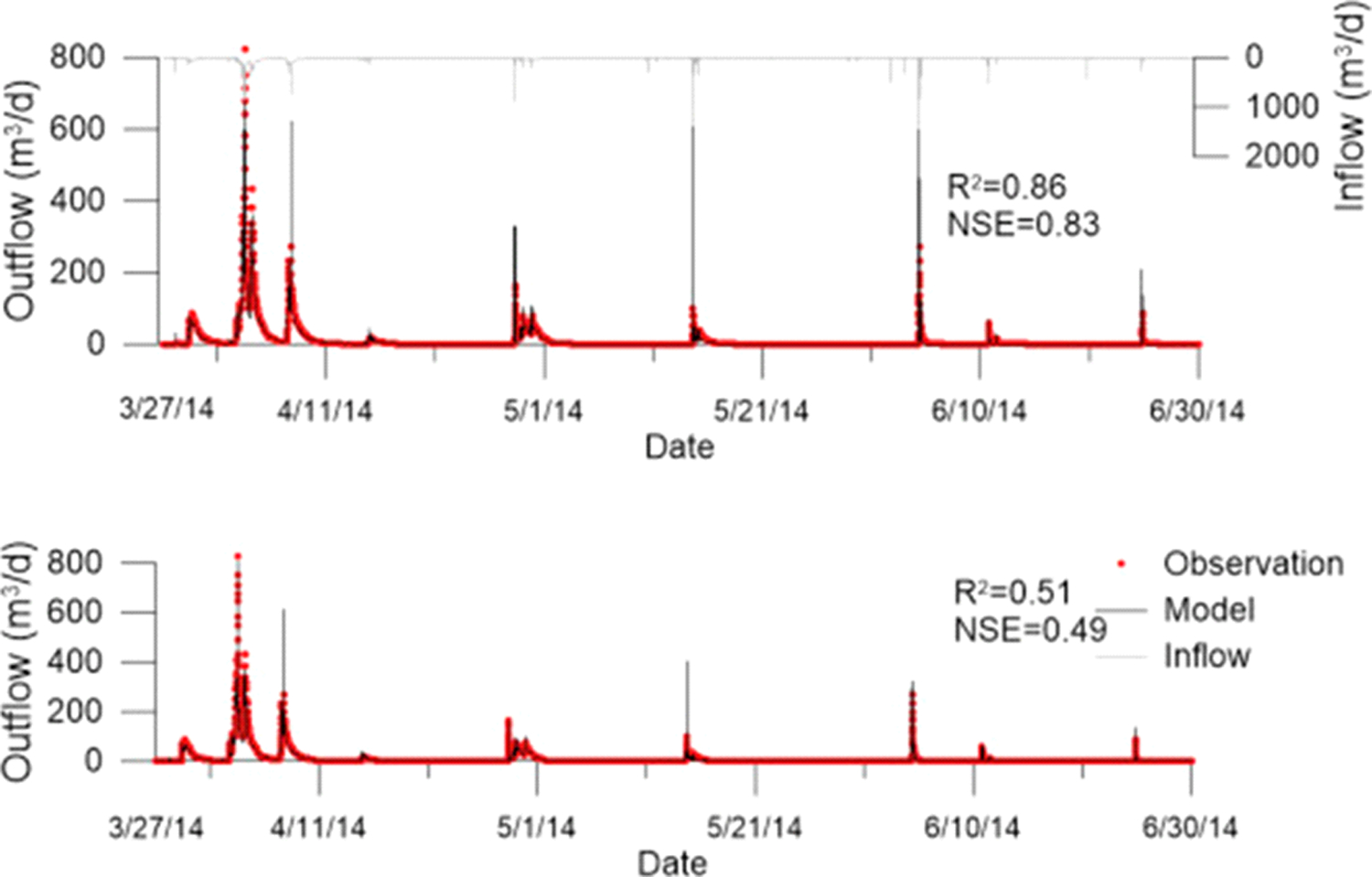
Comparison of the predicted outflow from the upper rain garden (top) and from the lower rain garden (bottom) with the observations. The inflow to the upper rain garden is also included.
The model outflow predictions are better for the upper rain garden with a coefficient of determination R2 = 0.86 and Nash-Sutcliffe efficiency coefficient NSE = 0.83 than the lower rain garden with R2 = 0.51 and NSE = 0.49. A rigorous systematic calibration and validation using another portion of the dataset is needed to obtain a set of more reliable calibrated model parameters or the uncertainty associated with the parameters; however, this is beyond the scope of this demonstration.
3.2. Application example 2: a porous pavement system
The second demonstration is the application of GIFMod to simulate the hydraulic processes within a porous pavement system installed in Louisville, Kentucky. The detailed description of the porous pavement system is provided by Lee et al. (2014).
Briefly, the porous pavement system was designed to receive runoff from a drainage area of 882 m2 that consisted of pervious surfaces (48.6% or 428.7 m2) and impervious surfaces (51.4% or 453.4 m2). The latter is mainly composed of paved roads (71.4%) and sidewalks (28.6%). The porous pavement itself is 16.76 m long (along the street) by 2.44 m wide. The slope of the surface of the pavement is 1.95% and 2.25% in the longitudinal direction and lateral directions, respectively. The underdrain soil texture is made of a gravel layer with a thickness of 0.46 m and a gravel trench with a thickness of 3.05 m. A schematic of the porous pavement cross section and the GIFMod representation are shown in Fig. 6. The gravel is surrounded by a homogeneous native soil, which is characterized as clay loam. The hydraulic head of the accumulated water at the bottom of the pavement was monitored for over 400 days (Lee et al., 2014).
Fig. 6.
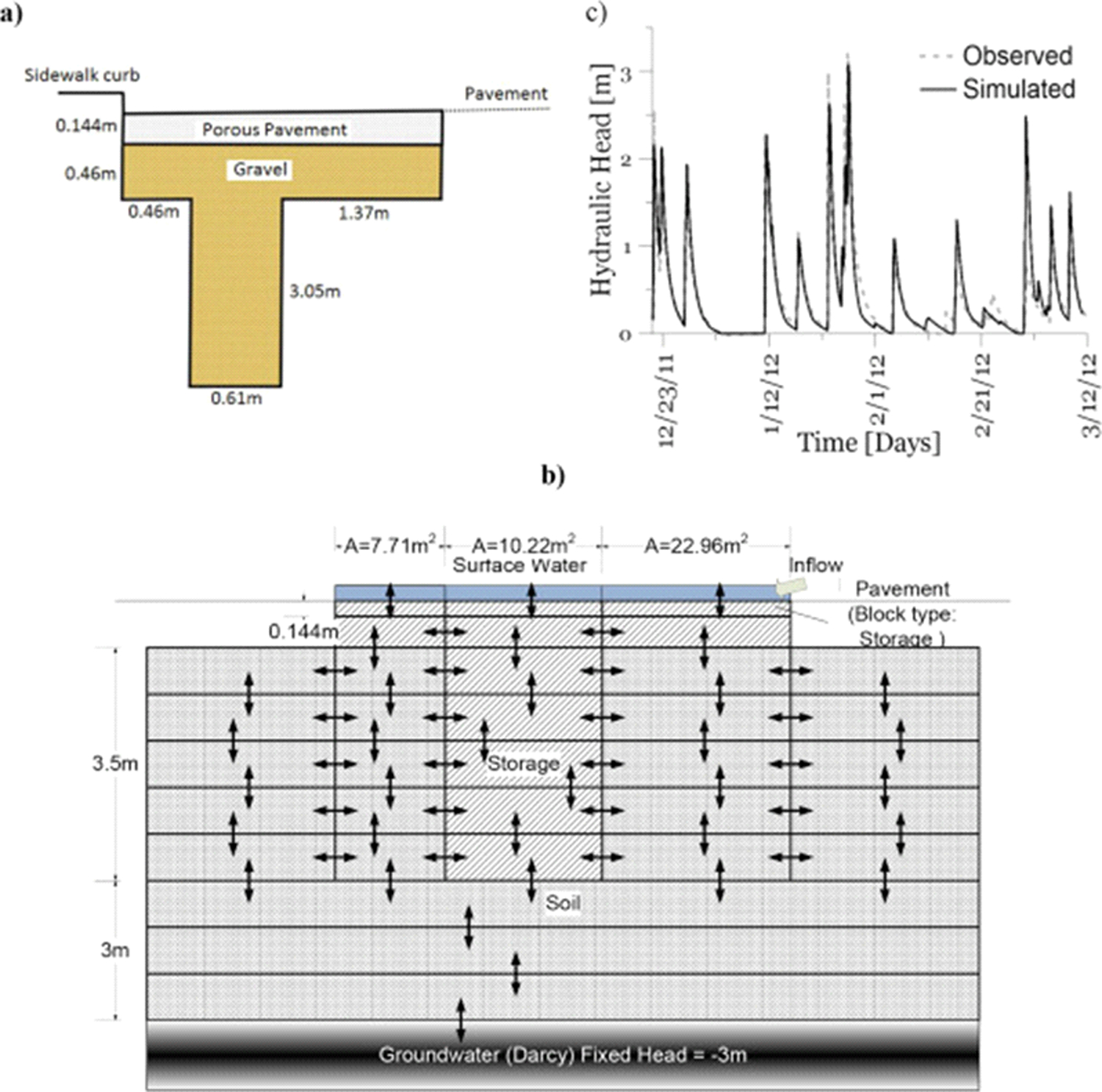
a) Cross sectional scheme of Adams Street porous pavement and b) the designed conceptual model. All the dimensions are in meter and are reported from Lee at al. (2014). c) Modeled vs. measured hydraulic head at the bottom of the storage layer during the course of simulation.
Since the length of the pavement system is substantially larger than its width (Fig. 6b), it was assumed that the hydraulic processes are uniform with respect to the longitudinal axis, and, therefore, 2 vertical dimensions (2D) would be an adequate representation of the system.
The time series for the runoff inflow through the surface block in the road side of the system was estimated roughly by multiplying the time series of the rainfall records by the total impervious area (i.e., 453.4 m2) and assuming a zero time of concentration. The runoff flow was then considered as an inflow to the system through the surface block on the road side of the system (Fig. 6b). In order to account for the lateral exfiltration into the surrounding natural soils, additional blocks were configured. Fig. 6c shows the modeled results versus measured water depth in the aggregate storage layer. The manually-calibrated parameter values used to obtain the match are given in Table 4.
3.3. Application example 3: the effect of a hypothetical infiltration basin/pond on groundwater recharge and quality
The third application models the flow and water quality underneath a hypothetical infiltration basin. Processes effecting water quality that are explicitly modeled include organic matter decomposition, oxygen uptake, nitrification, denitrification, colloid-transport of three classes of particles with different transport characteristics, and the transport of a hypothetical pollutant (zinc) with high sorption affinity to soil and colloidal particles. The infiltration basin is assumed to have a circular surface area with a radius of 5 m and the modeled domain is assumed to be a cylinder with a 25 m radius (Fig. 7a). The depth of the groundwater table is assumed to be 1.5 m below the surface which is assumed to not be affected by the recharge from the infiltration pond (i.e., groundwater mounding is ignored and the hydraulic head of the groundwater is assumed to be constant). The assigned values to model parameters are listed in Table 5. A multi-component reactive transport model considering transport and transformation of nitrate (NO3−), ammonia (NH4), Dissolved Oxygen (DO) and Dissolved Organic Matter (DOM) as well as multi-disperse particles (represented using three classes) and a hypothetical conservative pollutant (representing zinc) with a sorption affinity to solids is considered. As a simplifying assumption, the NO3−, NH4+, DO and DOM are assumed not to interact with the solid matrix. The reaction network controlling the transformation of NO3−, NH4+, DO and DOM is presented in Table 6. The reaction network is simplified here for the purpose of demonstrating the capability of the GIFMod framework. GIFMod allows for a number of reacting species and transformation processes to be modeled simultaneously that is only limited by computational resources. It should be noted that organic nitrogen is assumed to be part of DOM that is released as NH3 when organic matter mineralization occurs. An alternative approach would be to consider organic nitrogen as a separate pool from DOM. A hypothetical inflow is shown over a period of 30 d (Fig. 7b). To keep the temporal variation of flow rate realistic and the concentrations of the constituents reasonable, the inflow concentrations are adopted from another study where pollutographs were actually measured. The aeration rate in the pond and in the soil, are respectively modeled using the following expressions
| (10a) |
| (10b) |
where kA and ksA are aeration rate coefficients for surface water and soil respectively, O2,s is the saturated DO concentration, θs is the saturated moisture content, and θ is the moisture content. In effect, it is assumed that the air in the vadose zone is in a state of instantaneous equilibrium with the atmosphere. Because of the short period of simulation and the expectation of high atmospheric relative humidity during rain events, we expect the evapotranspiration effect from the surrounding soils to be negligible. Thus, to keep the model simple, the evaporation from the surrounding soils was neglected. For computing particle transport and particle-facilitated transport, the TSS entering the pond in the inflow is assumed to be uniformly distributed into three particle size-bins or classes with different settling velocities and attachment rate coefficients to the soil matrix. The adsorption and desorption characteristics of zinc on the suspended particles and to the soil matrix is assumed to be similar across particle types. In the inflow, it is assumed that zinc concentration is already in equilibrium with the incoming particles. Fig. 8 shows the variation in the percolation flow rate, concentrations of the constituents and colloids underneath the infiltration basin at the groundwater table and in the pond. Based on these results, the main model representing the transport of zinc to the groundwater is the colloid-bound model of transport. A more comprehensive presentation of the outcome of the model can be found in the supplementary information section of this paper that contains videos showing the spatiotemporal dynamics of moisture, water quality constituents, and colloid and colloid-bound heavy metals. The videos are made using MATLAB based on the model outputs and represent the dynamics of moisture and water quality constituents in the vadose zone underneath the infiltration basin.
Fig. 7.
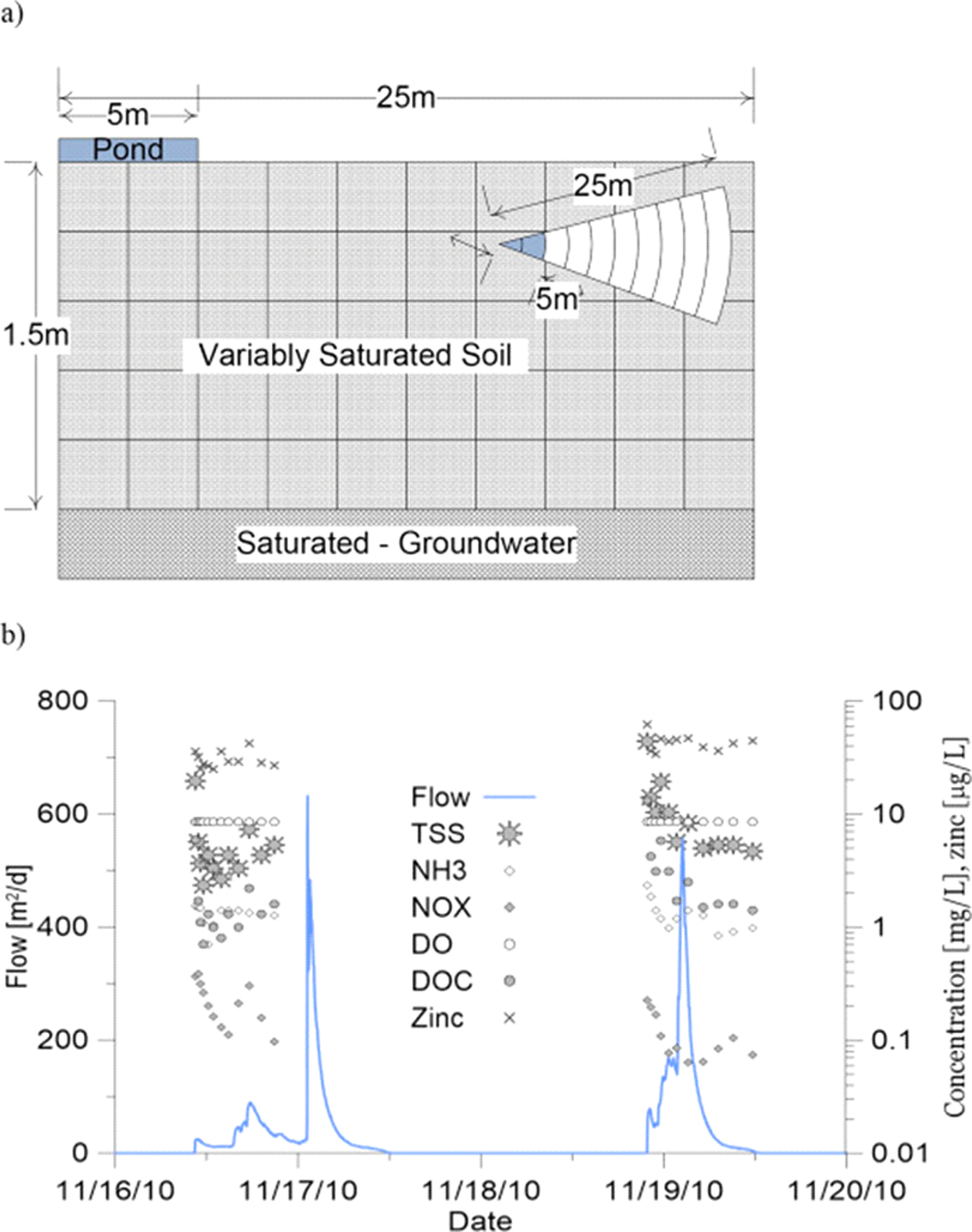
a) The schematic of the 2-D vertical representation of the infiltration basin model. The head of the groundwater table is assumed to be fixed and the domain is assumed axially symmetrical around the center of the pond (left edge of the figure). b) Influent flow rate and characteristics into the pond.
Table 5.
Model parameters used in the infiltration basin model. For definitions of the colloid transport parameters see Massoudieh and Ginn (2007).
| Horizontal Saturated Hydraulic Conductivity | 10 m/d |
| Vertical Saturated Hydraulic Conductivity | 1.1 m/d |
| Soil van Genuchten parameters α | 3.5 m−1 |
| Soil van Genuchten parameters λ | 0.5 |
| Soil van Genuchten parameters n | 3.19 |
| Soil Saturated moisture content θs | 0.37 |
| Soil Residual moisture content θr | 0.058 |
| Diffusion/Dispersion coefficient for all constituents | 0.005 m2/d |
| Maximum aerobic decomposition rate of DOM (μH) | 5 mg BOD/L.d |
| Maximum nitrification rate (μN) | 0.5 mg N/L.d |
| Maximum anoxic decomposition rate of DOM (μdn) | 3 mg BOD/L.d |
| DO half saturation constant for aerobic decay (Ko) | 1 mg BOD/L |
| DO half saturation constant for anoxic decay (Kon) | 1 mg BOD/L |
| Nitrate Half saturation constant for denitrification (Kdn) | 10 mg/L-N |
| Ammonia Half saturation constant for nitrification (Kn) | 0.1 mg/L-N |
| DOM half saturation constant (Ks) | 50 mg-L-BOD |
| Ammonia content of DOM (ηon) | 0.219 mg NH3-N/mg BOD |
| Aeration rate constant in soil (ksa) | 100 d−1 |
| Partitioning coefficient to air/water interface (kair) for colloid all colloid types | 10 water volume/air volume |
| Irreversible attachment fraction | 0.2 |
| Specific surface area | 104 m2/m3 |
| Effective attachment efficiency (ηα) for colloid type I, II, and III | 5 × 10−4, 5 × 10−5, 5 × 10−6 |
| Release rate coefficient (kdet) | 0.1 |
| Settling velocity (m/d) | 0.1, 0.01, 0.001 |
| Sorption rate coefficient of Zn to all solids | 0.6 d−1 |
| Partition coefficient of Zn to all solids (soil and colloids) | 1000 L/kg |
Table 6.
Reaction network used as the reactive transport component for the infiltration and wet pond model. The grey symbols in the reaction expressions represent constituents that are not explicitly considered in the model.
| Process | Reaction | Rate Expression |
|---|---|---|
| Aerobic decomposition of organic matter | ||
| Nitrification | ||
| Denitrification |
Fig. 8.
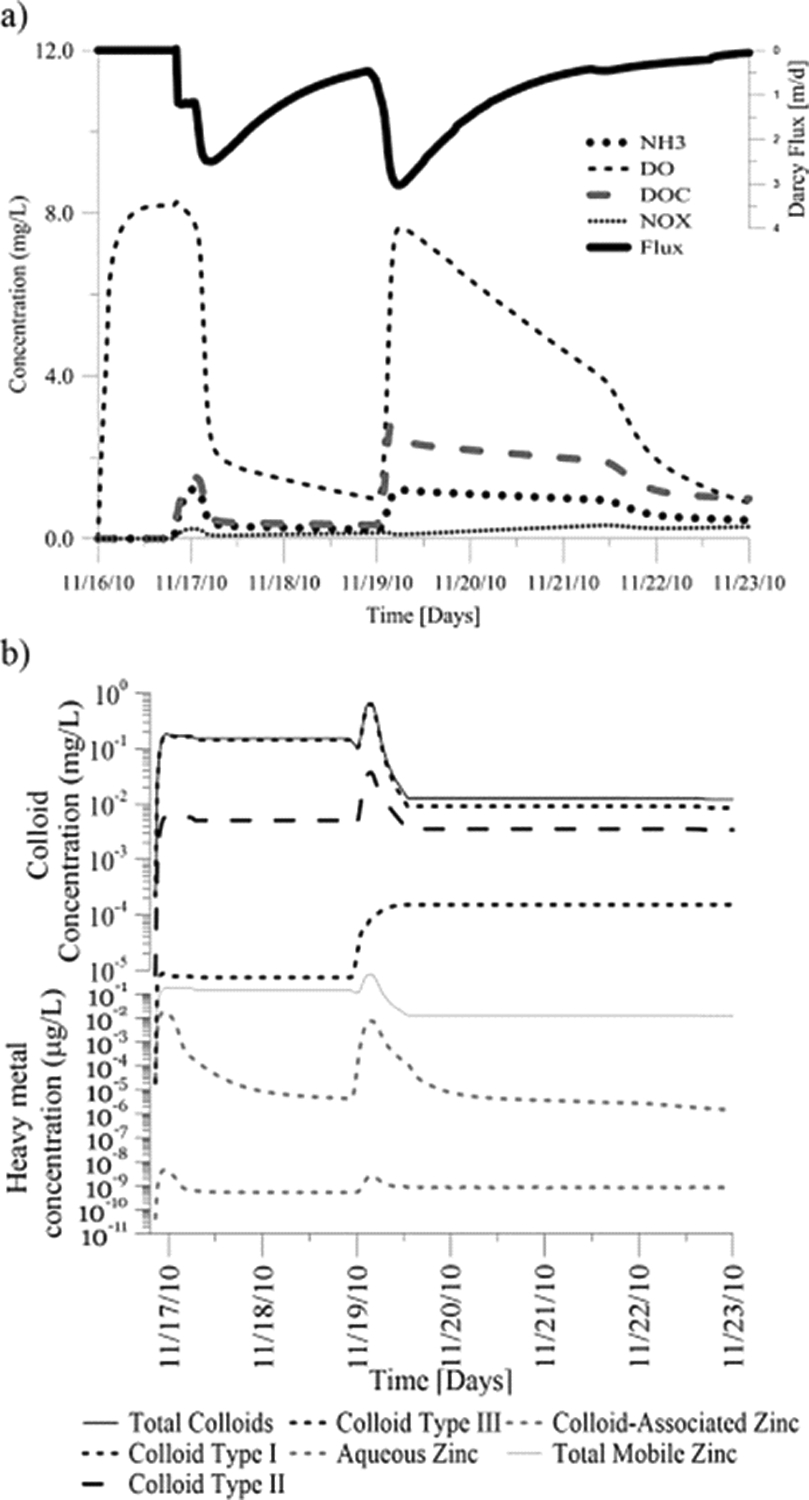
a) The variation of percolation flow rate, and constituent concentrations at the groundwater table underneath the infiltration basin. b) Concentration of mobile colloid and aqueous, colloidal and total heavy metal at the groundwater table underneath the infiltration basin. The spatiotemporal variation of concentrations and moisture content in the soil underneath and adjacent to the infiltration pond can be seen in the supplementary information.
3.4. Application example 4: evaluating the effect of a one-dimensional wet-pond on water quality of the discharge to a stream
The fourth and final application demonstrates how the hydraulic and water quality constituent cycling in a wet pond could be modeled using GIFMod. Although the example is hypothetical, the geometry of the wet pond (Fig. 9) is adopted from Comings et al. (2000). The wet-pond is modeled as a one-dimensional stream where routing is unidirectional between pond blocks and benthic sediments are considered to have a significant effect on denitrification due to a predominantly anoxic condition in the sediments. A Manning’s roughness coefficient of 0.035 s m−1/3 was considered for the channel. The depth of the active sediment layer is considered to be 10 cm and the diffusion rate coefficient through the water-sediment boundary layer is considered to be 0.0017 m2/d, which was assumed to encompass the effect of bioturbation and molecular diffusion. The same reaction network of Example 3 is considered for this case. To simplify the model, algae and plant growth and decay are not explicitly considered in the model. Instead, the production of organic matter due to plant and algae decay and the hydrolysis of particulate organic matter to dissolved (readily biodegradable) organic matter are taken into account by adding a source of DOM in the overlying waters and sediments. The biogeochemical transformation parameters are the same as in Example 3 (Table 5) with the addition of a DOM production rate of 0.03 g-Biological Oxygen Demand (BOD) m−2d−1 in the overlying water and 3 g-BODm−2d−1 in the sediments were used. Fig. 10 shows the temporal variation of water quality constituents considered in the model in pond blocks 1, 3 and 6 of the wet-pond both in the overlying water and in the sediments. The model output allows for the contemplation of effects on DO as well as NOx, and seems to be almost completely depleted in the sediments due to the high concentration of organic matter and some denitrification occurs in the sediments as well as in the water column.
Fig. 9.
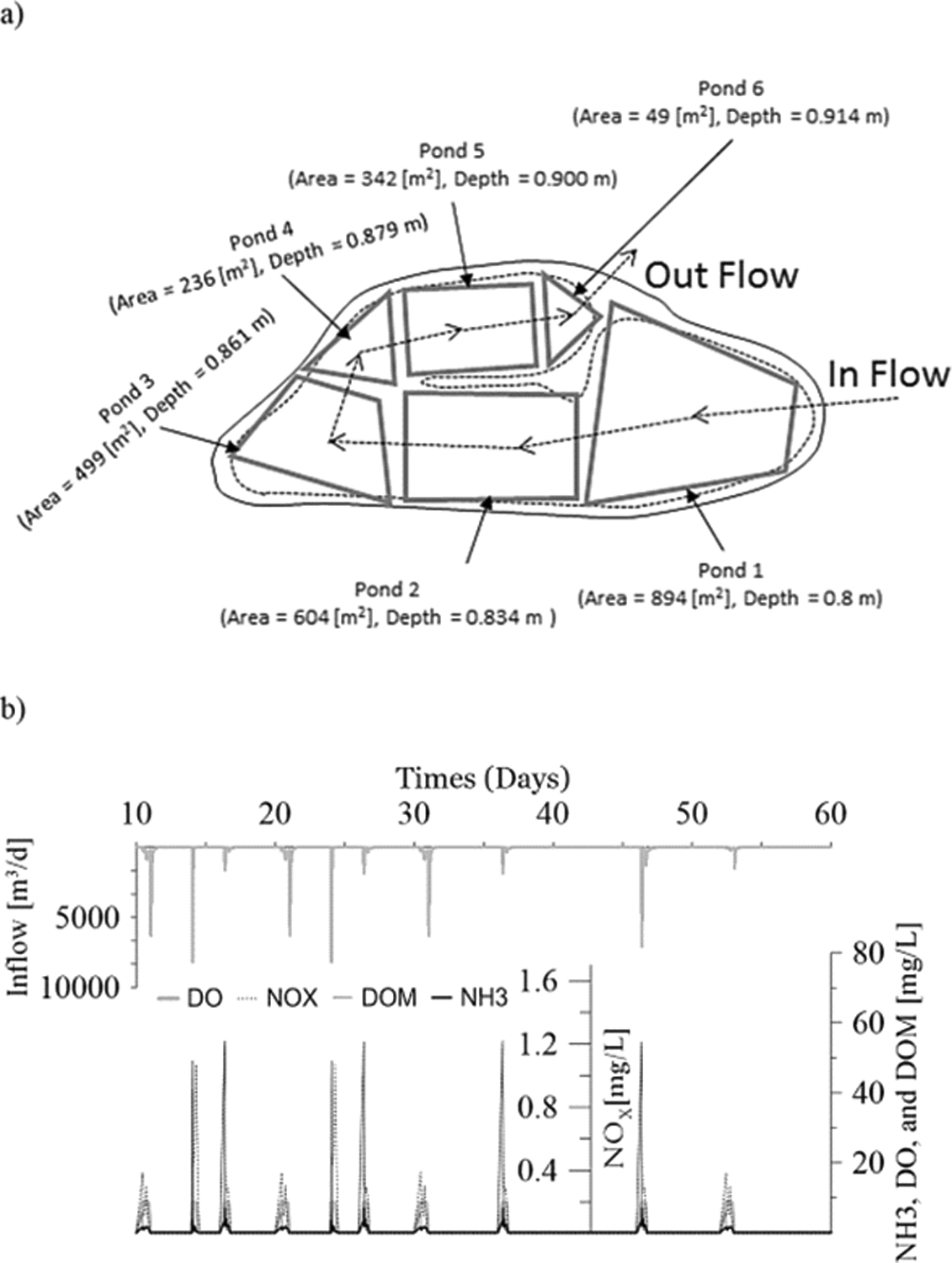
a) The diagram of the hypothetical water quality wetland, adopted from (Comings et al., 2000). b) Hypothetical inflow rate and characteristics into the wet pond.
Fig. 10.
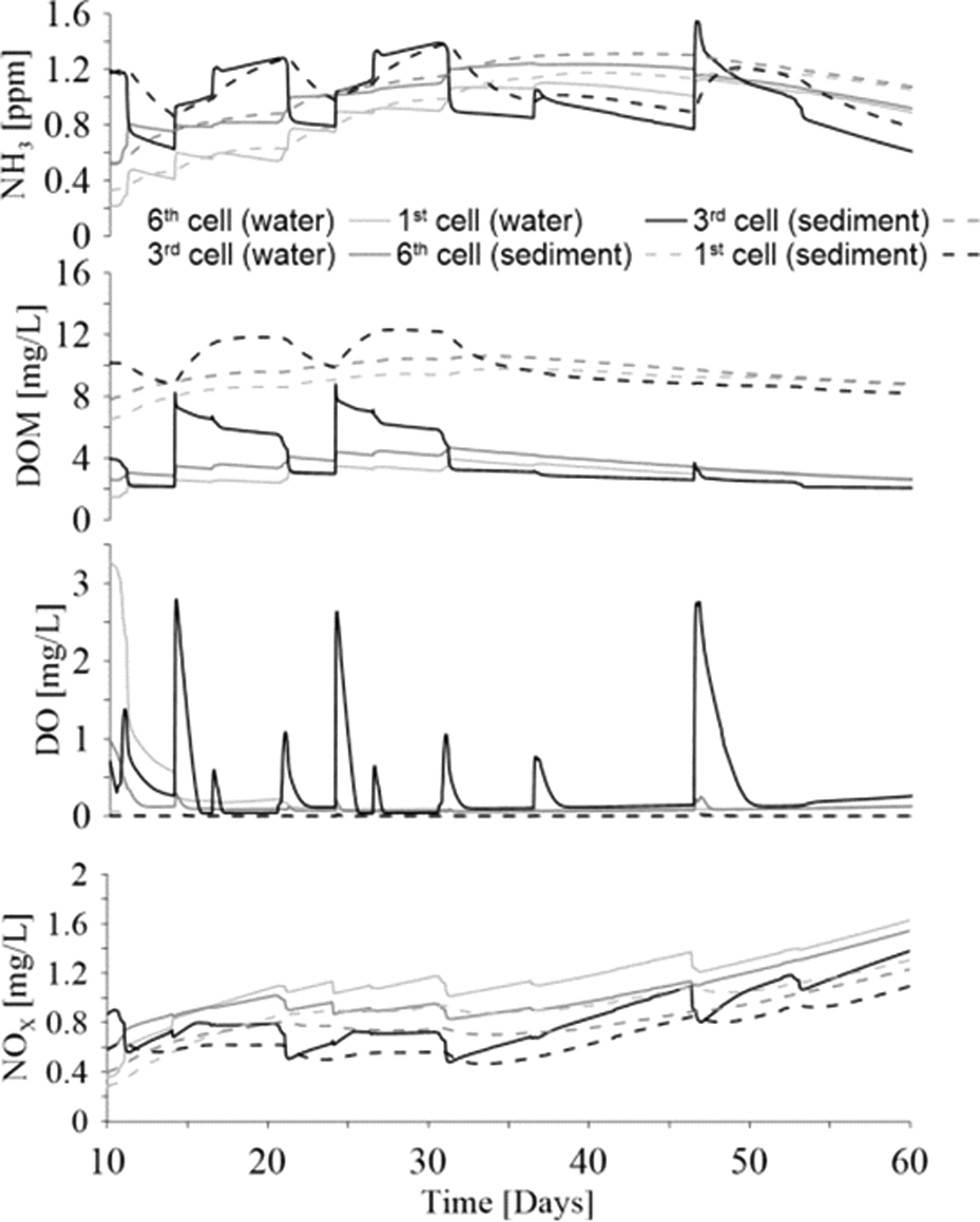
Modeled temporal variation of concentration of water quality constituents in segments (blocks), 1, 3 and 6 of the wet-pond.
4. Conclusions
A flexible modeling framework for constructing models of urban stormwater green infrastructure was presented in this paper. The framework uses an implicit Newton-Raphson algorithm to solve equations representing the hydraulic, particle transport (dissolve/particle-associated), and transformation of water quality constituents. The performance of the framework relies on an adaptive time-step solver that dynamically adjusts the time step-size during the simulation to preserve convergence and reduce the run-time. This feature is particularly important since GI systems experience time varying process dynamics such as long dry cycles and short wet periods. A user interface was also developed for the framework that couples the numerical solver with a GUI for conceptualization of the layout of GI systems and displaying the modeling outputs. The developed modeling tool, called GIFMod, is different from most of the existing tools used for modeling GI performance: First, GIFMod accommodates flexibility in the representation of the GI system, and, therefore, can be used to model specific real-world GI designs that are more often characterized by uniqueness of place issues difficult to represent adequately in tools that generalize GI construction. Second, a wide variety of hydraulic and pollution transport processes can be considered in the different media types commonly present in GI systems such as surface ponds, saturated and unsaturated subsurface layers, aggregate storage zones, and pipes. Third, GIFMod uses the aforementioned computationally efficient adaptive time step approach. Finally, the GIFMod framework includes the built-in capability to perform both deterministic and stochastic inverse modeling. Four demonstration cases were presented showing applications for a variety of common-type GI practices but unique system implementations including a bioretention-based system, a permeable pavement system, a hypothetical infiltration basin, and a hypothetical water quality wet-pond interacting with groundwater. These demonstrations showcase the ability of the GIFMod framework to effectively represent various processes affecting the flow as well as pollution transport and transformation within GI systems. GIFMod can be used in conjunction with existing watershed models such as SWAT (Arnold et al., 1998) and SWMM (Rossman, 2004, Rossman, 2015). For instance, the output hydrographs and/or pollutographs from these models could be used as input to GIFMod to consider the processes effecting performance in more detail. Similarly, GIFMod could be used to estimate effective parameters used by the watershed models such as water capture rate or pollutant removal rates based on the more detailed hydraulic and fate/transport relationships available to the modeler in GIFMod. These values would be used to parameterize the more simplified representation of GI in the watershed models.
The flexibility and expandability of the GIFMod framework means that the capabilities of the model will grow as multiple users model their unique GI projects. It is the vision of the model developers that the utility of GIFMod will grow with collaborative use.
Supplementary Material
Highlights.
A flexible modeling tool for analysis of green infrastructure performance is introduced.
The model allows users to conceptualize green infrastructure with desired complexity level.
The tools allows representing hydraulics, particle and constituent transport within GIs.
The applicability of the model is demonstrated using four case studies.
Acknowledgements
The authors wish to thank the helpful reviews of Drs. Joong Lee, President, Center of Urban Green Infrastructure Engineering, Milford, OH and Bradley Barnhardt, U.S.EPA, Office of Research and Development, National Health Effects and Ecology Laboratory, Western Ecology Division, Corvalis, OR. These reviews improved the manuscript significantly. Mr. Scott Jacobs, U.S. EPA, Office of Research and Development, National Risk Management Laboratory, Cincinnati, OH supplied the time series data used for the St. Francis rain gardens bioretention demonstration example, and helped with the surveying effort required for the model set-up. While model development and reporting was funded partially under contract of the U.S. EPA, Office of Research and Development, the data interpretation, ideas, and opinions made herein about modeling capabilities and performance are those of the authors alone and, therefore, do not reflect the policies of the U.S. EPA.
Footnotes
Software availability: The distribution package for GIFMod including additional examples and a detailed user’s manual are available at www.gifmod.com. The source code and installation package of the program can also be downloaded from the US EPA Github repository at: https://github.com/USEPA/GIFMod.
References
- Ackerman D, Stein ED 2008. Evaluating the effectiveness of best management practices using dynamic modeling J. Environ. Eng, 134 (8) (2008), pp. 628–639 [Google Scholar]
- Ahiablame LM, Engel BA, Chaubey I 2012. Representation and evaluation of low impact development practices with L-THIA-LID: an example for site planning Environ. Pollut, 1 (2) (2012), p. 1 [Google Scholar]
- Allen RG, Pereira LS, Smith M, Raes D, Wright JL 2005. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions J. Irrigation Drainage Eng, 131 (1) (2005), pp. 2–13 [Google Scholar]
- Arnold JG, Srinivasan R, Muttiah RS, Williams JR 1998. Large Area Hydrologic Modeling and Assessment Part I: Model Development 1 Wiley Online Library; (1998) [Google Scholar]
- Bicknell B, Imhoff J, Kittle J Jr., Jobes T, Donigian A Jr. 2001. Hydrological Simulation Program-FORTRAN, Version 12, User’s Manual US Environmental Protection Agency, National Exposure Research Laboratory, Athens, GA: (2001) (in cooperation with US Geological Survey. Water Resources Division, Reston, VA) [Google Scholar]
- Brooks RH, Corey AT 1964. Hydraulic properties of porous media and their relation to drainage design Trans. ASAE, 7 (1) (1964), pp. 26–0028 [Google Scholar]
- Brown R, Skaggs RW, Hunt W 2013. Calibration and validation of DRAINMOD to model bioretention hydrology J. Hydrology, 486 (2013), pp. 430–442 [Google Scholar]
- Campbell Scientific, 2014. Instruction Manual for ET107 Weather Station (2014)
- Chaudhry MH 2013. Applied Hydraulic Transients Springer; New York: (2013) [Google Scholar]
- Chow V, Maidment D, Mays L 2013. Applied Hydrology (second ed.), McGraw-Hill Companies,Incorporated; (2013) [Google Scholar]
- Clark MP, Kavetski D 2010. Ancient numerical daemons of conceptual hydrological modeling: 1. Fidelity and efficiency of time stepping schemes Water Resour. Res, 46 (2010) [Google Scholar]
- Comings KJ, Booth DB, Horner RR 2000. Storm water pollutant removal by two wet ponds in Bellevue, Washington J. Environ. Eng, 126 (4) (2000), pp. 321–330 [Google Scholar]
- Dickson DW, Chadwick CB, Arnold CL 2011. National LID Atlas: a collaborative online database of innovative stormwater management practices Mar. Technol. Soc. J, 45 (2) (2011), pp. 59–64 [Google Scholar]
- Dumouchelle DH, Darner RA 2014. Visualization of Soil-moisture Change in Response to Precipitation within Two Rain Gardens in Ohio (US Geological Survey; ) (2014) [Google Scholar]
- Dussaillant A, Cuevas A, Potter K 2005. Raingardens for stormwater infiltration and focused groundwater recharge: simulations for different world climates Water Sci. Technol. Water Supply, 5 (3–4) (2005), pp. 173–179 [Google Scholar]
- Dussaillant AR, Wu CH, Potter KW 2004. Richards equation model of a rain garden J. Hydrologic Eng, 9 (3) (2004), pp. 219–225 [Google Scholar]
- Elliott A, Trowsdale S 2007. A review of models for low impact urban stormwater drainage Environ. Model. Softw, 22 (3) (2007), pp. 394–405 [Google Scholar]
- Gamerman D, Lopes HF 2006. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference (second ed.), Taylor & Francis; (2006) [Google Scholar]
- Green WH, Ampt G 1911. Studies on soil phyics J. Agric. Sci, 4 (01) (1911), pp. 1–24 [Google Scholar]
- He Z, Davis AP 2010. Process modeling of storm-water flow in a bioretention cell J. Irrigation Drainage Eng, 137 (3) (2010), pp. 121–131 [Google Scholar]
- Hilten RN, Lawrence TM, Tollner EW 2008. Modeling stormwater runoff from green roofs with HYDRUS-1D J. Hydrology, 358 (3) (2008), pp. 288–293 [Google Scholar]
- Kavetski D, Binning P, Sloan SW 2001. Adaptive time stepping and error control in a mass conservative numerical solution of the mixed form of Richards equation Adv. Water Resour, 24 (6) (2001), pp. 595–605 [Google Scholar]
- Kavetski D, Binning P, Sloan SW 2002. Adaptive backward Euler time stepping with truncation error control for numerical modelling of unsaturated fluid flow Int. J. Numer. Methods Eng, 53 (6) (2002), pp. 1301–1322 [Google Scholar]
- Krebs G, Kokkonen T, Valtanen M, Setälä H, Koivusalo H 2014. Spatial resolution considerations for urban hydrological modelling J. Hydrology, 512 (2014), pp. 482–497 [Google Scholar]
- Lee JG, Borst M, Brown RA, Rossman L, Simon MA 2014. Modeling the hydrologic processes of a permeable pavement system J. Hydrologic Eng, 20 (5) (2014), p. 04014070 http://ascelibrary.org/doi/abs/10.1061/(ASCE)HE.1943-5584.0001088 [Google Scholar]
- Li K, De Jong R, Boisvert J, 2001. 2001 Comparison of Root-water-uptake Models, Sustaining the Global Farm: Selected Papers from the 10th Int. Soil Conservation Organization Meeting, pp. 1112–1117.
- Lim KJ, Engel BA, Kim Y, Bhaduri B, Harbor J 1999. Development of the Long Term Hydrologic Impact Assessment (LTHIA) www Systems Sustaining the Global Farm-Selected papers from the 10th International Soil Conservation Organization Meeting (1999), pp. 1018–1023 [Google Scholar]
- Liu J, Lucas W, Chan I, She N, Wu L 2015. Innovative Design of the LID Facilities of Congdu Ecological Grange International Low Impact Development Conference 2015@ sLID: It Works in All Climates and Soils ASCE (2015), pp. 331–341 [Google Scholar]
- Liu J, Sample DJ, Bell C, Guan Y 2014. Review and research needs of bioretention used for the treatment of urban stormwater Water, 6 (4) (2014), pp. 1069–1099 [Google Scholar]
- Massoudieh A, Aflaki S, Panguluri S 2016. User’s Manual for Green Infrastructure Flexible Model (GIFMod) (2016)
- Massoudieh A, Ginn TR 2007. Modeling colloid-facilitated transport of multi-species contaminants in unsaturated porous media J. Contam. hydrology, 92 (3) (2007), pp. 162–183 [DOI] [PubMed] [Google Scholar]
- Massoudieh A, Ginn TR 2008. Modeling colloid-enhanced contaminant transport in stormwater infiltration basin best management practices Vadose Zone J., 7 (4) (2008), pp. 1261–1268 [Google Scholar]
- Massoudieh A, Mathew A, Ginn TR 2008. Column and batch reactive transport experiment parameter estimation using a genetic algorithm Comput. Geosciences, 34 (1) (2008), pp. 24–34 [Google Scholar]
- Meng Y, Wang H, Chen J, Zhang S 2014. Modelling hydrology of a single bioretention system with HYDRUS-1D Sci. World J, 2014 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mualem Y 1976. A new model for predicting the hydraulic conductivity of unsaturated porous media Water Resour. Res, 12 (3) (1976), pp. 513–522 [Google Scholar]
- Neitsch SL, Arnold JG, Kiniry JR, Williams JR 2011. Soil and water Assessment Tool Theoretical Documentation Version 2009 Texas Water Resources Institute; (2011) [Google Scholar]
- Niazi M, Nietch C, Maghrebi M, Jackson N, Bennett BR, Tryby M, Massoudieh A 2017. Storm Water Management Model (SWMM): performance review and gap analysis J. Sustain. Water Built Environ (2017), p. 04017002 http://ascelibrary.org/doi/abs/10.1061/JSWBAY.0000817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Page J, Winston R, Hunt III WF, 2012. Stormwater monitoring of innovative street retrofits in urban Wilmington, NC, World Environmental and Water Resources Congress 2012: Crossing Boundaries.
- Palhegyi GE 2009. Modeling and sizing bioretention using flow duration control J. Hydrologic Eng, 15 (6) (2009), pp. 417–425 [Google Scholar]
- Penman HL 1948. Natural Evaporation from Open water, Bare Soil and Grass Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences The Royal Society (1948), pp. 120–145 [DOI] [PubMed] [Google Scholar]
- Pitt R, Voorhees J 2003. The Design, Use, and Evaluation of Wet Detention Ponds for Stormwater Quality Management (2003)
- Pitt R, Voorhees J, 2004. The use of WinSLAMM to evaluate the benefits of low impact development, Proceedings of the Low Impact Development Conference: Putting the LID on SWM, College Park, MD, USA. [Google Scholar]
- Priestley C, Taylor R 1972. On the assessment of surface heat flux and evaporation using large-scale parameters Mon. weather Rev, 100 (2) (1972), pp. 81–92 [Google Scholar]
- Qin H.-p., Li Z.-x., Fu G 2013. The effects of low impact development on urban flooding under different rainfall characteristics J. Environ. Manag, 129 (2013), pp. 577–585 [DOI] [PubMed] [Google Scholar]
- Rossman L 2015. Stormwater Management Reference Manual USEPA; (2015) [Google Scholar]
- Rossman L.a. 2004. Storm Water Management Model User’s Manual Version 5.0. (November) (2004), p. 245
- Russell DL 2006. Practical Wastewater Treatment Wiley; (2006) [Google Scholar]
- Skaggs R 1990. DRAINMOD User’s Manual North Carolina State University, Raleigh: (1990) [Google Scholar]
- Van Genuchten MT 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils Soil Sci. Soc. Am. J, 44 (5) (1980), pp. 892–898 [Google Scholar]
- Walter IA, Allen RG, Elliott R, Jensen M, Itenfisu D, Mecham B, Howell T, Snyder R, Brown P, Echings S, 2000. ASCE’s standardized reference evapotranspiration equation, Proc. of the Watershed Management 2000 Conference, June. [Google Scholar]
- Wong TH, Fletcher TD, Duncan HP, Coleman JR, Jenkins GA 2002. A model for urban stormwater improvement conceptualization Glob. Solutions Urban Drainage, 813 (2002) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


