Filament Nucleation Tunes Mechanical Memory in Active Polymer Networks

Abstract

Incorporating growth into contemporary material functionality presents a grand challenge in materials design. The F-actin cytoskeleton is an active polymer network which serves as the mechanical scaffolding for eukaryotic cells, growing and remodeling in order to determine changes in cell shape. Nucleated from the membrane, filaments polymerize and grow into a dense network whose dynamics of assembly and disassembly, or ‘turnover’, coordinates both fluidity and rigidity. Here, we vary the extent of F-actin nucleation from a membrane surface in a biomimetic model of the cytoskeleton constructed from purified protein. We find that nucleation of F-actin mediates the accumulation and dissipation of polymerization-induced F-actin bending energy. At high and low nucleation, bending energies are low and easily relaxed yielding an isotropic material. However, at an intermediate critical nucleation, stresses are not relaxed by turnover and the internal energy accumulates 100-fold. In this case, high filament curvatures template further assembly of F-actin, driving the formation and stabilization of vortex-like topological defects. Thus, nucleation coordinates mechanical and chemical timescales to encode shape memory into active materials.

Graphical Abstract

Structural and mechanical properties of reconstituted networks of protein polymers can be tuned by varying the amount of actin nucleator. Small and large concentrations of nucleators produce networks that relax easily, but at intermediate level of nucleation long lived topological defects are formed.

Introduction

In contrast to engineered materials, biological materials have the capacity to spontaneously grow and remodel. The cortical actin network in non-muscle cells is an apolar, disordered network of crosslinked filamentous actin (F-actin) coupled to the plasma membrane.^[1] The network is responsible for accumulating the internal active stresses that coordinate cortical flows and diverse changes in cell shape that occur during cell polarization, migration and division.^[2–4] The cortex is highly dynamic, constantly assembling and disassembling, renewing itself in seconds to minutes. ^[5–7] Assembly of cortical F-actin is in part mediated by formin nucleation, where linear polymers grow with accelerated assembly kinetics and entangle into a viscoelastic gel. In combination with F-actin disassembly which is modulated by depolymerization and severing, nucleated F-actin assembly determines F-actin network turnover.^[8–14] Turnover is linked to cortical tension through its ability to relax applied mechanical stress.^[15–17] However, altered assembly kinetics of F-actin have also been shown to alter the steady-state architecture of F-actin networks which in turn may influence network mechanics.^[18–20] Thus controlling turnover and mechanics simultaneously presents new possibilities for the engineering of active material.

Here, we present a novel, engineered biological material whose growth dynamics characteristically determine the architecture and mechanics of the material itself. First, we detail the coordinated assembly of an active and dynamic actin-membrane composite gel, composed of purified protein and lipid. Then, we vary the concentration of nucleating proteins coupled to a membrane surface, while retaining a constant and limiting concentration of total actin, restricting F-actin growth principally to the membrane surface. As the extent of nucleation is varied we measure the accumulation and dissipation of internal energies, which arises from F-actin polymerization forces. We explore how nucleation determines dissipation, through coordinating the timescales of mechanical relaxation and the timescales of chemical turnover. Finally, we determine how the balance of these timescales encodes structural memory.

Materials and Methods

Buffer Preparation.

G-buffer is composed of 2 mM Tris-HCl pH 8.0 and 0.1 mM CaCl₂, 0.2 mM ATP, 1 mM NaN₃, and 0.5 mM DTT. F-Buffer is composed of 10 mM Imidazole, 1 mM MgCl₂, 50 mM KCl, 0.2 mM EGTA, and 0.5 mM ATP at pH 7.5. The vesicle buffer is 100 mM NaCl, 20 mM HEPES, pH 7.3. The storage buffer for the myosin is 0.5 mM PIPES, pH 7.0, and 0.45M KCl. The Formin (mdia1) Buffer is 20 mM HEPES (pH 7.4), 1 mM EDTA, 200 mM KCl, 0.01% NaN₃, and the pH is set to 7.4 at room temperature with KOH and stored at 4C before use. The stock concentration of the formin used is 35 μM. The Profilin Buffer is as follows: 20 mM Tris/HCl, pH 7.5, 150 mM KCl, 0.2 mM DTT. The stock concentration of profilin is 200 μM.

Bilayer Preparation.

Egg Phosphatidyl Choline (EPC, Avanti Polar Lipids), FITC Green DHPE (Molecular Probes) and Nickel-NTA (Avanti Polar Lipids) are combined in chloroform and dried in a glass container under Ar gas. Bilayers are prepared in a ratio of 91% EPC /8.6% NTA /0.4% DHPE for formin attachment. These dried combinations are then resuspended in vesicle buffer and vortexed for 10s. The solution is then sonicated for upwards of 5 minutes to generate small, unilamellar vesicles (SUVs). The SUVs are then added to Piranha treated coverslips to coat them with a phospholipid bilayer in a custom-built imaging chamber (Chamlide). The phospholipid bilayer is maintained hydrated in approximately 500 μL ATP-free F-buffer.^[21]

Protein Preparation.

2.0 μM dark F-actin and 0.64 μM Alexa-568 actin are nucleated by mdia1 in F-buffer and crowded to the phospholipid bilayer surface with 0.25 % methyl-cellulose (MC) (14,000 MW, Sigma). The F-actin is allowed to polymerize for approximately 1 hour on the microscope at 25C.^{[21, 22]}

Imaging.

25 mm coverslips are sandwiched in a custom-built chamber (Chamlide). Sample fluorescence is monitored using a Ti-E microscope (Nikon) with a spinning disk confocal head (Yokagawa), a HQ2 Coolsnap CCD camera (Roper Scientific) and a 60× 1.4NA oil immersion objective lens (Nikon). The microscope and confocal head are controlled using Metamorph software (MSD Analytical Technologies).

Modelling filament assembly kinetics.

The simultaneous growth of multiple actin filaments is modelled using stochastic growth simulations. Linear actin filaments grow from a fixed number of formin nucleators and are released in the bulk, in a finite monomer pool shared by all the filaments. After releasing a filament, a formin nucleator can generate another filament. In an attempt to mimic diffusion limited growth, we limit the length of the filament produced by formin nucleator to be proportional to the amount of G-actin in bulk. Once released the filaments can polymerize further or depolymerize. Given a limited resource of monomers, the assembly rate of actin filaments is taken to be proportional to the available amount of monomers in solution.^{[23, 24]} We estimate the turnover time by calculating rate of change of filament length at long times, as this is a measure of how long it takes to renew the material in a filament. The details of the model are presented in the Supplementary Notes.

Results

F-actin Nucleation Determines Network Architecture

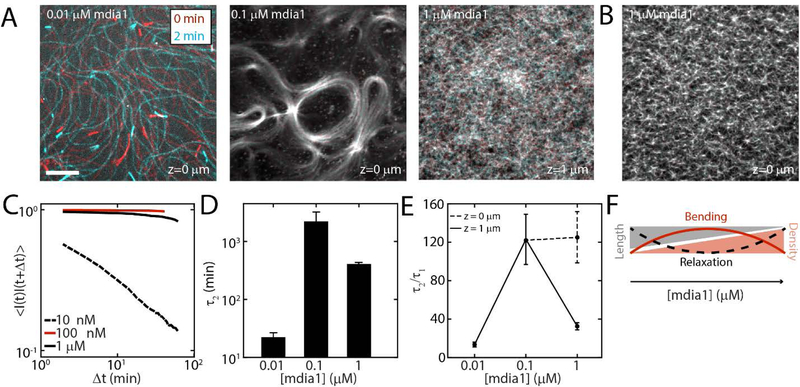
Here we use a simple, in vitro, quasi-two dimensional model of the cortex amenable to high resolution imaging.^[21] The model cortex is comprised of a minimal set of components, including G-actin, profilin, mdia1, and a model membrane (Figure 1A, Methods). Formin is attached to the membrane via an interaction between its purification His tag, and the NTA-Ni embedded in the membrane. Methylcellulose (MC, 0.25%) is kept in solution and used to keep the concentration of protein high at the membrane surface. The bulk concentration of formin is varied in the following concentrations: 10 nM, 100 nM, and 1 μM. The initial concentration of G-actin across different experiments is held constant at 2 μM dark G-actin and 0.6 μM Alexa-568 G-actin. A complete description of statistics and corresponding snapshots from experiments are available in the supplement (Figure S1, S2).

Figure 1. F-actin nucleation determines dynamics and architecture of network assembly.

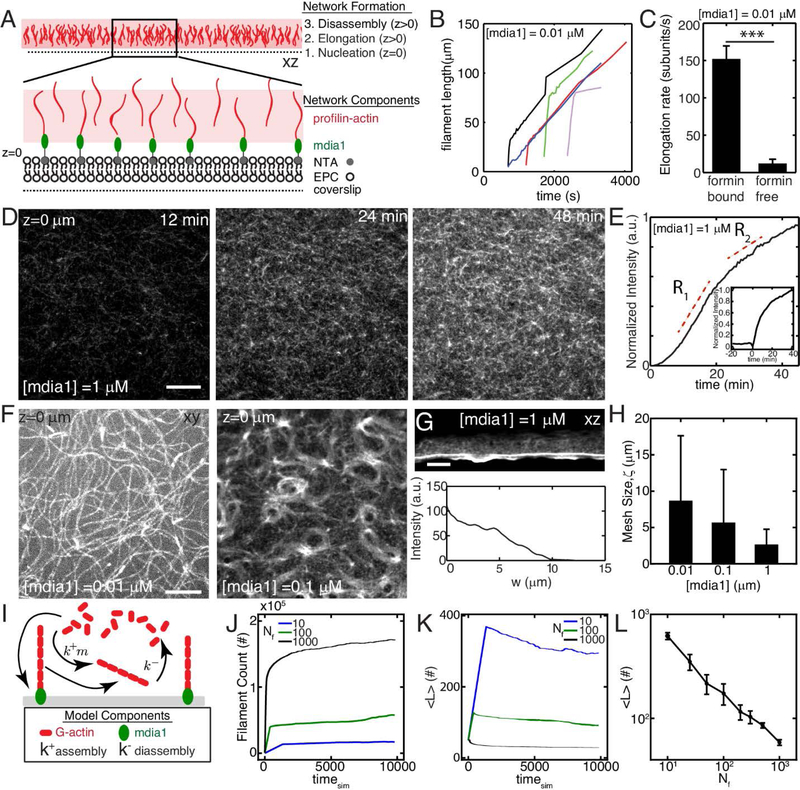
(A) Experimental setup where F-actin is nucleated from his-tagged mdia1 bound to NTA lipids within a model membrane. (B,C) Elongation rates of individual F-actin at 10 nM formin (N=4, 5, p<10⁻⁷). (D) F-actin fluorescence of network growth at 1 μM mdia1 concentration over time. (E) Normalized fluorescence intensity over time for the network in (D). (E,inset) Fluorescence intensity for a network where formin is added to proflin-actin at a later time (time=0 min). (F) Organization of F-actin for different concentrations of formin. (G) F-actin network nucleated from a microfluidic surface for a size view. (H) Mesh-size of the F-actin network as a function of formin concentration (N=3,4,3, p=ns) (I) Schematic of stochastic model for F-actin assembly from a limiting pool of G-actin. Model results for number of F-actin filaments (J), mean filament length (K), and equilibrium filament length for different number of nucleators (L). The pool size is 10⁷ monomers for results in J-L. All scale bars are 10 μm. All error bars are mean ± 1 standard deviation.

Formin will nucleate and elongate F-actin from the G-actin pool. Filament elongation occurs at different timescales. Individual filaments can only be observed at 10 nM formin. Initially, the filaments elongate quickly (~150 subunits s⁻¹) as expected by formin nucleated growth.^[25] However, they switch to a slow mode of elongation (~10 subunits s⁻¹) consistent with release from formin and slow elongation of profilin-actin alone (Figure 1B,C). Thus, at 10 nM formin, filaments are initially coupled to the membrane through their formin interactions but then released from the surface. At the network level, we measure the fluorescence of a field of view, and characterize the growth of the network as a whole (Figure 1D). Growth of the network shows an exponential behavior, growing quickly initially (R_1, ~0–20 min), and slowing down at long times (R_2, >20 min). The polymerization does not always fully plateau within experimental timescales (~ 1 hr) (Figure 1E). We further show that the rate of growth of the network is principally formin-dependent. Fast growth of the network does not proceed until formin is added (Figure 1E, inset).

At 10 nM, formin elongates F-actin from the surface, generating filaments approximately 100 μm in length (Figure 1F, Movie 1). The filaments remain adjacent to the membrane due to the effects of MC and entangle into a structurally homogeneous network. As the length of the filaments far exceed their persistence length, the filaments are floppy and fluctuate thermally.

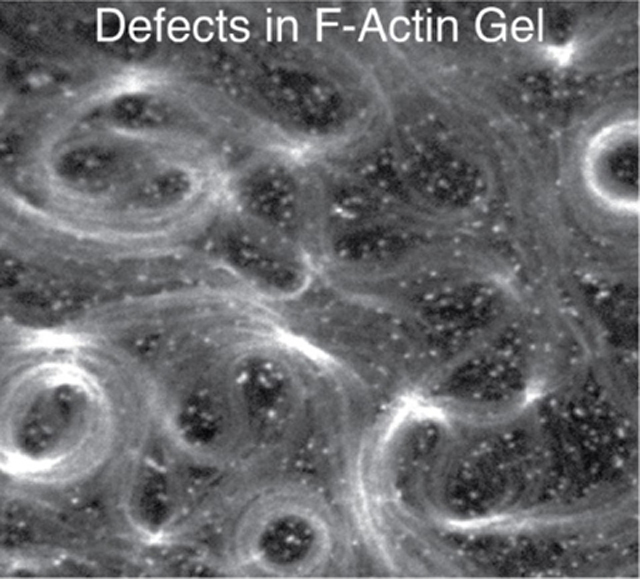
At 100 nM mdia1, F-actin fluorescence intensity is more spatially uniform than at 10 nM mdia1, indicating an increase in F-actin surface density (Figure 1F, Movie 2). At this concentration, spatial patterns can be observed in the F-actin network, such as circular arrays with lengthscales between 5 and 100 μm. These patterns are reminiscent of topological defects of the active gel model, in the activity-driven formation of spirals and vortices.^{[26, 27]} Often, the curvatures of the filaments observed can be much larger than what is expected based on the persistence length of F-actin (l_p ~ 15 μm), suggesting the accumulation of non-thermal energies.^[28]

At 1 μM, neither individual filaments nor spatial patterns in the F-actin network can be distinguished, as fluorescence intensity at the surface is spatially uniform (Figure 1D, Movie 3). Now, F-actin grows orthogonal to the surface of the membrane. Z-stacks indicate the F-actin density is highest at the membrane surface (z= 0 μm) and decreases with distance from the surface (Figure 1G, Movie 4). This can also be seen when formin is coupled to membranes that coat the inside of a rectangular microfluidic channel. This geometry allows for visualization across with thickness of the F-actin network within a single optical slice, which shows a very dense ‘gel-like’ network (Figure 1G inset).

With increasing density of formin, there is an increased density of F-actin (and likewise a decrease in F-actin mesh size) and a change in the pattern of F-actin, from entangled to gel (Figure 1H). Similarly, there is a change in the mean filament length, from approximately 100 μm as measured at 10 nM mdia1 (Figure 1B), to an estimated length of approximately 5–10 μm, for 1 μM mdia1 (Figure 1G). To understand the mechanism of F-actin length control by changing formin concentration, we implemented a stochastic model of filament assembly from a finite pool of nucleators, where the total amount of actin (F-actin + G-actin) is conserved. As a limiting pool of G-actin is shared by all growing filaments, the F-actin assembly rate is proportional to the amount of available monomers in solution (Figure 1I, Methods). As a result, the dynamics of F-actin network assembly can be altered by changing the concentration of membrane-bound formin. By simulating the model, we find that at long times the mean number of filaments is higher and filament length is smaller at larger concentration of formin (Figure 1J,K). For a fixed pool size, the mean filament length decreases with an increase in number of nucleators (Figure 1L).

F-actin Nucleation and G-actin Competition Govern Network Turnover

Turnover of F-actin and membrane (FITC-DHPE) is assessed using Fluorescence Recovery After Photo-bleaching (FRAP) (Figure 2 A,B, Movie 5). A circular region, approximately 10 μm in diameter is bleached with a 410 nm laser, and the fluorescence of either membrane or actin recovers over an exponential timescale, τ_{1 ,} (Figure 2C, Equation S6).

Figure 2. F-actin nucleation in a limited G-actin pool determines network turnover.

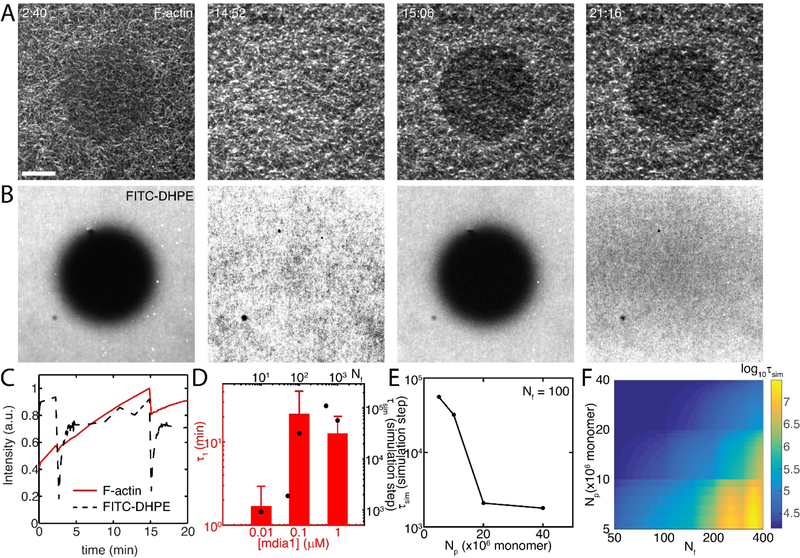
(A) Fluorescent F-actin (z=0 μm) over time, as FRAP is performed twice. Dark circles indicate FRAP region. Scale bar is 10 μm. (B) Fluorescence of FITC-DHPE within the phospholipid bilayer over time. Dark circles indicate FRAP region. (C) Quantification of data in A & B. F-actin recovers quickly for the first FRAP, more slowly for second FRAP, while membrane recovers equally well in both cases. (D) F-actin recovery times (τ₁) at different concentrations of formin (N=4,3,5), bars are experimental data and filled circles are the model result. (E) Recovery times for a fixed number of nucleators decrease with pool size (N_p). (F) Log of recovery time for various pool size and number of nucleator combinations. Pool size and nucleator number alter recovery time.

F-actin network recovery depends upon the concentration of surface bound formin. At 10 nM mdia1, F-actin network recovery is fast, τ₁=1.7 +/− 1.2 min (Figure 2D). Thus, the network recovers very quickly. By contrast, at 100 nM mdia1, the recovery time increases to 21.8 +/− 17.8 min. At 1 μM mdia1, the timescale is statistically indistinguishable from 100 nM at 12.6 +/− 7.3 min. Thus, at high formin concentrations, the network recovers more slowly than at lower concentrations. However, these timescales are much shorter than non-nucleated actin (Figure S4) and stabilized F-actin (Figure S5). In the cell, F-actin turnover is determined by factors that alter disassembly, such as severing proteins or proteins that accelerate depolymerization. Therefore, to understand how the turnover varies under the assumption of a constant disassembly rate, we turn to a computational model and explore the influence of a variable assembly rate.

In a stochastic model, turnover timescale (τ_sim) of F-actin is determined by the balance of F-actin assembly and disassembly. The rate of assembly depends on the concentration of formin molecules (N_f), and by the release rate of formin. Formin-mediated assembly elongates filaments quickly, until filaments reach approximately 100 μm, and the filament is released. The released filament continues to elongate at a slower pace, and new filaments are nucleated from the newly available formin molecule. Using this formalism, we find that the turnover of F-actin is very sensitive to formin concentration. As the concentration is increased, the turnover timescale increases. We find that the turnover timescale increases as the quantity of G-actin is exhausted from its limited pool (N_p), as this is when depolymerization occurs. Thus in this case, despite that the disassembly rate is presumed constant, the turnover is variable. We also suggest that depletion of G-actin causes the transition from fast growth in R1 to slower growth in R2 (Figure 1E). As pool size plays an important role in determining the turnover timescale, we plot the simulated turnover timescale as a function of pool size in stochastic simulations (Figure 2E). To better decipher the interplay between pool size (N_p) and number of nucleators (N_f) we plot the turnover timescale as a N_f and Np phase space (Figure 2F). These results show that turnover is slowest when the number of nucleators is high and pool size is low.

Templated F-actin Assembly Regulates Relaxation of Internal Energy

At intermediate concentrations of formin (100 nM), patterns and topological defects can be seen in the F-actin network (Figure 3A, Movie 4). The initial pattern and location of defects appears static, but broadens in width and increases in fluorescence intensity. This suggests that filament curvatures are established early during polymerization of the network, and serves as a ‘template’ for further growth of F-actin. We independently estimated the energy distribution by quantifying the curvature of structures (Figure 3C, Equation S2). We see that the mean radius of curvature (R) of filaments on the inner surface of defects depends upon the concentration of formin at the surface (Figure 3C inset). At 10 nM formin, filament curvature is low, corresponding to a maximum mean energy ~ 10⁻²⁰ J (Figure 3C). This energy is above k_BT (~ 10⁻²¹ J) presumably due to effects of crowding agents (MC) in two dimensions and mild entanglement. By contrast, at 100 nM formin, the curvature of filaments is higher and coarsens to an approximate mean energy of ~10⁻¹⁹ J. Thus, with an order of magnitude increase in formin concentration there is an order of magnitude increase in the mean bending energy. We also estimated the field energy stored in these structures using Frank Free energy equation (Equation S3) and considering the contributions both from bend and splay terms (Figure 3B, Equation S4). Temporal evolution of bend, splay, and total free energy is shown in Figure 3D. Comparing bending energies from Figure 3C and 3D we estimate the Frank constant, K₃₃ to vary between 1.38 to 4.6 pN. This is of the same order as that of a lyotropic liquid crystal.^[29] At steady state, these broadened filament structures remain fixed in time, despite continued steady-state polymerization dynamics. When photo-bleached the F-actin recovers its fluorescence intensity, although does not alter its structural organization (Figure 3E). The same filament organization can be seen qualitatively at the recovered state as can be seen prior to photo bleaching. Again, the structure does not change significantly, as the mean energy for the network remains nearly constant in time, while the F-actin continues to polymerize (Figure 3F).

Figure 3. Intermediate nucleation induces defect formation and resists relaxation by turnover.

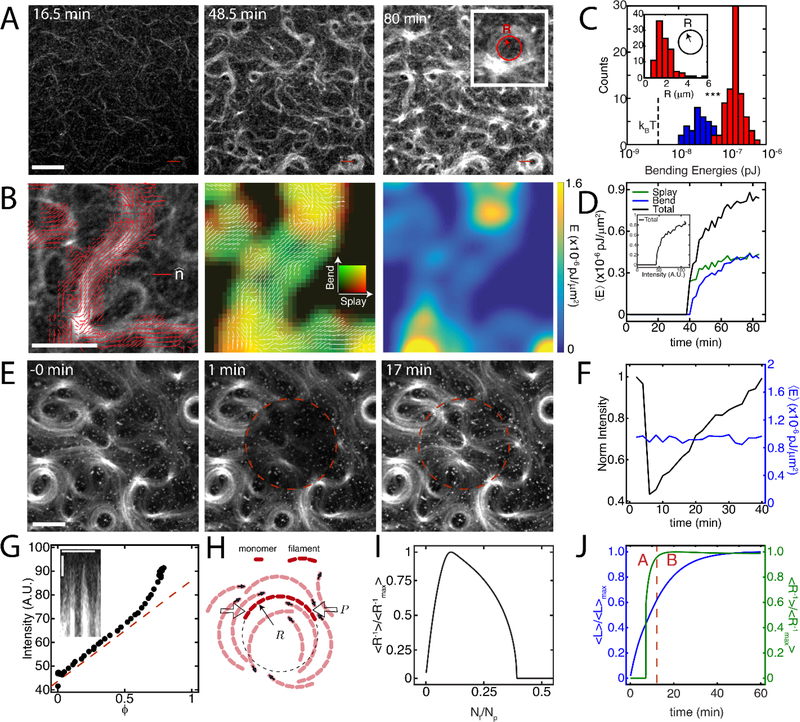
(A) F-actin fluorescence of the growth of a network from 0.1 μM mdia1. (B) Left panel depicts director vector field (red, $\widehat{n}$) over an actin bundle. The second and third panel are false color coded image of splay (red) - bend (green) energy density, and total distortion free energy density over the same bundle.(C) Bending energy of F-actin at the measured radii of curvature (R) (inset). N=4 independent experiments. Blue corresponds to [mdia1]=10 nM, red corresponds to [mdia1]=100 nM. (D) Temporal evolution of splay, bend, and total distortion free energy density. (E) Fluorescence recovery over time for the FRAP indicates structure experiences turnover but does not change its structural (vortex-like) organization. (F) Measurement of fluorescence intensity and distortion free energy density over FRAP region demonstrates that the local structure is preserved. (G) Non linear growth of intensity as a function of area fraction implies templating. (H) Schematic of growth pressure-driven buckling of F-actin. The growth pressure, P, depends on the local filament density. Filled arrows indicate the direction of filament growth. (I) Continuum model results show that normalized filament curvature is maximized at an intermediate formin concentration. (J) Model results show an initial increase in normalized filament curvature that reaches a steady-state at short times, while the filament keeps elongating at longer times. Region A indicates growth of curvature. Region B indicates templated assembly. This results in templated assembly of filaments. All scale bars are 10 μm, *** indicates a p-value of < 0.001.

As the bending energy increases from 10 to 100 nM formin, we seek to understand how this impacts the mechanics of the F-actin network. Plotting integrated intensity as a function of area fraction covered by filaments (φ) for the whole image in Figure 3G we show that coarsening occurs across the entire sample. This suggests that the vortex-like structures retain the same area but increase in intensity. We developed a continuum theory of growing soft filaments to explain curved F-actin assembly at intermediate formin densities (Supplementary Notes). The growth of actin filaments results in the accumulation of mechanical pressure acting on the surrounding filamentous network (Figure 3H, Supplementary Notes). This growth pressure (an increasing function of filament density) will not significantly affect network architectures at low formin densities due to negligible steric hindrance. Filament curvatures remain low at very high formin densities as the filaments are shorter than their persistence lengths. At intermediate formin densities, both the filament density and mean length are sufficiently high, such that the competition between filament polymerization and bending forces induces actin filament buckling (Figure 3I, Supplementary Notes). These curved filaments then polymerize while maintaining their curvatures, resulting in the observed templated assembly of F-actin (Figure 3J). Thus, the curvatures are highest at intermediate formin concentration (Figure 3I). The temporal dynamics of filament length and curvature from the continuum theory predicts that curvature sets in before the filaments reach an equilibrium length thus substantiating the idea of templating. We find that these results match experiments even without any explicit consideration of structure and may be pronounced further in case changes in organization or dimensionality are considered.

F-actin Nucleation Determines Mechanical Relaxation Time

We estimate network viscoelasticity by quantifying the thermal fluctuations of F-actin within the network as a function of time (Figure 4A,B). To this end, we take the autocorrelation of F-actin fluorescence intensity over time to determine a relaxation timescale τ₂ (Figure 4C, Equation S7). As we are interested in the trapping of bending energy, we chose to measure τ₂ for a 1 μM case at z = 1μm. This choice is motivated by the fact that due to tethering and out of plane growth of filaments there is no bending energy at z = 0 μm. At 10 nM formin, the filaments are long and floppy, and thus correlation is lost quickly. By contrast, at elevated levels of formin (100 nM & 1 μM), fluctuations are significantly reduced, and τ₂ increases. However, relaxation is the slowest for intermediate concentrations of formin, and likewise has the highest τ₂ (Figure 4C,D). We thus compare turnover timescales to relaxation timescales to understand the extent to which turnover is responsible for relaxation (Figure 4E). Thus, we suggest that turnover is sufficient to relax the F-actin network in the low and high concentrations of formin (where bending energy is low), but is decoupled at 100 nM (where the bending energy is high) (Figure 4F). We confirm the relaxation times for high concentrations of formin using MSD analysis of myosin embedded motors (Equation S1), which shows a transition to fluid like behavior at 10 minutes, matching the turnover timescale of 10 min for 1 μM formin (at z = 1 μm) (Figure S3). Thus, indeed it would appear that at concentrations other than 100 nM formin at which curvatures are inset, mechanical relaxation timescales are correlated to turnover timescales. However, a direct link between myosin motion and network mechanics is still unclear as motions of myosin are actively driven.

Figure 4. F-actin nucleation differentially mediates timescales of relaxation and turnover.

(A) Fluorescence image of F-actin at 0 min (red) and 2 min (cyan) for mdia1=10 nM (left), 100 nM (middle) and 1 μM (right) indicate motion of F-actin with time. Scale bar is 10 μm. (B) Color overlay for 1 μM F-actin at z=0 μm shows immobile F-actin. (C) Autocorrelation decay of fluorescence intensity and viscoelastic timescale τ₂. (D) Mean exponential timescale, τ₂ as a function of formin concentration (N = 3, 4, and 3 for 10 nM, 100 nM, and 1μM respectively). (E) Relaxation timescale divided by turnover timescale indicates the extent to which mechanical relaxation is induced by chemical turnover. The dashed line depicts the response of 1 μM network at z = 0 μm. The correlation timescales are significantly larger closer to surface due to possible tethering of filaments to formin nucleators. (F) Schematic of the relationship between geometric parameters, bending energy and timescales of relaxation.

Discussion

In our model system, the propensity to grow and remodel is principally determined by the dynamics of F-actin nucleation by formin nucleating proteins. The concentration of formin coupled to the membrane in combination with a limited supply of G-actin determines the length and density of F-actin, as well as the kinetics of F-actin network assembly. The combination of the release of F-actin by formins and a basal de-polymerization rate determines the balance of assembly and disassembly, what is termed turnover. We find that when surface nucleation is low, long filaments entangle to yield a low viscosity material with fast turnover. By contrast, when surface nucleation is high, filaments are short, and assemble into a viscoelastic gel with lower turnover. In these cases, the networks are structurally isotropic and the relaxation time of the networks scale with the turnover time, suggesting that internal energies are dissipated. However, at intermediate nucleation, there is a characteristic anisotropic structure formed that exhibits long-lengthscale spatial patterns, with high curvatures resembling vortices as predicted by active gel models.^{[26, 27]} These patterns emerge within the initial minutes of polymerization, and coarsen with time, retaining their initial curvatures. This suggests that F-actin curvatures are established and stabilized early, and guide the assembly of latter F-actin, a process we term templating. As a result of templating, the energies of bending and splaying are not dissipated but increase with time approximately 100-fold over thermal energy. Surprisingly, the system retains its structural organization despite its continued turnover. These results indicate that templating and the accumulation of bending energy are uniquely determined by a characteristic set of assembly conditions and resists relaxation by assembly driven turnover.

Filament nucleation by formin may play unique structural and mechanical roles in the cell. First, the accumulation of polymerization forces may be characteristic to formin-based nucleation, as we have yet to observe it with other nucleators. Furthermore as formin nucleation is putatively dependent upon load, the accumulation of internal forces may further feedback on its own assembly kinetics.^{[30, 31]} Alternatively, the increased F-actin curvature associated with this load may signal to well-known curvature sensing F-actin binding proteins to drive further biochemical events and downstream secondary effects, such as severing by cofilin.^{[32, 33]} Separately, the processivity of formin and release of F-actin may also be a feature actively used by the cell. As we show that loss of processivity increases the number of filaments which in turn competes for soluble G-actin to alter its own assembly rate, it may also establish a competition with other nucleators, or with myosin molecular motors.^[34] Also, as the probability of filament release by formin increases with filament length, filaments of different length will adhere differentially to the membrane. Thus formin alters myriad physical features of the cytoskeleton.

How to encode memory into programmable materials is an outstanding problem in materials science. Here, we show that nucleation as a single parameter can non-monotonically alter the storage or relaxation of internal energy, providing fine-tuned precision and control over the encoding of mechanical and structural information. As a mechanism for storage, the balance of kinetic and mechanical effects drives templating, the guided assembly of internal structure that follows F-actin bending due to polymerization forces. Thus, storage and erasure is explicitly an out-of-equilibrium property. These results provide new mechanisms and design principles gleaned from biological systems in the programming of memory into soft and active materials.