Doubly Robust Survival Trees

Abstract

Estimating a patient’s mortality risk is important in making treatment decisions. Survival trees are a useful tool and employ recursive partitioning to separate patients into different risk groups. Existing “loss based” recursive partitioning procedures that would be used in the absence of censoring have previously been extended to the setting of right censored outcomes using inverse probability censoring weighted estimators of loss functions. In this paper, we propose new “doubly robust” extensions of these loss estimators motivated by semiparametric efficiency theory for missing data that better utilize available data. Simulations and a data analysis demonstrate strong performance of the doubly robust survival trees compared to previously used methods.

1. Introduction

When contemplating the treatment of a given patient, a clinician will often factor in information related to a patient’s prognosis; such information may include, for example, the patient’s age, gender, various kinds of clinical and laboratory information, and increasingly biological variables like gene or protein expression. Risk indices can be used to predict a patient’s prognosis from such information; these are typically estimated from data previously collected on an independent cohort of patients with known covariates and outcomes. There are many statistical learning methods that might be used in building predictors of risk for a given outcome using covariate information. Recursive partitioning methods are an especially clinician-friendly tool for this purpose; [1] provides a comprehensive treatment and review.

Frequently, the outcome of interest represents the time to occurrence of a specified event; common examples in cancer studies, for example, include death and recurrence or progression of disease. Studies of this kind often result in outcomes that are right-censored on several subjects. Several learning methods for separating patients into prognostic risk groups in the presence of right-censored outcome data have been proposed; most represent variations on the original classification and regression trees (CART) algorithm of [2]. In the case of regression trees, the original CART algorithm uses recursive partitioning to construct a hierarchically-structured, covariate-dependent prediction rule. This prediction rule divides the covariate space into disjoint rectangles, typically through consideration of a splitting criterion derived from a loss function that compares observed responses to predicted values obtained under the indicated rule. For continuous response variables, it is common to use squared error loss for this purpose; associated decisions based on reductions in loss then correspond to maximizing within-node homogeneity. However, the squared error loss criterion cannot be directly used in the presence of right censoring, and this problem may be considered as one of the principal catalysts for methodological developments in the literature on survival regression trees with right-censored data. For example, in [3], trees are built by minimizing the distance between the within-node Kaplan-Meier estimator to a Kaplan-Meier estimator computed as if all failure times in the node occurred at the same time; in [4], a loss function based on the negative log-likelihood of an exponential model is used. Leblanc and Crowley [5] used a splitting statistic based on a one-step estimator of the full likelihood estimator for the proportional hazard model with the same within-node baseline hazard. These methods also focus on maximizing within-node homogeneity; alternatives focused on maximizing between-node heterogeneity include [6], who based the splitting rule on maximizing the two sample log-rank statistic, and [7], who proposed a pruning algorithm for trees built using the log-rank statistic. With some exceptions, developments in this area after [7] moved away from the basic process of building hierarchically constructed trees towards more complex modeling situations (e.g., clustering, discrete survival times, ensembles, alternative partitioning methods, etcetera); see [8] for a recent review.

The above-cited methods for survival regression trees all use decision rules that are specifically designed to deal with the presence of right-censored outcomes; none bear a strong resemblance to what would ordinarily be done if censoring were absent. This gap between tree-based regression methods used for censored and uncensored data was closed by [9], who used inverse probability censoring weighted (IPCW) theory (e.g., [10]) to replace a given “full data” loss function that would be used in the absence of right-censoring by an IPCW-weighted loss that (i) reduces to the full data when there is no censoring; and, (ii) is an unbiased estimator of the desired risk in the presence of censoring. However, such methods are essentially weighted complete case methods and thus ignore the partial information available on censored observations. In particular, splitting decisions and predictions do not make full use of the available information and it is reasonable to expect that methods that suitably incorporate more of the available information may have better performance.

Robins and Rotnitzky [11, Sec. 4] devised a semiparametric efficiency theory for missing data problems as a way to highlight the inefficiency of IPW estimators that fail to fully utilize information on observations with missing data. In particular, these authors show that the influence function for the most efficient estimator can be represented as a simple inverse probability weighted (IPW) estimator plus a certain correction term that depends on the observed data, providing important insight not only into how full efficiency can be recovered but also into how the efficiency of IPW estimators might be improved. The concept of augmented inverse probability weighted estimators was introduced in [12] (see also [13]), the focus being on improving efficiency in comparison to IPW estimators. Augmented IPW estimators require a model for both the missingness mechanism and the distribution of the “full” data, while the IPW estimators only require the missingness mechanism to be modeled. In order to be consistent the IPW estimators require the missingness mechanism to be consistently estimated, while [14] showed that the augmented inverse probability weighted estimators are consistent if either model is correct but not necessarily both, referred to as the “doubly robust” property. See [10] and [15] for further information on augmented IPW and IPCW estimators, where the problem of right censored outcomes is treated in detail.

Following these principles, and returning to the process of building survival trees, this paper proposes a new approach to building regression trees with right-censored outcomes. The method, doubly robust survival trees, generalizes the method developed in [9] by replacing the IPCW-weighted loss function with a doubly robust version of the loss function. We also introduce doubly robust cross-validation as a generalization of the IPCW cross-validation procedure in [9]; see also [16]. These novel substitutions improve the efficiency of the decision process that underpins the process of building and selecting a final tree. The performance of doubly robust survival trees, implemented via CART through a modification of the rpart package [17] in the R software [18], is evaluated in an extensive simulation study, where it is compared to the IPCW method in [9] and also that of Leblanc and Crowley [5]. The value of the methodology is also illustrated through analyzing data on death from myocardial infraction from the TRACE study [19].

2. Regression Trees, Loss Functions, and Censoring

2.1. Review of Regression Trees for Uncensored Outcomes

2.1.1. Basic procedure

Below, we briefly review how regression trees are calculated when there is no censoring; further details are available in [2]. In this section, it is assumed that we have n independent and identically distributed (i.i.d.) copies of (Z,W′)′, where $Z\in \mathbb{R}$ is the response and W is a d–dimensional covariate vector. As enumerated in [9] the tree building process consists of three main steps: (i) Choosing a loss function; (ii) Creating a sequence of candidate trees; and, (iii) Selection of the “best” tree from this sequence. A loss function L(Z, β(W)) = distance(Z, β(W)) defines a nonnegative measure of the discrepancy between a prediction function β(W) and a response Z. A popular choice, particularly with regression trees for continuous responses, is the squared error, or L₂, loss function L(Z, β(W)) = (Z – β(W))²; the absolute deviation, or L₁, loss L(Z, β(W)) = |Z – β(W)| is another of many possible choices. A regression tree recursively partitions the covariate space using binary splits, the decision to split on a given variable at a particular cutpoint being based on maximizing the reduction in the loss ${\sum }_{i=1}^{n}L(Z_i,\beta (W_i))$ (or, equivalently, average loss). At any given point in the splitting process, the data may be considered as being stratified into a set of nodes; splitting initially continues until some predetermined criterion is met (e.g., each node contains or exceeds a minimum number of observations), leading to a “maximal” tree, ψ_max, that may have many (terminal) nodes.

The recursive node splitting process just described creates a large, hierarchically-structured tree, say ψ_max. A method for pruning ψ_max is needed in order to reduce its propensity to overfit the data. A subtree of ψ_max is a tree ψ that can be obtained from ψ_max by collapsing some non-terminal nodes. Let a subtree ψ be given and let ${\widehat{\beta }}^{(\psi )}(W_i)$ be the prediction from ψ for a subject with covariate information W_i, that is, ${\widehat{\beta }}^{(\psi )}(W_i)$ is the prediction from the terminal node that W_i falls into when run down the subtree ψ. Let $L(Z_i,{\widehat{\beta }}^{(\psi )}(W_i))$ be the estimated error (i.e., loss) for subject i = 1, … , n and let |ψ| be the number of terminal nodes of the tree ψ. The cost complexity of the tree ψ is defined as

$${\mathcal{K}}_{\alpha }(\psi )=\sum _{i=1}^{n}L(Z_i,{\widehat{\beta }}^{(\psi )}(W_i))+\alpha |\psi |,$$ (1)

where α is a tuning parameter called the complexity parameter that serves to penalize the estimated error by the size of the tree. For a given α, the subtree ψ that minimizes ${\mathcal{K}}_{\alpha }(\psi )$ is said to be optimal; as α is varied, different subtrees of ψ_max become optimal. Varying α thus creates a sequence of subtrees ψ₁, … , ψ_l, each of which represents a candidate tree for the best (or final) tree. This process is called cost complexity pruning; see [2, Ch. 3.3].

The simplest way to select the best tree from the sequence of subtrees created by cost complexity pruning is to select the one with the smallest error (i.e., loss). In the absence of a completely independent test sample, cross-validation (e.g., [2], Ch. 8.5) is commonly used to estimate the error of each candidate tree. To be more specific, suppose cost complexity pruning generates the sequence of candidate trees ψ₁, … , ψ_l. Assume that the dataset D is split into V mutually exclusive subsets D₁, … , D_V. For a given v ∈ {1, … , V} let S_i,v be the indicator if observation i is in the subset D_v. For a given candidate tree ℓ ∈ {1, … , l} the tree ψ_ℓtrv is fit using the complexity parameter associated with ψ_ℓ using only the observations in the training set D \ D_v. Let ${\widehat{\beta }}^{({\psi }_{\ell ,t{r}_v})}(W)$ be the prediction from ψ_ℓ,trv for a subject with covariate information W. Then, we can define the cross-validated risk (or error) estimate for any candidate tree ψ_ℓ as

$$\widehat{\theta }(\ell )=\frac{1}{npV}\sum _{v=1}^V\sum _{i=1}^{n}I(S_{i,v}=1)L(Z_i,{\widehat{\beta }}^{({\psi }_{\ell ,t{r}_v})}(W_i)),$$ (2)

where p is the proportion of the total sample D included in each validation subset D₁, … , D_V. The estimated loss in (2) is calculated for each subject assuming ${\widehat{\beta }}^{({\psi }_{\ell ,t{r}_v})}(w)$ is a known function of w. The final tree (i.e., best candidate tree) is now taken to be ${\psi }_{\widehat{\ell }}$, where $\widehat{\ell }$ is the value of k that minimizes $\widehat{\theta }(k),k\in \{1,\mathrm{\dots },l\}$.

Let the predicted response obtained from the final tree be given by $\widehat{\beta }(W)={\sum }_{k=1}^{\widehat{K}}{\widehat{\beta }}_{k}I\{W\in {\widehat{\mathcal{N}}}_k\}$. It can be seen that this is a piecewise constant function of W; here, ${\widehat{\mathcal{N}}}_1,\mathrm{\dots },{\widehat{\mathcal{N}}}_{\widehat{K}}$ represent the set of terminal nodes (i.e., the chosen partition of the covariate space) and ${\widehat{\beta }}_k$ is estimated using the data within each terminal node (e.g., the node-specific sample mean, in the case of L₂ loss). The presence of “hats” in the definition of ${\widehat{\mathcal{N}}}_1,\mathrm{\dots },{\widehat{\mathcal{N}}}_{\widehat{K}}$ is meant to reflect the fact that the partition represented by the final tree is not prespecified but rather determined adaptively using the observed data.

2.1.2. Loss functions, risk, and their role in building regression trees

As described in Section 2.1.1, the specification of the loss function and corresponding terminal node estimators are key components in building the maximally sized tree, creating an associated sequence of candidate trees, and then using cross-validation to select the best tree among the candidate trees. In each of these steps, decisions are based on the principle of reducing the average loss, the underlying theoretical motivation being corresponding reduction in risk. In particular, given any fixed (i.e., prespecified, not adaptively determined) partition ${\mathcal{N}}_k$, k = 1 … K of the covariate space and assuming that $\beta (W)={\sum }_{k=1}^K{\beta }_{k}I\{W\in {\mathcal{N}}_k\}$, the average loss $n^{-1}{\sum }_{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}L(Z_i,{\beta }_k)$ is an unbiased estimator of the risk $\mathcal{R}(\beta )={\sum }_{k=1}^{K}E[I\{W\in {\mathcal{N}}_k\}L(Z,{\beta }_k)]$; see, e.g., [2, Ch. 9.3]. It is also not difficult to show that minimizing $\mathcal{R}(\beta )$ in β defines ${\beta }_0(W)={\sum }_{k=1}^K{\beta }_{k,0}I\{W\in {\mathcal{N}}_k\}$ as the main parameter of interest, where ${\beta }_{k,0}\in \mathbb{R}$ minimizes $E[L(Z,{\beta }_k)|W\in {\mathcal{N}}_k]$ in β_k for each k. For example, with L(Z, β(W)) = (Z – β(W))², the parameter β₀(W) that minimizes the risk is obtained with ${\beta }_{k,0}=E[Z|W\in {\mathcal{N}}_k],k=1\dots K$. Correspondingly, the minimizer of the average loss $n^{-1}{\sum }_{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}(Z_i-{\beta }_k{)}^2$ is $\widehat{\beta }(W)={\sum }_{k=1}^K{\widehat{\beta }}_{k}I\{W\in {\mathcal{N}}_k\}$, where ${\widehat{\beta }}_k$ is the sample mean of the Z_is for subjects falling into ${\mathcal{N}}_k$.

2.2. Estimating $\mathcal{R}(\beta )$ and β(W) with Right-Censored Data

Let T > 0 denote an event time of interest (e.g., time to death) and define the transformed survival time Z = h(T), where h(⋅) is a specified strictly increasing function that maps [0, ∞] to $\mathbb{R}$ (e.g., h(u) = log u). Following Sections 2.1.1 and 2.1.2, one can specify a suitable loss function L(Z, β(W)) and, in the case where each Z_i and W_j is fully observed, use the average loss $n^{-1}{\sum }_{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}L(Z_i,{\beta }_k)$ as the basis for building a regression tree. Just as before, this average loss is an unbiased estimator of the risk $\mathcal{R}(\beta )={\sum }_{k=1}^{K}E[I\{W\in {\mathcal{N}}_k\}L(Z,{\beta }_k)]$ assuming that $\beta (W)={\sum }_{k=1}^K{\beta }_{k}I\{W\in {\mathcal{N}}_k\}$.

However, in any time-to-event study, it is relatively common for the outcome T (hence Z) to be right-censored, e.g., due to a subject being administratively censored or lost to follow-up. In such cases, the event time T is not always fully observed and instead we observe $\tilde{T}$, the smaller of T and some censoring time C, and an event indicator Δ = I(T ≤ C) that specifies whether $\tilde{T}$ corresponds to a failure time or a censoring time. The presence of right-censoring means that not all of the Z_is are fully observed; instead, we observe the data $\mathcal{O}=(O_1,\mathrm{\dots },O_n)$, where $O_i=({\tilde{T}}_i,{\Delta }_i,{W^{\prime }}_i{)}^{\prime }$ is the observed data for subject i,i = 1, … , n and (O₁, … , O_n) are i.i.d. observations. Equivalently, $O_i=({\tilde{Z}}_i,{\Delta }_i,{W^{\prime }}_i{)}^{\prime }$ where ${\tilde{Z}}_i=\min (Z_i,h(C_i)),i=1,\mathrm{\dots },n$; a distinction will not be made between these two representations, as specifying h(⋅) allows them to be used interchangeably.

If only $\mathcal{O}$ is observed, the tree-building procedure of Section 2.1.1 cannot be applied directly because the loss function L(Z_i, β(W_i)) cannot be calculated for any subject i such that Δ_i = 0 (i.e., any censored subject). Below, we discuss two ways of extending the loss function and corresponding terminal node estimators to handle this situation. These extensions, respectively developed in Sections 2.2.1 and 2.2.2, are motivated from the perspective of constructing an unbiased estimator for the desired full data risk $\mathcal{R}(\beta )$. In Section 2.3, we discuss how these estimates are used in building survival regression trees and in developing novel extensions of existing cross-validation procedures. Similarly to Section 2.1.2, the developments of Sections 2.2.1 and 2.2.2 assume that (i) the partition ${\mathcal{N}}_k$, k = 1 … K is fixed (e.g., [2], Ch. 9.3); (ii) $\beta (W)={\sum }_{k=1}^K{\beta }_{k}I\{W\in {\mathcal{N}}_k\}$ and, (iii) the full data risk $\mathcal{R}(\beta )={\sum }_{k=1}^{K}E[I\{W\in {\mathcal{N}}_k\}L(Z,{\beta }_k)]$ is the quantity we wish to estimate using the information in $\mathcal{O}$. Viewed from this perspective, the parameter of interest ${\beta }_0(W)={\sum }_{k=1}^K{\beta }_{k,0}I\{W\in {\mathcal{N}}_k\}$ remains that defined in Section 2.1.2, that is, ${\beta }_{k,0}$ minimizes the full data conditional risk $E[L(Z,{\beta }_k)|W\in {\mathcal{N}}_k],k=1,\mathrm{\dots },K$.

To proceed, further assumptions are required. We make the standard identification assumption that T is conditionally independent of the censoring time C given the covariates W; this means that $P(\tilde{T}>u|W)=S_0(u|W)G_0(u|W)$ for every u ≥ 0, where $S_0(u|W)=P(T>u|W)$ and $G_0(u|W)=P(C>u|W)$ respectively denote the conditional survival functions for T and C given W. For reasons that will become clear shortly, we need to further assume the existence of ε > 0 such that

$$G_0(T|W)\ge \epsilon >0.$$ (3)

This positivity assumption (e.g., [11]) ensures each subject has a positive probability of being censored at their failure time, a fact that will be important in the next two subsections.

2.2.1. IPCW estimators

The basic idea behind IPCW theory is to weight the contribution of each uncensored observation by the inverse probability of being censored. In the context of loss estimation, each uncensored observation therefore contributes the loss L(Z_i, β(W_i)), weighted by Δ_i/G₀(T_i|W_i); that is, the full data loss weighted by the inverse of the corresponding probability that the observation Z_i was uncensored (e.g., [9]). Assuming (3) holds, both the average IPCW loss $n^{-1}{\sum }_{i=1}^n{\Delta }_{i}L({\tilde{Z}}_i,\beta (W_i))/G_0({\tilde{T}}_i|W_i)$ (a function of the observed data only) and the average full data loss $n^{-1}{\sum }_{i=1}^{n}L(Z_i,\beta (W_i))$ (a function of the full data) are easily shown to have the same marginal expectation, each being an unbiased estimator for $\mathcal{R}(\beta )$.

As defined, computation of the average IPCW loss requires knowing G₀ (⋅|⋅), an unknown nuisance parameter. Let $\overline{G}(\cdot |\cdot )$ be an estimator for G₀(⋅|⋅) derived using the observed data $\mathcal{O}=(O_1,\mathrm{\dots },O_n)$. Then, with $\beta (W)={\sum }_{k=1}^K{\beta }_{k}I\{W\in {\mathcal{N}}_k\}$, we define the empirical IPCW loss as

$$L_{\mathit{IPCW}}(\mathcal{O}|\overline{G})=\frac{1}{n}\sum _{k=1}^K\sum _{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}\frac{{\Delta }_{i}L({\tilde{Z}}_i,{\beta }_k)}{\overline{G}({\tilde{T}}_i|W_i)}.$$ (4)

With no censoring, (4) reduces to the average full data loss function. If $\overline{G}(\cdot |\cdot )$ is a suitably consistent estimate for G₀(⋅|⋅), the empirical IPCW loss function consistently estimates $\mathcal{R}(\beta )$ under certain regularity conditions. The predictor $\widehat{\beta }(W)={\sum }_{k=1}^K{\widehat{\beta }}_{\mathit{IPCW},k}I\{W\in {\mathcal{N}}_k\}$ that minimizes (4) is obtained by minimizing $n^{-1}{\sum }_{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}{\Delta }_{i}L({\tilde{Z}}_i,{\beta }_k)/\overline{G}({\tilde{T}}_i|W_i)$ in β_k for each k. For example, using the L₂ (full data) loss function (Z – β(W))², this solution reduces to ${\widehat{\beta }}_{\mathit{IPCW}}(W)={\sum }_{k=1}^K{\widehat{\beta }}_{\mathit{IPCW},k}I\{W\in {\mathcal{N}}_k\}$ where

$${\widehat{\beta }}_{IPCW,k}=\left(\sum _{i=1}^n\frac{{\Delta }_i{\tilde{Z}}_i}{\overline{G}({\tilde{T}}_i|W_i)}I\{W_i\in {\mathcal{N}}_k\}\right)/\left(\sum _{i=1}^n\frac{{\Delta }_i}{\overline{G}({\tilde{T}}_i|W_i)}I\{W_i\in {\mathcal{N}}_k\}\right).$$ (5)

As expected, and with no censoring, (5) reduces to the corresponding node-specific sample average of the Z_is.

2.2.2. Doubly robust estimators

Robins, Rotnitzky and Zhao [12] showed that simple IPW estimators are inefficient due to their failure to utilize all the information available on observations with missing or partially missing data. To improve efficiency, these authors proposed a class of augmented estimating equations that make better use of the available information. Below, we briefly summarize how these ideas are used to improve both loss and parameter estimation in the presence of censored data; further detail may be found in Section S.1.1 of the Supplementary Web Appendix.

By construction, the empirical loss $L_{\mathit{IPCW}}(\mathcal{O}|\overline{G})$ in (4) only makes use of complete cases, the information from censored observations being incorporated only through the estimation of G₀(⋅|⋅) by $\overline{G}(\cdot |\cdot )$. An augmented loss function, as developed in Section S.1.1 in the Supplementary Web Appendix, is designed to make greater use of the information available in censored observations. For the case of interest, namely $\beta (W)={\sum }_{k=1}^K{\beta }_{k}I\{W\in {\mathcal{N}}_k\}$, the empirical doubly robust loss function, derived directly from (S-6) in the Supplementary Web Appendix, is given by

$$L_{\mathit{DR}}(\mathcal{O}|\overline{G},\widehat{Q})=L_{\mathit{IPCW}}(\mathcal{O}|\overline{G})+\frac{1}{n}\sum _{k=1}^K\sum _{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}\left[\frac{(1-{\Delta }_i){\widehat{Q}}_k({\tilde{T}}_i,W_i)}{\overline{G}({\tilde{T}}_i|W_i)}-{\int }_0^{{\tilde{T}}_i}\frac{{\widehat{Q}}_k(u,W_i)}{\overline{G}(u|W_i)}d{\widehat{\Lambda }}_G(u|W_i)\right].$$ (6)

The doubly robust loss function (6) involves augmenting (4) with an additive “correction” term. As with (4), this augmentation term depends on $\overline{G}(\cdot |\cdot )$, an estimate derived from a model for the conditional censoring survivor function G₀(⋅|⋅), and its associated cumulative hazard function ${\widehat{\Lambda }}_G(\cdot |\cdot )$. In addition, the augmentation term further depends on a model for the conditional survivor function S₀(⋅|⋅). This can be seen directly from the definition of the function ${\widehat{Q}}_k(u,w)$, which estimates Q_k(u, w) = E[L(Z, β_k)|T ≥ u, W = w]; see (S-3) in the Supplementary Web Appendix. Specifically,

$${\widehat{Q}}_k(u,w)=-\frac{{\int }_u^{\infty }L(h(r),{\beta }_k)d\overline{S}(r|w)}{\overline{S}(u|w)},$$ (7)

where $\overline{S}(r|w)$ is a model-based estimate for S₀(r|w) = P(T > r|W = w). Importantly, similarly to (4), it can be shown that (6) also reduces to the average full data loss when there is no censoring.

The doubly robust nature of (6) stems from the fact that it consistently estimates $\mathcal{R}(\beta )$ under certain regularity conditions provided at least one of the models used for C|W and T|W has been correctly specified. For example, by construction, the second term on the right-hand side of (6) will be a consistent estimate of zero if $\overline{G}$ consistently estimates G₀; in this case, and under further regularity conditions, both (4) and (6) estimate $\mathcal{R}(\beta )$ whether or not $\overline{S}(\cdot |\cdot )$ is consistent for S₀(⋅|⋅). More generally, if $\overline{G}(\cdot |\cdot )$ fails to consistently estimate G₀(⋅|⋅), then (4) is an asymptotically biased estimator of $\mathcal{R}(\beta )$; however, if $\overline{S}(\cdot |\cdot )$ consistently estimates S₀(⋅|⋅), then it can be shown that the augmentation term corrects this bias and one still obtains a consistent estimate of $\mathcal{R}(\beta )$. When both $\overline{G}(\cdot |\cdot )$ and $\overline{S}(\cdot |\cdot )$ consistently estimate their population counterparts, (6) is an asymptotically efficient augmented estimate (i.e., for the specified loss function and predictor β(⋅)); in practice, one can anticipate reduced variance when reasonable models for G₀(⋅|⋅) and S₀(⋅|⋅) are selected.

For certain loss functions, the corresponding estimate of β(W) under (6) is also available in closed form. For example, consider again the important case of the L₂ full data loss (Z – β(W))²; then, it follows from arguments similar to those given in Section S.1.1 of the Supplementary Web Appendix that the minimizer ${\widehat{\beta }}_{\mathit{DR}}(W)$ of (6) is given by ${\widehat{\beta }}_{\mathit{DR}}(W)={\sum }_{k=1}^K{\widehat{\beta }}_{\mathit{DR},k}I\{W\in {\mathcal{N}}_k\}$ where

$${\widehat{\beta }}_{\mathit{DR},k}=\frac{{\sum }_{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}\left[\frac{{\Delta }_i{\tilde{Z}}_i}{\overline{G}({\tilde{T}}_i|W_i)}\text{+}\frac{1-{\Delta }_i}{\overline{G}({\tilde{T}}_i|W_i)}{\widehat{m}}_{\text{1}}({\tilde{T}}_i,W_i)-{\int }_0^{{\tilde{T}}_i}\frac{{\widehat{m}}_{\text{1}}(u,W_i)}{\overline{G}(u|W_i)}d{\widehat{\Lambda }}_G(u|W_i)\right]}{{\sum }_{i=1}^{n}I\{W_i\in {\mathcal{N}}_k\}},$$ (8)

and ${\widehat{m}}_1(s,w)$ estimates E[Z|T ≥ s, w] for each (s, w). For reasons similar to those discussed above, ${\widehat{\beta }}_{\mathit{DR}}(W)$ exhibits the doubly robustness property and so we will hereafter refer to it as the doubly robust mean. Like (5), and with no censoring, it can be shown that (8) also reduces to the corresponding node-specific sample average of the Z_is.

2.3. Survival Trees: Model Building and Cross-Validation

Similarly to the full data setting described in Section 2.1.1, justifications for the consistency of the IPCW and doubly robust loss functions obtained in the previous two subsections do not account for the adaptive nature of the tree building process. Nevertheless, with the results from Sections 2.2.1 and 2.2.2, regression trees for censored data can now be built exactly as described in Section 2.1.1, provided one replaces the average full data loss with either (4) or (6) throughout. We refer to the former as an IPCW survival tree and the latter as a doubly robust survival tree. The resulting “default” terminal node estimators respectively take the forms given by (5) or (8), though one may legitimately define and use any reasonable censored data estimate (e.g., Kaplan-Meier estimators) to summarize the final fit. The developments in Sections 2.2.1 and 2.2.2 show that the splitting decisions and associated terminal node estimators under (6) use more information in the observed data than do those under (4); hence, it is reasonable to anticipate improved performance of the doubly robust survival trees in comparison to the IPCW survival trees.

As described in Section 2.1.1, when full data are available cost complexity pruning uses the full data loss to create a sequence of subtrees (i.e., with respect to the maximum tree). Each tree in the sequence of subtrees created by cost complexity pruning is then a candidate for the final tree that will be selected and V-fold cross-validation is typically used to estimate the prediction error of each of the candidate trees and obtain the final tree. Following Sections 2.2.1 and 2.2.2, a straightforward extension of the basic procedure outlined in Section 2.1.1 suitable for censored data can be obtained by replacing the full data loss function in (2) with either the IPCW or doubly robust loss functions. In particular, given a full data loss function and following the developments of Section S.1.1 in the Supplementary Web Appendix, we can define a class of augmented cross-validated risk, or error, estimators for any candidate tree ψ_ℓ as

$$\widehat{\theta }(\ell )=\frac{1}{npV}\sum _{v=1}^V\sum _{i=1}^{n}I(S_{i,v}=1)\left(\frac{{\Delta }_{i}L(Z_i,{\widehat{\beta }}^{({\psi }_{\ell ,t{r}_v})}(W_i))}{\overline{G}(T_i|W_i)}+{\phi }_{\ell ,t{r}_v}(O_i)\right),$$ (9)

where φ_ℓ,trv (O_i) is some appropriate function of the observed training set for each i and ${\widehat{\beta }}^{({\psi }_{\ell ,t{r}_v})}(W_i)$ is the prediction from ψ_ℓ,trv (O_i) for a subject with covariate information W_i that is computed from a tree that is built using only the observations in the training set D \ D_v and then pruned using the complexity parameter associated with ψ_ℓ (i.e., the ℓ^th subtree obtained from the original tree fit). The error estimate (9) directly generalizes (2) for use with right-censored outcome data.

Using the above, we define two of several possible cross validation procedures below. First, suppose the original tree and all training set trees are built using the IPCW survival tree procedure; note that this means ${\widehat{\beta }}^{({\psi }_{\ell ,t{r}_v})}(W_i)$ is computed for each training set by calculating the terminal node estimates similarly to (5). Then, we obtain the IPCW cross-validation procedure upon setting φ_ℓ,trv (O_i) = 0 for each i in (9) above; this procedure is discussed in [9, 16]. Second, suppose the original tree and all training set trees are built using the doubly robust survival tree procedure described earlier; this means ${\widehat{\beta }}^{({\psi }_{\ell ,t{r}_v})}(W_i)$ is now computed for each training set by calculating the terminal node estimates similarly to (8). Then, we obtain the doubly robust cross validation procedure if we also define φ_ℓ,trv (O_i) in a manner that corresponds to (6); this cross-validation procedure is a novel extension of the cross-validation procedures discussed in [9, 16]. Further details on the computation of these measures can be found in Section S.1.2 of the Supplementary Web Appendix.

2.4. Computing the IPCW and Doubly Robust Loss Functions

Estimation of the conditional censoring distribution G₀(⋅|W) is required for both the IPCW loss (4) and doubly robust loss (6) functions for both model building and cross-validation. Use of (6) additionally requires a model and estimator for the conditional survivor distribution S₀(⋅|W). Methods for estimating G₀(⋅|W) and S₀(⋅|W) have not been discussed in detail; Section 3.2.1 reviews several possible approaches. Importantly, because of the repeated demand for these estimates in both model building and cross-validation, and in view of the assumptions used to justify various results in Section 2.2.2, estimates of these two distributions are to be computed in advance and treated as known throughout the entire tree building process for both the simulations and data analysis in Sections 3 and 4.

The use of pre-computed estimates $\overline{G}(\cdot |\cdot )$ and $\overline{S}(\cdot |\cdot )$ derived from the entire dataset during the tree-building and cross-validation phases merits further comment. When building trees, an alternative to using a pre-computed model-derived estimate $\overline{S}(\cdot |\cdot )$ is to dynamically recalculate this estimator as the doubly robust tree is being fit (i.e., using the current tree to estimate a new survivor function each time a split is considered). However, this approach suffers from two potential drawbacks. First, dynamic recalculation creates a significant additional computational burden in building a single tree that is only further compounded when using cross-validation for model selection. Second, splitting decisions made early in the tree building process do not use much of the available covariate information, increasing the chances that an incorrect model is used for (10) when making early decisions that govern the overall tree structure. In turn, this increases the susceptibility of the splitting process to misspecification of the censoring distribution, with early splits possibly being more sensitive to variables that influence censoring but not survival rates. Regarding cross-validation, it is well known that ensuring independence of the validation set from the tree fitting process in either the IPCW or doubly robust settings requires that both $\overline{G}(\cdot |\cdot )$ and $\overline{S}(\cdot |\cdot )$ to be derived using using only the training set. The reason why cross-validation forces the validation and the training set to be independent is that model estimation tends to adapt to the training set and therefore fits observations in the training set better than observations in an independent test set. However, using the whole dataset to compute $\overline{G}(\cdot |\cdot )$ and $\overline{S}(\cdot |\cdot )$ will clearly result in less variable estimates than might be obtained using only the training sample. More importantly, from the perspective of what is really being estimated using cross-validation, it is not obvious why using pre-computed estimators of these functions derived from the entire dataset should lead to overly optimistic risk estimators. Indeed, simulations (not shown) demonstrate that re-estimation for each training set generally results in worse performance. For all of these reasons, we have elected to use pre-computed estimates throughout the tree building and model selection phases in our simulations and data analyses.

3. Simulations

In this section we use simulation to compare the performance of the doubly robust and IPCW survival trees built using a L₂ full data loss function to each other as well as to trees built using the default exponential (Exp) method in rpart. The Exp method is equivalent to that proposed in [5], which is based on the negative log-likelihood for a Cox model with the same baseline hazard within each node. The doubly robust trees use a doubly robust loss function for splitting and cost complexity pruning and doubly robust cross-validation for selecting the final tree. The IPCW trees are fit using an IPCW loss function and IPCW cross-validation. Both methods are versions of CART and have been implemented within rpart by taking advantage of its flexibility in accommodating user-written splitting and evaluation functions [20]. The sections below describe the measures used to evaluate performance, the choices made when calculating the IPCW and doubly robust loss functions, and the results of the main simulation study.

3.1. Evaluation Measures

We now define several metrics that will be used to evaluate the performance of different tree building methods. We chose eight different measures based on the following two rules: (a) each measure contains information on how good the tree is; and, (b) each measure adds some information not contained in the other measures. For a test set consisting of n_test independent uncensored observations sampled from the full data distribution, the evaluation measures used are:

• Prediction Error (PE). Prediction error measures the ability of a regression tree to estimate the conditional expectation E[Z|W] for future observations. The prediction error for a tree ψ is defined as $\frac{1}{n_{\mathit{test}}}{\sum }_{i=1}^{n_{\mathit{test}}}{({\widehat{\beta }}^{(\psi )}(W_i)-E[Z_i|W_i])}^2$, where E[Z_i|W_i] is calculated from the underlying model used to generate the data.

• Pairwise Prediction Similarity (PPS). Pairwise prediction similarity (see [21]) measures the ability of each method to separate subjects into correct risk groups. Let I_T(i,j) and I_F(i,j) be an indicator if observations i and j have the same predicted outcome when run down the true tree and the fitted tree respectively. The pairwise prediction similarity is defined as

  $$1-\sum _{i=1}^{n_{\mathit{test}}}\sum _{j>i}^{n_{\mathit{test}}}\frac{|I_T(i,j)-I_F(i,j)|}{\left(\begin{array}{c}n\\ 2\end{array}\right)}.$$

  The range of this measure is [0,1], with higher being better. Hence, pairwise prediction similarity is the proportion of pairs of observations that get classified into the same risk group by the true and the fitted tree. This evaluation metric is independent of the actual prediction in the terminal node and thus depends mainly on the structure of the tree. For a given dataset, note that perfect similarity can be achieved even when the split points for the two trees are not exactly equal to each other.

• Absolute Survival Difference (ASD). Absolute survival difference measures how well a tree estimates the conditional survival distribution. For a given time t let S(t|W) and $\widehat{S}(t|W)$ be the true and estimated conditional survival function, respectively. The absolute t-th survival difference is defined as $\frac{1}{n_{\mathit{test}}}{\sum }_{i=1}^{n_{\mathit{test}}}|S(t|W_i)-\widehat{S}(t|W_i|$. We will use t equal to the 25th, 50th and 75th quantile of the true marginal survival distribution.

• |Size of fitted tree – size of true tree|. This metric measures how far away in absolute value the size of the fitted tree is away from the size of the true tree, hence measuring the ability of the tree building process to build trees of the correct size.

• Number of Splits on Noise Variables. This measures how often (on average) a tree includes variables that do not affect the survival time. Let n_sim be the number of simulations and NS_i be the number of times a tree includes variables that do not affect the survival time in simulation i. The number of splits on noise variables is defined as $\frac{1}{n_{\mathit{sim}}}{\sum }_{i=1}^{n_{\mathit{sim}}}N{S}_i$.

• Proportion of Correct Trees. A fitted tree will rarely be exactly equal to the correct tree; that is, it cannot be expected to split on the correct covariates at exactly the correct split points. We thus define a tree as being “correct” if it splits on all variables the correct number of times, independent of the chosen split point and the ordering of variable splits.

3.2. Calculating the IPCW and Doubly Robust Loss Functions

Below, we address several important issues related to the implementation of the IPCW and doubly robust survival methods.

3.2.1. Estimating S₀(⋅|⋅) and G₀(⋅|⋅)

As noted in Section 2.4, the IPCW and doubly robust loss functions respectively require estimates of G₀(⋅|⋅) and S₀(⋅|⋅) for implementation, the latter being needed only for calculating the function (7) that appears in the augmentation term. The Kaplan-Meier estimator can reasonably be used to estimate G₀(⋅|⋅) as long as it can be assumed that the censoring process is independent of covariates. However, it makes little sense to use this estimator for S₀(⋅|⋅) when building survival regression trees since such methods clearly presume that T depends on W in some way. Numerous parametric and semiparametric methods are available for estimating a conditional survivor function. In our simulations, we consider estimators for S₀(⋅|⋅) respectively derived from Cox regression, survival regression tree models, survival random forests, and parametric accelerated failure time (AFT) models. Each approach is described briefly below. We note here that while we focus on the problem of estimating S₀(⋅|⋅), any of the methods to be described below could just as easily be used to estimate G₀(⋅|⋅). However, as a general principle, one should try to avoid using an estimator for one of these functions that relies on the estimator for the other. This is because the incorrect specification of the model that underlies one of these estimators affects the consistency of the other, negatively impacting double robustness.

When using a Cox regression model, individual survival curves may be estimated using $\widehat{\mathbb{S}}(t|W_i)=e^{-{\widehat{\Lambda }}_0(t)e^{{\widehat{\eta }}^{\prime }{W}_i}}$, where $\widehat{\eta }$ is the estimated regression coefficient and ${\widehat{\Lambda }}_0(\cdot )$ is the estimated cumulative baseline hazard. As an alternative, one can use a survival regression tree model that employs the default exponential method (exp) in rpart; that is, the methodology proposed by [5]. In particular, suppose the fitted survival tree has K terminal nodes ${\mathcal{N}}_1,\dots ,{\mathcal{N}}_K$. Then, one first computes the Kaplan-Meier estimator ${\widehat{\mathbb{S}}}_k(t)$ using the original observations that fall into node ${\mathcal{N}}_k$ for each k; one can then define $\widehat{\mathbb{S}}(t|W_i)={\sum }_{k=1}^{K}I\{W_i\in {\mathcal{N}}_k\}{\widehat{\mathbb{S}}}_k(t)$ as the predicted survivor function under this fitted survival regression tree model. The use of a Kaplan-Meier estimator here is optional; for example, a separate parametric model could instead be used to estimate survivorship within each terminal node, the advantage being that $\widehat{\mathbb{S}}(t|W_i)$ is then guaranteed to be a proper survivor function. It is well known that ensemble procedures are able to improve upon single trees for purposes of prediction and are more nonparametric in nature than the Cox regression models. Consequently, a third option is to use the randomForestSRC package in R [22, 23] to estimate the individual survival curves. In our simulations, we used the rfsrc function, which uses the log-rank splitting rule introduced in [7]; similarly to both the Cox and regression tree methods, the associated predict function produces estimates of individual survivor curves at each ordered failure time in the observed data. Finally, one can use a parametric model to estimate S₀(⋅|⋅). For example, consider the parametric AFT model Z = μ + η′W + σΓ, where μ is an intercept, η is the model regression coefficient, σ is a scale coefficient, and Γ is a random variable with mean zero and unit variance. The model parameters can be estimated using maximum likelihood; doing so results in a survivor function estimate $\widehat{\mathbb{S}}(t|W_i)$ that is guaranteed to be proper for each i = 1, … , n.

3.2.2. Estimating (7) under L₂ loss

Regardless of how the survival curve is estimated, calculation of the augmentation term in (6) can proceed by substituting in the estimate $\widehat{\mathbb{S}}(t|W_i)$ for $\overline{S}(t|W_i)$ in (7). In the specific case of the full data L₂ loss function (Z – β(W))² with h(t) = log t, the calculation of (7) reduces to computing

$${\widehat{m}}_j(u,W_i)=\widehat{E}[Z^j|T\ge u,W_i]=-\frac{{\int }_u^{\infty }\log {(t)}^{j}d\widehat{\mathbb{S}}(t|W_i)}{\widehat{\mathbb{S}}(u|W_i)},j=1,2.$$ (10)

Usefully, all terms involving ${\widehat{m}}_2(\cdot ,\cdot )$ in (6) are actually independent of ${{\beta }^{\prime }}_{k}s$ and it can be shown that all such terms drop out of all required computations. As a result, implementation in practice for the L₂ loss only requires computation of ${\widehat{m}}_1(\cdot ,W_i),i=1,\mathrm{\dots },n$.

With the Cox, survival tree and random forest estimators for $\widehat{\mathbb{S}}(t|W)$, (10) is used provided $\widehat{\mathbb{S}}(u|W_i)-\widehat{\mathbb{S}}(+\infty |W_i)>0$ (i.e., there is at least one uncensored observation greater than u); otherwise, the estimator is taken to be equal to ${\max }_{i=1,\mathrm{\dots },n}\log {({\tilde{T}}_i)}^j$. For these methods, the integral in the numerator of (10) also reduces to calculating a finite sum since in each case $\widehat{\mathbb{S}}(t|W_i)$ only jumps at failure times. For the parametric AFT model, no adhoc adjustment to the calculation of (10) need to be made when there are no uncensored observations greater than u. For several common choices of parametric distributions for Γ, the required expectations are also available in a computationally convenient form. For example, under the indicated AFT model, calculations show that

$$m_1(u,w)=E[\log (T)|T>u,W=w]=\mu +{\eta }^{\prime }w+\sigma H(c(u,w)),$$

where H(u) = E[Γ|Γ] > u] and c(u, w) = σ⁻¹(log(u) − μ − η′w). In our simulations, we use m₁(⋅, ⋅) calculated assuming Γ, hence H(⋅), is an extreme value distribution and a standard log-logistic distribution (i.e., assuming failure times respectively follow a Weibull and a log-logistic distribution). For the extreme value distribution, calculation of the function H(⋅) relies on the ability to calculate the Exponential Integral (e.g., [24], Sec. 5.1); for the log-logistic distribution, we have H(u) = u + (log(1 + e^u) – u)(1 + e^u). Maximum likelihood estimates derived from the observed data $\mathcal{O}$ are then substituted in for all unknown parameters.

3.2.3. Selecting a truncation time τ to ensure positivity

Strictly speaking, the methodology summarized in Section 2.3 requires that an empirical version of the positivity assumption (3) holds for the observed data. It has been well documented in the causal inference literature that having probabilities in the denominator that are too close to zero can result in unstable finite sample performance for both IPCW and doubly robust estimators even when such an empirical version of this assumption holds. In practice, enforcing this assumption, hence bounding the IPCW weights, is often dealt with through the introduction of a truncation time τ (e.g., [11, 25]).

Independent of the simulation setting and the decisions that need to be made every time a full data regression tree is fit (e.g., selecting the various tuning parameters in the rpart function), one must consider the impact of introducing a truncation time τ. Two related methods of truncation, generically labeled Method 1 and Method 2, are discussed in Section S.1.3 of the Supplementary Web Appendix. Method 1 may be considered as the standard approach, and is most commonly used (e.g., [25]); Method 2 appears to be new and is of independent interest. To explore how the choice of τ and associated method of truncation influence performance under the set of metrics described in Section 3.1, we ran several preliminary simulations to help inform the choices made for the main simulation study. To ensure these evaluations reflect the modeling decisions made for S₀(⋅|⋅), performance is studied under all approximation methods in Section 3.2.2. The description of this study and the associated results may be found in Section S.2.1 of the Supplementary Web Appendix. Based on these preliminary simulation results, all simulations in the next subsection and in the data analysis of Section 4 will use truncation Method 2 with 10% truncation. This method of truncation does necessitate minor changes in the calculation of both the IPCW and doubly robust loss functions and associated terminal node estimators; this can be seen, for example, by respectively comparing (4) and (6) with (S-8) and (S-9) in Section S.1.3 of the Supplementary Web Appendix. Although little difference was observed for the method used to calculate the augmentation term in these preliminary simulations, results in the next section will be presented for all approaches described in Section 3.2.2.

3.3. Main Simulation Results

This simulation study intends to compare the performance of the doubly robust and IPCW survival trees built under L₂ loss using Z = logT to each other as well as to trees built using the default exponential (exp) method in rpart. We will summarize the results from two simulation settings. In both settings, a training set consisting of 250 independent observations from the observed data distribution and a test set of 2000 observations sampled using the full data distribution (no censoring) are generated 1000 times. Because the exp method in rpart is not based on a loss function that is minimized by some estimator of the mean survival time, a method for predicting the mean survival time is needed in order to calculate prediction error as described in Section 3.1. In an attempt to be consistent with how these particular trees are built, we first estimate the unscaled rate, say λ_k, within each terminal node ${\widehat{N}}_k$; we then estimate the mean of T for a given covariate W as if T has an exponential distribution with rate ${\sum }_k{\widehat{\lambda }}_{k}I\{W\in {\widehat{\mathcal{N}}}_k\}$.

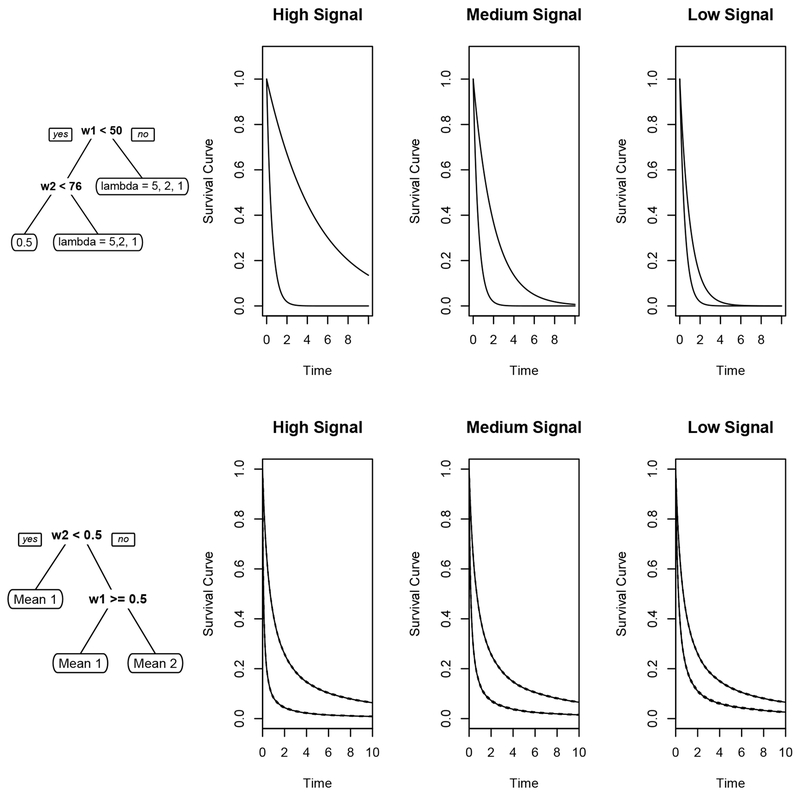
The first simulation setting (Simulation 1) is similar to the one used in [26] and is also the same setting as that used in Section 3.2.3 for determining a method and overall level of truncation. Assume there are five covariates W₁ – W₅ that are all uniformly distributed on the integers 1 – 100 and that Z = log T where the failure time T is exponential with mean parameter a equal to 5,2 or 1 if W₁ > 50 or W₂ > 75 and equal to 0.5 otherwise (i.e., high, medium, and low signal settings). The top row of Figure 1 provides a summary of the underlying models generating the survival data; observe that the correct tree has 3 nodes, with two of these on different branches having the same survival experience. Censoring is also assumed to have an exponential distribution with mean parameter chosen to achieve a 30% censoring rate; $\overline{G}$ is estimated using a Kaplan-Meier estimator. The performance of the different tree building methods for this setting is shown in Figure 2 and Table 1. The boxplots in Figure 2 show that the doubly robust trees perform better than the IPCW trees on almost all of the evaluation measures in the high and medium signal setting, and show similar performance in the low signal setting. The default method in rpart performs similarly or worse than the doubly robust methods in the high signal setting, especially in prediction error; however, it generally does as well or slightly better in the medium and low signal setting. When looking at Table 1, similar patterns emerge: the doubly robust trees tend to fit the correct tree more often, fit trees closer to the true size, and fit similarly often on noise variables compared to the IPCW tree. The proportion of trees of size 1, 2, 3, 4+ is shown in Table S-1 in Supplementary Web Appendix S.2.2. The sometimes superior performance of the exp method in rpart may be at least partly attributable to the fact that the proportional hazards assumption that underlies its development is satisfied in this setting.

Figure 1.

Summary of underlying survival models for Simulation 1 (top row) and Simulation 2 (bottom row).

Figure 2.

Boxplots for Simulation 1 for 30% censoring. Lower values imply better performance for all measures except PPS, where higher is better. IPCW is the IPCW tree building method, Exp is the default exponential rpart method, and Tree, Cox, RF, Weibull, and Log Log are the doubly robust trees fit using an augmentation term in which the required conditional expectation term is respectively estimated using a survival tree, Cox model, survival forest, and a Weibull and log-logistic parametric AFT model (see Section 3.2.2).

Table 1.

Results from Simulation 1 for 30% censoring showing proportion of correct trees (higher is better), |size – 3| (lower is better) and average number of noise variables used to split (lower is better). IPCW is the IPCW tree building method, Exp is the default exponential rpart method, and Tree, Cox, RF, Weibull and Log Log are the doubly robust trees fit using an augmentation term in which the required conditional expectation term is estimated using a survival tree, Cox model, survival forest, and a parametric Weibull and log-logistic AFT model, respectively (see Section 3.2.2).

		IPCW	Exp	Cox	Tree	Weibull	Log Log	RF
	Correct Trees	0.90	0.87	0.91	0.91	0.91	0.92	0.92
High	|Size - 3|	0.18	0.26	0.17	0.16	0.17	0.16	0.16
	Noise Var	0.10	0.12	0.09	0.09	0.10	0.10	0.09
	Correct Trees	0.60	0.81	0.74	0.75	0.73	0.73	0.72
Medium	|Size - 3|	0.37	0.32	0.35	0.35	0.36	0.37	0.42
	Noise Var	0.14	0.15	0.12	0.12	0.12	0.12	0.17
	Correct Trees	0.05	0.15	0.09	0.09	0.08	0.09	0.08
Low	|Size - 3|	1.66	1.36	1.53	1.55	1.55	1.58	1.56
	Noise Var	0.09	0.15	0.07	0.09	0.08	0.10	0.12

The second simulation setting (Simulation 2) involves a violation of the proportional hazard assumption and is similar to Setting D in [5]. Assume covariates W₁ – W₅ are independently uniformly distributed on the interval [0,1]. The event times are simulated from a distribution with survivor function S(t|W) = (1 + te^{λI(W₁≤0.5,W₂>0.5)+0.367})⁻¹ where λ = 1,1.5 and 2 respectively represents a low, medium, and a high signal setting. Denote the parameter defining this distribution as a = λI(W₁ ≤ 0.5, W₂ > 0.5); then, a = 1,1.5, or 2 when W₁ ≤ 0.5 and W₂ > 0.5 and is zero otherwise. The bottom row of Figure 1 summarizes the underlying models generating the survival data in this setting; as in Simulation 1, the correct tree has 3 nodes, with two of these on different branches having the same survival experience (i.e., for a = 0). Censoring times are uniformly distributed on [0, b] with b chosen to get a 30% censoring rate; $\overline{G}$ is again obtained using a Kaplan-Meier estimator. The results are shown in Figure 3 and Table 2. Table 2 again shows that the doubly robust trees fit a higher proportion of correct trees, build trees closer to the correct size, and fit less often on noise variables than both the IPCW and the exponential methods. Figure 3 shows that the doubly robust trees perform noticeably better than both the IPCW trees and exponential method in the high and medium setting; performance is comparable for all methods in the low signal setting. The proportion of trees of size 1, 2, 3, 4+ is shown in Table S-2 in Supplementary Web Appendix S.2.2. For both simulation settings similar trends occur when the censoring rate is 50%; see Supplementary Web Appendix S.2.2 for the corresponding figures and tables.

Figure 3.

Boxplots for Simulation 2 for 30% censoring. Lower values imply better performance for all measures except PPS, where higher is better. IPCW is the IPCW tree building method, Exp is the default exponential rpart method, and Tree, Cox, RF, Weibull and Log Log are the doubly robust trees fit using an augmentation term in which the required conditional expectation term is respectively estimated using a survival tree, Cox model, survival forest, and a parametric Weibull and log-logistic AFT model (see Section 3.2.2).

Table 2.

Results from Simulation 2 for 30% censoring showing proportion of correct trees (higher is better), |size – 3| (lower is better) and average number of noise variables used to split (lower is better). IPCW is the IPCW tree building method, Exp is the default exponential rpart method, and Tree, Cox, RF, Weibull and Log Log are the doubly robust trees fit using an augmentation term in which the required conditional expectation term is respectively estimated using a survival tree, Cox model, survival forest, and a parametric Weibull and log-logistic AFT model (see Section 3.2.2).

		IPCW	Exp	Cox	Tree	Weibull	Log Log	RF
	Correct Trees	0.68	0.64	0.82	0.82	0.82	0.82	0.81
High	|Size - 3|	0.54	0.62	0.33	0.29	0.29	0.29	0.33
	Noise Var	0.16	0.17	0.12	0.10	0.10	0.12	0.13
	Correct Trees	0.29	0.35	0.47	0.48	0.48	0.44	0.51
Medium	|Size - 3|	0.95	1.14	0.88	0.88	0.87	0.95	0.84
	Noise Var	0.12	0.16	0.16	0.15	0.15	0.17	0.13
	Correct Trees	0.05	0.08	0.11	0.11	0.10	0.09	0.10
Low	|Size - 3|	1.72	1.63	1.65	1.64	1.66	1.67	1.64
	Noise Var	0.07	0.17	0.07	0.08	0.08	0.09	0.09

Both Simulations 1 and 2 use a censoring distribution that is independent of covariates; the censoring distribution is also estimated accordingly with a product-limit estimator. In Supplementary Web Appendix S.2.3, we present additional results from simulations where the underlying censoring distribution depends on covariates and is estimated using a random survival forest procedure [23]. The results show similar trends to those summarized in this section; see Figures S-8 and S-9 and Tables S-7 and S-8 in Supplementary Web Appendix S.2.3.

Interesting features common to all simulation settings considered include (i) the general level of improvement that the doubly robust methods provide over the IPCW method, consistent with the goals of attempting to improve performance through better use of the available information; and, (ii) the relative insensitivity of these results to the choice of model used in the augmentation term, consistent with the desired double robustness property.

4. The TRACE dataset

In this section we use doubly robust trees to analyze the trace dataset, available in the R package timereg [27]. The dataset consists of 1878 randomly sampled subjects from 6600 patients collected by the TRACE study group [19]. The event of interest is death from acute myocardial infarction; subjects that were either alive when they left the study or died from other causes were considered censored. Two observations with an undefined censoring status were removed from the dataset, leaving 1876 patients. Information on age, gender, if the person had diabetes, if clinical heart pump failure was present, if the patient had ventricular fibrillation, and a measure of the heart pumping effect was also available.

Analyses in [19], conducted on the full dataset, separate out long-term (i.e., surviving beyond 30 days) and short-term survival, utilizing Cox regression for the former and logistic regression for the latter. Their analyses suggest that the effect of the ventricular fibrillation variable, an acute condition experienced in the hospital that increases the risk of death, is time-dependent with an effect that largely disappears after 60 days. The analyses in [27] utilize the first 5 variables only, excluding the information on heart pumping effect measure (a variable that appears to be strongly related to clinical heart pump failure). In the analyses presented below, we therefore focus on the subset of the data involving 1689 patients that survived beyond 30 days and include age (continuous), gender (male/female), diabetes (yes/no), clinical heart pump failure (yes/no) and ventricular fibrillation (yes/no) in our analyses. The censoring rate for this subset is 53.8%; a Cox regression model fit to the censoring distribution suggests that the censoring distribution is independent of all covariates, with a p-value from a likelihood ratio test equal to 0.536. No significant deviations from the proportional hazard assumption (i.e., for censoring) were found when tested using the cox.zph function. Hence, in the analysis below, the censoring distribution required for estimating the IPCW and doubly robust loss functions was estimated using a Kaplan-Meier estimator. In the Supplementary Web Appendix S.2.4 companion analyses on the subset of 1646 patients that survived beyond 60 days are also summarized.

We will analyze the data using several different tree building methods: the IPCW and Exp (default rpart) methods; doubly robust trees where the augmentation term is computed using four of the methods for estimating (10) as described in Section 3.2.2 (i.e., Cox, Tree, Weibull, and Log Log (log-logistic)) and also with a parametric AFT model using a log-normal distribution (Log Norm). Because most of the observations that are censored have large observed times, modifications of the survival regression tree method (i.e., Tree) and random survival forests method (i.e., RF) described in Section 3.2.2 were also considered. In particular, the TreeSM method uses the same tree as the Tree method, but estimates within-node survival curves using a node-specific parametric Weibull model in place of a Kaplan-Meier estimator; this facilitates calculation of the needed conditional expectations at larger time points. The RF SM method is a related modification of the RF procedure. Specifically, for each tree in the boostrap ensemble, we fit node-specific parametric Weibull models by maximum likelihood, obtaining an individualized set of parameter estimates for every subject in every boostrap sample; in order to have sufficient information to estimate these parameters, we set the minimum number of failures in each terminal node to be 50. It is now possible to process the resulting “forest” of parameter estimates obtained for each individual in several ways, each leading to a different final ensemble estimate of ${\widehat{m}}_1(\cdot ,W_i)$ in (10). For example, one can (a) average the Weibull parameter estimates for each individual over the boostrap samples to obtain an individual’s ensemble estimate of the Weibull parameters and then compute ${\widehat{m}}_1(\cdot ,W_i)$ using the approach described in Section 3.2.2; (b) estimate the corresponding survival curve for each subject for each boostrap sample, compute the resulting ensemble estimate $\widehat{S}(u|W_i)$ by averaging these curves over the bootstrap samples, and then use this estimate in (10) to compute ${\widehat{m}}_1(\cdot ,W_i)$; or, (c) compute a version of (10) for each bootstrap sample for each individual directly, averaging these bootstrap estimates to obtain an ensemble estimate of ${\widehat{m}}_1(.,W_i)$. Method (b) is closest to what is done in the RF method as implemented here and leads to the same final tree as Method (a). The results reported for RF SM in this section use method (c). With the exception of Exp, all trees are again estimated using L₂ loss and Z = log T using 10% Method 2 truncation. Using these choices, these analyses intend to separate patients into distinct risk groups on the basis of long-term survival, classified according to (truncated) mean log-survival time.

Using 10-fold cross-validation, the Exp method was observed to be particularly sensitive to how the dataset was partitioned into subsets, with different splits resulting in different estimates of the size of the optimal subtrees. The remaining methods demonstrated varying levels of sensitivity, with the IPCW method demonstrating greater sensitivity in comparison to the Tree, TreeSM, RF SM, Cox and the doubly robust AFT methods that make use of parametric models in computing (10), with the methods that use proper survival functions (AFT methods, TreeSM, and RF SM) being the most stable. To reduce the impact of this sensitivity on comparisons of results, we utilized repeated cross-validation for all methods, creating 100 different sets of 10-fold cross-validation sets. We calculated the cross-validation error for each of these 100 sets for each model size and averaged the results within size across the 100 different 10-fold partitions. The final tree is then selected as the tree that has the smallest average cross-validation error. This procedure has previously been shown to work well in reducing the variance of the cross-validation error in [28]. Barplots with the number of trees fit for each size for all nine methods can be found in Figure S-10 in the Supplementary Web Appendix S.2.4. These results confirm that the doubly robust trees with proper survivor functions used for computing (10) (i.e., Weibull, Log Log, Log Norm, TreeSM and the RF SM method) were the most stable and also the most conservative (i.e., fewest terminal nodes); this was followed by Cox, Tree, IPCW, and then Exp.

The four unique trees obtained using these various methods are shown in the top row of Figure 4. All of the trees built involve age; the only other variables selected, depending on the method, were clinical heart pump failure (CHF) and diabetes (Exp method only). The final trees obtained under the doubly robust AFT model (i.e., Weibull, Log Norm, Log Log), TreeSM and the RF SM methods were all the same, each having two terminal nodes with a primary split on age (< 75 vs. ≥ 75). The Cox and Tree methods built the same tree (5 terminal nodes), splitting on age first (< 72 vs. ≥ 72) in a manner similar to the doubly robust AFT, TreeSM, and RF SM methods; subsequent splits are made on CHF and then again on age (≥ 82 vs < 82) for those with CHF. This tree structure defines 3 risk groups among those with CHF by age, namely patients with ages < 72, [72, 81], and 82+ years. The terminal node estimates that appear in the trees for these 6 doubly robust methods are computed via (8) using the indicated choices of censoring and survival distribution estimators. The IPCW tree creates the same risk groups to those for the Cox and Tree methods for patients without CHF. For patients with CHF, the IPCW tree creates rather different risk groups, separating patients by ages < 68, [68,69], [70, 71], and 72+ years. Interestingly, the terminal node means in the < 68 and [70, 71] age groups are also estimated to be equal and considerably higher than the group with the shortest mean survival (i.e., those aged 68–69). The terminal node estimates that appear are computed using (5). The bottom row of Figure 4 shows the corresponding survivor curves, estimated via Kaplan-Meier within each terminal node. These curves are estimated from the untruncated survival data; that is, the truncation used to facilitate building the trees and defining the risk groups does not impact these estimated survival curves. The estimated survival curves show that the loss-based procedures (i.e., IPCW and doubly robust trees) generally do a good job of stratifying subjects into discrete, well-separated survival risk groups when compared to Exp method, which creates many overlapping survival curves and a significantly larger survival tree.

Figure 4.

Summary of results for the trace dataset restricted to patients surviving beyond 30 days obtained using different tree building methods. DR AFT represents the trees built where the required conditional expectation needed for the augmentation term is estimated using a parametric AFT model (see Section 3.2.2); the trees built in each case were all equal. The Tree, TreeSM, RF SM, and Cox methods also use doubly robust functions; see Section 3.2.2 for descriptions of the Tree,Cox and Section 4 for a corresponding description of the TreeSM and RF SM methods. The IPCW and Exp are the IPCW and exponential trees, respectively. The first row shows the final trees built for the different methods. The second row shows the Kaplan-Meier risk curves for the different trees, where each curve is estimated from the observed survival data falling into the corresponding terminal node. In the DR Cox, Tree, IPCW and Exp plots, the heavy dashed line denotes patient subgroups with CHF and the solid line denotes patient subgroups without CHF. The dotted line in the Exp and RF plots denotes terminal nodes for which no prior split was made on CHF.

We close this section with a few remarks:

1. The DR Cox and Tree methods present the most intuitively appealing stratification, with patients having CHF generally having worse survival compared to those that do not and older patients having worse survival compared to younger patients. The DR AFT, TreeSM, and RF SM methods also reflect a clear delineation by age. Such patterns are somewhat less evident with both the IPCW and Exp methods.

2. As might be anticipated from the analyses in [19], in particular Figure 3, the ventricular fibrillation variable does not add new information beyond the age and CHF variables in the above analyses. Boxplots of this variable by age (not shown) suggest that those that experienced ventricular fibrillation while in the hospital also tended to be younger by several years; the decreasing long-term risk associated with ventricular fibrillation (i.e., assuming one survives the initial event) combined with relative youth may help to explain why age and CHF, not ventricular fibrillation, appear as the most critical variables in these analyses.

3. The bottom row of Figure 4, in particular the results for the Tree and Cox, illustrates a strong similarity of the survival curves for older subjects without clinical heart pump failure and younger subjects with clinical heart pump failure; this suggests the possibility of being able to summarize these results using four rather than five groups. However, the suggested four-level risk model cannot be derived from these results because of the strongly hierarchical nature of trees (i.e., the exclusive use of ‘and’ statements in creating risk groups).

4. Results for companion analyses on the subset 1646 patients that survived beyond 60 days are summarized in the Supplementary Web Appendix S.2.4 and compared to the analyses described above. The results are generally consistent for the doubly robust and IPCW trees, in that the trees obtained for those surviving beyond 60 days can be obtained by collapsing the lowest-level pair of terminal nodes into a single group.

5. Discussion

We have proposed a modification of the IPCW-loss based recursive partitioning procedure introduced in [9] for right-censored outcomes that uses modern semiparametric efficiency theory for missing data to take better advantage of existing data. We have implemented these methods using a modification of rpart and demonstrated that the proposed methods tend to build more stable tree structures in both simulation and practice. The simulation results and data analysis suggest that these new methods are capable of building models with improved survival risk separation. Our simulation results demonstrate, in particular, the potential for substantial improvements in performance when compared to the IPCW survival tree procedure and (at worst) competitive performance with the methods of Leblanc and Crowley [5].

Some of the many interesting avenues for further research include: investigations of the impact of using alternative loss functions; improved techniques for estimating the augmentation term; studies involving the combination of doubly robust survival trees with ensemble procedures, providing an interesting competitor to methods developed in [22, 23] and [29]; extensions capable of dealing with more complex outcomes, such as competing risks and data obtained under case-cohort designs; and, asymptotic justifications of consistency (e.g., [7]). The underlying theory used to motivate these extensions does not rely on the platform for implementation; for example, exactly the same ideas can be applied to partDSA for survival outcomes [26], which currently uses IPCW loss functions to build models. The interest in extending partDSA for survival outcomes to doubly robust loss function is emphasized by the third remark at the end of Section 4, as it has the capability of constructing risk stratification rules through the use of both ‘and’ and ‘or’ statements. We intend to explore several of these extensions in subsequent work.