Networks for Joint Affine and Non-parametric Image Registration

Abstract

We introduce an end-to-end deep-learning framework for 3D medical image registration. In contrast to existing approaches, our framework combines two registration methods: an affine registration and a vector momentum-parameterized stationary velocity field (vSVF) model. Specifically, it consists of three stages. In the first stage, a multi-step affine network predicts affine transform parameters. In the second stage, we use a U-Net-like network to generate a momentum, from which a velocity field can be computed via smoothing. Finally, in the third stage, we employ a self-iterable map-based vSVF component to provide a non-parametric refinement based on the current estimate of the transformation map. Once the model is trained, a registration is completed in one forward pass. To evaluate the performance, we conducted longitudinal and cross-subject experiments on 3D magnetic resonance images (MRI) of the knee of the Osteoarthritis Initiative (OAI) dataset. Results show that our framework achieves comparable performance to state-of-the-art medical image registration approaches, but it is much faster, with a better control of transformation regularity including the ability to produce approximately symmetric transformations, and combining affine as well as non-parametric registration.

1. Introduction

Registration is a fundamental task in medical image analysis to establish spatial correspondences between different images. To allow, for example, localized spatial analyses of cartilage changes over time or across subject populations, images are first registered to a common anatomical space.

Traditional image registration algorithms, such as elastic [3, 24], fluid [5, 12, 28, 8, 30] or B-spline models [23], are based on the iterative numerical solution of an optimization problem. The objective of the optimization is to minimize image mismatch and transformation irregularity. The sought-for solution is then a spatial transformation which aligns a source image well to a target image while assuring that the transformation is sufficiently regular. To this end, a variety of different similarity measures to assess image mismatch have been proposed. For image pairs with a similar intensity distribution, Mean Square Error (MSE) on intensity differences is widely used. For multi-modal registration, however, Normalized Cross Correlation (NCC) and Mutual Information (MI) usually perform better. Besides, smooth transformation maps are typically desirable. Methods encouraging or enforcing smoothness use, for example, rigidity penalties [25] or penalties that encourage volume preservation [26, 21] to avoid folds in the transformation. Diffeomorphic transformations can also be achieved by optimizing over sufficiently smooth velocity fields from which the spatial transformation can be recovered via integration. Such methods include Large Displacement Diffeomorphic Metric Mapping (LDDMM) [5, 12] and Diffeomorphic Demons [28]. As optimizations are typically over very high-dimensional parameter spaces, they are computationally expensive.

Recently, taking advantage of deep learning, research has focused on replacing costly numerical optimization with a learned deep regression model. These methods are extremely fast as only the evaluation of the regression model is required at test time. They imitate the behavior of conventional, numerical optimization-based registration algorithms as they predict the same types of registration parameters: displacement fields, velocity fields or momentum fields. Depending on the predicted parameters, theoretical properties of the original registration model can be retained. For example, in Quicksilver [32], a network is learned to predict the initial momentum of LDDMM, which can then be used to find a diffeomorphic spatial transformation via LDDMM’s shooting equations. While earlier work has focused on training models based on previously obtained registration parameters via costly numerical optimization [6, 31], recent work has shifted to end-to-end formulations¹ [10, 14, 4, 9]. These end-to-end approaches integrate image resampling into their network and were inspired by the spatial-transformer work of Jaderberg et al. [13]. Non end-to-end approaches require the sought-for registration parameters at training time. To obtain such data via numerical optimization for large numbers of image pairs can be computationally expensive, whereas end-to-end approaches effectively combine the training of the network with the implicit optimization over the registration parameters (as part of the network architecture).

Existing deep learning approaches to image registration exhibit multiple limitations. First, they assume that images have already been pre-aligned, e.g., by rigid or affine registration. These pre-alignment steps can either be done via a specifically trained network [7] or via standard numerical optimization. In the former case the overall registration approach is no longer end-to-end, while in the latter the preregistration becomes the computational bottleneck. Second, many approaches are limited by computational memory and hence either only work in 2D or resort to small patches in 3D. Though some work explores end-to-end formulations for entire 3D volumes [4, 9], these approaches perform computations based on the full resolution transformation map, in which case a very simple network can easily exhaust the memory and thus limit extensions of the model. Third, they do not explore iterative refinement.

Our proposed approach addresses these shortcomings. Specifically, our contributions are:

• A novel vector momentum-parameterized stationary velocity field registration model (vSVF). The vector momentum field allows decoupling transformation smoothness and the prediction of the transformation parameters. Hence, sufficient smoothness of the resulting velocity field can be guaranteed and diffeomorphisms can be obtained even for large displacements.

• An end-to-end registration method, merging affine and vSVF registration into a single framework. This framework achieves comparable performance to the corresponding optimization-based method and state-of-the-art registration approaches while dramatically reducing the computational cost.

• A multi-step approach for the affine and the vSVF registration components in our model, which allows refining registration results.

• An entire registration model via map compositions to avoid unnecessary image interpolations.

• An inverse consistency loss both for the affine and the vSVF registration components thereby encouraging the regression model to learn a mapping which is less dependent on image ordering. I.e., registering image A to B will result in similar spatial correspondences as registering B to A.

Our approach facilitates image registration including affine pre-registration within one unified regression model. In what follows, we refer to our approach as AVSM (Affine-vSVF-Mapping). Fig. 1 shows an overview of the AVSM framework illustrating the combination of the affine and the vSVF registration components. The affine and the vSVF components are designed independently, but easy to combine. In the affine stage, a multi-step affine network predicts affine parameters for an image pair. In the vSVF stage, a U-Net-like network generates a momentum, from which a velocity field can be computed via smoothing. The initial map and the momentum are then fed into the vSVF component to output the sought-for transformation map. A specified number of iterations can also be used to refine the results. The entire registration framework operates on maps and uses map compositions. In this way, the source image is only interpolated once thereby avoiding image blurring. Furthermore, as the transformation map is assumed to be smooth, interpolations to up-sample the map are accurate. Therefore, we can obtain good registration results by predicting a down-sampled transformation. However, the similarity measure is evaluated at full resolution during training. Computing at low resolution greatly reduces the computational cost and allows us to compute on larger image volumes given a particular memory budget. E.g., a map with 1/2 the size only requires 1/8 of the computations and 1/8 of the memory in 3D.

Figure 1.

Our framework consists of affine (left) and vSVF (right) registration components. The affine part outputs the affine map and the affinely warped source image. The affine map initializes the map of the vSVF registration. The affinely warped image and the target image are input into the momentum generation network to predict the momentum of the vSVF registration model. The outputs of the vSVF component are the composed transformation map and the warped source image, which can be either taken as the final registration result or fed back (indicated by the dashed line) into the vSVF component to refine the registration solution.

We compare AVSM to publicly available optimization-based methods [19, 16, 23, 18, 2] on longitudinal and crosssubject registrations of 3D image pairs of the OAI dataset.

The manuscript is organized as follows: Sec. 2 describes our ASVM approach; Sec. 3 shows experimental results; Sec. 4 presents conclusions and avenues for future work.

2. Methods

This section explains our overall approach. It is divided into two parts. The first part explains the affine registration component which makes use of a multi-step network to refine predictions of the affine transformation parameters. The second part explains the vector momentum-parameterized stationary velocity field (vSVF) which accounts for local deformations. Here, a momentum generation network first predicts the momentum parameterizing the vSVF model and therefore the transformation map. The vSVF component can also be applied in a multi-step way thereby further improving registration results.

2.1. Multi-step Affine Network

Most existing non-parametric registration approaches are not invariant to affine transformations as they are penalized by the regularizers. Hence, non-parametric registration approaches typically start from pre-registered image pairs, most typically based on affine registration, to account for large, global displacements or rotations. Therefore, in the first part of our framework, we use a multi-step affine network directly predicting the affine registration parameters and the corresponding transformation map.

The network needs to be flexible enough to adapt to both small and large affine deformations. Although deep convolutional networks can have large receptive fields, our experiments show that training a single affine network does not perform well in practice. Instead, we compose the affine transformation from several steps. This strategy results in significant improvements in accuracy and stability.

Network:

Our multi-step affine network is a recurrent network, which progressively refines the predicted affine transformation. Fig. 2 shows the network architecture. To avoid numerical instabilities and numerical dissipation due to successive trilinear interpolations, we directly update the affine registration parameters rather than resampling images in intermediate steps. Specifically, at each step we take the target image and the warped source image (obtained via interpolation from the source image using the previous affine parameters) as inputs and then output the new affine parameters for the transformation refinement. Let the affine parameters be $\mathrm{\Gamma }$ = (A b) , where A ∈ ℝ^d×d represents the linear transformation matrix; b ∈ ℝ^d denotes the translation and d is the image dimension. The update rule is as follows:

$$\begin{array}{l}{A}_{(t)}={\tilde{A}}_{(t)}{A}_{(t-1)},b_{(t)}={\tilde{A}}_{(t)}{b}_{(t-1)}+{\tilde{b}}_{(t)},\\ s.t.A_{(0)}=I,b_{(0)}=0.\end{array}$$ (1)

Figure 2.

Multi-step affine network structure. As in a recurrent network, the parameters of the affine network are shared by all steps. At each step, the network outputs the parameters to refine the previously predicted affine transformation. I.e., the current estimate is obtained by composition (indicated by dashed line). The overall affine transformation is obtained at the last step.

Here, Ã_(t), A_(t) represent the linear transformation matrix output and the composition result at the t-th step, respectively. Similarly, $\tilde{b}$_(t) denotes the affine translation parameter output at the t-th step and b_(t) the composition result. Finally, if we consider the registration from the source image to the target image in the space of the target image, the affine map is obtained by ${\mathrm{\Phi }}_a^{-1}(x,\mathrm{\Gamma })=A_{\left(t_{last}\right)}x+b_{\left(t_{last}\right)}$ .

Loss:

The loss of the multi-step affine network consists of three parts: an image similarity loss L_a-sim, a regularization loss L_a-reg and a loss encouraging transformation symmetry L_a-sym. Let us denote I₀ as the source image and I₁ as the target image. The superscripts^st and^ts denote registrations from I₀ to I₁ and I₁ to I₀, respectively².

The image similarity loss L_a-sim(I₀, I_{1, ${\mathrm{\Phi }}_a^{-1}$}) can be any standard similarity measure, e.g., Normalized Cross Correlation (NCC), Localized NCC (LNCC), or Mean Square Error (MSE). Here we generalize LNCC to a multi-kernel LNCC formulation (mk-LNCC). Standard LNCC is computed by averaging NCC scores of overlapping sliding windows centered at sampled voxels. Let V be the volume of the image; x_i, y_i refer to the i^th (i ∈ {1, .., |V|}) voxel in the warped source and target volumes, respectively. N_s refers to the number of sliding windows with cubic size s × s × s. Let ${\zeta }_j^s$ refer to the window centered at the j^th voxel and ${\overline{x}}_j$, ${\overline{y}}_j$ to the average image intensity values over ${\zeta }_j^s$ in the warped source and target image, respectively. LNCC with window size s, denoted as κ_s, is defined by

$${\kappa }_s(x,y)=\frac{1}{N_s}\sum _j\frac{\sum _{i\in {\zeta }_j^s}\left(x_i-{\overline{x}}_j\right)\left(y_i-{\overline{y}}_j\right)}{\sqrt{\sum _{i\in {\zeta }_j^s}{\left(x_i-{\overline{x}}_j\right)}^2\sum _{i\in {\zeta }_j^s}{\left(y_i-{\overline{y}}_j\right)}^2}}.$$ (2)

We define mk-LNCC as a weighted sum of LNCCs with different window sizes. For computational efficiency LNCC can be evaluated over windows centered over a subset of voxels of V. The image similarity loss is then

$$\begin{array}{l}{L}_{a-sim}\left(I_0,I_1,\mathrm{\Gamma }\right)=\sum _i{\omega }_i{\kappa }_{s_i}\left(I_0°{\mathrm{\Phi }}_a^{-1},I_1\right),\\ \text{s}\mathrm{.}\text{t}\mathrm{.}{\mathrm{\Phi }}_a^{-1}(x,\mathrm{\Gamma })=Ax+b\text{and}\sum _i{\omega }_i=1,w_i\ge 0.\end{array}$$ (3)

The regularization loss L_a-reg($\mathrm{\Gamma }$) penalizes deviations of the composed affine transform from the identity:

$$L_{a-reg}(\mathrm{\Gamma })={\lambda }_{ar}\left(\Vert A-I{\Vert }_F^2+\Vert b{\Vert }_2^2\right),$$ (4)

where || • ||_F denotes the Frobenius norm and λ_ar ≥ 0 is an epoch-dependent weight factor designed to be large at the beginning of the training to constrain large deformations and then gradually decaying to zero. See Eq. 13 for details.

The symmetry loss L_a-sym($\mathrm{\Gamma }$,$\mathrm{\Gamma }$^ts) encourages the registration to be inverse consistent. I.e., we want to encourage that the transformation computed from source to target image is the inverse of the transformation computed from the target to the source image (i.e., $A^{ts}(Ax+b)+b^{ts}=x):$

$$L_{a-sym}\left(\mathrm{\Gamma },{\mathrm{\Gamma }}^{ts}\right)={\lambda }_{as}\left({\Vert A^{ts}A-I\Vert }_F^2+{\Vert A^{ts}b+b^{ts}\Vert }_2^2\right),$$ (5)

where λ_as ≥ 0 is a chosen constant.

The complete loss ${\mathcal{L}}_a\left(I_0,I_1,\mathrm{\Gamma },{\mathrm{\Gamma }}^{ts}\right)$ is then:

$$\begin{array}{l}{\mathcal{L}}_a\left(I_0,I_1,\mathrm{\Gamma },{\mathrm{\Gamma }}^{ts}\right)={\mathcal{l}}_a\left(I_0,I_1,\mathrm{\Gamma }\right)+{\mathcal{l}}_a\left(I_1,I_0,{\mathrm{\Gamma }}^{ts}\right)\\ +L_{a-sym}\left(\mathrm{\Gamma },{\mathrm{\Gamma }}^{ts}\right),\end{array}$$ (6)

where ${\mathcal{l}}_a\left(I_0,I_1,\mathrm{\Gamma }\right)=L_{\mathrm{a-}sim}\left(I_0,I_1,\mathrm{\Gamma }\right)+L_{a-reg}(\mathrm{\Gamma })$.

2.2. Vector Momentum-parameterized SVF

This section presents the momentum based stationary velocity field method followed by the network to predict the momentum. For simplicity, we describe the one step vSVF here, which forms the basis of the multi-step approach.

vSVF Method:

To capture large deformations and to guarantee diffeomorphic transformations, registration algorithms motivated by fluid mechanics are frequently employed. Here, the transformation map Φ ³ in source image space is obtained via time-integration of a velocity field v(x, t), which needs to be estimated. The governing differential equation is:${\mathrm{\Phi }}_t(x,t)=v(\mathrm{\Phi }(x,t),t),\mathrm{\Phi }(x,0)={\mathrm{\Phi }}_{(0)}(x)$ , where Φ₍₀₎ is the initial map. For a sufficiently smooth velocity field v one obtains a diffeomorphic transformation. Sufficient smoothness is achieved by penalizing non-smoothness of v. Specifically, the optimization problem is

$$\begin{array}{l}{v}^{*}=\underset{v}{\text{argmin}}{\lambda }_{vr}{\int }_0^1\Vert v{\Vert }_L^2\text{d}t+\text{Sim}\left[I_0◦{\mathrm{\Phi }}^{-1}(1),I_1\right]\\ \text{s}\mathrm{.}\text{t}\mathrm{.}{\mathrm{\Phi }}_t^{-1}+D{\mathrm{\Phi }}^{-1}v=0\text{and}{\mathrm{\Phi }}^{-1}(0)={\mathrm{\Phi }}_{(0)}^{-1},\end{array}$$ (7)

where D denotes the Jacobian and $\Vert v{\Vert }_L^2=\langle L^{†}Lv,v\rangle$ is a spatial norm defined by specifying the differential operator L and its adjoint L^†. As the vector-valued momentum m is equivalent to m = L^† Lv, one can express the norm as $\Vert v{\Vert }_L^2=\langle m,v\rangle$ . In the LDDMM approach [5], time-dependent vector fields v(x, t) are estimated. A slightly simpler approach is to use a stationary velocity field (SVF) v(x) [17]. The rest of the formulation remains the same. While the SVF registration algorithms optimize directly over the velocity field v, we propose a vector momentum SVF (vSVF) formulation which is computed as

$$\begin{array}{r}{m}^{*}=\underset{m_0}{\text{argmin}}{\lambda }_{vr}\langle m_0,v_0\rangle +\text{Sim}\left[I_0◦{\mathrm{\Phi }}^{-1}(1),I_1\right],\text{s}\mathrm{.}\text{t}\mathrm{.}\\ {\mathrm{\Phi }}_t^{-1}+D{\mathrm{\Phi }}^{-1}v=0,{\mathrm{\Phi }}^{-1}(0)={\mathrm{\Phi }}_{(0)}^{-1},v_0={\left(L^{†}L\right)}^{-1}{m}_0,\end{array}$$ (8)

where m₀ denotes the vector momentum and λ_vr > 0 is a constant. This formulation can be considered a simplified version of the vector momentum-parameterized LD-DMM formulation [29]. The benefit of such a formulation is that it allows us to explicitly control spatial smoothness as the deep network predicts the momentum which gets subsequently smoothed to obtain the velocity field, instead of predicting the velocity field v directly which would then require the network to learn to predict a smooth vector field.

Fig. 3 illustrates the framework of the vector momentum-parameterized stationary velocity field (vSVF) registration. We compute using a low-resolution velocity field, which greatly reduces memory consumption. The framework consists of two parts: 1) a momentum generation network taking as the input the warped source image, together with the target image, outputting the low-resolution momentum; 2) the vSVF registration part. Specifically, the predicted momentum and the down-sampled initial map are input into the vSVF unit, the output of which is finally up-sampled to obtain the full resolution transformation map. Inside the vSVF unit, a velocity field is obtained by smoothing the momentum and then used to solve the advection equation, ${\mathrm{\Phi }}_{(\tau )t}^{-1}+D{\mathrm{\Phi }}_{(\tau )}^{-1}v=0$, for unit time (using several discrete time points). This then results in the sought-for transformation map. The initial map mentioned here can be the affine map or the map obtained from a previous vSVF step, namely for the τ-th step, set ${\mathrm{\Phi }}_{(\tau )}^{-1}(x,0)={\mathrm{\Phi }}_{(\tau -1)}^{-1}(x,1)$.

Figure 3.

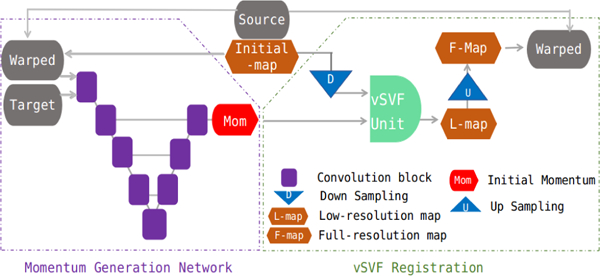
vSVF registration framework illustration (one step), including the momentum generation network and the vSVF registration. The network outputs a low-resolution momentum. The momentum and the down-sampled initial map are input to the vSVF unit outputting a low-resolution transformation map, which is then up-sampled to full resolution before warping the source image.

Momentum Generation Network:

We implement a deep neural network to generate the vector momentum. As our work does not focus on the network architecture, we simply implement a four-level U-Net with residual links [22, 15]. During training, the gradient is first backpropagated through the integrator for the advection equation followed by the momentum generation network. This can require a lot of memory. We use a fourth order Runge-Kutta method for time-integration and discretize all spatial derivatives with central differences. Therefore, to reduce memory requirements, the network outputs a low-resolution momentum. In practice, we remove the last decoder level of the U-Net. In this case, the remaining vSVF component also operates on the low-resolution map.

Loss:

Similar to the loss in the affine network, the loss for the vSVF part of the network also consists of three terms: a similarity loss L_v-sim, a regularization loss L_v-reg and a symmetry loss L_v-sym.

The similarity loss L_v-sim(I₀, I_1; Φ⁻¹) is the same as for the affine network. I.e., we also use mk-LNCC.

The regularization loss L_v-reg (m₀) penalizes the velocity field. Thus, we have

$$L_{v-reg}\left(m_0\right)={\lambda }_{vr}\Vert v{\Vert }_L^2={\lambda }_{vr}\langle m_0,v_0\rangle ,$$ (9)

where v₀ = (L^† L)⁻¹ m₀. We implement (L^† L)⁻¹ as a convolution with a multi-Gaussian kernel [20].

The symmetric loss is defined as

$$L_{v-sym}\left({\mathrm{\Phi }}^{-1},{\left({\mathrm{\Phi }}^{ts}\right)}^{-1}\right)={\lambda }_{vs}{\Vert {\mathrm{\Phi }}^{-1}°{\left({\mathrm{\Phi }}^{ts}\right)}^{-1}-id\Vert }_2^2,$$ (10)

where id denotes the identity map, λ_vs ≥ 0 refers to the symmetry weight factor, (Φ^ts)⁻¹ denotes the map obtained from registering the target to the source image in the space of the source image and Φ⁻¹ denotes the map obtained from registering the source image to the target image in the space of the target image. Consequentially, the composition also lives in the target image space.

The complete loss ${\mathcal{L}}_v\left(I_0,I_1,{\mathrm{\Phi }}^{-1},{\left({\mathrm{\Phi }}^{ts}\right)}^{-1},m_0,m_0^{ts}\right)$ for vSVF registration with one step is as follows:

$$\begin{array}{l}{\mathcal{L}}_v\left(I_0,I_1,{\mathrm{\Phi }}^{-1},{\left({\mathrm{\Phi }}^{ts}\right)}^{-1},m_0,m_0^{ts}\right)={\mathcal{l}}_v\left(I_0,I_1,{\mathrm{\Phi }}^{-1},m_0\right)\\ +{\mathcal{l}}_v\left(I_1,I_0,{\left({\mathrm{\Phi }}^{ts}\right)}^{-1},m_0^{ts}\right)\\ +L_{v-sym}\left({\mathrm{\Phi }}^{-1},{\left({\mathrm{\Phi }}^{ts}\right)}^{-1}\right),\end{array}$$ (11)

where:

$${\mathcal{l}}_v\left(I_0,I_1,{\mathrm{\Phi }}^{-1},m_0\right)=L_{\mathit{v-sim}}\left(I_0,I_1,{\mathrm{\Phi }}^{-1}\right)+L_{\mathit{v-reg}}\left(m_0\right).$$

For the vSVF model with T steps, the complete loss is:

$$\begin{array}{l}\sum _{\tau =1}^T{\mathcal{L}}_v\left(I_0,I_1,{\mathrm{\Phi }}_{(\tau )}^{-1},{\mathrm{\Phi }}_{(\tau )}^{ts-1},m_{0(\tau )},m_{0(\tau )}^{ts}\right)\text{s}\mathrm{.}\text{t}\mathrm{.}\\ {\mathrm{\Phi }}_{(\tau )}^{-1}(x,0)={\mathrm{\Phi }}_{(\tau -1)}^{-1}(x,1),\\ {\left({\mathrm{\Phi }}_{(\tau )}^{ts}\right)}^{-1}(x,0)={\left({\mathrm{\Phi }}_{(\tau -1)}^{ts}\right)}^{-1}(x,1).\end{array}$$ (12)

3. Experiments and Results

Dataset:

The Osteoarthritis Initiative (OAI) dataset consists of 176 manually labeled magnetic resonance (MR) images from 88 patients (2 longitudinal scans per patient) and 22,950 unlabeled MR images from 2,444 patients. Labels are available for femoral and tibial cartilage. All images are of size 384 × 384 × 160, where each voxel is of size 0.36 × 0.36 × 0.7mm³. We normalize the intensities of each image such that the 0.1th percentile and the 99.9th percentile are mapped to 0, 1 and clamp values that are smaller to 0 and larger to 1 to avoid outliers. All images are down-sampled to size 192 × 192 × 80.

Evaluation:

We evaluate on both longitudinal and cross-subject registrations. We divide the unlabeled patients into a training and a validation group, with a ratio of 7:3. For the longitudinal registrations, 4,200 pairs from the training group (obtained by swapping the source and the target from 2,100 pairs of images) are randomly selected for training, and 50 pairs selected from the validation group are used for validation. All 176 longitudinal pairs with labels are used as our test set. For the cross-subject registrations, we randomly pick 2,800 (from 1,400 pairs) cross-subject training pairs and 50 validation pairs; 300 pairs (from 150 pairs) are randomly selected as the test set. We use the average Dice score [11] over all testing pairs as the evaluation metric.

Training details:

The training stage includes two parts:

• 1)Training multi-step affine net: It is difficult to train the multi-step affine network from scratch. Instead, we train a single-step network first and use its parameters to initialize the multi-step network. For longitudinal registration, we train with a three-step affine network, but use a seven-step network during testing. This results in better testing performance than a three-step network. Similarly, for cross-subject registration we train with a five-step network and test with a seven-step one. The affine symmetry factor λ_as is set to 10.
• 2)Training momentum generation network: During training, the affine part is fixed. For vSVF, we use 10 time-steps and a multi-Gaussian kernel with standard deviations {0.05, 0.1, 0.15, 0.2, 0.25} and corresponding weights {0.067, 0.133, 0.2, 0.267, 0.333} (spacing is scaled so that the image is in [0, 1]³). We train with two steps for both longitudinal and cross-subject registrations. The vSVF regularization factor λ_vr is set to 10 and the symmetry factor λ_vs is set to 1e-4. For both parts, we use the same training strategy: 1 pair per batch, 400 batches per epoch, 200 epochs per experiment; we set a learning rate of 5e-4 with a decay factor of 0.5 after every 60 epochs. We use mk-LNCC as the similarity measure with (w, s) — {(0.3, S/4), (0.7, S/2)}, where S refers to the smallest image dimension. Besides, in our implementation of mk-LNCC, we set the sliding window stride to S/4 and kernel dilation to 2.

Additionally, the affine regularization factor λ_ar is epoch-dependent during training and defined as:

$${\lambda }_{ar}:=\frac{C_{ar}{K}_{ar}}{K_{ar}+e^{n/K_{ar}}},$$ (13)

where C_ar is a constant, K_ar controls the decay rate, and n is the epoch count. In both longitudinal and cross-subject experiments, K_ar is set to 4 and C_ar is set to 10.

Baseline methods:

We implement the corresponding numerically optimized versions (e.g., directly optimizing the momentum) of affine (affine-opt) and vSVF (vSVF-opt) registrations. We compare with three widely-used public registration methods: SyN [2, 1], Demons [28, 27] and NiftyReg [19, 16, 23, 18]. We also compare to the most recent VoxelMorph variant [9]. We report the performance of these methods after an in-depth search for good parameters. For Demons, SyN and NiftyReg, we use isotropic voxel spacing 1 × 1 × 1 mm³ as this gives improved results compared to using physical spacing. This implies anisotropic regularization in physical space. For our approaches, isotropic or anisotropic regularization in physical space gives similar results. Hence, we choose the more natural isotropic regularization in physical space.

Optimization-based multi-scale affine registration:

Instead of optimizing for the affine parameters on a single image scale, we use a multi-scale strategy. Specifically, we start at a low image-resolution, where affine parameters are roughly estimated, and then use them as the initialization for the next higher scale. Stochastic gradient descent is used with a learning rate of 1e-4. Three image scales {0.25, 0.5, 1.0} are used, each with {200, 200, 50} iterations. We use mk-LNCC as the similarity measure. At each scale k, let image size (smallest length among image dimensions) be S_k, here k ∈ {0.25, 0.5, 1.0}. At scale 1.0, parameters are set to (w, s) = {(0.3, S_k/4), (0.7, S_k/2)}, i.e., the same parameters as for the network version; at scales 0.5 and 0.25, (w, s) = {(1.0,S_k/2)}.

Optimization-based multi-scale vSVF registration:

We take the affine map (resulting from the optimization-based multi-scale affine registration) as the initial map and then numerically optimize the vSVF model. The same multiscale strategy as for the affine registration is used. The momentum is up-sampled between scales. We use L-BGFS, for optimization. In our experiments, we use three scales {0.25, 0.5, 1.0} with 60 iterations per scale. The same mk-LNCC similarity measure as for the optimization-based multi-scale affine registration is used. The number of time steps for the integration of the advection equation and the settings for the multi-Gaussian kernel are the same as for the proposed deep network model.

NiftyReg:

We run two registration phases: affine followed by B-spline registration. Three scales are used in each phase and the interval of the B-spline control points is set to 10 voxels. In addition, we find that using LNCC as the similarity measure, with a standard deviation of 40 for the Gaussian kernel, performs better than the default Normalized Mutual Information, but introduces folds in the transformation. In LNCC experiments, we therefore use a log of the Jacobi determinant penalty of 0.01 to reduce folds.

Demons:

We take the affine map obtained from NiftyReg as the initial map and use the Fast Symmetric Forces Demons Algorithm [28] via SimpleITK. The Gaussian smoothing standard deviation for the displacement field is set to 1.2. We use MSE as the similarity measure.

SyN:

We compare with Symmetric Normalization (SyN), a widely used registration method implemented in the ANTs software package [1]. We take Mattes as the metric for affine registration, and take CC with sampling radius set to 4 for SyN registration. We use multi-resolution optimization with four scales with {2100, 1200, 1200, 20} iterations; the standard deviation for Gaussian smoothing at each level is set to {3, 2, 1, 0}. The flow standard deviation to smooth the gradient field is set to 3.

VoxelMorph:

We compare with the most recent VoxelMorph variant [9], which is also based on deep-learning. VoxelMorph assumes that images are pre-aligned. For a fair comparison, we therefore used our proposed multi-step affine network for initial alignment. Best parameters are determined via grid search.

NiftyReg, Demons and SyN are run on a server with i9–7900X (10 cores @ 3.30GHz), while all other methods run on a single NVIDIA GTX 1080Ti.

Tab. 1 compares the performance of our framework with its corresponding optimization version and public registration tools. Overall, our AVSM framework performs best in cross-subject registration and achieves slightly better performance than optimization-based methods, both for affine and non-parametric registrations. NiftyReg with LNCC shows similar performance. For longitudinal registration, AVSM shows good performance, but slightly lower than the optimization-based methods, including vSVF-opt which AVSM is based on. A possible explanation is that for longitudinal registrations deformations are subtle and source/target image pairs are very similar in appearance. Hence, numerical optimization can very accurately align such image-pairs at convergence. VoxelMorph runs fastest among all the methods. Without initial affine registration, it unsurprisingly performs poorly. Once the input pair is well pre-aligend, VoxelMorph shows competitive results for longitudinal registrations, but is outperformed by our approach for the more challenging cross-subject registrations. To evaluate the smoothness of the transformation map, we compute the determinant of the Jacobian of the estimated map, J_ϕ (x) := |D_ϕ⁻¹ (x)|, and count folds defined by |{x : J_ϕ(x) < 0}| in each image (192 × 192 × 80 voxels in total). We also report the absolute value of the determinant of the Jacobian in these cases indicating the severity of the fold. Even though the regularization is used, numerical optimization (vSVF-opt) always results in diffeomorphisms, but very few folds remain in AVSM for cross-subject registration. This may be caused by numerical discretization artifacts, by very large predicted momenta, or by inaccuracies of the predictions with respect to the numerical optimization results. Fig. 5 shows the corresponding boxplot results. AVSM achieves small variance and high performance in both registration tasks and exhibits less registration failures (outliers). As AVSM only requires one forward pass to complete both the affine and the vSVF registration, it is much faster than using iterative numerical optimization.

Table 1.

Dice scores (standard deviation) of different registration methods for longitudinal and cross-subject registrations on the OAI dataset. Affine-opt and vSVF-opt refer to optimization-based multi-scale affine and vSVF registrations. AVSM (n-step) refers to a seven-step affine network and an n-step vSVF model. Folds (|{x : J_ϕ (x) < 0}|) refers to the average number of folds and corresponding absolute Jacobi determinant value in square brackets; Time refers to the average time per image registration.

Method	Longitudinal		Cross-subject
	Dice	Folds	Dice	Folds	Time (s)
affine-NiftyReg	75.07 (6.21)	0	30.43 (12.11)	0	45
affine-opt	78.61 (4.48)	0	34.49 (18.07)	0	8
affine-net (7-step)	77.75 (4.77)	0	44.58 (7.74)	0	0.20
Demons	83.43 (2.64)	10.7 [0.56]	63.47 (9.52)	19.0 [0.56]	114
SyN	83.13 (2.67)	0	65.71 (15.01)	0	1330
NiftyReg-NMI	83.17 (2.76)	0	59.65 (7.62)	0	143
NiftyReg-LNCC	83.35 (2.70)	0	67.92 (5.24)	203.3 [35.19]	270
vSVF-opt	82.99 (2.68)	0	67.35 (9.73)	0	79
VoxelMorph(w/o aff)	71.25 (9.54)	2.72 [1.57]	46.06 (14.94)	83.0 [18.13]	0.12
VoxelMorph(with aff)	82.54 (2.78)	5.85 [0.59]	66.08 (5.13)	39.0 [3.31]	0.31
AVSM (2-step)	82.60 (2.73)	0	67.59 (4.47)	5.5 [0.39]	0.62
AVSM (3-step)	82.67 (2.74)	3.4 [0.12]	68.40 (4.35)	14.3 [1.07]	0.83

Figure 5.

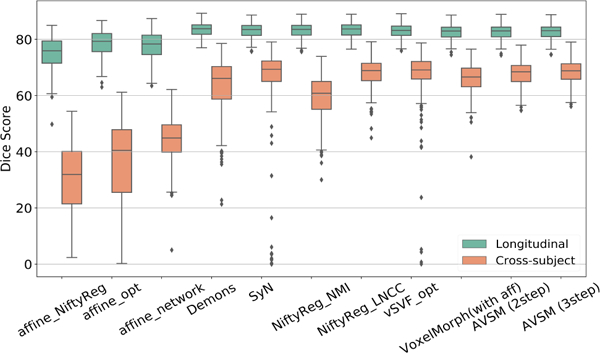
Box-plots of the performance of the different registration methods for longitudinal registration (green) and cross-subject registration (orange). Both AVSM and NiftyReg (LNCC) show high performance and small variance.

Tab. 2 shows results for an ablation study on AVSM. For the affine part, it is difficult to train the single-step affine network without the regularization term. Hence, registrations fail. Introducing multi-step and inverse consistency boosts the affine performance. Compared with using NCC as similarity measure, our implementation of mk-LNCC improves results greatly. In the following vSVF part, we observe a large difference between methods IV and VI, illustrating that vSVF registration results in large improvements. Adding mk-LNCC and multi-step training in methods VII and VIII further improves performance. The exception is the vSVF symmetry loss which slightly worsens the performance for both longitudinal and cross-subject registration, but results in good symmetry measures (see Fig. 6).

Table 2.

Ablation study of AVSM using different combinations of methods. Af- and vSVF- separately refer to the affine and to the vSVF related methods; Reg refers to adding epoch-dependent regularization; Multi refers to multi-step training and testing; Sym refers to adding the symmetric loss; MK refers to using mk-LNCC as similarity measure (default NCC). Except for the last approach which uses vSVF-Sym (last row) and encourages symmetric vSVF solutions, all other approaches result in performance improvements.

Method	Af-Reg	Af-Multi	Af-Sym	Af-MK	vSVF	vSVF-MK	vSVF-Multi	vSVF-Sym	Longitudinal	Better?	Cross-subject	Better?
I									-		-
II	✓								55.41	✓	28.68	✓
III	✓	✓							64.78	✓	36.31	✓
IV	✓	✓	✓						68.87	✓	37.54	✓
V	✓	✓	✓	✓					77.75	✓	44.58	✓
VI	✓	✓	✓	✓	✓				80.71	✓	59.21	✓
VII	✓	✓	✓	✓	✓	✓			81.64	✓	64.56	✓
VIII	✓	✓	✓	✓	✓	✓	✓		82.81	✓	69.08	✓
IV	✓	✓	✓	✓	✓	✓	✓	✓	82.67	✗	68.40	✗

Figure 6.

Illustration of symmetric loss for AVSM. The left column shows the source and target images. The right column shows the warped image from a network trained with and without symmetric loss. The deformation with symmetric loss is smoother.

We still retain the symmetric loss as it helps the network to converge to solutions with smoother maps as shown in Fig. 6. Instead of using larger Gaussian kernels, which can remove local displacements, penalizing asymmetry helps regularize the deformation without smoothing the map too much and without sacrificing too much performance. To numerically evaluate the symmetry, we compute $\left(\frac{1}{|V|}\Vert {\mathrm{\Phi }}^{-1}°{\left({\mathrm{\Phi }}^{ts}\right)}^{-1}-id{\Vert }_2^2\right)$ for all registration methods, where V refers to the volume size and Φ the map obtained via composition of the affine and the deformable transforms. Since different methods treat boundaries differently, we only evaluate this measure in the interior of the image volume (10 voxels away from the boundary). Fig. 7 shows the results. AVSM obtains low values for both registration tasks, confirming its good symmetry properties. Both Demons and SyN also encourage symmetry, but only AVSM shows a nice compromise between accuracy and symmetry.

Figure 7.

Box-plots of the symmetry evaluation (the lower the better) of different registration methods for longitudinal registration (green) and cross-subject registration (orange). AVSM (tested with two-step vSVF) shows good results.

Fig. 8 shows the average Dice sores over the number of test iteration steps of vSVF. The model is trained using a two-step vSVF. It can be observed that iterating the model for more than two steps can increase performance as these iterations result in registration refinements. However, the average number of folds also increases, mostly at boundary regions and in regions of anatomical inconsistencies. Examples are shown in the supplementary material.

Figure 8.

Multi-step vSVF registration results for two-step vSVF training. Performance increases with steps (left), but the number of folds also increases (right).

Conclusions and Future Work

We introduced an end-to-end 3D image registration approach (AVSM) consisting of a multi-step affine network and a deformable registration network using a momentum-based SVF algorithm. AVSM outputs a transformation map which includes an affine pre-registration and a vSVF non-parametric deformation in a single forward pass. Our results on cross-subject and longitudinal registration of knee MR images show that our method achieves comparable and sometimes better performance to popular registration tools with a dramatically reduced computation time and with excellent deformation regularity and symmetry. Future work will focus on also learning regularizers and evaluations on other registration tasks, e.g. in the brain and the lung.

Figure 4.

Illustration of registration results achieved by AVSM, each column refers to an example. The first five rows refer to source, target, warped image by AVSM, warped image with deformation grid (visualizing Φ⁻¹), warped image by multi-step affine respectively, followed by source label, target label and warped label by AVSM separately. There is high similarity between the warped and the target labels and the deformations are smooth.