Acoustic streaming vortices enable contactless, digital control of droplets

The switching of acoustic streaming vortices allows the contactless gating and routing of microliter droplets with scalability.

Abstract

Advances in lab-on-a-chip technologies are driven by the pursuit of programmable microscale bioreactors or fluidic processors that mimic electronic functionality, scalability, and convenience. However, few fluidic mechanisms allow for basic logic operations on rewritable fluidic paths due to cross-contamination, which leads to random interference between “fluidic bits” or droplets. Here, we introduce a mechanism that allows for contact-free gating of individual droplets based on the scalable features of acoustic streaming vortices (ASVs). By shifting the hydrodynamic equilibrium positions inside interconnected ASVs with multitonal electrical signals, different functions such as controlling the routing and gating of droplets on rewritable fluidic paths are demonstrated with minimal biochemical cross-contamination. Electrical control of this ASV-based mechanism allows for unidirectional routing and active gating behaviors, which can potentially be scaled to functional fluidic processors that can regulate the flow of droplets in a manner similar to the current in transistor arrays.

INTRODUCTION

For decades, the goal of laboratory automation and miniaturization has inspired the microfluidic community to develop integrated, programmable fluidic processors to automate complex reactions. To perform more sophisticated tasks, stackable fluid logic components (e.g., pneumatic valves and droplet-based units) have been integrated into fluidic processors to perform basic logic operations. Similar to the use of electrons or photons in digital materials, basic logic operations such as routing and gating encoded on rewritable media (i.e., electric circuits and optical waveguides) are essential for building functional modules and controlling any digital materials (1). Droplets, which are widely used as “micro–test beakers,” can be considered as an unconventional digital material (2) that share similar features with common digital materials but have adverse fluidic characteristics (e.g., adsorption and diffusion-induced contamination) that lead to random interference between operations. As a result, complicated setups are often required to overcome the difficulties associated with processing droplets as a digital material.

Generally, automated fluidic processors use a variety of different mechanism to manipulate droplets, including electrokinetics (3–7), acoustics (8–16), optics (17), magnetics (2, 18), mechanics (19), hydrodynamics (20, 21), and surface tension (22–24), leading to applications including on-chip bioassays, high-throughput compound screening, and biochemical synthesis (21), as well as various droplet processing strategies that follow serial (3, 21, 25), stepwise (4–6, 26), and digital logic rules (2, 27–29). One widely adopted droplet processing strategy is to regulate two-phase flow using microchannels and passive structures to sequentially generate, merge, mix, and split trains of droplets to perform high-throughput reactions (e.g., droplet barcoding) (25). Another popular strategy uses electrowetting forces to flexibly manipulate droplets on a two-dimensional (2D) surface using stepwise feedback control, allowing dynamic programmability and precise spatiotemporal control of droplet-based reactions (4–6, 26). Beyond those two well-established droplet processing strategies, the digital control of droplets has been explored to test the feasibility of droplet-based logic operations. Air bubble–based “computations” pioneered this concept on the basis of the hydrodynamic interactions between air bubbles in delicate microchannel networks (27). The digital logic control of water droplets was then demonstrated using similar concepts in microfluidics and the collision of water droplets falling along the tracks on a tilted, superhydrophobic substrate (29). In a more complex demonstration of digital droplet-based logics, the algorithmic control of water droplets was later realized by synchronizing the transport and interactions of ferrofluid droplets sandwiched between permalloy-patterned substrates using rotating global magnetic fields (2). Besides droplets, the digital logic control of fluids has also been achieved using microfluidic pneumatic valves, including microfluidic transistors, multiplexers, clock oscillators, and storage arrays (28, 30), based on the dynamic control or self-regulation of pressures within microfluidic channels. In addition, surfaces with anisotropic wetting nanostructures can transport fluids spontaneously with diode-like behaviors (i.e., topological liquid diodes) (23). Conclusively, those efforts exemplify the long pursuit of researchers to develop an integrated fluidic processor from stackable fluid logic components that can be programmed to perform automated matrices of biochemical reactions.

Despite these various innovations in droplet manipulation strategies, few mechanisms allow for the development of droplet-based logic units with rewritability, a necessary step in performing Boolean logic operations in fluidic circuits. The fluidic rewritability of droplet-based logic units is mostly constrained by contamination between droplets due to surface adsorptions on contacting solid structures (31) and the diffusion of small-molecule chemicals in the carrier oils (32), especially for applications involving oils with conventional surfactants. Ideally, a droplet actuation event should not adversely interfere with or contaminate future operations on the same unit to ensure the maximum reusability and integration potential of units. Mechanisms using long-range forces can eliminate solid-liquid contact and offer the potential for rewritable droplet processing. Acoustic levitation (9, 10, 16) uses acoustic radiation forces to suspend and transport aqueous droplets in open air via dynamic wave superposition but is limited by issues such as droplet evaporation, trapping instability, and complicated feedback control required for precision positioning in 3D space. Besides droplet manipulation in air, dielectrophoresis (4), magnetics (18), and streaming-induced hydrodynamic forces (33) have been demonstrated for the 2D manipulation of aqueous droplets floating on a dense oil layer in a stepwise manner.

Here, we present an acoustofluidic mechanism that allows the contact-free gating of individual droplets on rewritable fluid paths in oil via acoustic streaming vortices (ASVs), which are generated by increasing the excitation voltage amplitude over a critical threshold (V_T, at a nonlinear Reynolds number near 0.07). Different from the known acoustic streaming pattern of an immersed interdigitated transducer (IDT) (34), at an excitation amplitude above V_T, two ASVs will be formed along the two flanks of an IDT inside the oil layer and spin in the opposite direction to the direction of the surface acoustic wave (SAW) propagation. Therefore, a droplet in the vicinity of these ASVs will be translated toward an equilibrium point over the transducer between the vortices. By carefully aligning multiple ASVs generated by transducers with varied resonant frequencies, a long virtual channel for spatially translating the droplet will be formed over the transducer array inside the carrier oil. Using periodic multitonal signals, synchronized droplet transport is realized by shifting the hydrodynamic equilibrium positions continuously without external feedback control. By tuning the input period of multitonal signals and reconfiguring the layout of the IDTs, different fundamental operations necessary for droplet-based processing such as routing and gating are achieved, which can be analogous to electronic diode- or transistor-like behaviors. Furthermore, with ASVs, a single IDT can induce two distinct acoustic streaming patterns for biaxial droplet actuation with two types of input signals (i.e., low and high excitation amplitudes), which is consistent with particle tracking experimental results and numerical simulations. This ASV-based mechanism enables contactless, digital control of droplets on miniaturized, rewritable units and can potentially scale up to create functional fluidic processors that can control and regulate the flow of droplets similar to the current in transistor arrays.

RESULTS

Generation of ASVs

Figure 1A is a schematic illustrating a typical droplet processing unit that generates the ASVs. As shown in Fig. 1A, the interconnected array of IDTs is fabricated on a Y-128°–cut LiNbO₃ wafer that is immersed in a dense carrier oil (i.e., FC-40; ρ = 1.85 g·cm⁻³). The localized acoustic streaming is generated by the acoustic attenuation of leaky SAWs and locally coupled waves inside the thin layer of carrier fluid that covers the excited transducer.

Fig. 1. ASV-based droplet manipulation.

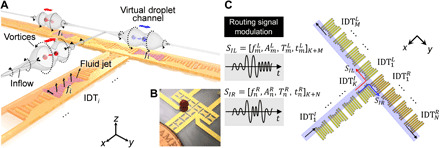
(A) Schematic showing a typical droplet processing unit. The droplets (i.e., red and blue spheres) over the transducers are guided into the center between the barrel-like ASVs (labeled as Vortices) following the recirculating inflow. These droplets are unidirectionally routed along the linear array of IDTs by shifting the sequence of working frequencies. The portions of the IDTs shaded in purple (e.g., IDT_i) indicate that they are being excited by a high-amplitude signal with frequency f_i. (B) The photo shows a bifurcated device with a particle floating above the transparent carrier oil layer. (C) The general control schematic for the droplet processing unit. The unit is composed of K + M + N interconnected IDTs [denoted as ${\text{IDT}}_k^I$, ${\text{IDT}}_m^L$, and ${\text{IDT}}_n^R$ (k = 1,2, …, K; m = 1,2, …, M; n = 1,2, …, N)] with tuned working frequencies. Multitonal signals (i.e., S_IL or S_IR) encoded with a series of different frequencies, amplitudes, durations, and initiation times (i.e., ${[f_m^L,A_m^L,T_m^L,t_m^L]}_{K+M}$ or ${[f_n^R,A_n^R,T_n^R,t_n^R]}_{K+N}$) are the excitation signals into the droplet processing unit and can direct the droplet from ${\text{IDT}}_1^I$ to the left or right port, respectively. The blue shaded area indicates the resulting virtual bifurcated channel for droplet translation. Photo credits: Peiran Zhang, Duke University.

Once a high-amplitude excitation signal is applied to the transducer, strong fluid jets will be generated in the oil layer above the transducer. When these fluid jets impinge on the air-oil interface, they will recirculate vigorously, interact with boundaries, and form “barrel-like” ASVs (labeled as “Vortices” in Fig. 1A) along the two flanks of the transducer. Conversely, in the far field, the immersed transducer acts to pump oil inward (labeled as “Inflow” in Fig. 1A) along the directions opposite to the SAW propagation. Therefore, a droplet near one aperture of an excited IDT_i will be rotated and guided into the ASVs by the inflow (Fig. 1A) and eventually be trapped at an equilibrium position. The transducers in the T-shaped array in Fig. 1A have different working frequencies (f₁, f₂, f₃…) and thus can be synchronized to generate ASVs for droplet trapping at designated times and positions via frequency-modulated signals. These resulting spatially overlapping ASV regions form a virtual channel to translate the droplet along the transducer array. The droplets (indicated by the red and blue spheres) floating on the virtual channel will be guided into the ASVs following the inflow and then are automatically routed along the IDT array, following the shifting of the input signals. A picture of the bifurcated device is shown in Fig. 1B. As shown in Fig. 1C, the input signal for exciting the bifurcated path consists of four independent parameters: frequency, amplitude, duration, and initiation time. Using the multitonal signals with predetermined parametric signal combinations, the droplet can be routed from ${\text{IDT}}_1^I$ to ${\text{IDT}}_M^L$ or ${\text{IDT}}_N^R$ using modulated signals of S_IL or S_IR, respectively, with minimum external feedback control.

To better understand this ASV-based droplet actuation mechanism, a finite-element method (FEM) simulation of the 3D acoustic streaming pattern for high-amplitude acoustic wave–fluid interactions (34, 35) is calculated (fig. S1 and note S1) in a 3 mm (x) by 3 mm (y) by 1.04 mm (z) space. This is spatially consistent with the particle tracing experiments using both low- and high-amplitude excitations. Here, we only show several 2D cross sections of the model (Fig. 2) to simplify the visualization, and the complete 3D acoustic streaming model is shown in fig. S1 and note S1. Figure 2 (A and B) shows the acoustic-induced streaming pattern in the xy plane obtained from the particle tracing experiments for low-amplitude (Fig. 2A and movie S1) and high-amplitude (Fig. 2B and movie S2) excitation. The corresponding simulation results are presented in Fig. 2 (C and E and D and F, respectively). The immersed transducer serves as a micropump that pushes fluid outward following the trajectories of the blue arrows, and the red arrows indicate inward flow. Under low-amplitude excitations (Fig. 2A), a butterfly-shaped streaming pattern forms, and the fluid is pumped inward along the ±x directions and outward in the ±y directions following the directions of SAW propagation. Under high-amplitude excitations (Fig. 2B), the directions of inflow and outflow are reversed (Fig. 2, A and B) and the ASVs will be generated along the two flanks of the immersed transducer. Simulation results in Fig. 2 (C to F) confirm the reversal of flow directions in the far field of the xz plane on the surface of oil layer under high-amplitude excitations; however, the positions of the symmetric hydrodynamic equilibrium points, or traps, remain similar (black asterisks).

Fig. 2. Mechanism of droplet actuation via ASVs.

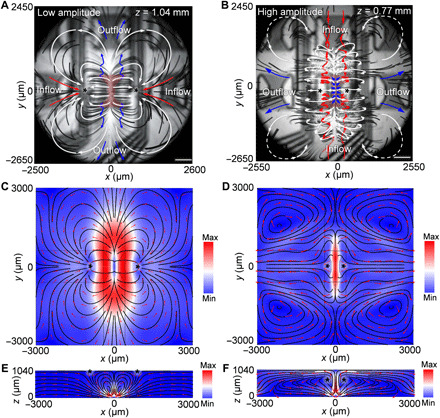
(A) The xy-plane composite image of particle trajectories generated from stacked, bottom-view images of particles near one flank of a transducer when excited by a low-amplitude signal near the surface of the oil (z = 1.04 mm). (B) xy plane of particle trajectories generated from the stacked, bottom-view images of particles near one flank of a transducer when excited by a high-amplitude signal beneath the surface of the oil (z = 0.77 mm). The blue arrows indicate the trajectories of fluid being pumped outward. Red arrows indicate the trajectories of fluid pumping inward. White arrows indicate the trajectories of recirculating flows. The shaded red areas indicate the location of the actuated transducers. (C) Numerical simulation results showing the acoustic streaming pattern in the xy plane (z = 1.04 mm) with a low-amplitude excitation signal. (D) Numerical simulation results showing the acoustic streaming pattern in the xy plane (z = 0.77 mm) with a high-amplitude excitation signal. Simulation results showing the acoustic streaming pattern in the xz plane (y = 0 mm) with (E) a low- and (F) a high-amplitude excitation signal. The black asterisks indicate the hydrodynamic equilibrium positions. Scale bars, 500 μm.

As seen in Fig. 2B, the ASVs can be decomposed into two parts: the inflow vortices (red arrows) and the channel vortices (white arrows outlining a barrel shape) along the two flanks of the transducer. Inside the two channel vortices, two pairs of inflow vortices (Fig. 2B, red arrows) gradually converge to the midpoints of the two flanks of the transducer near the surface of oil. Following the inflow vortices, a droplet near one aperture of the transducer will be rotated and guided inside the channel vortices (36) toward the equilibrium position at the midpoint of the flanks of transducer. At one equilibrium position, the ASVs converge and form highly localized vortices with gradually diminishing y velocities. This stabilizes the droplet in the y direction. In the x and z directions, a droplet, with a comparable size to the vortices, can be stably confined inside the vortices because of the zero time-averaged x and z acceleration.

2D particle image velocimetry (PIV) analysis is performed to characterize the transition of the acoustic streaming patterns from Fig. 2A (low amplitude) to Fig. 2B (high amplitude). Figure 3A shows the distribution of particle xy velocities in the region around the ASVs region (fig. S2) on the top surface of oil layer. The peak of the particle velocity distribution gradually shifts from 14 to 36 mm·s⁻¹ as the excitation voltage increases from 8.8 Vpp (Fig. 2A) to 14.8 Vpp (Fig. 2B). A switch in the directions of the inflow and outflow (Fig. 2, A and B) is clearly measured when sweeping the excitation voltages. As shown in Fig. 3B, the peak of the x-velocity distribution of the flow away from the flanks of the transducer (fig. S2) shifts from 1.8 to 2.5 mm·s⁻¹. At the threshold excitation voltage (i.e., V_T, 11.8 Vpp), particles are both approaching toward (x velocity < 0) and escaping from (x velocity > 0) the transducer, as observed in the particle tracking experiments and velocimetry analysis. A similar transition in the peak of the y-velocity distributions can be observed near the aperture region of the transducer (fig. S2), as measured in Fig. 3C. A mixed acoustic streaming pattern combining both low- and high-amplitude patterns can be observed at the threshold excitation voltage (i.e., V_T). The gradual transition of the acoustic streaming pattern from Fig. 2A to Fig. 2B is confirmed in our 3D acoustic wave–fluid interaction model as the SAW amplitude increases in a stepwise manner (fig. S3).

Fig. 3. PIV analysis with increasing excitation amplitude.

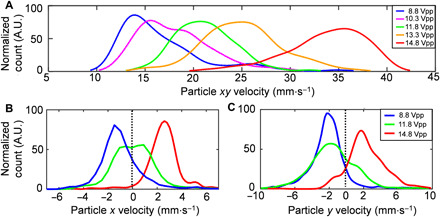
(A) The particle velocity distributions around the ASVs (z = 1.04 mm; on the oil surface) as the excitation voltage is increased. A.U., arbitrary units. (B) The velocity distribution of the particles, escaping from the transducer along x axis (i.e., x velocity) over the flanks of the transducer (z = 1.04 mm; on the oil surface), shifts toward the right side of the graph as the excitation voltage increases. (C) The velocity distribution of the particles moving away from the transducer along the y axis (i.e., y velocity) near the aperture of the transducer (z = 0.77 mm; inside the carrier oil) also shifts to the right in the graph as the excitation voltage increases. The dashed line indicates zero particle velocity (i.e., static particles). Note that the particle trajectories of the higher speed inflow are obscured by those of the overlapping channel vortices. (B) and (C) share the same legend. The normalized particle count is derived through PIV analysis on small regions of interest (ROIs) and then normalized simplified visualization of the data. The ROIs for (A) to (C) are indicated by dashed squares in fig. S2.

To further characterize the two acoustic streaming modes, we measured the typical acoustic pressures and streaming velocities under different excitation amplitudes from 2.8 to 14.8 Vpp and calculated the nonlinear Reynolds number (note S2) in our device. For the low-amplitude streaming pattern, the average acoustic pressure is 25 kPa (at 8.8 Vpp) and increases to 40 kPa for high-amplitude streaming (at 14.8 Vpp; fig. S4A). Calculated using the measured streaming velocity, the nonlinear Reynolds number is 0.04 for the low-amplitude excitation scenario and 0.1 for the high-amplitude excitation scenario (fig. S4B). Although both cases seem to correspond to slow streaming (37), at the higher acoustic power, the acoustic streaming shows an unusual experimentally observed phenomenon by generating a reverse fluid motion (Fig. 2B). Aktas and Farouk (38) also observed two different streaming patterns when the nonlinear Reynolds number was 0.08 and 0.1. A possible explanation is that when the nonlinear Reynolds number is about 0.1, the acoustic streaming is within the transition between slow and fast streaming, which may lead to irregular fluidic responses under the relatively high acoustic excitation. Our FEM simulation solved for the flow pattern for both cases, and these results show that the calculated flow fields indeed matched the experimental results.

To explore the phenomenon of reversion of flow at V_T, we further investigated the relationship between the oil thickness and the threshold voltage V_T for transiting from x-mode to y-mode acoustic streaming (fig. S5). Generally, as the thickness of oil increases, the threshold voltage V_T, as well as its associated nonlinear Reynolds number, decreases. In fig. S5, as the excitation voltage increasing, the threshold voltage V_T (b) (blue triangles) is defined as the voltage in the first frame in the particle tracing video when reversed flow appears near the flanks of the dual-mode IDT (dmIDT) (i.e., the region b shown in fig. S2) along the x axis. The threshold voltage V_T (c) (i.e., the red circles) is defined as the voltage in the first frame in the particle tracing video when reversed flow appears near the apertures of the dmIDT (i.e., the region c shown in fig. S2) along the y axis (i.e., the directions of SAW propagation). Below the excitation voltage V_T (b) (blue triangles in fig. S5), the dmIDT exhibits an x-mode acoustic streaming pattern (Fig. 2A) and the droplets can be actuated along the x axis. Above excitation threshold voltage V_T (c), the dmIDT demonstrates y-mode acoustic streaming (Fig. 2B) and the droplets can be actuated along the y axis. The transiting threshold voltage V_T is the mean value of V_T (b) and V_T (c), which involves a mixed mode of x-mode and y-mode acoustic streaming. For the scenarios with oil thickness lower or equals to 0.6 mm, the threshold excitation voltage V_T cannot be observed within 2 to 20 Vpp. As the oil thickness is increased above (or is equal to) 2.0 mm, the threshold excitation voltage V_T and the x-mode acoustic streaming disappear. This is probably due to the long distance between the air-oil boundary and the fact that the transducer plane is too far; in which case, the flows circulate locally near the transducer and cannot induce recirculating inflows in the observation plane (i.e., z = 1.4 mm) or attract a droplet along the x axis. However, V_T (c) and the transition to y-mode streaming can be clearly identified in the particle tracing video when the oil thickness is above 2.0 mm. Furthermore, as the excitation voltage was increased from 10 to 130 Vpp, another threshold voltage (V_T′) for the transition of fluidic behaviors was observed at a nonlinear Reynolds number within 1.8 to 2.8, which is discussed in detail in note S3 and figs. S6 to S8.

Dual-mode droplet actuation via ASVs

In this section, we demonstrate a dmIDT that can actuate droplets along both the x and y axes using one transducer. By applying different excitation amplitudes, the immersed transducer exhibits two distinct acoustic streaming patterns with reversed flow directions in the far field and can actuate droplets along the x and y axis (i.e., x and y mode, respectively). At a low excitation voltage (i.e., 8.8 Vpp), the transducer pumps fluid outward along the y axis and pumps fluid inward along the x axis. Two hydrodynamic potential wells are formed on the surface of the oil near the two flanks of the transducer. In this situation, a droplet near the flanks of the dmIDT will move toward one of the hydrodynamic potential wells located along the x axis and be repulsed along the y axis (fig. S9A, x mode). When a high excitation voltage (i.e., 14.8 Vpp) is applied, two pairs of symmetric ASVs are formed along the y axis near the two apertures of the dmIDT and extend to the flanks of the dmIDT. In this mode, a droplet near the two apertures will be translated along the y axis inside the ASVs and reach an equilibrium position near the midpoints of the flanks of the dmIDT (fig. S9B, y mode). Notably, the direction of the horizontal movement of the droplet is the opposite direction of the propagation directions of the SAWs on the LiNbO₃ substrate. Figure 4 (A and B) shows the experimentally obtained, time-elapsed images of droplet trapping using a single dmIDT (fig. S10) under x- and y-mode actuation along the x and y axes, respectively. Note that the geometry of the dmIDT is optimized for the robust trapping of droplets over a wide range of volumes (note S4 and figs. S11 and S12). Movie S3 shows the process of droplet trapping in y-mode actuation with particle trajectories to aid in tracing the flow direction. The trajectory of a droplet under y-mode actuation is shown in Fig. 4C. The droplet is rotated and translated to the flank of transducer following the inflow vortices, rendering a curved trajectory with high acceleration at the beginning and gradual deceleration as it approaches the equilibrium point. Note that the air-oil interface is not mandatory for generating ASVs for droplet actuation in y mode, which is further discussed in note S5 and fig. S13. For a trapped droplet, because of conservation of momentum at the immiscible oil-water interface and the small size of the droplet, the internal streaming (Fig. 4D and movie S4) within the trapped droplet enables efficient mixing of liquids and microparticles. As time goes by, those microparticles would gradually be concentrated to two separate equilibrium positions inside the droplet (Fig. 4E) when trapped by a y-mode–actuated dmIDT. For droplet trapping, evaporation-induced volume loss can be substantial, especially for droplets at nanoliter scale. However, the volume loss can be minimized when the droplet is being trapped beneath the oil surface by ASVs, allowing submicroliter droplet incubation on an open-chamber device (note S6 and fig. S14). Figure S15 shows the relationship between the droplet diameter and the step time (i.e., the time required to move a droplet by 1.9 mm) in the x and y mode. Generally, the droplet actuation speed in the y mode is faster than the speed in the x mode. Thus, the excitation duration of the dmIDTs need to be changed when moving the droplet along the different axes.

Fig. 4. Dual-mode droplet actuation via ASVs.

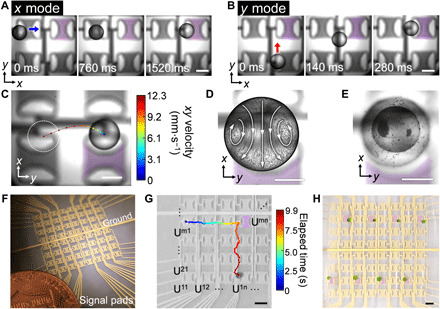
Time-lapse images showing the droplet actuation processes (A) along the x direction under low-excitation amplitudes (i.e., 8.8 Vpp, 49.125 MHz) and (B) along the y axis using high-excitation amplitudes (i.e., 14.8 Vpp, 49.125 MHz). (C) The time-elapsed trajectory of the nanoliter droplets actuated by the ASVs. The color scale indicates the horizontal velocity of the droplet. (D) Internal streaming inside a trapped droplet (observed from the bottom) is visualized by stacking the time-elapsed trajectory of 10-μm polystyrene particles. (E) Particles are concentrated within the droplet after 60 s of trapping. (F) Image of a contactless fluid processor with an array of 64 independent dmIDT units. (G) The time-elapsed motion of the droplet along the transducer array. The dmIDT units are denoted as U^mn (m, n = 1, 2, 3 …). The purple shading indicates a transducer unit (U⁴⁴) that initiates the change in the direction of droplet movement. As the droplet is being held by unit U⁴⁴, the excitation signal is switched from x mode to y mode. (H) Simultaneous trapping of eight droplets operating in y mode. Scale bars, 500 μm (A to E) and 1 mm (G and H). The purple shadings indicate excited IDTs. Photo credits: Peiran Zhang, Duke University.

As shown in Fig. 4F, a fluidic processor consisting of an 8 by 8 array of independent dmIDT units is realized on an area of 2 cm by 2 cm on the LiNbO₃ wafer. The actual measured operating voltage is below 10 Vpp for the x-mode actuation and 15 Vpp for y mode because of the lower viscosity of the carrier fluid (1.8 centistokes) and the smaller actual dimensions of the transducer. The horizontal movement of a droplet can be dynamically programmed by exciting the adjacent transducers with different amplitudes in a relayed manner, as shown by the time-elapsed droplet trajectory in Fig. 4G. When a transducer is broken in the array, the droplets can be actuated by a secondary neighboring transducer, which gives advantages in error recovery (note S7 and fig. S16). Figure S17 (A and B) demonstrates the influences of the thickness of the oil layer and the excitation voltage on the average speed of a 0.95-mm polystyrene sphere (density, 1 g·cm⁻³; volume, 450 nl) actuated a distance of one step (i.e., 1.9 mm) using a dmIDT in x and y mode. Basically, excitation voltages of 4.3 to 11.8 Vpp and oil thicknesses of 0.89 to 1.19 mm can be used to actuate the droplet using the x-mode dmIDT; excitation voltages of 14.5 to 20 Vpp (>20 Vpp will not be practical for devising controlling electronics) and oil thicknesses of 0.89 to 1.19 mm can be used to actuate the particle using the y-mode dmIDT. However, parameter combinations with high deviations in droplet speed (fig. S17, C and D) should be avoided. The current choice of oil thickness and excitation voltage for x-mode actuation (i.e., blue cross marks) has a good balance of speed and consistency. In addition, the range of workable excitation voltages for y-mode droplet actuation is much wider than that of x mode (i.e., >13.2 Vpp). Here, we chose a relatively lower excitation voltage (i.e., red cross marks) for y mode to ensure scalability of dmIDTs to reduce the heat generated for gating radio frequency signals.

Because of the low operating voltages (8.8 to 14.8 Vpp) to actuate the dmIDTs, simultaneous trapping (Fig. 4H) and movement (movie S5) of multiple droplets are realized. In the event that a droplet drifts away from the virtual fluidic path, the recirculating flows in the far field will restabilize the drifting droplet and consistently return it to the desired position, as shown in fig. S18. This feature adds robustness to the droplet manipulation mechanism yet raises issues concerning cross-talk between units, which may hinder the ability to simultaneously manipulate multiple droplets. Thus, as a tradeoff, this mechanism needs a larger spatial separation between neighboring droplets as compared with mechanisms like electrowetting on dielectrics to minimize acoustohydrodynamic interference, typically with the minimum droplet separation distances (for droplet trapping) of 1 mm along the x axis and 5.7 mm along the y axis (fig. S19). For independent droplet actuation, the minimum separation distance for independent actuation along the x axis is 3.8 mm (Fig. 4H) and 5.7 mm along the y axis to avoid acoustohydrodynamic interference.

Droplet merging via ASVs is feasible. As shown in fig. S20, the two droplets are first brought close to each other because of acoustic streaming and become trapped by a single transducer. Then, the transducer is switched off to allow the two droplets to contact one another following the “Cheerios effect” and eventually merge with each other. A floating droplet can also be on-demand split by the acoustic streaming but with relatively high excitation voltages (i.e., 60 to 100 Vpp). The details of droplet merging and splitting are further discussed in the Supplementary Materials (note S8 and fig. S21).

Contactless, unidirectional gating and routing of droplets via ASVs

As aforementioned in the first section, under high-amplitude acoustic excitations, the ASVs can extend to adjacent transducers to rotate and translate droplets inside the channel vortices. Those vortices effectively form a short virtual channel for droplet transportation. To achieve unidirectional routing function, we input different working frequencies into the transducers (i.e., f₁, f₂, f₃, …) to form a longer virtual path via acoustic streaming. In this configuration, the ASVs generated by different transducers will overlap coaxially in space to form a longer path for droplet transport. As shown in Fig. 5A, the three aligned transducers each have different working frequencies although they share the same electrical connections. When a periodic frequency-modulated signal (e.g., f₁ – f₂ – f₃ – f₁ – …) is applied to any row or column of transducers in the array, the immersed transducers are excited and ASVs are generated sequentially along the flanks of the series of excited transducers at the corresponding working frequencies. This is similar to the widely used “chirped IDT” or “slanted IDT” in principle yet with a different spatial arrangement and geometry. The key idea for designing the multitonal excitation signal is to ensure that the droplet is always close to the next excited transducer and its ASVs are actuated in the desired direction. Thus, the hydrodynamic equilibrium position will be periodically shifted from left to right along the flanks of the transducers, establishing a contact-free, unidirectional virtual channel for droplet transportation (movie S6). The original design has been further refined from a long chirped IDT (fig. S22) with a similar modulated frequency signal as it propagates along the transducer array to reduce nonspecific actuation and to enhance robustness.

Fig. 5. Contactless, unidirectional droplet gating and routing via ASVs.

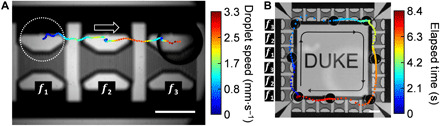
(A) Contactless, unidirectional droplet gating. The “f” indicates the working frequency of the corresponding transducer, from left to right: 45.125, 52.125, and 49.125 MHz. The initial position of the droplet is marked by the white dashed circle. (B) The time-elapsed unidirectional circular routing of a droplet using 24 interconnected dmIDTs triggered by periodic frequency-modulated signals. The device background is removed to show the droplets more clearly. The black arrows and lines indicate the directions of droplet motion. Scale bars, 1 mm. Photo credits: Peiran Zhang, Duke University.

Figure 5A demonstrates the time-elapsed trajectory of a droplet being transported unidirectionally, which can potentially serve as a passive gating unit. This gating direction can be reversed by reversing the frequency-shifting sequence of the frequency-modulated signal. The droplet transport speed can be tuned by adjusting the power and the time interval of the frequency shifting of the applied frequency-modulated signal. Movie S7 demonstrates the repetitive translation of a particle at a speed of two steps per second. Expanding on this unidirectional droplet routing unit, by generating these ASVs in a virtual closed loop (i.e., using 24 interconnected IDT units), the droplet can be automatically transported in a circular path in a contact-free manner with no external relay control (Fig. 5B and movie S8). Note that all the transducers share the same two electrical connections (i.e., the same signal path and the same ground wire) and the frequency-modulated signal synchronizes the transducers to shift the positions of the ASVs. The layout of the dmIDT units could be reconfigured to perform contactless, unidirectional droplet routing on programmable paths without external feedback control.

To validate the rewritability of these logic units, we measured any diffusion-induced contamination in the FC-40 carrier oil. Different from commonly used carrier oils used in microfluidics (e.g., mineral and silicone oil), Fluorinert FC-40 is oxygen permeable, chemically inert, and highly resistant to the diffusion of small molecules (note S9). Therefore, it is an ideal fluid to contain biosamples and to isolate the droplet from the piezoelectric substrate. Fluorescent dyes (i.e., fluorescein and rhodamine 6G) are used in the coincubation experiments with FC-40 to characterize diffusion. Our coincubation test results indicate that the signal from any diffused fluorescein into the FC-40 is close to the detection limit; therefore, it cannot be regarded as a viable marker to measure diffusion. Figure S23 demonstrates the diffusion of rhodamine 6G into FC-40 under different incubation times (0.5, 1, 2, 4, and 8 hours) and at different temperatures (room temperature, 30°C, and 55°C). The diffusion of rhodamine 6G is close to the detection limit of the plate reader at room temperature and does not exceed 8 × 10⁻⁵% in the worst-case scenario (8 hours, 55°C). Note that rhodamine 6G diffused most effectively in a lighter version of Fluorinert oil (Novec 7500) according to the study of Gruner et al. in 2016 (32), indicating a minimum risk of diffusion-induced cross-contamination for routine reagents that have a low molecular diffusivity. Furthermore, we performed on-chip coincubation experiments with two attached droplets on substrates (i.e., one droplet contains water only and the other one contains 100 μM rhodamine 6G) with ASVs and a separation distance of 4 mm. As shown in fig. S24, the diffusion from a dyed droplet to an empty droplet is below 2.5 × 10⁻⁴% (i.e., 11-hour coincubation). The detailed experimental procedure is shown in Materials and Methods. Thus, droplets filled with common reagents can be repetitively processed reusing the same fluidic paths with minimum diffusion into, and consequently cross-contamination from, the FC-40 carrier layer.

Active gating and bifurcated routing of droplets via ASVs

Gating and bifurcated routing (i.e., sorting) along reusable paths are fundamental functions necessary for optimized, automated fluidic processing. In this section, we demonstrate contactless droplet gating and bifurcated routing by programming ASVs. The active droplet gating unit consists of three subparts (Fig. 6A): (i) the input transducer array, (ii) the gating transducer, and (iii) the output transducer array. Similar to the unidirectional droplet transport in the previous section, for the input/output transducer arrays, the immersed transducers with different working frequencies are arranged periodically on the wafer (i.e., input array, f₁ – f₂ – f₃ – f₁ – f₂ – f₃; output array, f₂ – f₃ – f₁ – f₂ – f₃; Fig. 6A) so that the droplet will be automatically translated along the virtual paths following the sequence of different frequency components of the input signal. Then, a gap is added between the input and output transducer arrays to prevent the droplet from passing through the gate without the gating signal. A gating transducer with a working frequency of f₄ is placed at the gap between the input and output channels, of which the ASVs (Fig. 6A, red shaded area) can extend to the two adjacent transducers. Note that the input and output transducer arrays share the same two electrical connections (i.e., signal and ground wire) and, thus, all the transducers can receive the synchronized frequency-modulated signals. When applying a periodic series of multitonal signals (f₁ – f₂ – f₃ – f₁ …) to the input and output channel transducer arrays, the droplet on the input path (Fig. 6A, left) will be automatically translated to the right and then remain in the input path since the gating signal is OFF (Fig. 6B). When the gating pulse is ON, the ASVs are generated over the gating transducer and connect the ends of input and output channels, allowing the droplet to cross the gap (Fig. 6C). When the gating signal pulse is OFF, the droplet will be trapped by the first transducer (f₂) on the right side of the gap and then spontaneously move along the output path (Fig. 6D and movie S9), demonstrating an active gating behavior like early-stage transistors. Note that to release and transmit the trapped droplet through the gap, the timing of gating pulse needs to be synchronized with that of f₁ in the periodic frequency-modulated signal to avoid interfering with f₃, which is easily achieved using the same synchronized clock cycles. Similarly, this active gating behavior can be demonstrated in a reversed direction (Fig. 6E) by simply reversing the periodic multitonal signals (f₃ – f₁ – f₂ – f₃ – ….) on the input and output paths.

Fig. 6. Active gating and bifurcated routing of droplets via ASVs.

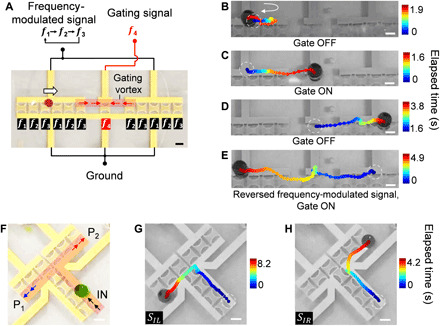
(A) Schematics and images of an active droplet gating device. The red arrows indicate the direction of droplet movement once the gating vortex is formed. The white arrow indicates the default droplet movement direction. (B to E) Time-lapse droplet trajectories when the gating signal (i.e., f₄, 41.59 MHz) is (B) OFF and (C to E) ON. (B) The droplet cannot pass the gate and remains in the input channel when the gate is OFF. (C and D) The droplet passes the gate when the gating signal is ON. (E) When the frequency-shifting signal is reversed, the droplet can move from the output channel to the input channel. (F) Schematics and device image of a bifurcated droplet routing unit via ASVs. The red shaded area indicates the location of the ASVs that form the virtual path for droplet transportation. Output port P₁, Port₁ (left turn); P₂, Port₂ (right turn). (G and H) Automatic bifurcated droplet routing using different frequency-modulated signals, S_IL [left turn (G)] and S_IR [right turn (H)]. Scale bars, 500 μm. Photo credits: Peiran Zhang, Duke University.

The bifurcated droplet routing unit is shown in Fig. 6F. The working frequencies of the transducer array of the channel on the left are arranged differently; thus, the distribution of ASVs can be changed by two series of multitonal signals with different frequencies and frequency sequences. The droplet can be guided to the left path (Fig. 6G, blue arrows) with the S_IL excitation signal or to the right path (Fig. 6H, red arrows) with the S_IR excitation signal (movie S10). Currently, the highest translation speed for gating and sorting is 300 to 340 ms per step, corresponding to the highest gating and sorting throughput of 0.18 event s⁻¹ (fig. S25A) and 0.5 event s⁻¹ (fig. S25, B and C), respectively. By actively controlling the spatial and temporal distribution of the ASVs with periodic and synchronized signals, these basic functional units have also enabled reusability of the same droplet paths. This has the potential of scaling up to create complex fluid processors by the rational stacking of these functional switching units with minimal external feedback control.

DISCUSSION

We have demonstrated contactless manipulation of individual droplets on rewritable units with digital switching functionality via programmable control of ASVs. In principle, the transducer immersed in oil demonstrates a counterintuitive flow pattern with scalable features of ASVs as the excitation voltage is increased over a critical voltage (V_T, at a nonlinear Reynolds number near 0.07). At the high amplitudes, two symmetric ASVs are established along the flanks of the immersed transducer and extend to adjacent transducers. Those vortices force a droplet near the transducer’s aperture area to be rotated, translated, and lastly trapped near the midpoints of the flanks of transducer, allowing for droplet motion along the y axis, which is counterintuitively in the opposite direction to the propagation directions of the SAWs in the xy plane.

The ASVs are barrel shaped and, when multiple transducers are sequentially actuated under high-amplitude excitation, can be connected to form a long virtual channel for droplet translation. By applying different working frequencies in a frequency-modulated signal to a linear array of high amplitude–mode transducers connected electrically in parallel, the generated ASVs enable unidirectional transportation and passive gating of the droplet along the transducer array. This is similar to the function of a diode in an electrical circuit that can be used for the passive gating and synchronized routing of individual droplets. On the basis of this unidirectional routing mechanism, droplets can be routed in an arbitrary prescribed pattern without external feedback control. As a simple demonstration, those virtual channels can also be designed in a bifurcated manner to allow the distribution of droplets using two sets of multitonal signals. Furthermore, by adding an independent gating transducer in the gap between two virtual paths, a unit has been developed with active gating functionalities. Conclusively, these contact-free droplet functional units (i.e., routing and gating) allow for rewritable, fundamental droplet processing units on reusable paths with minimized unit size and the need for external control and can potentially scale to functional fluidic processors by rational stacking like early-stage electronics. In addition, under low-amplitude excitations, the flow directions are reversed in the far field and can translate droplets along the x axis. Therefore, with these two different types of acoustic streaming patterns, droplets can be actuated along the x and y axes with low- and high-amplitude excitations using only one transducer. Moreover, our device’s ability to reuse virtual paths, which leads to “droplet rewritability,” is a major advantage of this fluidic handling method. With our approach, the floating droplets are isolated from the piezoelectric substrate, and thus, cross-contamination is effectively eliminated because of surface adsorption.

From the experiments on unidirectional droplet gating and routing using multitoned signals, each transducer unit will not have identical actuation under the same excitation amplitude because of frequency-dependent wave attenuation in the carrier oil. Therefore, it is necessary to compensate for this performance variation by adjusting the amplitudes of the excitation signals for individual transducers by using a programmable function generator. This is the reason why a series of different frequencies with varied amplitudes is required. In addition, the variation in the parasitic inductances and impedances from the electric interconnections of different transducers can be compensated by tuning the signal amplitude or adjusting the inductance and impedance of the transducers off-chip.

The advantages of contactless droplet routing and gating provided by this ASV-based design enable automated processing of fluids on rewritable paths with minimal external feedback control. As more ASV-based functional units are developed, they can be integrated into compact, rewritable fluidic processors. Leveraging the scalability of microelectronics fabrication techniques combined with the design analogy of computational logic units and reusable paths, our ASV-based devices can be used as the basic functional units of complex fluidic processors for biomedical and biochemical applications in the near future.

MATERIALS AND METHODS

Reagents and materials

The Fluorinert FC-40 carrier oil is purchased from Millipore Sigma Co., Merck KGaA, Darmstadt, Germany. The LiNbO₃ substrates are purchased from Precision Micro-Optics Inc., MA, USA. The flow tracers are silver-coated polymethyl methacrylate (PMMA) particles that are 30 μm in diameter (density, 1.8 g cm⁻³), and they are purchased from Cospheric LLC, CA, USA.

Electronics

The device is powered and controlled with a sinusoidal ac signal from a function generator (DG 3012C, Teletronics Technology Corporation, PA, USA) and an amplifier (25A250A, Amplifier Research, USA). A customized MATLAB code has been developed to control the function generator to generate the appropriate periodic frequency-modulated signals. The detailed descriptions of the supporting electronics are shown in note S10 and figs. S26 and S27. Furthermore, we devised an echo-based sensor for detecting the thickness of the oil (note S11 and fig. S28).

Device fabrication and operations

A 5-nm thick Cr and a 125-nm-thick Au were deposited on a Y-128°–cut lithium niobate wafer (Precision Micro-Optics, USA) after patterning using standard photolithography. The electrical connections between the chip and external wires were made using silver epoxy (MG Chemicals, USA). A network analyzer was used to determine the optimum device operating frequency before operation. The dimensions of the transducer were 1.18 mm in length and 0.87 mm in width. The pitch distance between transducers was 1.95 mm. The 64 IDTs share two ground wires and can be actuated individually via 64 signal wires. Table S1 presents an overview of the operational parameters of the device shown in Fig. 4F. Further considerations on the selection of parameters are discussed in note S12. For the transducer array and droplet gating devices, the wave propagation direction is coincident with the x axis of the Y-128° LiNbO₃ single crystal wafer. For the circular droplet translation and droplet routing on bifurcated paths, the SAW propagation direction is 45° rotated with respect to the x axis of the Y-128° LiNbO₃ single crystal wafers.

2D PIV

Silver-coated PMMA particles with a density similar to that of the Fluorinert oil were used for tracing the acoustic streaming. The bottom-view videos were captured using a digital camera at 500 frames per second in the bright field. Small regions of interest (ROIs) were selected to calculate the xy velocity of particles passing through the ROIs following fig. S2. The ROIs were meshed, and the velocity vectors were averaged in each element. The element counting results were normalized for display clarity. Details can be found in note S13.

Acoustic pressure measurement

The acoustic pressure generated by the dmIDT was measured using a hydrophone (HGL0085, Onda Corporation, USA) mounted on a customized 3D motorized stage with an oscilloscope (DPO4104, Tektronix, USA). We found that there is no significant change in acoustic pressure when changing the immersed medium (i.e., FC-40 or water) and when changing the position of the hydrophone within our amplitude range. Therefore, we used water for acoustic pressure measurements instead of oil and positioned the hydrophone directly above the dmIDT (1 mm) to avoid damaging the hydrophone. The measured amplitudes of the electric pulses were processed using a Fourier transform and then were calibrated to derive the acoustic pressure.

Diffusion characterization

Fluorescein and rhodamine 6G were dissolved in pure water to a final concentration of 100 μM. A total of 500 μl of dye solution was dispensed with 700 μl of Fluorinert FC-40 oil into 1.5-ml tubes for incubation. The incubation tests had different elapsed times (0.5, 1, 2, 4, and 8 hours) and environment temperatures (20°, 30°, and 55°C). After incubation, triplicate 200 μl of FC-40 oil were carefully transferred from each tube from bottom to top to a 96-well plate for fluorescence measurement using a plate reader (490-nm excitation/525-nm emission for fluorescein and 480-nm excitation/550-nm emission for rhodamine 6G; Synergy HT, BioTek Instruments Inc., USA). On-chip characterization of diffusion is as follows: A 2.5-μl rhodamine 6G droplet and a 2.5-μl water droplet were placed on the substrate of the y-mode transducer instead of being trapped by ASVs, which ensures long-period incubation with minimal volume loss due to evaporation. The two droplets were placed at the two apertures of the y-mode transducer with a separation distance of 4 mm (“IDT ON, 1 drop”; fig. S24). Another 2.5-μl water droplet was placed away from the transducer with a separation distance of 4 mm to minimize the influence of ASVs on cross-contamination, which represents scenarios of transducer OFF (“IDT OFF, 1 drop”; fig. S24). Three pairs of 2.5-μl rhodamine 6G droplets and 2.5-μl water droplets were tested using three y-mode transducers but in a single reservoir to characterize the scenarios of parallel droplet control (“IDT ON, 3 drops”; fig. S24). After 0.5, 1, 2, 4, and 11 hours of coincubation, those water droplets were carefully collected using a pipette and diluted to 50 μl using distilled water for the fluorescence measurement using plate reader (Synergy H1; 480-nm excitation and 550-nm emission). The detected fluorescence intensities were converted to the concentration of rhodamine 6G using calibration curves and then multiplied by the dilution factor 20 (i.e., to 50 μl) to obtain the final concentration of rhodamine 6G. As a control, the diffusion between 50-μl rhodamine 6G droplets and a 50-μl water droplet was characterized on a 24-well plate (“OFF, on plate”).

Droplet manipulation

For droplet manipulation using the transducer array, the transducers are excited in a relayed manner to move the droplets horizontally. The signal used for x-mode droplet actuation is 8.8 Vpp at 49.125 MHz for a single transducer. The signal used for y-mode droplet actuation is 14.8 Vpp at 49.125 MHz for a single transducer. The oil thickness is 1.17 mm. For the devices in which the wave propagation direction is rotated 45° with respect to the x axis of the Y-128° LiNbO₃ single crystal wafer, the signal frequency is changed to 44.59 MHz because of the change in the wave velocity in this direction. The wavelengths of the transducers used for droplet rotation are as follows: 74.5 μm (f₁), 80 μm (f₂), and 85.5 μm (f₃). The wavelengths of the transducers used for the gating device are as follows: 85.5 μm (f₁ and f_gate), 80 μm (f₂), and 74.5 μm (f₃). The wavelengths of the transducers used for the bifurcated droplet routing device are as follows: 74.5, 80, 85.5, and 112 μm. The wavelengths of the transducers were optimized to 60, 70, 90, and 112 μm for high-speed operation (fig. S25).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/24/eaba0606/DC1