Improving the reliability of computational analyses: Model-based planning and its relationship with compulsivity

Abstract

Background:

Computational models show great promise in mapping latent decision-making processes onto dissociable neural substrates and clinical phenotypes. One prominent example in reinforcement learning (RL) is model-based planning, which specifically relates to transdiagnostic compulsivity. However, the reliability of computational model-derived measures like model-based planning is unclear. Establishing reliability is necessary to ensure such models measure stable, trait-like processes, as assumed in computational psychiatry. Although analysis approaches affect validity of RL models and reliability of other task-based measures, their effect on reliability of RL models of empirical data has not been systematically studied.

Methods:

We first assessed within- and across-session reliability, and effects of analysis approaches (model estimation, parameterization, and data cleaning), of measures of model-based planning in patients with compulsive disorders (n=38). The analysis approaches affecting test-retest reliability were tested in three large generalization samples (healthy participants: ns=541/111; people with a range of compulsivity: n=1413).

Results:

Analysis approaches greatly influenced reliability: reliability of model-based planning measures ranged from 0 (no concordance) to above 0.9 (acceptable for clinical applications). The largest influence on reliability was whether model estimation approaches were robust and accounted for the hierarchical structure of estimated parameters. Improvements in reliability generalized to other datasets and greatly reduced the sample size needed to find a relationship between model-based planning and compulsivity in an independent dataset.

Conclusions:

These results indicate that computational psychiatry measures like model-based planning can reliably measure latent decision-making processes, but when doing so must assess the ability of methods to estimate complex models from limited data.

Introduction

Generative models of neurobehavioral processes, particularly reinforcement learning (RL) models, are increasingly used in psychiatric research. Components of these models represent unobservable latent processes that relate to neurobiological functioning, enabling translation between clinical and basic research(1). In particular, measures of model-based planning, a commonly used RL measure, show relationships with symptoms of obsessive-compulsive disorder, transdiagnostic compulsivity symptoms, and treatment effects(2–4). Model-based planning, as measured by the ‘two-step task’(5), assesses the degree of learning from cognitively flexible internal models of the world versus model-free learning from direct experience of reward.

This computational psychiatry approach assumes that generative models reliably measure a stable, trait-like latent process; however, this assumption is rarely tested. In contrast to self-report and clinical interview measures, which focus on reliability during measure development, development of task-based measures like model-based planning ignores reliability(6). Other task-based measures, such as dot-probe measures of attention bias, lack reliability despite their foundations in basic research on latent processes(7). In the case of attention bias, this poor reliability undermined confidence that these measures accurately represented latent processes and, by extension, whether they were appropriate to assess differences in psychopathology(8). Unfortunately, the reliability of many attention bias measures was not investigated in earnest until after studies, including clinical trials with patients, failed to show expected effects. Assessing whether computationally-derived measures like model-based planning can reliably measure constructs of interest prior to clinical deployment is necessary to avoid such translational failures. To date, test-retest and split-half reliabilities of computationally-derived learning and decision making measures, including model-based planning, range from poor to good(6,9–12). This pattern of findings suggests: 1) model-based planning varies within and across sessions and is unsuitable as a stable, trait-like measure, or 2) model-based planning is stable but poor measurement adds noise and decreases reliability. In addition to generative models, which directly map latent processes onto observed behavior, model-based planning is often measured with non-generative models approximating RL dynamics (i.e., trial-level logistic regression(2,5,13)). Non-generative approaches are simpler but whether this approximation reduces reliability is unclear. Work on validity of reinforcement learning models, using synthetic data, has shown that good validity is possible but depends on the quality of measurement(14,15). Hierarchical Bayesian models, which partially pool data and account for uncertainty within and across levels, perform better than non-hierarchical and non-Bayesian estimation approaches(14), Model parameterization further affects validity, with highly interrelated parameters more difficult to recover accurately(16,17). These investigations have focused primarily on assessing recovery of simulated data, but not whether measures assess stable constructs in empirical data from real participants (i.e., reliability). Factors affecting reliability may include model estimation and parameterization as well as removing data from contaminated trials and inattentive participants (which affects reliability in other performance-based measures(7)); however, the effects of these factors on reliability have not been systematically investigated.

Therefore, the goal of the present work was to assess reliability of model-based planning within and across sessions, focusing on a patient sample whose behavior is hypothesized to be sensitive to this measure. Specifically, we assessed measures of model-based planning on the ‘two step task’(5) in people with clinically elevated compulsive symptoms(2). We focused on model-based planning in the two-step task as a prominent example of a computational model-derived measure related to individual differences (e.g., (18–26)). Participants completed the task at two assessment points, approximately one week apart. We sought to answer two questions: 1) what is the maximum possible reliability of computationally-derived measures, particularly model-based planning, on this task? and 2) what approaches affect reliability? To develop empirical recommendations on how to optimize reliability in this task, we comprehensively tested combinations of different model estimation, model parameterization, and data cleaning approaches on between-session (test-retest) and within-session (split-half) reliability to determine which approaches affected reliability and which combination led to the best reliability. We then applied the approaches affecting reliability to three large generalization datasets to assess effects on reliability and strength of relationships with external clinical variables in these datasets.

Methods and Materials

Participants

The primary dataset comprised adults aged 18–55 who endorsed clinical levels of compulsive symptoms (N = 38); further participant details are described in the Supplement. All participants provided informed consent and all study procedures were approved by the University of Pittsburgh Institutional Review Board.

The primary dataset used participants tested in a controlled laboratory setting during a short test-retest interval (approximately one week) to minimize variance in performance. The strong relationship between model-based planning and compulsivity also motivated determining reliability in a clinical sample of interest. To determine if results found in this dataset generalized to other populations, reliability in two large, publicly available datasets of repeated assessments of the two-step task(6,11) was also assessed (N=541, N=111). Since the task administrations and populations systematically differed from the primary dataset, potentially leading to less stable measurement (adolescents tested 1–3 years apart, during which model-based learning shows developmental changes(23), and in online participants tested 4–6 months apart as part of an exhaustive task and self-report battery), the goal was establishing whether measures affecting reliability in our original dataset also affected reliability in these datasets. We additionally tested whether approaches differing in reliability affected the strength of relationships with clinical measures using a dataset (N=1413) from a previously published manuscript finding reductions in model-based learning with transdiagnostic compulsivity(2). Details on participants and procedures are reported in the Supplement.

Task

Participants in the primary sample completed 100 trials of the two-step task(5,23) (Figure 1), measuring model-based planning, as part of the task battery at each visit. The Supplement contains full task details; briefly, participants chose between two stimuli at the first stage, which each had a 70% probability of leading to one second stage option (common transition) and a 30% probability of leading to the other (rare transition). Transition probabilities for one option were the inverse of the other. Each second stage option had two additional stimuli, each leading to a probabilistic reward.

Figure 1. Task schematic.

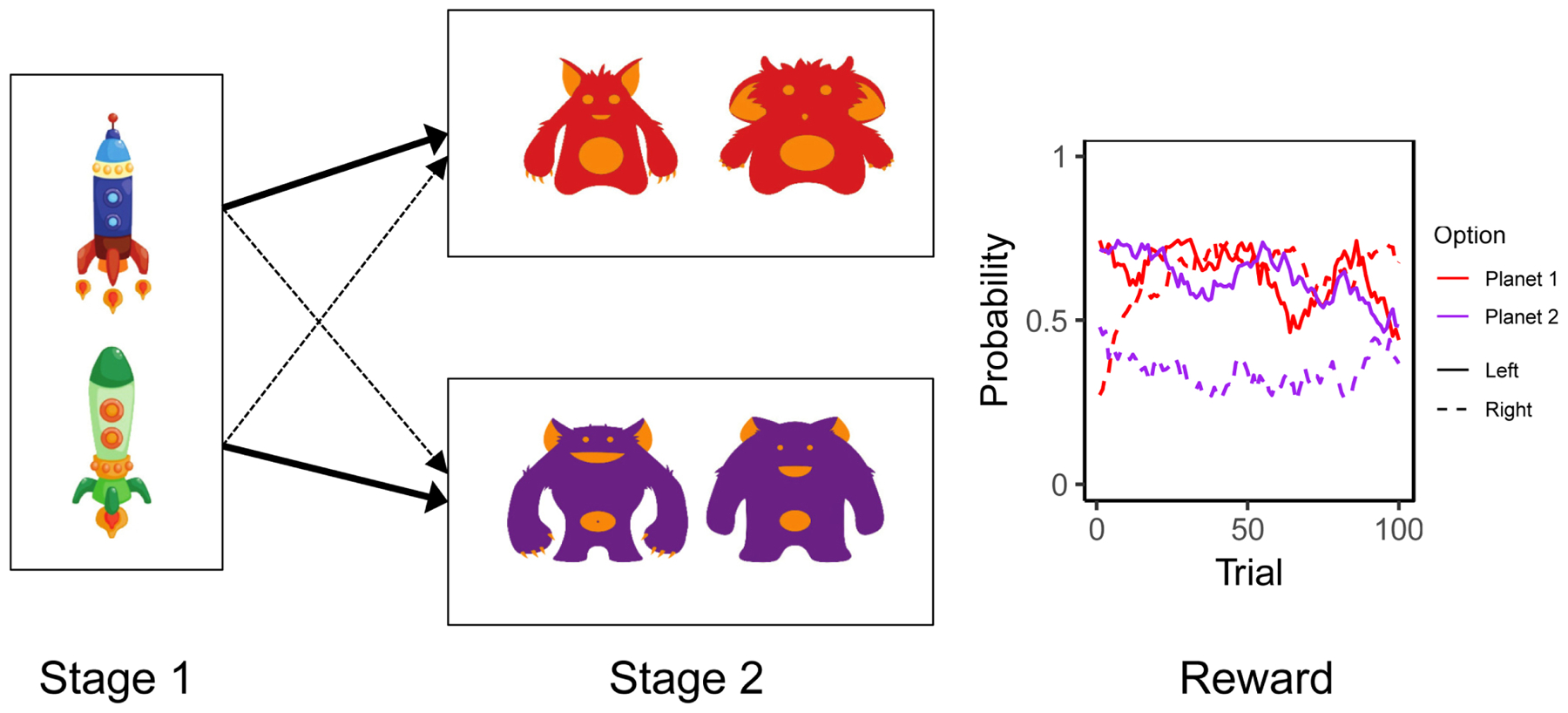
Each trial of the task consisted of two stages. At the first stage, participants chose between two stimuli (spaceships), which probabilistically led to one (70%, thick line) or the other (30%, dotted line) second stage set of stimuli (aliens on planets). The second stage stimuli led to reward based on a probability associated with each second stage stimulus (red vs. purple for aliens from Planet 1 vs. Planet 2; solid vs. dashed lines for the Left vs. Right alien on each planet). This probability drifts independently throughout the task for each stimulus, requiring continual learning. The effect of model-based planning is illustrated by behavior after a trial with a rare first-to-second-stage transition that results in reward: with high model-based planning, a participant using her internal model of the task, including knowledge of the transition probabilities, would realize that she needs to switch first-stage options to maximize the probability of entering the same second-stage state and receiving reward again. Meanwhile with low model-based planning, she would only use her direct experience of choosing an option and receiving a reward, and disregarding transition probabilities, she would stay with the same first stage option that had previously led to reward.

Data cleaning approaches

Based on approaches from other tasks measuring cognitive processes(7) and those used in previous studies with this task(2,5,27), two sets of methods to remove potentially problematic data were used. First, reaction time (RT)-based cleaning assumed trials with very fast (<250 ms) or slow (>2 seconds) reaction times on the first stage indicated inattention or poor responding; cutoffs were determined from previously published work on this task and from visual inspection of outliers on RT histograms. Lenient RT removal excluded individual trials with fast or slow RTs from analysis, while strict RT removal excluded participants with more than 20% of trials with fast or slow RTs.

Second, cleaning based on repetition probabilities (RPs) assumed participants who, after a common transition leading to a reward, did not select the same first stage option more than chance indicated inattention or poor learning. Lenient RP removal excluded participants whose probability of staying after common, rewarded trials was significantly worse than chance (defined as < 5% probability of fitting a binomial distribution with 50% probability and the subject-specific number of common, rewarded trials). Strict RP removal excluded participants who stayed after a rewarded, common transition less than 50% of the time. Supplementary Table 1 shows the amount of data excluded per visit (0–33% of trials) and when excluding subjects with poor data at either visit (15–26% of subjects).

Model parameterization approaches

Generative and non-generative models of model-based planning (5,18,23,28–30) were used to assess the effects of reward and transition type on choice. Both approaches are based in reinforcement learning theory: one approach uses a generative model with parameters representing learning components, while the other approximates learning dynamics using a logistic regression(13). The logistic regression estimated the probability of staying versus switching from a first-stage choice based on the presence of reward on the previous trial (main effect of reward), whether the transition on the previous trial was common or rare (main effect of transition type), and the interaction, which assesses model-based learning (reward*transition type interaction). Logistic regression was treated as one form of parameterization; three parameterizations of the generative model, differing on parameterization of model-based planning and overall model complexity and based on published work, were assessed (M1(5), M2(20), and M2(20); see Supplement for model equations).

Model estimation approaches

Logistic regression and generative models were each estimated with three approaches, resulting in six estimation approaches total. Models were estimated separately for each subject (‘single-subject LR’ for logistic regression and maximum likelihood estimation [‘MLE’] for the generative model) and with hierarchical estimation using other participants’ data to inform individual estimates (‘hierarchical LR’ for logistic regression and hierarchical Bayesian [‘HB’] for the generative model). Hierarchical approaches often lead to better parameter recovery(14) and better measurement but are more computationally complex. The shrinkage induced by hierarchical estimation improves estimation but also biases individual estimates, which may artificially suppress reliability values(31–33). Therefore, reliability values of hierarchical models were calculated by 1) correlating individual estimates (‘individual correlations’) and 2) calculating reliability values directly from each model (‘model-calculated’; see Supplement for details). We tested the accuracy of each generative estimation method using simulation (see Supplement).

Reliability calculations

Test-retest reliability correlated parameter estimates from the first and second visit, while split-half reliability correlated parameter estimates from odd and even trials from the first visit. Primary results for split-half correlations were reported without adjusting for the reduced number of trials (to give a more conservative estimation of reliability and due to differences by estimation approach on whether the reduced number of trials increased variance or biased correlations lower), but adjusted correlations using the Spearman-Brown correction are reported in Supplementary Tables 3 and 5.

The primary results report reliability of the primary construct of interest on this task, model-based planning. Median reliabilities and confidence/credible intervals (CIs) grouped by data cleaning, model parameterization, and model estimation approaches were reported. Median reliability of all parameters is also reported, with results from other individual parameters reported in Supplementary Tables 4 and 5. Reliability levels were benchmarked with <0.4 indicating poor, 0.4–0.7 fair, 0.7–0.9 good, and >0.9 indicating excellent reliability(34).

Generalization to other datasets

The approaches affecting reliability were applied to two additional test-retest datasets to test generalizability of results. To additionally test whether reliability affected the significance of relationships between model-derived measures and clinical variables, the effect of compulsivity on model-based planning was tested in subsets of participants from a previous study(2). The relationship between sample size and significance, and the resulting effect size assuming α=0.05 and 80% power, was then calculated in approaches differing in reliability (see Supplement for further information).

Results

Test-retest reliability: Model-based planning measures

We grouped all parameters and regression coefficients measuring model-based planning together and assessed factors affecting test-retest reliability in these measures (Figure 2). Reliability measures for these model-based measures ranged from nonexistent to excellent, with median reliability in the fair range (0.449 [CI: −0.054:0.752], range: −0.101 to 0.907). The largest effect on reliability was due to the model estimation approach; HB and hierarchical LR approaches with model-calculated reliability had good median reliability (0.718 [CI: 0.071:0.986] and 0.889 [CI: 0.453:0.989]), hierarchical LR with individual correlations and single-subject LR had fair median reliability (0.458 [CI: −0.152:0.774] and 0.401 [CI: −0.006:0.694]), and HB with individual correlations and MLE had poor median reliability (0.394 [CI: 0.000:0.686] and 0.125 [CI: −0.267:0.504]). Model parameterization and data cleaning had little effect overall or within measures from HB or LR model estimation (Supplementary Figure 1). Overall, the maximum test-retest reliabilities for model-based measures were good to excellent: 0.907 for the reward*transition interaction term ([CI: 0.398:0.989], estimated with LR, lenient RP data cleaning) and 0.865 for first level model-based beta parameter ([CI: 0.330:0.995], M3 estimated with HB, lenient RT and strict RP data cleaning; see Supplementary Table 2 for individual reliabilities and CIs of each combination of approaches by parameter).

Figure 2. Test-retest reliability of model-based measures.

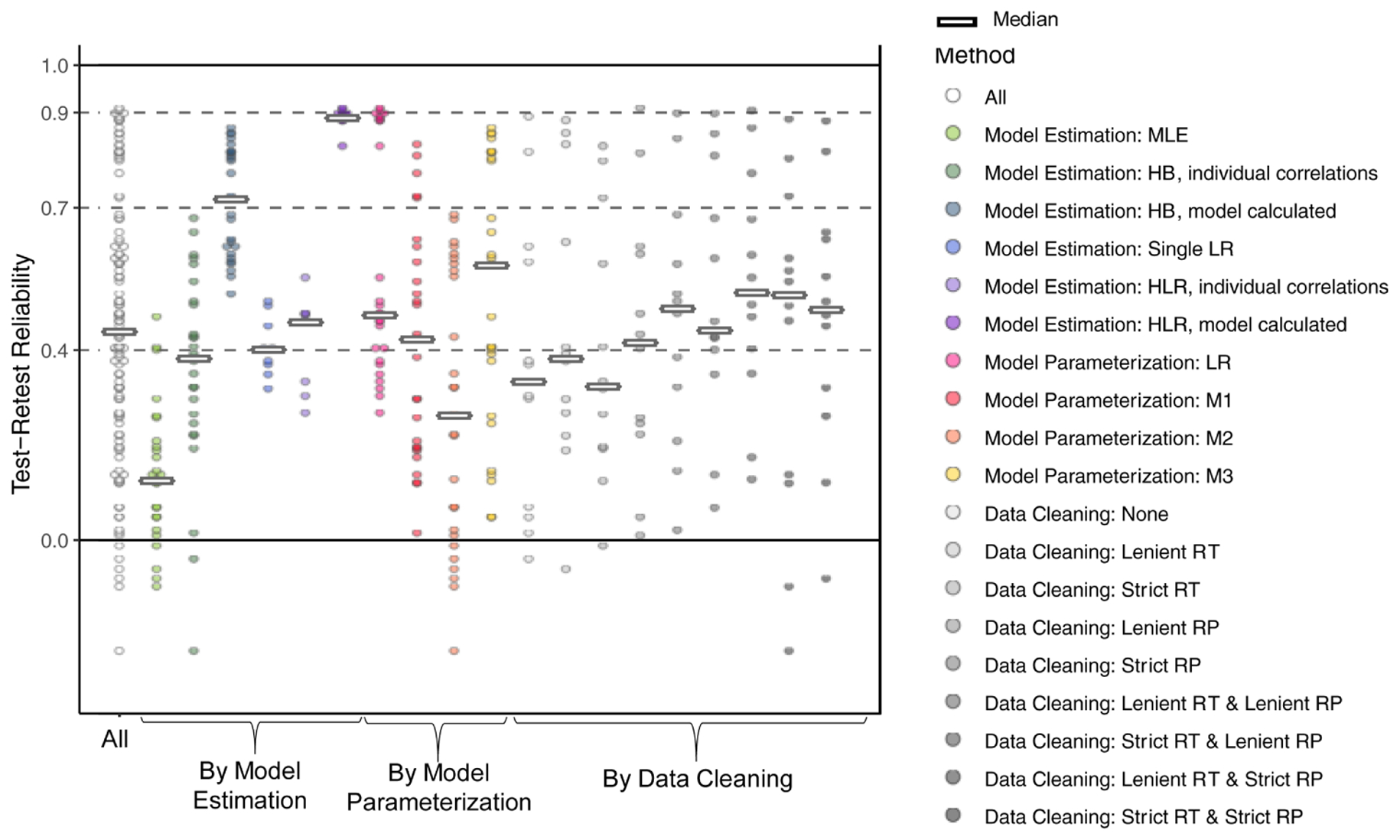
Reliability values are shown overall and grouped together by model estimation, model parameterization, and data cleaning approaches. Dots indicate reliability of individual combinations of approaches and thick horizontal lines the median for each approach. Parameters and regression coefficients measuring model-based learning were: reward x transition interaction for logistic regression, ω (model-based versus model-free weight) for M1, and β1 MB (model-based beta, signifying the influence of first stage model-based values on choices) for M2 and M3. Reliability values for each combination of approaches are reported in Supplementary Table 2.

Split-half reliability: model-based measures

Split-half reliabilities for all model-based measures were then assessed (Figure 3). Median reliability for these measures was fair (0.537 [CI: −0.321:0.868], range −0.172 to 0.922). Both model estimation and model parameterization approaches affected reliability. Hierarchical LR model estimation with model-calculated reliability had good median reliability (0.798 [CI: 0.305:0.992]), HB with model-calculated reliability, HB with individual correlations, hierarchical LR with individual correlations, and single-subject LR all had fair median reliability (0.621 [CI: −0.635:0.985, 0.539 [CI: 0.206:0.744], 0.414 [CI: −0.858:0.968], and 0.407 [CI: 0.004:0.721]), and single-subject MLE had poor median reliability (0.079 [CI: −0.377:0.482). For model parameterization, M2 had good median reliability (0.700 [CI: 0.307:0.884), while M1, M3, and LR all had fair median reliability (M1: 0.538 [CI: −0.417:0.774], M3: 0.424 [CI: −0.450:0.714], and LR: 0.441 [CI: 0.004:0.966]). Model parameterization and data cleaning had little consistent effect within measures from HB or LR model estimation (Supplementary Figure 2). Overall, the maximum split-half reliabilities for model-based measures were good to excellent and were 0.922 ([CI: 0.293:0.995], for LR with strict RT and lenient RP data cleaning) and 0.775 for model-based first stage beta ([CI: −0.291:0.993], M2 estimated with HB with lenient RT and strict RP data cleaning; see Supplementary Table 3 for individual reliabilities and CIs of each combination of approaches by parameter).

Figure 3. Split-half reliability of model-based measures.

Reliability values of odd compared to even trials from session 1 are shown overall and grouped together by model estimation, model parameterization, and data cleaning approaches. Dots indicate reliability of individual combinations of approaches and thick horizontal lines the median for each approach. Parameters and regression coefficients measuring model-based learning were: reward x transition interaction for logistic regression, ω (model-based versus model-free weight) for M1, and β1 MB (model-based beta, signifying the influence of first stage model-based values on choices) for M2 and M3. Reliability values for each combination of approaches are reported in Supplementary Table 3.

Maximum reliability across parameters

To assess whether other model parameters beyond those measuring model-based planning were reliable, the median reliability across all generative model parameters was assessed. The highest median test-retest reliability was excellent (0.922 [CI: 0.622:0.995]) and resulted from HB model estimation with model-calculated reliability, M2 parameterization, and lenient RT and lenient RP data cleaning. For split-half reliability, this combination of approaches also had good median reliability (median: 0.740 [CI: −0.023:0.990]), though the highest median split-half reliability was excellent and was achieved with HB estimation with model-calculated reliability, M1 model parameterization, and no data cleaning (median: 0.926 [CI: 0.635:0.994]). Supplementary Figures 3 & 4 show test-retest and split-half reliability, respectively, for all other parameters.

Test-retest reliability in other datasets

Findings in the primary dataset suggested that model estimation affected reliability values, but the small sample size led to imprecise estimates of reliability values. Therefore, the approaches most affecting test-retest reliability in the primary dataset (i.e., model estimation) were then tested in two other, large datasets (dataset 1(6); dataset 2(11)). For both datasets, applying the combinations of approaches that led to the best test-retest reliability in the primary dataset (HB model estimation with model-calculated reliability with M3 model parameterization and LR model-calculated model estimation, both with lenient RT and lenient RP data cleaning) led to meaningful improvements in reliability compared to other estimation approaches (Figure 4A and Supplementary Table 4).

Figure 4. Generalization of results to test-retest reliability in other datasets and to relationships with clinical variables.

(A) Test-retest reliability of approaches differing in reliability were tested in two independent datasets (S1: 111 participants; S2: 541 participants) and showed similar patterns of reliability. Dots indicate median reliability, colored by estimation method, and lines show 95% confidence or credible intervals (CIs). Reliability values and CIs are reported in Supplementary Table 6. (B) Estimation methods differing in reliability were used to test the relationship between model-based planning and compulsivity in subsets of participants from an independent dataset. X axis is number of participants, randomly drawn from the full sample (n = 1413) and y axis is the reduction in model-based planning with transdiagnostic compulsivity (z-scored). Dotted black horizontal lines indicate significance levels of p = 0.05, p = 0.01, and p=0.001. Colored lines indicate regression lines of the relationship between the number of subjects and the z-scored reduction in model-based planning with compulsivity, colored by estimation approach. Steeper lines reflect more precise estimation in methods with greater reliability. (C) Extrapolated effect sizes (f²) for the effect of compulsivity on model-based planning, extrapolated from the relationship between sample size and significance shown in Figure 4C, with small and medium effect sizes shown for reference.

Relationship with clinical measures

Analysis approaches with higher reliability should also measure relationships with external variables with less noise, resulting in a stronger relationship between sample size and strength of effects, thereby facilitating detection of significant findings with lower sample sizes. Therefore, the relationship between model-based learning and compulsivity was tested using subsets of participants from a large sample previously found to show this effect(2). As model estimation had the largest effect on reliability, different estimation approaches were used to estimate this relationship in randomly and independently selected subsets of participants (Figure 4B and 4C). Based on linear regressions predicting z-scores from sample size, the approximate sample size required for a significant effect (z < −1.96, p < .05) and the resulting effect size for each estimation approach ranged from approximately 200 participants (f² ≈ 0.065) for HB and hierarchical LR with model-calculated effects to over a thousand participants (f² ≈ 0.010) for MLE, HB with individual estimates, and hierarchical LR with individual estimates (where f² =0.02 is a small and f² =0.15 is a medium effect size(35)). As these data were collected online, lab-based studies in controlled environments would likely show larger effect sizes.

Recovery of simulated reliability values

Differences in reliability due to model estimation suggest that reliability depends on parameter recovery, such that approaches with poorer parameter recovery lead to misestimated reliability values. To test the impact of modeling approach on parameter recovery and the resulting ability to estimate true reliability values, reliability of parameters estimated from synthetic data were assessed with generative estimation approaches. HB model-calculated reliability estimated the true reliability significantly more accurately than MLE and somewhat more than individual correlations from HB estimates (median absolute difference between simulated and recovered reliability values: HB model-calculated 0.086, HB individual correlations 0.199, MLE 0.394; Wilcoxson rank sum test: p<.01 for HB model-calculated versus MLE, p=0.11 for HB model-calculated versus HB individual correlations; Supplementary Figure 5).

Discussion

In the present study, we investigated the test-retest and split-half reliability of measures of model-based planning from a common reinforcement learning task in a clinical sample in order to determine the best reliability possible with computationally-derived measures and how to achieve this best reliability. We found that the best reliability ranged from good to excellent, indicating that measures of model-based planning show reliability in a range appropriate for use in clinical research. The largest impact on reliability was how reliability values were estimated, with model-calculated hierarchical approaches leading to much higher reliability. These effects were similar for different constructs (model-based planning and other parameters) and for test-retest and split-half reliability. Improvements in reliability with this combination of approaches generalized to other datasets and were related to the strength of relationships with clinical measures.

Reinforcement learning models are increasingly used to measure processes hypothesized to be disrupted in psychiatric disorders. These models are on the cusp of clinical application(36); however, computationally-derived measures must first show acceptable psychometric properties. Although conditions for acceptable validity have been established, whether measures of model-based planning and other reinforcement learning measures reliably measure latent constructs in real-world empirical samples has been unclear. Low reliability would question whether these models measure their purported constructs and limit their use in clinical research. Research to this point has found a range of reliability values from poor to good(6,10–12). Through an exhaustive exploration of the impact of various analytic decisions, the present work establishes that measures of model-based planning and other constructs do have good reliability for clinical applications, and clarifies some of the variation in previous findings. Although the best reliability found in the present study was good to excellent, we found that the choice of analysis approaches, particularly in terms of estimation, led to large differences in reliability.

What leads to the good to excellent reliability found with reinforcement learning-based analyses, in contrast to the poor reliability found with other task-based measurements of constructs? Modern reinforcement learning approaches blend insights across levels of understanding(37–39) and use trial-level models to take advantage of conceptual and mathematical frameworks that may more accurately represent the underlying process. These RL measures also do not rely on contrast scores, unlike many other task based measures, which can impose inherent limits on reliability(8). Model-based planning is stable within individuals while showing meaningful inter-individual variability – a rare accomplishment for a task-derived measure(8,40). The present findings extend our previous work showing that another family of computational models, drift diffusion models, can represent attentional processes more reliably than conventional approaches(9). Taken together, these results suggest that computationally-informed measures of behavior may more accurately measure constructs than other approaches.

In contrast to the best possible reliability found, the range of reliabilities on any measure assessed ranged from nonexistent to excellent. This wide range lends caution to an optimistic assessment of the benefits of RL and other computational models but supplies recommendations for studies using these approaches. The primary factor affecting reliability, especially test-retest reliability, was the model estimation approach. Hierarchical approaches performed the best, with individual estimation-notably, of the same parameters with the same data- much worse. Hierarchical non-generative models (LR) had similar reliability as hierarchical generative models (HB), suggesting that model-based planning can be reliably assessed with either approach. Within hierarchical approaches, estimates of reliability that accounted for the hierarchical structure of estimation more accurately recovered simulated reliability values and resulted in higher reliability in empirical data than those that treated estimates as independent data points. Hierarchical parameter estimation may lead to better measurement and higher reliability on this task through partial pooling of estimates and Bayesian quantification of uncertainty. Recovery of parameters with known reliability values showed that reliability values of parameters estimated with HB were much closer to the true values than those estimated with MLE and did not artificially inflate estimates of reliability. This finding suggests that reliability of parameters will be partially based on whether simulated effects can be recovered by an estimation approach (whether HB, MLE, or others, including maximum a posteriori, variational Bayesian, or expectation maximization(41–43)) in a specific dataset and task. This conclusion means that one estimation method is not guaranteed to lead to high (or low) reliability, but that the quality of estimation should be assessed for each dataset and model to find the estimation approach that maximizes estimation quality while minimizing computational complexity. For example, in these analyses non-generative analysis approaches using hierarchical logistic regression had similar reliability to generative approaches using hierarchical Bayesian estimation, despite the latter requiring much more computational power.

Reinforcement learning models often require sophisticated, hierarchical estimation approaches because these models are ‘sloppy’- that is, parameters have complex, interrelated effects on behavior that make individual parameters difficult to estimate(17,29). In the present analyses, we found that using estimation approaches that were inadequate for the data and model used required two to seven times the sample size for a significant effect, compared to those with better estimation. Therefore, good measurement relies on either using powerful, often hierarchical, estimation approaches that can accurately recover parameters; combining multiple sources of data in other computationally complex ways (like combining RTs and choices in a structural equation model(11)); redesigning tasks and re-parameterizing models to facilitate estimation(17); or collecting larger amounts of data per participant(11).

As this study focuses on measures from a specific reinforcement learning task, future work should address whether similar reliability is found in other reinforcement learning tasks and populations. The model used here is relatively complex, so model estimation and other approaches may affect reliability for this task more than others; however, parameter recovery in other reinforcement learning tasks is similarly influenced by estimation approach(14). Future development of this task and similar measures(44–46) should also examine reliability. Both generative and non-generative models estimated model-based planning reliably, but whether non-generative models measure other learning processes in other tasks well requires further investigation. Since applications of the two-step task have assumed consistent measurement within and across sessions, we assessed both split-half and test-retest reliability, but tasks with low test-retest but high split-half reliability, including other learning tasks(47), could still be suitable for one-time assessments. Correlation-based measurements of reliability are also not appropriate in all contexts(40,48). The small sample and lower number of trials in the first set of analyses may have led to noisy estimates of reliability(49) and difficulty recovering parameters, but generalization of improvements in reliability to other datasets with larger samples and more trials per visit allays this concern. Future methodological work is also needed to determine how to best predict individual outcomes (e.g., treatment response) from hierarchically estimated models.

The present results lead to recommendations for ensuring the best possible reliability of measures derived from reinforcement learning and similar models (see Table 1). First, model estimation approaches that can estimate parameters well should be used; this should be documented with parameter recovery in simulated data or similar analyses. Quality of parameter recovery can be maximized prior to data collection using in silico optimization of task and computational model characteristics (similar to (15)). Additionally, reliability itself, as well as analysis approaches that affect reliability, including model estimation and parameterization, should be thoroughly documented in manuscripts, to allow comparisons and temper interpretations appropriately. With these recommendations in mind, the present results indicate that reinforcement learning and similar computational models can reliably measure constructs of interest in clinical populations, encouraging their use in clinical research.

Table 1.

Recommendations for maximizing reliability of measures from reinforcement learning and similar models

Optimize task design and modeling approaches (using e.g. in silico optimization) prior to data collection Ensure parameters are estimated well (using parameter recovery and other model assessments) and analyzed appropriately, particularly for hierarchical estimation Assess and document reliability (split-half, and if possible, test-retest) Fully document analysis approaches affecting reliability, including model estimation and parameterization