Displacement- and strain-based discrimination of head injury models across a wide range of blunt conditions

Abstract

Successful validation of a head injury model is critical to ensure its biofidelity. However, there is an ongoing debate on what experimental data are suitable for model validation. Here, we report that CORrelation and Analysis (CORA) scores based on the commonly adopted relative brain-skull displacements or recent marker-based strains from cadaveric head impacts may not be effective in discriminating model-simulated whole-brain strains across a wide range of blunt conditions. We used three versions of the Worcester Head Injury Model (WHIM; isotropic and anisotropic WHIM V1.0, and anisotropic WHIM V1.5) to simulate 19 experiments, including eight high-rate cadaveric impacts, seven mid-rate cadaveric pure rotations simulating impacts in contact sports, and four in vivo head rotation/extension tests. All WHIMs achieved similar average CORA scores based on cadaveric displacement (~0.70; 0.47–0.88) and strain (V1.0: 0.86; 0.73–0.97 vs. V1.5: 0.78; 0.62–0.96), using the recommended settings. However, WHIM V1.5 produced ~1.17–2.69 times strain of the two V1.0 variants with substantial differences in strain distribution as well (Pearson correlation of ~0.57–0.92) when comparing their whole-brain strains across the range of blunt conditions. Importantly, their strain magnitude differences were similar to that in cadaveric marker-based strain (~1.32–3.79 times). This suggests that cadaveric strains are capable of discriminating head injury models for their simulated whole-brain strains (e.g., by using CORA magnitude sub-rating alone or peak strain magnitude ratio), although the aggregated CORA may not. This study may provide fresh insight into head injury model validation and the harmonization of simulation results from diverse head injury models. It may also facilitate future experimental designs for better model validation.

Introduction

Traumatic brain injury (TBI) is a major public health problem in the world³⁸. Indisputably, TBI is a direct result of mechanical insult to the brain. Therefore, understanding the biomechanical mechanisms of TBI is critical for its prevention and detection. To this end, finite element (FE) models of the human head are increasingly employed to study TBI biomechanics, as they provide unparalleled rich information about impact-induced brain strain/strain rate thought to cause injury²⁷. These numerical surrogates serve as an important vehicle to bridge gaps among external impacts, tissue injury thresholds³⁶, and clinical outcomes of injury⁶. It is critical that these models are sufficiently biofidelic in order to ensure confidence in the estimated brain strains for the assessment of injury risks.

Recent studies have highlighted significant strain disparities among diverse “validated” head injury models. For example, Ji et al.²⁴ compared the Dartmouth Scaled and Normalized Model (DSNM), Simulated Injury Monitor (SIMon;⁴⁷) and Wayne State University Head Injury Model (WSUHIM⁵³). The three models differed significantly in strain and strain rate when simulating characteristic head impacts in ice-hockey (e.g., peak maximum principal strain (MPS) of ~0.4 vs. ~0.7 for one impact). Significant strain differences were also found among GHBMC³², THUMS²⁶ and two version of the KTH model¹⁶ when comparing against calculated cadaveric strains²¹ (e.g., more than 0.12 shear strain in GHBMC vs. 0.02–0.03 for the two KTH models¹⁶). Most recently, after incorporating white matter (WM) fiber reinforcement into the GHBMC model, MPS of the whole brain reduced up to 45% for a severe head impact but with negligible change in displacement-based validation score⁵⁰.

The substantial strain differences among “validated” models when simulating the same head impact suggest current model validations may not be effective in discriminating models for strain estimation. However, there is an ongoing debate on how best to validate a model. Particularly, no consensus exists on what experimental data is suitable for model validation and there is also inconsistent evaluation of validation quality. The majority of head injury models were validated against relative brain-skull displacements measured from high-rate cadaveric impacts^21,22 to study brain shear deformation for rotation-induced injuries^{14,16,25,32,33,51}. While relative brain-skull displacements are relevant to brain shear responses, it is their spatial gradient that defines strain thought important for brain injury²⁷. The difference between displacement and strain is analogous to displacement vs. velocity in the temporal domain. In part, therefore, these experiments on relative brain-skull displacements were recognized as not specifically designed for FE model validation^19,51.

Cadaveric strains are available^21,60; but there is a concern on quality⁵⁰. Although error sources in typically “noisy” cadaveric experiments⁶⁰ have been exhaustively discussed²⁰, a quantitative error estimate in strain, nevertheless, does not exist. The initially reported ~2–5% peak strains²¹ were rather low as they were of similar magnitude to other in vivo measurements⁴¹ from events with acceleration magnitudes one to two orders higher⁵⁵. The cadaveric strains were recently reanalyzed and reached a peak magnitude of ~10%⁶⁰. To-date, only the KTH model, GHBMC, and THUMS have been compared to cadaveric strains^16,60. It was found that validation quality against cadaveric strain did not correlate with validation quality against relative brain-skull displacements⁶⁰, suggesting that displacement-based validation alone is insufficient for brain strain validation^57,60. Nevertheless, they were limited to high-rate impacts but did not consider recent mid-rate head impacts^2,18,19 or in vivo datasets^8,29,30 across a wide-range of blunt conditions.

In vivo strains have been available for over a decade now^5,10,41. While some consider the dataset “not relevant” for studying injury¹⁶, others find it relevant to subconcussion⁵⁵ as the acceleration peak magnitude (244–370 rad/s²) was on the same order of the reported 25^th percentile subconcussive impacts in collegiate football (531–682 rad/s^{2 40}). The relevance to studying mild TBI (mTBI) may be further supported given the growing concern on the cumulative effects from repeated subconcussive impacts^4,44. The acceptance of in vivo strains appears to be growing^60,61. Nevertheless, their use in model validation remains limited^13,25,57, even though more extensive datasets have been recently reported for the purpose of “model validation”^8,29,30.

The ongoing debate is further confounded by differing rating methods using either Correlation Score (CS) based on normalized integral square error (NISE²⁶), or CORrelation and Analysis (CORA³³). The latter also has various settings that are not consistent throughout the literature^{3,16,33,50,57}. Given these controversies, there is little question about the need to converge to a common standard for model validation. To achieve this goal, it is important to first assess whether the available experimental data and validation strategies are sufficient to discriminate head injury models for their simulated whole-brain strain responses that are often used for injury prediction.

Therefore, the primary objective of this study is to scrutinize whether head injury models that report similar CORA scores or validation ratings based on either cadaveric displacement or strain would produce similar whole-brain strains across a wide range of blunt impact conditions. Both the magnitude and distribution of model-simulated strains are evaluated, as the latter is emerging as an important factor to consider in mTBI⁴⁹. Three versions of the Worcester Head Injury Model (WHIM) are used to simulate a total of 19 experimental tests/datasets, including eight high-rate cadaveric impacts²¹, seven mid-rate cadaveric head pure rotations designed to simulate impacts in contact sports^2,18,19, as well as four in vivo strain datasets from human volunteers^8,29,30. They provide valuable experimental data for potential model validation across a wide range of blunt impact conditions relevant to injury or subconcussion.

This study significantly extends previous work on model strain differences that were limited to strain magnitude alone using either high-rate cadaveric impacts only¹⁶ or characteristic²⁴ and reconstructed¹⁷ impacts drawn from live humans. For live human impacts^17,24, no experimental measurements are available (or possible) for potential model validation at the injury level. It also expands recent studies on cadaveric strain-based model validation^60,61 to further evaluate whether this validation strategy is sufficient to discriminate models in terms of simulated whole-brain strains. Therefore, findings from this work may provide fresh insight into how best to harmonize simulation results from diverse head injury models. In addition, they may potentially facilitate future experimental designs to improve model validations.

Methods

Worcester Head Injury Model (WHIM)

The previous isotropic²⁵ and anisotropic⁵⁷ versions of the Worcester Head Injury Model (WHIM) were used. In addition, a re-meshed brain⁵⁸ (Fig. 1) was also used to implement WM material anisotropy via tractography using the same earlier approach⁵⁷. Here, we referred to them as isotropic and anisotropic WHIM V1.0, and anisotropic WHIM V1.5, respectively. The re-meshed brain was considered to have converged in both strain magnitude and distribution⁵⁸. All WHIMs have identical head length, width, and brain volume (188.4 mm, 153.2 mm, and 1.5 L, respectively). Both WHIM meshes were co-registered with a WM atlas³⁵ and a separate gray matter (GM) atlas⁴³ using a previous technique^54,56 in order to localize specific brain regions of interest.

Fig. 1.

Brain meshes of the isotropic and anisotropic WHIM V1.0 (a) and anisotropic WHIM V1.5 (c), along with their corresponding direction-encoded, element-wise fiber orientations (b and d). The re-meshed WHIM V1.5 has a higher mesh resolution and a shorter spinal cord to align with the available tractography.

The earlier WHIMs employed C3D8R elements (constant strain with reduced integration) and enhanced hourglass control based on the enhanced assumed strain method¹. However, it does not allow the user to adjust the energy control¹. For WHIM V1.5, we adopted the same C3D8R elements but employed an integral viscoelastic form of hourglass control called “relax stiffness” in Abaqus¹. This choice was made as this type of hourglass control with high scaling factors was found to produce most similar strains relative to the baseline element, C3D8I (enhanced full integration with incompatible modes, thought to be the most accurate element type^1,58). We used the same iterative approach⁵⁸ to identify the appropriate scaling factors for the GM and WM to preserve simulation consistency compared to C3D8I benchmark elements, which led to 200 and 100, respectively. Table 1 summarizes the brain element/node numbers, average element sizes, brain material models and hourglass control types for the three WHIMs.

Table 1.

Summary of brain element/node numbers (excluding those for other components such as skull and face, as they are irrelevant when simplified into rigid bodies in simulation), average element size, hourglass (HG) control type, brain material models and their corresponding material property parameters for the three WHIMs. HGO: Holzapfel-Gasser-Ogden model; μ_i, α_i, G_0, G_∞, K, k_i, k, g_i, are material property parameters defined in Supplementary A (constitutive equations) and elsewhere^25,57.

	Isotropic WHIM V1.0		Anisotropic WHIM V1.0	(Anisotropic) WHIM V1.5
# of brain elements	55.1k			202.8 k
# of brain nodes	56.6 k			227.4 k
Avg. elm. Size (mm)	3.3±0.79			1.810.4
HG control type	Enhanced			Relax stiffness
Brain mat. model	2nd-order Ogden and viscoelastic		HGO and viscoelastic
Brain mat. prop.	μ1 (Pa)	271.7	G0 (Pa)	2673.23
	α1	10.1	G∞ (Pa)	895.53
	μ2 (Pa)	776.6	K (MPa)	219
	α2	−12.9	k1 (Pa)**	25459
	i = 1	7.69E-1	k2	0
	i = 2	1.86E-1	κ	Depending on FA* values
	i = 3	1.48E-2	g1	0.6521
	i = 4	1.90E-2	g1	0.0129
	i = 5	2.56E-3	τ1	0.0067
	i = 6	7.04E-3	τ2	0.0747

^*FA: Fractional anisotropy.

^**Property parameters for the gray matter are identical, except that k₁ was set to 0 as no fiber reinforcement existed in this region. k₁ was based on G₀/k₁ from experiment³⁷.

Experimental datasets

Eight high-rate cadaveric impacts²¹ were selected. They provide both relative brain-skull displacements and cadaveric strains. Head rotation in these experiments was induced by directly striking or stopping a cadaveric head, which led to short impulse durations with high magnitudes of rotational acceleration (~3–5 ms and ~3.9–26.3 krad/s²; Table 2). For each test, the first neutral density target (NDT) cluster was used to evaluate maximum principal Green-Lagrangian strain (MPS; to be consistent with earlier studies^60,61) due to measurement accuracy and data sufficiency considerations⁶⁰. Maximum shear strain was not evaluated, as it was largely similar to MPS⁶⁰.

Table 2.

Summary of 19 tests/datasets used for model response evaluation, including eight high-rate, seven mid-rate cadaveric head impacts and four in vivo head rotation/extension. The number of NDTs or crystals (for cadaveric impacts), primary plane of rotation, peak values of rotational acceleration/velocity ($a_{rot}^p$ and $v_{rot}^p$, respectively), and impulse durations (Δt) are reported. For the sonomicrometry datasets, case “Vrot20dt60” denotes an impact with a targeted $v_{rot}^p$ of 20 rad/s and Δt of 60 ms. Other cases are analogous.

	Case #	#of NDTs/crystals	Plane of rotation	$a_{rot}^p$ (krad/s2)	$v_{rot}^p$ (rad/s)	Δt (ms)	Ref.
High-rate	C288-T3	14 (7 used)	Sagittal	26.3	30.1	2.6	Hardy et al.(2007); Hardy (2007); Zhou et al. (2018) Hardy et al. (2007); Hardy
	C380-T1		Coronal	7.2	29.6	4.3
	C380-T2		Axial	5.7	24.1	5.0
	C380-T3		Coronal	6.5	22.4	4.9
	C380-T4			19.1	37.5	3.8
	C380-T6			13.7	31.7	4.6
	C393-T2			3.9	24.5	5.3
	C393-T3			11.8	26.6	3.9
Mid-rate	NDTA-T4	12	Sagittal	3.2	36.8	30.0	Guettler (2017); Guettler et al. (2018)
	NDTB-T2	11		1.3	22.0	30.9
	NDTB-T4	11		3.0	44.2	22.5
	Vrot20dt60	19 (3 avail.)	Coronal	1.4	22.3	34.4	Alshareef et al.(2018)
	Vrot20dt30			1.5	13.6	16.9
	Vrot40dt60			2.7	36.9	30.1
	Vrot40dt30			4.4	34.6	14.4
Low-rate	Sabet et al.	N/A	Axial rotation	~0.3	~13	~40	Sabet et al. (2008)
	Knutsen et al.			~0.2	~5		Knutsen et al. (2014)
	Chan et al.			~0.3	~3.9		Chan et al. (2018)
	Lu et al.		Extension	~0.2	~1.4		Lu et al. (2019)

Seven mid-rate non-contact, pure rotations designed to simulate impacts in contact sports were also used. They had two targeted peak angular speeds $v_{rot}^p$ of 20 and 40 rad/s and impulse durations (Δt) of 30 and 60 ms, respectively. One sub-group induced pure sagittal rotations using low mass NDTs^18,19. The NDTs were implanted in a “prescribed, scalable, and repeatable” manner to reduce experimental variation and to aid FE model validation. The procedure was repeated to determine the NDT locations in the WHIM space as detailed in Supplementary A (Fig. A1). Three impact cases (NDTA-T4, NDTB-T2, and NDTB-T4) from a total of 9 tests were selected to represent different levels of $v_{rot}^p$ and Δt (Table 2).

The other sub-group employed a sonomicrometry technique to conduct four tests on one cadaveric head². Relative brain-skull displacements were measured at crystals located across the brain. Usable displacement data were recorded at 19 receiver locations in a coronal rotation, but only those from 3 receivers have been reported (# 9, 16, and 31; Table 2). Their coordinates and displacements relative to a common head center of gravity were digitized and transformed into the WHIM model space after scaling to match brain cross-sections (Fig. 2). To be consistent with the NDT experiments, only displacements along the left-right, inferior-superior directions were used, as those along the anterior-posterior direction were negligible in the experimental data (and confirmed in simulation results; <1 mm)².

Fig. 2.

The cadaveric brain cross-sections (solid lines), head center of gravity, and crystal locations were digitized on the three anatomical planes from the experimental report². The WHIM was then scaled and repositioned so that its head center of gravity aligned with that of the cadaveric head (dashed lines represent brain cross-sections of WHIM V1.5; similar for WHIM V1.0, not shown). “S”: scaling factor along the corresponding anatomical direction.

Finally, four low-rate in vivo datasets were selected^8,29,30,41, all with a duration of ~40 ms. Knutsen et al.²⁹ optimized the previous tagged MRI technique⁴¹ to measure strains in an axial rotation. The more discretized area fractions of radial-circumferential shear strains on a representative mid-axial plane and at one time point were reported for one subject¹³. This work was further extended using double-trigger tagged MRI to measure strains in a cohort of 34 healthy human volunteers⁸. Regional volume fractions of the peak first and second principal strains and maximum shear strains were reported over the impulse duration. An in vivo head extension test was also simulated to report whole-brain peak radial-circumferential shear strain and peak maximum shear strain³⁰.

Table 2 summarizes a total of 19 tests/datasets used in this study, including 15 cadaveric impacts (with a total of 102 brain-skull displacement curves) and four in vivo datasets.

Impact simulations

For each cadaveric impact, the WHIM was scaled along the three anatomical directions to match with the reported head dimensions (summarized in Supplementary A, Table A1). Acceleration profiles were prescribed to the rigid skull through the head center of gravity (Fig. A2a in Supplementary A).

For in vivo Sabet et al. study, a subject-specific model was created via mesh warping²⁵. For the Knusten et al. and Lu et al. datasets, the generic WHIM was used as no MRI was available and no head/brain dimension was reported. For the Chan et al. study, the generic WHIM was scaled (by 0.918) to match the reported average brain volume and to simulate a representative subject. For axial rotations, acceleration profiles were prescribed about the inferior-superior axis, while the horizontal (left-right) axis close to the neck was used for head extension (graphically illustrated in Fig. A2b in Supplementary A).

CORA Rating

CORA (Version 4.0.4) was used to report validation quality, as it was found to produce less failure in correlation calculation than NISE¹⁶. Previous studies^33,55,57 utilized the default setting, which has a high exponent factor and weighting factor in shape¹⁶. In addition, the time interval for CORA calculation is automatically determined that could lead to inconsistent time intervals for different time traces. The default setting also combines ratings from both the corridor and cross-correlation methods. However, corridor data is not yet available for relative brain-skull displacements.

Therefore, recommended settings from (Giordano and Kleiven 2016)¹⁶ were adopted for the current study which uses a cubic exponent factor for shape rating and equal weights for curve shape, magnitude, and phase shift, and excludes the corridor method. At least 40 ms was recommended for “T_MAX”, which was used here for high-rate impacts as that was the length of the reported strain data 60. For all mid-rate cadaveric impacts, the initial zero acceleration/displacement portion of the history curves were truncated and the “T_MAX” value was uniformly extended to 130 ms to capture all displacement peaks (Table 2). For completeness, CORA scores using the default settings were also included. The detailed setting parameters are reported in Supplementary A (Table A2).

Model response comparisons: cadaveric data

For each cadaveric impact, we reported displacement-based CORA scores for the three WHIMs as averaged from all available NDTs or crystals. For the eight high-rate NDT datasets, model-simulated “cluster strains” were also compared with the recalculated strains⁶⁰. Briefly, the nearest brain nodes relative to cluster NDTs were localized to form a number of triangular shell elements or “triads”²¹. Their simulated nodal displacement trajectories were then prescribed to the corresponding NDTs, from which Green-Lagrangian strains were derived and averaged. Mid-rate NDT datasets were not included here because their cadaveric strains, unlike their high-rate counterparts, have not been reported (albeit, potentially our marker-based strain calculation could be applied to report regional strains in the future; more in Discussion).

For the four sonomicrometry datasets, measured displacements were only available from three crystal receivers at present². Therefore, MPS from a single triangular element was calculated using the nearest nodal displacements either from the head injury model simulation (“simulated”) or experimental measurements (“calculated”). For these 12 impact cases (8+4), CORA scores were then reported to compare between the “simulated” and “calculated” strains.

Model response comparisons: in vivo data

For the Sabet et al. study, the peak area fractions of radial-circumferential shear strains exceeding thresholds of 0.02, 0.04 and 0.06 on an axial imaging plane were compared with the experiment⁴¹. For the Knusten et al. study, we compared area fractions of circumferential shear strains exceeding a range of thresholds (−0.02–0.06¹³) on a representative mid-axial plane at 45 ms with the experiment. For the Chan et al. study, we compared volume fractions of the cumulative peak first and second principal strains as well as maximum shear strain over the entire simulation duration above a threshold of 0.03 in the whole brain, cortical/deep GM, and cerebral WM. Finally, for the Lu et al. study, we compared peak positive/negative radial-circumferential shear strain and peak maximum shear strain in the cerebral GM/WM, caudate, and putamen, as reported. For the Chan et al. and Lu et al. studies, comparisons in the deep GM thalamus region were excluded, as it was not included in the GM atlas used.

Whole-brain strain comparisons:

For all the 19 tests, we further compared their whole-brain strains in terms of linear regression slope (k) and Pearson correlation coefficient (r) to investigate differences in magnitude and distribution^49,58 over a wide range of impact conditions. This would extend earlier studies that focused on peak magnitude differences alone^21,24,50. To mitigate the disparity in mesh resolution, all MPS responses were resampled onto a same set of 3D grid points (at a spatial resolution of 1 mm³)⁵⁸. We chose the response from the anisotropic WHIM V1.0 as the reference (as the model was previously considered to be “validated”⁵⁷), without implying on strain “accuracy” relative to the unknown “ground-truth”.

Data analysis

All simulations were conducted using Abaqus/Explicit (Version 2016; Dassault Systèmes, France) double precision with 15 CPUs (Intel Xeon E5–2698 with 256 GB memory) and GPU acceleration (4 NVidia Tesla K80 GPUs with 12 GB memory). A typical head impact simulation runtime was 30 min for a 100 ms impact. All data analyses were performed in MATLAB (R2018b; MathWorks, Natick, MA). A permutation test (with 1000 samples)⁵⁴ was used to compare various averaged CORA scores. Statistical significance was reached when the p value was less than 0.05.

Results

Model comparison: relative displacement

Fig. 3 reports case-specific displacement-based average CORA scores using the revised settings for the three WHIMs. Results using the default setting are in Supplementary B (Fig. B1). With the same setting, all three WHIMs achieved similar average scores. However, the revised setting led to considerably higher scores than the default setting (average scores from 15 cadaveric cases ranged 0.43–0.44 increased to 0.69–0.70). Relative CORA scores between impact cases were consistent, and scores with the sonomicrometry data were higher than those from the NDT data, regardless of the CORA setting. Relative brain-skull displacement curves for the 7 mid-rate cadaveric impacts are reported in Supplementary B (Figs. B4–B10).

Fig. 3.

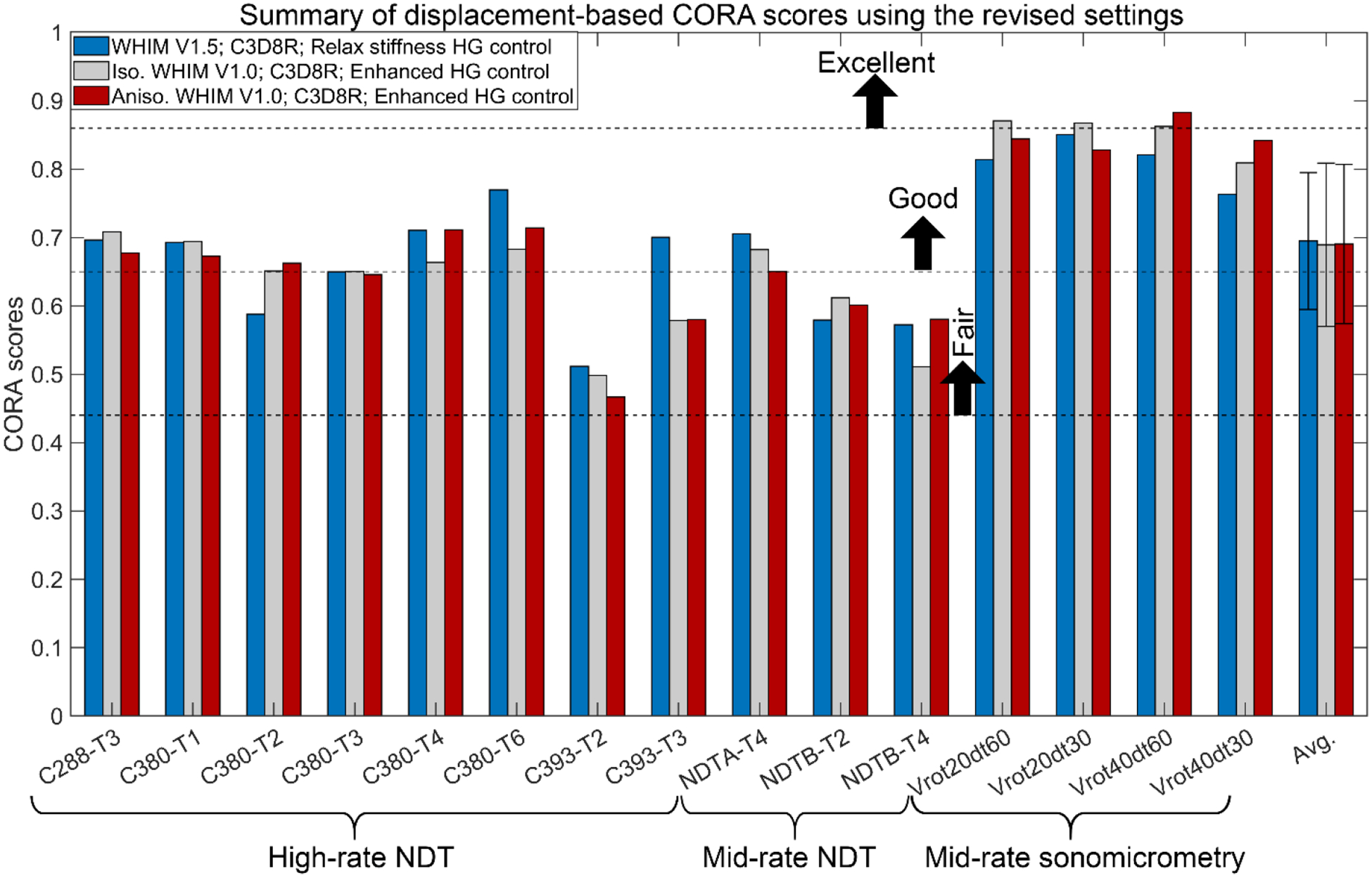
Case-specific displacement-based CORA scores for a total of 15 cadaveric head impacts based on simulated relative brain-skull displacements from the three WHIMs using the revised CORA setting¹⁶. The sliding scale for the CORA was adopted from the ISO/TR-9770²³ to rate model validation quality, as used previously^3,16. No statistically significant differences were found among the three average CORA scores (p > 0.1).

Model comparison: cadaveric brain strain

Fig. 4 reports case-specific average CORA scores based on cadaveric brain strains using the revised settings. Results using the default setting are in Supplementary B (Fig. B2). The average CORA scores of V1.0 models were slightly higher than that for WHIM V1.5 (0.86 vs. 0.78). For the 12 common cases, no significant correlation existed between displacement- and strain-based CORAs (p>0.1). The same occurred when limiting to the 8 high-rate cases, except for the isotropic WHIM V1.0 using the revised setting (correlation coefficient of 0.89, p=0.003).

Fig. 4.

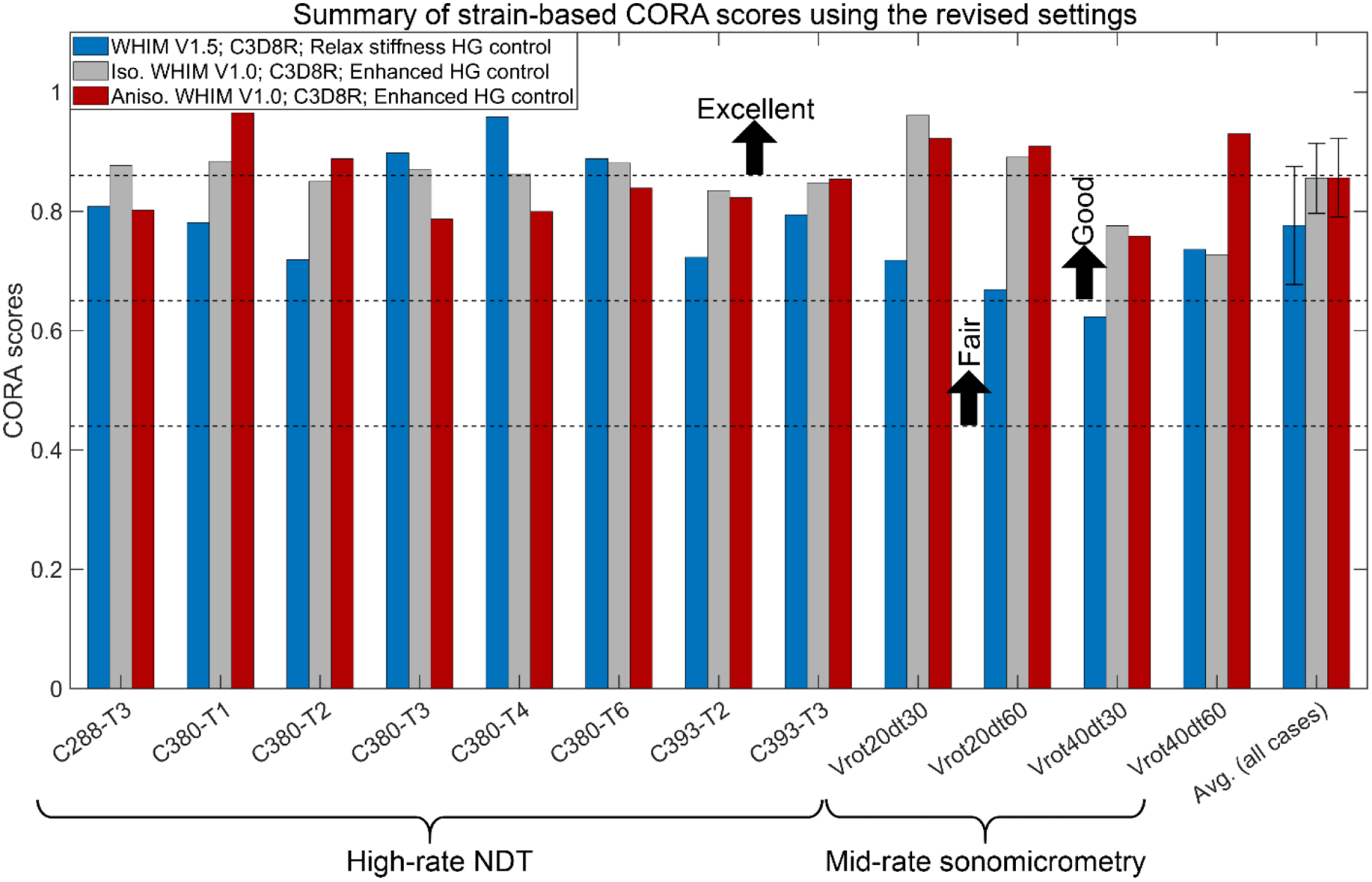
Case-specific strain-based CORA scores for the eight high-rate cadaveric head impacts and four mid-rate sonomicrometry datasets using the three WHIMs with the revised CORA setting. The sliding scale for the CORA was adopted from the ISO/TR-9770²³ to rate model validation quality, as used previously^3,16. The average CORA scores for the isotropic and anisotropic WHIM V1.0 were statistically higher than that for WHIM V1.5 (p < 0.05) when considering all the 12 cases; however, the statistical significance disappeared for the group of eight high-rate NDT cases.

Fig. 5 compares average cluster MPS from the three WHIMs with the recalculated strains for four high-rate NDT impact cases⁶⁰ (other four cases are reported in Fig. B11 in Supplementary B). Fig. 6 compares them against the experimental strains for the sonomicrometry datasets using the generalized marker-based approach. For most cases, the two V1.0 WHIMs achieved largely similar strains in peak values and curve shapes. However, WHIM V1.5 consistently produced peak strains ~1.32–3.79 (for C380-T1 and Vrot40dt30, respectively) times of those from the V1.0 models.

Fig. 5.

Comparison of average cluster MPS (Cluster 1, C1) from the three WHIMs with those recalculated from four selected high-rate impacts⁶⁰. Circles represent corresponding peak strains used to calculate magnitude ratios relative to those from the anisotropic WHIM V1.0 or the experiments.

Fig. 6.

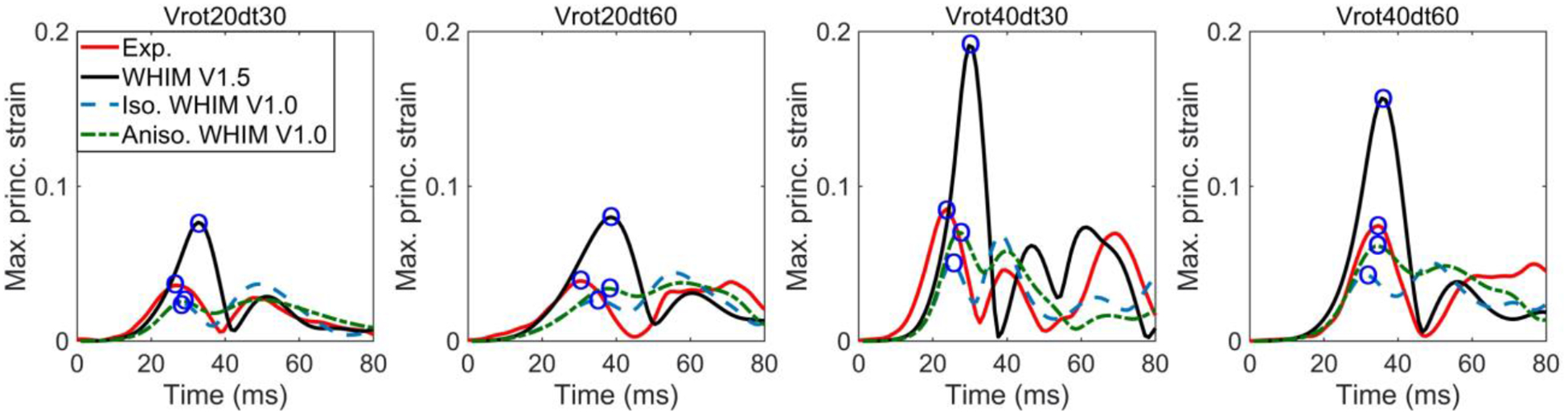
Comparison of surface MPS from the three WHIMs against the experimental counterparts for four sonomicrometry datasets. Circles represent corresponding peak strains used to calculate magnitude ratios relative to those from the anisotropic WHIM V1.0 or the experiments.

Model comparison: simulated whole-brain strain for cadaveric impacts

The three WHIMs were further compared in fringe plots in terms of peak MPS of the whole brain regardless of the time of occurrence for three selected cases (Fig. 7). The WHIM V1.0 models produced largely similar strains in magnitude and pattern between themselves. However, strains from the WHIM V1.5 were considerably larger along with degraded distribution similarity relative to the reference from the anisotropic WHIM V1.0 (linear regression slope, k, and Pearson correlation coefficient, r, ranged 1.17–2.69 (for C380-T3 and C288-T3, respectively) and 0.57–0.92 (for C380-T4 and C380-T3, respectively).

Fig. 7.

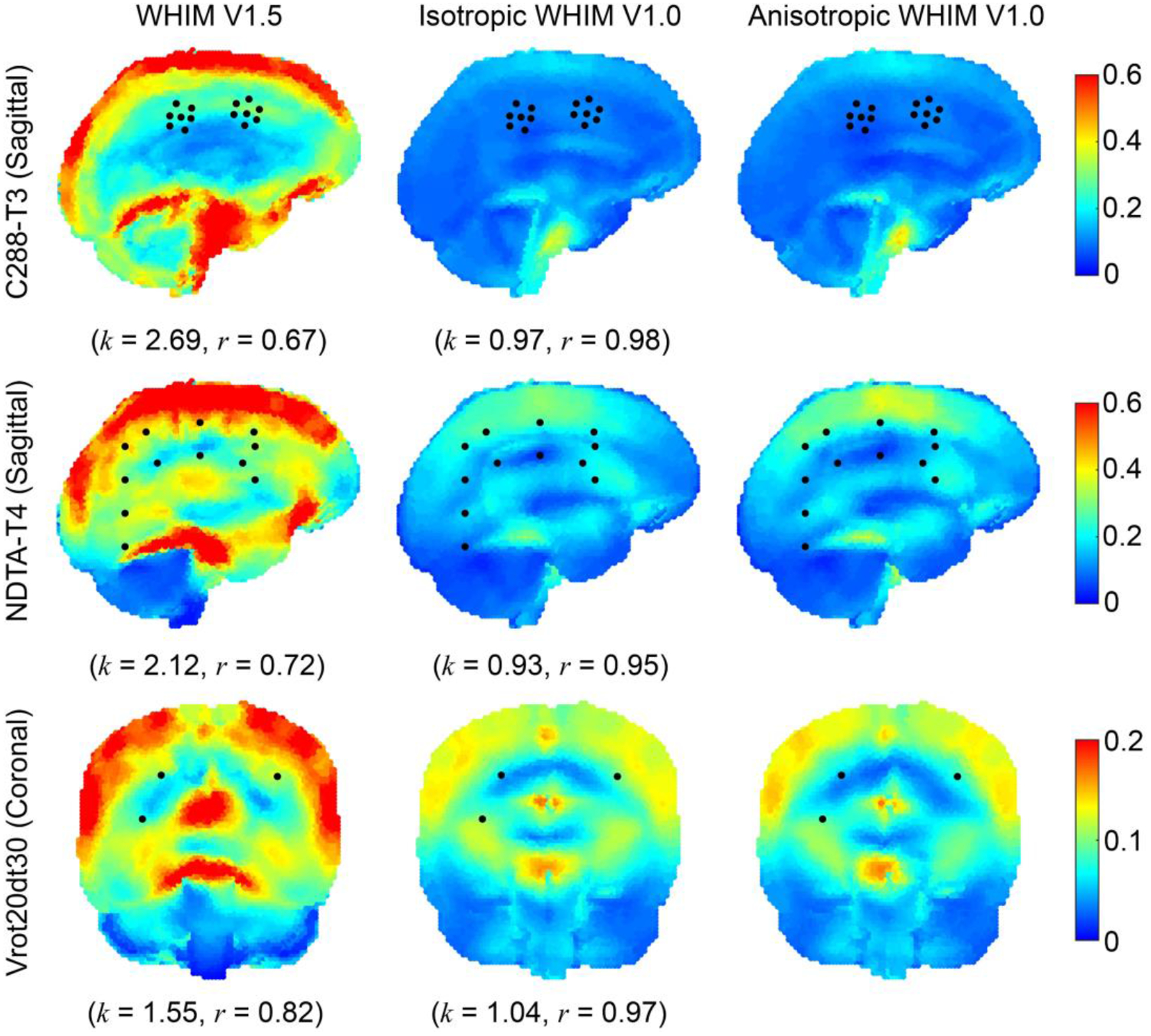
Cumulative peak MPS fringe plots for a high-rate impact (C288-T3, parasagittal plane in the middle of the right hemisphere through the cluster centroid; top) and two mid-rate cadaveric pure rotations (NDTA-T4, parasagittal plane in the middle of the right hemisphere; middle; and Vrot20dt30, coronal plane through receiver #16; bottom), along with projected locations of NDTs or crystals (shown as black dots) used to experimentally sample brain displacements. Comparisons in terms of linear regression slope (k) and Pearson correlation coefficient (r) relative to the anisotropic WHIM V1.0 reference are also reported.

Model comparison: in vivo strain

Fig. 8 compares responses using four in vivo datasets. Overall, the three WHIMs especially the two earlier variants agreed reasonably well with the experiments, at least they were on the same order of magnitude. However, the agreement varied for each dataset, and among the WHIMs.

Fig. 8.

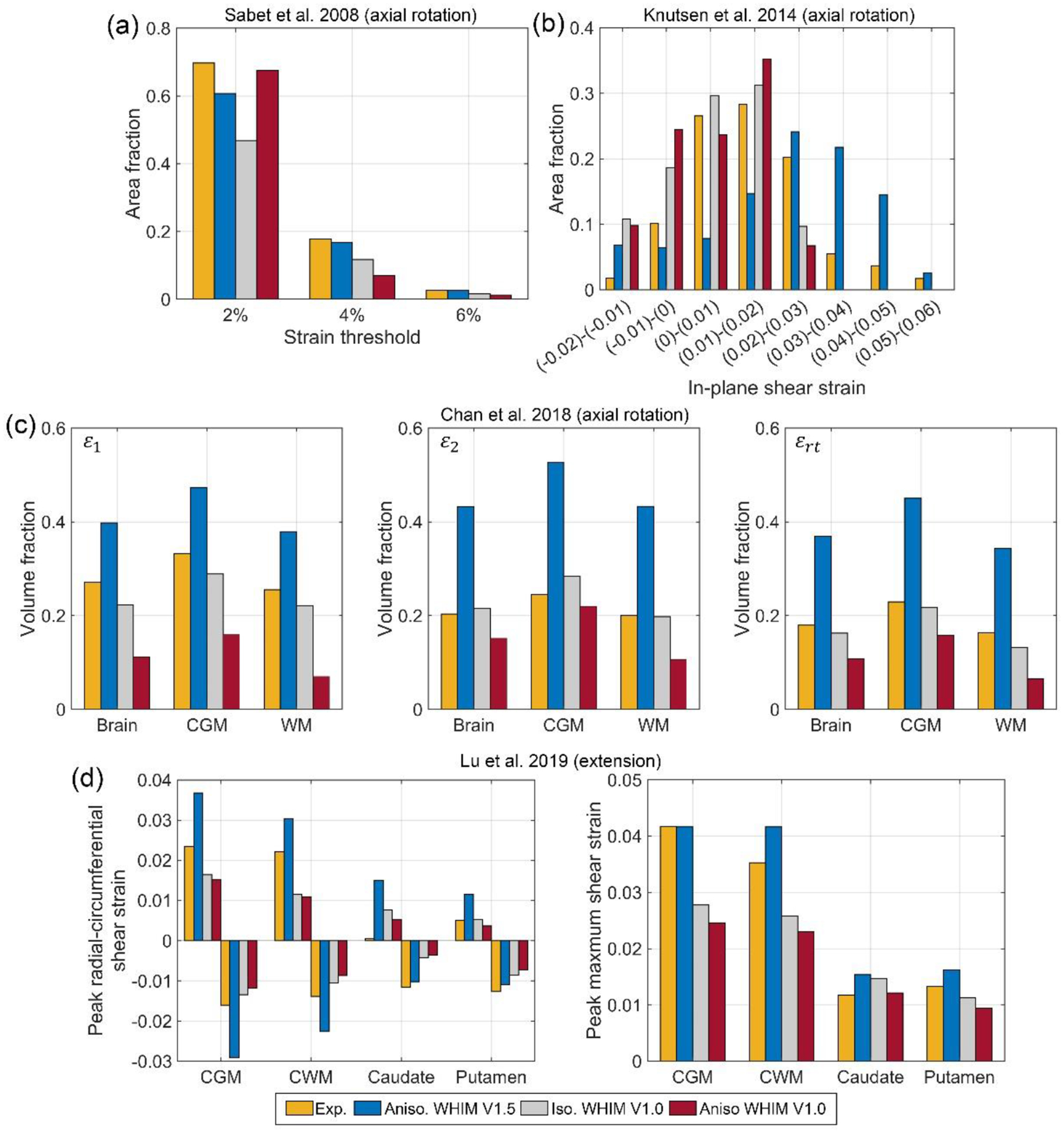
Summary of various above-threshold strain measures for three axial head rotations (a–c) and peak strain measures for a head extension test (d). CGM: cortical gray matter; CWM: cerebral white matter; ε₁: peak first principal strain; ε₂: peak second principal strain; ε_rt: maximum shear strain.

For the Sabet et al. study, the three WHIMs had largely comparable strains relative to the experiment, and among themselves (Fig. 8a). The Knutsen et al. dataset offered more refined strain thresholds. Estimated in-plane shear strains from WHIM V1.5 mostly underestimated at lower thresholds (<0.02), but mostly overestimated at higher thresholds (>0.02; Fig. 8b). At the high threshold (>0.05), the simulated result was largely comparable to the experiment. This was opposite for the two V1.0 WHIMs, however, where overestimation occurred at lower thresholds (<0.02) while underestimation occurred at higher thresholds (>0.02; Fig. 8b).

Compared to the Chan et al. dataset, WHIM V1.5 overestimated the above-threshold volume fractions by up to 116.4% relative to the three measured strains. In contrast, the anisotropic WHIM V1.0 mostly underestimated (by up to 72.4%), while the isotropic WHIM V1.0 agreed with the experiment the best (Fig. 8c).

When comparing with the Lu et al. test, WHIM V1.5 similarly overestimated the peak radial-circumferential shear strain in the cerebral GM and WM regions. Nevertheless, predictions of peak maximum shear strain were largely comparable. In contrast, responses from the two V1.0 WHIMs somewhat underestimated in the cortical GM and cerebral WM regions. However, responses between themselves were largely comparable (Fig. 8d). Finally, for each in vivo dataset, shear or MPS strain maps on a representative axial or parasagittal plane were compared among the three WHIMs along with that from the experiments (Fig. 9).

Fig. 9.

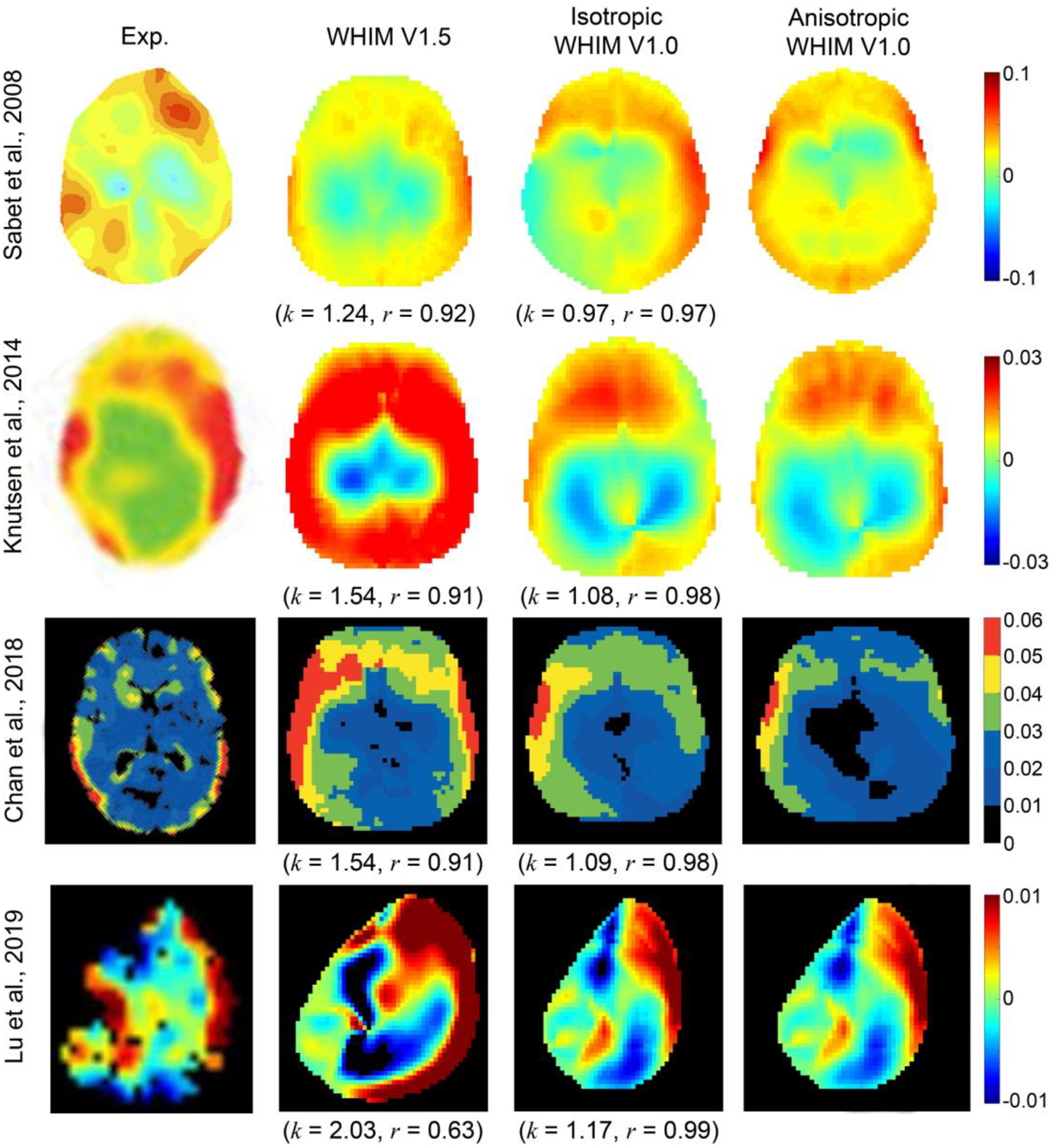
Representative strain maps from four in vivo datasets in comparison with their simulated counterparts using the WHIM V1.5 and the iso- and anisotropic WHIM V1.0. Temporal radial-circumferential shear strain was reported in the Sabet et al. (at 228 ms; axial plane of +2 cm), Knutsen et al. (at 45 ms; mid-axial plane), and Lu et al. (at 81 ms; para-sagittal plane of −39 mm) studies. Cumulative MPS over the entire simulation was reported in the Chan et al. study. Shown are also comparisons in terms of linear regression slope (k) and Pearson correlation coefficient (r) relative to the anisotropic WHIM V1.0 reference based on whole-brain MPS.

Discussion

The common approach to validating a head injury model relies on cadaveric relative brain-skull displacements. While some consider the approach more “robust”⁵⁰, others find it insufficient to evaluate strain accuracy⁶⁰. Therefore, cadaveric strain-based model validation was also proposed, using either a “triad”²¹ or a “tetra”⁶¹ approach. Nevertheless, it remains critical to evaluate whether “validated” head injury models, regardless of the validation approach, produce the same strain magnitude and distribution for the whole brain across the spectrum of blunt impact conditions. Such an investigation is important to assess the confidence when using simulated strains from diverse head injury models to assess injury risks based on experimental strain tolerances³⁶.

CORA-based model validation

The three WHIMs achieved similar average CORA scores based on relative brain-skull displacement (Fig. 3). The same occurred for marker-based strain with the default CORA settings, while WHIM V1.0 had a slightly higher average CORA score (by ~10%) than the WHIM V1.5 variant when using the revised settings (Fig. 4). Except for the isotropic WHIM V1.0 using the revised CORA setting based on the eight high-rate cases⁶⁰, no significant correlation existed between the displacement- and strain-based CORA scores (p>0.1), largely confirming the previous finding⁶⁰. The revised settings (Figs. 3–4) also led to considerably higher scores than the default settings (Figs. B1–B2 in Supplementary B) for both displacement and strain (e.g., average displacement-based CORA increased from 0.44 to 0.69), which was similarly observed before^3,16. The increase in CORA scores was, in part, due to the consistently saturated phase shift sub-rating with the revised setting (Tables B1–B3 in Supplementary B; further discussed below), which could compromise the CORA effectiveness.

Displacement-based CORA scores for the sonomicrometry dataset were also notably higher than those for the NDTs, regardless of the setting (e.g., range 0.83–0.88 vs. 0.47–0.71 using the anisotropic WHIM V1.0 with the revised setting; Fig. 3). However, the difference between strain-based CORA scores for the two datasets largely diminished for both settings (Fig. 4 and Fig. B2 in Supplementary B). These observations were limited to data from three crystals due to data availability. Further exploration is necessary using the complete sonomicrometry dataset.

Using displacement-based CORA, the WHIMs would be rated either as “good” or borderline “fair”, using the revised or default setting, respectively, according to a sliding scale²³ adopted recently³. Using strain-based CORA and the same rating method, the WHIMs would be rated as “good” to borderline “excellent” with the revised setting (Fig. 4) but “fair” with the default setting (Fig. B2 in Supplementary B). In comparison, the two V1.0 models were rated as “good” to “excellent”^25,57 according to NISE-based CS scores⁹ using six different impacts (the eight impacts selected here all had cadaveric strains reported that were not available in the other six). These inconsistent ratings on the same model suggest that caution should be exercised when comparing head injury model biofidelity ratings.

Comparison of simulated whole-brain strains

For simulated whole-brain strains, it is important to recognize that strain overestimation of WHIM V1.5 relative to the anisotropic WHIM V1.0 reference (linear regression slope, k, of ~1.17–2.69; Fig. 7) was similar to the peak cadaveric strain overestimation based on markers (~1.32–3.79; Figs. 5–6). This suggests that the marker-based cadaveric strains are capable of discriminating the WHIMs for their simulated whole-brain strains. WHIM V1.5 and V1.0 also differed considerably in strain distribution (r of 0.57–0.92; Fig. 7), suggesting that cadaveric strains with a higher spatial resolution such as the sonomicrometry datasets with all available crystal trajectories are desirable to discriminate region-specific strains in finer details. Strains from the two WHIM V1.0 variants were similar, because the anisotropic version was calibrated to produce the same MPS relative to its isotropic counterpart⁵⁷.

Nevertheless, when comparing the simulated cadaveric strains with the measured counterparts, the aggregated CORA from WHIM V1.0 was only slightly higher than that from WHIM V1.5 with the revised settings (0.86 vs. 0.78, by ~10%; p <0.04), despite statistical significance. The statistical difference also disappeared for the group of eight high-rate NTD cases (Fig. 4). In addition, when using the default settings, strain-based CORAs from the three WHIMs were statistically indistinguishable (Fig. B2 in Supplementary B). Collectively, these results suggest that aggregated strain-based CORA, itself, may not be effective or sufficiently effective in discriminating the simulated whole-brain strains from the WHIMs (e.g., 10% difference in CORA scores with the revised settings but up to 169% difference in whole-brain strain linear regression slope).

The aggregated CORA not only assesses the similarity in magnitude, but also phase shift and shape. Unlike the default settings with which phase shift sub-rating ranged from 0 to 1, the revised settings led to consistently high scores of phase shift sub-rating (0.8–1.0⁶⁰), and even consistently of 1.0 in this study (Tables B1–B3 in Supplementary B) when reporting displacement-based CORA scores. In part, therefore, this led to relative insensitivity of CORA to magnitude, especially with the revised settings. More work is necessary to understand how best to quantify validation quality. For example, whether to use CORA magnitude sub-rating alone or the peak magnitude ratios based on marker-based strains if and when the phase shift and shape sub-ratings are of sufficient quality. With the former approach, WHIM V1.0 models and V1.5 variant had a sub-rating of 0.71±0.15 and 0.50±0.21, respectively, which would be rated as “good” and “fair”, respectively (Fig. B3 in Supplementary B). This was consistent with the latter strategy when comparing peak strain magnitudes relative to those from markers, where WHIM V1.0 models and V1.5 variant reported an average ratio of 0.94±0.30 and 1.88±0.40 relative to the experiments, respectively (Figs. 5 and 6, Fig. B11 in Supplementary B).

Comparison with in vivo strains

All three WHIMs produced largely similar strains for the Sabet et al. dataset (Fig. 8a). However, WHIM V1.5 consistently overestimated regional shear or MPS from WHIM V1.0 (Fig. 8b–d). For the whole-brain MPS, the WHIM V1.5 also consistently overestimated by 1.24–2.03 times relative to WHIM V1.0 (Fig. 9), incidentally similar to the cadaveric data (1.17–2.69; Fig. 7). These findings suggest that the more recent in vivo datasets of higher resolutions in strain threshold and anatomical regions^8,29,30 improve the discrimination of model simulated strains than the previous Sabet et al. dataset⁴¹.

Some of the strain differences may be attributed to head dimensional mismatch, as either a generic, a subject-specific, or a scaled model was used. It warrants further investigation using subject-specific models (when MRI becomes available) to better identify sources of model-experiment mismatch. This may allow further improving model biofidelity (e.g., regional differences in brain material properties^11,12,31, brain-skull boundary conditions^42,59, etc.) under low-rate impact conditions to inform how models might be implemented for application at higher impact severities.

Cadaveric brain strains: a generalized marker-based strain validation approach

It is important to recognize the distinction between our cadaveric strain evaluation method and the “triad”²¹ or recent “tetra”⁶¹ approaches. Instead of outputting strains from head injury model simulation to compare with averaged strains from NDTs^21,61, we prescribed different sources of nodal trajectories directly to the same marker-based model for strain evaluation. This would avoid some limitations with the “triad” approach²¹ resulting from the mismatch between model volumetric strain vs. marker-based surface strain (which may not be compared directly, as noted⁶¹). It would also obliviate challenges with the “tetra” approach⁶¹ that requires sufficient brain mesh resolution to localize NDTs and preselected brain elements. Perhaps more importantly, maintaining the same marker-based model for strain sampling and interrogation may be more effective and versatile for strain validation. This is illustrated and discussed more extensively in Supplementary C.

Our technique was only applied to triangular surface elements for consistency and/or data availability reasons. However, it can be extended to a more generalized framework. Specifically, the group of markers can be tessellated into a number of volumetric tetrahedrons and/or surface triangular elements (e.g., via delaunay.m in MATLAB), along with pairwise linear elements between two arbitrary markers. Corresponding 3D volumetric, 2D surface and 1D linear strains can then be calculated using different sources of nodal trajectory data for convenient and direct model comparison and validation. Signed 1D linear strains may uniquely reveal local tissue compression/tension information not offered by direction insensitive MPS, as illustrated (Fig. B12 in Supplementary B).

Conceptually, the commonly adopted displacement-based CORA assesses marker motion coherence between model and experiment for each individual marker, and separately for each of the three components. In contrast, the generalized marker-based strain evaluation assesses the spatiotemporal motion coherence among a group of synchronously tracked markers. Potentially, the technique can be further extended to strain rate for model discrimination. A central question is how trustworthy the experimental strain/strain rate is to allow for “validation”, as errors in experimental strain/strain rate may be amplified due to displacement spatial/temporal differentiation. A sensitivity analysis quantifying displacement-strain/strain rate error relationship appears important to gain confidence in the quality of experimental data and subsequent validation⁵⁰.

Implications

Our findings suggest that strain measures of sufficient spatial resolution especially at high- and mid-rates may still be necessary to validate head injury models for strain estimation. Strain is the spatial derivative of displacement field. Regardless of how many embedded NDTs or crystals are available, displacement-based model validation assesses the motion spatiotemporal coherence of each individual marker between model and experiment, but not the coherence among the group of markers. Therefore, validation solely based on cadaveric relative brain-skull displacements may be considered as a first stage, “bronze-standard”. This first-stage validation does not infer strain biofidelity^60,61 and should remain discouraged for model quality ranking^3,34,57.

If a model exactly reproduces experimental displacements from all markers, then the model is perfectly “validated” (with a separate issue on “trustworthiness” due to experimental errors^2,19). Otherwise, a second stage validation against regional strains is necessary, which may be considered as a “silver-standard” especially if more markers in “strategic” locations (Fig. 7) are available to improve the spatial resolution. Cadaveric strains are capable of discriminating head injury models of their simulated whole-brain strains (Figs. 5–6). However, more work is necessary to identify an appropriate strain-based validation rating strategy, as the aggregated CORA may not be sufficiently effective in discriminating mode-simulated whole-brain strains (see earlier discussion). In addition, as strain depends on the non-rigid motion among markers, their group-wise rigid body motion⁶² may still need to be verified against that from the experiment to complete the model validation process.

A high-resolution, “gold-standard” biomechanical strain field may never be possible because the necessary injury-level experiments are not feasible on live humans. High-resolution in vivo strains^8,29,30,41, albeit insufficient for injury-level validation¹⁶, may be useful for validation at subconcussive levels⁵⁵. In addition, they may provide unique insight into how model biofidelity can be improved for potential application at higher impact severities.

The ineffectiveness of current model validation strategies highlights the challenge in defining a universal injury threshold applicable to all head injury models at present. As different “validated” head injury models based on displacements alone produce significantly different strains^16,24, conflicting findings on the risk of injury would occur based on a same injury threshold, either from experiment or a given model. Therefore, a model-specific injury threshold may be necessary, e.g., by fitting against real-world injury cases^15,55. Simulated strains from the same model can then be correlated with the risk of injury in reference to the model-specific threshold. Model-simulated strains, alone, without a corresponding threshold are not sufficient to evaluate the risk of injury, as threshold values from other sources may not be applicable.

Given the lack of strain data of sufficient resolution at injury levels and well-accepted for strain validation⁵⁰, validation against the combined dataset seems plausible to maximize model response confidence given the limitations of each individual piece (cadaveric vs. live; displacement vs. strain; low impact vs. high). In addition, the quality of head injury models may be partially assessed in terms of real-world injury prediction performance⁵⁷. In this case, an objective cross-validation measure is important (e.g., via leave-one-out^7,49 or k-fold cross-validation⁴⁸, appropriate when the sample size is either small or large, respectively; as opposed to a “training” performance commonly used at present^15,28,39,46). Otherwise, a perfect training AUC (area under the receiver operator’s curve) of 100% can be reached⁷, which is an obvious overfitting rather than a meaningful performance measure in practice. After all, objective injury prediction is perhaps one of the ultimate goals of developing and improving head injury models in the first place.

Limitations

This work was limited to one family of WHIMs. However, when considering other head injury models, strain disparities were, in fact, even larger. This is illustrated in Fig. 10 comparing cadaveric strains from THUMS, GHBMC, and KTH models with the experiments for the same four cases in Fig. 5. This would strengthen the notion that strain measures especially at high- and mid-rates are necessary to discriminate model strain responses. The impact case C288-T3 also has strain from a second NDT cluster in the coup side. It was not utilized here as only 39 ms of data is available⁶⁰ (less than the recommended minimum of 40 ms¹⁶). Regardless, we anticipate similar findings relative to the contrecoup to ensue. Certainly, it warrants further investigation whether the identified “strategic” regions (Fig. 6) remain identical in other models. Nevertheless, our findings do suggest the potential value of model simulations to facilitate experimental designs such as the placement of markers to maximize their effectiveness in model strain discrimination. A model-informed feedback on experiment seems logical but appears not to have been utilized.

Fig. 10.

Comparison of average cluster MPS among the THUMs, GHBMC, and KTH models digitized from a previous study¹⁶ and those recalculated from the same four cases⁶⁰ shown in Fig. 5. Strain disparities are even larger when comparing with the three WHIMs in Fig. 5.

Second, although a common standard for model validation is important, this is beyond the scope of the current study, as explorations are ongoing both experimentally^2,18,19 and in modeling^60,61. Nevertheless, by highlighting the large strain differences across a wide range of impact severities, we underscore the need for displacement spatiotemporal measures of sufficient resolution from which to derive regional strains at injury levels for future, improved model validation. The resulting implications on model applications also appear important to understand how best to harmonize model simulations at the current stage and to inform future experimental designs.

Third, while hourglass energy for all model simulations was less than 10% of the total energy (excluding external and other work in Abaqus)^52,59, WHIM V1.0 could lead to ~40–60% ratios relative to the internal energy¹⁵ resulting from enhanced hourglass control that is Abaqus-recommended but not user-adjustable. In comparison, WHIM V1.5 typically reported up to ~40% ratios relative to the internal energy for high-rate impacts, while ~5%, and ~2% for mid-rate impacts and in vivo loading cases, respectively. It was possible to control the relax stiffness scaling factor to reach a ratio <10% for high-rate cases⁵⁸; albeit, at the expense of strain overestimation relative to the baseline from C3D8I elements that are immune to hourglass issue¹. Regardless, the different types of hourglass controls do seem to affect brain strains substantially^17,45.

Fourth, all cadaveric data (marker locations, displacements, and brain shapes) had to be digitized manually (albeit, not necessarily a limitation of our own study). This was not only repetitive and laborious but also prone to errors. It is recommended that experimentalists^2,18,19 and modelers^16,60,61 alike publish their data in modern digital forms so that to best facilitate their use. This is explored here using an interactive MATLAB figure to embed marker locations and displacement time histories (Supplementary D; along with example code to generate an animated 1D linear strain field).

Finally, the WHIM V1.5 was only minimally upgraded. Other advanced modeling features have already emerged, such as a multi-scale approach to represent the pia-arachnoid complex⁴², fluid-structure interaction at the brain-skull interface⁵⁹, and mesh conformity of ventricles and deep brain structures³. They can be candidates for future WHIM development.