Abstract
Image post-processing is used in clinical-grade ultrasound scanners to improve image quality (e.g., reduce speckle noise and enhance contrast). These post-processing techniques vary across manufacturers and are generally kept proprietary, which presents a challenge for researchers looking to match current clinical-grade workflows. We introduce a deep learning framework, MimickNet, that transforms conventional delay-and-summed (DAS) beams into the approximate Dynamic Tissue Contrast Enhanced (DTCE™) post-processed images found on Siemens clinical-grade scanners. Training MimickNet only requires post-processed image samples from a scanner of interest without the need for explicit pairing to DAS data. This flexibility allows MimickNet to hypothetically approximate any manufacturer’s post-processing without access to the pre-processed data. MimickNet post-processing achieves a 0.940±0.018 structural similarity index measurement (SSIM) compared to clinical-grade post-processing on a 400 cine-loop test set, 0.937±0.025 SSIM on a prospectively acquired dataset, and 0.928±0.003 SSIM on an out-of-distribution cardiac cine-loop after gain adjustment. To our knowledge, this is the first work to establish deep learning models that closely approximate ultrasound post-processing found in current medical practice. MimickNet serves as a clinical post-processing baseline for future works in ultrasound image formation to compare against. Additionally, it can be used as a pretrained model for fine-tuning towards different post-processing techniques. To this end, we have made the MimickNet software, phantom data, and permitted in vivo data open-source at https://github.com/ouwen/MimickNet.
Keywords: Clinical Ultrasound, CycleGAN, Image Enhancement, MimickNet, Ultrasound Post-Processing
I. Introduction and Background
IN the typical clinical B-mode ultrasound imaging paradigm, a transducer probe will transmit acoustic energy into tissue, and the back-scattered energy is reconstructed via beamforming techniques (e.g., delay-and-sum [1], minimum variance [2], delay-multiply-and-sum [3]) into a human eye-friendly image. This image attempts to faithfully map spatial changes in tissue’s acoustic impedance, which is a property of its bulk modulus and density. Unfortunately, there are many sources of image degradation such as electronic noise, speckle from sub-resolution scatterers, reverberation, and de-focusing caused by heterogeneity in tissue sound speed [4]. In the literature, these sources of image degradation can be suppressed through better focusing [5], [6], spatial compounding [7], harmonic imaging [8], [9], [10], and coherence imaging techniques [11], [12], [13].
In addition to beamforming, image post-processing is a significant contributor to image quality improvement. Reader studies have shown that medical providers largely prefer post-processed images over delay-and-sum (DAS) imagery [12], [14]. Unfortunately, commercial post-processing algorithms are proprietary, and implementation details are typically kept as a black-box to the end-user. Thus, researchers that develop image improvement techniques on highly configurable research systems, such as Verasonics (Kirkland, USA) and Cephasonics (Santa Clara, USA) scanners, face challenges in presenting their images alongside current clinical system scanner baselines. The current status quo for researchers working on novel image forming techniques is to compare against DAS images, which are not typically viewed by medical providers. Contrast ratio (CR) and Contrast-to-noise (CNR) are commonly provided metrics; however, these can be sensitive to arbitrary dynamic range alterations, which have motivated the development of new metrics [15], [16], [17].
Researchers looking to translate clinically-relevant image enhancement should ideally compare their images against an existing scanner’s full post-processing pipeline. Of course, this is difficult. Researchers would either need access to proprietary post-processing code or hack into raw channel data from difficult-to-configure commercial scanners for a fair, direct pixel-wise comparison. To combat this difficulty, we aim to mimic a significant portion of a commercial scanner’s post-processing pipeline by leveraging deep learning methods.
Deep learning based post-processing using convolutional neural network (CNN) generators [18], [19] have become immensely popular in the image restoration problem [20], [21]. One popular network architecture used is an encoder-decoder network with skip connections commonly referred to as a Unet [22]. In the image restoration problem, the encoder portion of Unet takes a noisy image as input and creates feature map stacks which are subsequently down-sampled through max pool operations. The decoder portion up-samples features and attempts to reconstruct an image of the same size as the input. Usage of skip connections in Unet has been shown to better maintain high-frequency information in the original image [23]. Other encoder-decoder Unet flavours exist which exploit residual learning [24], [25], wavelet transforms [26], and dense blocks [27], [28]. Encoder and decoder network parameters are optimized with gradient descent which minimizes a distance function between the reconstructed and ground truth image [29].
Adversarial objective functions are a unique class of distance functions that have shown success in the related field of image generation [30]. The adversarial objective optimizes two networks simultaneously. Given training batch sizes of m with individual examples i, G is a network that generates images from noise z(i), and another network, D, discriminates between real images x(i) and synthetically generated images G(z(i)). D and G play a min-max game since they have competing objective functions shown in Eq. 1 and Eq. 2 where θg are parameters of G and θd are parameters of D. If this min-max game converges, G ultimately learns to generate realistic synthetic images that are indistinguishable from the perspective of D. In the literature, these networks are referred to as generative adversarial networks (GANs) [31], [32]. Conditional GANs (cGANs), which take in a structured input, such as a corrupted image instead of noise, have seen success in image restoration and style transfer problems [33].
| (1) |
| (2) |
In the field of ultrasound, CNNs and cGANs have been applied in many versatile ways to B-mode imaging. CNNs have been applied to achieve better motion estimation, which in turn enables better construction of a high-resolution image from a temporal window of low-resolution ultrasound frames [34]. CNNs have been shown to improve the quality of in vivo single plane-wave images through training only on simulated data [35]. GANs have been shown to process images from 3 compounded plane-waves to look similar to an image compounded with 10 plane-waves [36]. CNNs have been shown to directly beamform images and perform speckle reduction on simulated data as well as in vivo images [37]. In recent work, GANs have shown the same beamforming ability on simulated data [38], though a comparison to simpler CNN approaches has not yet been performed. GANs have shown the ability to generate a multi-focus image from a single-focus image [39]. Finally, GANs have approximated the non-local low-rank (NLLR) speckle reduction algorithm [40].
While the results of higher quality images from CNNs and GANs are promising, these studies do not compare against current clinical-grade post-processing. These and future image formation studies would benefit from a pixel-wise comparison to a clinical-grade baseline. Unfortunately, this is not a luxury available in most research environments. To this end, we present an easy and robust method to mimic clinical-grade post-processing without the need for explicit image registration through cycle-consistent GANs (CycleGAN) [41].
CycleGANs excel at the problem of style transfer where images are mapped from one domain to another without necessitating explicitly paired images. CycleGANs consist of two key components: forward-reverse domain generators, Ga and Gb, and forward-reverse domain discriminators, Da and Db. The generators translate images from one domain to another, and the discriminators distinguish between real and synthetically generated images in each domain. We show the objective functions for one direction of the cycle in Eq. 3 and Eq. 4 where a(i) is an image from domain A, and b(i) is an image from domain B. In Eq. 3 and Eq. 4, the variables and are the parameters for the domain A forward generator and domain B discriminator respectively. In Eq. 3, f can represent any distance metric to compare two images.
| (3) |
| (4) |
As an overview, we investigate approximation of a clinical-grade post-processing algorithm under the following schemes:
When before-and-after image pairs are available: This scheme is only feasible if DAS beams can be accessed immediately before any post-processing. We can directly optimize this scheme with respect to a pixel-wise loss. We call this training scheme the gray-box constraint.
When before-and-after image pairs are not available: This training scheme equates to acquisitions from one scanner with easily accessible DAS data, and acquisitions from another scanner that only provides post-processed images ready for clinical use. We can only indirectly optimize in this scheme through the cycle-consistency loss in [41]. However, this scheme is more practical to implement compared to the gray-box scheme. We call this training scheme the black-box constraint. MimickNet refers to the trained model under black-box constraints.
We assess MimickNet (black-box constrained) on the test set and prospectively acquired data. Our training set only includes DAS liver, fetal, and phantom data; thus, to further assess generalizability, we also evaluate on out-of-distribution cardiac data.
Our results suggest that clinical-grade post-processing can be well approximated using the MimickNet framework using data acquired through a clinical scanner’s intended use. Once trained, we hypothesize MimickNet can be used as a pretrained model for other post-processing, or downstream prediction tasks.
II. Methodology
We start with 1500 unique retrospective ultrasound cine-loop acquisitions over 59 subjects consisting of a total of 39200 frames from fetal, phantom, and liver targets from studies [12], [42], [43], [44]. 78 frames from a cardiac cine-loop acquired in [6] were used for out-of-distribution evaluation. 67 unique prospective scans are gathered for further evaluation. Each study was IRB approved by Duke University, and each study subject provided written informed consent prior to enrollment in the study.
Cine-loops are split into a train-validation-test-split of 1000–100-400 cine-loops; however, structures across unique cine-loop acquisitions may contain displacement shifted repeats. Cine-loop frames are processed by a proprietary post-processing algorithm known as Dynamic Tissue Contrast Enhancement (DTCE™), to form before-and-after pairs. DTCE™ is commercially advertised by Siemens (Malvern, USA), to perform speckle reduction, contrast enhancement and improve the conspicuity of anatomical structures.
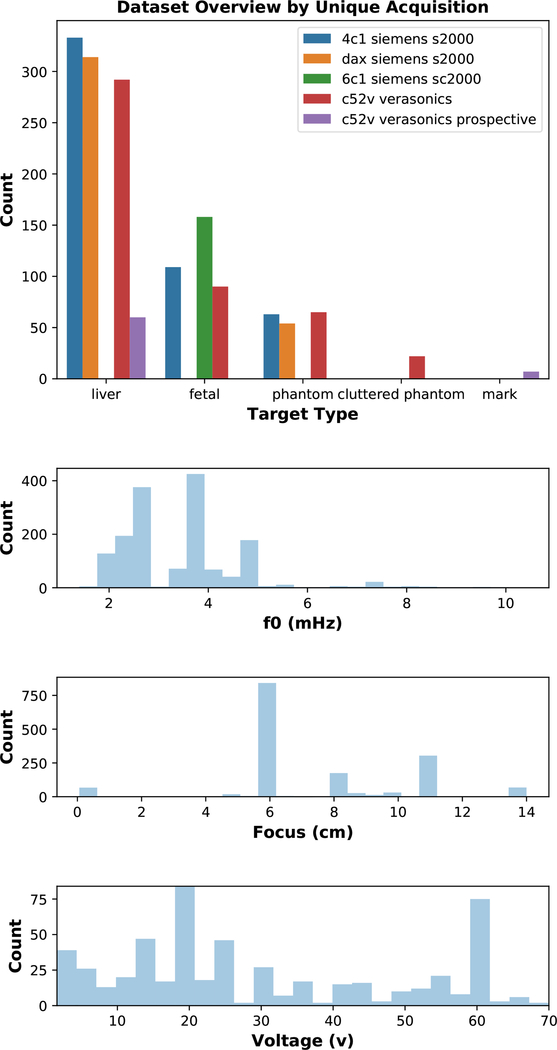
Our dataset is highly heterogeneous which enables training and performance assessment over a large input domain. Table I shows the data split at per-frame granularity. Fig. 1 shows a sample distribution of what scan parameters differ across the dataset for each uniquely acquired cine-loop.
TABLE I.
Dataset Overview by unique scan and individual frames for train-test distribution and prospectively acquired data.
| Type | Unique Scans | Frames | Train | Val | Test |
|---|---|---|---|---|---|
| Train-Test | 1500 | 39200 | 25986 | 2393 | 10821 |
| Prospective | 67 | 2810 | 2810 |
Fig. 1.
Overview of our highly heterogeneous dataset and distribution across different acquisition parameters. Phantom data, permitted in vivo data, and acquisition parameter metadata at a per-frame granularity are available in the Supplemental Materials Metadata Section.
A. Gray-box Training with Paired Images
In the gray-box case where before-and-after paired images are available, our problem can be seen as a classic image restoration problem where our input DAS beamformed data is “corrupted”, and our clinical-grade post-processed image is the “uncorrupted ground truth”. We use the generator found in Fig. 2 replacing LeakyReLU activations with ReLU activations, and optimizing for mean-absolute-error (MAE). MAE is the summed pixel-wise absolute difference between a ground truth pixel y(i) in image y and estimated pixel x(i) in image x. These residuals are averaged by all pixels m.
| (5) |
We use an ADAM optimizer [45] with a learning rate λ of 0.002, first moment β1 of 0.9, and second moment β2 of 0.99. See Supplemental Materials Code Section for more details.
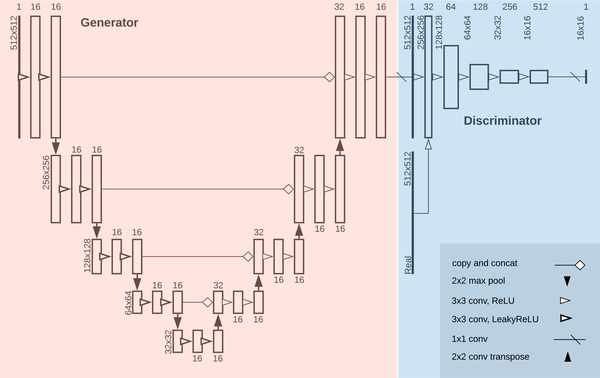
Fig. 2.
Above is a diagram of the generator and discriminator structure for MimickNet in one translation direction of our black-box training scheme. The reverse direction uses an identical mirrored structure. Under the gray-box training constraint, only the generator is used since pixel-wise ground truth is available. The gray-box and black-box training schemes use the same generator architecture except LeakyReLU activations are ReLU in the gray-box scheme.
B. Black-box Training with Unpaired Images
To simulate the more realistic black-box case where paired before-and-after images are unavailable, we take whole cine-loops from the training set and split them into two groups. The first group removes paired DAS data, and the second group removes paired clinical-grade post-processed data. This data removal ensures there are never any registered image pairs during training, and that other transmit parameters vary in a similar distribution across the two groups.
We train a CycleGAN using MAE for our generators’ cycle-consistency loss (Eq. 3) and identity loss [33]. We weight the cycle-consistency loss 10 times greater as originally defined in [33]. We use the discriminator architecture on the right side of Fig. 2, which combines the PatchGAN and LSGAN approaches used in [19], [33] to optimize for least-squares on patches of linearly activated final outputs. The discriminator is only used to facilitate training in the black-box case where no paired images are available, and it is not used in the gray-box case since ground truths are available.
We use an ADAM optimizer with a learning rate λ of 0.0002, first moment β1 of 0.5, and second moment β2 of 0.99. See Supplemental Materials Code Section for more details.
C. Training Details
Before training, we preprocess detected DAS data frames by log compression and clipping to an 80dB noise floor. Processed frames are shuffled and randomly cropped to 512×512 axial by lateral beams with a padded reflection if the dimensions are too small. Constraining dimensions enables batch training, which leads to faster and more stable training convergence. During inference time, images can be any size as long as they are divisible by 16 due to required padding in our CNN architecture. We use a TensorFlow [46] backend to train models built with the Keras [47] interface.
D. Performance Evaluation, Sampling, and Breakdown
We evaluate the full test set of unpadded MimickNet post-processed beams before scan conversion against clinical-grade post-processed beams using structural similarity index measurement (SSIM) which ranges from 0 to 1. SSIM was first proposed in [48] as a metric more representative of human perceived similarity. SSIM is defined in Eq. 6 and is the product between two images’ luminance l, contrast c, and structure s (Eq. 7–9).
| (6) |
| (7) |
| (8) |
| (9) |
Similarity is calculated between X and Y which are two 11×11 kernels from their respective images. These kernels slide across the two images, and the output values are averaged to get the SSIM between two images. Variables μX, and μY, are the mean and variance of each kernel patch, respectively. Variables c1, c2, and c3 are the constants (k1L)2, (k2L)2, and c2/2 respectively. L is the dynamic range of the two images, k1 is 0.01, and k2 is 0.03. All SSIM constants are the default values originally formulated in [48].
We plot the kernel density estimate of SSIM compared to clinical-grade ground truth per individual frame across our entire test set and prospectively acquired dataset. We show the SSIM distribution of DAS frames, gray-box model frames, MimickNet frames, and MimickNet prospective frames.
We investigate the individual components of SSIM, luminance l, contrast c, and structure s, to better understand which component is most degrading to our approximation. Since the equations for contrast Eq. 8 and structure Eq. 9 are highly related in examining variance between and within patches, we can algebraically simplify these two equations into a single equation we call contrast-structure cs (Eq. 10).
| (10) |
We acquire prospective data solely for evaluation shown in Table I and Fig. 1. Lastly, we display sample images from the worst to best SSIM metric.
III. Results
A. Overview
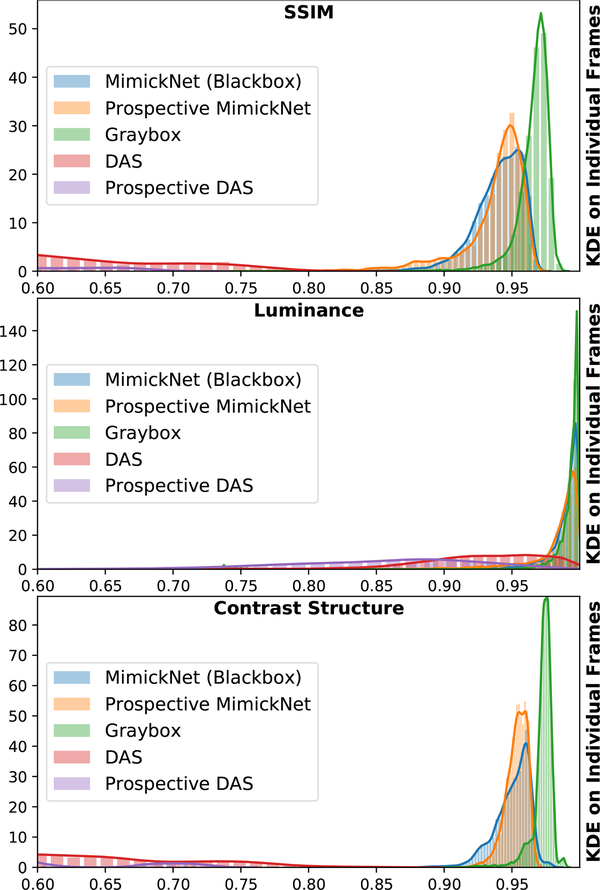
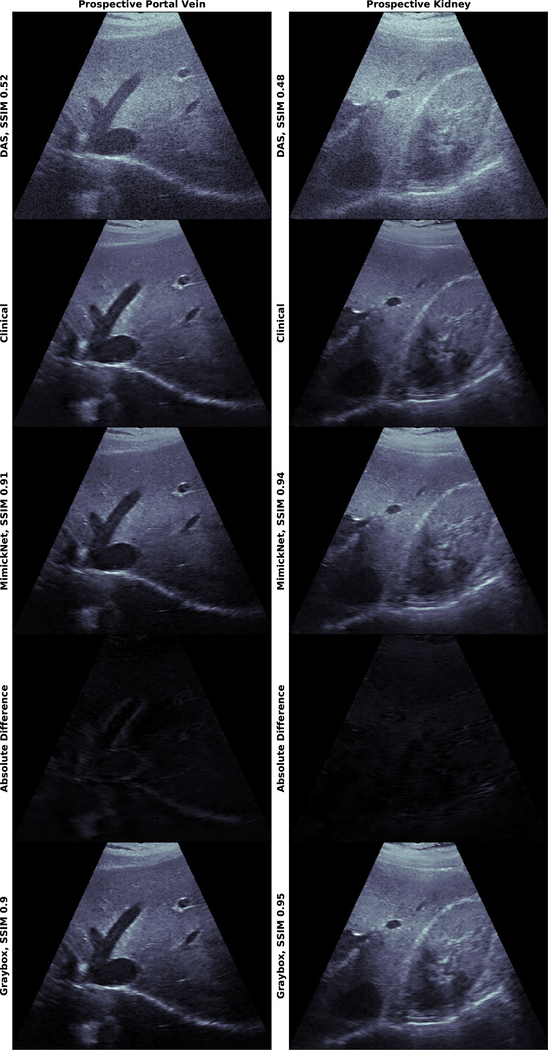
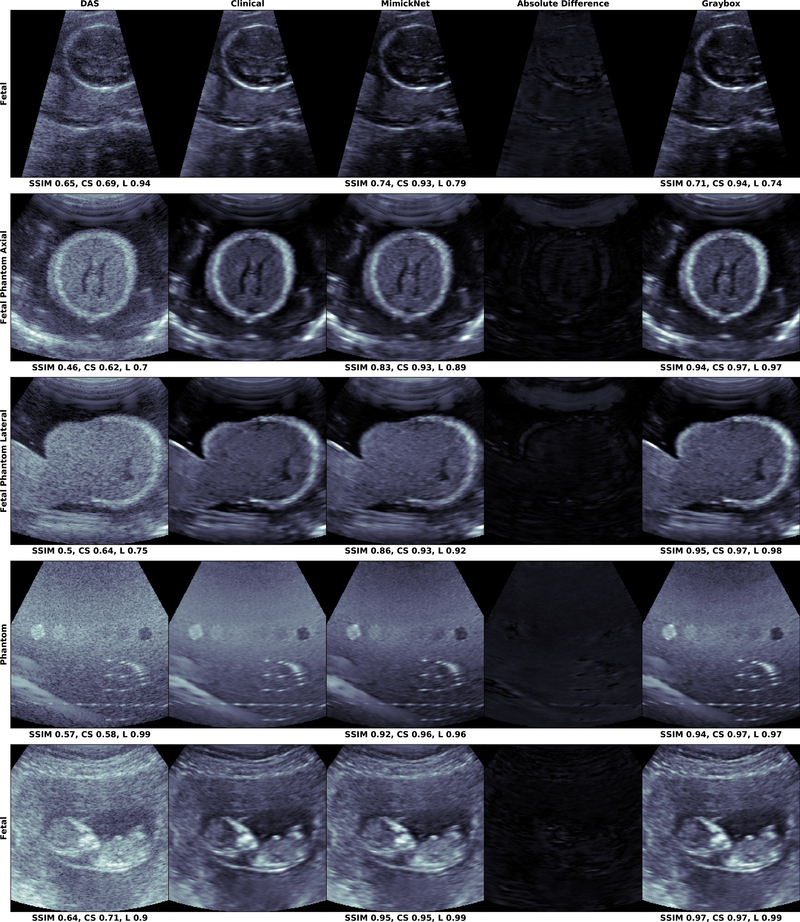
The distribution of SSIM across retrospective and prospective test sets is shown in Fig. 3. Mean and standard deviation of these distributions are reported in Table II. Prospectively acquired images of the hepatic portal vein and kidney are in Fig. 4. We show images from the worst (0.74) to best (0.95) SSIM along with their breakdowns in luminance and contrast-structure in Fig. 5. Notice the artificially-enhanced bright edges apparent in the Clinical-grade and Gray-box post-processing on the hepatic portal vein in (Fig. 4, left), and chin of the lateral view fetal phantom (Fig. 5, 3rd row). MimickNet’s post-processing does not introduce artificial structures not present in the DAS data.
Fig. 3.
The KDE distribution of SSIM (top), luminance (middle), and contrast-structure (bottom) across all cine-loop frames in our test dataset. All metrics are available in the Supplemental Materials Metrics Section at a frame level granularity. Metrics compare images produced under the following conditions to clinical ground truth: “MimickNet (Blackbox)” refers to black-box optimization on the retrospective test set. “Prospective MimickNet” refers to black-box optimization on the prospective test set. “Graybox” refers to gray-box optimization on the retrospective test set. “DAS” refers to delay-and-sum beamformed data from the retrospective test set. Prospective DAS refers to delay-and-sum beamformed data on the prospective test set.
TABLE II.
Summary metrics on different evaluation schemes. Mean ± Standard Deviation of post-processed test set images compared to clinical ground truth are reported. “Pro” refers to prospective test set.
| Scheme | SSIM | Contrast-Structure | Luminance |
|---|---|---|---|
| MimickNet | 0.940±0.018 | 0.951±0.013 | 0.989±0.013 |
| (Pro) MimickNet | 0.937±0.025 | 0.953±0.008 | 0.982±0.023 |
| Graybox | 0.965±0.013 | 0.973±0.008 | 0.993±0.010 |
| DAS Baseline | 0.557±0.105 | 0.598±0.102 | 0.924±0.056 |
| (Pro) DAS | 0.465±0.077 | 0.533±0.065 | 0.852±0.074 |
Fig. 4.
Prospectively acquired harmonic in vivo images on the hepatic portal vein (left) and kidney (right) self-acquired by Dr. Mark Palmeri. Images were acquired on a Verasonics C5–2v probe with a 4.7 MHz center frequency spanning 49.75 degrees. All images are shown on a dynamic range of 80dB. The Absolute Difference between MimickNet and Clinical images are shown on the same 80dB scale as other images. Images were acquired for evaluation only and not used in any training capacity. Notice the difference between Clinical and MimickNet images near the hepatic portal edges. These artificially-enhanced bright edges are not apparent in the original DAS image (images are best viewed electronically).
Fig. 5.
The mean SSIM over our test distribution of images was 0.940±0.018, but we display the worst-case SSIM outliers (top) to the expected case SSIM (bottom). We also display the contrast-structure (CS) and luminance (L) components of SSIM. All images are shown on a dynamic range of 80dB. The Absolute Difference between MimickNet and Clinical images are shown on the same 80dB scale as other images. Graybox refers to the gray-box training constraint when direct optimization is possible while MimickNet is the black-box case when only indirect optimization is possible. Notice the artificially-enhanced bright edges apparent in the Clinical and Graybox post-processing on the chin of the lateral view fetal phantom in (3rd row). Also notice the bright reflector present in the phantom (4th row) in all except the Clinical image.
B. SSIM Performance Distribution
SSIM from gray-box and MimickNet (black-box) training schemes are shown in Table II. The gray-box performs slightly better and serves as an upper bound of what our generator can achieve when direct pixel-wise optimization is possible. We also provide the SSIM on DAS images as a baseline. We see that the majority of image improvement is captured by the contrast-structure component of SSIM.
In Fig. 3, we show kernel density estimates (KDE) of SSIM for individual frames across our test set and prospectively acquired dataset. In statistics, KDE is a non-parametric method to estimate the probability density function (PDF) of a random variable. In the best case scenario, the entire PDF would exist at 1.00. DAS is far from the ideal while MimickNet is well centered around 0.94. The gray-box upper bound performs slightly closer to the ideal than black-box. The PDF of SSIM performance between prospective data and black-box data highly overlap, thus MimickNet’s performance on retrospective testing data generalize to our prospective data.
Other metrics are available at frame level granularity in the Supplemental Materials Metrics Section. Additionally, in the gray-box case, we varied loss function and filter depth hyperparameters. However, these hyperparameter changes did not result noticeable improvements. These results are available in the Supplemental Material Tables I and II.
C. Runtime Performance
In Table III, the runtime was examined for MimickNet on different hardware, input sizes, and their intended use case during benchmarking. MimickNet contains 52993 trainable parameters and uses 0.105 MFLOPS. MimickNet has not undergone any inference optimization such as quantization or floating point 16 optimization.
TABLE III.
Runtime Performance of MimickNet on Different Hardware, Input Sizes, and Intended Use Case.
| Hardware | Input Size | Use case | FPS (Hz) |
|---|---|---|---|
| Nvidia P100 | 512×512 | Training Pipeline | 142 |
| Nvidia Titan V | 1808×208 | Verasonics C5-2v | 65 |
| Huawei Mate 10 | 288×240 | Cardiac | 8 |
D. Out of Dataset Distribution Performance
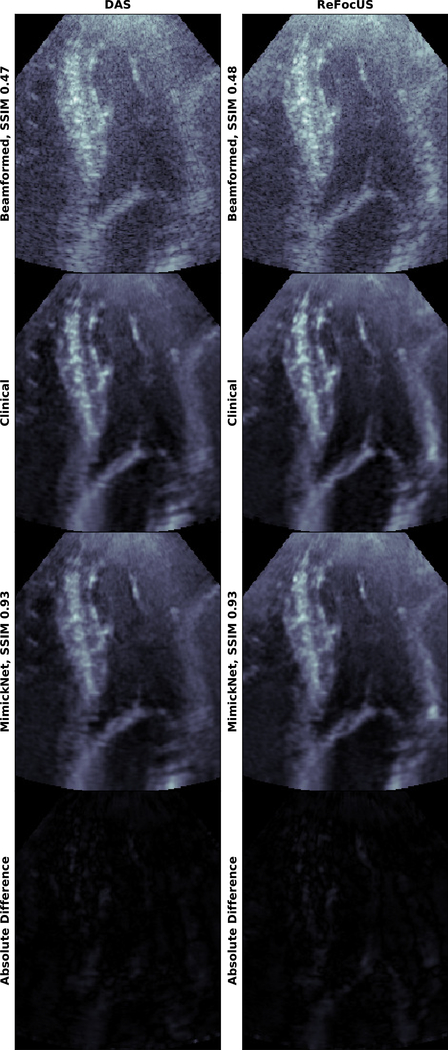
We applied MimickNet post-processing to a 78 frame cardiac cine-loop to assess MimickNet’s generalizability. MimickNet is never trained on cardiac data. MimickNet achieves a 0.928±0.003 after gain correction despite only training on phantom, fetal, and liver targets. Table IV shows SSIM with and without gain correction (GC). In Fig. 6 we show images with gain correction which highlights the importance of contrast-structure.
TABLE IV.
Out of Distribution Cardiac Data metrics with and without gain correction (GC). Mean ± Standard Deviation of post-processed test set images compared to clinical ground truth are reported.
| MimickNet Input | SSIM | Luminance | Contrast Structure |
|---|---|---|---|
| DAS Data | 0.746±0.009 | 0.746±0.009 | 0.944±0.002 |
| DAS (GC) | 0.928±0.003 | 0.982±0.002 | 0.944±0.002 |
| REFoCUS Data | 0.749±0.016 | 0.794±0.016 | 0.943±0.002 |
| REFoCUS (GC) | 0.937±0.002 | 0.992±0.001 | 0.943±0.002 |
Fig. 6.
MimickNet applied to out of distribution cardiac data on DAS and REFoCUS ultrasound beamformed images. Gain correction is performed. MimickNet is never trained on cardiac data and is only trained on fetal, liver, and phantom data. All images are shown on a dynamic range of 80dB. The Absolute Difference between MimickNet and Clinical images are shown on the same 80dB scale as other images. Note the contrast improvements in the heart chamber, and resolution improvements in the mitral valve due to REFoCUS are preserved after MimickNet and DTCE™ post-processing. The full cine-loop is provided in the Supplemental Materials Media Section.
MimickNet and DTCE™ were developed with DAS beamformed images as input. To further assess MimickNet’s generalization, we applied MimickNet on data beamformed by REFoCUS without additional training. Cardiac data was acquired with a P4–2v Verasonics Probe with 2.25MHz center frequency spanning 75.3 degrees. REFoCUS is a recent novel beamforming method that allows for transmit-receive focusing everywhere under linear system assumptions resulting in better image resolution [6].
We see that both MimickNet and DTCE™ generalize to REFoCUS beamformed data, despite point spread function differences between DAS training data and REFoCUS. We qualitatively see that contrast improvements in the heart chamber, and resolution improvements in the mitral valve due to REFoCUS are preserved after MimickNet and DTCE™ post-processing in Fig. 6. We envision MimickNet can be used to improve the image quality of other novel beamforming methods by providing a comparable post-processing algorithm to what is used in clinical practice.
IV. Discussion
A. MimickNet Generalizes Well
MimickNet is successful at approximating a clinical-grade post-processing algorithm, DTCE™, which is commercially advertised by Siemens to simultaneously perform speckle reduction, contrast enhancement and improve the conspicuity of anatomical structures. Quantitatively, MimickNet takes DAS beams as an input with initial SSIM of 0.557±0.105 and post-processes them to achieve an SSIM of 0.940±0.018 against clinical-grade processed ground truth in our test dataset. SSIM ranges from 0 to 1, and was formulated to be reflective of human perceived similarity. Qualitatively, we show images with low to high SSIM in Fig. 5. Our sampling extends the full range of SSIM from 0.74 (worst case) to 0.97 (best case). Even for post-processed images with the worst SSIM performance, it is difficult to discern differences without looking closely at the Absolute Difference image between MimickNet and Clinical images. We acquire prospective data solely for evaluation in Fig. 4, and see similar qualitative and quantitative (0.937±0.002) results to our test set.
We apply MimickNet to out-of-distribution data to further assess generalization. MimickNet was never trained on cardiac data, but it achieves a 0.928±0.003 SSIM on cardiac data after gain correction which is similar to in-distribution performance. MimickNet was also only trained on DAS beamformed data. We were curious if differently beamformed data would result in reasonable output. We choose to post-process REFoCUS data, a recently developed beamforming method, and achieve 0.937±0.002 SSIM after gain correction which is also similar to in-distribution data performance.
Our results on test data and prospectively acquired data show that MimickNet generalizes to in-distribution anatomical data. Additionally, while MimickNet can be used to fine-tune towards new anatomical structures or beamforming methods, our out-of-distribution cardiac image results show SSIM similar to in-distribution performance even without fine-tuning.
B. MimickNet Use Case
MimickNet’s envisioned use case is to transfer a post-processing pipeline approximation from a clinical-grade scanner to a target scanner (e.g. research-grade or cheaper portable scanner). To achieve this transfer, known scan parameters (e.g. focus, transmit frequency, and voltage) from both scanners should be similarly distributed. From MimckNet’s perspective, any differences in parameter distributions are considered “post-processing” to approximate. Sweeping a selected distribution of parameters, a researcher can acquire post-processed images on the clinical-grade scanner, and beamformed-only images on the target scanner. These two collections of unregistered images can be used as input to train or fine-tune MimickNet under a black-box training scheme.
If before-and-after post-processing pairs are available, the researcher can simply use a gray-box training scheme. However, this option may not always be easily accessible. In the worst case, gray-box training requires a researcher to hack into a scanner system to siphon DAS data immediately before post-processing. The black-box scheme equates to acquiring images from ultrasound scanners via their intended use, no hacking required. This ease in data collection costs a slight trade-off of 0.025 SSIM performance.
We envision MimickNet can be used to help close the clinical translation gap by producing a clinically comparable image baseline familiar to medical providers. This can be used to better highlight the benefits of novel beamforming methods like REFoCUS, or highlight the similarities of images formed on differing hardware that is potentially cheaper or more portable.
C. MimickNet Observed Differences
Closer qualitative inspection of minor differences suggest MimickNet maintains original DAS contrast better than Clinical post-processing. We choose to represent SSIM over other metrics available in the Supplemental Materials Metric Section because it provides an interpretable breakdown of where we fail to match the ground truth image. However, SSIM has limitations like any other metric, and minor structural differences are not well represented. Thus, we take time to qualitatively discuss minor, but present, image differences. Future work in the form of clinical reader studies are needed to formally examine the clinical significance of differences between DTCE™ and MimickNet.
We find it interesting that clinical-grade post-processing produces such artificially-enhanced bright edges found in the hepatic portal vein (Fig. 4, left), and chin of the lateral fetal phantom view (Fig. 5, 3rd row) when they are not present in the original DAS image. While it is out of the scope for this paper to discuss which image is clinically better, we note that MimickNet better preserves the original relative contrast found in the physics-based DAS image than clinical-grade post-processing.
One of the theoretical mechanisms MimickNet leverages to prevent information removal is its unique cycle-consistency loss. While on one hand, the discriminator loss encourages MimickNet images to look indistinguishable from a clinical-grade post-processed image, the cycle-consistency loss penalizes irreversible transformations. MimickNet’s choice of maintaining instead of brightening certain edges found in Fig. 4, and Fig. 5 may be to keep information such that it can return to the original DAS intensity. We see that the gray-box images, which are not under cycle-consistency loss pressure, are able to brighten corresponding edges.
The cycle-consistency loss enforces the interesting property that for any forward transformation, such as post-processing a physics-based DAS image, there must exist a reverse transformation that minimizes information loss. Future work should investigate leveraging the cycle-consistency loss as a conditional input parameter that modulates the amount of desired post-processing at inference time. A related mechanism has been proposed by [49] to modulate the diversity of GAN generated images. Conceptually, this parameter would modulate the bias a neural network is allowed to move an image away from underlying physics. Although, creating this mechanism is challenged by the cycle-consistency loss being closely tied with model convergence. We may require some method to disentangle convergence from modulation. An example of the modulation parameter’s use case can be seen in the 4th row of Fig. 5. Clinical-post-processing removes the bright reflectors in the left-most phantom lesion, but both black-box and gray-box do not mimic this removal. Whether it is a clinically good idea to remove such strong physical signal is beyond the scope of this paper, but it would be desirable to have the flexibility to modulate the amount of removal while maintaining a reduced speckle background.
D. MimickNet Mobile Runtime
MimickNet can be run in real-time and shows promise for mobile device use. It runs in real-time at 142 FPS on a P100 (Nvidia, Santa Clara, USA), has been used to process DAS beams from a Verasonics C5–2v in real-time at 65 FPS, and has been shown to run on a Mate 10 (Huawei, Shenzhen, China) mobile phone at 8 FPS. This runtime is relevant since more ultrasound systems are being developed for mobile phone viewing [50]. Future work will investigate inverted residuals and linear bottlenecks [51] to increase computational speed on mobile devices.
E. Future Works
MimickNet is meant to be a simplistic architecture useful for downstream fine-tuning to new tasks, and future work can explore better modeling architectures. The architecture we used for our generator is meant to be simplistic to best showcase initial feasibility. One immediate improvement that comes to mind is to explicitly model the scan conversion process so beam geometries are disentangled from the training scheme. This can be accomplished through spatial transformer networks (STNs) which resample images from a predefined or learned transformation matrix [52]. Learning the transformation matrix may enable better beam interpolation beyond bilinear or bicubic approaches. Another improvement would be to explicitly model depth dependent de-focusing. This could be accomplished by appending coordinate features following the same scheme as used in [53]. Our results with ultrasound data suggest it should also be possible to approximate medical image post-processing under black-box constraints in CT and MR images as similar encoder-decoder architectures have been used to denoise CT [54], and MR [55] in the direct optimization, gray-box case.
Future work will look into increasing the capacity of MimickNet to perform multiple types of specialized post-processing. It will also be valuable to assess how much data is required to successfully train under black-box constraints, as well as how much data domains can diverge before training fails to converge. We provide pretrained model weights of MimickNet for researchers to fine-tune towards other clinical post-processing algorithms.
V. Conclusion
This work’s main contribution is in decreasing the clinical translation barrier for future image enhancement research. MimickNet closely approximates DTCE™, a particular clinical-grade post-processing algorithm, in the black-box case without before-and-after post-processed image pairs. Beamformed data previously only largely understood by research domain experts can be translated to clinical-grade images widely familiar to medical providers. MimickNet can run in real-time, works for out-of-distribution cardiac data, and thus shows promise for practical production use. We also present MimickNet as a flexible image matching tool that can provide fair comparisons of novel image formation techniques to a clinical baseline mimic. We specifically demonstrate MimickNet’s application in comparing DAS and REFoCUS beamforming methods, and we showed that resolution improvements from REFoCUS are carried over into the MimickNet post-processed image. We provide the pretrained model weights of MimickNet to make it easy for researchers to fine-tune towards other clinical post-processing algorithms in future research endeavours. The MimickNet software, phantom data, and permitted in vivo data are open-source at https://github.com/ouwen/MimickNet.
Supplementary Material
Acknowledgment
This work was supported by the National Institute of Biomedical Imaging and Bioengineering under Grant R01-EB026574, and National Institute of Health under Grant 5T32GM007171-44. The authors would like to thank Siemens Medical Inc. USA for in kind technical support, including access to complied DTCE™. The authors would like to thank the team at Google Cloud for providing compute resources.
References
- [1].Thomenius KE, “Evolution of ultrasound beamformers,” in 1996 IEEE Ultrasonics Symposium. Proceedings, vol. 2, November 1996, pp. 1615–1622 vol.2. [Google Scholar]
- [2].Synnevag JF, Austeng A, and Holm S, “Benefits of minimum-variance beamforming in medical ultrasound imaging,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 56, no. 9, pp. 1868–1879, Sep. 2009. [DOI] [PubMed] [Google Scholar]
- [3].Matrone G, Savoia AS, Caliano G, and Magenes G, “The delay multiply and sum beamforming algorithm in ultrasound b-mode medical imaging,” IEEE Trans. Med. Imaging, vol. 34, no. 4, pp. 940–949, Apr. 2015. [DOI] [PubMed] [Google Scholar]
- [4].Pinton GF, Trahey GE, and Dahl JJ, “Sources of image degradation in fundamental and harmonic ultrasound imaging using nonlinear, full-wave simulations,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 58, no. 4, pp. 754–765, Apr. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Thiele K, Jago J, Entrekin R, and Peterson R, “Exploring nsight imaging, a totally new architecture for premium ultrasound,” Philips, Tech. Rep. 4522 962 95791, June 2013. [Online]. Available: https://www.usa.philips.com/healthcare/resources/feature-detail/nsight [Google Scholar]
- [6].Bottenus N, “REFoCUS: Ultrasound focusing for the software beamforming age,” in 2018 IEEE International Ultrasonics Symposium (IUS), Oct. 2018, pp. 1–4. [Google Scholar]
- [7].Trahey GE, Allison JW, Smith SW, and von Ramm OT, “Speckle reduction achievable by spatial compounding and frequency compounding: Experimental results and implications for target detectability,” in Pattern Recognition and Acoustical Imaging, vol. 0768. International Society for Optics and Photonics, Sep. 1987, pp. 185–192. [Google Scholar]
- [8].Thomas JD and Rubin DN, “Tissue harmonic imaging: why does it work?” J. Am. Soc. Echocardiogr, vol. 11, no. 8, pp. 803–808, Aug. 1998. [DOI] [PubMed] [Google Scholar]
- [9].Desser TS and Jeffrey RB, “Tissue harmonic imaging techniques: physical principles and clinical applications,” Semin. Ultrasound CT MR, vol. 22, no. 1, pp. 1–10, Feb. 2001. [DOI] [PubMed] [Google Scholar]
- [10].Anvari A, Forsberg F, and Samir AE, “A primer on the physical principles of tissue harmonic imaging,” Radiographics, vol. 35, no. 7, pp. 1955–1964, Nov. 2015. [DOI] [PubMed] [Google Scholar]
- [11].Lediju MA, Trahey GE, Byram BC, and Dahl JJ, “Short-lag spatial coherence of backscattered echoes: imaging characteristics,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 58, no. 7, pp. 1377–1388, Jul. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Long W, Hyun D, Choudhury KR, Bradway D, McNally P, Boyd B, Ellestad S, and Trahey GE, “Clinical utility of fetal Short-Lag spatial coherence imaging,” Ultrasound Med. Biol, vol. 44, no. 4, pp. 794–806, Apr. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Morgan MR, Hyun D, and Trahey GE, “Short-lag spatial coherence imaging in 1.5-d and 1.75-d arrays: Elevation performance and array design considerations,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, Mar. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Ahman H, Thompson L, Swarbrick A, and Woodward J, “Understanding the advanced signal processing technique of Real-Time adaptive filters,” J. Diagn. Med. Sonogr, vol. 25, no. 3, pp. 145–160, May 2009. [Google Scholar]
- [15].Dei K, Luchies A, and Byram B, “Contrast ratio dynamic range: A new beamformer performance metric,” in 2017 IEEE International Ultrasonics Symposium (IUS), Sep. 2017, pp. 1–4. [Google Scholar]
- [16].Rindal OMH, Austeng A, Fatemi A, and Rodriguez-Molares A, “The effect of dynamic range alterations in the estimation of contrast,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 66, no. 7, pp. 1198–1208, Jul. 2019. [DOI] [PubMed] [Google Scholar]
- [17].Rodriguez-Molares A, Rindal OMH, Drhooge J, Masoy S-E, Austeng A, Bell MAL, and Torp H, “The generalized contrast-to-noise ratio: a formal definition for lesion detectability,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, Nov. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Xu L, Ren JSJ, Liu C, and Jia J, “Deep convolutional neural network for image deconvolution,” in Advances in Neural Information Processing Systems 27, Ghahramani Z, Welling M, Cortes C, Lawrence ND, and Weinberger KQ, Eds. Curran Associates, Inc., 2014, pp. 1790–1798. [Google Scholar]
- [19].Mao X, Li Q, Xie H, Lau RYK, Wang Z, and Smolley SP, “Least squares generative adversarial networks,” in 2017 IEEE International Conference on Computer Vision (ICCV), October 2017, pp. 2813–2821. [Google Scholar]
- [20].Takeda H, Farsiu S, and Milanfar P, “Robust kernel regression for restoration and reconstruction of images from sparse noisy data,” in 2006 International Conference on Image Processing, Oct. 2006, pp. 1257–1260. [Google Scholar]
- [21].Tomasi C and Manduchi R, “Bilateral filtering for gray and color images,” in Sixth International Conference on Computer Vision (IEEE Cat. No.98CH36271), Jan. 1998, pp. 839–846. [Google Scholar]
- [22].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” Med. Image Comput. Comput. Assist. Interv, 2015. [Google Scholar]
- [23].Yamanaka J, Kuwashima S, and Kurita T, “Fast and accurate image super resolution by deep CNN with skip connection and network in network,” in Neural Information Processing. Springer International Publishing, 2017, pp. 217–225. [Google Scholar]
- [24].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [Google Scholar]
- [25].Zhang Z, Liu Q, and Wang Y, “Road extraction by deep residual U-Net,” IEEE Geoscience and Remote Sensing Letters, vol. 15, no. 5, pp. 749–753, May 2018. [Google Scholar]
- [26].Liu P, Zhang H, Zhang K, Lin L, and Zuo W, “Multi-level Wavelet-CNN for image restoration,” 2018.
- [27].Huang G, Liu Z, Van Der Maaten L, and Weinberger KQ, “Densely connected convolutional networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 4700–4708. [Google Scholar]
- [28].Jégou S, Drozdzal M, Vazquez D, Romero A, and Bengio Y, “The one hundred layers tiramisu: Fully convolutional densenets for semantic segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2017, pp. 11–19. [Google Scholar]
- [29].Vincent P, Larochelle H, Lajoie I, Bengio Y, and Manzagol P-A, “Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion,” J. Mach. Learn. Res, vol. 11, no. December, pp. 3371–3408, 2010. [Google Scholar]
- [30].Brock A, Donahue J, and Simonyan K, “Large scale GAN training for high fidelity natural image synthesis,” in International Conference on Learning Representations, 2019. [Online]. Available: https://openreview.net/forum?id=B1xsqj09Fm [Google Scholar]
- [31].Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, and Bengio Y, “Generative adversarial nets,” in Advances in Neural Information Processing Systems 27, Ghahramani Z, Welling M, Cortes C, Lawrence ND, and Weinberger KQ, Eds. Curran Associates, Inc., 2014, pp. 2672–2680. [Google Scholar]
- [32].Radford A, Metz L, and Chintala S, “Unsupervised representation learning with deep convolutional generative adversarial networks,” CoRR, vol. abs/1511.06434, 2016. [Google Scholar]
- [33].Isola P, Zhu J-Y, Zhou T, and Efros AA, “Image-to-image translation with conditional adversarial networks,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 1125–1134. [Google Scholar]
- [34].Abdel-Nasser M and Omer OA, “Ultrasound image enhancement using a deep learning architecture,” in Proceedings of the International Conference on Advanced Intelligent Systems and Informatics 2016 Springer International Publishing, 2017, pp. 639–649. [Google Scholar]
- [35].Perdios D, Vonlanthen M, Besson A, Martinez F, and Thiran J-P, “Deep convolutional neural network for ultrasound image enhancement,” in 2018 IEEE International Ultrasonics Symposium (IUS), Oct. 2018, pp. 1–4. [Google Scholar]
- [36].Zhang X, Li J, He Q, Zhang H, and Luo J, “High-quality reconstruction of plane-wave imaging using generative adversarial network,” in 2018 IEEE International Ultrasonics Symposium (IUS), October 2018, pp. 1–4. [Google Scholar]
- [37].Hyun D, Brickson LL, Looby KT, and Dahl JJ, “Beamforming and speckle reduction using neural networks,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 66, no. 5, pp. 898–910, May 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Nair AA, Tran TD, Reiter A, and Bell MAL, “A generative adversarial neural network for beamforming ultrasound images : Invited presentation,” in 2019 53rd Annual Conference on Information Sciences and Systems (CISS), March 2019, pp. 1–6. [Google Scholar]
- [39].Goudarzi S, Asif A, and Rivaz H, “Multi-focus ultrasound imaging using generative adversarial networks,” in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), April 2019, pp. 1118–1121. [Google Scholar]
- [40].Dietrichson F, Smistad E, Ostvik A, and Lovstakken L, “Ultrasound speckle reduction using generative adversial networks,” in 2018 IEEE International Ultrasonics Symposium (IUS), Oct. 2018, pp. 1–4. [Google Scholar]
- [41].Zhu J-Y, Park T, Isola P, and Efros AA, “Unpaired image-to-image translation using cycle-consistent adversarial networks,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2223–2232. [Google Scholar]
- [42].Kakkad V, Dahl J, Ellestad S, and Trahey G, “In vivo application of short-lag spatial coherence and harmonic spatial coherence imaging in fetal ultrasound,” Ultrason. Imaging, vol. 37, no. 2, pp. 101–116, Apr. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Deng Y, Palmeri ML, Rouze NC, Trahey GE, Haystead CM, and Nightingale KR, “Quantifying image quality improvement using elevated acoustic output in B-Mode harmonic imaging,” Ultrasound Med. Biol, vol. 43, no. 10, pp. 2416–2425, Oct. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Long J, Long W, Bottenus N, Pintonl GF, and Trahey GE, “Implications of lag-one coherence on real-time adaptive frequency selection,” in 2018 IEEE International Ultrasonics Symposium (IUS) IEEE, 2018, pp. 1–9. [Google Scholar]
- [45].Kingma D and Ba J, “Adam: A method for stochastic optimization in: Proceedings of the 3rd international conference for learning representations (ICLR’15),” San Diego Law Rev., 2015. [Google Scholar]
- [46].Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, Ghemawat S, Goodfellow I, Harp A, Irving G, Isard M, Jia Y, Jozefowicz R, Kaiser L, Kudlur M, Levenberg J, Mané D, Monga R, Moore S, Murray D, Olah C, Schuster M, Shlens J, Steiner B, Sutskever I, Talwar K, Tucker P, Vanhoucke V, Vasudevan V, Viégas F, Vinyals O, Warden P, Wattenberg M, Wicke M, Yu Y, and Zheng X, “TensorFlow: Large-scale machine learning on heterogeneous systems,” 2015, software available from tensorflow.org [Online]. Available: http://tensorflow.org/
- [47].Chollet F et al. , “Keras,” https://keras.io, 2015.
- [48].Bovik AC, Sheikh HR, and Simoncelli EP, “Image quality assessment: from error visibility to structural similarity,” IEEE Trans. Image Process, vol. 13, no. 4, pp. 600–612, Apr. 2004. [DOI] [PubMed] [Google Scholar]
- [49].Yang D, Hong S, Jang Y, Zhao T, and Lee H, “Diversity-Sensitive conditional generative adversarial networks,” Jan. 2019.
- [50].Hewener H and Tretbar S, “Mobile ultrafast ultrasound imaging system based on smartphone and tablet devices,” in 2015 IEEE International Ultrasonics Symposium (IUS), Oct. 2015, pp. 1–4. [Google Scholar]
- [51].Sandler M, Howard A, Zhu M, Zhmoginov A, and Chen L, “Mobilenetv2: Inverted residuals and linear bottlenecks,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, June 2018, pp. 4510–4520. [Google Scholar]
- [52].Jaderberg M, Simonyan K, Zisserman A, and Kavukcuoglu K, “Spatial transformer networks,” in Advances in Neural Information Processing Systems 28, Cortes C, Lawrence ND, Lee DD, Sugiyama M, and Garnett R, Eds. Curran Associates, Inc., 2015, pp. 2017–2025. [Google Scholar]
- [53].Liu R, Lehman J, Molino P, Petroski Such F, Frank E, Sergeev A, and Yosinski J, “An intriguing failing of convolutional neural networks and the CoordConv solution,” in Advances in Neural Information Processing Systems 31, Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, and Garnett R, Eds. Curran Associates, Inc., 2018, pp. 9605–9616. [Google Scholar]
- [54].Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, Zhou J, and Wang G, “Low-Dose CT with a residual Encoder-Decoder convolutional neural network,” IEEE Trans. Med. Imaging, vol. 36, no. 12, pp. 2524–2535, Dec. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Zbontar J, Knoll F, Sriram A, Muckley MJ, Bruno M, Defazio A, Parente M, Geras KJ, Katsnelson J, Chandarana H, Zhang Z, Drozdzal M, Romero A, Rabbat M, Vincent P, Pinkerton J, Wang D, Yakubova N, Owens E, Zitnick CL, Recht MP, Sodickson DK, and Lui YW, “fastMRI: An open dataset and benchmarks for accelerated MRI,” 2018.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.