Estimating the undetected infections in the Covid-19 outbreak by harnessing capture–recapture methods

Abstract

Objectives

A major open question, affecting the decisions of policy makers, is the estimation of the true number of Covid-19 infections. Most of them are undetected, because of a large number of asymptomatic cases. We provide an efficient, easy to compute and robust lower bound estimator for the number of undetected cases.

Methods

A modified version of the Chao estimator is proposed, based on the cumulative time-series distributions of cases and deaths. Heterogeneity has been addressed by assuming a geometrical distribution underlying the data generation process. An (approximated) analytical variance of the estimator has been derived to compute reliable confidence intervals at 95% level.

Results

A motivating application to the Austrian situation is provided and compared with an independent and representative study on prevalence of Covid-19 infection. Our estimates match well with the results from the independent prevalence study, but the capture–recapture estimate has less uncertainty involved as it is based on a larger sample size. Results from other European countries are mentioned in the discussion. The estimated ratio of the total estimated cases to the observed cases is around the value of 2.3 for all the analyzed countries.

Conclusions

The proposed method answers to a fundamental open question: “How many undetected cases are going around?”. CR methods provide a straightforward solution to shed light on undetected cases, incorporating heterogeneity that may arise in the probability of being detected.

Introduction

Currently, health systems across the globe are challenged by the ongoing Covid-19 pandemic. It is not a simple task to assess the efficiency of current health systems in detecting, treating, and preventing onward transmission of Covid-19, as the number of undetected infections is by definition unknown. Understanding the diffusion of the epidemic and assessing the number of real infections of Covid-19 is crucial for implementing effective public and health policies in tackling the virus. Unfortunately, official reporting and statistics significantly underestimate the true number since there exists a vast proportion of asymptomatic infected patients including those with mild symptoms among all infected individuals who are not detected. Indeed, the infected individuals with low–mild symptoms are likely not going to get in contact with the health care system and will also not be recorded in official statistics.

For example, reports estimate the number of infected in Italy to be around 3.5 times higher than reported (Tuite et al., 2020). Slightly lower estimates have been given for Germany (Ranjan, 2020). Another study discusses that Italy mostly focuses on testing in hospitals with symptoms; hence, the roughly 50% asymptomatic are not covered by this approach (Onder et al., 2020). The same percentage of asymptomatic is also reported in Iceland (Shahan, 2020). The asymptomatic individuals in fact can be a direct transmitter of the virus and their unawareness can indirectly strengthen and increase the transmission of Covid-19. Indeed, it seems fair to say that the undetected cases are the major driver in spreading the disease as detected cases are and will be systematically contained.

Most of the existing analyses performed a secondary data analysis from several sources of data already in the public domain (Menkir et al., 2020). Because published estimates of the distribution of Covid-19 vary widely, with estimates of the basic reproduction number, R0, alone ranging from subcritical (i.e., <1) to >3 (Giordano et al., 2020, Li et al., 2020a, Li et al., 2020b, Maugeri et al., 2020, Zhao et al., 2020, Zhou et al., 2020), mathematical models of infectious diseases, such as Susceptible-Infected-Recovered models, computing the theoretical number of people infected with a contagious illness in a closed population over time, needs to be evaluated on a range/grid of simulated values, each based on different assumptions and adjusted based on data from different geographic areas (Chen et al., 2020). Other much simpler (Nishiura et al., 2020) or sophisticated (Flaxman et al., 2020) approaches are also used to estimate the number of undetected cases, but with large, almost unacceptable, uncertainty on the obtained estimates.

As mentioned above, several methods have been proposed to estimate the undetected number of infections but none has yet suggested to use capture–recapture methods, which is, in some sense, the most obvious method to estimate a dark number. For more details see Böhning (2016). Hence, the purpose of this contribution is to propose a lower bound estimator for the number of people affected by Covid-19 but not detected for various reasons, the major one being that they are asymptomatic. In other words, the aim is to estimate the size of an elusive, i.e., partially unobserved, population. Capture–recapture (CR) methods are designed to achieve this goal. In a nutshell, capture–recapture methods use the capture history of individuals to estimate those who have never been caught. The method suggested uses only the frequencies of those caught once and those caught twice. In the Covid-19 application, these are the ones newly identified at some day and the ones caught twice are those newly identified the day before (and surely still infected one day later, so that they are considered as twice identified) subtracted by the number of deaths at the given day. Hence, our proposal is developed using the cumulative distribution of the observed cases and deaths. The use of CR methods is not straightforward as we are dealing with an open population, subject to deaths, and heterogeneity in the probability of being detected. A modified version of Chao's estimator under a geometric distribution, suitable for the setting here, is introduced. It accounts for heterogeneity in a simple way and can be easily computed starting from data collected by all government sources. In this way, the policy makers can have benchmark, statistically valid, estimates of the lower bound for the total number of cases and, accordingly, adjust their interventions.

This short note is organized as follows. In Section “Basic notation and date”, we introduce the basic notation and how we are going to work with the cumulative distribution of observed cases and deaths. Section “Statistical methods” provides all the necessary details to obtain the estimates. An example to Austrian data is provided in Section “Application to the Austrian situation”. A discussion showing other interesting insights on several European countries concludes.

Basic notation and data

We will denote with N(t) the cumulative count of infections at day t where t  =  t ₀, …, t _m. Hence ΔN(t) =  N(t) −  N(t  − 1) are the number of new infections at day t where t  =  t ₀  + 1, …, t _m. Also, let D(t) denote the cumulative count of deaths at day t where t  =  t ₀, …, t _m. t ₀ defines the beginning of the observational period and t _m defines the end. We assume the trivial assumption t _m  >  t ₀, so that the observational window is not empty. Again, we denote with ΔD(t) =  D(t) −  D(t  − 1) the count of new deaths at day t where t  =  t ₀  + 1, …, t _m. To illustrate, we look at these data (taken from https://www.worldometers.info/coronavirus/country/austria/) for the country of Austria as provided in Table 1 for the infections and in Table 2 for the deaths.

Table 1.

Cumulative counts of infections with Covid-19 for Austria starting at t₀ = 15 March 2020 to t_m = 6 April 2020.

t	15/03	16/03	17/03	18/03	19/03	20/03	21/03	22/03
N(t)	860	1,018	1,332	1,646	2,179	2,649	2,922	3,582
t	23/03	24/03	25/03	26/03	27/03	28/03	29/03	30/03
N(t)	4,474	5,283	5,588	6,909	7,697	8,271	8,788	9,618
t	31/03	01/04	02/04	03/04	04/04	05/04	06/04
N(t)	10180	10,711	11,129	11,524	11,781	12,051	12,297

Table 2.

Cumulative counts of deaths from Covid-19 for Austria starting at t₀ = 15 March 2020 to t_m = 7 April 2020.

t	15/03	16/03	17/03	18/03	19/03	20/03	21/03	22/03	23/03	24/03	25/03	26/03
D(t)	1	2	4	4	6	6	8	16	21	28	31	49
t	27/03	28/03	29/03	30/03	31/03	01/04	02/04	03/04	04/04	05/04	06/04
D(t)	58	68	86	108	128	146	158	168	186	204	220

Statistical methods

The question arises how this can be linked to a capture–recapture approach. For this purpose we briefly review the capture–recapture model we like to harness here. Suppose a target population is sampled for units of interest repeatedly. Let X denote the number of times a unit is identified in this sampling process. Also, let p _x denote the probability of identifying a unit x times where x  = 0, 1, …. In the capture–recapture world the following mixture model is quite common:

$$p_x=\theta {(1-\theta )}^x.$$ (1)

In (1) occurs the geometric distribution as a suitable count distribution. Now we can find p ₀, the probability for missing a unit of interest (infection) as $p_0=p_1^2/p_2$, the ratio of the square of the probability of identifying a unit twice divided by the probability of detecting a unit once. Replacing p ₁ and p ₂ with the observed frequencies f ₁ of those identified exactly once and f ₂ of those identified exactly twice leads to an estimate of the hidden units ${\hat{f}}_0=f_1^2/f_2$. The validity of the estimate depends on the validity of the geometric distribution (1). To weaken this assumption we allow the parameter θ to vary in the population with arbitrary unknown distribution f(θ) to reflect varying identification probabilities across the target population:

$$p_x=\int \theta {(1-\theta )}^{x}f(\theta )d\theta .$$ (2)

Often the Poisson distribution is used in (2) instead of the geometric distribution. However, we prefer to use the latter as we think of the geometric distribution as a Poisson distribution mixed with an exponential density, hence the geometric is able to incorporate already some of the likely present heterogeneity in the population.

We assume that model (2) is valid which we consider as a weak assumption. Then, using the Cauchy–Schwarz inequality for moments, it is possible to show that for the probability p ₀ of missing a unit of interest the following inequality holds:

$$p_0\ge \frac{p_1^2}{p_2}.$$ (3)

Replacing p ₁ and p ₂ on the right-hand side of (3) with the observed frequencies f ₁ of those identified exactly once and f ₂ of those identified exactly twice leads to the lower bound estimate of Chao (Chao, 1987, Chao, 1989, Chao and Colwell, 2017):

$${\hat{f}}_0=\frac{f_1^2}{f_2}.$$ (4)

Here f ₀ is the frequency of units that remains unobserved or hidden for which (4) is a lower bound estimate. In the case of no heterogeneity, (4) is a direct estimate of f ₀. Chao's lower bound has been also generalized to include covariate information such as regional information (Böhning et al., 2016) but we do not follow up on this aspect at this stage.

The idea is to apply this estimator (4) day-wise. We take an arbitrary day t. At this day we have ΔN(t) new infections. This will be viewed as f ₁, the infected people identified just once. If we look at ΔN(t  − 1), then this is the count of new infections the day before. But these will still be infected at day t unless they decease. So, f ₂ corresponds to ΔN(t  − 1) − ΔD(t). We can ignore the number of recoveries as we are looking at infections which are very recent (notified at day t or t  − 1). Hence we are able to give the estimate for the number of hidden infections at day t as

$$H(t)=\frac{{[\mathrm{\Delta }N(t)]}^2}{\mathrm{\Delta }N(t-1)-\mathrm{\Delta }D(t)}$$ (5)

and global estimate of hidden infections is achieved by summing up over all days in the observational period:

$$H_{t_0}=\sum _{t=t_0+1}^{t_m}\frac{{[\mathrm{\Delta }N(t)]}^2}{\mathrm{\Delta }N(t-1)-\mathrm{\Delta }D(t)}.$$ (6)

We will use a bias-corrected form of (5) suggested by Chao (1989) and given as

$$H_{t_0}=\sum _{t=t_0+1}^{t_m}\frac{\mathrm{\Delta }N(t)[\mathrm{\Delta }N(t)-1]}{1+\mathrm{\Delta }N(t-1)-\mathrm{\Delta }D(t)}.$$ (7)

We define the understanding that ΔN(t  − 1) − ΔD(t) is set to 0 if it becomes negative, in other words we use max{0, ΔN(t  − 1) − ΔD(t)}. The final estimate of the total size of infection is then given as what has been observed at the end of the observational window t _m and the estimate of the hidden numbers:

$$\mathrm{total}\mathrm{size}\mathrm{of}\mathrm{infections}=N(t_m)+H_{t_0}.$$ (8)

We need to address the uncertainty involved in the estimator (7). A variance estimate of (5) has been provided in Niwitpong et al. (2013) and is given here as

$$\begin{array}{cc}\widehat{\mathrm{Var}}H(t)\hfill & =\frac{{[\mathrm{\Delta }N(t)]}^4}{{[1+\mathrm{\Delta }N(t-1)-\mathrm{\Delta }D(t)]}^3}+\frac{4{[\mathrm{\Delta }N(t)]}^3}{{[1+\mathrm{\Delta }N(t-1)-\mathrm{\Delta }D(t)]}^2}\hfill \\ \hfill & +\frac{{[\mathrm{\Delta }N(t)]}^2}{[1+\mathrm{\Delta }N(t-1)-\mathrm{\Delta }D(t)]},\hfill \end{array}$$ (9)

so that the final variance estimate of $H_{t_0}$ is given as

$$\sum _{t=t_0+1}^{t_m}\widehat{\mathrm{Var}}H(t)$$ (10)

assuming stochastically independence of the H(t) terms over observation time t. A 95% confidence interval can then be constructed by means of

$$H_{t_0}\pm 1.96\sqrt{\sum _{t=t_0+1}^{t_m}\widehat{\mathrm{Var}}H(t)}.$$

Application to the Austrian situation

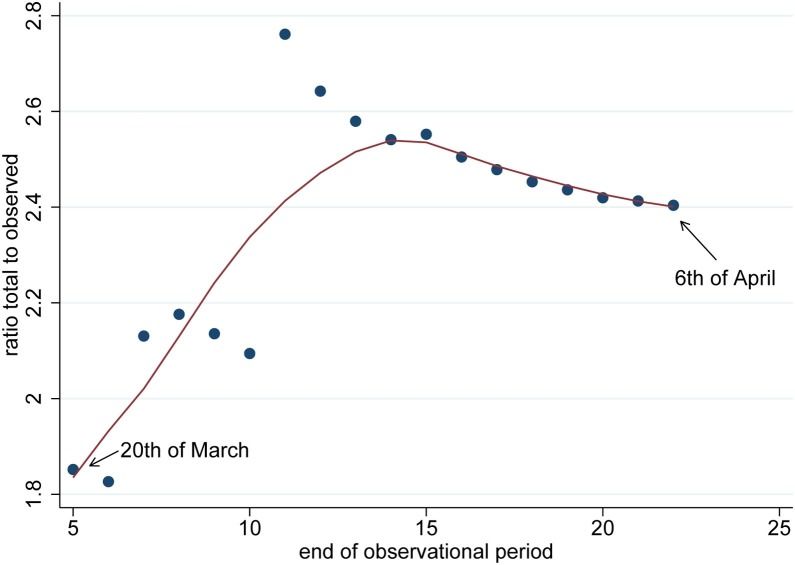
The results are provided in Table 3 for the country of Austria which includes estimates of the hidden and total (observed + hidden) cases with 95% confidence intervals. At the 6th of April the number of infections was 12,297 which is the observed number. We have chosen the 15th of March as beginning of the observational period. However other dates are possible as well so that we looked at estimates in dependence of the beginning of the observation period. It can be seen that results change slightly. Of course, if the window is made too small estimates of hidden numbers will only refer to observations made in this window. The major question arises if the estimates of Table 3 are realistic and do they represent a reasonable estimate of the true size of the undetected infections. The best comparison would give a representative sample of the target population where sampling is done to find infection with a valid diagnostic test. For Austria we have an independent study on the size of the Covid-19 outbreak (https://www.sora.at/nc/news-presse/news/news-einzelansicht/news/covid-19-praevalenz-1006.html). The study was led by Günther Ogris and Christoph Hofinger (SORA Institute for Social Research and Consulting) and is known as the dark number study. The study was rolled out during the 1 April and 6 April 2020 and sampled 1544 persons across Austria covering all ages up to 94 years. The study used a PCR-test for diagnosing infection which is assumed to be accurate. According to the study, the proportion of infected people was 0.0033. If this proportion is applied to the population of Austria, as study in media release points out, during the study period there were 28,500 infected persons in Austria. The study estimates that we have provided match very well with the results of the study, independent where we start the observational window. The dark number study also reports a 95% confidence interval for the proportion of infected persons which ranges from 0.0012 to 0.0076, corresponding to 10,200 and 67,400 infected persons, respectively. Clearly, the capture–recapture estimate is included in this large interval but as we are able to utilize much larger routinely collected data on infected persons, the uncertainty provided by the capture–recapture approach is considerably reduced which is reflected in the relative short confidence intervals. The ratio of the total estimated cases to the observed cases is interesting in itself. A ratio of 2.5 would mean that for every observed patient there are 1.5 infected persons unseen. The reason for this can be manifold as these unseen cases might be without symptoms or show very mild signs of infection. It is also interesting to investigate how this ratio changes over the duration of the pandemic. In Figure 1 we see a scatter-plot of this ratio against a varying end point of the observational period starting at day 5 (20th of March) and ending at day 23 (6th of April). As the ratio shows quite a bit of random variation, in particular for early days, we have also included a LOWESS smoother. It becomes clear in Figure 1 that the ratio stabilizes around day 15 as the end of the observational period which can be also taken as guidance for choosing the size of the observational period.

Table 3.

Estimated hidden and total cases of Covid-19 for Austria and various sizes of the observational window ranging from t₀ = 15 March 2020 to t₀ = 18 March 2020; the second part of the table contains the associated proportions of total population in Austria (8.859 million).

t0	Hidden cases	Total cases	95% CI
15	17,264	29,561	28,412–30,709
16	16,638	28,935	27,800–30,069
17	16,326	28,623	27,491–29,754
18	15,420	27,716	26,602–28,831
15	0.0019	0.0033	0.0032–0.0035
16	0.0019	0.0033	0.0031–0.0034
17	0.0018	0.0032	0.0031–0.0034
18	0.0017	0.0031	0.0030–0.0033

Figure 1.

Ratio of total to observed case as a function of the end of the observational period starting at day 5 which is the 20th of March 2020; the solid line is a LOWESS smoother.

Discussion

The proposed method answers to a fundamental open question: “How many undetected cases are going around?”. Of course, we provide a lower bound, but this information may be treated as a starting point whenever interventions and tools to dampen the spread of the epidemic are rolled out. CR methods are easy to apply in practice, and this is one of the merits of the method. Moreover, we simply use time series of cumulative data, readily available from official sources. Given that individual data are not publicly available, CR methods provide a straightforward solution to shed light on undetected cases, incorporating heterogeneity that may arise in the probability of being detected simply considering the widely known and used geometric distribution.

We have applied the capture–recapture approach using Chao's estimator for large entities such as countries in Europe. However, the approach can be also utilized to indicate regional variation, in other words application to smaller geographical or administrative units. In addition, if age-specific numbers are provided Chao's estimator can be applied in an age-stratified way.

Another question relates to the size of the observational period. In the case, study we have used 3 weeks as this would cover a period where a person infectious at the first day might still be so at the end of the period. Hence we are trying to estimate the hidden population which is infectious and not a mix of persons being infectious and persons having passed the infection. An interesting thought which was contributed by an anonymous referee was to take a period starting from the very first case and ending with the very last one. Applying the estimator would give an estimate of the size of the population who has passed the infections (and potentially have reached immunity).

The example provided here relies on Austrian data, but many other countries can be analyzed even if there are not benchmark survey studies to compare with. For example, taking data up to 17/04/2020 from https://github.com/open-covid-19/data on several European countries and considering data from the day which we record the first death, we obtain the estimates of undetected cases for Italy, Germany, Spain, UK and Greece (see Table 4 ). The last column in Table 4 shows the ratio of the total estimated cases to the observed cases. There is a remarkable stability around the value of 2.3.

Table 4.

Estimated hidden and total cases of Covid-19 for several European countries, at 18/04/2020.

Country	Hidden cases	Total cases	95% CI	Total/observed
Italy	211,768	384,201	381,649–386,762	2.23
Germany	178,451	315,890	312,429–319,350	2.30
Spain	232,057	423,783	421,112–426,454	2.21
UK	149,150	257,842	255,482-260,202	2.37
Greece	2,901	5,108	4,718–5,499	2.31
Austria	17,264	29,560	28,412–30,709	2.40

All the obtained estimates are surrounded by some uncertainty. Confidence intervals for the modified Chao's lower bound have been provided and are seemingly reliable, in particular compared to those presented in other studies. We emphasize that the estimates provided are conservative, in the sense that they provide lower bounds on the size of undetected infections. However, we have provided some evidence such as in the situation of Austria that these lower bounds are not far away from the true size of infection in the target population. This needs to be followed up by further comparisons with representative sampling studies on target population infection.

This is just a first evidence on the use of capture–recapture methods to study Covid-19 data. Another question is still open: “is there a way of estimating an upper bound for the number of undetected cases?”. Again capture–recapture methods could be implemented to provide an answer to this question and help policy makers to evaluate the Covid-19 epidemic situation locally and at the current phase of its development.

Ethical approval

Not required.

Funding

None declared.

Conflict of interest

We declare that we have no conflict of interest.

Appendix A. Supplementary data

The following are the supplementary data to this article: